Introduction

Quantitative image analysis in time-resolved electron or X-ray diffraction is a cornerstone for the successful reconstruction of atomic structures of far-from-equilibrium systems. It allows direct observation of the atomic motions accompanying structural transitions, which are the primary forces behind chemical, biological, and condensed phase processes. Fundamentally, the image analysis comprises the extraction of differences between the image acquired during the structural dynamics and a static one, which is translated into real space information in later steps by assuming that the measured changes of the diffraction signal solely originate from atomic structural changes1. Such a central assumption in the time-resolved studies, however, could be challenged in the event other processes contribute to the differential signal2,3. In the case of electron diffraction, this problem arises when the charged electron probe interacts with optical pump-induced field effects. Ultrafast electron diffraction (UED) experiments often require high excitation intensity beyond 1011 W cm−2 to drive an observable structural change, mainly due to the ultrashort laser pulses on sub-picosecond time scales4,5,6. Depending on the material, the resulting high peak power can lead to significant photoinduced emission from a solid surface7,8,9,10,11,12 and generation of a surface field at the charge-separated region13,14,15,16,17,18, capable of affecting electron trajectories. This well-known effect has been exploited in finding time zero for ultrafast low-, high-, and even MeV-electron diffraction19,20,21. Nonetheless, the combination of two independent physical mechanisms that can cause time-dependent changes of the diffraction image following photoexcitation, namely the atomic structural change of interest and the surface field effect, could mislead the interpretation of UED data. The lifetime of such surface field effects is in the range of a few tens to hundreds of picoseconds13,22. The associated dynamics fall in the same range as the structural dynamics of interest. Hence, it covers the typical time window accessed in UED experiments, making it difficult to separate each contribution to image formation without correcting this effect or ensuring it is negligible with respect to the determination of the structural dynamics.

The relative contribution of the surface field effect to the differential signal above background depends strongly on the scattering geometry and electron energy, which can give rise to a shift or distortion of the diffraction pattern, or to intensity changes at the electron detector13,14,15,16,17,18. The shift or change in deflection angles has been observed mostly in grazing incidence geometries, showing for example mrad deflection magnitudes of 30 keV electrons traveling in a tangential direction13,16. For this geometry, the charge-separated region has been described by a capacitor-type model, allowing one to estimate the strength of the presumed spatially uniform field to be in the 104–106 V m−1 range13,16. By comparison, the intensity effect observed mostly in transmission geometry has been deemed unlikely to affect diffracted electrons16. This is because, in transmission geometry, the surface field effect nearly cancels out with respect to transverse deflection as the field is confined to the charge-separated region and scattering angles are small for high-energy electrons, typically only tens of mrads. Nonetheless, the inversely proportional relation between the kinetic energy and the deflection of an electron at a given field makes ultrafast low-energy electron diffraction (ULEED) much more susceptible to the surface field effect than higher-energy electrons, as is found to be the case in this work. This means that ULEED, the emerging technique capable of exploring surface atomic motions selectively20,21,23, needs to be restricted to excitation conditions that can avoid the field effect, or otherwise run the risk of misinterpretation. In the case of inevitable aberrations, the effect needs to be quantified and corrected in order to extract the structural dynamics of interest; yet, a means for the quantitative analysis is presently lacking.

Here, we investigate the surface field effect on the intensity of transmission-mode ultrafast low-energy electron projection and diffraction images at various excitation conditions by varying fluence, F, and duration, D, of ultrashort laser pulses, allowing effective control of optical irradiance on target samples. Based on the analysis of intensities measured in a time series of the projection images, we extract characteristic parameters associated with the surface field effect-driven intensity changes. With this information, we determine whether the observed diffraction kinetics is the result of the surface field effect, or the expected Debye–Waller response defining thermally excited atomic motions, or a mixture of both. In case of combined effects, we demonstrate their quantitative separation. Using particle tracking simulations with electric fields calculated for various spatial distributions of the surface emitted electrons, we explain the observed intensity variations at the detector by the geometrical characteristics of the charge-separated region.

Results and discussions

Experiment

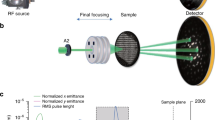
For imaging and diffraction conditions, we use, respectively, a divergent direct electron beam and a focused electron beam with a kinetic energy of 2.0 keV, generated with a custom-designed low-energy electron gun featuring a directly integrated electrostatic Einzel lens as depicted in Fig. 1a and Supplementary Fig. 1. The electron projection and diffraction images are recorded with a time delay ∆t between the excitation laser pulse and electron pulse at the sample plane. We chose a copper mesh grid as the imaging object, and a free-standing graphene film suspended on the same type of the grid as the diffraction target (see “Methods” for details). The excitation source was pulses of visible light (515 nm central wavelength) with a Gaussian intensity profile in space and time. The excitation conditions are controlled by varying either F (0.95–29.3 mJcm−2 for imaging and 4.0–12.1 mJ cm−2 for diffraction) at a fixed D (180 fs for imaging and 2.0 ps for diffraction, FWHM) or D (180 fs–3.1 ps for imaging and 500 fs–2.5 ps for diffraction) at a fixed F (22.8 mJcm−2 for imaging and 12.1 mJcm−2 for diffraction), allowing investigation of the F– or D–dependence on the direct and diffracted beam image.

Fig. 1: Conceptual illustration of the study of the surface field effect on ultrafast low-energy electrons.
figure 1

a Schematic of the experimental layout. A femtosecond laser excitation pulse is incident either on a standard TEM copper mesh grid or on freestanding monolayer graphene suspended on the same type of the grid. Upon photoexcitation, a divergent direct ultrafast low-energy electron beam forms a projection image of the copper grid at the screen (left panel), while a low-energy electron beam focused by an electrostatic Einzel lens integrated into the photocathode produces a graphene diffraction image (right panel). The images are recorded as a function of the delay time, ∆t, between the excitation pulse and the electron beam. b Typical example of the difference map (a “static” image without excitation subtracted from a time-resolved image with excitation) before (∆t = 0) and after (∆t = 50 ps) excitation. The left and right pairs of maps correspond to the direct and diffracted beam case, respectively. The color bars indicate pixel intensity variations (∆I) of the maps. c Time trace of the relative intensity difference (∆I/I) measured at the regions-of-interest (ROI) indicated by the red box in b (left panel), and at the (10) diffraction spots (right panel, average of six spots). Each measurement condition for panels b and c is (F = 22.8 mJ cm−2, D = 550 fs), and (F = 12.1 mJ cm−2, D = 500 fs), respectively.

Full size image

The standard pump-probe protocol generates time-resolved intensity difference maps from which the spot intensity, I, can be time-traced. Typical difference maps from the imaging and diffraction measurements with a negative and positive ∆t are shown in the left and right panel of Fig. 1b. On the difference maps, regions-of-interest (ROI) are defined for the integration of spot intensities, and the temporal behavior of the integrated intensities is monitored by calculating the relative spot intensity change (∆I(∆t)/I(∆t < 0)). For projection imaging, a single ROI near the center of the image is used, as indicated by the red box in the left panel. For diffraction, ∆I/I at the (10) and the (11) reflections (shown in the right panel) are determined independently. Typical examples of observed intensity time traces are presented in Fig. 1c. Both time traces feature a sudden intensity drop after ∆t = 0 at the initial phase, and undergo a gradual recovery during the subsequent tens of ps. Details of data collection and image processing are provided in Supplementary Note 1.

Surface field effect on the intensity of the low-energy electron projection image

As shown in the difference map of the projection image (left panel of Fig. 1b), electron depletion (blue color) close to the beam center and accumulation (red color) at the periphery of the depletion region clearly indicates spatial deflection caused by the surface field effect affecting the central part of the diverging electron beam. Intensity line profiles of the projection images provide a more detailed view of the effect (Supplementary Fig. 2); the difference of the line profiles measured at positive and negative ∆t shows regions of increasing and decreasing intensities, whereas the integral over the total area is almost constant (independent of ∆t). This implies that the total charge arriving at the electron detector is conserved while the position of individual particles in the beam is redistributed due to the surface field effect.

The two main features of the intensity curve obtained for the projection image (left panel of Fig. 1c) should be associated with the expected transient surface field dynamics: 1) the intensity drop marking the onset of surface field generation at the initial phase and 2) the subsequent intensity recovery resulting from charge recombination to the mesh grid. To quantify these characteristics for different excitation conditions, we fit the measured time traces of the relative intensity (i.e., I(∆t)/I(∆t < 0)) with a two-exponential model that describes the surface field effect from a phenomenological point of view (see Supplementary Equation 9 in Supplementary Note 2). From this model fitting, a surface field strength factor, XSF, and two-time constants for the initial and the recovery phase, τSF,ini and τSF,rec, could be extracted. The entire set of the time-traces and fit curves is presented in Supplementary Fig. 3, and the resulting fit parameters as a function of F and D are summarized in Fig. 2 and Supplementary Table 1.

Fig. 2: Quantitative analysis of projection image intensity.
figure 2

a Surface field-effect strength factor, XSF, as a function of F (black circles) at a fixed D of 180 fs and a function of D (blue squares) at a fixed F of 22.8 mJ cm−2. The power regression fits to the measured data are indicated by the black and blue curves. The exponent of the fit is evaluated as 0.94 ± 0.02 and −0.34 ± 0.01 for the F- and D-dependence measurements, respectively. b F- and D-dependence of XSF displayed as functions of the calculated peak electronic temperature, Te,peak. The black solid line is the calculated XSF of the F-series measurement with the analytical equation developed by Riffe et al.10, featuring a range of linear behavior above Te,peak ≅ 3000 K, and thus indicating the regime (white background) of space charge limited (SCL) thermionic emission (TE). The calculated XSF is scaled down by a factor of 0.35 to qualitatively match the first five data points (from the left) of the D-series, and shown as blue broken line. The blue solid line connecting the remaining three data points is drawn as guide to the eye. c, d Time constant of the initial, τSF,ini (black circle), and recovery τSF,rec (red square) phase as a function of F and D, respectively. The SCL TE regime is indicated by the white background region, determined in b. The broken horizontal lines indicate the weighted averages of τSF,ini and τSF,rec, which were used as fixed parameters in the analysis of the diffraction data (see the main text). The error bars correspond to ±1 standard deviation of the fitting results.

Full size image

Using the F- and D-dependence of XSF we first investigate the electron emission mechanism responsible for surface field generation. For this purpose, we assume that XSF is related to the yield of surface-confined electrons (via image charge), Q. For pulsed visible laser excitation of a solid target (below ablation threshold), three distinctive electron emission mechanisms are expected depending on F and D7,8,9,10,11,12: thermionic emission, multiphoton photoemission (MPPE), or thermally-assisted MPPE. For the case of MPPE, our excitation conditions with a photon energy of 2.4 eV and a work function of 4.5–4.6 eV (copper target24) would imply two-photon photoemission. Thus, Q and the parameters of laser excitation should be related according to25:

$${X}_{{{{{{\rm{SF}}}}}}}={CQ}\propto {F}^{2}{D}^{-2}$$
(1)

with the unknown scaling factor C. For a constant C, XSF should depend quadratically on both F and D−1. As shown in Fig. 2a, the expected second-order dependence is not exhibited.

For thermionic emission theory applied to thermal equilibrium in steady-state conditions between the electron and phonon distributions, the charge yield is characterized by a rapid increase with the equilibrium temperature. This relation is described by the Richardson–Dushman equation26 in which the thermal energy is compared to a potential barrier for the removal of an electron from a metal surface. In the case of femtosecond excitation, by comparison, emission takes place at the sub-picosecond time scale before thermal equilibration of the electronic subsystem with the lattice, resulting in an extraordinarily high current density at the emission site. This ultrafast process gives rise to space-charge-limited (SCL) emission that has been described by a modification of the Richardson–Dushman equation, which adds a space-charge-field-induced potential to the inner potential barrier, lowering the charge yield for a given electronic temperature10. According to this study10, the linear dependence between Q and the peak electronic temperature on the surface, Te,peak, is a clear signature of the SCL thermionic emission regime starting at a threshold Te,peak of 0.2–0.3 eV (2300–3500 K) for materials of work functions around 4.4 eV. In Fig. 2b, XSF is plotted as a function of Te,peak in the target, as determined from the temperature evolution (Supplementary Fig. 4) calculated for the given laser excitation conditions (see “Methods” for details). First, we compare the XSF values extracted from the F-dependent measurements with the theoretically predicted values (black solid line) calculated according to the modified Richardson-Dushman equation developed by Riffe et al. (see “Methods” for details)10. For this comparison we assumed a proportional relation between XSF and Q, introducing a constant scaling factor C. The comparison shows that data points of the F-series follow the expected linear dependence above Te,peak ≅ 3000 K and thus SCL thermionic emission starts close at this temperature for our measurements.

In case of the D-dependent measurements (blue squares), XSF first drops rapidly with decreasing Te,peak from the highest point at 23.8% (overlapping with the F-series data), shows a sharp bend at 8.7% (corresponding to D = 1.0 ps), and then continues decreasing at a more moderate rate. This variation clearly deviates from the theoretically calculated XSF values for the D-series (blue broken line, downscaled by the factor 0.35 relative to the black line), implying that C may not be constant for the D-series. Our calculations (see Supplementary Fig. 4) show that the duration, τ, of the electronic temperature profile is changed from 2.2 ps to 5.0 ps through the entire D-series range, while it is almost constant (≅ 2 ps) for all fluences at D = 180 fs (Supplementary Fig. 5 and Supplementary Table 2). Given that the varying τ dictates the spatial distribution of surface electrons and, thus, the resulting surface field, the simple linear relation between XSF and Q, introduced for the F-series analysis, may not be valid for the measurement with different D and τ conditions.

The fitted time constants τSF,ini and τSF,rec for the F- and D-dependence measurements are shown in Fig. 2c, d. While τSF,ini presents no clear signature of F- or D-dependence, the data for τSF,rec suggest a systematic increase of the recovery time towards the side of low surface field effect (small F or large D), although the uncertainties are increasing due to the decreasing signal-to-noise ratio of the corresponding measurements. Under conditions of strong surface field effect, τSF,rec is fairly constant and close to the average overall data points (using variance weights). For the final analysis of the diffracted beam intensities, we used the weighted averages of τSF,ini and τSF,rec as fixed parameters as it turned out that only conditions of high XSF had a strong impact on the diffraction data. Calculations with linearly varying values of τSF,rec did not lead to significantly different results.

Separation of structure dynamics and surface field effect in diffraction images

Femtosecond excitation of freestanding graphene with visible light drives larger rms motions of the carbon atoms of graphene, leading to variation of the lattice temperature over time, Tl(∆t)27. With the space and time resolving capabilities of ULEED, we tried to capture the expected structure dynamics by using the Debye–Waller model, which relates the lattice temperature Tl(∆t) at a given ∆t with the intensity of Bragg reflections, I(hk)(∆t) = I(hk)(Tl(∆t)), where (hk) are the 2D Miller indices (in our case, (hk) = (10) and (11)). If the Debye–Waller effect is the only physical effect in operation, the intensity changes of the (10) and (11) reflections are strictly related by the Debye–Waller equation. Deviations from this relation indicate the presence of another effect. Thus, in view of the similarity of intensity variations expected for surface field and Debye-Waller effects, simultaneous analysis of the (10) and (11) intensity traces is the key for deciding whether diffraction is affected by surface fields or not, and opens the door for quantitative separation of the two effects.

The time traces of the (10) and (11) reflection intensities are fitted simultaneously with a function that combines the surface field effect, formally described in the previous section, and the Debye–Waller effect. It is assumed that both effects change the intensities I(hk)(∆t)/I(hk)(∆t < 0) by independent factors xSF(Δt) and xDW(Δt). The Debye–Waller factors for the two reflections depend on the excursion of the lattice temperature after photoexcitation, ΔTl(∆t), according to x(10),DW = exp(−ΔTl) ≈ 1 − ΔTl and x(11),DW = exp(−3 ΔTl) ≈ 1–3 ΔTl if temperatures are measured in appropriate units (see Supplementary Equations 8 and 9 in Supplementary Note 3). The changes in lattice temperature are described by the same type of bi-exponential function as the surface field effect, with three parameters: an overall temperature scale factor XT and two-time constants for the rising and the recovery part. This temperature function can be interpreted as the solution of a differential equation that describes a system in thermal contact with a heat bath at an equilibrium temperature that receives thermal energy at a constant rate from another system (the electronic sub-system), which temporarily stores the absorbed energy of the pump pulse. Consequently, the parameter XT should be proportional to the absorbed energy. (For more details about modeling and fitting see Supplementary Notes 2–7).

Figure 3 summarizes the results of simultaneous fitting. In Fig. 3d an example of fitted time traces is shown where the surface field effect contributes significantly to the total intensity changes (D = 0.5 ps, F = 12.2 mJcm−2). The curves in Fig. 3d represent the best fit to the observed intensities and the decomposition of the total effect into contributions from the surface field and pure Debye–Waller effect. The entire set of the time-traces and fit curves for all measurements is available in Supplementary Fig. 6. The fit parameters are tabulated in Supplementary Table 3.

Fig. 3: Quantitative analysis of the diffracted beam intensity.
figure 3

a D-dependence of XT, and XSF, the overall scale factors of the temperature excursion and the surface field effect after photo-excitation, for a fixed F of 12.2 mJ cm−2. Black circle and red box indicate XT and XSF, respectively. The black dashed line is the weighted average of XT. b F-dependence of XT and XSF for a fixed D of 2.0 ps. The black dashed line is a weighted linear fit of XT through (0,0). The upper horizontal axis indicates the calculated peak lattice temperature, Tl,peak, of graphene. The error bars in a, b correspond to ±1 standard deviation of the fitting results. c Degree of the surface field effect contamination as a function of D for the (10) (blue bar) and (11) reflections (gray bar) for a fixed F of 12.2 mJ cm−2. The error bars in c indicate calculated uncertainties from the error propagation analysis for the combination of independent errors of the extracted XT and XSF. d Separation of the surface field effect and the Debye–Waller effect for F = 12.2 mJ cm−2 and D = 0.5 ps. Black circles are the measured ∆I/I as a function of ∆t for the (10) (upper panel) and the (11) (bottom panel) reflections. The solid red curves are the results of a simultaneous fit of both time traces. Solid blue and cyan curves indicate the individual contributions of the surface field and Debye-Waller effect, respectively. Dotted red and black lines correspond to the corrections applied for intensity drift and time zero shift.

Full size image

As shown in Fig. 3a the pre-factor XSF, which measures the strength of the surface field effect, varies a lot with D at fixed F (12.2 mJcm−2). At D ≥ 2.0 ps, the fitted value tends to zero, while at D ≤ 1.5 ps it rapidly grows, such that it exceeds the value of XT at the shortest D (=0.5 ps). This is consistent with the direct beam experiments. In contrast to XSF, the overall scale factor of the temperature effect, XT, is almost constant over the entire range of D. There are deviations where it is not exactly constant, which could be attributed to our simplistic modeling of the temperature excursion. However, the fact that XT decreases with decreasing D at constant F, while it is exactly proportional to F at constant D (see below) suggests that the slight variation of XT is due to a nonlinear effect such as saturable absorption of graphene28 or depression of Tl,peak caused by hot plasma generation with respect to the electrons in the near-surface region.

The variation of XT in the F series with constant D of 2.0 ps is shown in Fig. 3b. In agreement with the results in Fig. 3a, all-time traces of this series were fit to values of XSF close to zero within the accuracy of the fit parameters. Thus, for the final calculation XSF was not fitted but set to zero (indicated in Fig. 3b by the red squares without error bars at zero level). The variation of XT closely follows the regression line through zero, showing that XT is proportional to F, which itself is proportional to the calculated peak lattice temperature, Tl,peak, displayed in the upper horizontal axis of Fig. 3b (see “Methods”). This validates the adequacy of the proposed model, and further corroborates the assumption XSF = 0 for the entire series of F-dependent measurements at this longer D.

Figure 3a, b shows that the alteration of reflection intensities by the surface field effect is below detectability at relatively long pulses of 2 ps for all F ranges we tested. However, at shorter Ds, the contribution of the surface field effect to the measured intensities gradually increases, and eventually exceeds the contribution of the Debye–Waller effect. In Fig. 3c, the relative contribution of the surface field effect (defined as XSF/XT for the (10) reflection, XSF/3XT for the (11) reflection) is shown for the D-dependent measurements. Although the surface field effect is independent of the diffraction order in the present model, the relative contribution is smaller for the higher order, as the temperature effect increases according to the Debye-Waller theory.

Intensity modulation from a geometrical perspective

The initial spatial distribution of the emitted electrons via SCL thermionic emission can be approximated as a quasi-two-dimensional thin disc10,13,16. These well-localized characteristics of the emitted electrons above the surface originate from the fast emission time, comparable to the femtosecond laser excitation time, and the effective emission area dictated by the beam spot size (few tens to hundreds of μm) and the intensity profile. The subsequent evolution of the distribution in both transverse and horizontal directions is, however, governed not only by the initial distribution, but also by the nonlinear self-forces and the kinetic energy spread of the electrons13,22,29. Given that concomitant changes of the surface field alter the trajectories of the probe electrons onto the electron detector, it is important to investigate the relation between the intensity modulation and geometrical characteristics of the charge-separated region. In order to gain this insight, we calculated surface fields in the charge-separated region for various spatial distributions of emitted electrons, and simulated trajectories of probe electrons in the calculated field (see “Methods” for details). The emitted electrons were modeled as a charged plasma with a cylindrical volume of diameter φ and thickness δ, floating above the sample plane at the distance d, as illustrated in Fig. 4a.

Fig. 4: Simulation study of the surface field effect on electron image.
figure 4

a Simulation model of the experimental geometry including electron gun, sample grid, and screen. The simulated low-energy electrons are colored according to their kinetic energy. The inset shows the magnified view of the charge-separated region where the electron plasma creating the surface field (sky blue color) is modeled as a cylinder with diameter φ and thickness δ, separated from the sample grid by the distance d. b Representative two-dimensional position distributions of low-energy electrons at the screen plane. The modeling parameters of the plasma shape are (φ = 10 μm, δ = 1 μm, d = 20 μm), (φ = 200 μm, δ = 1 μm, d = 20 μm), (φ = 10 μm, δ = 150 μm, d = 20 μm), and (φ = 200 μm, δ = 150 μm, d = 20 μm), from the left to the right panel, and the plasma charge is 160 fC. c Corresponding electric field map to panels shown in b in respective order and d electric potential distribution in the charge-separated region to the same panels shown in b in respective order. The scale bar indicates 100 μm. ∆I/I in the depletion zone as a function of φ and δ for the plasma charge of 160 fC and d = 20 μm (e), 160 fC and d = 70 μm (f), and 16 fC and d = 20 μm (g). h Depletion zone size at the screen plane as a function of δ for different d and plasma charge.

Full size image

The two-dimensional distribution of particle positions at the screen plane (x, y plane) has been investigated for varying φ and δ, and for two values of d (20 μm, 70 μm) and two uniformly distributed volume charges (16 fC = 105 electrons, and 160 fC). The justification of these parameter settings is described in “Methods”. The full data set is presented in Supplementary Figs. 7–9. As shown in Fig. 4b, probe electrons near the central part of the screen seem to be swept away, leading to the formation of a depletion zone with a decreased density of particles compared with the reference condition of zero plasma charge. These particles are redistributed towards the rim of the depletion zone, consistent with the excess density observed in the difference map of the surface field effect (Fig. 1b).

Our simulations show that the particle distribution at the screen is closely correlated with the magnitude and the direction of the surface field, both of which are controlled by the simulation parameters of the electron plasma. Electric field and potential calculations with diameters φ = 10 µm and φ = 200 µm for given δ and plasma charge (Fig. 4c, d) show that the magnitude of the field decreases (as indicated by the false-color scale) and the direction of the field changes from transverse to vertical in the vicinity of the plasma center with expanding φ. This effect causes the central electrons of the beam to gain less transverse momentum, with the result that they land statistically more often inside the depletion zone. This explains the smaller ∆I/I at the depletion zone for larger φ, as summarized in Fig. 4e–g. The φ-dependence of ∆I/I is more prominent for shorter d and lower plasma charge. Furthermore, the size of the depletion zone is largely dependent on δ for given d and plasma charge (Fig. 4e). This is ascribed to the interaction time of the probe electrons with the surface field. Comparison of simulations with δ = 1 µm and δ = 150 µm (Fig. 4c) shows that thicker plasmas generate longer charge-separated regions in the propagation direction, allowing probe electrons to gain larger transverse momenta.

Geometrical characteristics of the charge-separated region is provided by comparison of the simulation to our experimental results. For d = 20 μm and the plasma charge = 16 fC (Fig. 4g), ∆I/I is −27.0 % with the plasma dimensions of φ = 200 μm and δ = 1 μm, which is larger than ∆I/I of the projection image measured in the entire ∆t range with the highest irradiance (Supplementary Fig. 3, F = 27.3 mJcm−2, D = 0.18 ps). The calculated Te,peak based on this excitation condition is 0.45 eV, corresponding to the propagation speed of 0.4 μm/ps for emitted electrons. Within the approximations of this approach, the observed magnitude of the depletion zone indicates d ≅ 20 μm at ∆t = 50 ps for which the observed maximum ∆I/I (−21.0 %) best matches the calculated response. Also, the yield of the emitted electrons at Te,peak = 0.45 eV is expected to lie between the lower and upper limit range set in our simulation, according to ref. 10. These parameter values deduced from experimental conditions and the inversely proportional trend between ∆I/I and φ (Fig. 4g) from our simulation imply the transverse dimension is larger than 200 μm for the plasma floating on the expected location from the surface for the given ∆t and the excitation condition. In addition, depletion zone size of the projection image recorded at the same ∆t, in Fig. 1b (left panel), is ~ 3 mm, larger than the calculated one for the electron plasma with δ = 150 μm for both cases of plasma charge = 16 and 160 fC (Fig. 4h). Given the proportional relation between the depletion zone size and δ from our simulation, δ larger than 150 μm of the plasma is expected. This indicates that the space charge-induced expansion speed should be larger than 3 μmps−1 in the propagation direction. This is ~5 times larger than the deduced number from studies with high energy electrons13,16. Therefore, the plasma dimensions implied from our study is far from the thin disc shape adapted in the capacitor model. However, this model provides qualitative insight into the magnitude and effect of the resulting surface fields.

The information obtained from projection imaging, diffraction, and simulation helps to devise several practical ways of eliminating the surface field effect in ULEED. On the experimental front, a spatially uniform intensity profile (rather than Gaussian) of the excitation pulse would reduce Te,peak of the diffraction sample for a given irradiance, possibly avoiding SCL thermionic emission. The same effect can be expected by increasing D for a given F that is required to trigger an observable structural change: as shown in Fig. 2b for example, adjusting D from 180 fs to 1.0 ps reduces Te,peak to such an extent that the surface field is significantly mitigated—this sub-picosecond regime is still below the electron bunch duration limited temporal resolution of ULEED achieved by state-of-the-art apparatuses20,21,30.

In certain cases, increasing D is not an option as high time resolution is required for the surface process of interest. A more fundamental approach can be conceived for this case that consists of the correction of surface field effect-contaminated diffraction intensities. By compensation of surface field effect-induced intensity changes using data measured independently at the same ∆t and at the same ROI, in projection imaging, the surface field can be determined and its effect on diffraction intensities corrected. The nonlinear effects need to be taken into account but are manageable. In the present work, the first steps have been taken along this line. Using monolayer graphene as a test sample, correction of the surface field effect has been achieved implicitly by fitting the diffraction data with a function that combines the simulated structural effect and the surface field effect; the latter was described with parameters deduced from independent measurements in projection geometry. In this way, the degree of obfuscation with the surface field effect could be quantified, and subsequently separated from the structural effect with high confidence. This separation was possible by fitting two diffraction orders simultaneously, and exploiting the restrictions imposed by the Debye–Waller equation. Graphene is a particularly simple example, as it is a mono-atomic material; this largely restricts structural variations to changes in atomic displacement parameters. Nevertheless, a similar procedure should be applicable to more complicated cases where constraints between the relevant structure parameters are known, for example a Debye–Waller contribution or known structural endpoints to provide constraints. The key point here is that the surface fields are non-negligible and we give a prescription on how to remove these effects from the structural dynamics of interest.

Overall, the present work strengthens the method in reliably extracting structural dynamics from ULEED signals where surface field effects are significant. In this manner, we have widened the scope of ULEED as an emerging technique for directly observing atomic motions at surfaces that are central to understanding surface chemistry, heterogeneous catalysis, and exotic two-dimensional collective effects at discontinuities defined by surface boundary conditions. The development of sample delivery systems for preparing nanoscale liquid layers thin enough for ULEED studies even promise to open up in situ studies of interfacial chemistry31,32. The methodology developed in this work will enable capturing the critical atomic motions defining these processes.

Methods

Experimental design

We adopted the conventional stroboscopic optical pump-electron probe protocol, running both series of experiments, the projection imaging, and diffraction measurements, at 1 kHz repetition rate. The measurements were carried out in transmission geometry. We used a femtosecond laser system operating at 1030 nm. Electron bunches were generated from a photocathode upon irradiation by the 4th harmonic of the fundamental laser pulse, and accelerated to beam energies ranging from 0.5 to 2 keV via the extraction plate of an electrostatic Einzel lens directly integrated into the photocathode. In case of the diffraction measurement, the generated electron beam was maximally focused on the detector plane by tuning this lens. The beam spot size at the sample plane approximately 7 mm away from the photocathode was 98 μm (horizontal) × 93 μm (vertical) FWHM, measured by the standard knife-edge method. In the case of projection imaging an unfocused diverging beam was used by turning off the lens. The number of electrons per bunch was 7.5 × 104, and the total number of electrons accumulated for each projection and diffraction image was 6 × 108 and 7.5 × 107, respectively. The electron bunch duration at the sample plane is about 12 ps FWHM (in case of D = 180 fs), independently measured by a home-built streak camera33,34. The 2nd harmonic of the fundamental laser pulse was used for exciting the sample. The spot size of the excitation beam at the sample plane was 359 μm (horizontal) × 285 μm (vertical) FWHM. Further details of the experimental setup are available in Supplementary Fig. 1. The data collection and image processing scheme are described in Supplementary Note 1.

Statistical analysis

The procedures used for statistical data analysis of direct and diffracted beam experiments are described in full detail in Supplementary Note 2–7.

Samples

An ultrafine mesh grid of copper from Ted Pella Inc. served as object for low-energy electron projection imaging (hole size 6.5 μm, bar size 6 μm, thickness 25 ± 2 μm). For diffraction measurements, we used CVD-grown monolayer graphene from Ted Pella Inc., supported by the same type of copper grid, without additional treatment.

Calculation of T e,peak of the copper grid after laser excitation

In order to describe the temporal evolution of Te and Tl, the electronic and lattice temperature of the copper grid after excitation, we solved a pair of coupled equations of the standard two-temperature model. In solving the equations, we neglected the spatial dependence of the temperature evolution, yielding a simplified version:

$${C}_{{{{{{\rm{e}}}}}}}\left({T}_{{{{{{\rm{e}}}}}}}\right)\frac{\partial {T}_{{{{{{\rm{e}}}}}}}}{\partial t}=-G\left({T}_{{{{{{\rm{e}}}}}}}\right)\left({T}_{{{{{{\rm{e}}}}}}}-{T}_{{{{{{\rm{l}}}}}}}\right)+P\left(t\right)$$
(2)
$${C}_{{{{{{\rm{l}}}}}}}\left({T}_{{{{{{\rm{l}}}}}}}\right)\frac{\partial {T}_{{{{{{\rm{l}}}}}}}}{\partial t}=G\left({T}_{{{{{{\rm{e}}}}}}}\right)\left({T}_{{{{{{\rm{e}}}}}}}-{T}_{{{{{{\rm{l}}}}}}}\right)$$
(3)

where, Ce, Cl, and G denote the electronic and lattice heat capacity, and electron-lattice coupling factor. We used the Te dependent Ce and G of copper from ref. 35, in which the constants were calculated with the consideration of the thermal excitation of 3d band electrons of copper at high Te under the density-functional-theory framework. For Cl, the Dulong–Petit value (=3.4 × 106 J m−3 K−1)36 of copper was adopted, considering its weak dependence on temperature at high Tl. P(t) in Eq. (2) is a source term, equal to P(t) = F(t)(1 − γ)/Λ, where γ and Λ are reflectivity and skin depth of copper, respectively. The temperature-dependent optical constants were adopted from ref. 37. F(t) was assumed to follow a Gaussian profile in time (t) with the laser parameters (F and D) corresponding to each excitation condition. Equations (2) and (3) were integrated numerically, and Te,peak was determined from the Te(t) curves calculated for different excitation conditions (Supplementary Fig. 4).

Theoretical prediction of X SF as a function of T e,peak

For this calculation, we refer to the modified Richardson–Dushman equation10,11 that relates the yield, Nesc (equivalent to Q of Eq. (1) in the main text), of surface escaping electrons to Te,peak of a metal target, derived from the standard Richardson–Dushman equation by considering suppression of the total charge yield due to space charge fields occurring near the surface region during the ultrafast (≤10 ps) emission process:

$${N}_{{{{{{\rm{esc}}}}}}}=\frac{{k}_{B}{T}_{{{{{{\rm{e}}}}}},{{{{{\rm{peak}}}}}}}}{a{e}^{2}{R}_{1}^{2}}\times {{\log }}\left[1+4{h}^{-3}{{{{{{\rm{\pi }}}}}}}^{2}{m}_{{{{{{\rm{e}}}}}}}{e}^{2}{R}_{2}a\tau {k}_{{{{{{\rm{B}}}}}}}{T}_{{{{{{\rm{e}}}}}},{{{{{\rm{peak}}}}}}}\times {{\exp }}\left\{-\frac{{\varepsilon }_{{{{{{\rm{F}}}}}}}-\mu +e\phi }{{k}_{{{{{{\rm{B}}}}}}}{T}_{{{{{{\rm{e}}}}}},{{{{{\rm{peak}}}}}}}}\right\}\right]$$
(4)

denoting by kB, h, me, e, εF, μ, eϕ the Boltzmann constant, Planck constant, electron mass, elementary charge, and Fermi energy, chemical potential, and work function of the target. R1 and R2 are the radii of an elliptical excitation spot size (FWHM) at the target. The term, a, is a geometric parameter (=1–2) that depends on the shape of the escaping electron cloud. Here, τ is the pulse duration of the Te profile, defined by the full width at 80% of Te,peak11. Note that this analytical equation features relatively insensitive dependencies on the parameters inside the log term.

We first calculated Nesc by adapting, in the above equation, our experimental parameters, R1 = 98 µm, R2 = 93 µm, eϕ = 4.55 eV (for Cu), and the theoretical values, a = 1.7 (for a uniform thin disk shape) and τ = 2.1 ps (determined from the calculated Te profiles for the F-dependence measurement in Supplementary Fig. 4, see Supplementary Fig. 5 and Supplementary Table 1). Here, εF − μ were set to 0 (following ref. 10). Next, we determined an overall scale parameter that accounts for the unknown proportionality factor C relating XSF with Nesc by fitting the calculated Nesc to the F-series data points (black circles in Fig. 2b). With the extracted C, the theoretical XSF (=CNesc) is plotted as a black solid line in Fig. 2b. In case of the D-dependence measurement, a hypothetical XSF curve (plotted as a blue broken line in Fig. 2b) was calculated with τ = 5.0 ps and a scale parameter reduced by a factor of 0.35 relative to the C extracted from the F-measurement.

Estimation of T l,peak of graphene after laser excitation

The peak lattice temperature, Tl,peak, of graphene was estimated with the assumption that the absorption efficiency at 515 nm wavelength is 2.3% for monolayer graphene38. According to ref. 39, the specific heat of monolayer graphene above 100 K is constant and identical to that of graphite (≈0.7 J g−1 K−1). The thickness and density of graphene were taken as 0.355 nm and 2.3 g cm−3, respectively.

Electric field calculation and particle trajectory simulation

The probe electrons with 2.0 keV kinetic energy travel with a speed of 2.6 × 107 ms−1 along the propagation direction, whereas the plasma electrons, creating the surface field, leave the sample surface (copper grid) at 105–106 ms−1, depending on F and the work function of the sample13. This order of magnitude difference in speed implies a “snapshot” of the transient surface field seen by the probe electrons during their interaction time with the plasma at a specific Δt. With this consideration, we performed electrostatic field calculations by using a commercial software package (CST EM Studio®) based on the finite integral technique.

In Fig. 2b of the main text, Te,peak ≅ 0.26 eV (=3000 K) is determined as the threshold to generate SCL thermionic emission. The study on the charge yield as a function of Te,peak in the SCL thermionic emission regime indicates the range of the yield from 105 to 106 electrons for Te,peak = 0.3–1.0 eV10. An independent study13 reports the surface charge density ranges at 0.54–1.9 × 106 mm−2 for the excitation fluence range of 13.5–67.7 mJ cm−2 for Silicon, comparable with ref. 10. Referring to this range, we set the lowest and largest surface charge as 105 to 106, respectively. This parameter range can mostly cover the experimentally accessible charge yield for femtosecond excitation cases.

The exact plasma evolution dynamics was beyond the scope of this study. However, in order to estimate reasonable geometrical parameters of the plasma for our field calculation, we took into account the initial plasma velocity and the longitudinal expansion speed, deduced from the capacitor model, as summarized in Supplementary Table 2: both quantities are tabulated in the table as the order of 1 μm ps−1. Also, from our direct beam intensity traces (see Supplementary Fig. 3), the elapsed Δt to reach the observed maximum ΔI/I was evaluated as 50–75 ps (depending on F and D). This time scale indicates that the floating distance d from the target surface should be in the order of few tens of micrometer, leading us to study two cases of d (=20 and 70 μm) in the field calculation. As shown in our particle trajectory simulation result (see Fig. 4h), the larger value of d induces the stronger surface field effect for a given plasma charge and shape, resulting in the larger depletion zone size.

Given the time scale to reach d and the deduced longitudinal expansion speed of 1 μm ps−1, the thickness of the plasma δ can also be estimated to be on the order of a few tens of micrometers. In our field calculation, by setting the wider parameter range of 1–150 μm, we could check the geometrical effect on the particle trajectory more clearly. The parameter range (1–200 µm) for φ is determined by considering the approximate excitation laser beam spot size at the sample plane. It is noteworthy that the effective emission area can be smaller than the given spot size due to the inhomogeneous laser intensity profile and whether the final φ for a given ∆t is dictated by the emission area or the lateral expansion speed of the plasma, which is subject to the particle density during the propagation dynamics.

In order to simulate the trajectories of the probe electrons, we first calculated the electric field distribution corresponding to the experimental setup with a plasma of electrons included. The parameters describing the experimental setup were set according to the dimensions of each mechanical component, as measured directly or deduced from the recorded images (camera length = 35 mm, sample-to-electron source distance = 7 mm, Einzel lens inner diameter = 1 mm, diameter of the sample plane = 3 mm, etc.). The plasma was modeled as a vacuum object containing a negative volume charge, and the sample plane was treated as a perfect electric conductor. The photocathode plane voltage was set to −2.0 kV, and the voltage of the other conductor components (i.e., Einzel lens, sample plane, screen) was set to 0 (ground).

The calculated field data was imported in a particle tracking solver (CST PS Studio®) for simulation of the electron beam trajectory in stationary mode. In the simulator, the electron source was modeled as a circular region with a diameter of 100 µm, corresponding to the photo-injection laser beam size, where homogenously distributed 105 emission sites are defined to generate electrons. By setting the plasma charge to zero, we compared the simulated electron beam spot size at the screen plane with the measured one in projection imaging to ensure that the parameters used in the solver reproduce the experimental conditions. For both steps, the field calculation and the trajectory simulation, an adaptive hexahedral mesh element was used, and the total mesh number was over 3.5 × 106 in each computation run with a different set of plasma parameters.