Introduction

Materials with reprogrammable properties have attracted the continued interest of researchers in a wide range of fields, such as materials science, physics, and engineering. This is not only due to the rich physics of these reprogrammable materials, but also because of the great potential for engineering applications enabled by their in situ control of material properties in unprecedented ways1,2. In recent years, by mimicking such material behavior, reconfigurable mechanical structures have been developed at the macroscopic level. Their programmable shape changes can be implemented by leveraging the reconfigurability of the constituent architectures. For example, recent studies have shown highly transformable morphological properties by employing origami/kirigami3,4,5,6,7,8, compliant mechanisms9,10,11, and inflatable structures12,13,14.

Such reconfigurable mechanical structures can also offer tunable mechanical properties (e.g., stiffness15,16, wave guide17,18,19, etc) associated with their deformation. However, reconfigurability in mechanical systems usually achieves versatility at the sacrifice of structural rigidity. Recently, origami-based structures with self-locking behavior have shown significant enhancement of load-bearing capabilities depending on their folded configurations3,20. Such an origami structure shows flexible folding motions without deforming each surface in a limited folding range. Once the structure reaches its locking point, it exhibits high rigidity due to the contact between its surfaces and creases.

In previous studies, high stiffness has been achieved either by the collision of vertices in the waterbomb origami21 or by employing Miura-ori to induce self-locking3,20,22. Although such stiffening response can be achieved without modifying predefined design parameters, once this stiffening response is implemented in the design, it is extremely difficult to remove this feature after fabrication. This implies that the foldable range is always limited significantly by introducing the stiffening property.

Here, we study a reconfigurable 3D origami structure with reversible stiffness control induced by the vertex contact within the structure. We analytically and experimentally demonstrate the vertex contact and thus the stiffening of this origami structure from the level of a unit cell to a multicell tessellation. From the unit cell analysis, we show that our origami unit cell can be transformed into multiple phases: a self-contacting configuration with a rapid increase of its stiffness, and flexible configurations in which self-contact nature is completely removed throughout the entire folding range. Then, we build a 3D space-filling origami tessellation, which inherits the transformability of the unit cell. Interestingly, we find that the origami tessellation can support not only homogeneous configurations (i.e., all unit cells are in the identical phase, which exhibits the same folding motion within the tessellation), but also highly heterogeneous configurations (i.e., different phases of origami unit cell coexist in the same tessellation while maintaining its reconfigurability) by virtue of phase transformation. This extrinsic heterogeneity proffers rich morphology changes as well as finely controllable stiffness in the self-contact regime, which has been extremely challenging, especially after assembly, as mentioned earlier.

The versatile conversion between homogeneous and heterogeneous states in origami is phenomenologically analogous to the structural phase transformation of the crystal structure. In a metal alloy, for example, the change in the crystal structure induces its material property change. Similarly, the shape change of unit cells induces the variations of its mechanical property—specifically variable and reversible stiffness—in our origami tessellation. This hints that the design principles of our heterogeneous origami tessellations could open the broader possibility of new programmable mechanical structures and materials.

Results

Unit cell analysis

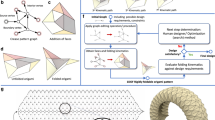
We start by demonstrating the transformable nature of our origami unit cell structure by characterizing its geometry. Our origami unit cell consists of two flat sheets folded, whose crease patterns are defined by the length parameters (l, m, d) and angle (α) (see Fig. 1a). The crease lines are folded according to mountain and valley folds denoted in Fig. 1a. The upper and lower sheets are bonded together such that the outer rims denoted as red solid lines are always aligned and in contact during the folding behavior (see Methods, Supplementary Note 3, and Supplementary Fig. 5 for the detail of the actual prototyping using the paper sheet). Starting from the flat state, by selecting appropriate crease lines to be used, we obtain three different resultant shapes of the unit cell. If all crease lines are used, the unit cell is folded into the Tachi-Miura polyhedron23,24 (TMP; red-colored unit cell in Fig. 1b). Interestingly, if some of the crease lines are kept flat, the unit cell can be folded into two additional phases, the origami tubes (OTs) (see blue and green-colored unit cells in Fig. 1b). For instance, selecting green lines as a flat crease results in the blue-colored unit cell in Fig. 1b, and the same for the blue lines in the green-colored unit cell, but with the opposite tilted angle (see Supplementary Movie 1 for folding motions of each configuration). Therefore, we obtain three different phases: one TMP and two OT phases.

Fig. 1: Reconfigurable rigid origami structure.
figure 1

a The flat crease patterns of the origami unit cell, and b three possible phases: TMP, OT(−) and OT(+). When crease lines denoted by blue (green) color are forced to be flat, unit cell is folded into OT(+) (OT(−)). c Reconfigurable behavior is shown in the configuration space. Energy landscape for each configuration is plotted along its folding path. The geometrical parameters are (l, m, d, α) = (30, 30, 30, 65°) (see Supplementary Note 1 for the detail of the energy calculation). d Folding motion of TMP and OT(+) with l = 30 (back) and l = 22.5 (front). The other parameters are the same as those in c.

Full size image

To analyze the folding motion of each phase closely, we introduce the folding angles θM and θS defined as half of the angle between adjacent surfaces connected by the horizontal and inclined creases, respectively (see Fig. 1b and Supplementary Fig. 1). Note that these angles can be obtained from one another (see Supplementary Note 1 and Supplementary Fig. 1). To characterize three different phases (TMP and OTs), we use θS1 and θS2 specifically for the blue and green inclined crease lines in Fig. 1a-b. Note that θS1 (or θS2) is constant at π/2, if corresponding inclined creases are kept flat. We refer to the above two OT configurations as OT(+) if θS1 = π/2 and OT(−) if θS2 = π/2. While the TMP configuration obtained from this crease pattern has been studied in previous research23,24, this transformation into the OT configurations has not yet been reported. Also, such phase transformation is achieved while each transformed unit cell maintains the rigid foldable behavior, i.e., deformation takes place only along the crease lines.

Figure 1c shows the folding paths of TMP and OT unit cells in the configuration space as a function of the folding ratio (γ = 1 − θM/(π/2)) and angle difference (θS1 − θS2). The design parameters used in this analysis are (l, m, d, α) = (30, 30, 30, 65°). The TMP exhibits its folding motion along θS1 − θS2 = 0, whereas the folding motion of the OT(+) (OT(−)) unit cell takes place in the positive (negative) θS1 − θS2 regime as the structure is folded from its flat state (γ = 0; please see Supplementary Fig. 2 for the posture of the unit cell and the corresponding γ). By modeling the creases as a linear torsion spring, we plot the energy landscape for each configuration along its folding path (Fig. 1c; see also Supplementary Note 1 and Supplementary Fig. 3 for the detail of the energy calculation). We find a minimum energy state for each configuration, which means that there are three stable states.

Next, we examine the kinematics of origami unit cells, specifically TMP and OT(+). Figure 1d shows the folding motions of TMP and OT(+) phases for two different l values: l = 22.5 (in the front) and l = 30 (in the back), while the other parameters (m, d, α) being kept consistent with the aforementioned analysis. If l = 30, both the TMP and OT(+) can be folded from a flat state (γ = 0) to another flat state in the 1–2 plane (γ = 1). However, if l = 22.5 is chosen, the TMP exhibits the contact between some of its vertices (denoted by the dashed circle in TMP at γ = 0.62; see also Supplementary Fig. 4 for closeup illustration), in sharp contrast to the OT configuration that shows the complete folding motion observed for l = 30. Therefore, the further folding in TMP can be halted due to this vertex contact, which can lead to the stiffening response.

We analyze this self-contacting behavior by considering the vertex spacing w as shown in Fig. 2a. Based on the geometry of the TMP and OT, we analytically obtain this vertex spacing (see Supplementary Note 2 for the derivation detail). In particular, for the TMP phase (i.e., θS1 = θS2 = θS), the vertex spacing is expressed as

$$\frac{w}{d}=-2(\lambda +\mu )+\cot \alpha +4\mu {\sin }^{2}\alpha {\cos }^{2}{\theta }_{S},$$
(1)

where λ = l/d and μ = m/d are nondimensional design parameters for center and side lengths. Note that θS is calculated from θM. Then, by considering w/d = 0, we obtain the critical folding ratio (γc) at which the vertex contact occurs as follows:

$${\theta }_{S,c}={\cos }^{-1}\left[\sqrt{\frac{2\left(\lambda +\mu \right)-\cot \alpha }{4\mu {\sin }^{2}\alpha }}\right],$$
(2)

if

$$\lambda \le \frac{1}{2}\cot \alpha -\mu \cos 2\alpha .$$
(3)

See Supplementary Note 2 for more detail. Note that the critical folding angle (γc) can be calculated from this critical folding angle θS,c. To build a physically valid origami structure, we also require

$$\frac{1}{2}\cot \alpha \le \lambda .$$
(4)

By imposing these conditions on our analysis, we explore the self-contacting behavior of our origami unit cells.

Fig. 2: Origami unit cell with self-contacting vertices.
figure 2

a We examine the vertex spacing (w) of the (red) TMP and (green) OT(+) unit cells with (l, m, d, α) = (22.5, 30.0, 30.0 mm, 65°). b The 3D diagram shows the tunability of the contact point altered by the design parameters. The dashed curves indicate the boundary between rigid foldable without contacting vertex configurations (green and blue-colored areas) and self-contact regimes (color intensity represents the critical contact points) bounded by Eq. (3). Here, the blue-colored regions indicate a foldable configuration without self-contact, but with load-bearing capability due to auxetic behavior25. The grey colored areas indicate the invalid design parameters. The inset illustrations show TMP unit cells with α = 45° (green: noncontacting regime) and α = 65° (blue: No self-contact, but load-bearing capability) at λ = μ = 1.2. c Compression test on the TMP and OT unit cell prototypes. The black vertical line indicates the prediction of a critical contact point from Eq. (2). We approximate the force-displacement curve for the TMP by using two models: the torsion spring origami model, in which the crease lines of the TMP are modeled as a torsion spring, whose spring constant is kθ = 43.99 Nrad−1 (dash-dotted line); the modified torsion spring model with the repulsive force field to model the vertex contact (dashed line), whose constants are kθ = 43.99 Nrad−1 and ke = 8.889 × 104 Nm.

Full size image

Figure 2a shows the normalized vertex spacing w/d as a function of the folding ratio γ for TMP and OT(+) phases. Our analysis shows that w becomes zero if the TMP is folded to γ = 0.62, which indicates that two vertices (denoted as blue dots in Fig. 2a) are in contact. On the contrary, the OT(+) phase shows nonzero w throughout the whole folding motion.

We further explore various designs of our origami unit cell for the self-contacting behavior, particularly its tailorable critical contact point. Figure 2b shows the tunable critical folding ratio (γc) denoted by the color intensity in the three-dimensional design space (λ, μ, α). In this figure, the black dashed curves indicate the boundaries obtained from Eq. (3). For example, the value of γC decreases as we increase μ or α, which means that the self-contact can be triggered in an earlier folding stage. The gray-colored areas indicate the invalid design parameters (i.e., origami cannot be built physically) as expressed mathematically by Eq. (4). Note that both blue- and green-colored regions are a noncontacting design, but blue areas yield re-entrant TMP with a negative Poisson’s ratio. While such re-entrant TMP is collapsible in the 3-axis direction (which is the direction of our primary interest in this study), it can provide load-bearing capability in the two-axis direction due to the auxeticity (see ref. 25 for more details).

Given the kinematic analysis and design space for the self-contacting unit cell, we now explore the static response of TMP and OT phases to verify the stiffening response induced by the vertex contact. We conduct the uniaxial compression test along the 3-axis by fabricating prototypes made of paper. The design parameters used in this test are (l, m, d, α) = (22.5, 30.0, 30.0, 65°), which gives a critical folding ratio of γc = 0.62 (see Methods and Supplementary Note 3 for details). In Fig. 2c, we show experimentally measured force-displacement curves for the TMP (red solid line) and OT(+) (green). Here, we clearly observe that the TMP phase exhibits a drastic increase of the force after the predicted contact point, while the force profile remains plateau for the OT(+) phase even after the contact point.

To further analyze this behavior, we employ a torsion spring model of the TMP unit cell in which its crease lines are modeled as a linear torsion spring (with spring constant kθ). We fit the model function to the experimental results (see the black dash-dotted curve in Fig. 2c). Note that this model provides the analytical force solely based on the folding angle changes regardless of the vertex contact. Thus, this model expresses the experimentally measured force curve very well up to the predicted critical point, but it starts to deviate drastically from the experiment result after the the vertices make contact.

With this deviation being revealed, we now introduce a repulsive force field to model the stiffness increase within the post-contact regime26,27, such that the total force is now Ftotal = F + frepulsive where F is the force from the conventional torsion spring model. We assume the force field of the form,

$${f}_{{{repulsive}}}=\left\{\begin{array}{l}\kern-13pc0\quad (u < {u}_{c})\\ \frac{{k}_{e}\pi }{4{\delta }_{0}^{2}}N\left[\pi ({\delta }_{0}-\delta (u))-2{\delta }_{0}\cot \left(\frac{\pi \delta (u)}{2{\delta }_{0}}\right)\right]\frac{d\delta }{du}\quad (u\ge {u}_{c})\end{array}\right.$$
(5)

where u is the displacement in axis-3 direction, uc is the critical displacement where the vertex contact occurs, δ(u) = w(θS(u)) − w(H0), δ0 = δ(uc), N is the number of layers, H0 is the initial height of the unit cell (Nd), and ke is the magnitude of the virtual potential. The derivative \(\frac{d\delta }{du}\) can be evaluated using the relationships Eq. (1) and \({\theta }_{M}={\sin }^{-1}\left(1-\frac{u}{Nd}\right)\). This force guarantees the C1 continuity, given that frepulsive = 0 and \(\frac{d}{du}{f}_{{{repulsive}}}=0\) at u = uc. For more detail of the derivation, please refer to Supplementary Note 2.

We again fit the modified model to the curve obtained from the experiment. The dashed line in Fig. 2c shows the modified model function with two fitted parameter kθ and ke. We can see that modified model collapses with the conventional torsion spring model until the theoretically predicted critical point, and start to deviate by following the experimental result within the post-contact regime.

Experimental demonstration of stiffness variation

Based on the unit cell analysis above, we demonstrate very fine tunable stiffness induced by the vertex collision, by building an origami tessellation. Here, an origami tessellation can be designed through two different assembly approaches: close-packed and square assemblies (see Supplementary Note 4, Supplementary Figs. 8-10). In this study, we employ the close-packed assembly to build a prototype of 3 × 3 tessellation, which can transform into different configurations. Figure 3a shows four exemplary configurations composed of different numbers of the TMP unit cells: (i) nTMP = 0, (ii) 3, (iii) 6, and (iv) 9 (see Supplementary Fig. 6 for other examples of possible configurations and Supplementary Movie 2 for the transformations between these four configurations). In addition to these four configurations, this 3 × 3 tessellation can transform into 32 different configurations composed only of TMP and OT(+) phases (e.g., see the bottom right illustrations in Fig. 3a for some of the examples). The number of possible transformation patterns increases as we increase the total number of origami unit cells constituting a tessellation (see Supplementary Note 5 and Supplementary Fig. 11).

Fig. 3: Origami tessellation with in situ tunable self-contacting vertices.
figure 3

a 3 × 3 close-packed assembly can transform from its flat state into multiple configurations containing different numbers of TMP cells nTMP (red-colored cells): (i) nTMP = 0, (ii) nTMP = 3, (iii) nTMP = 6, and (iv) nTMP = 9 (all TMP configuration). In addition to these four configurations, the lower right inset illustrations show other possible transformed shapes. The inset photographs with scale bar of 100 mm show our paper prototypes of their corresponding configuration. b Experimentally measured force-displacement relationships for the above four configurations. The force is normalized by the torsion spring constant obtained from the unit cell compression test (Fig. 2b), and the displacement is normalized by the initial height of the prototype before compression is applied. We extract the slope of each force curve in the rigid folding and contact regimes (see the dashed lines). c The values of slope in the rigid folding regime (kn) and contact regime (Kn) are plotted as a function of the number of TMP cells (nTMP) contained in the tessellation. The slope is normalized by k0, i.e., no TMP case.

Full size image

We then conduct uniaxial compression tests on these transformed patterns to study how this structural morphology changes the mechanical properties of our origami, specifically stiffness in the 3-axis direction (see Methods, Supplementary Note 3, and Supplementary Fig. 7 for the detail). Figure 3b shows the experiment results for four different configurations, which correspond to the configuration i–iv, transformed from the same design. These four configurations initially show a similar static response, but after the critical point, we observe drastically different evolution of force among different configurations. In particular, the slope of each force curve in the post-contact regime increases as the number of self-contacting TMP cells increases.

To quantify this variation, we extract the slope via linear regression using the least-squares approach (denoted as a dashed line in Fig. 3b), and plot it as a function of the number of TMP unit cells (n) as shown in Fig. 3c. Let Kn and kn be the slope obtained from post-contact and rigid folding regimes, respectively. We measure Kn and kn by considering eight different transformed configurations, including the four patterns above (i.e., nTMP = 0, 2, 3, 4, 5, 6, 7, 9; see Supplementary Note 3 for more detail). In Fig. 3c, the slope values normalized by k0 are shown. In the rigid folding regime, these transformed patterns show very similar slope levels regardless of nTMP. In the contact regime, however, we clearly observe the significant changes of the slope value depending on the number of TMP cells. Although the static response after a critical point is difficult to control at the unit cell level due to nonrigid origami behavior, this tessellation analysis demonstrates the feasibility of highly tunable bulk material properties induced by phase transformation of the origami tessellation (see conceptual illustration in Supplementary Fig. 15 for this highly tunable bulk stiffness).

Shannon information entropy

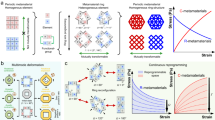
The fine tunable self-contacting behavior is achieved due to transformation between different configurations. More specifically, the finely programmable mechanical property (i.e., stiffness in the current study) is dependent upon the number of configurations that the tessellation can achieve. Therefore, it is crucial that we identify how the tessellation changes its shape, regardless of which mechanical property we would tune. To quantify this unique morphological transformability of the origami tessellation, we characterize these various transformed configurations as geometrically stored information28. Here, we employ the Shannon information entropy S to quantify the geometric information capacity (i.e., number of configurations). Even if we use the same numbers of TMP and OT(+/−) cells, the tessellation can take multiple different transformable configurations. Let ρTMP be the TMP density for a N × N tessellation defined by ρTMP = nTMP/N2, the information capacity is calculated as \(S({\rho }_{{{{{{\mathrm{TMP}}}}}}})={{{{{{{\mathrm{log}}}}}}}\,}_{b}W({\rho }_{{{{{{\mathrm{TMP}}}}}}})\) where W(ρTMP) is the number of possible configurations for a given TMP density ρTMP. Also, b = 3 is chosen in this study because our origami unit cell can transform into three phases, which means that if S > 1, the information capacity of a tessellation is greater than that of a single unit cell component.

 Figure 4a shows the Shannon entropy change for two-phase only configurations (TMP and OT(+)) of a 5 × 5 tessellation, i.e., OT(−) density is zero (ρOT(−) = nOT(−)/52 = 0). All TMP (or all OT(+)) tessellation has only one possible configuration so that the Shannon entropy is zero. As ρTMP approaches 0.5, the Shannon entropy value becomes large (here we define large entropy state of our origami structure as S > 3), which means that multiple different geometrical configurations can be obtained even if we use the same number of TMP cells in the tessellation (see the inset illustrations in the dashed box in Fig. 4a). Therefore, the large Shannon entropy combinations can store more information geometrically in an origami tessellation compared to its unit cell component itself.

Fig. 4: Reprogrammable geometric information capacity of a 5 × 5 origami tessellation.
figure 4

a The tessellation composed of TMP and OT(+) cells (i.e., no OT(−) cell) shows b the drastic change of the Shannon entropy S as a function of ρTMP = nTMP/25. The maximum entropy is achieved at ρTMP = 0.48 (see the example configurations in the dashed box). c All possible configurations for the 5 × 5 origami tessellation are characterized by the entropy S and the results are plotted in the ternary diagram, which represents a three-component origami system. The color intensity of each hexagonal marker indicates the value of the Shannon entropy S. Note that the empty region bounded by the dashed line in the ternary diagram indicates no configuration. The plot shown in b, represents the change of S along the bottom axis in this plot, i.e., ρOT(−) = 0. By embedding different phases in the tessellation, the origami system can transit to the medium entropy combinations (S ≈ 2). See the example configurations in the dashed boxes. In addition to the three-component system, defect unit cells can be embedded in the tessellation (see the left two inset illustrations for the defect phases).

Full size image

We then extend this entropy calculation to the three-component system in the same setting of the 5 × 5 tessellation. In Fig. 4c, we map the calculation results to a ternary diagram in which the color intensity of each hexagonal marker represents the Shannon information value S as a function of three different density variables: TMP density (ρTMP), OT(+) density (ρOT(+)), and OT(−) density (ρOT(−)). Similar to the two-phase configurations, as we discussed above, the origami tessellation can transform into various heterogeneous configurations ranging from small Shannon entropy to large Shannon entropy regimes, as well as zero-entropy homogeneous configurations (see Supplementary Movie 3 for the folding motion of heterogeneous origami tessellations). In particular, three different phases can be embedded in the same tessellation (see the dashed box for three-phase combinations, which are close to the center of the ternary diagram). Note that conventional rigid origami (e.g., all TMP tessellation) without transformation typically has only a single folding configuration, i.e., zero Shannon entropy. As demonstrated here, the reconfiguration from zero to large entropy combinations without redesigning the system is the unique feature of our origami tessellation.

Interestingly, our analysis reveals the so-called “no configuration regime” (i.e., empty area enclosed by the black dashed lines in the ternary diagram in Fig. 4c) bounded by the small entropy combinations. In this regime, there is no possible configuration due to the geometrical constraints among the three phases in the same tessellation. One of the natural questions here is whether there is a way to access this forbidden area. Here, we consider one potential approach to answering this question by introducing an additional phase of the origami unit cell, specifically a defect phase with zero volume (see Supplementary Note 6 and Supplementary Fig. 12 for more details). For example, if we introduce two defect cells in a tessellation, it can enable the formation of OT(−) phase surrounded by TMP and OT(+) cells (see the left inset illustration “Introduce defects” in Fig. 4c). Also, if multiple defect cells are introduced, a two-phase configuration composed of only OT(+) and OT(−) cells can be obtained (see the left inset illustration “Multi-defect phase” in Fig. 4c), which is not allowed in the original three-component origami tessellation (See Supplementary Note 6 and Supplementary Fig. 13 for more details; see also Supplementary Movie 4 for its folding motion).

Discussion

In conclusion, we have analytically and experimentally demonstrated reconfigurable self-contacting behavior of a volumetric origami unit cell, which arises from its multi-transformable nature. Our unit cell analysis results have revealed highly tailorable self-contacting behavior, specifically tunable contact points and switching between contacting and noncontacting configurations. At a multicell level, we have designed origami tessellations transformable between multiple configurations, and we have shown the in situ tunable static response of our origami tessellation by controlling the number of contacting origami cells within the tessellation. Along with the experimental demonstration, we have systematically analyzed the transformability of the tessellation by quantifying the heterogeneity using the Shannon information entropy. Unlike existing materials composed of multiple elements (e.g., recently proposed high-entropy alloys29,30 typically consist of five or more principal elements), our origami tessellation can alter its mixing ratio of different elements via multiphase transformability, even after being manufactured. Our design and analysis strategies suggest a new approach for designing high- and variable-entropy materials with in situ reconfigurability. In analogy to conventional alloys that use multiple elements, our origami also allows intrinsic heterogeneity, in which different unit cell designs can be implemented in a tessellation. This further widens the design freedom of our origami, for instance, with the multistep vertex contact introduced (see Supplementary Note 7 and Supplementary Fig. 14 for more detail. See also Supplementary Movies 5 and 6 for the folding motions of intrinsic heterogeneous designs.). Our findings have great potential not only for engineering applications, such as deployable space structures, reconfigurable robots, and surgical medical devices, but also for physics platforms to explore analogous material-level phenomena at a macroscopic scale, which can provide new insight in various research areas.

Methods

Fabrication and experiments

The TMP unit cell is folded according to the crease pattern as shown in Fig. 1a. For the actual prototype, we replace the crease lines with the compliant mechanism and create the laser cutting pattern. The laser cutting pattern is then cut from a paper sheet (3-ply Strathmore 500 Series Bristol Board), which is thick enough to fulfill the rigid foldable condition, using the laser cutter (Universal Laser Systems, Inc. VLS4.60). To assemble upper and lower sheets (see Fig. 1a) into the unit cell, we use the adhesive sheet (Grafix Double Tack Mounting Film) on the small triangular adhesive areas (see Supplementary Note 3 for the detail). The constructed unit cell is then fused into a 3 × 3 tessellation to form a complete tessellation using the same adhesive sheet used for the unit cell assembly. The design parameters of l = 22.5 mm, m = 30.0 mm, d = 30.0 mm, and α = 65° (equivalent to λ = 0.75, μ = 1.0) are chosen. The fabricated unit cell and tessellation are then loaded under the uniaxial compression test. Each prototype is compressed for 60 mm along the third axis controlled by a linear stage (Velmex, Inc. Bislide motorized linear stage MN10), and force is measured through the load cell (Kyowa Compact Tension/Compression Load Cell LUX-B-50N-ID).