Abstract
Despite mounting evidence that materials imperfections are a major obstacle to practical applications of superconducting qubits, connections between microscopic material properties and qubit coherence are poorly understood. Here, we combine measurements of transmon qubit relaxation times (T1) with spectroscopy and microscopy of the polycrystalline niobium films used in qubit fabrication. By comparing films deposited using three different techniques, we reveal correlations between T1 and intrinsic film properties such as grain size, enhanced oxygen diffusion along grain boundaries, and the concentration of suboxides near the surface. Qubit and resonator measurements show signatures of two-level system defects, which we propose to be hosted in the grain boundaries and surface oxides. We also show that the residual resistance ratio of the polycrystalline niobium films can be used as a figure of merit for qubit lifetime. This comprehensive approach to understanding qubit decoherence charts a pathway for materials-driven improvements of superconducting qubit performance.
Similar content being viewed by others
Introduction
Two decades of continuous improvement in device performance have established superconducting qubit technology as a promising platform for fault-tolerant quantum computation. Significant enhancements in qubit coherence have mostly been achieved through novel device designs and improved fabrication processes. However, performance improvements by these means have started to plateau, indicating that the dominant sources of decoherence are not well understood1. This has led to a recent surge of interest in understanding the limiting loss mechanisms in qubit materials2,3,4,5,6,7,8,9,10,11,12,13,14,15,16.
An increasing number of studies highlight the central role played by uncontrolled surfaces and interfaces in the decoherence of transmon qubits2,3,4,5,6,7,8,17,18. Proposed mechanisms for loss at surfaces and interfaces involve interactions between the qubit and microscopic objects such as impurity-based paramagnetic defects19, charge-trapping defect sites20, and two-level systems (TLS)9,10,11,17,18,21,22,23 characterized by atoms or charges tunneling between two metastable states. Several studies have quantified the macroscopic impact of such interactions by showing a proportionality between relaxation and participation ratios at various interfaces2,3,4,5. Other studies have mapped interactions between the qubit and TLS to fluctuations in relaxation, dephasing, and qubit frequency10,11,12,13,14. However, plausible identifications of specific defects or impurities associated with such phenomenological findings are rare. To address this challenge, a substantial scope of multidisciplinary research is required to explore the large phase space of potentially relevant materials properties and identify connections with qubit performance.
In this study, we bridge the gap between qubit performance and microscopic materials properties through a combined materials-and-device investigation of transmon qubits. Using spatially resolved x-ray spectroscopy and microscopy, we characterized the structural and electronic properties of the niobium (Nb) thin films used to fabricate transmon qubit devices. We compared three different deposition methods for the Nb films, yielding a quantifiable variation in the nanostructure, surface oxide composition, and transport properties. Several of these film properties correlate with the measured qubit relaxation time T1. Specifically, for qubits with shorter relaxation times, the corresponding films exhibit smaller grain size, larger voids at grain boundaries, enhanced oxygen diffusion along grain boundaries near the surface, and excess suboxides at the interface between the Nb metal and the Nb2O5 passivation layer. Additionally, longer relaxation time correlates to higher residual resistance ratio in the Nb films. We discuss mechanisms that link the observed microscopic features to residual resistance and relaxation times. In particular, our results are consistent with a significant role for TLS-induced dissipation due to defects hosted at grain boundaries and in the suboxides near the surface. These results are a critical first step in connecting precise materials properties with microscopic models for decoherence and establishing a materials-based approach to enhance qubit performance.
Results
Qubit design and performance
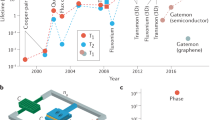
Qubit characterization was performed on transmon qubits, which are widely used for quantum computing and quantum simulation applications1,10,11,24,25,26,27,28. Transmons consist of a Josephson junction—implemented with a thin aluminum oxide barrier between superconducting wires—shunted by a large capacitor (Fig. 1a). The Josephson junction acts as a non-linear inductor, creating an anharmonic oscillator where the two lowest-lying states can be used as a coherent qubit24. Transmons are controlled and measured in a circuit quantum electrodynamics platform, where the qubit is capacitively coupled to a coplanar waveguide resonator and operated in the dispersive regime (Fig. 1b). Measurements are performed by monitoring transmission at the resonator frequency, which shifts as a function of qubit state29.
a False color optical image of a representative transmon qubit from our study. Niobium regions include the center-pin of the coplanar waveguide resonator (green), the transmon capacitor pads (purple), and the ground plane (gray). The aluminum Josephson junction is shown in white. Black areas indicate where the metal has been etched away, and the sapphire substrate is exposed. b Effective circuit diagram of a transmon qubit coupled to a resonator. Each circuit element is schematically colored as in (a). The resonator is comprised of a center-pin coupled to ground via a capacitor (Cr) and an inductor (Lr). EJ and C refer to the Josephson energy and the capacitance of the qubit respectively. The qubit is capacitively coupled to the center-pin of the resonator (Cc) and to ground (Cg). c Measured relaxation times (T1) for three rounds of devices fabricated with sputtered (purple circles), HiPIMS optimized (blue diamonds), and HiPIMS normal (green squares) niobium films, for a total of nine devices. Error bars indicate standard deviation across all T1 measurements taken on a particular device.
We employ three different deposition methods for the Nb films used to fabricate the coplanar waveguide resonators, qubit capacitor pads, and ground plane in the transmon devices. All films are deposited on sapphire substrates. First, we use direct current (DC) sputter deposition, which is common in superconducting qubit fabrication. We additionally study two variations of high-power impulse magnetron sputtering (HiPIMS), where the DC ionization voltage is replaced with short, high-power pulses, potentially leading to a higher degree of ionization and denser films30,31,32. The average cathode power in HiPIMS is typically chosen to be similar to standard DC sputtering; such a process was performed on our first HiPIMS variation, which we refer to as “HiPIMS normal”. Our second variation, “HiPIMS optimized”, involves an optimized geometry of the Nb target and sapphire substrate and a higher peak current, resulting in triple the average power.
We performed relaxation (T1) measurements to characterize the dependence of qubit performance on deposition technique. Since T1 is limited by microwave losses in the superconductors and substrate, it is a valuable probe of materials-induced loss channels. We measured three devices per film type, where a given round consisted of one device made with each Nb deposition technique, to maintain as consistent fabrication, packaging, and shielding as possible within each round. Details of qubit fabrication, measurement setup, and qubit performance are in Supplementary Notes 1–3, Supplementary Tables 1, 2, and Supplementary Figs. 1–3.
The measured T1 times of all devices are shown in Fig. 1c. Their relative distribution shows a clear statistical separation between the three deposition techniques. The sputtered niobium qubit consistently performs the best, followed by the HiPIMS optimized qubit, then the HiPIMS normal qubit. The average qubit relaxation times are displayed in Table 1 along with the standard deviation across the three rounds for each film. The measured relaxation times exhibit temporal fluctuations (Supplementary Fig. 3), which have been previously explained by coupling to near-resonant TLS10,11,13,14.
For the three films, we employ a wide range of characterization techniques to understand the possible microscopic origins of these coherence differences. All characterization was performed on films that underwent the same fabrication processes as the qubits, as detailed in Supplementary Note 1.
Surface oxides
The surface oxides on the three types of Nb films were investigated using a combination of soft and hard X-ray photoemission spectroscopy (PES) and resonant inelastic X-ray scattering (RIXS). The experimental details can be found in the Methods section. Figure 2a shows a representative spectrum of the spin-orbit-split Nb 3d3/2 and 3d5/2 core levels, measured on the sputtered film with an incident energy of 3330 eV. Also shown are the fits to distinct materials components. The PES spectra are best fit with five doublet components, revealing that there are four coexisting oxidation states besides Nb metal: NbOx (x < 1), NbO, NbO2, and Nb2O5, with respective shifts in binding energy of +0.5 eV, +1.8 eV, +3.8 eV, and +5.6 eV compared to Nb metal. The presence of five total oxidation states including Nb metal is consistent with previous PES studies33. Figure 2b shows the spectra measured on all three types of film at 3330 eV, revealing clear variations in the concentrations of different oxidation states among the different deposition techniques.
a Representative PES spectrum of the Nb 3d3/2 and 3d5/2 core levels, measured on the sputtered film for a photon energy (hν) of 3330 eV (black dots) and fit with five components. b Measured spectra for all three film types at 3330 eV, normalized to the intensity of the Nb2O5 component. For each film, the measured intensity of the Nb (c) and Nb2O5 (d) peaks are plotted at several photon energies. The sum of the signals from the different oxidation states in a given film is normalized to one, and the error bars show a 1% error, as estimated from the signal-to-noise of measured data. The intensity of Nb and Nb2O5 increase and decrease with energy, respectively, indicating the presence of a surface oxide layer.
PES measurements of the Nb 3d core levels were performed for seven values of the incident photon energy between 420 eV and 5000 eV. Since higher incident photon energies probe deeper into the film, this energy range resulted in surface sensitivity from the topmost monolayers down to a depth of ≈ 20 nm. The relative intensities of the signals from the five oxidation states were extracted for different photon energies, as shown for Nb metal and Nb2O5 in Fig. 2c and d, respectively. As expected, the Nb and Nb2O5 components respectively increase and decrease with increasing photon energy, which is consistent with the presence of a surface oxide layer. To reconstruct a depth profile of the concentrations of the oxides, we applied a maximum-entropy method algorithm, which obtains the most likely depth profile with minimal user input from the energy-dependent fits to the spectra. It has been commonly applied to angle-resolved PES34 and, more recently, to variable photon energy PES35,36 as in the present study.
The resulting depth profiles of the relative concentrations of the different oxidation states are shown in Fig. 3. For all three film types, we observe a surface oxide layer with Nb2O5 as the main constituent, followed by a transition layer of lower oxidation states whose thickness, depth distribution, and composition vary between the different films. The oxide/metal interface is sharpest for the sputtered film and is increasingly diffuse for the HiPIMS optimized and then the HiPIMS normal film. The HiPIMS optimized film shows some Nb2O5-NbO2 interdiffusion in the 2–6 nm range, as seen from the respectively decreasing and increasing profiles of Nb2O5 and NbO2, and it also shows a thicker NbOx layer than the sputtered film. The Nb2O5–NbO2 interdiffusion is strongest in the HiPIMS normal film, and the formation of NbO is also evident around 6 nm. Significantly, the NbOx penetrates most deeply in the HiPIMS normal film, extending beyond the 20 nm depth sensitivity allowed by this technique. The relative concentrations of the different Nb oxidation states, estimated by integrating over the 20 nm depth profiles and expressed in percents, are displayed in Table 1.
The profiles for the sputtered (a), HiPIMS optimized (b), and HiPIMS normal (c) Nb films were reconstructed from PES data using a maximum-entropy method algorithm. Each film shows a surface layer of a few nm of Nb2O5, a transition layer with varying concentrations of different suboxides, and the Nb metal bulk. In particular, the HiPIMS normal film shows significant concentrations of NbO and NbO2 in the transition layer and deeper penetration of NbOx into the metal.
RIXS is a complementary probe of the electronic structure that offers sensitivity to low-energy excitations of the electronic and lattice degrees of freedom (phonons)37. RIXS spectra were measured on all three films at room temperature and at a grazing incident angle of 10°, yielding a depth sensitivity of ≈ 10 nm. Measurements were performed at the oxygen K-edge (O-K), a band edge corresponding to excitations from the oxygen 1s core level into unoccupied valence states, thereby providing chemical sensitivity to the oxide layer. The spectra in Fig. 4a were collected for an incident photon energy tuned to the resonance of the O-K absorption, shown for the sputtered film in the inset. They are normalized in intensity to the area under the peak of the emission line (not shown), which spans the ≈3–11 eV energy loss range.
a RIXS measurements at the oxygen K-edge resonance for an incident energy of 531 eV. The inset shows the O-K absorption spectrum of the sputtered film with a vertical dashed line at the resonance. b Close-up view of the RIXS spectra after subtraction of the elastic line, with the phonon density of states (DOS) calculated for Nb2O5 from45. The overall scaling factor of the DOS was chosen to aid visualization. The DOS was reported to arise from both niobium and oxygen up to ≈70 meV, and mostly from oxygen at higher energies, as represented by the blue and pink bands, respectively. The lower intensity at higher energies for the HiPIMS films indicates a larger concentration of oxygen vacancies.
Figure 4b shows a close-up view of the low-energy features after removing the elastic peak, achieved by subtracting the negative-energy-loss tail mirrored about zero energy. The energy range and broad profile of the inelastic features are reminiscent of a multi-phonon shake-up process38,39, specifically phonons in the surface oxides, dictated by the use of the O-K-edge resonance at grazing incidence. The inelastic features are similar in energy and lineshape across the three films, with a slightly higher intensity in the 0.1–0.3 eV energy loss range for the sputtered film. These spectra are in stark contrast to the multiple vibrational modes extending up to ≈2 eV that would be expected from OH groups40, which indicates that there are no detectable hydrogen bonds in the surface oxides of these films. This finding, which is consistent with previous reports that the surface Nb oxide layer acts as a barrier against hydrogen diffusion41, is significant as hydrogen bonds in Al2O3 have been proposed as one of the primary sources of TLS resonant absorption in superconducting qubits42,43,44. This suggests that TLS from hydrogen bonds in particular are unlikely to be a dominant source of loss in our Nb films.
Figure 4b also shows the phonon density of states (DOS) of Nb2O5 calculated using density functional theory, taken from ref. 45. The main features of the DOS are consistent with the energy and relative intensities of the experimental peaks. Reference 45 showed that both niobium and oxygen vibrations contribute to the features below 70 meV (blue region), whereas the higher-energy phonons mostly arise from oxygen because of its smaller atomic mass (pink region). The two HiPIMS films show a lower intensity at higher energies, indicating a larger quantity of oxygen vacancies in the Nb2O5 layer. This lower intensity cannot be explained by a lower oxidation state, as the theoretical phonon DOS of suboxides have a stronger, and not weaker, relative intensity for the high-energy features compared with Nb2O5, as shown for NbO2 in ref. 46.
Structural and chemical imaging
In order to correlate our surface oxide spectroscopy findings with morphology and grain size, we performed transmission electron microscopy (TEM), spatially resolved electron-energy loss spectroscopy (EELS), and atomic force microscopy (AFM) measurements on all three types of Nb films. The results are summarized in Fig. 5. In panels (a)–(c), we present high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) images of film cross-sections at the surface. This measurement confirms the presence of a ≈ 5 nm thick oxide layer at the surface of all three films. The near-surface morphology of the HiPIMS normal film is visibly different, with the oxide layer conforming to smaller grains.
All measurements are shown for the sputtered, HiPIMS optimized, and HiPIMS normal films, respectively. Panels (a)–(c) show high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) measurements at cross-sections of the films' surfaces, revealing a ≈ 5 nm oxide layer and variations in grain size. Panels (d)–(f) show O-K-edge electron-energy loss spectroscopy (EELS) spectra measured at the locations indicated on the HAADF-STEM images. For the sputtered and HiPIMS optimized films, both the EELS spectra within a grain (left) and the spectra taken along a grain boundary (right) show a transition from a double peak (Nb2O5) to a single peak (suboxides) to a negligible peak (metal). However, for the HiPIMS normal film, EELS spectra along the grain boundary reveal similar oxidation peaks to the surface oxide layer, indicating that oxygen has diffused into the grain boundary to form oxides. Panels (g)–(i) show TEM bright-field images of cross-sections of the films' surfaces, where the white dotted lines delineate grain boundaries for the sputtered and HiPIMS optimized films, and the yellow arrow points to a gap at the grain boundary for the HiPIMS normal film. The grainy, light gray layer above the surface is platinum, which protects the surface during sample preparation. Panels (j)–(l) show atomic force microscopy (AFM) images measured over a 500 nm x 500 nm area. It is visually evident that the sputtered film grain size is the largest, and the HiPIMS normal film grain size is the smallest.
To characterize local chemical properties near the surface, we performed spatially resolved EELS. Panels (d)–(f) show O-K-edge EELS spectra that were measured at the locations indicated by colored dots on the HAADF-STEM images. In each EELS panel, the left plot shows chemical variation from the surface into the grain, and the right plot shows variation along grain boundaries. The main O-K-edge feature near 534 eV shows a transition from a clear double-peak lineshape near the surface to a single broad peak near the interface with Nb metal. Based on EELS spectra previously reported for different Nb reference oxides47, this indicates a change from Nb2O5 to lower oxidation states, in agreement with the PES measurements. For the sputtered and HiPIMS optimized films, spectra along grain boundaries (locations 8–10 and 6–8, respectively) do not reveal a stronger oxidation than in the Nb metal away from the grain boundaries (locations 4 and 5 in both films). However, for the HiPIMS normal film, the presence of the oxide in the boundary is clear, as seen from the stronger signal in locations 5–7 compared with location 4. These results are consistent with the overall picture from PES profiles shown in Fig. 3, which show significant oxygen diffusion for the HiPIMS normal films. By contrast, further TEM-EELS analysis reveals that for all films, the Nb/sapphire and Al/Nb interfaces are chemically sharp, with no oxides observed at grain boundaries (See Supplementary Figs. 4–6). This highlights the fact that, besides the grain size which is a bulk feature, the differences between the three film types are primarily concentrated around the Nb/air interface.
To further characterize grain boundaries near the film surface, bright-field TEM images that rely on a diffraction contrast from the transmitted beam were taken at cross-sections of each sample, as shown panels (g)-(i) of Fig. 5. Grain boundaries, indicated by white dotted lines for the sputtered and HiPIMS optimized films, are observed in each case. The grain structure observed using TEM appears to be largely columnar, with grains extending through the thickness of the films (see Supplementary Fig. 7). The HiPIMS normal film is distinguished by smaller grain sizes, and it exhibits a lower packing density with apparent gaps along some of the grain boundaries (yellow arrow). The EELS measurements suggest that these gaps host oxidized Nb near the film surface.
Further information about the grain morphology and size can be extracted from the complementary, top-down view provided by the AFM images shown in panels (j)-(l) of Fig. 5. First, it appears that the grains are elongated and not spherical. Second, the grain size decreases between the sputtered and HiPIMS optimized films, and even more significantly between the HiPIMS optimized and normal films. This observation is quantified by estimating the mean grain surface areas using a watershed algorithm48, as reported in Table 1. We also used AFM to measure short-range film roughness, which is found to be approximately 1 nm root mean square for all three films.
Auxiliary device measurements
Measured values of residual resistance ratio (RRR) for all three film types are displayed in Table 1. RRR is defined as the ratio between the values of the resistivity near room temperature and just above the superconducting critical temperature Tc. It is a measure of the temperature-independent residual resistance in a bulk film attributable to sample-specific defects. We specifically report RRR values as the ratio of measured resistivity between 295 K and 10 K. The sputtered film has the highest RRR, followed by HiPIMS optimized, and then HiPIMS normal. We also report measured Tc, which shows a similar trend.
In order to isolate the microwave loss from the Nb films from contributions from the aluminum-based Josephson junction, we fabricated a set of coplanar waveguide resonators for each Nb film type, as detailed in Supplementary Note 4 and Supplementary Table 3. Measurements of the internal quality factor (Qi) as a function of input microwave power qualitatively match the standard tunneling model describing TLS at weak fields (Supplementary Fig. 8)9,15,49,50. We place bounds on the TLS-induced loss tangent for the three types of film: the upper bound assumes that all low-power loss comes from TLS, and the lower bound assumes a non-TLS loss contribution at lower power which is equal to the maximum measured Qi (Supplementary Eqs. 2 and 3, respectively). While the bounds for the three film types have significant overlap, we find a rough agreement with the trend in qubit T1: the sputtered film resonators have the lowest upper bounds, and the HiPIMS normal resonators have the highest lower bounds (Supplementary Fig. 8). Additionally, we observe shifts in Qi over time, especially in the HiPIMS resonators, which we attribute to individual near-resonant TLS16. These findings are consistent with TLS being a relevant loss channel.
Discussion
We observe a clear correlation between qubit T1 and Nb film characteristics such as RRR, grain size, and suboxide concentration near the surface, as shown in Table 1. The total qubit relaxation rate is the sum of multiple mechanisms including microwave losses associated with the Nb films, the sapphire surface and bulk, and the aluminum-based Josephson junction, as well as other effects such as radiative losses. In the present study, the key constituents of the qubit devices are nominally identical, except for the Nb film regions. The correlations in Table 1 suggest that the properties of the Nb films dominate loss. We focus our discussion on relaxation mechanisms associated with the Nb films.
RRR has long been used as a gauge of the quality of Nb films for the construction of superconducting radiofrequency cavities51,52, capturing the impact of impurities, defects and other factors such as grain boundaries on the bulk resistivity. The impact of bulk resistivity and other, surface or intergranular oxide-specific mechanisms such as TLS, on microwave loss is determined by the field penetration into the film and can be described by an effective surface resistance [14]. Seminal studies of radiofrequency cavities with superconducting Nb walls have shown that residual surface resistance limits the cavity quality factor at low temperatures53,54,55,56,57. Our finding that RRR correlates with T1 suggests that residual resistance can also serve as a gauge for superconducting qubit performance. In the following, we discuss plausible mechanisms by which the observed materials properties, grain boundaries and suboxides, can lead to residual resistance, particularly TLS loss, and thus limit T1.
The correlation we observe between grain size, RRR, and Tc is consistent with a body of literature that links these quantities in polycrystalline Nb thin films58,59,60. The relationship between grain size and radiofrequency surface resistance in Nb films has been understood by describing grain boundaries as Josephson weak-links61,62. Under the assumption that the grain boundaries’ critical current and shunt resistance are independent of grain size, the surface resistance simply depends on grain boundary density61. This scaling is consistent with the observed grain size/RRR/T1 trend between films, pointing to grain boundary dissipation as a relevant relaxation mechanism. We expect that dissipation at grain boundaries is caused by structural defects (dislocations, vacancies, dangling, or extra bonds) and chemical defects (oxidation, impurities), both of which can contribute to TLS loss.9
In addition to grain size, grain boundary composition differs between the three film types. The HiPIMS normal film exhibits the lowest packing density, leading to significant grain boundary voids. These voids host sub-surface NbOx, which penetrates into the metal (Figs. 3 and 5). Since NbOx forms through the migration of interstitial oxygen defects resulting in local lattice distortions63,64, its presence in the grain boundaries can contribute to microwave absorption. By contrast, in the sputtered and HiPIMS optimized films, the NbOx penetrates only a few nanometers (Fig. 3), and no oxides are detectable in the grain boundaries with EELS (Fig. 5). This suggests relatively less impact on microwave absorption in these films. Overall, we expect an accumulation of structural and chemical defects along the grain boundaries, especially in the HiPIMS normal film, to create a fertile ground for tunneling material defects, which can potentially lead to TLS loss.
Another potential dissipation channel involves the quality of the intragrain surface oxide layer, which could also affect the density of TLS defects. A correlation between the thickness of the surface oxide layer and Qi of Nb resonators was recently reported65, which highlights the importance of microwave losses induced by surface oxides. Here, the Nb2O5 passivation layer is found to have the lowest concentration of oxygen vacancies and to be most homogeneous in the sputtered film (Figs. 4 and 3, respectively). The Nb2O5 layer is least homogeneous in the HiPIMS normal film, where NbO2 and NbO are observed at the interface with Nb. The presence of different oxidation states is expected to result in a more complex oxide-metal interface, where mismatches in crystalline parameters lead to increased strain and dislocation density. NbO itself is a source of defects, as it crystallizes in a naturally defective structure with a quarter of the Nb and O sites vacant. All of these defects (vacancies, dislocations, etc) have the potential to enhance TLS loss.9,23. Additionally, while NbO is a superconductor, NbO2 is not, further contributing to loss.
In Table 1, we report the sum of the relative concentrations of the suboxides NbOx, NbO, and NbO2, which exhibits a negative correlation with T1. This observation indicates that the total suboxide concentration could limit relaxation times in superconducting qubits, potentially through the introduction of TLS defects. We note that the difference between the T1 of the sputtered and HiPIMS optimized films may not be explained entirely by the small difference in suboxide concentration between these two films, but rather by a combination of the difference in suboxide concentration, grain size, and oxygen vacancy density in the Nb2O5 layer.
Thus far, we have identified potential materials-based defect sites for TLS-driven dielectric dissipation; next, we highlight markers of TLS loss in our device measurements. The power dependence of resonator quality factors matches the TLS model. Specifically, the plateauing of internal quality factor at low power suggests that the resonators are dominated by TLS loss at the single-photon level. Also, our observation of temporal fluctuations in both resonator quality factor and qubit T1 is consistent with the TLS mechanism10,11,13,14,16. The scaling of T1 fluctuations with relaxation time and the correlation to Nb film characteristics connects those fluctuations to TLS centers associated with the Nb pads. These results are consistent with the proposed relaxation mechanisms, namely that the grain boundaries and surface suboxides host defects which contribute to TLS loss in the qubits.
Conclusion
This study establishes a significant link between the performance of superconducting transmon qubits and the materials' properties of Nb films, a critical component in qubit fabrication. Our investigation exploits microscopic variations among Nb thin films, which were deposited using three sputtering techniques. Our experimental findings reveal correlations between qubit relaxation time and structural and chemical Nb film properties, specifically grain size, suboxide intergranular penetration, and suboxide intragrain concentration near the surface. Our combined analysis of microscopic materials properties and device performance further establishes RRR as a phenomenological proxy for the qubit lifetime in studies using polycrystalline superconducting films.
We anticipate that further improvements in relaxation times will arise from grain size optimizations in Nb deposition and from exploring the use of other superconductors with more chemically homogeneous surface oxide layers, such as tantalum66. More broadly, the connections between material properties and relaxation mechanisms uncovered in this work form a solid basis for physical models to guide the development of materials for superconducting qubits. Future multidisciplinary efforts can also leverage the multimodal spectroscopy and microscopy approach used here to make further progress toward identifying microscopic mechanisms for decoherence and engineering high-performance qubits.
Methods
Materials characterization
Synchrotron measurements were carried out at the National Synchrotron Light Source II (NSLS-II)67, in Brookhaven National Laboratory. Hard X-ray photoemission spectroscopy measurements were performed on beamline 7-ID-2 of the National Institute of Standards and Technology using a 400 mm diameter hemispherical electron-energy analyzer with a 300 μm slit, mounted at 90° with respect to the beam propagation, and operating at 200 eV pass energy. A double crystal monochromator was used for x-ray energy selection, with Si (111) crystals used for 2600 eV photon energy, and Si (220) crystals for all higher photon energies. Samples were mounted at a 10° x-ray incidence angle (80° takeoff angle).
Soft X-ray PES measurements were performed using the ambient pressure PES endstation at the 23-ID-2 (IOS). The samples were mounted on a sample holder by carbon tape and all measurements were performed in ultra-high vaccuum at room temperature. The endstation has a base pressure of 3 × 10−7 Pa and it is equipped with a SPECS PHOIBOS 150 NAP analyzer. The incidence angle of the X-ray beam and the photoemission angle were 50° and 20° from the sample normal, respectively. Survey spectra were measured at a photon energy of 1260 eV while Nb 3d spectra were measured at 420 eV and 1260 eV. All spectra were measured with a pass energy of 10 eV.
RIXS measurements were performed using the Soft Inelastic X-ray (SIX) 2-ID beamline68,69. Varied line spacing gratings with line spacings of 500 mm−1 and 1250 mm−1 were, respectively, used on the beamline and spectrometer which, coupled with a 20 μm exit slit, provided a combined resolution of 32 meV. The spectra were measured with σ-incident polarization, where the polarization is perpendicular to the scattering plane. The incident angle was set to 10° to enhance the surface contribution, and the scattering angle was set to 90°.
Transmission electron microscopy work (bright-field imaging, HAADF-STEM imaging, and STEM-EELS) was performed at the Center for Functional Nanomaterials (CFN) in Brookhaven National Laboratory using an FEI (Thermo-Fisher Scientific) Talos F200X at an accelerating voltage of 200 kV and Gatan Enfinium EELS. TEM samples were prepared with a focused ion beam method using FEI Helios NanoLab DualBeam, via the standard in-situ lift-out method.
Temperature dependence of the resistivity of the Nb films, from 295 K down to 4 K, was performed in a Janis (model ST-3T) micromanipulated probe station at the CFN. The pressure during measurement was kept in the low 10−4 Pa range. The Nb films had an approximate length and width of 7 mm and 3 mm, respectively. Contacts to the films were established with 25 μm Al wires in a 4-point-measurement configuration. Silver paint was used to expand the current leads across the width of the films to achieve homogeneous longitudinal current flow. Current-voltage curves, from which the resistance of the films was extracted, were measured with three Keithley source-meter units (model 2636A) as current sources (one for each Nb film) and a Keithley nanovoltmeter (model 2182A).
AFM measurements were performed at the CFN at room temperature using a commercial Park NX20-AFM instrument in tapping mode. Standard Si cantilevers with nominal resonant frequency of 330 kHz were used for scanning topography. The XEI software was used for image analysis.
Niobium deposition
Sputtered niobium
Niobium was deposited on 530 μm thick C-plane sapphire from CrysTec GmbH Kristalltechnologie. Prior to deposition, the sapphire was sonicated for 2 min each in toluene, acetone, methanol, and isopropanol, then rinsed in deionized water and blow-dried with nitrogen. The wafer was then loaded into an AJA hybrid deposition system, where it was heated to 350° C for 20 min, then cooled for 20 min. Sputter deposition was performed at a pressure of 1.1 Pa, a power setpoint of 300 W, and a shutter delay of 60 s after reaching full power. The deposition was run for 252 s, resulting in a film thickness of 185 nm.
HiPIMS Niobium
Niobium was deposited on 530 μm thick C-plane sapphire from CrysTec GmbH Kristalltechnologie. At Princeton University, the sapphire wafers were sonicated for 2 min each in toluene, acetone, methanol, and isopropanol, then rinsed in deionized water and blow-dried with nitrogen. Then, the substrates were sent to Angstrom Engineering for HiPIMS deposition of Nb. Detailed deposition parameters and photographs are presented in Supplementary Table 1 and Supplementary Fig. 1. The primary changes in deposition parameters between the normal and optimized processes were substrate geometry and peak current. We hypothesize that a face-on rather than a confocal substrate geometry and higher peak currents during the HiPIMS pulse lead to higher critical temperatures. These two alterations necessitated the other process changes. In particular, the fixture fabricated by Angstrom for the face-on geometry did not allow for substrate rotation. The deposited thicknesses were 182 nm and 135 nm for HiPIMS normal and HiPIMS optimized, respectively.
Data availability
The data that support the findings of this study are available from the corresponding authors upon request.
References
Kjaergaard, M. et al. Superconducting qubits: current state of play. Annu. Rev. Condens. Matter Phys. 11, 369–395 (2020).
Wang, C. et al. Surface participation and dielectric loss in superconducting qubits. Appl. Phys. Lett. 107, 162601 (2015).
Dial, O. et al. Bulk and surface loss in superconducting transmon qubits. Supercond. Sci. Technol. 29, 044001 (2016).
Gambetta, J. M. et al. Investigating surface loss effects in superconducting transmon qubits. IEEE Trans. Appl. Supercond. 27, 1–5 (2017).
Woods, W. et al. Determining interface dielectric losses in superconducting coplanar-waveguide resonators. Phys. Rev. Appl.12, 014012 (2019).
Calusine, G. et al. Analysis and mitigation of interface losses in trenched superconducting coplanar waveguide resonators. Appl. Phys. Lett. 112, 062601 (2018).
Nersisyan, A. et al. Manufacturing low dissipation superconducting quantum processors. In 2019 IEEE International Electron Devices Meeting (IEDM) 31.1.1–31.1.4.
Mcrae, C. R. H. et al. Dielectric loss extraction for superconducting microwave resonators. Appl. Phys. Lett. 116, 194003 (2020).
Muller, C., Cole, J. H. & Lisenfeld, J. Towards understanding two-level-systems in amorphous solids: Insights from quantum circuits. Rep. Prog. Phys. 82, 124501 (2019).
Burnett, J. J., Bylander, J., Bengtsson, A., Scigliuzzo, M. & Niepce, D. Decoherence benchmarking of superconducting qubits. npj Quantum Inform. 5, 1–8 (2019).
Schlör, S. et al. Correlating decoherence in transmon qubits: low frequency noise by single fluctuators. Phys. Rev. Lett. 123, 190502 (2019).
Barends, R. et al. Coherent Josephson qubit suitable for scalable quantum integrated circuits. Phys. Rev. Lett. 111, 080502 (2013).
Muller, C., Lisenfeld, J., Shnirman, A. & Poletto, S. Interacting two-level defects as sources of fluctuating high-frequency noise in superconducting circuits. Phys. Rev. B 92, 035442 (2015).
Klimov, P. V. et al. Fluctuations of energy-relaxation times in superconducting qubits. Phys. Rev. Lett. 121, 090502 (2018).
McRae, C. R. H. et al. Materials loss measurements using superconducting microwave resonators. Rev. Sci. Instrum. 91, 091101 (2020).
de Graaf, S. E. et al. Two-level systems in superconducting quantum devices due to trapped quasiparticles. Sci. Adv. 6, 51 (2020).
Oliver, W. D. & Welander, P. B. Materials in superconducting quantum bits. MRS Bulletin 38, 816–825 (2013).
Martinis, J. M. & Megrant, A. UCSB final report for the CSQ program: review of decoherence and materials physics for superconducting qubits. Preprint at http://arxiv.org/abs/1410.5793 (2014).
Lee, D., Dubois, J. & Lordi, V. Identification of the local sources of paramagnetic noise in superconducting qubit devices fabricated on α-Al2O3 substrates using density-functional calculations. Phys. Rev. Lett. 112, 017001 (2014).
Van Harlingen, D., Plourde, B., Robertson, T., Reichardt, P. & Clarke, J. In Quantum Computing and Quantum Bits in Mesoscopic Systems (eds Leggett, A. J., Ruggiero, B. & Silverstrini, P.) 171–184 (Springer, 2004). https://doi.org/10.1007/978-1-4419-9092-1_19.
Gao, J. et al. Experimental evidence for a surface distribution of two-level systems in superconducting lithographed microwave resonators. Appl. Phys. Lett. 92, 152505 (2008).
McDermott, R. Materials origins of decoherence in superconducting qubits. IEEE Trans. Appl. Supercond. 19, 2–13 (2009).
Paz, A., Lebedeva, I., Tokatly, I. & Rubio, A. Identification of structural motifs as tunneling two-level systems in amorphous alumina at low temperatures. Phys. Rev. B 90, 224202 (2014).
Koch, J. et al. Charge-insensitive qubit design derived from the Cooper pair box. Phys. Rev. A: At. Mol. Opt. Phys. 76, 1–19 (2007).
Arute, F. et al. Quantum supremacy using a programmable superconducting processor. Nature 574, 505–510 (2019).
Ma, R. et al. A dissipatively stabilized Mott insulator of photons. Nature 566, 51–57 (2019).
Mundada, P., Zhang, G., Hazard, T. & Houck, A. Suppression of qubit crosstalk in a tunable coupling superconducting circuit. Phys. Rev. Appl. 12, 054023 (2019).
Guo, Q., Cheng, C. & Sun, Z. et al. Observation of energy-resolved many-body localization. Nat. Phys. 17, 234–239 (2021).
Blais, A., Huang, R. S., Wallraff, A., Girvin, S. M. & Schoelkopf, R. J. Cavity quantum electrodynamics for superconducting electrical circuits: An architecture for quantum computation. Phys. Rev. A: At. Mol. Opt. Phys. 69, 1–14 (2004).
Alami, J. et al. High-power impulse magnetron sputtering of Ti–Si–C thin films from a Ti3SiC2 compound target. Thin Solid Films 515, 1731–1736 (2006).
Kouznetsov, V., Macak, K., Schneider, J. M., Helmersson, U. & Petrov, I. A novel pulsed magnetron sputter technique utilizing very high target power densities. Surf. Coat. Technol. 122, 290–293 (1999).
Souček, P. et al. Superhard nanocomposite nc-TiC/a-C:H coatings: the effect of HiPIMS on coating microstructure and mechanical properties. Surf. Coat. Technol. 311, 257–267 (2017).
Tian, H. et al. Surface studies of niobium chemically polished under conditions for superconducting radio frequency (SRF) cavity production. Appl. Surf. Sci. 253, 1236 (2008).
Chang, J. et al. Profiling nitrogen in ultrathin silicon oxynitrides with angle-resolved x-ray photoelectron spectroscopy. J. Appl. Phys. 87, 4449 (2000).
Weiland, C. et al. Nondestructive compositional depth profiling using variable-kinetic energy hard x-ray photoelectron spectroscopy and maximum entropy regularization. Surf. Interface Anal, 46, 407 (2014).
Weiland, C., Rumaiz, A. K., Pianetta, P. & Woicik, J. C. Recent applications of hard x-ray photoelectron spectroscopy. J. Vac. Sci. Technol. A 34, 030801 (2016).
Ament, L., van Veenendaal, M., Devereaux, T., Hill, J. & van der Brink, J. Resonant inelastic x-ray scattering studies of elementary excitations. Rev. Mod. Phys. 83, 705 (2011).
Bisogni, V. et al. Bimagnon studies in cuprates with resonant inelastic x-ray scattering at the O-K edge. I. Assessment on La2CuO4 and comparison with the excitation at Cu L3 and Cu K edges. Phys. Rev. B 85, 214527 (2012).
Lee, W. et al. Role of lattice coupling in establishing electronic and magnetic properties in quasi-one-dimensional cuprates. Phys. Rev. Lett. 110, 265502 (2013).
Ertan, E. et al. Theoretical simulations of oxygen K-edge resonant inelastic x-ray scattering of kaolinite. Phys. Rev. B 95, 144301 (2017).
de Graaf, S. et al. Hydrogen absorption and its effect on low- temperature electric properties of niobium. J. Appl. Phys. 51, 4460 (1980).
Jameson, J. et al. Dielectric relaxation study of hydrogen exposure as a source of two-level systems in Al2O3. J. Non-Crys. Solids 357, 2148 (2011).
Gordon, L., Abu-Farsakh, H., Janotti, A. & Van de Walle, C. G. Hydrogen bonds in Al2O3 as dissipative two-level systems in superconducting qubits. Sci. Rep. 4, 7590 (2015).
de Graaf, S. et al. Direct identification of dilute surface spins on Al2O3: Origin of flux noise in quantum circuits. Phys. Rev. Lett. 118, 057703 (2017).
Cheng, Z. et al. Diffuson-driven ultralow thermal conductivity in amorphous Nb2O5 thin films. Phys. Rev. Mater. 3, 025002 (2019).
O’Hara, A. & Demkov, A. A. Nature of the metal-insulator transition in NbO2. Phys. Rev. B 91, 094305 (2015).
Bach, D., Schneider, R., Gerthsen, D., Verbeeck, J. & W., S. EELS of niobium and stoichiometric niobium-oxide phases-part I: Plasmon and near-edges fine structure. Microsc. Microanal. 15, 505 (2009).
Rabbani, A. & Ayatollahi, S. Comparing three image processing algorithms to estimate the grain-size distribution of porous rocks from binary 2D images and sensitivity analysis of the grain overlapping degree. Spec. Top. Rev. Porous Media—Int. J. 6, 71–89 (2015).
Phillips, W. A. Two-level states in glasses. Rep. Prog. Phys. 50, 1657 (1987).
Wang, H. et al. Improving the coherence time of superconducting coplanar resonators. Appl. Phys. Lett. 95, 233508 (2009).
Russo, R., Catani, L., Cianchi, A., Tazzari, S. & Langner, J. High quality superconducting niobium films produced by an ultra-high vacuum cathodic arc. Supercond. Sci. Technol. 18, L41–L44 (2005).
Valderrama, E. et al. High-RRR thin-films of Nb produced using energetic condensation from a coaxial, rotating vacuum arc plasma. AIP Conf. Proc. 1434, 953 (2012).
Turneaure, J. & Weissman, I. Microwave surface resistance of superconducting niobium. J. Appl. Phys. 39, 4417–4427 (1968).
Broom, R. & Wolf, P. Q factor and resonance amplitude of Josephson tunnel junctions. Phys. Rev. B 16, 3100–3107 (1977).
Halbritter, J. Surface residual resistance of high-Q-superconducting resonators. J. Appl. Phys. 42, 82–87 (1971).
Schmüser, P. Superconductivity in high energy particle accelerators. Prog. Part. Nucl. Phys. 49, 155–244 (2002).
Romanenko, A. & Schuster, D. Understanding quality factor degradation in superconducting niobium cavities at low microwave field amplitudes. Phys. Rev. Lett. 119, 264801 (2017).
Bose, S., Raychaudhuri, P., Banerjee, R., Vasa, P. & Ayyub, P. Mechanism of the size dependence of the superconducting transition of nanostructured Nb. Phys. Rev. Lett. 95, 147003 (2005).
Bose, S. et al. Size induced metal-insulator transition in nanostructured niobium thin films: intra-granular and inter-granular contributions. J. Phys.: Condens. Matter 18, 4553–4566 (2006).
Bose, S., Raychaudhuri, P., Banerjee, R. & Ayyub, P. Upper critical field in nanostructured Nb: competing effects of the reduction in density of states and the mean free path. Phys. Rev. B 74, 224502 (2006).
Bonin, B. & Safa, H. Power dissipation at high fields in granular RF superconductivity. Supercond. Sci. Technol. 4, 257–261 (1991).
Attanasio, C., Maritato, L. & Vaglio, R. Residual surface resistance of polycrystalline superconductors. Phys. Rev. B 43, 6128–6131 (1991).
Dosch, H., Schwerin, A. & Peisl, J. Point-defect-induced nucleation of the ω phase. Phys. Rev. B 34, 1654 (1986).
Delheusy, M. et al. X-ray investigation of subsurface interstitial oxygen at Nb/oxide interfaces. Appl. Phys. Lett. 92, 101911 (2008).
Verjauw, J. et al. Investigation of microwave loss induced by oxide regrowth in high-Q Nb resonators. Preprint at https://arxiv.org/abs/2012.10761 (2020).
Place, A. et al. New material platform for superconducting transmon qubits with coherence times exceeding 0.3 milliseconds. Nat. Commun. 12, 1779 (2021).
Hill, J. et al. Future trends in synchrotron science at NSLS-II. J. Phys. Cond. Matter 32, 374008 (2020).
Dvorak, J., Jarrige, I., Biosgni, V., Coburn, S. & Leonhardt, W. Towards 10 meV resolution: the design of an ultrahigh resolution soft X-ray RIXS spectrometer. Rev. Sci. Instrum. 87, 115109 (2016).
Jarrige, I., Bisogni, V., Zhu, Y., Leonhardt, W. & Dvorak, J. Paving the way to ultra-high-resolution resonant inelastic x-ray scattering with the SIX beamline at NSLS-II. Synch. Rad. News 31, 7 (2018).
Acknowledgements
This research used the SST-2, IOS, and SIX beamlines of the National Synchrotron Light Source II, and the electron microscopy facilities of the Center for Functional Nanomaterials, U.S. Department of Energy (DOE) Office of Science User Facilities operated for the DOE Office of Science by Brookhaven National Laboratory under Contract No. DE-SC0012704. Qubits were fabricated in the Princeton Institute for the Science and Technology of Materials (PRISM) cleanroom and the Quantum Device Nanofabrication Laboratory at Princeton University. A.P. acknowledges the National Science Foundation Graduate Research Fellowship, B.J. acknowledges the Humboldt Foundation, A.P.M.P. acknowledges the National Defense Science and Engineering Graduate Fellowship, and all Princeton authors acknowledge the Materials Research Science and Engineering Center (MRSEC) Grant No. DMR-1420541 and the Army Research Office Grant No. W911NF-1910016. Certain commercial equipment, instruments, or materials are identified in this paper in order to specify the experimental procedure adequately, and do not represent an endorsement by the National Institute of Standards and Technology.
Author information
Authors and Affiliations
Contributions
I.J. and A.A.H. designed research, A.P., C.W., S.H., I.J., B.J., A.P.M.P., I.W., A.H., V.B., J.P., A.B., M.M., P.R., F.C., K.K., X.T. performed research, A.P., C.W., S.H., I.J., M.H. analyzed data, M.H. advised, A.P., I.J., M.H. wrote the main text of the manuscript. All authors reviewed the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Communications Materials thanks the anonymous reviewers for their contribution to the peer review of this work. Primary Handling Editor: Aldo Isidori.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Premkumar, A., Weiland, C., Hwang, S. et al. Microscopic relaxation channels in materials for superconducting qubits. Commun Mater 2, 72 (2021). https://doi.org/10.1038/s43246-021-00174-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43246-021-00174-7
This article is cited by
-
High-quality superconducting α-Ta film sputtered on the heated silicon substrate
Scientific Reports (2023)
-
A Review of Developments in Superconducting Quantum Processors
Journal of the Indian Institute of Science (2023)
-
Towards practical quantum computers: transmon qubit with a lifetime approaching 0.5 milliseconds
npj Quantum Information (2022)