Introduction

Superconducting qubits are a leading platform for quantum computing1,2. This has been driven, in part, by improvements in coherence times over five orders of magnitude since the realization of coherent dynamics in a Cooper-pair box3. However, further improving coherence times remains crucial for enhancing the scope of noisy superconducting quantum processors as well as the long-term challenge of building a fault tolerant quantum computer. Recent advances4,5,6,7 in two-qubit gate control have placed their fidelities at the cusp of their coherence limit, implying that improvements in coherence could directly drive gate fidelities past the fault tolerant threshold. In this context, coherence stability and its impact on multi-qubit device performance is also an important theme, since superconducting qubits have been shown to display large and correlated temporal fluctuations (i.e., 1/fα) in their energy relaxation times T18,9,10,11,12,13,14. This places additional challenges for benchmarking the coherence properties of these devices13, and also for error mitigation strategies such as zero noise extrapolation12.

The fluctuations of qubit T1 are often attributed to resonant couplings with two-level systems (TLSs) that have been historically studied in the context of amorphous solids15,16 and their low temperature properties. More recently, TLSs have attracted renewed interest due to their effect on the coherence properties of superconducting quantum circuits11,13,14,17,18,19,20, and are attributed to defects in amorphous materials at surfaces, interfaces, and the Josephson junction tunnel barrier. Frequency resolved measurements of T1 in flux and stress tunable devices11,19,20,21 have also displayed fluctuations, suggesting an environment of TLSs with varying coupling strengths around the qubit frequency. The variability of T1 over time is explained11,16, at least in part, by temporal fluctuations in this frequency environment, associated with the spectral diffusion of the TLSs15,22.

Furthermore, two-qubit gates that involve frequency excursions5,11,23 can also interact with TLSs near the qubit frequency leading to additional incoherent error. The fluctuations in TLS peak positions, therefore, can also introduce fluctuations in two-qubit fidelity. Spectroscopy of defect TLS is, therefore, central to understanding the short and long time T1 and gate fidelity of qubits.

Single Josephson junction transmons with fixed frequency couplings represent a successful device architecture achieving networks of over 60 qubits1 with all microwave control and state of the art device coherence. The single junction configuration offers advantages such as reduced sensitivity to flux noise, while preserving the transmon charge insensitivity and also reducing system complexity with fewer control inputs. However, there is little TLS spectroscopy of single junction transmons because of the limited tunability, despite the central importance of understanding the TLS environment both for device and process characterization.

In this work, we introduce an all-microwave technique for the fast spectroscopy of TLSs in single junction transmon qubits that requires no additional hardware resources. In contrast to flux-based approaches to TLS spectroscopy, we employ off-resonant microwave tones to drive AC-Stark shifts of the fundamental qubit transition and spectrally resolve qubit relaxation times. Dips in relaxation times serve as a probe of the frequency location of a strongly coupled TLS. We use repeated frequency sweeps to probe the time dynamics of the relaxation probabilities including tracking the spectral diffusion of strongly coupled TLS. Across 10 qubits, we observe strong correlations between the long time mean, averaged over several months \({\langle {T}_{1}\rangle }_{T}\), and the short time mean, averaged around the local qubit frequency \({\langle {T}_{1}\rangle }_{\omega ,t}\).

This strong correlation suggests a quasi-ergodic behavior of the TLS spectral diffusion in the nearby frequency neighborhood of the qubit. In contrast, there is lower correlation between \({\langle {T}_{1}\rangle }_{T}\) and T1 measured over a single day. The \({\langle {T}_{1}\rangle }_{\omega ,t}\) can provide, therefore, a more rapid estimate of long-time behavior.

Results

Device and spectroscopy technique

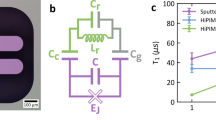
The experiments reported in this letter were performed on ibmq_almaden, a 20 qubit processor based off single junction transmons and fixed couplings. The device topology is shown in Fig. 1a, and qubit frequencies are around ~5 GHz. Figure 1b depicts the characteristic spread of the qubit T1s and their mean, from ~250 measurements over 9 months. The base plate (to which the device was mounted) temperature of the dilution refrigerator was typically ~13 mK excepting several temperature excursions to ~1 K, which were not observed to have any significant effects on the long time T1 time series or distributions of T1 values discussed in this work, discussed later. Several qubits on the device display mean T1s exceeding 100 μs. However, the large spread in individual qubit T1s highlights the challenge for rapid benchmarking of device coherence, since any single T1 measurement can disagree substantially from its long-time mean.

Fig. 1: Device map and T1s.
figure 1

a Map of a 20 qubit device including the qubit number, two-qubit connectivity, and the qubit frequency in (GHz). b Box and whisker plot of T1’s measured daily.

Full size image

We study the spectral dynamics of these T1 times by employing off-resonant microwave tones24 to induce an effective frequency shift Δωq in single junction transmons by the AC Stark effect. This has been employed previously for coherent state transfer between coupled qubits that are Stark shifted into resonance25. In this work, shifting the qubit frequency into resonance with a defect TLS induces a faster relaxation time, which in turn is used to detect the frequency location of the TLS26, as depicted in Fig. 2a. The Stark shift can be described analytically by a Duffing oscillator model27,28

$${{\Delta }}{\omega }_{q}=\frac{{\delta }_{q}{{{\Omega }}}_{s}^{2}}{2{{{\Delta }}}_{qs}({\delta }_{q}+{{{\Delta }}}_{qs})}$$
(1)

where δq is the qubit anharmonicity, Ωs is the drive amplitude and Δqs = ωq − ωs is the detuning between the qubit frequency and the Stark tone.

Fig. 2: Stark tone implementation.
figure 2

a Schematic of qubit T1 response to shift in qubit frequency (red traces), at different times, t. The qubit frequency is tuned by an amount Δωq by an off-resonant tone placed ∣Δqs∣ above the qubit frequency ωq. The dependence of the frequency shift on the off-resonant tone amplitude Ωs is depicted by the blue trace. The T1 dips are indicative of the qubit coming into resonance with a strongly coupled TLS, at the frequency ωTLS. The TLS frequency shifts in time due to spectral diffusion, schematically indicated by changes in the T1 dips at different time snapshots. b Schematic of a Ramsey pulse sequence used to calibrate Δωq as a function of Ωs (top); and (bottom) schematic pulse sequence for the relaxation time spectroscopy. For each Ωs (i.e., Δωq), the \(\left|1\right\rangle\) occupation is measured at a fixed time (i.e., τ = 50 μs in this work). c An illustrative case of the 01 transition dependence on ωs for constant Ωs. The 01 qubit frequency, ωq + Δωq, uses an unperturbed frequency of ωq = 5.0 GHz and an anharmonicity of δq = −340 MHz. The locations of the unperturbed 01 and 12 transitions are shown as vertical lines overlaid with 5 MHz offsets to make their locations more visible on the figure. Negative and positive qubit shifts can be produced and large shifts can be induced depending on Δqs. d Measured Δωq as a function of normalized DAC amplitude, Ωs using the AC Stark shifted Ramsey technique. Solid line is a quadratic fit functionally consistent with a perturbative model.

Full size image

As seen from the expression above, the magnitude and sign of the Stark shift can be manipulated by the detuning and the drive amplitude of the Stark tone, Fig. 2c. Very large frequency shifts can be obtained by driving close to the transmon transitions, but this typically leads to undesired excitations/leakage out the two-state manifold. In this work, we obtain Stark shifts of 10’s of MHz, with modest drive amplitudes and a fixed detuning Δqs of ±50 MHz. The frequency shifts are experimentally measured using a modified Ramsey sequence29, schematically shown in Fig. 2b, and display good agreement with the quadratic dependence of the perturbative model in the low-drive limit. A representative case is shown in Fig. 2d.

We focus on the spectrally resolved T1 measurements in Fig. 3 that we use as a probe of defect TLS transition frequencies. However, instead of measuring the entire T1 decay, we use the excited state probability, P1, after a fixed delay time as a measure of T1. This speeds up the spectral scans significantly. Our experiments are performed at a repetition rate of 1 kHz, but our scheme can be further accelerated with reset techniques30, which can be crucial for probing faster TLS dynamics. For an effective frequency sweep, we run an amplitude sweep with off-resonant pulses at fixed detuning (±50 MHz) and duration (delay time of 50 μs), after exciting the qubit with an initial π pulse. The pulsed Stark sequence enables faster spectroscopy by circumventing the need to re-calibrate the π, π/2 pulses at every frequency. The off-resonant pulses have Gaussian-square envelopes with a 2σ rise-fall profile, where σ = 10 ns. This pulse sequence is shown in Fig. 2b. The amplitude points in the sweep are then related to Stark shifts by Ramsey sequences. Figure 3 shows representative data of such a sweep on qubit 19 (Q19) with distinctive dips in P1 that we attribute to strongly coupled TLS at their transition frequencies. T1 measurements at Stark tone amplitudes corresponding to high/low P1 points, as seen in the bottom panel of Fig. 3, explicitly show the substantial variation in T1 as a function of frequency and the consistent tracking of T1 with P1.

Fig. 3: Representative example of relaxation time dependence on frequency.
figure 3

a Measured probability of being in the \(\left|1\right\rangle\) state, P1, at 50 μs wait time with varying Δωq and tone detuned 50 MHz above ωq/2π for Q19. b Example of Ramsey measurements used to extract frequency shifts Δωq/2π from pulse amplitudes. The two curves result from starting the Ramsey oscillations with a Xπ/2 or Yπ/2. c and d are T1 measurement with Stark shifts Δωq/2π = −18.9 and −5.3 MHz, respectively. e T1 measurement with no Stark shift (i.e., no Stark tone).

Full size image

Variations in P1 can potentially be caused by sources other than TLS. In our experiments, P1 is spectrally resolved to ~± 25 MHz around the individual qubit frequencies. The narrow frequency range combined with measuring non-neighbor sets of qubits simultaneously avoids strong P1 suppression from resonances with neighboring qubits, the coupling bus or common low-Q parasitic microwave modes. Control experiments show that time insensitive features in the P1 fingerprint are robust to choice of the Stark tone detuning, ruling out a power dependence for the power range used in this work. Finally, while a recent report31 modeled their broadband T1 scatter as arising from quasi-particle fluctuations, this is not sufficient to explain the sharp frequency-dependent P1 features depicted, for instance in Fig. 3. Furthermore, recent experiments on our qubits suggest a quasi-particle limit to T1 that exceeds several milliseconds32.

TLS dynamics and correlations of P 1(ω, t) and 〈T 1〉T

We repeat the line traces of Fig. 3 for both positive and negative 50 MHz detuning, approximately once every 3–4 h, extended over hundreds of hours for all the qubits. A representative example of the cumulative scans is shown in Fig. 4 for Q15. Spectroscopy of the other qubits is shown in the supplemental information S1. The TLS dynamics around the qubit frequency are qualitatively similar to previous TLS spectroscopy using flux or stress tunable devices16.

Fig. 4: Time dependence of energy relaxation spectroscopy.
figure 4

Time dependence of the energy relaxation spectroscopy for Q15 using Δωs = ± 50 MHz and varying Ωs over 501 different j amplitude points, Ωs,j, to sweep Δωq(Ωs,j) in a positive or negative direction (see Eqn. (1)). The P1 is measured at 50 μs.

Full size image

In the case of Q15, Fig. 4, there are prominent dips in relaxation probability around positive 1 MHz, negative 5–10 MHz, and negative 15–20 MHz. The spectral diffusion of the positions of the T1 dips can vary between order of 1 to 10 MHz over the 272 h of measurement providing a qualitative measure of linewidths. A more quantitative discussion of linewidths can be found in supplemental information S2. The background is covered by an ensemble of smaller dips of relaxation, Fig. 3, that also dynamically evolve, with features that are larger than the sampling noise in the measurement.

As discussed previously, T1 fluctuations introduce uncertainty in the coherence benchmarking, stability of multi-qubit circuit performance and process optimization of superconducting qubit devices. In this context of better estimator, we examine if the long-time averages (T ~ 9 months) \({\langle {T}_{1}\rangle }_{T}\) and \({\langle {P}_{1}\rangle }_{T}\) are correlated with the frequency neighborhood of the qubit \({\langle {T}_{1}\rangle }_{\omega ,t}\) and \({\langle {P}_{1}\rangle }_{\omega ,t}\), respectively. The averaged relaxation probabilities and T1s are defined as

$${\langle {P}_{1}\rangle }_{T}=\frac{1}{N}\mathop{\sum }\limits_{i=1}^{N}{P}_{1}({\omega }_{q},\tau ,{T}_{i})$$
(2)
$${\langle {T}_{1}\rangle }_{T}=\frac{1}{N}\mathop{\sum }\limits_{i=1}^{N}{T}_{1}({\omega }_{q},{T}_{i})$$
(3)
$${\langle {P}_{1}\rangle }_{\omega ,t}=\frac{1}{n}\mathop{\sum }\limits_{i=1}^{n}\frac{1}{2{{\Delta }}\omega }\mathop{\sum }\limits_{{\omega }_{j}=-{{\Delta }}\omega }^{{{\Delta }}\omega }{P}_{1}({\omega }_{q}+{\omega }_{j},\tau ,{t}_{i})d{\omega }_{j},$$
(4)
$${\langle {T}_{1}\rangle }_{\omega ,t}=\frac{1}{n}\mathop{\sum }\limits_{i=1}^{n}\frac{1}{2{{\Delta }}\omega }\mathop{\sum }\limits_{-{{\Delta }}\omega }^{{{\Delta }}\omega }\frac{-\tau }{\ln ({P}_{1}({\omega }_{q}+{\omega }_{j},\tau ,{t}_{i})d{\omega }_{j})},$$
(5)

where definitions of variables can be found in Table 1.

Table 1 List of symbols.
Full size table

We compare \({\langle {P}_{1}\rangle }_{\omega ,t}\) to \({\langle {P}_{1}\rangle }_{T}\) from the daily T1 measurements over \({T}_{\max } \sim\) 9 months evaluated at τ = 53 μs, shown in Fig. 1. The \({\langle {P}_{1}\rangle }_{\omega ,t}\) are calculated for a T1 delay time of τ = 50 μs for 10 qubits in the device for the first time slice and a cutoff frequency Δω/2π = 5 MHz. A qualitatively close agreement for all 10 qubits is observed, see Fig. 5a.

Fig. 5: Correlation between different T1 estimators.
figure 5

a Comparison of \({\langle {P}_{1}\rangle }_{\omega ,t}\) at 50 μs and \({\langle {P}_{1}\rangle }_{T}\) averaged for ~9 months and evaluated at a τ of 53 μs decay time. \({\langle {P}_{1}\rangle }_{\omega ,t}\), is averaged over Δω/2π = 5 MHz after a single measurement that took ~ 20 min. (inset) A scatter plot using \({\langle {T}_{1}\rangle }_{T}\)’s averaged over 9 months of measurement as the dependent variable and \({\langle {T}_{1}\rangle }_{\omega ,t}\) or T1s from a single day. The line is a guide to the eye showing a 1:1 correlation. b The Pearson R dependence on time averaging of the T1’s of the odd numbered qubits up to time, T, for three cases: (i) the entire time series (dash), (ii) the time series between temperature excursion B and D (dash-dot), lettered locations indicated in the inset, and (iii) the time series between C and D for which no temperature excursions were recorded (solid). The intermediate time series are shifted in time index to compare more directly at short times with the full-time series. The differences in R are within the standard deviation calculated for sampling T1 time series with a Gaussian-distributed range of values, see supplemental information S4. (inset) The T1 (black, left) and mixing chamber temperature (blue, right) time series for Q13. Spacing of measurements is non-uniform. The minimum spacing is ~ 24 h apart. Each temperature excursion is labeled with a letter. c Pearson correlation, R, dependence on time slice averaging and frequency range, Δω, of the odd numbered qubits.

Full size image

A \({\langle {T}_{1}\rangle }_{\omega ,t}\) can also be estimated for each \({\langle {P}_{1}\rangle }_{\omega ,t}\) at τ = 50 μs by assuming an exponential decay. The approximate equivalence of \({\langle {T}_{1}\rangle }_{\omega ,t}\) and \({\langle {T}_{1}\rangle }_{T}\) is seen in the scatter plot of Fig. 5a inset. A near 1:1 relationship is observed when this approach is applied more broadly across many IBM devices, see supplemental information S3. Furthermore, the poorer correlation between \({\langle {T}_{1}\rangle }_{T}\) and a single instance of T1 measurements, is also shown by larger scatter, as seen in Fig. 5a inset.

To quantify with a single value the correlation between \({\langle {T}_{1}\rangle }_{T}\) or \({\langle {P}_{1}\rangle }_{T}\) and their estimators for many qubits, we use a Pearson R measure across the ten odd-labeled qubits,

$$R=\frac{\mathop{\sum }\limits_{k=0}^{d-1}({\langle X\rangle }_{T,{Q}_{i}}-\overline{{\langle X\rangle }_{T}})({\langle X\rangle }_{\omega ,t,{Q}_{i}}-{\overline{\langle X\rangle }}_{\omega ,t})}{\sqrt{\mathop{\sum }\limits_{k=0}^{d-1}{({\langle X\rangle }_{T,{Q}_{k}}-\overline{{\langle X\rangle }_{T}})}^{2}\mathop{\sum }\limits_{k=0}^{d-1}{({\langle X\rangle }_{\omega ,t,{Q}_{i}}-{\overline{\langle X\rangle }}_{\omega ,t})}^{2}}}$$
(6)

where d is the number of qubits in the device or analysis, 10 in this case, and X is the observable P1 or T1. The Pearson correlation is a normalized covariance between two variables reflecting a linear correlation from 1 to −1, where R = 1 (−1) represents a 100% positive (negative) correlation and R = 0 indicates no correlation. Strong R correlation can therefore signal the existence of a potential linear mapping between the estimator and \({\langle {T}_{1}\rangle }_{T}\), in particular, possibly one that is 1:1 or a scaling factor that will reliably estimate \({\langle {T}_{1}\rangle }_{T}\).

For a single frequency sweep that takes ~20 min, we obtain 0.76 < R(ti) < 0.84 correlation between \({\langle {T}_{1}\rangle }_{T}\) and \({\langle {T}_{1}\rangle }_{\omega ,t}\) for 0.5 MHz < Δω < 5 MHz. Using the P1 values without assuming an exponential dependence leads to stronger correlations of 0.87 < R(ti) < 0.91. Both of these are substantially stronger than the correlation found between the representative instance of T1 and \({\langle {T}_{1}\rangle }_{T}\), which was R = 0.29. We note this instance of R can have a large spread, as seen by simulations of Gaussian-distributed fluctuations in supplemental information S4.

A better estimate of the \({\langle {T}_{1}\rangle }_{T}\) for each qubit, Qk, in the device can be obtained from a moving average of multiple, N, measurements. We show the evolution of \({\langle R\rangle }_{{T}_{0\to N}}\) using a moving average of the T1(Ti) measurements, \({\langle {T}_{1}\rangle }_{{T}_{0\to N}}\), for each qubit, Fig. 5b. The \({\langle R\rangle }_{{T}_{0\to N}}\) exceeds R ~ 0.8 (i.e., strong correlation) after ~10 measurements, corresponding to a time exceeding 100 h. Approximately 10 independent measurements is sufficient for fluctuations with magnitude \(\sim 0.2{\langle {T}_{1}\rangle }_{T}\) to obtain a strong correlation, R ~ 0.8, between an estimator (e.g., \({\langle {T}_{1}\rangle }_{{T}_{0}\to N}\)) and \({\langle {T}_{1}\rangle }_{T}\). The details of R dependence on fluctuation magnitude and number of measurements in the moving average are discussed more completely in supplemental information S4.

Autocorrelation between T1(Ti) and T1(Ti−1) measurements is an underlying challenge to fast estimation of \({\langle {T}_{1}\rangle }_{T}\). Evidence of autocorrelation can be seen for example in long-term drifts in the average and short-term correlations between T1, inset of Fig. 5b. On shorter time scales, our experimental data shows evidence of stronger autocorrelation frustrating faster accurate estimation of \({\langle {T}_{1}\rangle }_{T}\) and that the fastest R ~ 0.8 can be obtained on order of 1–2 days, see supplemental information S5 and S6. We conclude that \({\langle {T}_{1}\rangle }_{\omega ,t}\) shows promise as a method for faster estimation of \({\langle {T}_{1}\rangle }_{T}\) than repeated T1(ω = ωq) measurements at only the qubit frequency. Extending the \({\langle {T}_{1}\rangle }_{\omega ,t}\) estimator to a set of many qubits, {Qk}, in a device result in larger R, in the same time, compared to relying only on T1(ωq) measurements for each qubit. The R value simply being a quantitative single value expression of the high correlation between each \({\langle {T}_{1}\rangle }_{\omega ,t}\) and \({\langle {T}_{1}\rangle }_{T}\) across the entire set of qubits.

It is important to note that our calculations of \({\langle {T}_{1}\rangle }_{\omega ,t}\) employ an equal weighting of P1 associated with every frequency bin and the same choice of Δω for every qubit. However, it is not a priori clear that equal weighting is a representative choice over the Δω range. For example, how evenly does the spectral diffusion of each TLS contribute to the T1 of the qubit? The strong correlation of \({\langle {T}_{1}\rangle }_{\omega ,t}\) with \({\langle {T}_{1}\rangle }_{T}\) with equal weighting suggests that an ergodic-like sampling of the TLSs near the qubit frequency is a reasonable first approximation. The ergodic behavior of the T1 estimators is examined more completely in supplemental information S7 and supplemental information S8. Central to the question of assigning a T1 estimate to any qubit, we observe that \({\langle {T}_{1}\rangle }_{T}\) behaves ergodically for all the qubits despite short-term 1/fα correlated behavior (i.e., a constant mean \({\langle {T}_{1}\rangle }_{T}\) can be identified). Assignment of any T1 estimate could alternatively be made impossible in the presence of drift, which is not observed in these qubits, see supplemental information S9 and supplemental information S7 for further details about weak stationarity and ergodicity. Furthermore, the strong correlation of \({\langle {T}_{1}\rangle }_{T}\) to \({\langle {T}_{1}\rangle }_{\omega ,t}\) using only the P1(ω, τ, t) spectrum around the qubit is consistent with a leading hypothesis that the \({\langle {T}_{1}\rangle }_{T}\) is dominated by TLS behavior rather than other stochastic or static contributions.

Correlation dependence on frequency and measurement time

A natural question about the estimator \({\langle {T}_{1}\rangle }_{\omega ,t}\) is, what are the optimal parameter choices for frequency range Δω, n autocorrelated samples and the spacing in time, Δt = ti − ti−1, to obtain sufficiently weakly autocorrelated measurements and a fast, accurate measure of \({\langle {T}_{1}\rangle }_{T}\). Since the optimum choices are presently not known a priori, we evaluate and plot \({\langle R\rangle }_{{t}_{0\to n}}\) versus Δω and ti in Fig. 5c to guide future application of this approach. Equal frequency bin weighting of P1 is used. While this order of magnitude choice of Δω produces a reasonably good first approximation for correlation across the entire range, the plot displays several unexplained features (e.g., non-monotonic dependence on Δω) indicating the unsurprising insufficiency of these two globally applied parameters (i.e., Δω and t) alone to weight the frequency contribution of all the qubits and approach R ~ 1. Additional sensitivity analysis in supplemental information S8 also examines correlation between frequencies and highlights that individual qubits have different sensitivity to the range sampled, Δω. We see that a wide span of Δω produces high \({\langle R\rangle }_{{t}_{0\to n}}\), comparable or better than R(Ti) from a single T1(ωq) measurement. We further show that not only is there a strong R correlation (e.g., linear dependence) but that \({\langle {T}_{1}\rangle }_{\omega ,t}\) approaches 1:1 quantitative agreement with \({\langle {T}_{1}\rangle }_{T}\). The degree to which a T1 estimator, from sampling the nearby frequency space, is quasi-ergodic and would converge to 1:1 agreement is addressed in much more detail in supplemental information S8 and supplemental information S3.

Discussion

Implications for process characterization

The strong correlation between \({\langle {T}_{1}\rangle }_{\omega ,t}\) and \({\langle {T}_{1}\rangle }_{T}\) suggests that long-time T1 averages might be estimated relatively rapidly using spectroscopy. This is in contrast to overcoming correlation times in T1 at a single ωq to obtain a representative \({\langle {T}_{1}\rangle }_{T}\) for the qubit.

Identification of better choices of Δω and n in this study were made with pre-knowledge of what \({\langle {T}_{1}\rangle }_{T}\) was. These parameters will have to be chosen without this pre-characterization for future implementation of this method. Encouragingly, the R dependence on both these parameters appears to be relatively weak suggesting that a heuristic choice for a single Δω and n might be sufficient to obtain useful estimates (i.e., R > 0.8) of \({\langle {T}_{1}\rangle }_{T}\) for new processes when using this simple equal weighting approach until improved choices can be formulated (i.e., different frequency spans for each qubit and or weighted averaging over frequency).

More specifically we observe that \({{{\mathcal{O}}}}\)(10) independent measurements is sufficient to obtain an R ~ 0.8 or higher, see supplemental information S4. We conjecture that one can obtain 10 approximately independent samples, S, in a single scan by sampling at frequency spacings, χ, that are greater than the autocorrelation frequency width (i.e., a frequency spacing where correlation drops below ~ 0.2). In this work, we found the correlation to become weak for \({{{\mathcal{O}}}}\)(1 MHz), see supplemental information S8. Then by this heuristic, a single spectroscopy scan would require a Δω = \(\frac{(S-1)}{2}\chi\), where S = 10 for the target of R ~ 0.8. We assume one of the measurements is done at the qubit frequency, T1(ωq), so for a χ ~ 1 MHz, a scan from ± 4.5 MHz would be suggested by such a heuristic. Extra n measurements can be obtained by waiting longer than the autocorrelation time. The autocorrelation width, furthermore, can be evaluated in the same scan as that used for the \({\langle {T}_{1}\rangle }_{T}\) estimate as long as a sufficiently wide range is sampled. Alternatively, a second scan can be taken if the initial Δω guess was too small.

Empirically we see diminishing gains in using ever larger Δω. Further research is needed to guide better limits on Δω beyond the operational observation that \(S \sim {{{\mathcal{O}}}}(10)\) produces a quasi-ergodic result for qubits with \({\langle {T}_{1}\rangle }_{T}\) in the range of 10–200 μs, see supplemental information S8 for more details on quasi-ergodicity. Since we do find ~ 1:1 agreement using a relatively small Δω ~ 10 MHz for the ~9 month time series and we observe that the distribution of T1(ωq, Ti) produces a constant standard deviation, see supplemental information S9, rather than growing (e.g., proportional to a random walk \(\propto \sqrt{t}\)), we speculate that optimal Δω is bounded rather than growing indefinitely from spectral diffusion processes. Notably, Klauder et al. calculate that dipole-coupled ensembles that are proposed for TLS spectral diffusion22, will produce a truncated linewidth33.

Remarks on technique, correlations, and ergodicity

In this work, we probe the temporal and spectral dynamics of superconducting qubit relaxation times. We study these dynamics in high coherence, single-junction transmons by developing a technique for energy relaxation spectroscopy of defect TLSs via the AC Stark effect. Our technique requires no additional hardware resources and can be easily sped up further by integration with reset schemes. Autocorrelation of T1 frustrates rapid characterization of the long-time average \({\langle {T}_{1}\rangle }_{T}\) and therefore accurate characterization of devices. Our analysis of the dynamics identifies a strong correlation between \({\langle {T}_{1}\rangle }_{T}\) and its short time average over the local frequency span, \({\langle {T}_{1}\rangle }_{\omega ,t}\). The strong correlation of \({\langle {T}_{1}\rangle }_{T}\) with \({\langle {T}_{1}\rangle }_{\omega ,t}\) is also consistent with a TLS dominated T1 that quasi-ergodically samples the qubit local frequency neighborhood in contrast to static or uncorrelated stochastic processes. This work opens up several new promising directions for rapid process characterization and evaluation of device stability.