Introduction

The tremendous success of Si electronics has driven research and development on Si-based electronic–photonic integrated circuits (EPICs), the so-called “superchips” combining photonic applications with electronics that can be seamlessly fabricated in a complementary metal–oxide–semiconductor (CMOS)-compatible processes1,2. Si-based EPICs prepared using group-IV semiconductors, including Si, Ge, and their alloys, have achieved great success in the near-infrared region spanning from 0.7 to 1.4 µm3,4,5. The operating wavelength of Si-based EPICs is currently being expanded to the mid-infrared (MIR) spectral region (typically defined as the 1.8–5 µm wavelength range6) for a broad range of applications such as high-speed optical communications, bio-medical sensing, environmental monitoring, astronomy, and long-range light detection and ranging (LiDAR) detection6,7,8,9. MIR EPICs require the monolithic integration of light sources, waveguides, amplifiers, modulators, switches, and photodetectors on a single Si substrate. Although significant progress has been made on MIR Si-based waveguides10, light emitters11,12,13,14,15,16, and photodetectors17,18,19,20, efficient MIR optical modulators on Si remain elusive because group-IV semiconductors do not exhibit the linear electro-optical (Pockels) effect21,22.

The electric field effect is the ideal control mechanism for optical modulators because it requires little or no electric current (and therefore little power) and delivers fast response suitable for >100 GHz high-speed modulation21,22. An applied electric field can induce a change in either the real (Δn) or the imaginary part of the refractive index (Δα) of some materials, known as electro-refraction or electro-absorption, respectively. The Franz–Keldysh effect is an electro-absorption phenomenon in which the modulation wavelength is determined by the direct-gap absorption edge of the material. However, there are fundamental challenges to achieve efficient MIR optical modulation using group-IV semiconductors. If we examine the free-carrier plasma dispersion effect in group-IV semiconductors Si and Ge as a competing electro-absorption modulation mechanism22,23,24,25, the free-carrier approach is weaker because it requires a larger interaction length than the Franz–Keldysh effect and usually consumes a significant amount of power up to hundreds of milliwatts. While excellent Ge-based electro-absorption modulators have been reported26,27,28, the 0.8 eV direct bandgap in Ge limits its operating wavelength to only approximately 1600 nm. The quantum-confined Stark effect in Ge quantum wells29,30 has a similar limitation. Although the Franz–Keldysh effect in GeSn alloys can be effective for implementing on-chip MIR optical modulation31 and the Franz–Keldysh effect in GeSn alloys has been observed32, MIR modulation has not yet been experimentally realized.

In this paper, we present a series of experimental results on the achievement of electro-absorption modulation on Si using GeSn alloys offering high performance in the 1.95–2.25 μm MIR wavelength range, which can be extended readily to 5 μm in modified versions. The GeSn alloy used here is part of the group-IV photonics approach, an expanded version of silicon photonics employing SiGeSn materials. Unlike Ge, which has an indirect bandgap, GeSn alloys have nearly direct or direct bandgap, which can be easily tuned by varying the alloy composition. The device is comprised of a small circular mesa that has free-space light incident normally upon it. A reverse-biased p-i-n diode structure modulates the intensity of light transmitted through the Si substrate. This device is a p-Ge/i-GeSn/n-Ge heterostructure diode grown upon Ge-buffered Si substrates and is a CMOS-compatible device that utilizes the Franz–Keldysh effect to shift the zero-field absorption spectrum of the GeSn active region. The detailed measurements presented here, which are confirmed by our theoretical modeling, demonstrate that GeSn alloys can be efficient MIR optical modulators on Si. We show that control of the Sn content in the GeSn active layer provides a tunable modulation range across the MIR range with a broadband operating range of >140 nm and a good figure-of-merit (FOM) of Δα/α0 ~ 1.5. We also theoretically study the effect of Sn content and strain on the Franz–Keldysh effect in GeSn. These results experimentally demonstrate a practical and competitive group-IV photonics approach for achieving MIR optical modulation on Si using GeSn alloys, thus opening up avenues for Si-based MIR EPICs.

Results

Material growth and characterization

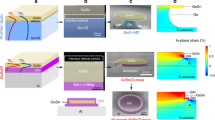
In this study, we investigated GeSn double-barrier heterostructures with different Sn contents for MIR electro-absorption modulation. The heterostructure consists of a pseudomorphic p-i-n Ge/GeSn/Ge diode structures grown on a double-side polished (001) silicon substrate via a Ge virtual substrate using low-temperature molecular beam epitaxy (see the “Methods” section). To study the effect of Sn content on the Franz–Keldysh effect in GeSn, two samples (N1, N2) were epitaxially grown with N2 having a higher Sn content than N1. Figure 1a shows a cross-sectional transmission electron microscopic (XTEM) image of sample N1 overlapped with secondary ion mass spectrometry (SIMS) atomic distribution profiles of Ge, Sn, B, and Sb. From the XTEM image, defects were observed to be confined at the interface near the Si substrate, indicating the strain relaxation of Ge virtual substrate. Clear, flat, and sharp interfaces between the Ge and GeSn layers were observed, indicating a good-quality Ge/GeSn/Ge heterostructure. An average threading dislocation density of 3.9 × 107 cm−2 was obtained for the grown samples via etch-pit density experiments, which is comparable with the typical value of ~2 × 107 cm−2 in good quality Ge-on-Si materials33. In addition, the SIMS results reveal a homogenous distribution of Sn atoms in the GeSn layer. X-ray diffraction (XRD) was employed to measure the lattice constants of the layers to determine Sn composition and strain. The (224) reciprocal space mapping (RSM) of sample N1 is displayed in Fig. 1b. Three distinct peaks associated with the Si substrate, Ge layers, and GeSn active layer are observed. The Ge and GeSn peaks share the same Qx, confirming that the GeSn layer is fully strained to the underlying Ge virtual substrate, which is consistent with the XTEM results. Figure 1c shows high-resolution XRD ω–2θ scans of the samples. The out-of-plane and in-plane lattice constants of the layers are determined using the Bragg angle (θ) and the pseudomorphic growth condition; the Sn composition and strain are then extracted using these results (Supplementary Note 1). The characterization results for the epitaxially grown samples are summarized in Table 1. Additionally, although the GeSn active layers were unintentionally doped, defects as vacancies or dislocations may introduce a p-type background carrier concentration. To obtain the background carrier concentration, a reference sample containing a 400-nm-thick Ge0.955Sn0.045 layer was pseudomorphically grown on a Si substrate via a Ge virtual substrate under the same growth conditions, and Hall measurements showed a p-type background carrier concentration of 6.47 × 1016 cm−3.

Fig. 1: Material characterization of the grown samples.
figure 1

a Cross-sectional transmission electron microscopic (XTEM) image of sample N1 overlapped with secondary ion mass spectrometry (SIMS) atomic distribution. Inset: a high-resolution XTEM image of the Ge/GeSn interface, revealing pseudomorphic growth. b (224) reciprocal space mapping (RSM) of sample N1, showing pseudomorphic GeSn/Ge heterostructures. c ω–2θ scans of samples N1 (red line) and N2 (blue line), showing shifted GeSn peaks with increasing Sn composition.

Full size image
Table 1 Characterization results obtained for the epitaxially grown samples.
Full size table

Device design and MIR modulation principle

Figure 2a shows a schematic diagram of the designed normal incident GeSn p-i-n diode for optical modulation. The device consists of a pseudomorphic p-Ge/i-GeSn/n-Ge heterostructure grown on a silicon substrate via a Ge virtual substrate in which the narrow-bandgap GeSn layer is employed as an active layer. The application of a reverse bias to the device increases the electric field in the GeSn active layer, triggering the Franz–Keldysh effect to modify the absorption coefficient near the direct-gap absorption edge of the GeSn active layer. Therefore, when light is normally incident on the surface of the device, the intensity of the transmitted light can be altered to achieve optical modulation. Figure 2b shows a schematic band diagram of the Ge/GeSn/Ge p-i-n heterostructure. Because the GeSn active layer has a smaller bandgap than that of Ge, a type-I band alignment at the Γ symmetry point in the momentum space can be achieved. In addition, the pseudomorphic growth of GeSn on Ge virtual substrate imposes a compressive strain in the GeSn active layer, thereby removing the degeneracy of heavy-hole (HH) and light-hole (LH) bands such that the top valence band is HH-like. As a result, the lowest direct-gap transition is from the HH band to the Γ-conduction band (HH → cΓ), and the lowest indirect-gap transition is from the HH band to the L-conduction band (HH → L). Note that the bandgap energies of the GeSn active layer can be widely tuned by controlling the Sn content. Thus, the modulation range of GeSn is expected to be “tunable” in the MIR region, enabling a wide range of applications. In this study, we investigated the Franz–Keldysh effect and optical modulation characterization in the GeSn devices with different Sn contents (devices N1 and N2). Figure 2c shows the calculated lowest direct- and indirect-bandgap energies at T = 300 K as a function of Sn composition of the GeSn active layer, which is obtained from our k·p calculations (Supplementary Note 2). As the Sn content increases, both direct- and indirect-bandgap energies decrease. With a Sn content of >3.6%, the direct bandgap can be reduced to <0.688 eV, thereby pushing the modulation range into the MIR region. In addition, a further increase in the Sn content allows bandgap shrinking and redshifting of the modulation range across the MIR region.

Fig. 2: GeSn p-i-n diodes on silicon for mid-infrared electro-absorption modulation.
figure 2

a Schematic of our designed normal-incident GeSn p-i-n diode on (001) silicon for optical modulation (not to scale). The mid-infrared (MIR) light beam is incident on the top of the device and transmitted through the GeSn active layer. AC bias voltage is applied to the p-i-n diode to modulate the MIR light based on the Franz–Keldysh effect. b Schematic band diagram of Ge/GeSn/Ge heterojunction with an applied electric field. The compressive strain in the GeSn active layer splits the valence band. c Evolution of the lowest direct-gap transition energy (from the heavy-hole (HH) to Γ-conduction band) and indirect-gap transition energy (from HH to L-conduction band) for pseudomorphic GeSn on Ge at 300 K as a function of Sn composition calculated using deformation potential theory. The epitaxially grown GeSn heterostructure samples N1 and N2 are indicated by the dashed lines. d Current–voltage characteristics of the fabricated GeSn p-i-n diodes with D = 250 μm using samples N1 (solid blue line) and N2 (dashed red line). The inset shows a top-view scanning electron microscopy (SEM) image of the fabricated diode.

Full size image

The device fabricated in this study is composed of a GeSn heterostructure p-i-n diode arranged vertically through two circular mesas of different diameters (D) and two ring-shaped Cr/Au metal pads. The device was fabricated using a standard CMOS-compatible process (see “Methods” section). A scanning electron microscopic image of the fabricated device with D = 250 μm is displayed inset of Fig. 2d. Figure 2d shows the current–voltage characteristics of the fabricated GeSn p-i-n diodes; clear rectifying behavior was observed. In addition, device N2 exhibited higher dark current than that of the device N1 under reverse bias conditions, because of the higher Sn content that results in a lower bandgap energy34.

Experimental evidence of electro-absorption modulation in the MIR region

The electro-absorption modulation properties of the GeSn devices are presented in Fig. 3. Figure 3a shows the measured modulation depth of the devices, which is defined as \({\Delta}T\left( F \right)/T_0 = \left[ {T_0 - T\left( F \right)} \right]/T_0\)35, where T0 and T(F) are the transmittance of the devices measured at zero bias (corresponding to a built-in electric field of F0 = 6 kV cm−1 estimated using the depletion theory21) and at different electric fields (F), respectively. The zero-bias transmittance spectra and absorption coefficient (α0) spectra obtained from responsivity characterization (Supplementary Note 3) are presented in Fig. 3b, c, respectively. At \(F = 30\;{\mathrm{kV}}\;{\mathrm{cm}}^{ - 1}\), the modulation depth spectra clearly show significant oscillation characteristics in the 1500–2300 nm spectral range in which the positive peaks (indicated by the arrows) are associated with the HH → cΓ direct-gap transitions, which match the absorption edges in Fig. 3c. The HH → cΓ transition energies were determined to be \(E_{{\mathrm{HH}}}^{c{\Gamma}} = 0.639\;{\mathrm{eV}}\) for device N1 and \(E_{{\mathrm{HH}}}^{c{\Gamma}} = 0.605\;{\mathrm{eV}}\) for device N2. These results confirmed the narrowing of direct-bandgap energies due to Sn alloying. As the electric field increases, the modulation depth significantly increases. With \(F = 150\;{\mathrm{kV}}\;{\mathrm{cm}}^{ - 1}\), the modulation depth values are 0.84% (87.1 dB mm−1) at λ = 1950 nm for device N1 and 0.64% (77.4 dB mm−1) at λ = 2080 nm for device N2. In addition, the modulation depth spectra exhibit redshift as the electric field increases because of the electric-field-induced tilting of the energy bands. These observations provide strong evidence for the Franz–Keldysh effect in GeSn alloys. Figure 3d shows the alternating current (AC) modulation signal at λ = 2000 nm for device N1 with a swing voltage between 0 and −2.37 V at 100 kHz and clear dynamical modulation is observed. These results exhibit optical modulation in the MIR region with the GeSn heterostructure devices. Figure 3e shows the normalized radio frequency (RF) response at λ = 2000 nm of device N1. A 3-dB bandwidth (f3dB) of 19.06 MHz was obtained, which is sufficient for many MIR applications such as LiDAR, remote-sensing, and imaging6,9. As the bandwidth of electro-absorption optical modulators is limited by RC time delay22, it is anticipated that the modulation bandwidth can be increased by further reducing the device footprint (Supplementary Note 4).

Fig. 3: Modulation characteristics at room temperature.
figure 3

a Modulation depth spectra of the GeSn devices measured at different electric fields. Clear variations in transmittance are observed, providing strong evidence of the Franz–Keldysh effect. The lowest direct transition energies are indicated by the solid black arrows. b Transmittance spectra for the GeSn devices and c absorption spectra under zero-bias conditions for the GeSn active layers. d Applied AC bias voltage (upper panel) and AC optical modulation signal (lower panel) at 100 kHz at λ = 2000 nm for device N1. e Normalized radio frequency response of device N1 (D = 250 µm) at λ = 2000 nm showing a 3-dB bandwidth of 19.06 MHz.

Full size image

Electro-absorption Franz–Keldysh effect in GeSn

To further analyze the Franz–Keldysh effect, the change in absorption coefficient (Δα) with different electric fields for the GeSn active layer was extracted from the modulation depth spectra using \({\Delta}\alpha = - \frac{1}{t}\ln \left[ {1 + {\Delta}T\left( F \right)/T_0} \right]\), and the results are shown in Fig. 4a. The Δα spectra clearly exhibit characteristic oscillation features that are very similar to the Franz–Keldysh effects in III–V direct-bandgap materials21. The observed positive Δα peaks are located near λ = 1940 nm for device N1 and λ = 2060 nm for device N2, and the effect of the electric field on Δα is shown inset of Fig. 4a. The absorption coefficient increases with increasing electric field but tends to saturate in high electric fields. For the electric field range of 6–50 kV cm−1, we obtain \({\Delta}\alpha /{\Delta}F\sim 3.1\,{\mathrm{cm}}^{ - 1}\,{\mathrm{kV}}^{ - 1}\) for the devices, which is close to \({\Delta}\alpha /{\Delta}F\sim 3\,{\mathrm{cm}}^{ - 1}\,{\mathrm{kV}}^{ - 1}\) at λ = 1647 nm in the 14–70 kV cm−1 range for Ge36. At \(F = 150\;{\mathrm{kV}}\;{\mathrm{cm}}^{ - 1}\), significant Δα = 437 cm−1 at λ = 1940 nm for device N1 and Δα = 316 cm−1 at λ = 2060 nm for device N2 were achieved. It is noted that the obtained Δα values decreases as the Sn content increases. This observation is attributed to the compressive strain in the GeSn layer, which will be discussed later.

Fig. 4: Franz–Keldysh effect in GeSn.
figure 4

a Change in the absorption coefficient in the GeSn active layers at different electric fields for devices N1 (upper panel) and N2 (lower panel). The inset shows the change in the absorption coefficient for device N1 and device N2 at λ = 1940 and λ = 2060 nm, respectively, as a function of electric field. b Figure-of-merit (FOM) Δα/α0 for the GeSn active layer at different electric fields for devices N1 (upper panel) and N2 (lower panel). The lowest direct bandgap is indicated by the dashed blue lines. The inset shows the absorption coefficient spectrum under the zero-bias condition of device N2.

Full size image

While a high extinction ratio is favorable for optical modulators, a low insertion loss is equally essential. Thus, the FOM, defined as \({\Delta}\alpha /\alpha _0\), is usually used for characterizing materials for electro-absorption modulators and for determining the optimal spectral working region. Figure 4b shows the FOM spectra for the devices with different electric fields. The FOM increases with increasing wavelength and reaches a maximum at a photon energy of ~25 meV below the lowest direct bandgap \(\left( {E_{{\mathrm{HH}}}^{c{\Gamma}}} \right)\) as indicated by the dashed blue lines. It then decreases again as the wavelength increases further. As the electric field increases, the FOM increases with an increase in Δα. At \(F = 150\;{\mathrm{kV}}\;{\mathrm{cm}}^{ - 1}\), the FOM peaks at 1.51 at λ = 2110 nm for device N1 and 1.50 at λ = 2160 nm for device N2. These values are comparable to, or even slightly better than, those of Ge-based electro-absorption modulators27,28. This behavior can be explained by the contribution of the indirect transition to the background absorption coefficient. In pure Ge, the L-conduction band lies below the Γ-conduction band by a significant energy separation of \({\Delta}E_{{\Gamma}{\rm{L}}} = 136\,{\rm{meV}}\). As a result, there is usually a long indirect absorption tail extending below the direct transition band edge, which contributes to a permanent high absorption coefficient below the direct-gap absorption edge \(\left(\right.{\alpha _{\rm{L}} \propto ({\hbar \omega - E_{\rm{g}}^{\rm{L}} \pm E_{{\mathrm{ap}}}})^2}\), where \(E_{\rm{g}}^{\rm{L}}\) is the indirect bandgap and \(E_{{\mathrm{ap}}}\) is the acoustic phonon energy37). Consequently, Ge-based electro-absorption modulators usually suffer from relatively high insertion losses and thus, low FOMs. In contrast, the energy difference \({\Delta}E_{{\Gamma}{\rm{L}}}\) between the direct and indirect conduction bands in the GeSn devices is considerably reduced to 70 and 58 meV for devices N1 and N2, respectively. This significantly reduced \({\Delta}E_{{\Gamma}{\rm{L}}}\) suppresses \(\alpha _{\rm{L}}\) below the direct-gap absorption edge, as shown in the inset of Fig. 4b. As a result, the FOM is enhanced, suggesting the potential for low insertion-loss and high extinction-ratio MIR optical modulation. We can also define the optimal modulation range of the devices based on the FOM. For device N1 (4.82% Sn), as shown in Fig. 4b, the FOM at F = 150 kV cm−1 is always >1 across a wavelength range of 1964–2190 nm. This implies that the extinction ratio can indeed be greater than the insertion loss in this spectral range, which is beneficial for achieving high-performance optical modulation. Thus, we identify this 226-nm-wide spectral range as the operating regime of this device. For device N2 with a higher Sn content (5.76% Sn), the adequate modulation range is from 2090 to 2236 nm with a 146-nm-wide optimal modulation width. The corresponding scaling performance for device N1 (N2) is 66.32 dB mm−1 (95.9 dB mm−1) extinction ratio and 49.8 dB mm−1 (64.7 dB mm−1) insertion loss at λ = 2070 nm (λ = 2160 nm) (Supplementary Note 5). These results emphasize several unique advantages of MIR GeSn optical modulators. First, the adequate modulation range of these devices with a FOM > 1 is much larger than the modulation width of ~20 nm for Ge(Si) electro-absorption modulators26,27,28,29,30 and free-carrier Si Mach–Zender optical modulators38, highlighting the broadband optical modulation capability of GeSn in the MIR range. Second, the optimal modulation range of the GeSn devices can be controlled by varying the Sn composition in the GeSn active layer to achieve optical modulation at other spectral ranges in the MIR region. Third, the optimal modulation range of our devices perfectly matches the emerging 2 μm MIR optical communication band (λ = 1900–2100 nm)6,24 and 2 μm ultra-long range LiDAR9, making our devices ideal for MIR optical communication applications.

Theoretical modeling of the Franz–Keldysh effect in GeSn

After the experimental verification of the Franz–Keldysh effect and MIR electro-absorption modulation in GeSn, understanding the effect of GeSn alloy composition on the Franz–Keldysh effect is essential for the design of efficient GeSn MIR electro-absorption modulators for MIR EPICs. Here, we discuss the effect of Sn composition up to 15% on the Franz–Keldysh effect in GeSn. In addition, we also investigate the strain effect by comparing the electric-field-induced Δα for pseudomorphic Ge1−xSnx on Ge and unstrained Ge1−xSnx. The theoretical models for strained band structures and electric-field-independent absorption coefficients are presented in Supplementary Notes 2 and 621,39,40. Figure 5a shows the calculated Δα spectra for pseudomorphic Ge1−xSnx on Ge (which has a compressive strain of 0.143% per 1% Sn) with different Sn compositions and electric fields. For a fixed Sn content, Δα increases with an increase in the electric field due to the Franz–Keldysh effect. As the Sn content of the GeSn alloy increases, the direct bandgap decreases despite the compressive strain, redshifting the Δα spectrum. For x > 3.6%, the direct bandgap can be reduced to <0.688 eV, shifting the modulation range into the MIR region. For x = 15%, the modulation range can be shifted to ~3.1 μm. In addition, the magnitude of Δα near the direct-bandgap edge is significantly dependent on the Sn content. When the Sn content increases from 0 to 5%, the magnitude of Δα near the direct-bandgap edge decreases. This behavior is attributed to the compressive strain that splits the HH and LH bands. Thus, Δα arising from HH → cΓ and LH → cΓ transitions occurs at different photon energies. As a result, Δα near the direct-bandgap edge is only governed by the HH → cΓ transition, leading to a weaker Franz–Keldysh effect (Supplementary Fig. 5). This analysis matches our experimental observation (Fig. 4a). As the Sn content increases further from 5 to 15%, Δα near the direct-bandgap edge again increases. This behavior is attributed to the increased joint density-of-states caused by the larger effective masses of electrons and holes that significantly enhance the direct-gap absorption coefficient (Supplementary Fig. 5), thereby enhancing Δα. In contrast, for unstrained Ge1−xSnx, the Δα spectrum also redshifts with an increase in the Sn content but with a higher rate compared to the case of pseudomorphic Ge1−xSnx on Ge. Thus, the modulation range can be widely tuned across the entire MIR region by varying the Sn content in the 2.8–15% range. In addition, the HH and LH bands are still degenerate in the unstrained Ge1−xSnx alloys. Thus, both HH → cΓ and LH → cΓ transitions can contribute to Δα near the direct bandgap, leading to a larger Δα compared to pseudomorphic Ge1−xSnx on Ge. In addition, Δα monotonically increases with an increase in the Sn content. This highlights the importance of the strain effect on Franz–Keldysh modulation in GeSn. The results of these GeSn strain and alloy composition experiments provide useful guidelines for designing high-performance GeSn MIR electro-absorption modulators.

Fig. 5: Theoretical modeling for Franz–Keldysh effect in GeSn.
figure 5

Calculated change-in-absorption coefficient Δα at T = 300 K for a pseudomorphic Ge1−xSnx on Ge and b unstrained Ge1−xSnx with different Sn contents and electric fields.

Full size image

Discussion

We have experimentally demonstrated MIR electro-absorption modulation using GeSn alloys on Si. The Franz–Keldysh effect in the MIR region was clearly observed by engineering the bandgap of GeSn alloys with Sn alloying. Electro-absorption modulation in the MIR region was achieved with a good FOM of >1.5 and a broadband modulation spectral range of >140 nm. In addition, our experimental and theoretical analyses verified that the modulation range can be tuned by adjusting the Sn composition to enable efficient optical modulation in the entire MIR spectrum. Room-temperature Si-based MIR EPICs can be utilized for a broad range of applications, such as high-speed optical communications, remote sensing, environmental monitoring, astronomy, infrared imaging, and long-range LiDAR detection over the entire MIR range, but more particularly in the 2-μm communications band6. Another advantage of our GeSn heterostructure MIR device is its low-cost manufacturability and scalability using CMOS-compatible fabrication processes.

For the GeSn devices fabricated in this study, the mesa can be thought of as one pixel in an N × M-pixel spatial light modulator. But, moving away from the space scenario, it is a straightforward procedure to modify the heterostructure presented here to create an effective electro-absorption modulator within a strip-channel waveguide integrated on a Si chip. For example, a strip could be formed by etching a layered structure on Si, where those layers would be formed by successive epitaxial growth of Ge and GeSn layers on the chip. Using doping at some epitaxy steps, a p-i-n diode strip could be formed whose cross-section is, for example, 1.0 μm in width and 0.5 μm in height. The resulting waveguided electro-absorption modulators (or several such modulators) could be seamlessly or monolithically integrated with a variety of “cooperating” on-chip photonic components to form EPICs. Because the response of the present electro-absorption modulation begins at 1.9 μm and extends to longer wavelengths, it is ideal for 1.8–5.0 μm MIR applications.

Methods

Sample growth

The samples used in this study were grown on p-type double-side polished Si(001) substrates using molecular beam epitaxy at a base pressure of <2 × 10−10 torr. The first step of the epitaxy process was the growth of a strain-relaxed Ge virtual substrate using a two-step growth technique, consisting of two 100-nm-thick Si layers grown at 650 and 350 °C, a 60-nm-thick Ge seed layer grown at 350 °C, followed by in situ annealing at 800 °C for 5 min, and a 60-nm-thick Ge buffer layer grown at 550 °C. Then, a B-doped p-type Ge layer was grown at 550 °C. The growth temperature was subsequently decreased to 150 °C for the growth of a GeSn active layer, followed by the growth of a Sb-doped n-type Ge layer. The epitaxial growth was completed with the growth of a 3-nm-thick Si cap layer. The nominal doping in the p- and n-Ge layers is 5 × 1018 cm−3.

Device fabrication

The grown samples were fabricated into p-i-n diodes using CMOS-compatible processing technology. Circular mesas with different diameters in the 250–1000 μm range were created using standard optical lithography and reactive ion etching methods. A SiO2 passivation layer with a thickness of 400 nm was then deposited using an e-beam evaporator. Contact windows were then opened by wet etching using buffered oxide etchant, which provides high etching selectivity between Ge and SiO2. Cr/Au bilayer metal a thickness of 20/200 nm were deposited using an e-beam evaporator and ring-shaped electrodes were then patterned using lift-off techniques for electrical contact.

Transmission experiments

The transmission experiments were carried out at room temperature using a broadband quartz–tungsten–halogen lamp as the light source. The light was filtered using a 1200-nm high-pass filter and dispersed using a monochromator equipped with a 600-line/mm grating blazed at 1600 nm. The dispersed light was then reshaped using an adjustable aperture and focused onto the top surface of the device using a ×20 objective; this process ensured that the beam size was smaller than the window of the device. A square-wave AC bias with a frequency of 1 kHz was applied to the devices using an arbitrary wavefunction generator (Fluke, 282). The light transmitted through the device was then sent to a LN2-cooled InSb photodetector (1–5 μm detection range) and converted to an electrical signal, which was read out using a lock-in amplifier (Stanford Research System, SR830) to determine the transmittance. The electric field applied to the GeSn active layer was estimated from the applied voltage (V) using \(F = F_0 + V/t\), where \(F_0\) is the built-in electric field in the p-i-n junction.

AC experiments

The AC experiments were carried out at room temperature using a 2-µm laser (Thorlabs, LFL2000) as the light source. The laser was focused onto the top surface of the device using a 20× objective. The transmitted light through the device was then sent to an extended InGaAs photodetector (Thorlabs, DET10D2) with a photodetection cutoff wavelength of 2600 nm and a 3-dB bandwidth of 14.5 MHz. The electrical signal from the photodetector was then preamplified (Standard Research System, SR 560) and monitored using an oscillator (Tektronix, MSO 2000B).

For the 3-dB bandwidth experiments, we evaluated the 3-dB bandwidth at a 2000-nm wavelength. A 2000-nm laser (Thorlabs, LFL2000) was used as the light source. A vector network analyzer (Anritsu MS4647B) with a bias tee to combine direct current bias and high-speed RF signals was used to generate the RF signals fed into the GeSn devices. The intensity of the transmitted light was then detected using a high-speed amplified extended InGaAs photodetector (Electro-Optics Technology, ET-5000A) with a rated bandwidth of >12.5 GHz and the signal was sent to the vector network analyzer for S21 parameter (the ratio between the modulated optical signals and the RF signal) measurements.