Abstract
Everywhere in our surroundings we increasingly come in contact with nanostructures that have distinctive complex shape features on a scale comparable to the particle itself. Such shape ensembles can be made by modern nano-synthetic methods and many industrial processes. With the ever growing universe of nanoscale shapes, names such as “nanoflowers” and “nanostars” no longer precisely describe or characterise the distinct nature of the particles. Here we capture and digitise particle shape information on the relevant size scale and create a condensed representation in which the essential shape features can be captured, recognized and correlated. We find the natural emergence of intrinsic shape groups as well-defined ensemble distributions and show how these may be analyzed and interpreted to reveal novel aspects of our nanoscale shape environment. We show how these ideas may be applied to the interaction between the nanoscale-shape and the living universe and provide a conceptual framework for the study of nanoscale shape biological recognition and identity.
Similar content being viewed by others
Introduction
It is now clear that man-made nanoscale objects are processed by the whole range of endogenous biological machinery, in part via their in situ biomolecular corona surface1,2,3,4,5,6. The idea that “biology sees nanoscale shape” and that certain shape features could also specifically regulate (or even target) given biological pathways is an intriguing but still emerging concept7,8,9,10,11,12,13. Various aspects of shape at different length scales have always been implicitly involved in nanoscience14,15,16,17,18,19,20; nanostructures are never smooth and spherical (on an atomic or few-atom scale) by virtue of their synthetic or other origin, and also some highly non-spherical (for example rod-like) objects are quite well studied21,22,23,24,25,26,27,28. However, everywhere in our surroundings we increasingly make (purposefully or by accident, as in 3D printing) nanoscale shape ensembles, that possess complex features on length-scales comparable to the particle itself29,30,31,32,33,34,35. Also, advancing synthetic methods now potentially offer “unlimited” freedom to controllably make a new universe of such complex geometrical ensembles that cannot be described, recognized or characterized with only a few length parameters36,37,38,39,40,41,42. We currently find ourselves unable to even name and share information, let alone carry out many systematic investigations of them. These general limitations become very significant barriers to understanding the link between nanoscale shape ensembles and biology, and progress there now requires new ways of thinking, new concepts, as well as practical innovations.
As a basic step we require a quantitative statistical definition of nanoscale shape that can ensure complex shape ensembles are meaningfully reproduced and their properties communicated. Such a quantitative framework with the capacity to describe the relevant aspects of shape ensembles might also link nanoparticle shape statistics to biological function in new and hitherto undiscovered ways. Thereby, arenas extending from the science of immunological adjuvants to the biological and clinical impacts of environmental dusts (currently phenomenological in approach, lacking any substantive quantitative basis for development) may be advanced.
While many disciplines will value a quantitative framework for nanoscale shape, here we discuss the two interwoven arenas of nanoscale shape statistics, nanoparticle synthetic control (framed by quantitative measures of shape), and the resulting linkage of those well-controlled shape ensembles to cellular read-outs. We will use that discussion to raise the question of “biological shape identity”.
We first introduce the concept of statistically defined nanoscale geometries that go beyond the current practice of borrowing “family” names from common objects (“nanoflowers”’ “nanostars”, “urchin-like”, etc.)43,44,45,46. It should be stressed that the ideas we describe do not replace conventional experimental nanoparticle fingerprints such as differential centrifugal sedimentation, and spectroscopic methods (i.e. single-particle extinction and scattering), all of which still give valuable basic information47,48,49,50,51. However, by using digitized transmission electron microscopy-derived images of shapes, combined with concepts of computational geometrical analysis, we are now able to capture particle shape information that leads to a quantitative definition of shape ensembles. Based on this approach we then define simplified parameters that generalise familiar concepts of particle averages, measures of heterogeneity, and correlation for nanoparticle shape ensembles.
Those developments, when implemented, impose significant discipline on particle preparation, even for well-established particle shape syntheses (such as the gold particle system used here), and lead to optimization of shape homogeneity and reproducibility.
We illustrate the overall approach by analysing whole transcriptome readouts of cells that have been exposed to sufficiently well-defined and homogeneous shape ensembles. We find that distinct shapes (nominally composed of the same materials, prepared under the same conditions) can elicit distinct and non-overlapping biological responses, raising the possibility of shape-targeted regulation of biological pathways. We finally discuss the potential to isolate canonical nanoscale (structural) biological control parameters.
Results
Nanoparticle population shape identity and shape groups
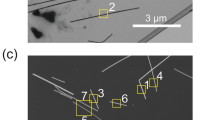
In contrast to molecules, nanoparticle (NP) shapes do not have a single well-defined and unique geometry. For fixed average reaction conditions they are formed by largely irreversible nucleation and growth processes, with particle-to-particle shape fluctuations derived from local growth kinetics around a population of initial seeds52,53,54,55,56,57. Progressive methodological improvement of the synthetic method eliminates many factors (such as mesoscopic mixing heterogeneities) ultimately leading to relatively reproducible populations in which each particle, while being slightly different, possesses an apparently recognizable “typical” shape (see an illustrative selection of NPs in Fig. 1a–c). Transmission electron microscopy (TEM) allows the capture of NP shapes that are appropriately (and homogenously) presented on grids, followed by image digitization in three dimensions (tomography) or two (contour) dimensions (see Supplementary Figs. 1–4)58,59,60. Various mathematical representations of the volume, surface or the contour of the NPs may then be used, but given the typical length scales and organization of synthetic surface features, we can efficiently capture information in a Discrete Fourier Transform (DFT, see more details in “Methods” and Supplementary Table 1)61,62,63,64,65,66. There is nothing unique about such a representation, and in the future others will be found useful. Still, it is noteworthy that (for the shape families studied here, and likely many others) this representation allows contour descriptions of shape using relatively few (two or three) parameters in a low dimensional setting, instead of the many hundreds of points defining the original contour.
TEM micrographs illustrating a library of different gold NPs with a regular geometrical shapes and b branched shapes. c Four representative NPs shapes used in this work. From the left: GNP1 (“nanospheres”), GNP2 (“nanorods”), GNP3 (“nanourchins”), and GNP4 (“nanostars”). Scale bars are 100 nm. d Schematic representation of the hyperspace geometrical identity and definition of shape groups (basins of similarity).
We first introduce the concept of shape probability distributions (along axes in the generalized hyperspace of shape parameters) and discuss the idea of population shape distinctiveness (identity) and measures of shape difference (see Fig. 1d for a schematic illustration of the concept).
In this picture, “similar” nanoparticles within a given ensemble (possibly derived from identical syntheses, or other common origins) are manifested as distinct probability maxima (or “basins” in an equivalent entropic-free-energy description). If sufficiently homogeneous, and well separated from others, such ensembles may be considered as distinct pure “shape groups”. In some cases, these probability maxima certainly map onto known terms (e.g., the so-called “nanoflowers”, “nanostars” or “urchin-like” particles)44,45,67 but there is no necessity that they do so, and any ensemble can be statistically characterized leading to nanoscale shape-substance definitions. Evidently, the specifics of the geometrical description and presentation somewhat affects the details of this picture, and different applications (from biology to plasmonics) may require different conventions about what constitutes a separate shape group. For instance, within the Fourier representation, it is convenient to normalise with the first (zeroth-order) coefficient, which (in the biological examples discussed later) means that particles with similar features such as “tip sizes”, inter-tip separations (tip density), are considered to be from the same shape group, even if the particles are of different overall average size. That appears to be an appropriate choice for some of the biological readouts explored below.
We should also differentiate between complete 3D information that must be captured to fully describe the shapes involved (see Supplementary Figs. 3, 4 and Supplementary Methods), and much more practicable reduced representations that may be sufficient to classify and frame “shape identity”, and (possibly) the biological identity of shape. Here we will show that to statistically distinguish some shape groups, it is sufficient to capture, digitise and analyse only the 2D projected contours from particle populations. This approach essentially samples smaller segments of correlated surface curvature via their statistically presented contours. In general then, the aim is to create minimal (low-dimensional) shape descriptors by progressive simplifications in both data collection and analysis, providing the outcome still parameterises those differences (and similarities) between shape ensembles that are relevant to the purpose.
Nevertheless, one has to be attentive to the choices made. For some classes of structure specific over-simplifications of geometrical representation may subordinate (obscure) too much biologically relevant information, and the underlying biological control parameters may not be captured. Within that (under-determined) representation, materials could then be (wrongly) identified as similar while eliciting quite distinct biological read-outs. In our current studies, this is not relevant, but in future one should bear in mind the general concepts of shape definition presented here, rather than only the specific choices made.
Distance in shape space and identification of groups
To meaningfully attribute concepts of “shape ensemble difference” one must choose appropriate definitions of “distance” between particles in shape ensembles using the geometrical coefficients that were used to capture and describe them. In the present case, a generalized (complex coordinate) shape descriptor is defined using tens or hundreds of Fourier coefficients obtained by a DFT (see Supplementary Fig. 5, “Methods” and Supplementary Methods for details) of the contours. The Fourier representation is of course equivalent to the full spatial (discrete) contour itself, but for many classes of shape a given representation may require only a few coefficients (instead of hundreds of real-space points) to sufficiently capture the key information. We, therefore, now define a distance (so-called Lnnorm, see “Methods” and Supplementary Fig. 6) based on differences between these Fourier coefficients. Using this concept of “distance” between particle contours (for example for the material ensembles of Fig. 1) “spatial proximity” becomes a proxy for geometrical similarity, and particles visually identified as members of the same group indeed cluster with each other. Those recognizably different populate other separate clusters. Also, the same particle syntheses (when sufficiently optimized) are reproducibly assigned to the same location in shape space, and “spatial” proximity (in this space) maps well onto shared particle group identity, as well as measures of ensemble quality and reproducibility. This all now imposes some conceptual order on nanoscale shape ensembles.
More striking is the a priori identification of shape groups (Fig. 2a) starting only with a large contour database of different shapes derived from numerous different syntheses but randomized so that our visually based prejudices are eliminated. To illustrate, we then apply an efficiently connected cluster algorithm (see Supplementary Methods) in which this concept of distance can be applied computationally to progressively identify all near neighbors, neighbors of neighbors, and so forth, until the process terminates, and there are no further unidentified neighbors. We can then extract well-defined “connected clusters” (of identity), each element of which is within some chosen threshold distance from one or more other elements of the same cluster. One can then check that the overall outcome is not highly sensitive to the threshold (see “Methods” and Supplementary Figs. 7 and 8). Several variants of the approach are discussed in Supplementary Fig. 9, but the basic outcome is that when we apply the method (Fig. 2a) to particle contour databases (from which all knowledge of particle synthetic origin has been eliminated) shape families (highlighted there with separate colors) readily re-emerge in a low dimension space of principal components composed of the Fourier coefficients.
a Clustering using center of gravity method (CGCM—see “Methods”) represented as scatter plots for the first three principal components (PCs). Each dot represents one individual NP. Shape group colors are GNP1 (blue), GNP2 (orange), GNP3 (green), GNP4 (red). The first three PCs with magnitude and phase are represented in the expanded space (variance = 88%); b normalized probability distribution function (PDF) of shape variability for each shape group. c Graphical representation of the contours of 5 particles from the center (red) and 5 particles from the periphery (black) of the cluster of GNP1 and GNP2. On top of each GNP1 particle, the relative values of compactness (1 for a perfect sphere) and on top of each GNP2 particle the relative values of aspect ratio. d Distribution of aspect ratio for GNP2 and compactness for GNP1. e Clustering and f normalized PDF histogram for a “poorly controlled batch” of GNP3. g Clustering and h normalized PDF histogram for a “good synthetic batch” of GNP3. Green bars/dots define the particles belonging to GNP3 shape group and purple bars/dots define the particles that are at the edge of the basin of similarity (the cut-off distance is calculated as the half height of the distribution). The inset in e illustrates three representative contours from the center of the cluster (green) and three representative contours outside the cluster (purple), related to the dots highlighted with a black border in the scatter plot.
Interestingly (by visual inspection) we see that for a priori clustering, rare aberrant particles (arising from anomalous synthetic events in a single batch) now appear to be more correctly assigned to shape groups than by reliance only on their synthetic origin. We can thereby fingerprint (to a level appropriate to the given application) the geometrical variability of the ensemble, batch-to-batch reproducibility, and detect (within the limits of the contour sampling itself) “shape impurities”, making contact with all of the familiar ideas of particle “characteristics and quality” commonly applied for spherical particle ensembles.
Besides the overview provided by scatter plots along principal component axes (Fig. 2a) we can also define simpler analogs to familiar experimental “probability distribution indices” (Fig. 2b). There the “PDI” widths no longer represent the dispersion in radius (as for spheres) but the ensemble spread of important shape related properties, ranked within the principal component analysis, or important in the specific application. Since that “width” (Fig. 2b) of such shape distributions is not a familiar concept we use a specific example to illustrate the physical meaning of geometrical fluctuations (or dispersity) along a geometrical principal component axis. Thus, we use connected cluster analysis to identify the vicinities of the clusters (“basins”) of spheres (GNP1) and rods (GNP2). In Fig. 2c we show representative particles from the center (red) and outliers at the periphery (black) of each cluster (GNP1-blue and GNP2-orange). As expected, the actual structures derived from the center of each cluster are (respectively) nearly ideal rods and spheres, while the fluctuations from these shapes are localized outside the two main clusters. Moreover, these fluctuations represent the tails of the distributions of aspect ratio and sphericity (compactness), respectively for GNP2 and GNP1 (Fig. 2d). Further detailed insights into the nature of sub-ensemble shape fluctuations could be obtained by calculating an average shape of these objects (see “Methods” and Supplementary Fig. 10). This could be very useful for small groups of outliers having some specific biological action (absent in the larger ensemble) as one searches for the conceptual (shape) equivalent of “impurity” classifications.
We now also apply these ideas (Fig. 2e–h) to more disordered particle ensembles that could, for instance, model environmentally derived or process derived nanoscale dusts. As an example, we show a poorly controlled synthesis of the same type (GNP3) as used throughout the paper, in which many of the resulting particles have no discernible “group name” such as those commonly used in particle synthesis. Applying the same methods used in Fig. 2a, with appropriate principal component analysis (PCA, see Fig. 2e, g) and probability functions (PDF—Fig. 2f, h), we detect a well-defined sub-population cluster sharing similar properties to GNP3 admixed with many separated more isolated and apparently random structures. Interestingly, for comparison (Fig. 2f, h), we can restore the synthetic conditions closer to those for “good” batches of GNP3, and again see emerging the strong representation of those particle types. These results are quite typical and illustrate how well-defined sub-populations often occur against a significant background of (un-noticed) “broad-band shape noise”. One should be aware that many syntheses are carried out without the benefit of these analyses and, from our typical experience, the results can be quite heterogenous, when analyzed by the measures described here.
Other characteristic phenomena can be observed in synthesis of nanoparticle shapes that extend beyond population dispersity or “impurity”, and touch on the question of how many shapes groups may arise from a given class of material syntheses. For instance, efforts to tune some reaction conditions between well-defined shape groups appears to form a type of macroscopic distinct shape group coexistence (often regarded as undesirable), rather than a smooth evolution to new shape groups. These effects have not been systematically investigated, but it is possible that they arise from constraints on specific seed faceting that, along with fixed reaction parameters and concentrations, lead to a “reaction-induced shape phase-separation”, and thereby essentially “shape transitions” between some shape groups. As systematic shape studies become more quantitative, we may expect such phenomena to be classified in reaction mixtures, and described as mixtures derived from “pure shape” basins (see Fig. 1a), mirroring aspects of traditional macroscopic phase behavior.
Biological functional responses derived from distinct basins
We stress one aim in this work is to establish a conceptual and practicable framework to enable shape identity to play a role in different arenas, including biology. The biological results we describe below are intended to illustrate the idea that ensemble geometry can be meaningfully fixed and causally linked to biological outcomes. We are therefore using high-dimensional cellular (transcriptomic) read-outs as measures of “material identity” rather than performing an exhaustive biological study that claims downstream consequences. There is a great deal of detailed exhaustive biological, surface, and materials science to be done before such claims, carefully made, would be appropriate. However, we hope the present work will frame such studies, and help ensure that they become a durable contribution to the science of shape in biology.
To link biological outcomes to nanoscale geometry there are several key issues that should be addressed. Firstly, particle shape heterogeneity is potentially of such variety and complexity that (using methods of the type described here) we should capture and report on the reproducibility of shape samples including “average shape”, shape dispersity and potentially levels of “shape impurity”. Obviously, these new issues do not lessen the importance of conventional requirements such as maintaining chemically and immunologically clean conditions (Supplementary Fig. 11), quality and stability of protein (or other) particle dispersion method (Supplementary Figs. 12 and 13), nor the numerous other physiochemical methods in use. However, alone, those are insufficient to prescribe the material properties, in the biological context.
We present data (Figs. 3, 4) for three characteristic shape groups (GNP1, 3, 4) that illustrate their structural properties, basic global biological read-outs, and the link between them. The (occasional) use of legacy “family” names may temporarily assist the reader to make connections to previous literature, but in reality their structural and biological identity lies in the geometrical parameterization, presented in the PC scatter plots, Fig. 3b, c. Nanospheres (GNP1) are included as a conventional reference point, as well as two types of shape ensemble with similar architectures (many tips protruding from a central core but with different overall sizes; “large nano-urchins”—GNP3a and “small nano-urchins”—GNP3b), and another branched shape family (“nanostar”—GNP4) with far fewer and much more developed tips, though of comparable overall size to GNP3b. The principal component scatter plots (Fig. 3b, c) for the different optimized particle ensembles reproducibly lead to probability distributions that are well separated. Recall that (since Fourier coefficients were normalized by the zeroth order-roughly speaking a mean radius) GNP3a and GNP3b, ensembles in this representation overlap, implying they have nearly identical architectures, with different overall (average) sizes. Conventional characterization of these shape ensembles were performed using differential centrifugation measurements (Fig. 3e) and UV-Vis-NIR absorption spectroscopy, showing the typical localized plasmon resonance peaks (Fig. 3f) that “fingerprints” the size and some aspects of architecture of the nanomaterials.
a Representative TEM images and cartoon for GNP1, 3a, 3b, and 4 (scale bars are 50 nm). b 3D and c 2D scatter plot of the principal components, d intra-batch probability density distribution, e differential centrifugal sedimentation (DCS) analysis expressed as relative number, f normalized UV–Vis-IR absorption spectra. Qualitatively, GNP3a and GNP3b have 15–20 tips (GNP3a tip length = 15–25 nm, GNP3b tip length = 10–15 nm) while GNP4 have 3–5 tips (tip length = 15–25 nm). g Representative TEM images for three independent batches of GNP3b (scale bars are 50 nm), h 3D and i 2D scatter plot of the principal components, j intra-batch probability density distribution, k DCS analysis expressed as relative number, and l normalized UV–Vis–IR absorption spectra.
The cells were treated with GNPs for 24 h. a Heatmap of genes identified in the microarray. Z-score hierarchical clustering based on Euclidean distance and average linkage. b Principal coordinate analysis (PCoA) illustrating the difference in transcriptome between treatment groups. The PCoA was conducted using Bray-Curtis dissimilarity matrices. c, d Volcano plot showing differentially expressed genes in comparison to untreated cells after incubation with GNP1 (c, in blue) and GNP3b (d, in green). e Gene ontology (GO) enrichment analysis for differentially expressed genes by Metascape. Bar graph showing top ten GO terms (biological process aspect) for GNP1 and GNP3b. f Network enrichment analysis by Metascape. Each term represents a node and colored by its cluster. Terms with similarity score >0.3 are linked by an edge, and the thickness of the edge represents the similarity score. The immunological response-related clusters impacted by GNP3b are highlighted.
It is worth stressing that the discipline and constraints imposed by these quantitative probability distribution analyses bring shape syntheses to a new level of reproducibility that is suitable for biological study. This occurs in part because the syntheses, even when already known in general outline, are now optimized with an approach (more reminiscent of conventional synthetic organic chemistry) in which we seek to reproduce the shape statistics, rather than conventional macroscopic physiochemical measurement. This guides the nature of the optimizations, but also presents a much stronger reproducibility constraint than merely overlapping of macroscopic measurements. Thus, (Fig. 3h, i) principal component shape scatter plots of three independent preparations of GNP3b-type particles have no discernible structural differences, nor any measurable difference in conventional physiochemical characterization. Other results (Supplementary Figs. 12 and 13) show a high level of time-dependent stability in different protein-stabilized dispersions used in biological studies. Such considerations allow us to design studies with the expectation that biological experiments should attain their intrinsic level of reproducibility. Then the reproducible biological read-outs can legitimately be causally connected to (the equally reproducible) nanoscale shape ensembles.
Shape ensembles differentiate biological responses at cell level
For illustration, we screen high-dimensional biological read-outs using the transcriptome of a murine dendritic cell line (JAWS II) exposed to quantified shape distributions. We use highly reproducible shape ensembles (Fig. 3) of fixed particle number, possessing narrow shape distribution, stably dispersed in ovalbumin, prior to presentation in the relevant mouse dendritic cell medium (see Supplementary Fig. 13). The whole cell transcriptomes for the three shape families (Fig. 4) have a high level of biological reproducibility in entirely independent experiments (Fig. 4a) and reveal considerable differentiation in the transcriptome between the particle shapes and the relevant controls. From the heatmap the particle ensembles exhibit three distinct profiles (Fig. 4a). The shape groups GNP1, GNP3a, and GNP3b result in significant overall changes in the cellular transcriptomes, but even with the more pronounced “tip” features, GNP4 has relatively few detectable impacts. Strikingly, despite their difference in overall size, the particle ensembles of GNP3a and GNP3b elicited similar cellular responses, suggesting that they may be considered (as they were defined structurally) to have similar biological identity. Principal coordinate analysis (PCoA) graphically illustrates the relationships between the transcriptomic profiles induced by the particle ensembles (Fig. 4b). Again, we see the high level of biological reproducibility (reflected in the repeat triangles) and separation (in the major principal component sub-space) in their biological profiling. Significantly, the near-orthogonality of regulation induced by groups GNP1 and GNP3 points towards a qualitatively different biological outcome. Volcano plots further highlight the differentially expressed genes (DEGs) in comparison to the untreated cells (Fig. 4c and d). With the thresholds of p-value <0.05 and fold-change of 1.5, the DEGs (colored dots) for GNP1 and GNP3b are 561 and 2725, respectively. Furthermore, when Metascape is used to infer enriched biological pathways and networks of the DEGs (Fig. 4e and f) the top ten gene ontology (biological process) enrichment terms show no overlap between the two shape groups, and these results together suggest quite distinct (orthogonal) biological shape-dependent outcomes.
We note carefully the stipulation that the purpose of such studies is to establish causal relationships between shape ensembles and cellular read-outs, and not to draw general conclusions for the biology. However, it is noted that four of the unique gene ontology (GO) terms in the dendritic cells response to GNP3b treatment are strongly associated with immunological processes. In Fig. 4f the intra- and inter-cluster interactions are further visualized by network enrichment analysis where GO terms are represented as nodes (colors based on their clusters) and their interactions represented by the strength of the links between the nodes. The results suggest that GNP3 ensembles stimulated three distinct immunological processes. Thus, while the two clusters of “inflammatory response” and “positive regulation of innate immune response” form a compact local large cluster, the other two enrichments of “response to interferon-gamma” and “adaptive immune response” are not linked, suggesting separate regulated processes of GNP3.
Whatever their broader biological implications, such results clearly suggest the potential for differentiated causal shape-dependent impact on sub-groups of biological pathways. It might be argued that, since the particles are nominally of the same material (gold), with same initial stabilizing protein (ovalbumin) and exchangeable cell culture medium dispersant, the results shed light also on the mechanism. However, to ensure clarity, and cast light on future investigations, we suggest such interpretations are premature, and the results do not even establish the level at which the causal linkage occurs. While one can speculate that aspects of the shape directly induce biological differentiation (via receptor clustering or local cytoskeleton stressing) it is also feasible that the shape is causally linked to other (for instance material surface) or surface corona organization aspects. Indeed, the fact that group GNP3 has a high density of features (and gaps between them) of the same size scale as the proteins adsorbed to them, may lead to an in situ corona not previously envisaged, and not presently understood. These are therefore complex questions that require significant efforts to unravel them, and in-depth in vivo investigation to understand the broader significance. Hopefully, the investment in such studies will be justified by the well-defined conceptual framework, and highly reproducible causal link between shape and biology.
Discussion
Since the work here represents quite new and possibly unfamiliar concepts in the quantitative linkage of nanoscale shape to biological (and potentially other) outcomes it is also worth considering thoughtfully and critically the issues that will frame the future. We see the absence of any such framework as currently limiting the fields capacity to create (meaningful) “reproducible” scientific research, to protect intellectual property or advance towards regulation as medical products.
However, it is fair to ask what level of detail we need to “define” material shapes (say for biological applications) beyond existing experimental approaches such as plasmonics, differential centrifugation times, and various forms of scattering. Evidently, such methods, currently used to minimally fingerprint materials in an effort to make them reproducible, are not useful proxies for population shape differences (especially subtle ones). They instead pick up generic particle differences (mostly quite unrelated to shape) and while it is reassuring if material batches have overlapping spectra, they cannot describe shape, capture its biologically relevant characteristics nor track evolution of shape distributions that correlate to biological outcomes. We, therefore, propose that shape features on this scale, if they are control factors in biological function, must now be captured by structural information that goes beyond such experimental measurements, or the “visual impressions” of electron microscope images.
Succinctly put, currently published results that cite “names of shapes” may (even unknowingly to the authors) refer in detail to complex and irreproducible mixtures, or label as “identical” quite different shape distributions that significantly and differentially affect the biology. That could confound the future development of the field.
That situation is very evident for crude heterogeneities. They, and their biological impacts, can be identified, eliminated, and those facts communicated within the framework presented here. For instance, a simple mixtures of quite distinct structures (an extreme example would be GNP1, GNP3b) can be quantified by (multiple peaks or anomalous line shapes) in even the simplest representation of the present method and limits of detection are set by (controllable) image capture statistics rather than resolution or representation limitations. Heterogenous populations composed of distinct sub-populations, each with different functional biological outcomes (for example GNP1,3b mixtures) when correlated with macroscopic averages of the biological endpoints (such as whole transcriptomes, proteomes, etc.) will be confounded by appearing as multiple additive pathway activation, or worse, interpreted in bioinformatics as non-existent connected pathways and should be eliminated. That much is clear.
There are, however, more subtle questions on which the broader future of the biological study of shape will depend. Thus, given the type of information captured here, to what level can quasi-homogenous (single shape group) but well spread shape distributions (parameterized by some median or average and principal component widths) be structurally distinguished from a “nearby” distribution with comparable widths, and how relevant will that resolution be in the exploration of shape-dependent biology. The answer to the first question is already relatively clear within the current paper, and populations that look “similar” can be definitively (and reproducibly) made, captured and recorded as distinct by virtue of the methods outlined here. Indeed, that is the power of high dimensional (e.g., Fourier) representations condensed (e.g., via principal components) to reduced representational dimensions for they have the capacity to capture, detect and quantify complex population differences that are otherwise hard to describe, or even observe.
The second question is whether that capacity to recognise multiple subtle, and (qualitatively) difficult-to-define changes will materially affect the destiny of nanoscale-shape-dependent biology. The answer to that question resides partly in understanding whether nanoscale shape-dependent biology will itself allow quite new and independent biological interventions. For example, if overall changes in shape are found to differentially and specifically target distinct biological outcomes (pathways, systems) then rather narrow and well-controlled (shape-surface) populations will amount to active agents (“drugs”), in a background of rather similar but less interesting nanostructures of the same chemical identity. We believe that is indeed the paradigm to expect, and that in the absence of methods such as those presented here we face the impossible task of searching for, identifying, and reporting on an “active agent” in a shape landscape by qualitative visual inspection. Evidently, the causal assignment linking those structural changes to biological (e.g., immunological or other) outcomes would also be challenging, and it would be impossible in a synthesis to recover identical shape populations. More fundamental (and with more profound long-term significance) the lack of a low dimensional quantitative structural “order parameter” that can be correlated with the biological outcome currently inhibits the development of “structure-function” hypotheses in which specific (low dimensional) aspects of the structure can be (meaningfully) associated with the biology, and act as the basis for further improvement on design.
Besides these specific interests, we may also credibly hypothesize a significant (if still poorly understood) role for particle shape in other important arenas. This includes environmental pollution, and the many associated (and growing) mysteries of human health (including immune regulation) involved there. Durable advances throughout will require the same quantitative approach to environmental dusts in terms of “substance definition” to help frame the strategy of investigations and reliably report the outcomes.
We believe, in time, these points will be established with growing clarity, as future research develops along more quantitative lines.
Methods
NPs contour extraction
All the TEM images were analyzed using the Open Source Computer Vision Library (https://opencv.org/). In particular, for the contour extraction the function cv2.findContours was employed. This function is an implementation of the algorithm for contour extraction proposed by Suzuki et al.68 Before extracting the contours, the original TEM grayscale images were transformed to binary and filtered (using again OpenCV). A threshold of 160 was used for the binary transformation and to smooth the image contours a blurring low-pass filter kernel was applied using a blur size of 16. Care was taken to manually confirm that all the contours extracted corresponded to NPs. Objects that were not NPs (e.g., the scalebars, see Supplementary Fig. 1) were manually removed from the database. The contours extracted, considering the resolution of the TEM images contain on average between 500 and 800 points. An example of an image and the resulting contour extraction is shown in Supplementary Figs. 1 and 2.
Contour normalization and resampling
The contours obtained are closed curves in 2D with coordinates ordered counter-clockwise. The coordinates are integer numbers (corresponding to the position of the pixels that make the contour in the image) connected horizontally, vertically or diagonally. Each shape was centered so that its center of mass lies on the origin, and the contours were transformed so that each pair of consecutive points were one-unit distance apart. This required adding a point between two diagonally connected points to form an L-shaped connection of three equally spaced points.
Discrete Fourier Transform (DFT) calculations
Each contour is made of N points. The njh point of the curve has coordinates xn, yn which are used to define the complex coordinate as zn =xn + iyn (where i is imaginary number). We then use the complex coordinates to perform a Discrete Fourier Transform (DFT) of a contour defined as:
where \(\hat z_k\) is kth Fourier coefficient and 1<k<N.
Average shape calculation
For each contour, the N Fourier coefficients calculated by using Eq. 1 were normalized for unitary L1norm. Also, a global phase was applied to all coefficients to make the first non-zero coefficient a pure real number. The number of coefficients thus obtained is the same as the number of points on the original contours. Since this number was not constant, the number of coefficients was decreased or increased by eliminating or adding zero-valued coefficients on the high frequency part of the Fourier transform, around the position N/2 and renormalizing to unity. If not stated otherwise, 1024 Fourier coefficients were used to describe the shapes.
For a set of N shapes belonging to a single group, a representation of the average shape of this group was extracted by finding a Fourier representation for each one that minimizes the sum over the whole set of the L1norm distance to the average (see Eq. 3). There are three operations that do not alter the shape itself but affect the phases of the Fourier coefficients: rotation, starting point, and mirroring. Any rotation in real space is equivalent to multiplying all the coefficients in Fourier space by a single imaginary number of unit norm, which affects the phase of each coefficient equally. This global phase was fixed by requiring, on the normalization procedure, that z2 is real.
The second operation, changing the starting point, results in a cyclical permutation of the ordered set {zn} which affects the phases of \(\left\{ {\hat z_n} \right\}\) in the following manner.
Let Tm be the operator that changes the starting point from z1 to zm then the new set of Fourier coefficient is given by:
Which only differ from the original set by their phase.
Finally, mirroring is equivalent to taking the complex conjugate of the coefficients. For these last two operations (mirroring and starting point), we iteratively tried every combination to obtain the desired coefficients, by minimizing the sum of the distances between each particle in the known (or training) set to the average shape of its group.
Average shape classification method (ASCM)
After calculating the average shape for each group, we compare the distance from the unknown shape’s Fourier coefficients to each average shape using the complex-valued coordinates of the Fourier space. The same restriction of real-valued \(\hat z_N\)(z2) was applied for rotation, and the distance was calculated for every combination of mirroring plus starting point permutation of the unknown particle. The particles were classified as belonging to the group with the minimum distance to its average shape.
In order to classify an unknown shape, we compare its L1norm distance to the center of each basin and assign it to the closest group. The L1norm on the complex coefficients is defined as usual. Let \(\left\{ {\hat a_n} \right\}\) and \(\left\{ {\hat b_n} \right\}\) be the N Fourier coefficients representing two different shapes, A and B. The L1norm distance between them is given by:
where \(\Re \left( z \right)\) and \(\Im \left( z \right)\) are the real and imaginary parts of the complex number z.
Nearest neighbor classification method (NNCM)
The Fourier coefficients obtained by using Eq. 1 are not directly useful for classification as they are scale, rotational and starting point dependent as pointed out before. One way to avoid this limitation is by the alignment explained above. Another option is to perform a normalization as the one reported by Sokic et al.64 This normalization first starts by calculating the normalization factor γ,
Then the normalized Fourier coefficients are:
Notice that the normalized coefficients \(\hat c_i\) are now real numbers and that the element n = 1 is not used. This shape signature was chosen as it is invariant under translation, under rotation and it does not depend on which point of the contour is selected as the initial point. In addition, the coefficients are also scale invariant.
Similar to the ASCM, to compare two contours using the normalized coefficients defined in Eq. 5, the L1norm distance between their set of \(\hat c_i\) was calculated. Considering two different shapes labeled as 1 and 2 and described by their set of normalized Fourier coefficients \(c_i^1\) and \(c_i^2\) where i = 2….N, the L1norm between them is calculated as follow:
From the experimental procedure and the image analysis developed, we obtained a number of contours for each type of NP studied (4 types in total). With the obtained contours a database for each NP type is generated by randomly selecting K contours of each type. Then an unknown NP is classified based on the following procedure: (1) The distances D (Eq. 6) between the unknown NP and each of the elements of the database are calculated. This will give 4K distances. (2) The unknown NP is then classified as the type for which the D is minimum.
Center of gravity classification method (CGCM)
We will call type A a database of any type of GNPs. This database is composed of M contours. We calculate the average normalized Fourier coefficient \(\hat c_i\) as:
The set of \(\left\langle {\hat c_i} \right\rangle \left( {i = 2 \ldots .N} \right)\) correspond to the Fourier coefficients’ Center of Gravity (CG) for the NP type A. Then the distance of any contour, say contour j, to the CG of the NPs of type A is given by:
Similar to the NNCM, a database of K contours for each NP type is generated. Then for each type of NP, the average normalized Fourier coefficient (Eq. 7) are calculated. Then an unknown NP is assigned to a shape group as follow: (1) The distances DA (Eq. 8) between the unknown NP and the average normalized Fourier coefficient for the 4 types of NPs are calculated. This gives 4 distances. (2) The unknown NP is then classified as the shape group for which the DA is minimum.
Principal component analysis (PCA)
In order to evaluate the particle classification methods, we performed a principal component analysis (PCA) on the space of the Fourier coefficients. In this way we can measure which coefficients contained more of the information necessary for the classification of the shapes. With the particles represented by complete Fourier coefficients in the way done for the calculation of the average shapes, in a 1024-dimensional space with complex coordinates, PCA is able to find a suitable base set of axes in this multidimensional space ranked in order of projections containing most of the statistical variance between samples, which in other words means the most information.
For example, one particular coefficient that has the same value for all particles obviously is of no help when trying to distinguish between them, and can safely be ignored, whereas a coefficient that has a wide range of values over all the particles may have a particular range of values associated with each particle group, and be instrumental in separating them. We are also interested in measuring how much information is lost by using only the magnitude of the Fourier coefficients (see above for details) as real-valued coordinates for the particles.
By interpreting each particle as a sample, and each Fourier coefficient as an independent variable, first, we subtract the center of mass of the whole set of particles in order to make them distributed around the origin with zero mean, then we calculate the covariance matrix of the entire population and find its eigenvectors which will be the principal components, in decreasing order of eigenvalue. Principal components are always orthogonal and normalized. In order to facilitate the comparisons and plotting between the different geometrical spaces, the full complex Fourier coefficients versus real-valued magnitudes, we treated each part of the complex number for the full coefficients as different variables \(\left\{ {\hat \zeta _n} \right\}\)by separating each Fourier coefficient into its real and imaginary parts, which doubles the number of coordinates but now both spaces have a similar range of values, and the same scale, so their variances are directly comparable for further analysis.
where \(\Re \left( z \right)\) and \(\Im \left( z \right)\) are the real and imaginary parts of the complex number z.
It is remarkable that a small number of principal components are able to accurately separate the particles into groups, even if in the analysis we considered the whole set of particles as “database” for classification. Because the phase of the Fourier coefficients of the particles have been aligned explicitly to calculate the representation with the minimal spread around the center of gravity for each group, the number of misclassified particles is very small, and composed of some malformed particles that are not very good representatives of their respective groups. It is also noticeable (see Supplementary Table 2) that the principal components are almost entirely aligned with just two Fourier coefficients, suggesting that these two coefficients would be enough to classify an unknown particle in a computationally cheap way that involves very little calculation.
The first two principal components (Fig. 2a) for the \(\hat \zeta\) add up to 95% of their respective magnitudes:
where \(\vec \zeta\) is to be interpreted as a unitary vector in the direction of this coefficient, and \({\it{\epsilon }}\) is a small contribution from other coefficients. Likewise, for the \(\left| {\hat z} \right|\) space (real normalized coefficients), the first 2 principal components are:
As we can see, they are practically the same, and furthermore they are practically aligned with the coefficients \(\left| {\hat z_2} \right|\) and \(\left| {\hat z_{1024}} \right|\) that we labeled 1st PC and 2nd PC in Fig. 2a, which shows that we can achieve a good separation in clusters without losing much information by using only these two descriptors for each particle.
Transcriptome analysis
A mouse dendritic cell line, JAWS II, was purchased from ATCC (ATCC® CRL-11904™). The cells were maintained in complete culture medium consisting of Alpha MEM with ribonucleotides, deoxyribonucleosides (Gibco) with 10% heated-inactivated fetal bovine serum (FBS) (Gibco), 4 mM l-glutamine (Gibco), 10 U mL−1 penicillin and 100 μg mL−1 streptomycin (Gibco), 1 mM sodium pyruvate (Gibco), and 5 ng mL−1 murine GM-CSF (pre-Protech).
For treatment with GNPs, 1.5 × 105 cells were seeded in 12-well plates in the complete culture media for 48 h prior to the treatment. 3 × 1010 OVA-coated GNPs were dispersed in 1 mL of serum free mouse dendritic cell culture media (Celprogen), added to each well, and incubated with the cells for 24 h. The GNP treatment was performed in replicates and repeated independently 2 or 3 times. Subsequently, the cells were washed with 500 µL of PBS once, and total RNA was extracted according to the manufactory instructions of InviTrap® Spin Universal RNA Mini Kit. The concentration and purity of extracted RNA were confirmed by Bioanalyzer. The samples were then transferred to RNA stable tubes (Sigma Aldrich), dried out in a vacuum, and ready for Whole-Mouse Genome One-Color Microarray (Agilent) analysis.
After correcting background and filtering low intensity signals, 16418 probes were identified. Data are expressed in the mean of replicates in log2 scale. p-value was calculated by one sample T-Test. Differentially Expressed Genes (DEGs) in comparison to untreated were determined by fold-change > = 1.5 and p-value < 0.05. The heatmap was generated by Morpheus (https://software.broadinstitute.org/morpheus). The Gene ontology (GO) enrichment analysis was performed by Metascape (http://metascape.org/gp/index.html#/main/step1).
Data availability
The datasets generated and analyzed during the current study are available in the Figshare repository, https://doi.org/10.6084/m9.figshare.11948886. The deposit is entitled: Supplementary dataset for “Classification and Biological Identity of Complex Nano Shapes”—a submission to Communications Materials.
Code availability
The code used to generate the data produced in this study is available in the Figshare repository, https://doi.org/10.6084/m9.figshare.11948886. The deposit is entitled: Supplementary dataset for “Classification and Biological Identity of Complex Nano Shapes”—a submission to Communications Materials.
Change history
10 May 2021
A Correction to this paper has been published: https://doi.org/10.1038/s43246-021-00155-w
References
Salvati, A. et al. Transferrin-functionalized nanoparticles lose their targeting capabilities when a biomolecule corona adsorbs on the surface. Nat. Nanotechnol. 8, 137–143 (2013).
Lundqvist, M. et al. Nanoparticle size and surface properties determine the protein corona with possible implications for biological impacts. Proc. Natl Acad. Sci. USA 105, 14265–14270 (2008).
Monopoli, M. P., Aberg, C., Salvati, A. & Dawson, K. A. Biomolecular coronas provide the biological identity of nanosized materials. Nat. Nanotechnol 7, 779–786 (2012).
Monopoli, M. P. et al. Physical−chemical aspects of protein corona: relevance to in vitro and in vivo biological impacts of nanoparticles. J. Am. Chem. Soc. 133, 2525–2534 (2011).
Lara, S. et al. Identification of receptor binding to the biomolecular corona of nanoparticles. ACS Nano 11, 1884-1893 (2017).
Alnasser, F. et al. Graphene nanoflakes uptake mediated by scavenger receptors. Nano Lett. 19, 1260-1268 (2019).
Talamini, L. et al. Influence of size and shape on the anatomical distribution of endotoxin-free gold nanoparticles. ACS Nano, 11, 5519-5529 (2017).
Castagnola, V. et al. Towards a classification strategy for complex nanostructures. Nanoscale Horiz. 2,187–198 (2017).
Xu, M. et al. How entanglement of different physicochemical properties complicates the prediction of in vitro and in vivo interactions of gold nanoparticles. ACS Nano 12, 10104–10113 (2018).
Chithrani, B. D., Ghazani, A. A. & Chan, W. C. Determining the size and shape dependence of gold nanoparticle uptake into mammalian cells. Nano Lett. 6, 662–668 (2006).
Wang, J. et al. Physical activation of innate immunity by spiky particles. Nature Nanotechnol. 13, 1078-1086 (2018).
Decuzzi, P. et al. Size and shape effects in the biodistribution of intravascularly injected particles. J. Control. Release 141, 320–327 (2010).
Rivera Gil, P., Oberdörster, G. N., Elder, A., Puntes, V. C. & Parak, W. J. Correlating physico-chemical with toxicological properties of nanoparticles: the present and the future. ACS Nano 4, 5527–5531 (2010).
Tang, M. L., Liu, N., Dionne, J. A. & Alivisatos, A. P. Observations of shape-dependent hydrogen uptake trajectories from single nanocrystals. J. Am. Chem. Soc. 133, 13220–13223 (2011).
Glotzer, S. C. Nanotechnology: shape matters. Nature 481, 450 (2012).
Libbrecht, K. G. The physics of snow crystals. Rep. Prog. Phys. 68, 855 (2005).
Kelly, K. L., Coronado, E., Zhao, L. L. & Schatz, G. C. The optical properties of metal nanoparticles: the influence of size, shape, and dielectric environment. The J. Phys. Chem. B 107, 668–677 (2003).
Zhao, Y. et al. Shape-controlled deterministic assembly of nanowires. Nano Lett. 16, 2644–2650 (2016).
Nakayama, K., Tanabe, K. & Atwater, H. A. Plasmonic nanoparticle enhanced light absorption in GaAs solar cells. Appl. Phys. Lett. 93, 121904 (2008).
Horton, M. R., Manley, S., Arevalo, S. R., Lobkovsky, A. E. & Gast, A. P. Crystalline protein domains and lipid bilayer vesicle shape transformations. J. Phys. Chem. B 111, 880–885 (2007).
Yang, P. & Lieber, C. M. Nanorod-superconductor composites: a pathway to materials with high critical current densities. Science 273, 1836–1840 (1996).
Osberg, K. D. et al. Dispersible gold nanorod dimers with sub-5 nm gaps as local amplifiers for surface-enhanced Raman scattering. Nano Lett. 12, 3828–3832 (2012).
Horsch, M. A., Zhang, Z. & Glotzer, S. C. Self-assembly of polymer-tethered nanorods. Phys. Rev. Lett. 95, 056105 (2005).
Nikoobakht, B. & El-Sayed, M. A. Preparation and growth mechanism of gold nanorods (NRs) using seed-mediated growth method. Chem. Mater. 15, 1957–1962 (2003).
Murphy, C. J. et al. Gold nanoparticles in biology: beyond toxicity to cellular imaging. Acc. Chem. Res. 41, 1721–1730 (2008).
Durr, N. J. et al. Two-photon luminescence imaging of cancer cells using molecularly targeted gold nanorods. Nano Lett. 7, 941–945 (2007).
Grabinski, C. et al. Effect of gold nanorod surface chemistry on cellular response. ACS Nano 5, 2870–2879 (2011).
Ye, X. et al. Improved size-tunable synthesis of monodisperse gold nanorods through the use of aromatic additives. ACS Nano 6, 2804–2817 (2012).
Lin, H. et al. Clathrate colloidal crystals. Science 355, 931–935 (2017).
Grzelczak, M., Pérez-Juste, J., Mulvaney, P. & Liz-Marzán, L. M. Shape control in gold nanoparticle synthesis. Chem. Soc. Rev. 37, 1783–1791 (2008).
Cozzoli, P. D. et al. Colloidal synthesis and characterization of tetrapod-shaped magnetic nanocrystals. Nano Lett. 6, 1966–1972 (2006).
Ahmadi, T. S., Wang, Z. L., Green, T. C., Henglein, A. & El-Sayed, M. A. Shape-controlled synthesis of colloidal platinum nanoparticles. Science 272, 1924 (1996).
Sun, Y. & Xia, Y. Shape-controlled synthesis of gold and silver nanoparticles. Science 298, 2176–2179 (2002).
Xia, Y. & Halas, N. J. Shape-controlled synthesis and surface plasmonic properties of metallic nanostructures. MRS Bull. 30, 338–348 (2005).
Li, N., Zhao, P. & Astruc, D. Anisotropic gold nanoparticles: synthesis, properties, applications, and toxicity. Angew. Chem. Int. Ed. 53, 1756–1789 (2014).
Lee, H.-E. et al. Amino-acid-and peptide-directed synthesis of chiral plasmonic gold nanoparticles. Nature 556, 360 (2018).
Han, D. et al. DNA origami with complex curvatures in three-dimensional space. Science 332, 342–346 (2011).
Gentleman, D. J. & Chan, W. C. A systematic nomenclature for codifying engineered nanostructures. Small 5, 426–431 (2009).
Bigdeli, A., Hormozi-Nezhad, M. R., Jalali-Heravi, M., Abedini, M. R. & Sharif-Bakhtiar, F. Towards defining new nano-descriptors: extracting morphological features from transmission electron microscopy images. RSC Adv. 4, 60135–60143 (2014).
Rice, K. P., Saunders, A. E. & Stoykovich, M. P. Classifying the shape of colloidal nanocrystals by complex Fourier descriptor analysis. Cryst. Growth.Des. 12, 825–831 (2012).
Miernicki, M., Hofmann, T., Eisenberger, I., von der Kammer, F. & Praetorius, A. Legal and practical challenges in classifying nanomaterials according to regulatory definitions. Nature Nanotechnol. 14, 208 (2019).
Ling, H. & Jacobs, D. W. Shape classification using the inner-distance. IEEE T Pattern Anal. Mach. Intell. 29, 286–299 (2007).
Liang, H. et al. Asymmetric silver “nanocarrot” structures: Solution synthesis and their asymmetric plasmonic resonances. J. Am. Chem. Soc. 135, 9616–9619 (2013).
Yuan, H. et al. Gold nanostars: surfactant-free synthesis, 3D modelling, and two-photon photoluminescence imaging. Nanotechnology 23, 075102 (2012).
Zhao, L. et al. Formation and stability of gold nanoflowers by the seeding approach: the effect of intraparticle ripening. J. Phys. Chem. C 113, 16645–16651 (2009).
Bakr, O. M., Wunsch, B. H. & Stellacci, F. High-yield synthesis of multi-branched urchin-like gold nanoparticles. Chem. Mater. 18, 3297–3301 (2006).
Wang, R. et al. Experimental determination and analysis of gold nanorod settlement by differential centrifugal sedimentation. RSC Adv. 6, 43496–43500 (2016).
Carney, R. P. et al. Determination of nanoparticle size distribution together with density or molecular weight by 2D analytical ultracentrifugation. Nat. Commun. 2, 335 (2011).
Sharma, V., Park, K. & Srinivasarao, M. Shape separation of gold nanorods using centrifugation. Proc. Natl Acad. Sci. USA 106, 4981–4985 (2009).
Brown, P. H. & Schuck, P. Macromolecular size-and-shape distributions by sedimentation velocity analytical ultracentrifugation. Biophys. J. 90, 4651–4661 (2006).
Potenza, M. et al. Detecting the shape of anisotropic gold nanoparticles in dispersion with single particle extinction and scattering. Nanoscale 9, 2778–2784 (2017).
Finney, E. E. & Finke, R. G. Nanocluster nucleation and growth kinetic and mechanistic studies: a review emphasizing transition-metal nanoclusters. J. Colloid Interf. Sci. 317, 351–374 (2008).
Frens, G. Controlled nucleation for the regulation of the particle size in monodisperse gold suspensions. Nature 241, 20–22 (1973).
Thanh, N. T., Maclean, N. & Mahiddine, S. Mechanisms of nucleation and growth of nanoparticles in solution. Chem. Rev. 114, 7610–7630 (2014).
Turkevich, J., Stevenson, P. C. & Hillier, J. A study of the nucleation and growth processes in the synthesis of colloidal gold. Discuss. Faraday Soc. 11, 55–75 (1951).
Gast, A. P. & Monovoukas, Y. A new growth instability in colloidal crystallization. Nature 351, 553 (1991).
Jana, N. R., Gearheart, L. & Murphy, C. J. Seed-mediated growth approach for shape-controlled synthesis of spheroidal and rod-like gold nanoparticles using a surfactant template. Adv. Mater. 13, 1389 (2001).
Bals, S., Goris, B., Liz‐Marzán, L. M. & Van Tendeloo, G. Three‐dimensional characterization of noble‐metal nanoparticles and their assemblies by electron tomography. Angew. Chem. Int. Ed. 53, 10600–10610 (2014).
Levin, B. D. et al. Nanomaterial datasets to advance tomography in scanning transmission electron microscopy. Sci. Data 3, 160041 (2016).
Midgley, P. A., Ward, E. P., Hungría, A. B. & Thomas, J. M. Nanotomography in the chemical, biological and materials sciences. Che.Soc. Rev. 36, 1477–1494 (2007).
Bowman, E. T., Soga, K. & Drummond, W. Particle shape characterisation using Fourier descriptor analysis. Geotechnique 51, 545–554 (2001).
Sokic, E. & Konjicija, S. in Content-Based Multimedia Indexing (CBMI), 2014 12th International Workshop on Content-Based Multimedia Indexing (CBMI). 1–4 (IEEE).
Vranic, D. & Saupe, D. 3D Shape Descriptor Based n 3D Fourier Transform in Proceedings of the EURASIP Conference on Digital Signal Processing for Multimedia Communications and Services, Budapest, Hungary, pp. 271–274, (2001).
Zhang, D. & Lu, G. A comparative study of curvature scale space and Fourier descriptors for shape-based image retrieval. J. Visual Commun. Image R. 14, 39–57 (2003).
Zhang, D. & Lu, G. Shape-based image retrieval using generic Fourier descriptor. Signal Process. Image Commun. 17, 825–848 (2002).
Zhang, H. & Fiume, E. in Shape Modeling International, 2002. Proceedings. 261-268 (IEEE).
Li, J. et al. Controllable synthesis of stable urchin-like gold nanoparticles using hydroquinone to tune the reactivity of gold chloride. J. Phys. Chem. C 115, 3630–3637 (2011).
Suzuki, S. Topological structural analysis of digitized binary images by border following. Comput. Vis. Graph. Image Process. 30, 32–46 (1985).
Acknowledgements
This work was supported by Science Foundation Ireland under SIRG (Funding Agency Ref. No: 15/SIRG/3423) (Y.Y., V.A.G.) and SFI-NSFC Partnership (Funding Agency Ref. No: 17/NSFC/4898) (K.A.D.). K.A.D. acknowledges the funding of Guangdong Provincial Education Department Key Laboratory of Nano-Immunoregulation Tumor Microenvironment (2019KSYS008). H. L., V.C., and Q.C. acknowledge financial support from the Irish Research Council (H.L., EPSPD/2015/5; V.C., GOIPD/2016/128; Q.C., GOIPG/2014/874). Q.C. and W.Z and J.L. acknowledge Chinese Scholarship Council (agreement no. 201408300003 and 201706220062 and 201508300009). J.M.A. acknowledges CNPq for support through Bolsa de Produtividade em Pesquisa No. 313431/2018-3. The work described in this article, prior to reaching this level, evolved over some years with contributions from Authors and other previous researchers at the Center for BioNano Interactions (CBNI), University College Dublin. They were helpful in bringing the work to the present stage of development. Inge Nelissen performed the gene array measurements. Marco Monopoli and Zeljka Krpetic were involved in early phases when syntheses and dispersions of shape particles were quite irreproducible, and helped parameterize the nature of the problems involved. Marco Monopoli played a significant role in the early thinking on dispersion stability. Camila P. Silveira also played a significant role in collaboration with Q.C. in unravelling various aspects of the irreproducibility. More recently, James Behan played a significant role, working with L.B. and V.C., in supporting the transition to fully reproducible syntheses. Ban Zhan (visiting student to CBNI) collaborated with Y.Y. on running the PCoA analysis. Zengchun Xie and Eoin O’Neill both extracted and analyzed contours.
Author information
Authors and Affiliations
Contributions
Y.Y. and K.A.D. conceived and developed the overall concept of shape specification and its relationship to biology, developed the methods and approaches, lead the overall project. Y.Y. lead the project overall, including biological development, established working methods for the materials in biology, interpreted and supervised the experiments. Both wrote the paper. L.B. and V.C. helped develop the ideas behind the work and played a leading role in that. V.C. was central to design of overall approach to synthesis, including implementing numerous technical developments that lead to reproducibility, supervised the synthesis experiments for part of the projects evolution, and wrote the paper. V.C. and L.B. supported and carried out some of the synthetic and characterization experiments, and Q.C. persisted with many of the key experiments during the transition to more reproducible phase of synthesis, during which the problems were more fully clarified. L.B. and W.Z. worked together to achieve highly reproducible syntheses, and W.Z. finally achieved almost complete reproducibility for the shapes reported. All three extracted contours of nanoparticles. H.L. was central to the design and writing the codes, and perform the computational experiments, and contributed to the paper. H.L, A.M. and J.M.A. helped design some of the computational experiments and interpretations. H.L, A.M., and J.M.A. tested the reproducibility of the computational analysis. All of the above contributed to the writing of the paper. V.A.G. and J.L. independently extracted the RNA, and worked with Y.Y. to reproduce the biological data. J.C. performed the 3D tomography.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Boselli, L., Lopez, H., Zhang, W. et al. Classification and biological identity of complex nano shapes. Commun Mater 1, 35 (2020). https://doi.org/10.1038/s43246-020-0033-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43246-020-0033-2
This article is cited by
-
Chiral self-assembly of cellulose nanocrystals is driven by crystallite bundles
Nature Communications (2022)
-
Current understanding of biological identity at the nanoscale and future prospects
Nature Nanotechnology (2021)
-
The route towards nanoparticle shape metrology
Nature Nanotechnology (2020)