Abstract
Weyl semimetals are characterized by the presence of massless band dispersion in momentum space. When a Weyl semimetal meets magnetism, large anomalous transport properties emerge as a consequence of its topological nature. Here, using in−situ spin- and angle-resolved photoelectron spectroscopy combined with ab initio calculations, we visualize the spin-polarized Weyl cone and flat-band surface states of ferromagnetic Co2MnGa films with full remanent magnetization. We demonstrate that the anomalous Hall and Nernst conductivities systematically grow when the magnetization-induced massive Weyl cone at a Lifshitz quantum critical point approaches the Fermi energy, until a high anomalous Nernst thermopower of ~6.2 μVK−1 is realized at room temperature. Given this topological quantum state and full remanent magnetization, Co2MnGa films are promising for realizing high efficiency heat flux and magnetic field sensing devices operable at room temperature and zero-field.
Similar content being viewed by others
Introduction
When electric and thermal currents flow through a ferromagnet, an electric field emerges orthogonally to the current path. The two effects are, respectively, called the anomalous Hall (AHE) and Nernst (ANE) effects and are exploited as operating mechanisms in various novel applications such as energy harvesting1,2, magnetic sensor3, and heat flux sensing4. The associated transverse voltage of the electric field is empirically proportional to its spontaneous magnetization. In contrast to the general belief, recent discoveries of both large AHE and ANE, which do not scale with magnetization, have elicited great surprise5,6,7,8,9,10. In particular, the observed ANE thermopower of single crystalline bulk Co2MnGa at room temperature, ~6.0 μV K−1 is an order of magnitude larger than that of other ferromagnets with similar magnetizations7,9. These transverse properties are postulated to arise from a Berry curvature emerging within band structures near the Fermi energy (EF)11,12.
Topologically non-trivial Weyl semimetals possessing spin-split massless fermions characterized by zero-gap and linear band dispersions are promising candidates featuring a large Berry curvature13,14,15. Weyl fermions in solids can be realized in materials that break inversion symmetry or time-reversal symmetry. With the breaking of such symmetries, Weyl nodes appear as pairs in momentum space and act as magnetic monopoles with positive and negative chiralities16. To date, Weyl fermions have been verified in experiments in non-centrosymmetric (e.g., TaAs-family) and magnetic materials (e.g., Mn3Sn) through angle-resolved photoelectron spectroscopy (ARPES) and magneto-transport measurements8,17,18,19,20,21,22,23,24,25,26.
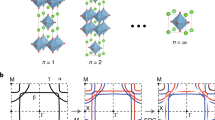
Recently, a Co2MnGa Heusler alloy has also been theoretically predicted to be a ferromagnetic Weyl semimetal with a high Curie temperature and has been experimentally demonstrated in the bulk form to exhibit large anomalous transport properties under an external magnetic field7,9,27. The nature of this highly symmetric crystal (Fig. 1a) creates mirror-symmetry-protected Weyl nodal lines in the band structure as encountered by theory and experiments28,29. However, the nodal lines lead to vanishing Berry curvature when integrated over the whole Brillouin zone30,31 and cannot explain the observed phenomena. One way to obtain a large Berry curvature is to gap out their nodal lines using remanent magnetization or an external magnetic field (specifically, to break the mirror symmetry). Yet, the experimental evidence for broken mirror symmetry was not provided by the recent ARPES measurement on bulk Co2MnGa crystal because the remanent magnetization was negligible as applying external magnetic fields is not permitted in this measurement. For practical applications in which zero-field operation and gigantic outputs are a requirement, it is thus indispensable to truly understand the band structure responsible for the anomalous transport properties in films with full remanent magnetization.
a Schematic of the L21-ordered structure of Co2MnGa. Dependence on perpendicular external magnetic field (Hz) of b \({\rho }_{yx}^{{\rm{A}}}\) and c \({E}_{xy}^{{\rm{A}}}\) normalized by given temperature gradient ∇Tx in the Co2MnGa films. d \({E}_{xy}^{{\rm{A}}}\) measured by giving the perpendicular temperature gradient ∇Tz and sweeping the in-plane magnetic field Hx for the sample with Nv = 28.5. Dependence on total valence electron number Nv of e ρxx, f \({\rho }_{yx}^{{\rm{A}}}\), g \({\sigma }_{xy}^{{\rm{A}}}\), h Sxx, i \({S}_{xy}^{{\rm{A}}}\), SI and SII and j \({\alpha }_{xy}^{{\rm{A}}}\). Green dashed lines in e–j indicate Nv for the stoichiometric composition. All error bars represent standard deviation. k Relationship between \({\alpha }_{xy}^{{\rm{A}}}\) vs. \({\sigma }_{xy}^{{\rm{A}}}\) in our Co2MnGa films (red circles) and different magnets (gray squares: taken from ref. 34).
Here, we experimentally and theoretically investigated the topological band structure and anomalous transport properties of ferromagnetic Co2MnGa thin films. Growth of high-quality thin films possessing full remanent magnetization and in situ spin-resolved ARPES (SARPES) measurements permit access to their non-trivial band structures modified by the broken mirror symmetry. We observed spin-polarized Weyl cones located mostly at a Lifshitz quantum critical point and a flat band of surface states. Furthermore, when the energy associated with the massive Weyl cone approaches EF, the anomalous Hall and Nernst conductivities systematically increase as the electron number rises. In particular, the ANE reaches thermopower of ~6.2 μV K−1 at room temperature, which is the highest amongst magnetic films to the best of our knowledge.
Results and discussion
AHE and ANE properties of epitaxial Co2MnGa films
To examine the influence of the relative location of the Weyl cone-associated energy with respect to EF on the transverse transport properties, we grew epitaxial Co2MnGa films with different compositions and investigated their AHE and ANE properties. Highly L21-ordered structure was confirmed in all Co2MnGa films by the quantitative analysis of X-ray diffraction patterns with taking the off-stoichiometry in each film into account (Supplementary Fig. 1 and the associated text). Figure 1b, c show the dependence on the perpendicular external magnetic field μ0Hz of the anomalous Hall resistivity \({\rho }_{yx}^{{\rm{A}}}\) and the normalized transverse thermoelectric voltage \({E}_{xy}^{{\rm{A}}}\) for Co2MnGa films with different compositions labeled H8, H7, H5, H1, and E2 (see Table 1), leading to a different number of valence electrons (Nv) ranging from 25.6 (H8) to 28.5 (E2). These curves clearly show that for all these films the respective magnitude of the AHE and the ANE changes significantly depending on the composition ratio of Co2MnGa regardless of its atomic ordering. It should be mentioned that here we apply the ∇Tx and Hz for evaluating the thermopower of the ANE strictly, causing no ANE signal at μ0Hz = 0 as the spontaneous magnetization does not appear to the z-direction due to the strong demagnetization field. Thus, we also measured ANE signal by applying the ∇Tz and sweeping the magnetic field in the plane and observed clear ANE voltage at zero-field due to the perfect spontaneous in-plane magnetization as shown in Fig. 1d, which is advantageous to thermoelectric applications such as heat flux sensor4.
Resistivity \({\rho }_{yx}^{{\rm{A}}}\) and thermopower \({S}_{xy}^{{\rm{A}}}\) (Fig. 1f, i) were estimated by finding the intercept of the linear-fitted curve for the saturation region in Fig. 1b, c, respectively. From Fig. 1e, f, ρxx monotonically decreases with increasing Nv, whereas \({\rho }_{yx}^{{\rm{A}}}\) has a maximum value of 22.5 μΩ cm at around Nv = 27.3–27.4. \({\sigma }_{xy}^{{\rm{A}}}\) evaluated from \({\sigma }_{xy}^{{\rm{A}}}\) = \({\rho }_{yx}^{{\rm{A}}}\)/(\({\rho }_{xx}^{2}\) + \({{\rho }_{yx}^{{\rm{A}}}}^{2}\)) exhibits a nearly monotonic increase from 2 S cm−1 at Nv = 25.6 to 485 S cm−1 at 28.5 (Fig. 1g).
Figure 1h displays the Nv dependence of the Seebeck coefficient Sxx. In the small Nv region, Sxx is positive and gradually decreases with Nv changing sign at Nv = 26.7. A very tiny ANE is observed in the small Nv region (Fig. 1i); for instance, 0.3 μV K−1 at Nv = 25.6. Interestingly, \({S}_{xy}^{{\rm{A}}}\) increases steeply with increasing Nv with the largest \({S}_{xy}^{{\rm{A}}}\) achieved being 6.2 μV K−1 at Nv = 27.3, which is the highest in the ferromagnetic thin films32,33 and slightly smaller than the highest value in bulk Co2MnGa ~ 8.0 μV K−134. \({S}_{xy}^{{\rm{A}}}\) is obtained from the linear response equation
Here, αxx and \({\alpha }_{xy}^{{\rm{A}}}\) are the longitudinal and transverse thermoelectric conductivities, respectively. This equation indicates that there are two different phenomenological contributions to ANE. To simplify our explanation, we denote the associated terms as SI = \({\rho }_{xx}{\alpha }_{xy}^{{\rm{A}}}\) and SII = \(-{\rho }_{yx}^{{\rm{A}}}{\alpha }_{xx}\). As mentioned in refs. 35,36, SII is regarded as the contribution of AHE to ANE induced by a Seebeck-driven longitudinal current. Similarly, SI stems from the direct conversion from a temperature gradient to a transverse current via \({\alpha }_{xy}^{{\rm{A}}}\). SII can be converted to \(-{S}_{xx}{\rho }_{yx}^{{\rm{A}}}/{\rho }_{xx}\), enabling a direct estimate from experimental data plotted in Fig. 1i. One clearly views the contribution of SII to \({S}_{xy}^{{\rm{A}}}\) to be very limited. Therefore, SI\((={S}_{xy}^{{\rm{A}}}-{S}_{{\rm{II}}})\) dominates the observed \({S}_{xy}^{{\rm{A}}}\) over the whole range of Nv. Transverse thermoelectric conductivity \({\alpha }_{xy}^{{\rm{A}}}\) estimated from SI and ρxx increases enormously with Nv in a similar way to \({\sigma }_{xy}^{{\rm{A}}}\) and has a maximal value of 3.3 A m−1K−1 at Nv = 28.5 (Fig. 1j). Figure 1k shows the relationship between \({\alpha }_{xy}^{{\rm{A}}}\) and \({\sigma }_{xy}^{{\rm{A}}}\) at 300 K for Co2MnGa films compared to other magnets. A previous study by Xu et al.34 clarified that many topological magnets have a universal relationship \({\alpha }_{xy}^{{\rm{A}}}/{\sigma }_{xy}^{{\rm{A}}} \sim {k}_{{\rm{B}}}/e\). Thus, we examined this ratio in our present samples as shown in Fig. 1k. While both \({\alpha }_{xy}^{{\rm{A}}}\) and \({\sigma }_{xy}^{{\rm{A}}}\) are enhanced more than one order of magnitude by increasing Nv from 25.6 to 28.5, we confirmed that the \({\alpha }_{xy}^{{\rm{A}}}/{\sigma }_{xy}^{{\rm{A}}}\) ratios of our Co2MnGa films also follow this universal behavior. It signifies that the main origin of AHE and ANE in all Co2MnGa films comes from the intrinsic topological nature34.
We also found that ρxx decreases with increasing Nv whereas \({S}_{xy}^{{\rm{A}}}\) increases in our Co2MnGa films (Fig. 1e, i). This relation between ρxx and \({S}_{xy}^{{\rm{A}}}\) is opposite to that reported in Co3Sn2S2, where \({S}_{xy}^{{\rm{A}}}\) is enhanced by increasing ρxx37. It is worth mentioning that this discrepancy arises from a difference in an origin of enlargement of \({S}_{xy}^{{\rm{A}}}\). Namely, Ding et al. prepared Co3Sn2S2 single crystals having different impurity concentrations and found that the impurity scatterings in Co3Sn2S2 enlarge ρxx but preserve \({\alpha }_{xy}^{{\rm{A}}}\), resulting in the enlargement of \({S}_{xy}^{{\rm{A}}}\) through SI term. On the other hand, this study tunes the position of EF by adjusting the composition of Co2MnGa film, leading to a drastic enlargement of \({\alpha }_{xy}^{{\rm{A}}}\) with Nv which is large enough to overcome the reduction of ρxx, thus \({S}_{xy}^{{\rm{A}}}\) is enhanced through SI term as well.
Theoretical calculations
To understand the origin of the strong Nv dependence of AHE and ANE, we have performed ab initio calculations. Figure 2a shows the band structure of Co2MnGa along the X–K line at kz = 2π/a and along the K–Γ–W line at kz = 0 plane in the Brillouin zone (Fig. 2h). The red and blue dashed lines represent the majority- and minority-spin bands, respectively, in the absence of the spin–orbit interaction (SOI). A large minority-spin hole pocket is found around Γ, whereas majority-spin bands dominate near EF around X, K, and W and form crossing bands, labeled A through E. Previous studies have shown that such majority-spin band structures have three types of Weyl nodal loops in the Brillouin zone reflecting mirror symmetries with respect to the ki = 0 planes (i = x, y, z)9,15,28,38,39. For example, the nodal points of bands C and D in Fig. 2a are connected by the nodal loop shown in Fig. 2h.
a Band structures and calculated, b \({\sigma }_{xy}^{{\rm{A}}}\), and c \({\alpha }_{xy}^{{\rm{A}}}\) of L21-ordered Co2MnGa. d−g Berry curvatures Ωz(k) calculated at E − EF = 0.05, 0.03, 0, and −0.08 eV, respectively. h Three-dimensional view of the Weyl nodal lines in the first and second Brillouin zones of Co2MnGa, where the kz = 0 and kz = 2π/a planes are highlighted, in the absence of SOI. Color corresponds to the location of the Weyl node. i Same as h but with SOI and magnetization along [100]. The blue arrow indicates the direction of magnetization.
When the SOI and the magnetization along the [100] direction are taken into account, only the mirror plane kx = 0 remains; the other planes disappear. This is because the mirror plane perpendicular to the magnetization conserves the direction of spins whereas that parallel to the magnetization does not9,15,38,39. Once the SOI is present, the energy gaps open at all points of the Weyl cones A–E, since the mirror symmetry is broken with respect to the kz = 0 and the kz = 2π/a planes (Fig. 2a, gray curves). Specifically, several Weyl nodal loops collapse and become massive (gapped) Weyl cones, and only those protected by kx = 0 mirror symmetry survive (Fig. 2i and Supplementary Fig. 7). Here, we emphasize that the gapped Weyl cones A and C are tilted, most being at a Lifshitz quantum critical point between type-I and type-II Weyl fermions.
From the calculated anomalous Hall conductivity \({\sigma }_{xy}^{{\rm{A}}}\) (Fig. 2b), we see that \({\sigma }_{xy}^{{\rm{A}}}\) has large values of ~103 S cm−1 and exhibit a peak near EF, consistent with previous results7,9. In Fig. 2c, we show the calculated transverse thermoelectric conductivity \({\alpha }_{xy}^{{\rm{A}}}\). Around E = EF, \({\alpha }_{xy}^{{\rm{A}}}\) increases with increasing E − EF (i.e., by electron doping) and takes a maximum at E − EF = 0.07 eV, near to where \({\sigma }_{xy}^{{\rm{A}}}\) sharply drops (Fig. 2b). This is reasonable as \({\alpha }_{xy}^{{\rm{A}}}\) is approximately proportional to \(-{\rm{{d}}}{\sigma }_{xy}^{{\rm{A}}}/{\rm{{d}}}E\) (see “Methods” section, Eq. (4), and the Sommerfeld expansion40).
To discuss the correlation between the large \({\sigma }_{xy}^{{\rm{A}}}\) around E = EF (Fig. 2b) and the band structures (Fig. 2a), we plotted the (kx, ky) dependences of the Berry curvature Ωz(k) (Fig. 2d–g); the nodal loops at the kz = 0 and 2π/a planes are marked as highlighted areas in Fig. 2i. At E−EF = 0.05 and 0.03 eV (Fig. 2d and e), the Berry curvature has large values on the X–K line but has small values on the K–Γ–W line, because the gap of Weyl cone A mainly contributes to the Berry curvature at these energies (Fig. 2a). In contrast, at the lower energy of E − EF = −0.08 eV (Fig. 2g), large values of the Berry curvature are obtained close to the W point on the Γ–W line, which is determined by the gap of Weyl cone D (Fig. 2a). From these results, we conclude that both gaps open on two different nodal loops in the kz = 0 and kz = 2π/a planes and yield a large Berry curvature at E = EF (Fig. 2f), leading to a large anomalous Hall conductivity. The calculated \({\sigma }_{xy}^{{\rm{A}}}\) and \({\alpha }_{xy}^{{\rm{A}}}\) qualitatively explain the experimental results (Fig. 1g, j). Specifically, the electron-doped sample exhibits large anomalous transport properties. However, the simple EF shift that follows the rigid band model based on the stoichiometric Co2MnGa gives a quantitative discrepancy with the Nv dependence of \({\sigma }_{xy}^{{\rm{A}}}\) and \({\alpha }_{xy}^{{\rm{A}}}\) obtained from experiments. For example, the calculated negative \({\alpha }_{xy}^{{\rm{A}}}\) in the E − EF < 0 region is not observed in the experimentally hole-doped samples. This discrepancy may be caused by an extrinsic mechanism or the formation of anti-site defects arising from off-stoichiometric compositions, which is not taken into account in the calculations.
Band structures of an electron-doped Co2MnGa film
We performed ARPES experiments for the E2 (Nv = 28.5) sample as it exhibits the highest \({\sigma }_{xy}^{{\rm{A}}}\) and \({\alpha }_{xy}^{{\rm{A}}}\), to determine the EF location and the band structure with the mirror-symmetry breaking that yields a large Berry curvature as well as anomalous transport properties. Figure 3a shows the observed Fermi surface recorded at 80 eV photon energy after magnetization along [100] (Supplementary Movie 1 for a detailed continuous change in constant energy maps). Around the Γ point, a circular-shaped contour is evident. At each X point of the first Brillouin zone, we recognize a point-like structure. The calculated constant energy contour of the stoichiometric Co2MnGa (Nv = 28.0) with the SOI along [100] was also plotted (Fig. 3a). Except for the intensities in between Γ and K, the features observed in the experiments are well reproduced by the calculation when the chemical potential shifts by +70 meV (Supplementary Fig. 5 and the associated text). Figure 3b shows the ARPES images and the band dispersions calculated at several momentum cuts (Fig. 3a, white dashed lines). At cut 1 (Γ–K line), we confirmed the large hole-pocket crossing EF around Γ. One also finds distinct features that get closer to the K points with increasing E − EF and finally cross EF, indicated by a red inverted triangle. These features are consistent with the calculated minority-spin hole band at Γ point and one branch of the tilted majority-spin Weyl cone C (Fig. 2a). In going from cut 1 to cut 3, the slope of the Weyl cone evolves to be sharper for both experiment and calculation. Here we also emphasize that an almost non-dispersive band is observed just below EF around the Γ point represented by a gray inverted triangle at cut 1. This flat band corresponds to the Fermi surface between the Γ and K points (Fig. 3a) and is not reproduced by the calculations. At the cut 4 (X–X line), we can confirm the hole bands with energy maximum of E−EF ~ −100 and −350 meV around \({k}_{| | }^{\prime}\) = 0 and ±0.8 Å−1, respectively, in both experiment and calculation. We also realize that the bottom of the electron bands located near EF at the X points create prominent point-like structures on the Fermi surface (Fig. 3a).
a Fermi surface of sample E2 (Nv = 28.5) obtained at 80 eV with p-polarized light. The calculated Fermi surface of the stoichiometric Co2MnGa (Nv = 28.0) with 70 meV chemical potential shifted is overlaid. b Observed and calculated band structures along cuts 1–4 marked by white dashed lines in a. c, d Wide ARPES images along the Γ–K–X line recorded at 80 eV with p- and s-polarizations, respectively. e ARPES image with p-polarized light c is added with that with s-polarized light d. f Second derivative ARPES image of e with respect to the energy and momentum directions. The calculated band dispersion is overlaid. g Magnified ARPES image (upper) in the frame in e and corresponding calculation (lower). h Photon-energy-dependent EDCs at k∣∣ = −0.5 Å−1 taken at 50, 60, 70, and 80 eV with p-polarized light.
Figure 3c, d shows the wide range ARPES images along the Γ–K–X line (cut 1) taken at 80 eV energy for incident photons with p- and s-polarization, respectively. With s-polarized light, a sharp electron-pocket is markedly enhanced around the X points, whereas the photoemission intensities of the tilted Weyl cone C and the flat band observed by p-polarization have mostly diminished. In Fig. 3e, f, we present the ARPES image and its second derivative with the calculated band structure. Here, to eliminate the effect of the light polarization-dependent matrix-element, these images acquired with p- and s-polarized light are mixed. The experimental result is well reproduced by the calculations with EF shifted upward by 70 meV (i.e., electron doping). This chemical potential shift is consistent with a higher Nv of 28.5 for this sample than the stoichiometric one (Nv = 28.0). Small discrepancies are noted between the observed and calculated band dispersions (Fig. 3f), for instance, the location of the bottom of the band of the sharp electron-pocket around the X points. The differences may arise through correlation or kz broadening effects41,42.
Figure 3g shows the magnified ARPES image in the frame shown in Fig. 3e. With suppression through the matrix-element effect, the band structure around the X point at the kz = 2π/a plane in the second Brillouin zone are clearly visualized. In a comparison with the calculation (Fig. 3g, lower panel), we realized that the observed band structure around the X point resembles the tilted and gapped Weyl cone A (Fig. 2a). Because the upper part of the Weyl cone cannot be seen, EF is probably located in the gap of the massive Weyl cone A.
Here, we turn our attention to the flat band observed around the Γ point. To clarify the origin of the flat band, we show the photon-energy-dependent energy distribution curves (EDCs) at k∣∣ = −0.5 Å−1 taken after magnetization (Fig. 3h). The prominent peaks caused by the flat band do not show a clear photon-energy (kz) dependence. Details of the photon energy dependence are shown in Supplementary Fig. 6 and the associated text. We therefore conclude that the observed flat band just below EF belongs to a surface state.
To gain deeper insight into the Weyl fermion and the peculiar surface state in the Co2MnGa film, we performed spin-resolved measurements. Since the light spot size (>1 mm) is much larger than the magnetic domain, we carried out SARPES measurements before and after magnetizing the sample. Figure 4a and b shows the spin-resolved EDCs and spin-polarizations at θ∣∣ = −4∘ (k∣∣ ~ −0.3 Å−1) taken before and after magnetizations, respectively. Although the spin-polarization is negligible over the whole energy region before magnetization due to the formation of magnetic domains, it is enhanced enormously after magnetization. In particularly, the large negative spin-polarization (~40%) originating from the flat surface state has been observed at EF. Figure 4c shows the calculated band structures (left) and the experimentally observed spin-polarization map along the Γ–K–X line overlaid with the calculated band structures (right). Here the positive (negative) spin-polarizations are marked in red (blue). Also, the spin-resolved band structures in the majority (left) and minority (right) spin channels (Fig. 4d) feature a large hole band around the Γ point having a minority-spin component. There are bands having a strong majority-spin component around the K point near EF. From calculations, the Weyl cone C is characterized by the majority-spin component and tilting (see Fig. 2a). Furthermore, because Weyl cones A and C are mostly at Lifshitz quantum critical points, they have a large density of states at EF when the Weyl node approaches EF7. These features are confirmed by our ARPES and SARPES measurements, and therefore we conclude that the observed spin-polarized feature with positive spin-polarization near the K point can be ascribed to one flatter branch of the tilted spin-polarized Weyl cone C induced by broken mirror symmetry.
a, b Spin-resolved EDCs and spin-polarizations at θ∣∣ = −4∘ (k∣∣ ~ −0. 3 Å−1) taken before and after magnetization at 80 eV with p-polarized light. All error bars represent standard deviation. The insets show the schematics of multi-magnetic domains and a single-magnetic domain. c Calculated band dispersion with EF shifted upward by 70 meV (left) and spin-polarization map along the Γ–K–X line (right). d Spin-resolved ARPES images of the majority (left) and minority (right) spin states. e Spin-resolved EDCs taken from θ∣∣ = 0∘ to 20∘ (Γ–K–X). The background signal of the secondary electrons was subtracted. Inverted triangles indicate the peak position of the minority spin-polarized flat band.
In addition, we find that the flat surface state has a minority-spin component (Fig. 4d, right), the sign of which is opposite to that of the Weyl cone (Fig. 4d, left). Figure 4e shows the spin-resolved EDCs taken from θ∣∣ = 0∘ to 20∘, which corresponds to the k-line from Γ to X. The clear minority-spin peaks persist over a wide momentum region marked with inverted triangles. There are two main possibilities for the origin of this peculiar surface state. One is the topologically non-trivial Fermi-arc surface state17,18,19,20,23,25,26. The other is a trivial surface resonance state, which was predicted for half-metallic Co-based Heusler alloys43,44. Having considered the location of the Weyl node before magnetization, it seems that the minority-spin surface state connects the Weyl cones at positive and negative momenta although further study is needed to elucidate the origin of the surface state.
Band structures of a hole-doped Co2MnGa film
In order to compare the band structures of electron-doped and hole-doped samples, we also performed SARPES experiments for the sample H3* (Nv = 27.3). Figure 5a, b show the observed Fermi surface and wide range ARPES image along Γ–K–X line recorded at 50 eV photon energy with p-polarized light. At X point, the electron-pocket crossing EF can be seen while the large hole-pocket is located at Γ point. These features are in good agreement with the electron-doped sample (Fig. 3). In Fig. 5c, d, we present the magnified ARPES image along the Γ–K–X direction and its second derivative along the momentum axis. Around −0.60 Å−1 near EF, one can see a tilted band, in which the node is slightly located above EF (see gray arrow in Fig. 5d). As we can see in Fig. 5f, this tilted band has a strong majority-spin component. These experimental results agree with the results of the calculation, shown in Fig. 5e with the position of EF shifted downward by 220 meV. Therefore, we conclude that the tilted cone close to K point belongs to the Weyl cone E (see Fig. 2a).
a Fermi surface of the sample H3* (Nv = 27.3) recorded at 50 eV with p-polarized light. b Wide ARPES image along the Γ–K–X line indicated by the white dashed line in a. c, d Magnified ARPES image in the frame in b and its second derivative. e Calculated band dispersion with EF shifted downward by 220 meV. f Spin-polarization map along the Γ–K–X line.
Finally, we discuss the role of the Fermi energy tuning in optimizing the anomalous transport properties. From ARPES measurements from two samples, we determined the relative EF shifts from the stoichiometric condition (Nv = 28.0), specifically, +70 meV for the sample E2 (Nv = 28.5) and −220 meV for the sample H3* (Nv = 27.3). The latter has lower \({\sigma }_{xy}^{{\rm{A}}}\) and \({\alpha }_{xy}^{{\rm{A}}}\) than the former. These results reasonably explain the observed and calculated large anomalous transport properties presented in Fig. 1 based on our calculations given in Fig. 2. In detail, because EF of sample E2 is closely located at the gapped region of the Weyl cones A and C through slight electron doping, it satisfies a criterion whereby a large Berry curvature in both kz = 0 and kz = 2π/a planes is generated and thereby results in a gigantic ANE because the \({\alpha }_{xy}^{{\rm{A}}}\) is large. Therefore, we have clearly confirmed that enhancing the anomalous transport properties of topological ferromagnets involves two key features: (1) the creation of a massive (gapped) Weyl cone from the nodal loop by mirror-symmetry breaking and (2) the tuning of the Fermi energy.
Conclusion
In summary, we have experimentally and theoretically investigated a one-to-one correspondence between the electronic structure and the anomalous transport properties in the film form of Co2MnGa topological ferromagnets. By in situ SARPES, we provided a direct visualization of the spin-polarized and massive Weyl cones and the peculiar surface state under mirror-symmetry breaking. When EF approaches the gap of the massive Weyl cones by the electron doping, we have recorded the highest anomalous Nernst thermopower (6.2 μV K−1) at room temperature among ferromagnetic films to the best of our knowledge. Our findings signify the insufficient EF position tuning against the Weyl cone is the most probable cause for the smaller anomalous Nernst thermopower in the Co2MnGa films reported in previous studies32,33 and provide the reliable guiding principle to maximize the Nernst thermopower by the band engineering utilizing the SARPES, transport measurements, and ab-initio calculations, for the first time. From an applications perspective, our work facilitates the implementation of various novel applications based on the thin film form of topological magnets; namely, the large transverse electric and thermoelectric conversions without an external magnetic field, which cannot be realized in the bulk form because of the formation of magnetic domains, are promising for novel thermoelectric applications such as heat flux sensor.
Methods
Thin film growth
Epitaxial thin films of (001)-oriented Co2MnGa having different compositions were deposited on a MgO(001) single crystalline substrate at 600 ∘C using a co-sputtering technique with Co, Mn, and Co41.2Mn27.5Ga31.3 sputtering targets. The films were designed to be 50 nm thick. To prevent the film from oxidizing for transport measurements, a 1.5 nm-thick Al-capping layer was deposited by rf magnetron sputtering. The base pressure of the deposition chamber was near 2 × 10−7 Pa. The thickness and the composition of the film were evaluated by wavelength dispersive X-ray fluorescence analysis. Table 1 shows the result of the composition analysis and the evaluated total valence electron number for all prepared Co2MnGa films.
For SARPES measurements, uncapped films were deposited on a MgO substrate with a buffer layers of Cr (10 nm) and Ag (100 nm) to smooth the surface. To avoid surface contaminations, grown films were transferred from the magnetron-sputtering chamber to the preparation chamber of the SARPES instrument using a portable suitcase chamber to avoid exposure to air (<1 × 10−6 Pa). Note that sample H3* was deposited on the MgO(001) substrate with buffer layers at room temperature, and then post-annealed at 550 °C for 30 min.
Measurement of transport and magnetic properties
The magnetic properties of the Co2MnGa films were measured with a superconducting quantum interference device-vibrating sample magnetometer (SQUID-VSM, Quantum Design Co. Ltd). The crystal structure was revealed through X-ray diffraction with a Cu Kα X-ray source and a two-dimensional detector (PILATUS 100K/R, Rigaku Co.). The substrate was cleaved to a size with lateral dimensions of ~7.0 × 10.0 mm2, and then the film was patterned into a Hall bar structure with a width of 2.0 mm and a length of 7.0 mm through photolithography and Ar ion milling. The AHE was measured at 300 K applying a 1 mA electric current along the [110] direction and a magnetic field was applied perpendicular to the [001] direction of the Co2MnGa film using a Physical Property Measurement System (PPMS, Quantum Design Co., Ltd.). The ANE was also measured at 300 K applying a temperature gradient ∇Tin along the [110] direction and a magnetic field along the [001] direction of the Co2MnGa film in PPMS. To evaluate ∇Tin, the Seebeck coefficient Sxx in the Co2MnGa film was obtained outside the PPMS by measuring the ∇Tout using an infrared thermal camera and a black-body coating to calibrate the emissivity. Then, ∇Tin can be estimated from the Seebeck voltage obtained in the PPMS and Sxx. The accuracy of this method to evaluate ANE has been confirmed in the previous studies35,36.
Theoretical calculations
We calculated the electronic structure of L21-ordered Co2MnGa applying the full-potential linearized augmented plane-wave method including SOI, which is implemented in the WIEN2k program45. The lattice constant of the cubic unit cell was set to the experimentally determined value of 5.755 Å and the k-point number in the self-consistent-field calculation was chosen as 20 × 20 × 20 after confirming the convergence of the total energy. Using the electronic structure obtained, we calculated the anomalous Hall conductivity \({\sigma }_{xy}^{{\rm{A}}}\) using46
where n and \(n^{\prime}\) denote band indices, Ωz(k) denotes the Berry curvature, px(py) the x(y) component of the momentum operator, ψn,k the eigenstate with the eigenenergy En,k, and f(En,k, ϵ) the Fermi distribution function for the band n and the wave vector k at the energy ϵ relative to the Fermi energy. In the calculation of \({\sigma }_{xy}^{{\rm{A}}}\), the direction of the magnetization was set along the [100] direction (Fig. 1a) and 90 × 90 × 90 k points were used for the Brillouin zone integration ensuring good convergence for \({\sigma }_{xy}^{{\rm{A}}}\).
From Boltzmann transport theory, we calculated the transverse thermoelectric conductivity \({\alpha }_{xy}^{{\rm{A}}}\) for a given temperature T by substituting the obtained \({\sigma }_{xy}^{{\rm{A}}}\) into the following expression:
where \(f=1/[\exp ((\epsilon -\mu )/{k}_{{\rm{B}}}T)+1]\) denotes the Fermi distribution function with μ the chemical potential. Here, μ = 0 corresponds to the Fermi level.
Spin-resolved and angle-resolved photoelectron spectroscopy
ARPES and SARPES measurements were performed at the ESPRESSO end-station (BL-9B) in the Hiroshima Synchrotron Radiation Center47,48. The base pressure of the SARPES chamber was 5 × 10−9 Pa. The photoelectrons were acquired using a hemispherical electron analyser (R4000, Scienta-Omicron). The spin-polarization was measured using a very low-energy electron diffraction-type spin detector. The experimental geometry is shown in Supplementary Fig. 4. The energy and angular resolutions for ARPES (SARPES) were set to 45 meV (55 meV) and ±0.3° (±1.5°), respectively. The effective Sherman function was 0.28 for the SARPES measurements.
During all SARPES measurements, the temperature was maintained below 40 K. Before each ARPES and SARPES measurement, the sample was annealed at 550 °C for 30 min at the preparation chamber (base pressure ~ 4 × 10−8 Pa). The quality and cleanliness of the annealed sample was checked by low-energy electron diffraction (Supplementary Fig. 3 and the associated text). A magnetic field as large as ~0.1 T was applied to the samples along the [100] for sample E2 ([110] for sample H3*) easy-axis using a permanent magnet in the preparation chamber at room temperature. A 0.1 T magnetic field was sufficiently high to saturate the magnetization (Supplementary Fig. 2 and the associated text). The ratio between the remanent and saturation magnetizations along the [100] easy-axis of the sample E2 is 0.96. Therefore, a single magnetic domain was overall obtained for SARPES measurements.
Data availability
The data presented in this paper are available from the authors on reasonable request.
References
Bell, L. E. Cooling, heating, generating power, and recovering waste heat with thermoelectric systems. Science 321, 1457 (2008).
Sakuraba, Y. Potential of thermoelectric power generation using anomalous Nernst effect in magnetic materials. Scr. Mater. 111, 29 (2016).
Vilanova Vidal, E., Stryganyuk, G., Schneider, H., Felser, C. & Jakob, G. Exploring Co2 MnAl Heusler compound for anomalous Hall effect sensors. Appl. Phys. Lett. 99, 132509 (2011).
Zhou, W. & Sakuraba, Y. Heat flux sensing by anomalous Nernst effect in Fe–Al thin films on a flexible substrate. Appl. Phys. Express 13, 043001 (2020).
Nakatsuji, S., Kiyohara, N. & Higo, T. Large anomalous Hall effect in a non-collinear antiferromagnet at room temperature. Nature 527, 212 (2015).
Ikhlas, M. et al. Large anomalous Nernst effect at room temperature in a chiral antiferromagnet. Nat. Phys. 13, 1085 (2017).
Sakai, A. et al. Giant anomalous Nernst effect and quantum-critical scaling in a ferromagnetic semimetal. Nat. Phys. 14, 1119 (2018).
Liu, E. et al. Giant anomalous Hall effect in a ferromagnetic kagome-lattice semimetal. Nat. Phys. 14, 1125 (2018).
Guin, S. N. et al. Anomalous Nernst effect beyond the magnetization scaling relation in the ferromagnetic Heusler compound Co2 MnGa. NPG Asia Mater. 11, 16 (2019).
Guin, S. N. et al. Zero field Nernst effect in a ferromagnetic Kagome lattice Weyl semimetal Co3Sn2S2. Adv. Mater. 31, 1806622 (2019).
Xiao, D., Yao, Y., Fang, Z. & Niu, Q. Berry-phase effect in anomalous thermoelectric transport. Phys. Rev. Lett. 97, 026603 (2006).
Xiao, D., Chang, M.-C. & Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 82, 1959 (2010).
Wan, X., Turner, A. M., Vishwanath, A. & Savrasov, S. Y. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 83, 205101 (2011).
Soluyanov, A. A. et al. Type-II Weyl semimetals. Nature 527, 495 (2015).
Manna, K. et al. From colossal to zero: controlling the anomalous Hall effect in magnetic Heusler compounds via Berry curvature design. Phys. Rev. X 8, 041045 (2018).
Yan, B. & Felser, C. Topological materials: Weyl semimetals. Annu. Rev. Condens. Matter Phys. 8, 337 (2017).
Xu, S.-Y. et al. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science 349, 613 (2015).
Lv, B. Q. et al. Observation of Weyl nodes in TaAs. Nat. Phys. 11, 724 (2015).
Lv, B. Q. et al. Experimental discovery of Weyl semimetal TaAs. Phys. Rev. X 5, 031013 (2015).
Belopolski, I. et al. Discovery of a new type of topological Weyl fermion semimetal state in MoxW1−xTe2. Nat. Commun. 7, 13643 (2016).
Xu, S.-Y. et al. Discovery of Lorentz-violating type II Weyl fermions in LaAlGe. Sci. Adv. 3, e1603266 (2017).
Kuroda, K. et al. Evidence for magnetic Weyl fermions in a correlated metal. Nat. Mater. 16, 1090 (2017).
Belopolski, I. et al. Signatures of a time-reversal symmetric Weyl semimetal with only four Weyl points. Nat. Commun. 8, 942 (2017).
Wang, Q. et al. Large intrinsic anomalous Hall effect in half-metallic ferromagnet Co3Sn2S2 with magnetic Weyl fermions. Nat. Commun. 9, 3681 (2018).
Borisenko, S. et al. Time-reversal symmetry breaking type-II Weyl state in YbMnBi2. Nat. Commun. 10, 3424 (2019).
Liu, D. F. et al. Magnetic Weyl semimetal phase in a Kagome crystal. Science 365, 1282 (2019).
Kübler, J. & Felser, C. Weyl points in the ferromagnetic Heusler compound Co2 MnAl. EPL 114, 47005 (2016).
Chang, G. et al. Topological Hopf and chain link semimetal states and their application to Co2MnGa. Phys. Rev. Lett. 119, 156401 (2017).
Belopolski, I. et al. Discovery of topological Weyl fermion lines and drumhead surface states in a room temperature magnet. Science 365, 1278 (2019).
Noky, J., Xu, Q., Felser, C. & Sun, Y. Large anomalous Hall and Nernst effects from nodal line symmetry breaking in Fe2MnX (X = P, As, Sb). Phys. Rev. B 99, 165117 (2019).
Noky, J. & Sun, Y. Linear response in topological materials. Appl. Sci. 9, 4832 (2019).
Reichlova, H. et al. Large anomalous Nernst effect in thin films of the Weyl semimetal Co2MnGa. Appl. Phys. Lett. 113, 212405 (2018).
Park, G.-H. et al. Thickness dependence of the anomalous Nernst effect and the Mott relation of Weyl semimetal Co2MnGa thin films. Phys. Rev. B 101, 060406 (2020). (R).
Xu, L. et al. Anomalous transverse response of Co2 MnGa and universality of the room-temperature \({\alpha }_{ij}^{A}/{\sigma }_{ij}^{A}\) ratio across topological magnets. Phys. Rev. B 101, 180404 (R) (2020).
Nakayama, H. et al. Mechanism of strong enhancement of anomalous Nernst effect in Fe by Ga substitution. Phys. Rev. Mater. 3, 114412 (2019).
Sakuraba, Y., Hyodo, K., Sakuma, A. & Mitani, S. Giant anomalous Nernst effect in the Co2MnAl1−x Six Heusler alloy induced by Fermi level tuning and atomic ordering. Phys. Rev. B 101, 134407 (2020).
Ding, L. et al. Intrinsic anomalous Nernst effect amplified by disorder in a half-metallic semimetal. Phys. Rev. X 9, 041061 (2019).
Wang, Z. et al. Time-reversal-breaking Weyl fermions in magnetic Heusler alloys. Phys. Rev. Lett. 117, 236401 (2016).
Noky, J., Gooth, J., Felser, C. & Sun, Y. Characterization of topological band structures away from the Fermi level by the anomalous Nernst effect. Phys. Rev. B 98, 241106 (2018).
Ashcroft, N. W. & Mermin, N. D. Solid State Physics. (Saunders College, Philadelphia, 1976).
Nawa, K. & Miura, Y. Exploring half-metallic Co-based full Heusler alloys using a DFT+U method combined with linear response approach. RSC Adv. 9, 30462 (2019).
Strocov, V. N. Intrinsic accuracy in 3-dimensional photoemission band mapping. J. Electron Spectrosc. Relat. Phenom. 130, 65 (2003).
Wustenberg, J.-P. et al. Surface spin polarization of the nonstoichiometric Heusler alloy Co2 MnSi. Phys. Rev. B 85, 064407 (2012).
Braun, J. et al. Monitoring surface resonances on CO2 MnSi(100) by spin-resolved photoelectron spectroscopy. Phys. Rev. B 91, 195128 (2015).
Blaha, P. et al. WIEN2k: An APW+lo program for calculating the properties of solids. J. Chem. Phys. 152, 074101 (2020).
Yao, Y. et al. First principles calculation of anomalous Hall conductivity in ferromagnetic bcc Fe. Phys. Rev. Lett. 92, 037204 (2004).
Okuda, T. et al. Efficient spin resolved spectroscopy observation machine at Hiroshima Synchrotron Radiation Center. Rev. Sci. Instrum. 82, 103302 (2011).
Okuda, T., Miyamoto, K., Kimura, A., Namatame, H. & Taniguchi, M. A double VLEED spin detector for high-resolution three dimensional spin vectorial analysis of anisotropic Rashba spin splitting. J. Electron Spectrosc. Relat. Phenom. 201, 23 (2015).
Acknowledgements
The SARPES measurements were performed with the approval of the Proposal Assessing Committee of Hiroshima Synchrotron Radiation Center (Proposals Nos. 18BG038 and 19AG054). This work was financially supported by KAKENHI (Nos. 16H02114, 17H06152, 17H06138, and 18H03683). K.S. was financially supported by a Grant-in-Aid for JSPS Fellows (No. 19J00858). Y.S. was financially supported by a JSPS KAKENHI Grant-in-Aid for Young Scientists (A) (No. JP2670945) and PRESTO from the Japan Science and Technology Agency (No. JPMJPR17R5). We thank S. Kurdi, A. Sakuma, K. Nawa, K. Uchida, and K. Hono for valuable discussions and N. Kojima and B. Masaoka for a technical support.
Author information
Authors and Affiliations
Contributions
K.S., T.K., and M.K. performed the SARPES experiments with the assistance of K.Mi and T.O. Y.S., K.G., and W.Z. synthesized the thin films and performed the transport measurements. K.Ma and Y.M. performed the ab initio calculations. K.S., Y.S., and K.Ma wrote the manuscript with inputs from all authors. A.K. supervised the work.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Primary handling editor: Aldo Isidori
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sumida, K., Sakuraba, Y., Masuda, K. et al. Spin-polarized Weyl cones and giant anomalous Nernst effect in ferromagnetic Heusler films. Commun Mater 1, 89 (2020). https://doi.org/10.1038/s43246-020-00088-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43246-020-00088-w
This article is cited by
-
Intrinsic magnetic topological materials
Frontiers of Physics (2023)
-
Unusual Kinetic Properties of Usual Heusler Alloys
Journal of Superconductivity and Novel Magnetism (2022)
-
Topological magnets—their basic science and potential applications
AAPPS Bulletin (2022)
-
Berry curvature origin of the thickness-dependent anomalous Hall effect in a ferromagnetic Weyl semimetal
npj Quantum Materials (2021)
-
Magneto-optical design of anomalous Nernst thermopile
Scientific Reports (2021)