Abstract
Coupling of quantum emitters in a semiconductor relies, generally, on short-range dipole-dipole or electronic exchange type interactions. Consistently, energy transfer between exciton states, that is, electron-hole pairs bound by Coulomb interaction, is limited to distances of the order of 10 nm. Here, we demonstrate polariton-mediated coupling and energy transfer between excitonic states over a distance exceeding 2 μm. We accomplish this by coupling quantum well-confined excitons through the delocalized mode of two coupled optical microcavities. Use of magnetically doped quantum wells enables us to tune the confined exciton energy by the magnetic field and in this way to control the spatial direction of the transfer. Such controlled, long-distance interaction between coherently coupled quantum emitters opens possibilities of a scalable implementation of quantum networks and quantum simulators based on solid-state, multi-cavity systems.
Similar content being viewed by others
Introduction
Energy transfer between quantum emitters, such as excitons in a semiconductor, relies on a coupling through short-range dipole–dipole (Förster)1 or electronic exchange (Dexter)2-type interactions. The distance of these interactions is typically of the order of 10 nm in III–V or II–VI semiconductors3,4. As shown in the pioneering work by Agranovich et al.5, the spatial range of energy transfer in semiconductor systems can be enhanced utilizing the light–matter coupling effects. In the strong light–matter coupling regime, the exciton and the optical mode of the microcavity exchange energy in a reversible way, which leads to a superposition of their wave functions and the emergence of a new eigenstate called an exciton–polariton6,7,8,9,10,11,12. When several excitonic states are strongly coupled to a common optical mode, their wave functions hybridize enabling their mutual coupling. In this way, polariton-mediated transfer of energy between distant excitons is possible. The energy transfer remains efficient as long as the strong coupling conditions and hybridization of the initial and final excitonic states of the process are maintained13. As such, it enables an enhancement of the energy transfer range by orders of magnitude with respect to the Förster limit13,14,15,16,17.
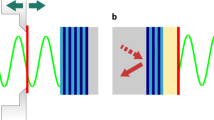
In this work, we report on magnetic field-controlled, polariton-mediated energy transfer between 2D exciton states over a distance as large as 2.15 μm. We achieve this in structures containing (Cd,Zn)Te and (Cd,Mn,Zn)Te quantum wells (QWs) strongly coupled to the modes of two coupled microcavities separated by a semi-transparent Bragg mirror (see Fig. 1a). In such a system, the polariton wave function contains a component originating from exciton in two different QWs and from the two coupled optical modes. As a result, the polariton relaxation from a level with a dominant contribution by the exciton from one QW to a level with a dominant contribution by the exciton from another well is accompanied by a change in the spatial position of the exciton. In this way, the polariton relaxation is accompanied by energy transfer between different, separated in space, QWs. Doping of the QWs in one of the microcavities with a small amount of Mn2+ ions enhances the exciton Zeeman splitting in magnetic field due to the s,p–d exchange interaction between the extended band states and the localized spins of the Mn2+ ions18 (see Fig. 1b and Supplementary Note 1). To maximize exciton splittings, we choose the Faraday geometry with magnetic field applied along the sample growth direction, thus parallel to the quantization axis. In consequence, we are able to tune the energy of the excitons in the Mn-doped QW (QWDMS) below or above the energy of the excitons in the non-magnetic QW using a magnetic field19. Since the exciton density transfer between the wells is assisted by energy relaxation, by adjustment of the relative energy order of the excitons in the QWDMS and QW one gains control of the direction of the transfer, as schematically shown in Fig. 1a.
a Coupled microcavity structure hosting spatially delocalized symmetric (CS) and antisymmetric (CAS) optical modes (respective distributions of the squared electric field shown with green and brown lines). Three non-magnetic quantum wells (QW) are placed in the upper and three magnetically doped quantum wells (QWDMS) are placed in the lower microcavity. Under strong coupling conditions a four-level polariton system emerges inducing hybridization of excitons in the QWDMS and QW. Long-distance transfer of energy between the QW and QWDMS is possible owing to the optical mode-mediated coupling of the initial and final excitonic states of the process. b Energy levels of the QW (blue line) and QWDMS (red line) as a function of the magnetic field. The energy of the excitons in the QWDMS can be tuned below or above the energy of the excitons in the QW; the crossing occurs at Bcrit. Below Bcrit, exciton density transfer assisted by energy relaxation occurs predominantly from the QW to the QWDMS, while above Bcrit the transfer direction is reversed.
Results
Four-level polaritonic system
As shown in Fig. 2a–c, three 10-nm-wide non-magnetic (Cd,Zn)Te QWs and three 12-nm-wide, Mn2+-doped (semimagnetic) (Cd,Mn,Zn)Te QWs are, as intended, embedded in the center of the upper and lower microcavity, respectively. Incorporation of the Mn2+ ions only in the QWDMS is confirmed by the transmission electron microscopy (TEM) images shown in Fig. 2d, e.
a The structure comprises two (Cd,Zn,Mg)Te microcavities coupled by a semi-transparent Bragg mirror. Three (Cd,Zn)Te and three (Cd,Mn,Zn)Te quantum wells are embedded in the upper and lower microcavities, respectively, as confirmed by the energy-dispersive X-ray spectroscopy investigations of spatial distribution of Mg atoms (b, c) and Mn atoms (d, e) in the sample cross-section.
In order to prove evidence for the formation of a four-level polaritonic system in the studied sample, in Fig. 3 we show emission spectra of the structure resolved in in-plane photon momentum space k∥. The spectra are registered at consecutive positions on the sample along the direction of the microcavity thickness gradient, that is, as a function of the detuning between the coupled, symmetric (CS) and antisymmetric (CAS), optical modes of the structure and the QW and QWDMS excitons. For an even number of Bragg pairs separating the microcavities, as in the present case, the CS mode is higher in energy than the CAS one (see Supplementary Note 2).
Emission spectra resolved in in-plane photon momentum k∥ (shown on a logarithmic intensity scale). Dotted lines represent the uncoupled exciton states in the QW and QWDMS, as well as the optical modes CS and CAS delocalized spatially over the two coupled microcavities. Solid lines represent polariton levels calculated as eigenvalues of the Hamiltonian H (Eq. (1)). Detuning between the optical modes and exciton levels increases from a to c.
The case of a large negative detuning between the excitons and microcavity modes is shown in Fig. 3a. Exciton–photon mixing is negligible here, and individual components contributing to the four-level polaritonic system are clearly distinguished. The approximately parabolic dispersion identifies the CS and CAS modes. The QW transition with a negligible dispersion is seen at ~1640 meV, while the QWDMS one occurs at 1645 meV. Excitation energy below the bandgap energy of any layer of the structure except the QW and QWDMS (see Supplementary Fig. 2) ensures that the excitation penetrates both microcavities. The absorption of the QWs in the upper microcavity is below 10%, which means that carriers are generated in the QWs in the upper and lower microcavities with comparable efficiency. Emission from the QWDMS is vanishingly weak, however, due to its filtering by the stopbands of the middle and upper Bragg mirrors. When the coupled modes approach the excitonic levels, anticrossing is observed (see Fig. 3b), which testifies to strong light–matter coupling conditions. Figure 3c shows the case of modes–excitons resonance. In contrast to the case shown in Fig. 3a, all four emitting levels exhibit a clear dependence on k∥, proving a non-negligible contribution by the photonic part to each state of the four-level polaritonic system.
In order to describe the observed polariton dispersion quantitatively, we introduce the Hamiltonian H (Eq. (1)) representing a four coupled oscillator model20,21,22. The Hamiltonian H written in the basis of the exciton states QW and QWDMS, with mode M localized in the upper and mode MDMS localized in the lower microcavity, takes the form:
Off-diagonal elements of the matrix represent couplings in the system, κ describes the strength of the interaction between the (degenerate) M and MDMS giving rise to the emergence of the CS and CAS optical modes20,23,24,25 delocalized spatially over the two microcavities (the respective squared electric field distributions for the CS and CAS modes are shown in Fig. 1a), Ω is the coupling constant between the QW exciton and the mode M of the upper microcavity and ΩDMS represents the coupling between the QWDMS exciton and the MDMS mode of the lower microcavity. Direct coupling of the excitons with the optical mode confined in the adjacent microcavity is neglected20,21,22.
Fitting the energies obtained from diagonalization of the Hamiltonian H to the energies of the optical transitions reported in Fig. 3 determines the value of κ to be 13 meV. Such a value is, in fact, expected for a microcavity separation of 16 distributed Bragg reflector (DBR) pairs25,26, as in the present case. The vacuum Rabi splitting Ω for the QW exciton is (10.0 ± 0.4) meV, and ΩDMS for the QWDMS exciton is (12.5 ± 0.4) meV. In simulations, only the bare-level energies are changed by detuning, while the coupling constants remain fixed (they change by <10% when changing the position on a 7 mm × 20 mm sample). In terms of the splitting energy per QW, the values obtained are consistent with previous reports on II–VI polariton systems8,27,28,29,30.
We note that the coupling constants are of the same order as the energy separation between the QW and QWDMS excitons. This means that the coupling with the delocalized optical modes of the structure indeed ensures hybridization of the QW and QWDMS states, being a prerequisite for efficient polariton-mediated energy transfer between the QWs.
In previous studies, the magnetic field applied in Faraday geometry enabled lowering of the polariton condensation threshold31,32 or, when applied in the Voigt geometry, controlling of the polariton condensate propagation in single microcavities33. Here, we demonstrate photon-mediated exciton interaction and energy transfer between the macroscopically distant QWs in double microcavity structure and use the magnetic field as a mean to control of the transfer direction.
Photon-mediated interaction between magnetic and non-magnetic exciton
Figure 4 shows the emission spectra resolved in circular polarization, registered as a function of magnetic field for consecutive detunings between the microcavity modes and QW excitons decreasing from panels a to d. Corresponding Hopfield coefficients34 determined from the diagonalization of the Hamiltonian H (Eq. (1)) are shown below the spectra (note the labels run from 1 to 4 in order of increasing level energy). Below, we analyze the emission energy and intensity of the dependencies observed in the experiment.
Photoluminescence spectra as a function of the magnetic field for consecutive values of the detuning between the microcavity modes and quantum well excitons, decreasing from a to d. Circular polarizations of the detection are indicated. The bare levels of the excitons in the QW and QWDMS (simulated following Eqs. (2) and (3), respectively), as well as the optical modes M and MDMS of the upper and lower microcavities are shown by the dashed blue, red, yellow, and light-green lines, respectively. Delocalized optical modes CAS and CS arising from the coupling between M and MDMS are denoted by the dashed orange and olive lines, respectively. Calculated polariton levels are shown by solid white lines. Hopfield coefficients vs. magnetic field determined in the basis of the QWDMS, QW, M and MDMS for polariton levels from 1 to 4 are provided below the photoluminescence maps with the respective color code. The “transfer on” case, where the coupled modes are tuned to resonance with the QW and QWDMS excitons enabling long-distance, polariton-mediated energy transfer is shown in b, c. The “transfer off” case, where the coupled modes are detuned with respect to the excitons, which precludes the interaction and energy transfer between magnetic and non-magnetic exciton states is shown in a, d.
The non-resonant case, where the coupled modes are far detuned to higher energy with respect to the QW excitons (~20 meV at B = 0 T), is shown in Fig. 4a. In this case, the observed emission arises predominantly from the exciton confined in the QW, as indicated by only a slight change in the emission energy and intensity upon application of the magnetic field (at B = 10 T, σ− intensity Iσ− is higher than the σ+ intensity Iσ+ by a factor of ≲2. Such a small splitting, as well as only weak (below 30%) and negative polarization of the emission (=(Iσ+ − Iσ−)/(Iσ+ + Iσ−)) is expected in the case of a non-magnetic QW, since only linear Zeeman splitting (excitonic g-factor of 0.7, consistent with ref. 35) and diamagnetic shift (γ = 0.018), both of relatively small magnitude, affect the exciton energy \({E}_{\,\text{QW}\,}^{\sigma \pm }(B)\):
In the case of the QWDMS, the exciton energy \({E}_{{{\rm{QW}}}_{{\rm{DMS}}}}^{\sigma \pm }(B)\) varies much more upon application of magnetic field due to an additional contribution coming from the s,p–d exchange interaction between the exciton spin and the localized 5/2 spins of the Mn2+ ions:
In Eq. (3) the term Esat = xMn(N0α − N0β)S0 represents exciton giant Zeeman splitting at saturation, defined by the Mn dopant concentration xMn, the s–d and p–d exchange integrals N0α = 0.22 eV and N0β = −0.88 eV, respectively, for electrons and holes, and S0 = 2.12 being the effective spin of the Mn2+ ion in (Cd,Mn)Te36. The B5/2 is the modified Brillouin function36 with parameters: Mn2+ ion Landé factor gMn = 2, Bohr magneton μB, effective temperature of the Mn spins Teff = 2.3 K, and the Boltzmann constant kB.
It is worth to note that crossing of the QW and QWDMS exciton levels occurring at around Bcrit = 0.8 T at σ+ polarization in Fig. 4a does not affect the energy of the emission. This indicates that when the mode is far detuned from the excitons, no interaction between excitons in the QW and QWDMS occurs. The negligible hybridization of the QW and QWDMS states in the non-resonant case is reflected by a sharp exchange of the QW and QWDMS components in the polariton states 1 and 2 when the magnetic field passes Bcrit (see the Hopfield coefficients for levels 1 and 2 in Fig. 4a). The emission from the QWDMS in the non-resonant case is filtered out by the middle and upper DBRs. Thus, despite being excited by the laser, it is not manifested in the spectrum. In the non-resonant case, the emission spectral width is just the linewidth of the QW confined neutral exciton transition. It is larger than the radiative lifetime defined limit due to a sample structural disorder. An additional broadening of the emission towards lower energy seen in Fig. 4a is attributed to a presence of transition of charged exciton37,38 confined in the QW.
The resonant case, where either the CAS or CS mode is tuned to the close spectral vicinity of the QW levels, is shown in Fig. 4b or c, respectively. The spectra reveal an anticrossing of the polariton states for which a contribution from the QW and QWDMS exciton dominates (they are, respectively, levels 1 and 2 in Fig. 4b and levels 2 and 3 in Fig. 4c). The anticrossing occurs at polarization σ+ at Bcrit = 0.8 T, where the uncoupled QW and QWDMS exciton levels cross, proving the photon-mediated interaction between the macroscopically distant, magnetic and non-magnetic, excitons. The Hopfield coefficients confirm enhanced hybridization of the QW and QWDMS excitons in the resonant case. In the resonant case, the emission spectral width is the average of the QW exciton and the mode linewidths weighted by the respective contributions of the two components to the emitting state. In the following discussion by conditions “below Bcrit”, we mean B > Bcrit in σ+ polarization, while by “above Bcrit” we mean the remaining field range and polarization of the signal (i.e., B < Bcrit in σ+ and B > 0 T in σ− polarization).
Magnetic field-controlled, polariton-mediated energy transfer over a macroscopic distance
Let us now consider the emission intensity dependences, starting from the resonant (“transfer on”) case shown in Fig. 4b. Below Bcrit, the dominant contribution to level 1 comes from the exciton confined in the QWDMS, while the dominant contribution to level 2 comes from the exciton confined in the QW. QWs in both microcavities are excited with comparable intensity, and the QWDMS emission is not as efficiently filtered out by the DBRs stopband as it was in the non-resonant case. Thus, if there were no exciton density transfer between the QW and QWDMS, one would expect a comparable emission intensity from levels 1 and 2. This is clearly not the case: the emission occurs mostly from the lowest in energy, polariton level 1. The observed enhancement of the population of level 1 and depletion of the population of level 2 reflects the efficient relaxation of the polaritons to level 1 from level 2. This points toward efficient exciton density transfer from the QW placed in the upper microcavity to the QWDMS placed in the lower microcavity, 2.15 μm away. The observed behavior, in particular the depletion of the polariton level 2, cannot result from intrawell spin relaxation of the exciton in the QW, since its spin polarization is weak (see Fig. 4a) and it is not affected by a superposition with the optical mode (at least below the polariton condensation density, as in the present case)39,40,41.
Exciton density transfer between the QW and QWDMS does not require exciton spin relaxation. It is assisted, however, by its energy relaxation. The energy difference between the QW and QWDMS excitons is relatively small (up to 5 meV, depending on the magnetic field), which facilitates its efficient dissipation by acoustic phonons and ensures high exciton density transfer rates42. Measurements of time-resolved micro-photoluminescence from the cleaved edge of the sample indicate that the lifetime of the exciton in either the QW or QWDMS is ~200 ps (see Supplementary Fig. 3). We thus state that the transfer time is much smaller than this value, in the range of tens of ps or shorter.
In turn, above Bcrit in Fig. 4b the contribution to the lowest polariton level 1 from the QW exciton dominates over the contribution from the QWDMS exciton. A dominant population of level 1 above Bcrit indicates that the direction of the transfer is reversed and the exciton density shifts from the QWDMS to the QW. Here, due to the large splitting of the QWDMS exciton for B > 0 T, an additional contribution to the depletion of the σ− polarized exciton in the QWDMS exciton appears, resulting from spin and energy exciton relaxation within the QWDMS18. The excitation, kept constant during the magnetic field-dependent measurements, is linearly polarized and non-resonant, so that it does not introduce any imbalance between σ+ and σ− populations of the photocreated excitons.
The energy and intensity dependences of the resonant (“transfer on”) case presented in Fig. 4c are similar to the case in Fig. 4b. Excitons contributing to polaritons on the most populated level 2 originate predominantly either from the QW (for B below Bcrit) or the QWDMS (for B above Bcrit). Comparable dependencies in Fig. 4b, c point towards their similar interpretation and indicate that both coupled modes CS and CAS mediate the energy transfer between the QWs with comparable efficiency. Such a result is consistent with comparable intensities of the electric field associated with CS and CAS at the centers of the microcavities, as seen in Fig. 1a. Analysis of the Hopfield coefficients in Fig. 4c reveals that feeding of the polariton levels indeed occurs through the QW excitons, as polariton level 2, of strongly excitonic character, is much more populated than the lowest, but mostly photonic in nature, level 1. Consistently, emission from the level 1 in σ+ polarization, where a net exciton component is present (see the Hopfield coefficients) is stronger than in σ− polarization, where the exciton content to level 1 is negligible.
Finally, Fig. 4d shows that when the optical modes are far detuned to lower energy with respect to the QW excitons (“transfer off” case), the ordinary crossing of exciton energy levels of QWs occurs. This indicates that the photon-mediated interaction and energy transfer between the QW and QWDMS exciton states have been turned off again. Also in this case, a net exciton content results in enhancement of the σ+ polarized with respect to σ− polarized emission of the level 2.
Discussion
Photon-mediated hybridization of excitonic states and enhanced energy transfer efficiency over distances of the order of 100 nm have been studied so far in microcavities with embedded layers of organic molecules13,14,15,16,43,44,45,46 or hybrid structures involving perovskite or two-dimensional transition metal dichalcogenides layers47,48,49,50,51. Very recently, use of a hybrid organic–inorganic coupled microcavity enabled the energy transfer on a distance reaching 1.5 μm17.
A long-distance, spin-dependent interaction and polariton-mediated energy transfer between quantum emitters demonstrated in the present work are promising for deterministic designing of novel photonic devices such as, for example, bosonic Josephson junctions52,53,54, so far limited to disordered polaritonic systems. Formation of spatially delocalized polaritons in a coupled multi-cavity structure and the possibility of their manipulation by a magnetic field makes the presented system useful for studies and implementation in the recently intensively developing areas of quantum polariton networks55, quantum simulators56 and production of hyper-entangled photons with a strongly reduced noise background57.
The present study has been performed in a linear regime, where interactions between the polaritons are negligible due to their small density. An exciting extension of this work would be a study of the presented four-level polaritonic system to the high excitation limit, where stimulated scattering in a non-linear regime induces such effects as the polariton Bose–Einstein condensation. Such a study should not only answer the question whether the condensate can boost a long-distance energy transfer in a semiconductor, but it should also enable observation of new phenomena, such as magnetic field tunable polariton parametric scattering between polariton branches or switchable, multiple wavelength polariton lasing. Enhancement of optical nonlinearities owing to the exciton hybridization should enable an ultra-low threshold for lasing.
Conclusions
We have accomplished magnetic field-controlled coupling and energy transfer between semiconductor QWs over a distance exceeding 2 μm. The distant interaction is ensured by the strong coupling of the excitons to a common optical mode delocalized over the two coupled microcavities. The magnetic field enables control of the strength of the coupling and the energy order of the semimagnetic QW exciton with respect to the non-magnetic QW exciton. This makes possible control of the direction of the polariton-mediated energy transfer by an external magnetic field, which is promising for magnetic field-controlled routing of the excitation in a semiconductor. The multilevel system presented is attractive for further studies of non-linear polariton effects and for a wide range of applications in optoelectronics and quantum information science.
Methods
Sample
The structures are grown by molecular beam epitaxy on a ZnTe buffer layer deposited on a (100)-oriented GaAs substrate, with real-time monitoring of the thickness of the layers by in situ reflectivity during ~12 h of growth. The structure contains two (Cd,Zn,Mg)Te 3λ/2 microcavities (ncav = 2.7 at λ = 750 nm). The microcavities are sandwiched between and separated by DBRs made of 30, 16, and 28.5 pairs of alternating refractive index layers in the case of the lower, the middle, and the upper mirrors, respectively (see Fig. 2a). High (nhigh = 2.95 at 750 nm) and low (nlow = 2.4 at 750 nm) refractive index layers are made of (Cd,Zn,Mg)Te with, respectively, 10% and 50% Mg content. Both microcavities are of wedge type, which results in a gradient of the mode energy of 10.5 meV/mm, as deduced from reflectivity spatial mapping. At every point on the sample the microcavities share the same thickness, which ensures a maximum degree of coupling between their optical modes. The quality factor of the microcavities deduced from the coupled modes linewidth observed in reflectivity exceeds 2000. The energy gradient of a QW-confined exciton amounts to ~0.6 meV/mm. The concentration of the manganese in QWDMS is determined to 0.8% by fitting a modified Brillouin function36 to the QWDMS exciton shift in the magnetic field (see Supplementary Fig. 1).
Experiment
Photoluminescence is non-resonantly continuous wave excited at 1.81 eV (λexc = 685 nm). For far-field distribution of the emission measurements, the sample is placed inside a helium-flow cryostat at 8 K. The laser beam is focused to a 1–2-μm diameter spot at the sample surface using a microscope objective (numerical aperture of 0.7). The in-plane photon momentum k∥ is registered in the range from −4.5 to 4.5 μm−1 by imaging the Fourier plane of the microscope objective on the entrance slit of the spectrometer. For magnetic field-dependent measurements, the sample is placed inside a pumped helium cryostat at 1.8 K equipped with a superconducting split-coil magnet producing a magnetic field of up to 10 T. The measurements are performed in the Faraday configuration. The combination of a quarter-wave plate and a linear polarizer allows for the detection of two circular polarizations. The laser beam is focused to a 0.1 mm diameter spot at the sample surface using a 500 mm focal length lens. The lens is mounted on an automated XY translation stage, which enables spatial mapping of the photoluminescence with a step of 0.01 mm. The range of registered k∥ vectors is limited to 0.42 μm−1 in this case. A CCD camera coupled to a grating spectrometer serves as a detector (0.1 meV of the overall spectral setup resolution).
TEM observations are conducted on a FEI Talos F200X microscope operating at 200 kV. The measurements are performed in scanning TEM mode using a high-angle annular dark-field detector and energy-dispersive X-ray spectroscopy on a Brucker BD4 spectrometer. Cross-sectional TEM specimens are prepared by a standard method of mechanical pre-thinning followed by Ar ion milling.
TMM simulations
The spatial distribution of the electric field in the structure shown in Fig. 1a is calculated using the transfer matrix method. Complex refractive indices of the layers are assumed following the literature58.
Data availability
Data related to the figures can be found at https://doi.org/10.6084/m9.figshare.12981383. Other data related to this work are available from the authors upon reasonable request.
References
Förster, T. Zwischenmolekulare Energiewanderung und Fluoreszenz. Ann. Phys. 437, 55 (1948).
Dexter, D. L. A theory of sensitized luminescence in solids. J. Chem. Phys. 21, 836 (1953).
Heimbrodt, W. et al. Tunneling and energy transfer in ZnSe-based semimagnetic double quantum wells. Phys. Rev. B 58, 1162 (1998).
Itskos, G. et al. Efficient dipole-dipole coupling of Mott-Wannier and Frenkel excitons in (Ga,In)N quantum well/polyfluorene semiconductor heterostructures. Phys. Rev. B 76, 035344 (2007).
Agranovich, V., Benisty, H. & Weisbuch, C. Organic and inorganic quantum wells in a microcavity: Frenkel-Wannier-Mott excitons hybridization and energy transformation. Solid State Commun. 102, 631 (1997).
Weisbuch, C., Nishioka, M., Ishikawa, A. & Arakawa, Y. Observation of the coupled exciton-photon mode splitting in a semiconductor quantum microcavity. Phys. Rev. Lett. 69, 3314 (1992).
Dang, L. S., Heger, D., André, R., Bœuf, F. & Romestain, R. Stimulation of polariton photoluminescence in semiconductor microcavity. Phys. Rev. Lett. 81, 3920 (1998).
Kasprzak, J. et al. Bose–Einstein condensation of exciton polaritons. Nature 443, 409 (2006).
Amo, A. et al. Superfluidity of polaritons in semiconductor microcavities. Nat. Phys. 5, 805 (2009).
Kavokin, A., Baumberg, J. J., Malpuech, G. & Laussy, F. P. Microcavities (Oxford Univ. Press, 2017).
Klembt, S. et al. Exciton-polariton topological insulator. Nature 562, 552 (2018).
Stepanov, P. et al. Dispersion relation of the collective excitations in a resonantly driven polariton fluid. Nat. Commun. 10, 1 (2019).
Zhong, X. et al. Energy transfer between spatially separated entangled molecules. Angew. Chem. Int. Ed. 56, 9034 (2017).
Coles, D. M. et al. Polariton-mediated energy transfer between organic dyes in a strongly coupled optical microcavity. Nat. Mater. 13, 712 (2014).
Feist, J. & Garcia-Vidal, F. J. Extraordinary exciton conductance induced by strong coupling. Phys. Rev. Lett. 114, 196402 (2015).
Zhong, X. et al. Non-radiative energy transfer mediated by hybrid light-matter states. Angew. Chem. Int. Ed. 55, 6202 (2016).
Jayaprakash, R. et al. A hybrid organic-inorganic polariton LED. Light Sci. Appl. 8, 1 (2019).
Furdyna, J. K. Diluted magnetic semiconductors. J. Appl. Phys. 64, R29 (1988).
Sadowski, J., Mariette, H., Wasiela, A. & d’Aubigné, Y. M. Multiple quantum well exciton Bragg mirrors, tunable by magnetic field. Thin Solid Films 306, 296 (1997).
Panzarini, G. et al. Exciton-light coupling in single and coupled semiconductor microcavities: polariton dispersion and polarization splitting. Phys. Rev. B 59, 5082 (1999).
Richter, S. et al. Maxwell consideration of polaritonic quasi-particle Hamiltonians in multi-level systems. Appl. Phys. Lett. 107, 231104 (2015).
Dufferwiel, S. et al. Tunable polaritonic molecules in an open microcavity system. Appl. Phys. Lett. 107, 201106 (2015).
Stanley, R. P., Houdré, R., Oesterle, U., Ilegems, M. & Weisbuch, C. Coupled semiconductor microcavities. Appl. Phys. Lett. 65, 2093 (1994).
Armitage, A. et al. Optically induced splitting of bright excitonic states in coupled quantum microcavities. Phys. Rev. B 57, 14877 (1998).
Ściesiek, M. et al. Design and control of mode interaction in coupled ZnTe optical microcavities. Cryst. Growth Des. 17, 3716 (2017).
Bayindir, M., Kural, C. & Ozbay, E. Coupled optical microcavities in one-dimensional photonic bandgap structures. J. Opt. A 3, S184 (2001).
Sebald, K. et al. Strong coupling in monolithic microcavities with ZnSe quantum wells. Appl. Phys. Lett. 100, 161104 (2012).
Klein, T. et al. Polariton lasing in high-quality selenide-based micropillars in the strong coupling regime. Appl. Phys. Lett. 107, 071101 (2015).
Rousset, J.-G. et al. Strong coupling and polariton lasing in Te based microcavities embedding (Cd, Zn)Te quantum wells. Appl. Phys. Lett. 107, 201109 (2015).
Sawicki, K. et al. Triple threshold lasing from a photonic trap in a Te/Se-based optical microcavity. Commun. Phys. 2, 38 (2019).
Kochereshko, V. P. et al. Lasing in Bose-Fermi mixtures. Scientific Rep. 6, 20091 (2016).
Rousset, J.-G. et al. Magnetic field effect on the lasing threshold of a semimagnetic polariton condensate. Phys. Rev. B 96, 125403 (2017).
Caputo, D. et al. Magnetic control of polariton spin transport. Commun. Phys. 2, 1 (2019).
Hopfield, J. J. Theory of the contribution of excitons to the complex dielectric constant of crystals. Phys. Rev. 112, 1555 (1958).
Zhao, Q. X., Oestreich, M. & Magnea, N. Electron and hole g-factors in CdTe/CdMgTe quantum wells. Appl. Phys. Lett. 69, 3704 (1996).
Gaj, J., Planel, R. & Fishman, G. Relation of magneto-optical properties of free excitons to spin alignment of Mn2+ ions in Cd1−x Mnx Te. Solid State Commun. 29, 435 (1979).
Kossacki, P. Optical studies of charged excitons in II VI semiconductor quantum wells. J. Phys. Condens. Matter 15, R471 (2003).
Muszyński, M., Teisseyre, H., Sobczak, K. & Suffczyński, J. Stable charged exciton in a ZnO/(Zn,Mg)O quantum well at near room temperature. Appl. Phys. Lett. 117, 033102 (2020).
Fischer, J. et al. Anomalies of a nonequilibrium spin or polariton condensate in a magnetic field. Phys. Rev. Lett. 112, 093902 (2014).
Sturm, C. et al. Nonequilibrium polariton condensate in a magnetic field. Phys. Rev. B 91, 155130 (2015).
Król, M. et al. Giant spin Meissner effect in a nonequilibrium exciton-polariton gas. Phys. Rev. B 99, 115318 (2019).
Price, P. Two-dimensional electron transport in semiconductor layers. I. Phonon scattering. Ann. Phys. 133, 217 (1981).
Lidzey, D. G., Bradley, D. D. C., Armitage, A., Walker, S. & Skolnick, M. S. Photon-mediated hybridization of Frenkel excitons in organic semiconductor microcavities. Science 288, 1620 (2000).
Lodden, G. H. & Holmes, R. J. Long-range, photon-mediated exciton hybridization in an all-organic, one-dimensional photonic crystal. Phys. Rev. Lett. 109, 096401 (2012).
Orgiu, E. et al. Conductivity in organic semiconductors hybridized with the vacuum field. Nat. Mater. 14, 1123 (2015).
Schachenmayer, J., Genes, C., Tignone, E. & Pupillo, G. Cavity-enhanced transport of excitons. Phys. Rev. Lett. 114, 196403 (2015).
Wenus, J. et al. Hybrid organic-inorganic exciton-polaritons in a strongly coupled microcavity. Phys. Rev. B 74, 235212 (2006).
Lanty, G. et al. Hybrid cavity polaritons in a ZnO-perovskite microcavity. Phys. Rev. B 84, 195449 (2011).
Slootsky, M., Liu, X., Menon, V. M. & Forrest, S. R. Room temperature Frenkel-Wannier-Mott hybridization of degenerate excitons in a strongly coupled microcavity. Phys. Rev. Lett. 112, 076401 (2014).
Flatten, L. C. et al. Electrically tunable organic–inorganic hybrid polaritons with monolayer WS2. Nat. Commun. 8, 14097 (2017).
Waldherr, M. et al. Observation of bosonic condensation in a hybrid monolayer MoSe2-GaAs microcavity. Nat. Commun. 9, 3286 (2018).
Albiez, M. et al. Direct observation of tunneling and nonlinear self-trapping in a single Bosonic Josephson junction. Phys. Rev. Lett. 95, 010402 (2005).
Lagoudakis, K. G., Pietka, B., Wouters, M., André, R. & Deveaud-Plédran, B. Coherent oscillations in an exciton-polariton Josephson junction. Phys. Rev. Lett. 105, 120403 (2010).
Abbarchi, M. et al. Macroscopic quantum self-trapping and Josephson oscillations of exciton polaritons. Nat. Phys. 9, 275 (2013).
Liew, T. C. H. & Rubo, Y. G. Quantum exciton-polariton networks through inverse four-wave mixing. Phys. Rev. B 97, 041302 (2018).
Berloff, N. G. et al. Realizing the classical XY Hamiltonian in polariton simulators. Nat. Mater. 16, 1120 (2017).
Portolan, S., Einkemmer, L., Vörös, Z., Weihs, G. & Rabl, P. Generation of hyper-entangled photon pairs in coupled microcavities. N. J. Phys. 16, 063030 (2014).
André, R. & Dang, L. S. Low-temperature refractive indices of Cd1−x Mnx Te and Cd1−y Mgy Te. J. Appl. Phys. 82, 5086 (1997).
Acknowledgements
We gratefully acknowledge sample preparation for the TEM measurements by Jolanta Borysiuk (deceased). This work was partially supported by the Polish National Science Center under projects DEC-2013/10/E/ST3/00215 and DEC-2017/25/N/ST3/00465. The research was carried out with the use of CePT, CeZaMat, and NLTK infrastructures financed by the European Union—the European Regional Development Fund within the Operational Program “Innovative economy” for 2007–2013.
Author information
Authors and Affiliations
Contributions
M.Ś. was involved in all steps of this work. J.S. was involved in all steps of this work apart from the sample growth. W.P. epitaxially grew the samples. K.S. and T.K. participated in optical measurements. A.G. participated in design of the studies and interpretation of the results. K.So. performed TEM measurements. J.S. wrote and all authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Primary handling editor: Aldo Isidori.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ściesiek, M., Sawicki, K., Pacuski, W. et al. Long-distance coupling and energy transfer between exciton states in magnetically controlled microcavities. Commun Mater 1, 78 (2020). https://doi.org/10.1038/s43246-020-00079-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43246-020-00079-x