Abstract
Future population projections of urban agglomerations furnish essential input for development policies and sustainability strategies. Here, working within the Shared Socioeconomic Pathways (SSPs) and using a simple urban-growth model, we estimate population trends throughout the 21st century for ~20,000 urban agglomerations in 151 countries. Our results suggest that urban growth in this century will produce increasingly concentrated cities, some growing to enormous sizes. We also demonstrate that, although detailed urbanization trajectories differ for different SSP scenarios, in all cases, the largest projected agglomerations of the future are more populous than the largest agglomerations today. Our projection strategy advances urban-population research by producing urban-size projections—for agglomerations around the world—that correctly obey empirically observed distribution laws. Although our method is very simple and omits various aspects of urbanization, it nonetheless yields valuable insight into long-term SSP-specific urbanization trends to inform discussion of sustainable urban policies.
Similar content being viewed by others
Introduction
Explosive growth in urban populations presents a wide range of societal, environmental, and economic consequences; in developing nations, in particular, many aspects of urban infrastructure are inadequate already for the needs of today’s population, and accommodating rapid future growth will require major improvements in urban planning1, for which accurate population estimates are essential. As just one example, the 11th item in the United Nations’ Sustainable Development Goals2 pledges to “make cities and human settlements inclusive, safe, resilient and sustainable,” and the associated 2030 objectives have spurred cities to introduce a variety of initiatives—in areas such as housing, transportation, public health, and environmental protection—whose implementation depends crucially on urban-population projections; needless to say, urban-population growth is projected to continue well beyond 20303, while the consequences of climate change will affect the sustainability and resilience of cities on even longer timescales4,5, and thus urban-population projections must extend not only into the near term, but ideally several decades into the future. Beyond their key role in urban planning, long-term projections of the spatial distribution of future populations have been used to assess risks associated with phenomena such as climate-change-induced flooding6,7, heat waves8, malaria epidemics9, food security10, biodiversity11, and freshwater availability12, and have also been researched for more general purposes13,14,15; in contrast to the regional scope of urban-planning applications, the global scope of such research studies often demands future projections of worldwide urban populations, and this is the challenge we address in this study. Of course, future projections of urban populations or any other statistics necessarily entail uncertainties, and thus an additional desideratum for population projections is an estimate of the ranges over which a given projection may vary—due, for example, to variations in future social, political, and environmental conditions, such as those envisioned by the Shared Socioeconomic Pathways (SSPs)16.
To date, a wide variety of methods have been used to project future urban populations. In particular, since Alonso-Muth-Mills17,18,19,20, a vast number of studies have investigated urban morphology (for reviews, see refs. 21,22,23), which estimates the spatially detailed population distribution within a city. These studies clarified that the spatial distribution of population and urban land use can be modified by policies and technologies affecting land and transport, but studies considering applications to realistic cities have typically assumed given total populations for target urban agglomerations. For individual nations or regions, these include cohort-component methods24, which incorporate autoregressive integrated moving-average models, and nationally averaged growth rates grounded in past estimates25; such methods, while useful for localized modeling, do not readily extend to the global scales of interest in this work due to data limitations. Other authors have used grid-based approaches based on heuristic functions15 to downscale the IPCC Special Report on Emissions Scenarios26, gravity-type models13, or cellular automata14. They are capable of yielding global-scale projections, but such methods may be suboptimal for some purposes: the grid-based populations they predict may not map readily onto population projections for actual cities, and—more disturbingly—the resulting distribution of urban populations may fail to reproduce the well-known power-law (Pareto) distribution observed for actual cities (Zipf’s law)27. An additional drawback of some methods is a failure to evaluate uncertainties in the model itself: while uncertainties in future input conditions can be evaluated with these models, most global-scale grid-based population models have not been validated to represent historical trends or to incorporate SSP-like variations in background conditions, preventing accurate estimates of uncertainty ranges in projection results. Thus, at present, there are few if any population-projection methods capable simultaneously of (a) operating on global scales, (b) furnishing predictions for individual cities, (c) guaranteeing a realistic distribution of urban populations and successfully reproducing historical data as validation, and (d) incorporating SSP-like scenarios to quantify uncertainties.
In this study, we propose a method that satisfies all of these criteria. As discussed in more detail in “Methods” below, our technique is global in scope, but eschews the use of territorial grids in favor of estimating populations of individual cities—or, more precisely, individual urban agglomerations. The notion of an urban agglomeration—defined by the United Nations to be “a type of urban settlement defined by the de facto population contained within the contours of a contiguous territory inhabited at urban density levels without regard to administrative boundaries”3—offers a more intuitive image than grid-level population distributions and is frequently chosen as the appropriate spatial unit for understanding urban activity and planning or assessing infrastructure installations. As a specific technique for estimating populations of urban agglomerations, we use an urban-growth model28 that we have previously developed to guarantee proper power-law scaling of urban-population distributions, in accordance with Zipf’s law. In essence, this model is based on reasoning similar to that of the Simon model29, which assesses changes in city populations using a proportional distribution based on urban scale; thus, our model assumes that the population of an agglomeration itself acts as the driver of further population growth. Zipf’s law for cities is by now the subject of an extensive and growing literature (for a review, see ref. 30), with power-law distributions observed not only for urban populations but also for urban geographical footprints; among studies of the latter, we note in particular refs. 31,32, which proposed a stochastic simulation model designed to yield power-law scaling for the sizes of urban land clusters, similar to what we do here for urban populations. Our approach and that of refs. 31,32 are thus complementary; however, despite the obvious correlation between the populations and geographical sizes of cities, urban land clusters and agglomerations are defined in different ways, and it is not clear that the stochastic simulation approach is applicable to population projection. Indeed, to our knowledge, no previous study has used deterministic power-law methods to project future populations of individual urban agglomerations. The original models of Simon29 (quoted by33) and Gibrat (quoted by34) employ random processes to assign growing urban populations to individual cities, thus yielding power-law population distributions. However, this randomness produces nondeterministic estimates for both past and future populations of individual urban agglomerations, complicating the task of validating population estimates for individual cities. Our approach yields deterministic projections by assigning populations to urban agglomerations based on the expected preferential attachment share. An advantage of focusing on populations of actual cities is that we can validate our method by comparison to observed historical data, which we do quite successfully, as described below. Finally, to account for variations in background conditions and accurately estimate uncertainties, we formulate our model in a manner consistent with the SSPs—a long-term (extending to 2100) projection of socioeconomic trends, established to advance research on methods for addressing climate change, comprising 5 distinct scenarios encompassing a wide variety of conceivable patterns for future development35.
In attempting to identify initial data to seed our model—as well as reference data to use for validation tests—we encounter the difficulty that there exists no comprehensive database encompassing the full set of urban agglomerations around the world. For this reason, we used the data sources World Urbanization Prospects (WUP) 2018, Gridded Population of the World (GPW) v. 436, and OpenStreetMap to construct a dataset containing population and location information, for the year 2010, for 21,424 urban agglomerations in 151 countries. We also extracted population and coordinates, as of 2010, for 68,196 nonurban human settlements. With our model thus seeded by empirical data for 2010, we may run the model backward to obtain postdictions of urban populations prior to 2010, or forward to project future populations, and we use both of these possibilities to validate the accuracy of our model, as discussed in the “Validation” section below.
Having constructed, seeded, and validated our model, we next use it to project future populations for the full set of 89,620 worldwide urban agglomerations and nonurban settlements, throughout the remainder of this century, for each of the five SSP scenarios. We emphasize that this dataset includes both urban and rural populations, and that our projections cover both of these, as described in the “Methods” section. As discussed in more detail in the section “Projection of global urban agglomerations”, our results reveal a number of intriguing trends, including that populations will continue to concentrate in larger agglomerations, with the largest urban agglomerations in 2100 swelling to populations of at least 40 million and possibly significantly greater (with precise details differing for distinct SSPs).
Finally, the construction, validation, and results of our model entail a number of points worthy of further comment, including the implications for sustainable policies under the SSPs, which we address in “Discussion” below.
Results
Model validation and error estimation
In this section, we validate the accuracy of our model by comparing its postdictions and projections with WUP data, then use the results of this comparison to estimate expected errors in our urban-growth model.
To validate the accuracy of the model, we first use Eqs. (7) and (8) in “Methods” below to obtain postdictions, based on year 2010 and extending as far back as 1950, for the populations of 1794 urban agglomerations for which historical data are available in WUP. Table 1 lists the mean absolute percent errors (MAPEs) by year for all agglomerations and for agglomerations with populations of 100,000 or more. Past estimates are calculated sequentially backward in time, so naturally the MAPE increases as time goes back. MAPEs for all cities grow extremely large at long times in the past—for 1950, for example, the MAPE is 1281%. This is due to the right-skewed distribution of absolute percent errors (APE) in subnational population forecasts37. When observed populations are small, APEs for some cities tend to extreme values. The minimum population in the 2010 WUP data is 137,000, while that for 1950 is just 5. If we restrict attention to cities with populations of 100,000 or more in all years, the MAPEs fall in a reasonable range. These MAPEs are comparable to those of empirical prediction models for United States county data38,39,40. More sophisticated approaches, such as cohort change with an autoregressive integrated moving-average model, have been reported to estimate subregional populations more accurately25; however, such models require detailed panel data by age group that is not practical to obtain for all agglomerations worldwide.
Supplementary Fig. 1 in the Supplementary Information shows population trajectories for some selected urban agglomerations from 1950 to 2010 as observed by the United Nations and as estimated by our method. Our estimates for some urban agglomerations reproduce observed data quite well, while estimates for other cities diverge widely from observations. As discussed above, the population blooming of certain small cities is a major source of inaccuracy in population forecasts39. For instance, the APE of Shenzhen, China, is 31600% in 1950 where the statistical population is 3148 and postdicted population is 1 million. Shenzhen was designated as a special economic zone in 1980, after which it attracted huge amounts of foreign investment that spurred explosive migration in the 1990s. Another example in which our estimation model fails is Glasgow, UK, which has negative correlation between observed and postdicted population. The population of Glasgow decreased almost monotonically from 1960 to 2000 due to the decline of the ship-building industry; such political and socioeconomic factors clearly affect future populations, but are not taken into account by our projections. Nonetheless, overall estimation errors and prominent failures for some cities notwithstanding, we find significant positive correlation between observed data and the postdictions produced by our model for 98% of agglomerations.
As a second validation of our model, we compare its projections for future urban populations to the projections recorded in the UN WUP database, which extend to 2035. Table 2 lists MAPEs and mean algebraic percent errors (MALPEs) for this comparison; note that these MAPEs—10% for 10-year projections and 16% for 25-year projections—are lower than those of our model’s postdictions. Indeed, most agglomerations grow in population during the period covered by UN WUP data, whereupon the right skew of MAPE distribution is lower than those of postdictions. The positive values observed for MALPEs indicate that our model tends to underestimate urban populations on average compared to UN WUP projections. One possible reason for this is that our estimates assume that the spatial extent of urban agglomerations remains fixed; in fact, of course, urban areas typically expand geographically as their population grows. In this study, we fix the spatial boundaries of urban agglomerations at 2010 values, and the positive values observed for MALPEs suggest that the accuracy of our model could be improved by accounting for geographic expansion accompanying population increase—a possibility we consider in “Discussion”.
As discussed above, APEs tend to be higher for lower-population agglomerations and projections further into the future. Referring to Tayman et al.39, we adopt a model in which APEs are explained by population and temporal distance (years past base year); according to this model, the APEs expected for a city of 1 million are 5% for 10-year projections and 24% at 90 years, or 1.7% and 8.6%, respectively, for a city of 10 million. Using this model, we can estimate the uncertainty of our estimates. Details of this APE estimation model are described in “Methods” and “Data availability” sections below.
Projection of global urban agglomerations
Using this model, with input values for urban populations and GDP taken from nation-specific SSP data from the International Institute for Applied Systems Analysis (IIASA), we project future populations for individual cities through the year 2100. According to the narratives of SSPs35 and associated national urbanization prospects41, SSP1 describes a sustainable future and assumes fast urbanization in all countries, SSP2 is intermediate between other pathways with a moderate pace of urbanization, SSP3 assumes a regionalized world and slow urbanization, and SSP4 describes inequal, stratified economies with moderate urbanization in high-income countries and rapid urbanization in medium- and low-income countries. SSP5 describes rapid growth of the global economy and fast urbanization in all countries. Fertility declines with increasing economic growth, so the total populations of SSPs reflect economic-growth narratives (see Supplementary Fig. 2). The urban-population scenarios in the SSPs also contain uncertainties. Details of country-level population scenarios can be found in KC and Lutz42.
Segregating cities by population scale for cities with populations of 100,000 or above, Table 3 shows the number of cities in each of several population classes (A), and the total population of those cities (B) as projected for 2050 and 2100. This subset consists primarily of urban populations, but also includes some rural populations depending on nation-specific definitions of minimum urban population, as explained in “Methods”. Under all SSPs, the total number of cities with projected populations of 100,000 or more in 2050 is greater than in the base year 2010. From 2050 to 2100, this number decreases in all scenarios except SSP3. Considering the class of cities with populations more than 500,000, we find that the number of cities in this population range increases from 2010 to 2050 in all scenarios; however, only for SSPs two, three, and four does this number continue to grow from 2050 to 2100, instead declining for SSPs one and five. Meanwhile, in all scenarios except SSP1, we find that the number of megacities—with populations of 10 million or more—remains on a trajectory of steady growth throughout the century to 2100. SSP1 and SSP5 have similar trajectories for the total urban-population share (Supplementary Fig. 2) but different trajectories for the number of cities. The storylines of these SSPs describe different trends in fertility rates and migration patterns: SSP1 assumes moderate fertility levels for rich OECD countries and moderate migration levels for all countries, while SSP5 assumes high levels of both fertility and migration. The primary impact of this difference is seen in the number of cities in rich OECD countries.
Among all SSPs, SSP3 sees the largest number of cities with populations above 500,000, but the smallest fraction of the overall population accounted for by urban dwellers. SSP3 is also the only pathway to exhibit growth in the number of cities with populations below 500,000 toward 2100. Nonetheless, despite the increasing number of smaller cities in SSP3, the share of the overall population living in larger agglomerations increases as 2100 approaches. In summary, the urban population is expected to reside in larger agglomerations. This trend is most significant in SSP5.
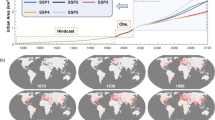
Figures 1 and 2 plot the worldwide spatial distribution of urban agglomerations—of population 100,000 or above—as observed in 2010 and as projected for 2100 within the five SSP scenarios. All scenarios predict prominent urban expansion in South Asia and sub-Saharan Africa. In India—particularly in the Ganges basin—both megacities and slightly smaller cities of 1–5 million exhibit significant growth. Meanwhile, smaller cities—of populations below 1 million—decrease in number for all scenarios except SSP3. These trends imply that large-scale migration from rural areas to large cities is to be expected. In Africa, all scenarios predict prominent growth of cities with population 1–5 million in Nigeria and Democratic Republic of the Congo. SSP4 sees a significant emergence of megacities in sub-Saharan Africa. SSP5 projects the formation of numerous megacities in North America and a greater prevalence of megacities in the developed nations of Europe and Oceania as compared to the other SSPs.
From these results, we see that SSPs 1 and 5 predict that, although the total worldwide urban-population peaks and subsequently declines, the trend toward increasing urban concentration continues apace. For SSP3, on the other hand, mid-size and small cities are relatively numerous. For SSP4, the urban population increases, mainly in high-fertility-rate countries. This spurs urban-population growth in sub-Saharan Africa and a dramatic increase in the numbers of megacities and cities of 1–5 million residents. For SSP2, projections for numbers of cities and urban-population distributions lie intermediate between those of SSPs 3 and 5. Although SSPs do not give insight into the circumstances of individual cities, one plausible narrative that might explain this outcome is that cities in SSP3 become less attractive due to limited interregional mobility and imperfections in urban planning35; this contrasts with the case of SSP5, in which—according to this interpretation—large-scale urban initiatives enhance the attractiveness of cities. These storylines are consistent with the results of this study. On the other hand, the narrative underlying SSP1 assumes that compact spatial footprints produce efficient cities. Our results indicate increasing urban populations residing in fewer cities, implying an increase in the average population of agglomerations by 2100. However, this study does not account for variations in the geographical extent of cities, and further analysis is required to evaluate the consistency of our results with the SSP1 storyline.
Table 4 lists the population of the world’s ten most populous cities, as observed in 2010 and as projected for 2050 and for 2100 within the various SSP scenarios. As is clear from the table, the cities with the highest populations differ from year to year and from scenario to scenario, but in most cases, they are large cities in developing countries. Delhi is ranked as the largest city in most cases, with other Indian cities also ranking among the top ten in many cases. In SSP5, two US cities, New York and Los Angeles, are among the top ten in 2100, with the former approaching 50 million residents.
Note that, while the world’s highest-population city in 2010 was Tokyo with 36.86 million, projections for all scenarios except SSP3 indicate that the most populous urban agglomerations in 2050 will be larger, and all the scenarios indicate that the largest urban agglomerations in 2100 exceed 40 million. These results highlight major challenges awaiting such growing cities, including enormous increases in housing demand and the need to invest in key infrastructure facilities supporting transport, water, sewage, waste disposal, and other essential services.
Finally, we estimate MAPE values for our SSP-specific population projections (Supplementary Fig. 3). For agglomerations of 100,000 or more, the MAPE is 24–25% in 2050 and 42–44% in 2100. As mentioned in “Methods”, APEs tend to be larger for smaller agglomerations. MAPEs for the various SSPs do not differ significantly before 2050, but do vary slightly from one SSP to another between 2050 and 2100. MAPE is the highest in SSP3 and lowest in SSP4, a result attributable to differences in the sizes of agglomerations; indeed, upon restricting consideration to agglomerations of 1 million or more, the differences between SSPs nearly vanish, falling below the 1% level. The MAPE for agglomerations above 1 million is about 10% in 2050 and 18% in 2100. We expect our population projections contain substantial errors for smaller cities, but are reasonably precise for large cities, giving an accurate picture of long-term global trends in urbanization.
Discussion
As noted in the Introduction, this study adopts a simplified viewpoint in which urban agglomerations are defined solely by population and geographical size, ignoring the multitude of other factors—political, economic, technological, and environmental—that affect real-world cities. Nonetheless, despite this minimal framework, for most agglomerations in the UN dataset, our method correctly reproduces key trends in population evolution, suggesting that our approach successfully captures essential drivers of urbanization at the level of global aggregation.
In our method, the dominant driver of urban growth is population itself. Our approach is highly abstract, but implicitly assumes the urbanization mechanisms of the knowledge-based economy43, in which urban competitiveness depends on the scale and variety of the labor market, which in turn is expected to depend on population.
By focusing on the populations of urban agglomerations—as opposed, for example, to grid-based modeling—we are necessarily influenced by ambiguities present in the term “urban” itself44. This is a notion that admits multiple framings and may vary considerably from one era to another; indeed, by the end of this century, the nature of urban existence will have changed in crucial ways due to technological, economic, and lifestyle progress. For instance, in an SSP5 future with globally averaged GDP per capita surging above $100,000, the day-to-day activities of citizens—for work, travel, and leisure—may bear little or no resemblance to anything we would recognize today; for the urban planners and policymakers tasked with facilitating large-scale urbanization amidst such a transformed future landscape, perhaps, the most valuable asset will be a firm grasp of challenges likely to arise. This will require reframing notions of urbanity—but in ways that remain hotly contested among experts. Our projections are based on the United Nation’s traditional definition of urban agglomeration throughout the period covered by our projections; we hope our results will be useful as referential cases to compare with future figures under new urbanization contexts.
A final point of note is that, in the simple model used in this study, future population changes are allocated on the basis of present-day urban populations; strictly speaking, the relative rankings of cities cannot change in such an approach. Batty45 considered this point and concluded, based on long-term observational data on the past evolution of urban populations, that the actual situation was in fact entirely different. However, as this study shows, even this simple-minded approach suffices to reproduce, with impressive accuracy, historical population trajectories for individual urban agglomerations over the past 50 years, suggesting that the model correctly captures the mechanisms of urban-population growth to a significant extent. Moreover, pairing this model with a model describing the expansion of urban spatial footprints allows us to consider mergers between cities, whereupon we can predict changes in the domestic rankings of cities within nations; similarly, by considering variations in SSPs from one nation to another, we can predict future changes in the international ranking of cities as well. Because the circumstances of urbanization in different countries are influenced by a wide variety of factors, our estimates and projections do not depend solely on a systematic model-based methodology; instead, by basing our analysis on a range of scenarios—such as those encompassed by the SSPs—we obtain results that reflect multiple possible future outcomes, a property of great value to long-term studies of urban policy. As for the decay of urban populations, in many cases, such events are precipitated by industrial decline—as exemplified by the example of ship-building town—but to make accurate long-term predictions of declining industrial or economic activity in a given city is itself an extremely challenging task. Of course, urban growth is not determined solely by present-day values of urban-population ratios, but is rather influenced by a broad array of societal, economic, and environmental factors, whose full consideration will require more detailed models; needless to say, more complicated models have more input parameters, whose validation alone can be extremely labor-intensive. Meanwhile, the model of this paper, despite its extreme simplicity, nonetheless reproduces past urban-growth trajectories with considerable accuracy, suggesting that it correctly captures key aspects of the mechanisms governing urban growth.
One topic for future research on urban-population projection is the question of how best to account for variations in the geographical extent of cities. As discussed above, in this study, we bypassed this question by assuming fixed geographical footprints for all urban agglomerations at all future times; in reality, of course, cities typically expand geographically as their populations grow, occasionally merging with neighboring cities to consolidate labor and housing markets. If the model of this paper were extended to incorporate such phenomena, the occurrence of such mergers might produce truly enormous agglomerations—larger, both in population and geography, than the largest cities found in the projections of our model. Technically, one way to incorporate spatial expansion in a projection model would be to use a road-travel-distance model prepared to reproduce the base-year dataset; this would require that the model accounts for various factors affecting the geographic extent of cities, such as progress in transportation policy and technology.
Our findings revealed the distinct possibility that the 21st century will witness an urbanization—primarily in developing countries—that proceeds on a scale more massive than has ever been seen before. We also found that the appropriate perspectives needed to accommodate the needs of future cities, differ significantly in different SSPs, suggesting that alternative urban-policy strategies may be needed for long-term sustainability.
The variation of projected populations by SSPs, as described in “Projection of global urban agglomerations” above, may stimulate further discussion of anticipated urban problems and possible countermeasures toward their solution. Of the various scenarios, SSP4 has the most significant urban concentration in Africa, as shown in Figs. 1 and 2 (more detailed maps can be found in the links indicated in the data availability statement). The storyline assuming inequal and stratified economies in this scenario may cause the most severe urban crises and may require international cooperation to solve the urban problems in these countries. On the other hand, SSP5 has more megacities in current developed nations—especially the United States—reflecting the storyline of a high level of migration. In this case, for example, New York grows to a population of almost 50 million at the end of this century (Table 4). In combination with the exponential economic growth of this scenario, these megacities may see high-density development. Meanwhile, the SSP1 storyline assumes that global population peaks around 2070, as shown in Supplementary Fig. 2b, and thus that urbanization approaches saturation levels after 2050. The storyline of SSP1 describes a sustainable future, and this is reflected in our projections of relatively moderate population concentration in megacities. These results are among the most significant differences between SSPs. On the other hand, India is expected to have extensive urbanization in all SSPs. For instance, the population of Delhi is projected to exceed 40 million by 2100 for all scenarios (Table 4). Therefore, urban management studies to address the unprecedented size of megacities will be needed—at least for India—under the range of all SSPs.
These urban-growth scenarios raise concerns regarding the achievement of sustainable development goals (SDGs)2. Even if the SDGs are temporarily achieved by 2030, continuous urbanization may degrade indices in subsequent years. Goal 11 is the goal most closely related to urban population, covering issues, such as affordable housing, accessible transport systems, disaster prevention, and reduced environmental impact. Rapid population increase often causes housing demand in excess of supply, as well as severe transportation congestion that degrades the service level and reliability of transportation systems. In rapidly growing cities, residential areas may be developed at sites vulnerable to natural hazards or anthropogenic pollutants. Housing in such vulnerable locations is usually occupied by poor people. Congestion and unplanned development cause inefficiency and increase environmental impacts. In addition, management of water and sanitation (Goal 6), facilitation of sustainable and resilient infrastructure development (Goal 9), and climate-change adaptation (Goal 13) are directly affected by urban population. Other targets, such as ensuring healthy lives, preventing marine pollution, and protecting ecosystems and biodiversity, are indirectly affected by population. Although a full discussion of SDGs and their achievement under projected urban populations is beyond the scope of this paper, we expect that our global projections of urban agglomerations will provide perspectives illuminating possible risks of urban problems.
Regarding infectious diseases, we note that COVID-19 has had devastating impacts on urban activities throughout the world. Indeed, 90% of reported COVID-19 cases are estimated to have occurred in urban areas, where population density and high interaction levels increase the chances of transmitting the virus46. Clearly, planning is required to rebuild urban systems for post-COVID-19 recovery47. However, it is far too soon to assess the impact on urban-population distributions of initiatives currently underway to combat the pandemic and rethink post-pandemic urban planning. One of the major centripetal forces gathering people in cities is the agglomeration economy48,49. Locating in large cities saves transaction and transportation costs, increases access to other businesses and other entities, and probably entails benefits from knowledge or technological spillovers. Before COVID-19, most of these activities were based on face-to-face communications. During the pandemic period, remote work has replaced a substantial portion of face-to-face business activities, except for essential jobs such as medical care, retail, and transportation. If the agglomeration economy is realized through this kind of online communication, then some aspects of the centripetal force to cities would disappear, and city-size distributions might be altered drastically. In contrast, if people still prefer face-to-face communication, then urban-growth trajectories may largely return to their original course before COVID-19. Looking at historical data for city-size distributions in the United States and the United Kingdom (Supplementary Fig. 5), we see remarkable stability during the past 60 years, despite tremendous technological progress and considerable fluctuations of risks in cities. This observation regarding city-size distributions may reflect deep-rooted principles of urban-system formation. If city-size distributions change drastically post COVID-19, this would mean that key principles of urban-system formation have shifted—in which case alternative models to explain the distorted size distribution must be developed. Clearly, global urban trends in the post-COVID-19 era will demand careful monitoring. Although further research is needed to incorporate various additional factors—including the impact of infrastructural, environmental, economic, and societal factors on urban-system growth, as well as the appropriate reframing of “urban” concepts in a sustainability context—nonetheless we believe that this study, yielding long-term projections of urban futures supported by a substantial evidentiary basis, will furnish valuable input to discussions of urban planning, infrastructure design, energy and environmental policy, and sustainability.
Methods
Data
For raw data on populations and coordinates, we used the resources “Population of Urban Agglomerations with 300,000 Inhabitants or More in 2018”3 from the UN’s World Urbanization Prospects 2018 (referred to below as WUP), “Population Count v4.11 (referred to below as PC)”, and “Administrative Unit Center Points with Population Estimates v4.11(referred to below as AUCP)” from Gridded Population of the World, v436 (referred to below as GPW). WUP records urban populations and geographical coordinates, at 5-year intervals between 1950 and 2035, for 1860 urban agglomerations spanning 154 nations or territories around the world. GPW-PC is a global raster of population count at 30 arc-second resolution. GPW-AUCP records coordinates for 8,342,421 worldwide sites, spanning 241 nations or territories, and populations at 5-year intervals from 2000 to 2020. We use World Gazetteer and GeoNames to provide seeds of urban agglomeration. Each dataset contains 88,549 and 99,181 named locations with coordinates, respectively.
GDP per-capita data are compiled using OECD.stat and Global Metro Monitor for data-available agglomerations and World Development Indicators to set national average GDP per capita for the other agglomerations. OpenStreetMap (referred to below as OSM) is used to determine major roads in and around agglomerations to estimate urban extents. We extracted the roads classified as motorways, trunk roads, and primary roads.
For SSP scenarios, we use the IIASA-SSP database16, which lists city populations and per-capita GDP values, organized by nation, at 5-year intervals from 2010 to 2100.
Workflow
Figure 3 shows the overall workflow used in this study to project future populations for all agglomerations. First, we estimate the maximum road-travel distance for each agglomeration in WUP to determine its spatial urban boundaries (see Supplementary Fig. 4). We rasterize the OSM major road links to 30 arc-second grid and assume travel speeds of 50 km/h for road-covered and 10 km/h for nonroad meshes. We assume that each agglomeration is centered at its WUP coordinates and map-travel times from agglomeration centers to the surrounding grid. The maximum road-travel time of agglomeration i is denoted as tmax,i, which we determine based on WUP populations according to \(\mathop {\sum }\nolimits_{g \in {{\Omega }}_i} n_g = N_i\), \({{\Omega }}_i = \left\{ {g{\mathrm{|}}t_{ig} \le t_{{\mathrm{max}},i}} \right\}\), where ng is the population at grid point g, Ni is the population of agglomeration i, and tig is the time required to reach grid point g from the center of agglomeration i. For some agglomerations, the WUP location and GPW-CP grid are inconsistent, in which case we arbitrarily assume a worst-case road-travel time of 2 h.
The flow consists of data (UN WUP, GPW-PC, GPW-AUCP, Urban seeds by geoNames and World gazetteer, OpenStreetMap, GDP per capita by OECD.stat, Global Metro Monitor, and World Development Indicators), scenarios (shared socioeconomic pathways), models (maximum road-time model and random growth urban model), and output (urban-population projections).
Second, we estimate the model of the maximum road time explained by population, GDP per capita, and major road-grid ratio in the urban extent. Here, we select 151 countries for which these data are available. If the center of an agglomeration is within the time contour of the other larger agglomeration, we assume that the smaller agglomeration belongs to the larger agglomeration and merge them in the dataset. Additional explanation can be found in Supplementary Fig. 4. As a result, the original WUP agglomerations are merged into 1794 agglomerations. We applied the same procedure to GeoNames, World Gazetteer, and GPW-AUCP data to merge agglomerations or human settlements. We obtained 415,886 settlements. Among these, we select 89,620 settlements that have populations of 5000 or more to reduce calculation cost. These selected agglomerations/settlements cover a total population of 6.6 billion, or 95% of the total 2010 population of the GPW-AUCP dataset. The observed global urban-population share is 52% in 2010, with our dataset of course including rural populations. Urban and rural settlements are distinguished by population size, and we set the dividing thresholds to yield urban populations consistent with 2010 observations for each country. These dividing thresholds—the minimum population sizes of urban agglomerations—are described in “Random-growth urban model” section below.
Third, we apply our random-growth model to these selected agglomerations/settlements to project future populations for each agglomeration through the year 2100 under each SSP. The original projection assumes fixed urban extent.
Models
In this study, we mainly use two models: a maximum road-travel time model and a random-growth model. In addition, we model absolute percentage errors (APEs) to assess uncertainty.
As noted in the workflow section, we estimate maximum road-travel times for agglomerations in WUP. Following Makse et al.50, we quantify the maximum road-travel time via the formula \(T_i = \alpha _0N_i^{\alpha _N} \cdot G_i^{\alpha _G} \cdot R_i^{\alpha _R}\) with Ti, Ni, Gi, and Ri, respectively, denoting the maximum road time, population, per-capita GDP, and major road-grid area ratio of urban agglomeration i; the quantities α0, αN, αG, and αR are parameters. We determine parameter values via linear regression analysis after applying a logarithmic transformation to the model. Table 5 lists the results of our parameter-estimation procedure. Signs of parameters indicate that, as expected, road-travel times increase with increasing population and GDP per capita, and also increase with decreasing road coverage of grid regions.
Using dynamical equations describing the temporal evolution of urban populations, the Random-growth urban model29 asymptotically approaches the Pareto distribution of city population scales. The original model is described as follows:
Here, Ni denotes the population of agglomeration i, n denotes the rate of increase of the national urban population, \(\mu _i\) is a geographical fitness parameter, N0 is the minimum population of a city, m is the average geographical fitness, and \({{\Omega }}_t\) is the set of all cities in a nation at time t. This model asymptotically approaches a Pareto distribution for urban populations. The probability that agglomeration’s population exceeds N is expressed as follows:
Our primary interest is the upper tail of the size distribution, so we utilize Eq. (1) to project future populations for each agglomeration. However, in this study, we use scenarios describing the urban populations of individual nations at 5-year intervals to estimate variations in the urban populations of existing cities and geographical locations, taking the urban-population distribution in 2010 as a basis of reference. Thus, we consider the following discretized version of the model.
In cases where the urban population increases, we express the population of urban agglomeration i at time t + 1 in the form
where \(N^t_i\) and NUct denote the population of urban agglomeration i, and the urban population of the nation as a whole, at time t. Here we assume \(\mu _i - N_0 \ll N_i\) and thus neglect this quantity in Eq. (1). In this equation, the quantity r(t) that enters the summation limits is the rank of the smallest city at time t, and we put \(N_{Uc}^t = \mathop {\sum}\nolimits_{j = 1}^{r(t)} {N_j^t}\). If \(N^t_i\) in this equation is Pareto-distributed, then Nit + 1 will be as well. Here, the increase in a nation’s total urban population is the sum of the population increases in existing cities plus the populations of any newly added cities; all cities with ranks between r(t) + 1 and r(t + 1) will be newly added. In our estimation procedure, r(t + 1) is not known in advance; instead, we initially set r(t + 1) = r(t) + 1, use Eq. (6) to compute \(N_{r(t + 1)}^{t + 1}\), and then repeatedly increase the value of r(t + 1) by 1 until we have \(N_{r(t + 1)}^{t + 1}\) < Nmc, where Nmc is the minimum population size of urban agglomerations, which varies from nation to nation. If r(t + 1) > r(t), then r(t + 1) − r(t) rural settlements become urban agglomerations, as their populations now exceed Nmc. Thus, our method simulates the emergence of new urban agglomerations from the seeds of rural settlements, while the total number of urban and rural settlements remains fixed through the analysis. The emergence of entirely new cities—with no predecessors in 2010—is not simulated in this study. This assumption will affect the lower tail of the population-size distribution, which falls outside the scope of this study. If, at any time point, the sum of the populations of the cities we include in our analysis exceeds the total population of the nation given by the SSP scenario, we correct the discrepancy by forcibly setting to zero the population of first the smallest city, then that of the second smallest city, and so on until the total population agrees with the SSP value.
In cases where the urban population decreases, we assume that the number of cities decreases as well, and we put
Mirroring the procedure described above, as r(t + 1) is not known in advance, we initially put r(t + 1) = r(t) − 1, then repeatedly decrease r(t + 1) by 1 until the condition Nr(t+1)t + 1 > Nmc is satisfied.
For postdiction, if NUct + 1 > NUct we put
while if NUct + 1 < NUct we instead put
Because r(t) is unknown, in the former case, we initialize r(t) = r(t + 1)–1 and then repeatedly decrease r(t) by 1 until Nr(t)t > Nmc; in the latter case, we initialize r(t) = r(t + 1)+1 and then repeatedly increase r(t) by 1 until Nr(t)t < Nmc.
We estimate absolute percentage errors (APEs) of our projections by comparing them to UN-WUP data. APEs tend to larger values for urban agglomerations of smaller populations and for projections further into the future. Referring to Tayman et al.39, we model APEs according to
where \(N_i^t\) is the population of agglomeration i at time t and T is the temporal distance from 2010 (i.e., T = | t − 2010 | ). Here we use APE and N values for 1736 agglomerations at 5-year intervals from 1950 to 2035, excluding the base year 2010. Table 6 shows the estimated parameters, and Fig. 4 shows the estimated APE for a range of population and time horizon. According to the estimate, APEs are substantial for small cities, but decrease for larger populations. For the year 2100 (time horizon 90 years), the APE for agglomerations with populations of 1 million or more is 24%, while that for agglomerations with populations of 10 million or more is estimated at 8.7%.
Reporting summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Data availability
The data generated and analyzed during this study are described in the following data record: https://doi.org/10.6084/m9.figshare.1311812351. The following resources, which were among the sources of the data analyzed in the study, are available from the links below: postdiction results for 1794 urban agglomerations. Temporal evolution from 2010 to 2100 of the geographical distribution of urban agglomerations, arranged by population scale, as predicted within the various SSP scenarios (http://stwww.eng.kagawa-u.ac.jp/~kii/Research/UPP_2020/UPP_2020.html). Available urban-population data include the UN’s World Urbanization Prospects 20183 (https://population.un.org/wup/) and Gridded Population of the World, v436. Available settlement-point data include, in addition to the above urban-population sources, World Gazetteer (https://www.arcgis.com/home/item.html?id=346ce13fa2d4468a9049f71bcc250f37) and GeoNames (https://www.geonames.org/). GDP per-capita data are available from OECD.stat (https://stats.oecd.org/), Global Metro Monitor (https://www.brookings.edu/research/global-metro-monitor/), and World Development Indicators (http://datatopics.worldbank.org/world-development-indicators/). OpenStreetMap is available at https://www.openstreetmap.org/. Scenario data for SSPs are available at the IIASA-SSP database16.
Code availability
The R codes developed for preparing the global urban agglomeration dataset and for the population projection of agglomerations are available at the same URL provided in the “Data availability” section.
References
van Ginkel, H. Urban future. Nature 456, 32–33 (2008).
United Nations Economic and Social Council. Progress towards the sustainable development goals. Report of the Secretary-General, E/2016/75 (2016).
World Urbanization Prospects: The 2018 Revision. World Urbanization Prospects: The 2018 Revision. https://doi.org/10.18356/b9e995fe-en (2019).
Bai, X. et al. Six research priorities for cities and climate change. Nature 555, 23–25 (2018).
Revi, A. et al. Urban areas. Clim. Chang. 2014 Impacts, Adapt. Vulnerability Part A Glob. Sect. Asp. 535–612, https://doi.org/10.1017/CBO9781107415379.013 (2015).
Arnell, N. W. & Lloyd-Hughes, B. The global-scale impacts of climate change on water resources and flooding under new climate and socio-economic scenarios. Clim. Change 122, 127–140 (2014).
Jongman, B. et al. Declining vulnerability to river floods and the global benefits of adaptation. Proc. Natl. Acad. Sci. USA 112, E2271–E2280 (2015).
Dong, W., Liu, Z., Liao, H., Tang, Q. & Li, X. New climate and socio-economic scenarios for assessing global human health challenges due to heat risk. Clim. Change 130, 505–518 (2015).
Caminade, C. et al. Impact of climate change on global malaria distribution. Proc. Natl. Acad. Sci. USA 111, 3286–3291 (2014).
Huang, Q. et al. The occupation of cropland by global urban expansion from 1992 to 2016 and its implications. Environ. Res. Lett 15, 084037 (2020).
Seto, K. C., Güneralp, B. & Hutyra, L. R. Global forecasts of urban expansion to 2030 and direct impacts on biodiversity and carbon pools. Proc. Natl. Acad. Sci. USA 109, 16083–16088 (2012).
McDonald, R. I. et al. Urban growth, climate change, and freshwater availability. Proc. Natl. Acad. Sci. USA 108, 6312–6317 (2011).
Jones, B. & O’Neill, B. C. Spatially explicit global population scenarios consistent with the Shared socioeconomic pathways. Environ. Res. Lett. 11, 084003 (2016).
Zhou, Y., Varquez, A. C. G. & Kanda, M. High-resolution global urban growth projection based on multiple applications of the SLEUTH urban growth model. Sci. Data 6, 1–10 (2019).
Grübler, A. et al. Regional, national, and spatially explicit scenarios of demographic and economic change based on SRES. Technol. Forecast. Soc. Change 74, 980–1029 (2007).
Riahi, K. et al. The shared socioeconomic pathways and their energy, land use, and greenhouse gas emissions implications: an overview. Glob. Environ. Chang. 42, 153–168 (2017).
Alonso, W. Location and Land Use (Harvard University Press, Cambridge, MA, 1964).
Muth, R. F. Cities and Housing (University of Chicago Press, Chicago, IL, 1969).
Mills, E. S. An aggregative model of resource allocation in a metropolitan area. Am. Econ. Rev. 57, 197–210 (1967).
Mills, E. S. Studies in the Structure of the Urban Economy (John Hopkins Press, Baltimore, MA, 1972).
Acheampong, R. A. & Silva, E. A. Land use–transport interaction modeling: a review of the literature and future research directions. J. Transp. Land Use 8, 11–38 (2015).
Iacono, M., Levinson, D. & El-Geneidy, A. Models of transportation and land use change: a guide to the territory. J. Plan. Lit. 22, 323–340 (2008).
Kii, M., Nakanishi, H., Nakamura, K. & Doi, K. Transportation and spatial development: an overview and a future direction. Transp. Policy 49, 148–158 (2016).
Colby, S. L. & Ortman, J. M. Projections of the Size and Composition of the US Population: 2014 to 2060: Population Estimates and Projections. (US Census Bureau, 2017).
Hauer, M. E. Population projections for U.S. counties by age, sex, and race controlled to shared socioeconomic pathway. Sci. Data 6. https://doi.org/10.1038/sdata.2019.5 (2019).
Nakicenovic, N. & Swart, R. Special Report on Emissions Scenarios (Cambridge University Press, UK, 2000).
Zipf, G. K. Human Behaviour and the Principle of Least Effort (Addison-Wesley, Cambridge, 1949).
Kii, M., Akimoto, K. & Doi, K. Random-growth urban model with geographical fitness. Physica A 391, 5960–5970 (2012).
Simon, H. A. On a class of skew distribution functions. Biometrika 42, 425–440 (1955).
Arshad, S., Hu, S. & Ashraf, B. N. Zipf’s law and city size distribution: a survey of the literature and future research agenda. Physica A 492, 75–92 (2018).
Fragkias, M. & Seto, K. C. Evolving rank-size distributions of intra-metropolitan urban clusters in South China. Comput. Environ. Urban Syst. 33, 189–199 (2009).
Huang, K., Li, X., Liu, X. & Seto, K. C. Projecting global urban land expansion and heat island intensification through 2050. Environ. Res. Lett. 14, 114037 (2019).
Krugman, P. Confronting the mystery of urban hierarchy. J. Jpn. Int. Econ. 10, 399–418 (1996).
Favaro, J. M. & Pumain, D. Gibrat revisited: an urban growth model incorporating spatial interaction and innovation cycles. Geogr. Anal. 43, 261–286 (2011).
O’Neill, B. C. et al. The roads ahead: narratives for shared socioeconomic pathways describing world futures in the 21st century. Glob. Environ. Chang. 42, 169–180 (2017).
Center for International Earth Science Information Network - CIESIN - Columbia University. Gridded population of the world, version 4 (GPWv4): Population density, revision 11. Palisades, NY: NASA Socioeconomic Data and Applications Center (SEDAC) (2018).
Swanson, D. A., Tayman, J. & Bryan, T. M. MAPE-R: a rescaled measure of accuracy for cross-sectional subnational population forecasts. J. Popul. Res. 28, 225–243 (2011).
Rayer, S., Smith, S. K. & Tayman, J. Empirical prediction intervals for county population forecasts. Popul. Res. Policy Rev. 28, 773–793 (2009).
Tayman, J., Smith, S. K. & Rayer, S. Evaluating population forecast accuracy: a regression approach using county data. Popul. Res. Policy Rev. 30, 235–262 (2011).
Rayer, S. & Smith, S. K. Factors affecting the accuracy of subcounty population forecasts. J. Plan. Educ. Res. 30, 147–161 (2010).
Jiang, L. & O’Neill, B. C. Global urbanization projections for the shared socioeconomic pathways. Glob. Environ. Chang. 42, 193–199 (2017).
KC, S. & Lutz, W. The human core of the shared socioeconomic pathways: population scenarios by age, sex and level of education for all countries to 2100. Glob. Environ. Chang. 42, 181–192 (2017).
Westlund, H. Urban-rural relations in the post-urban world. in The Post-Urban World. (eds Haas, T. & Westlund, H) 70–81 (Routledge, London, 2018).
Parnell, S., Elmqvist, T., McPhearson, T., Nagendra, H. & Sörlin, S. Situating Knowledge and Action for an Urban Planet. in Urban Planet. (eds Elmqvist, T. et al.) 1–16 (Cambridge University Press, Cambridge, 2018).
Batty, M. Rank clocks. Nature 444, 592–596 (2006).
United Nations. Policy Brief: COVID-19 in an Urban World (United Nations, 2020).
Acuto, M. et al. Seeing COVID-19 through an urban lens. Nat. Sustain. https://doi.org/10.1038/s41893-020-00620-3 (2020).
Rosenthal, S. S. & Strange, W. C. Geography, industrial organization, and agglomeration. Rev. Econ. Stat. 85, 377–393 (2003).
Fujita, M. & Krugman, P. The new economic geography: past, present and the future. Pap. Reg. Sci. 83, 139–164 (2004).
Makse, H. A., Havlin, S. & Stanley, H. E. Modelling urban growth patterns. Nature 377, 608–612 (1995).
Kii, M. Metadata record for the manuscript: Projecting future populations of urban agglomerations: around the world and through the 21st century. figshare https://doi.org/10.6084/m9.figshare.13118123 (2020).
Acknowledgements
This work was partly supported by JSPS Grants-in-Aid for Scientific Research (KAKENHI) 16KK0013, JST SICORP JPMJSC16E1, Japan, Science and Technology Research Partnership for Sustainable Development (SATREPS), JST/JICA JPMJSA1704, and JSPS and DAAD under the Japan-Germany Research Cooperative Program JPJSBP120183515. We thank K. Akimoto for useful discussion, H. Reid for translating and editing of this paper, and the anonymous reviewers for their valuable comments.
Author information
Authors and Affiliations
Contributions
M.K. contributed to the conception and design of the work, analysis and interpretation of the data, and drafted the work.
Corresponding author
Ethics declarations
Competing interests
The author declares no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kii, M. Projecting future populations of urban agglomerations around the world and through the 21st century. npj Urban Sustain 1, 10 (2021). https://doi.org/10.1038/s42949-020-00007-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42949-020-00007-5
This article is cited by
-
IoT-enabled co-integration analysis of foreign trade and environmental sustainability in Quanzhou city
Soft Computing (2024)
-
AI-Based on Machine Learning Methods for Urban Real Estate Prediction: A Systematic Survey
Archives of Computational Methods in Engineering (2024)
-
Nature-based solutions potential for flood risk reduction under extreme rainfall events
Ambio (2024)
-
Projecting spatial interactions between global population and land use changes in the 21st century
npj Urban Sustainability (2023)
-
A review on factors influencing fog formation, classification, forecasting, detection and impacts
Rendiconti Lincei. Scienze Fisiche e Naturali (2022)