Abstract
The reconstruction of complex time-evolving fields from sensor observations is a grand challenge. Frequently, sensors have extremely sparse coverage and low-resource computing capacity for measuring highly nonlinear phenomena. While numerical simulations can model some of these phenomena using partial differential equations, the reconstruction problem is ill-posed. Data-driven-strategies provide crucial disambiguation, but these suffer in cases with small amounts of data, and struggle to handle large domains. Here we present the Senseiver, an attention-based framework that excels in reconstructing complex spatial fields from few observations with low overhead. The Senseiver reconstructs n-dimensional fields by encoding arbitrarily sized sparse sets of inputs into a latent space using cross-attention, producing uniform-sized outputs regardless of the number of observations. This allows efficient inference by decoding only a sparse set of output observations, while a dense set of observations is needed to train. This framework enables training of data with complex boundary conditions and extremely large fine-scale simulations. We build on the Perceiver IO by enabling training models with fewer parameters, which facilitates field deployment, and a training framework that allows a flexible number of sensors as input, which is critical for real-world applications. We show that the Senseiver advances the state-of-the-art of field reconstruction in many applications.
Similar content being viewed by others
Main
The goal of sparse data reconstruction is to take a few sensor values from a space that we cannot fully observe, and use them to reconstruct the global field. Reconstructing spatial fields from sensor data has been a grand challenge in a wide range of applications in industry, medicine and science1,2,3. Some examples include laboratory experiments4, monitoring industrial plants5, precision agriculture6, design of limb orthoses and prostheses7, structural health monitoring in aircraft8 civil infrastructure9, subsurface sensing10, tectonic motion estimation11, weather and climate monitoring12, and identification of abandoned wells13, among others.
Common features of these applications are low-spatial-sensor coverage (typically less than 1%), three-dimensional (3D) domains, noisy data, nonlinear dynamical phenomena and a scarcity of available processing power within the sensor. These sensing assets are often deployed in areas with scarce or non-existent network connectivity, necessitating edge computing. For this reason, low-resource, field-ready devices such as drones require machine learning approaches that are computationally efficient and accurate. While some applications can be fully described by physics-based partial differential equations (PDEs), incorporating field observations (for example, sensor measurements) back to the PDEs is challenging. A variety of techniques have been developed using PDE-based14,15 and statistical16,17,18 approaches. Still, widespread success has been elusive due to a lack of a generic framework to incorporate measured data at arbitrary times and locations. As a result, machine learning models have become an attractive alternative16,17,18 as these have the capacity to learn complex relationships from data in a great many problems. Some notable examples include optimization of sensor placement19,20,21. Machine learning models have the potential to be successful even when the governing PDEs of the system are not available. Still, real-world sensors often have physically limited sensor positions (for example, floating buoys in the ocean22, Earth-based asteroid sensing23, the inlet/outlet for a laboratory experiment24), and covering a field exhaustively can be prohibitively expensive, if not impossible. Furthermore, low-power sensors are often preferred when operating off the grid (for example, mobile sensing with drones), and so computational resources are precious.
With recent advances in machine learning algorithms, complex reconstruction problems have become more tractable25,26. Although fully connected networks could be used for this task, their rigid architecture has difficulty handling sensors that move around the field and/or go on and off with time. Another key challenge for reconstructing fields from sparse data is that the field itself does not always lie on a Cartesian grid, so methods that assume structured data, such as convolutional neural networks, must impose an artificial structure to the field values. Conversely, methods that overcome this problem by explicitly including the geometry of the data, such as graph neural networks27, require a choice of a graph topology, which may be problem and/or dataset specific. This aspect of the problem adds additional decisions to make and hyperparameters when applying a graph network method to new problems. Data-driven methods generally require a dense set of observations and training time and a sparse set of observations at inference time. Techniques such as the popular physics-informed neural networks28,29 become prohibitively expensive for even small, canonical two-dimensional (2D) datasets30 and success has therefore been limited in leveraging them for sparse sensing9.
A few notable works stand out. Manohar et al.19 describes methods where the low-rank structure of the dataset can be exploited if it exists. They specifically target cases where the number of sensors is greater than the number of modes used in reconstruction, by introducing the idea of QR pivoting. They employ this mechanism to leverage known patterns in the data to optimize the sensor positioning. However, for chaotic, multiscale systems such as 3D turbulence, the number of modes for effective reconstruction are often quite high, and there could be fewer sensors in practice. In another recent approach, Güemes31 proposed constructing low-resolution fields using moving averages from accessible sparse sensor data that then are mapped to higher resolutions using a learned mapping. In a similar vein, Fukami et al.32 introduced a method based on Voronoi tessellation of observations onto the prediction domain, followed by a refinement using a convolutional network. Their approach has the attractive upsides of allowing arbitrary sensor placement within a 2D mesh, and allowing inference using sensor locations that differ from the ones used during training. Nevertheless, this approach inherits the hurdles of deep convolutional networks, such as the assumption of a regular grid and high memory costs for 3D domains33, which are features prevalent in real-world problems. Extending convolutional neural network approaches to 3D or large 2D datasets would be very computationally expensive, and may require considerable efforts in engineering implementation. This is a common denominator for methods currently in literature: they struggle to work in chaotic, high-dimensional datasets without demanding excessive compute resources. As a result, there is a major gap in literature between proposed models and the practical application to real-world data.
Attention mechanisms34 have greatly improved the baselines over other architecture for a variety of problems35,36,37,38, and recently, the Perceiver IO framework39 overcame a crucial computational bottleneck using cross-attention with latent arrays, thereby constraining the bulk of the network activations to a fixed-sized space regardless of input size. While this was viewed as a way to handle a large set of inputs (for example, every pixel in an image), we exploit the fact that it also allows us to scale down the quantity of information fed into a network, resulting in a framework we call the Senseiver. For our applications, we need to make near real-time decisions on drones or other field-deployed instruments with limited processing power, and current machine learning architectures are too computationally expensive. By incorporating sparsity and refining the network architecture to drastically reduce the number of parameters needed, the Senseiver is able to accurately learn and process an entire field with a far smaller amount of resources. Crucially, sparse processing can treat spatial data that do not live on a fixed, regular, Cartesian-type mesh. Our approach also overcomes a limitation of earlier of graph element networks27, which produce bad estimates when a denser set of sensors is used at inference time.
In this Article, we demonstrate examples of these advantages on several datasets, and we compare the Senseiver to the recent successes of ref. 32, showing remarkable improvements in accuracy, scalability and efficiency in the limit of low sensor coverage. Beyond these improvements, we discuss additional benefits of the sparse processing model of the Senseiver, such as prediction of partial information, reduced memory requirements, and faster performance during training and inference. We demonstrate this on large 3D cases, where even convolutional networks are not practical. The model is also computationally efficient by not processing invalid locations in irregular geometries where there are regions without data, such as in solid boundaries in porous media and continents; sparse processing allowing for training to domains of arbitrary size and structure.
Workflow
Overview
The first aim of the Senseiver is to learn a compact representation of the state of a system from a small number of sensor observations at a given time. This encoded representation can then be used to decode the state of the full system from sensor data. The input to our model is a set of Ns sensor observations si taken at time t, \({\{{{{{\bf{s}}}}}_{1},{{{{\bf{s}}}}}_{2},\ldots {{{{\bf{s}}}}}_{{N}_{{\mathrm{s}}}}\}}_{t}\), with \({{{{\bf{s}}}}}_{i}\in {{\mathbb{R}}}^{{N}_{{\mathrm{I}}}}\), where NI corresponds to the number of channels recorded by the sensors (for example, 1 for temperature, 3 for a velocity vector in 3D). The system has a domain Ω where a set of sensor locations \(\{{{{{\bf{x}}}}}_{1},{{{{\bf{x}}}}}_{2},\ldots ,{{{{\bf{x}}}}}_{{N}_{{\mathrm{s}}}}\}\)\({{{{\bf{x}}}}}_{i}\in {{\mathbb{R}}}^{{N}_{{\mathrm{D}}}}\) are extracted. Throughout the paper, we use bold lowercase letters to denote vectors, bold uppercase letters to denote matrices, italic uppercase letters to represent functions, and italic lowercase letters to denote scalars.
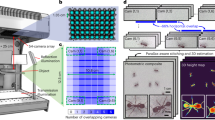
The Senseiver workflow, shown in Fig. 1a, has three main components. (1) A spatial encoder PE that maps a spatial coordinate xs to an array of spatial encodings a, that allow us to encode a precise n-dimensional spatial position to a vector. (2) An attention-based encoder E that maps the spatial encodings of the sensor positions ai and their values si to a latent matrix Z, which is a compressed representation of the system at time t. 3) An attention-based decoder D, which outputs the reconstructed field value at arbitrary query position xq that are also represented using the spatial encoder. As equations, this process is given by:
a, The workflow of the Senseiver innovations for the sparse-sensing problem. We use sensor values and precise query locations that are sparse in the field domain and allow greater computational efficiency. The sensor values are processed by an encoder, and the resulting latent representation is passed along with the query information to a decoder, which estimates the field at a new location. In this example, the output is decoded into a structured grid. b, Overview of applications in this work.
where the subscripts s and q stand for the sensor and query positions. These items are explained in detail (Methods).
The Senseiver is well suited to the demands of many real-world applications (some of which are shown in Figure 1b). First, it is agnostic to spatial dimensionality, as it can work in one, two or three dimensions, with no code or hyperparameter modifications. Second, we can train our model without specialized feature engineering, that is, no problem-specific processing of input features or labels is required, as the direct sensor observations can be used as input to the network. Third, our model is resolution/grid agnostic, as it works with arbitrary, continuous sensor locations. This addresses a key limitation in real-world problems, where we can place sensors only in locations such as the boundaries and edges, making the reconstruction problem harder. In addition, our model can treat not only sparse input but also sparse output, which allows training to large 3D fields using less memory by stochastically subsampling the output space. These features show promise in scaling our approach to datasets across a variety of scientific domains with arbitrary size, meshing and geometry.
Brief review of attention-based models
Attention-based neural networks process information by re-weighting a set of inputs, the sequence, such that each sequence element is weighted to take larger contributions from certain elements in the sequence (to ‘attend’), while effectively ignoring others34. It is important to note that the term sequence need not represent a one-dimensional array of variables; in fact, attention layers can have arbitrary connections between the elements composing the sequence. Because of this fact, attention layers can model the interactions of n sensors among themselves and additional information using a pair-wise interaction modelling approach40. In practice, this is not memory efficient because it corresponds to a complete graph of connections between all sequence elements. This is especially relevant for applications that involve learning from large inputs (for instance, images or videos), as the memory requirements for complete pair-wise self-attention scale quadratically with input size.
However, attention mechanisms are very flexible, and this can be exploited. The Perceiver IO41 presented an alternative to avoid the quadratic bottleneck by utilizing a latent sequence array (\({{{{\bf{Q}}}}}_{{\mathrm{in}}}\in {{\mathbb{R}}}^{{N}_{{{{{\bf{Q}}}}}_{{\mathrm{in}}}}\times {N}_{{\mathrm{I}}}}\)) to process arbitrarily sized inputs into a compact latent sequence representation of the same size as the latent array. The same principle is employed at the output to project the latent sequence into the desired output shape and dimensionality. Thus the model can use arbitrarily shaped inputs and outputs, while the bulk of latent computations are of fixed shape and computational cost (Fig. 2). This approach allows for non-local processing across input sequences and makes no assumptions about the structure of the data. This allowed the Perceiver IO to have a core network that is domain agnostic, so that different input/output branches can be used to process qualitatively different data streams, such as text, audio or image. For the Senseiver, it allows the treatment of partial information and frees the network from any assumption about the input domain geometry, unlike, for example, convolutional networks.
Training procedure
During training, a batch of data is used to optimize the weights of the model by minimizing the mean square error:
where t is time, and xs and \({{{{\bf{x}}}}}_{{{\mathrm{q}}}_{j}}\) are the spatial coordinates of the sensors and the queries, respectively. A batch of data is composed by a selection of \({{{{\bf{x}}}}}_{{{\mathrm{q}}}_{j}}\) in the training dataset. In our experiments, we used batches of randomly selected points through the training dataset—first sampling a time frame and then sampling query points within that time frame. Shuffled data samples proved much more effective versus ordered points (axis or patches) for training performance. Note that dense observations are required to train the model, while at inference time only sparse observations are necessary. We trained the model until the minimum loss value over the training period did not change for 100 consecutive epochs. As this is a nascent class of problems, the mean L2 error norm:
across all the time steps of the test set is reported for comparison with recent work32. Here, \(\hat{s}\) is the prediction of the model.
Results
Cyclic and quasi-cyclic dynamical phenomena
The first dataset considered is a simulation of a 2D unsteady flow past a cylindrical obstacle42. This results in a von Kármán vortex street, that is, an alternating shedding of left- and right-handed vortices in the flow field behind the cylinder. The dataset was created utilizing a numerical simulation that solves the incompressible Navier–Stokes equation at a Reynolds number of 100. The simulation is periodic in the x and y coordinates and its computational size is a 192 × 112 grid with 5,000 time frames, which approximately spans four vortex shedding periods. The domain spans 10 cylinder diameters vertically and 15.7 cylinder diameters horizontally. The recorded output is the vorticity field of the fluid, which is impacted by having a solid obstacle.
We trained our model to reconstruct the simulation based on three different sensor location configurations as inputs. During training, each batch observes the field at only a sparse set of locations, but collectively the batches sample the whole training field. The first configuration uses eight sensor locations as proposed by ref. 32. The second configuration uses only the first four sensors to show the impact of having less input information. The third proposed configuration sets the sensor locations at the inlet/outlet boundaries, motivated by sensing limitations of lab-on-a-chip experiments. In this case, for the approach proposed by ref. 32, the Voronoi-tessellated image would contain almost no information, as the values at the boundaries are very close to zero at every time step. Even when the variance of the values is very small, the attention layers are able to construct a robust representation. All these configurations are shown in Fig. 3. We trained our model using only 50 frames (1% of the dataset) and the remaining frames are used as the test set. The results are shown in the bar plot of Fig. 3. In comparison with the VoronoiCNN (the model proposed in ref. 32) trained on the same amount of data and with the same amount of sensors, our model achieves approximately ten times lower error. Even with just four sensors at the boundary, the Senseiver is able to reconstruct the entire simulation faithfully with a negligible drop in accuracy compared with the eight-sensor configuration. Higher errors are present where the vorticity magnitude changes the most, partly due to the fact that these locations are far away from the sensors. It is worth noting that the model in ref. 32 has over 682,000 trainable parameters, while ours is composed by less than 5% of that number. A complete hyperparameter analysis for this problem can be found in the Supplementary Information.
Left: test error (equation (5)) with different sensor configurations and number of training frames and comparison with VoronoiCNN32. The bars with diagonal lines indicate the error of our model. Note that the colour in the inset plot on the left is artificially limited to highlight the von Karman vortices. Right: sensor locations, a frame with an error closest to the mean error and the mean error throughout the test set. The values of the field at each frame go from −1 to 1; colorbars in the error plots represent the reconstruction error on this field.
The second dataset that we considered is the National Oceanic and Atmospheric Administration sea surface temperature43. This real-world dataset was collected from satellite and ship-based observations over time. The data comprise weekly observations of the sea surface temperature of Earth at a spatial resolution of 360 × 180 (longitude and latitude, respectively)—giving a resolution of 1° longitude and 1° latitude. For training, we use 1,040 snapshots spanning from the year 1981 to 2001, and then we tested on snapshots from 2001 to 2018. During training, we do not use any information about field values on the continents, because there is no recorded value to reconstruct, which saves computational time (as the continents are 32% of the computational domain). For each batch of data, we select 1 to 100 sensors using a uniform distribution with the goal of training the model to be robust under different number of sensors and spatial configurations. Again, each batch during training observes a sparse set of observations, but collectively the batches with random sensor configurations sample from the whole field. For testing, we placed sensors randomly following the same procedure as ref. 32.
In our results, we see that just 10 sensors allows for a very strong reconstruction performance of ϵ = 0.047. Ten sensors constitute a total spatial coverage of 0.0154%. By adding more sensors, the overall test error goes down and missing details are added to the local temperature field as seen in Supplementary Fig. 2. It also noticeable that as we use random sensors during training, the model does not take a big performance hit in the scenarios with fewer sensors (Ns < 50) compared with ref. 32. The forecasting capabilities show that with good coverage (Ns > 50), the trained model can perform estimates up to 18 years into the future with error substantially less than 1 °C. This shows that the Senseiver architecture can cope with real-world situations, including forecasting. All these results are shown in detail in the Supplementary Information.
Acyclic and nonlinear chaotic phenomena
The third dataset considered is a simulation of turbulent fluid flow through a channel44. The flow field data are obtained by a 3D numerical simulation of incompressible flow in a channel at a Reynolds number of 180. A slice is taken at the middle of the channel, which yields a computational domain of size 128 × 48, with 128 cells in the streamwise direction of the flow. The domain is non-dimensionalized using the half-width of the channel (δ), and the length of channel is 4π times the half-width. The target of interest is the velocity of the fluid in the direction of flow.
To make the model robust to changes in sensor locations, at each training time iteration we picked a random number of sensors (Ns) from the training pool, which ranged from 25 (low coverage) to 300 (medium coverage). We train our model with all the available simulation data and test its ability to reconstruct it. Similar to the previous datasets, 25–300 locations are sampled in each batch, but aggregating the locations sampled across all batches in an epoch results in the whole field being sampled. Of course, only sparse observations are used at inference time. In addition, we ran a case were we multiplied the value of the loss function (the mean squared error, or MSE) at each mini-batch times the number of sensors used in the forward pass, namely (\({{{\mathcal{L}}}}={\mathrm{MSE}}\times {N}_{{\mathrm{s}}}\)). We found that this increases performance for cases where more than 150 sensors are provided to the model. We show that the Senseiver is able to provide excellent qualitative reconstructions, as illustrated by the cross-sections in Fig. 4. This training scheme also allows us to move the sensors at inference time. The model obtains the main features accurately, even with a small number of sensors as can be seen in the reconstructions of Fig. 4. A study of how temporal coverage and number of sensors affect the performance of the trained model is shown in Supplementary Fig. 3.
The x axis depicts number of sensors used to reconstruct the field. We tested our trained model with ten different random sensor locations (using fixed seeds) for each x coordinate. The plot shows the 10th and 90th percentiles as bounds of the error (equation (5)) and the average of the 10 with a line. Insets: predictions for the same time frame are shown to depict how the prediction accuracy increases qualitatively with more sensor coverage. All the colorbars are normalized from −1 to 1. δ, half-width of the channel.
The fourth dataset considered is a simulation of two fluids flowing through a complex 3D medium comprised of spherical obstacles with periodic boundary conditions. A simulation was run using the lattice-Boltzmann method library MPLBM45 for 4 days using 120 central-processing-unit cores. A non-wetting fluid was placed at the inlet and driven through the domain where its density was recorded during the simulation. The goal of this test case is to assess the capabilities of our model to train with very large arrays with extremely sparse inputs (0.0006% of spatial coverage). The computational domain is 128 × 128 × 512 (with a resolution of 3.5 μm) and we collected 100 frames (one every millisecond) totalling over 1.6 billion points. Three 3D snapshots throughout the simulation are illustrated in Supplementary Fig. 4.
Similar to the sea-temperature dataset, in this domain around 70% of the grid cells have no property value to reconstruct (that is, the cells inside the solid), hence the training is sped-up by a substantial factor compared with convolutional neural network approaches, which are forced to scan the whole domain. It is also worth noting that the 3D version of the approach in ref. 32 allocated the entire memory of a 24 Gb graphics processing unit for a mini-batch of only one sample, slowing down the training and being unable to train with bigger images. In contrast, our model uses only 4 Gb. The results of the abstraction performance of the model with different amounts of training data are shown in Fig. 5. Fifty per cent temporal coverage is enough to train a model that is able to provide accurate reconstructions (ϵ < 0.3) throughout the dataset. One important highlight is that the model is not predictive in highly non-stationary acyclic flows with transient dynamics46, for instance, frames far away from the training data (>100 in Fig. 5). The model has periodic boundary conditions so the fluid reaching the outlet is re-injected at the inlet, a situation not contemplated by the training data.
The fifth and last dataset is a contaminant being advected by a turbulent field. This set-up reflects the case were a pollutant is being transported and sparse velocity measurements are available. This example demonstrates the flexibility of the framework to model the relationship between a vector and a scalar. By withholding the concentration of the pollutants from the inputs, this example also illustrates the ability for the model to predict quantities that are unobserved. In this example, the velocity vector (vx, vy, vz, which yields in NI = 3) is measured in 1% of the 1283 domain and the task of the model is to predict the concentration of the pollutant. In contrast to previous datasets, where the whole field is sampled across many batches in training, with this dataset we sample only 75% or 50% of spatial locations across all batches during training, to test scenarios where not all the ground truth is available. In Fig. 6, we observe that the model reconstructs larger-scale variations in the passive scalar fairly well, but does not reproduce the fine-scale structure. The overall R2 for reconstruction is approximately 0.75, which is remarkable given that there is virtually no correlation between velocity, which is observed, and the tracer concentration, which is predicted (Supplementary Fig. 5).
Left: error (equation (5)) of the model versus temporal coverage. The 3D sensor locations are depicted in the top left corner. In the plot, each line represents a trained model and the points represent the training data used for each line. The dashed line represents the training data coverage boundary. Right: reconstructions for time step 55 using models trained with a different number of time frames. The colorbars are fixed in the range between −1 and 1.
Discussion
The flexibility of the Senseiver architecture allows the exploration of many uses cases, and although we aimed to cover as much ground as possible, there are many things still to explore. For instance, non-Cartesian or unstructured grids can be used during training and/or inference. In the same vein, the resolution of the field prediction can be increased by computing the desired property at intermediate intervals, thus repurposing the architecture for super-resolution. Multiple decoding heads can be trained to predict outputs with different boundary conditions or different downstream tasks (for example, segmentation or classification). Additional research could be carried out so that positional encodings can be used to train a model to have forecasting capabilities. During the development of this project, an attempt was made to encode time using sine–cosine encodings without success. However, we tried utilizing a trainable array where each time increment (dt) corresponded to one vector; this was successful but we found it impractical as it requires the model to visit every time increment (dt) during training.
Conclusion
With the advent of widespread access to satellite data and cheap sensors, we have an opportunity to address several problems in Earth sciences and engineering in a manner not possible before. However, these powerful data sources are typically sparse, and leveraging them requires specialized approaches that can map the measured local data to the physics of the global field under observation. The limitations of current approaches introduce large uncertainties in myriad applications such as aviation safety, forecasting accuracy in adverse weather predictions, migration patterns of wildfire, contaminant tracing and tracking sequestered CO2 plumes. Having a general class of algorithms that is able to estimate and reconstruct the global field from sparse, local measurements will be a major advancement in this field. In this work, we present an efficient and effective deep learning approach to reconstruct fields from such sparse measurements.
From an information theoretic perspective, sparse sensing is an inverse modelling problem that maps sparse, low-dimensional measurements to a dense high-dimensional state. The goal of sparse-sensing algorithms is to obtain the best possible estimates useful enough to inform practical applications, as there are few other viable alternatives. We propose an attention-based neural network architecture, the Senseiver, to encode a compact representation of large systems. We validated the effectiveness of our method with extensive demonstrations on different datasets of interest to the sparse-sensing community, and also on a complex, realistic 3D fluids dataset. Our approach offers improved capabilities for large, practical applications compared with the state-of-the-art convolutional neural network architectures by demonstrating higher accuracy with a lower memory footprint. Five examples of global field reconstruction from local sensor measurements demonstrated the accuracy and robustness of our method. Sparse sensing of fluid flow data, especially turbulence, is extremely challenging due to nonlinearity and chaos. In addition, a low sensor coverage makes the task harder as the sensors can have non-unique reconstructions. Compared with previous efforts, our model scales effectively in large domains of high dimensionality.
Besides the greatly reduced memory footprint, compared with previous efforts, a key advantage of the Senseiver is using a query-based decoder, which allows us to predict domains of arbitrary sizes in a sequential manner. This decoupling of the query process from the dimensionality of the dataset makes it extremely memory efficient and allows our model to scale effectively to large domains. In summary, this work only scratches the surface of what is possible with attention-based architectures for sparse sensing.
Methods
Encoder–decoder architecture
Our encoder–decoder architecture is built upon Perceiver IO. The encoder module takes the locations and values of the sensors and maps them to a latent space (of size \(N_f\)) through scaled dot-product attention layers. First, the sensor data si from a number of sensors observations Ns and their corresponding positional encodings ai are concatenated to form the input \({{{{\bf{E}}}}}^{(0)}\in {{\mathbb{R}}}^{{N}_{{\mathrm{s}}}\times {N}_{{\mathrm{I}}}+2{N}_{{\mathrm{D}}}{N}_{{\mathrm{f}}}}\), where the superscript indicates each box/layer in Fig. 2. E(0) is then processed using a fully connected linear layer to create \({{{{\bf{E}}}}}^{(1)}\in {{\mathbb{R}}}^{{N}_{{\mathrm{s}}}\times {N}_{{\mathrm{c}}}}\) where Nc is a hidden dimension used throughout the architecture. Next, E(1) is processed with an attention block. Within each block is a multi-headed cross-attention layer (Fig. 2) that uses a trainable query array \({{{{\bf{Q}}}}}_{{\mathrm{in}}}\in {{\mathbb{R}}}^{{N}_{{{{{\bf{Q}}}}}_{{\mathrm{in}}}}\times {N}_{{\mathrm{c}}}}\). The attention block preserves the dimension such that the output Z of the encoder is of a fixed dimension \({N}_{{{{{\bf{Q}}}}}_{{\mathrm{in}}}}\times {N}_{{\mathrm{c}}}\), regardless of the number of sensor observations. In summary, the steps of the encoder are given by
The dimensions inside the attention blocks are provided in Supplementary Information, along with definitions of multi-head attention mechanisms. Qin is the latent query array in each block, and θ and ϕ are the weights of the multi-layer perceptrons (MLPs) within each attention block. We also note that the second and third attention-block modules share weights, and therefore this is a recurrent step in the architecture. This has the benefit of reducing the parameters. Furthermore, our preliminary experiments re-using the weights recurrently resulted in a small increase in accuracy (~10%) without any additional parameters. Linear refers to a simple linear layer with bias, although it is important to note that this projection decreases the dimension before the attention mechanism, that is, we have Nc < < NI + 2NDNf. This dimension reduction improves computational efficiency while preserving key information—similar to low-rank methods or the Johnson–Lindenstrauss lemma, but further empowered by the use of attention. The number of channels output by the linear layer is a key hyperparameter that, while small, is somewhat application dependent. While increasing Nf is used to capture higher spatial resolution (Supplementary Table 1), increasing the number of channels can be used to capture more complex temporal dynamics (Supplementary Table 2).
Next, in the decoder block, the encoded position of the query aq is concatenated with a trainable query vector \({{{{\bf{q}}}}}_{{\mathrm{out}}}\in {{\mathbb{R}}}^{{N}_{{\mathrm{c}}}}\). However, more frequently we consider multiple query points, denoted Nq. In this case, the query vector is repeated row-wise (once for each query point aq) to make a matrix, Qout. We denote the concatenated positions and Qout as \({{{{\bf{D}}}}}^{(0)}\in {{\mathbb{R}}}^{{N}_{{\mathrm{q}}}\times 2{N}_{{\mathrm{f}}}{N}_{{\mathrm{d}}}+{N}_{{\mathrm{c}}}}\). This query matrix is process by a linear layer to output \({{{{\bf{D}}}}}^{(1)}\in {{\mathbb{R}}}^{{N}_{{\mathrm{q}}}\times {N}_{{\mathrm{c}}}}\). D(1) serves as the queries in a multi-head cross-attention. The keys and values for this cross-attention are provided by the latent input representation Z, which yields the output \({{{{\bf{D}}}}}^{(2)}\in {{\mathbb{R}}}^{{N}_{{{{{\bf{Q}}}}}_{{\mathrm{out}}}}\times {N}_{{\mathrm{c}}}}\). D(2) is processed by a linear layer, which yields an output \(\hat{{{{\bf{s}}}}}\in {{\mathbb{R}}}^{{N}_{{\mathrm{o}}}}\). In summary, the steps of the decoder are given by:
For details of the attention layers, the network implementation and the design decisions in the Senseiver, see Supplementary Information. The end-to-end forward pass is illustrated in Fig. 2.
Spatial encodings
The attention mechanism does not explicitly account for the spatial location of the sensors or queries. To include this information, we encode the spatial position of these (equation (1)) using sine–cosine positional encodings34. These are visualized graphically in Fig. 2. For each d of the ND spatial dimensions, we specify a set of spatial frequencies \({\{\,{f}_{k}\}}_{d}\) of size k over which to build the sine–cosine positional encodings. A position \({{{\bf{x}}}}\in {{\mathbb{R}}}^{{N}_{{\mathrm{D}}}}\) is decomposed into a vector \({{{\bf{a}}}}\in {{\mathbb{R}}}^{2\times {N}_{{\mathrm{D}}}\times {N}_{{\mathrm{f}}}}\), where each entry in a is the value of a corresponding sine or cosine (hence the factor 2) at the specified frequency f and Nf is the number of frequencies in the encoding. For each dimension d, there are 2Nf entries in a; the first are \(\sin (\uppi {f}_{k}{x}_{d})\) and the second are \(\cos (\uppi {f}_{k}{x}_{d})\).
This design choice does not require any additional training parameters, and the computational work required to produce them is negligible. In many applications, having a large Nf is required to accurately encode the position of the sensors and query points—especially in three dimensions. The number of parameters increases rapidly for Perceiver IO as Nf increases. Senseiver avoids this problem, making it more suitable in applications where precise locations are important—see Supplementary Table 2 for a comparison. In the examples used in this work, the data are located in Cartesian grids, so an array with components denoting the centre of each grid point in each coordinate direction is created, and then indexed during training and inference. Having a Cartesian grid is not a prerequisite to use our model; the sine–cosine spatial encodings can be evaluated on any mesh, or on arbitrary continuously variable points in space. A strong advantage of this flexibility is that it makes it possible to construct field predictions at arbitrary subsets of the full domain, which allows predictions to be made with very few computational resources, as a domain prediction can be constructed piece by piece. We take advantage of this fact during training, as described in ‘Training procedure’. In addition, recent work in explainable artificial intelligence has shown that neural networks appear to learn Fourier representation of fluid flows internally47, supporting our assumption that these encodings are appropriate for many problems of interest.
Data availability
The data are available at https://zenodo.org/records/8290040 (ref. 53).
Code availability
The code is available on Zenodo at https://doi.org/10.5281/zenodo.8364148 (ref. 54).
References
Shen, H. et al. Missing information reconstruction of remote sensing data: a technical review. IEEE Geosci. Remote Sens. Mag. 3, 61–85 (2015).
Klingensmith, M., Dryanovski, I., Srinivasa, S. S. & Xiao, J. CHISEL: Real time large scale 3D reconstruction onboard a mobile device using spatially-hashed signed distance fields. In Robotics: Science and Systems Vol. 11 (MIT Press Journals, 2015).
Zhang, P., Nevat, I., Peters, G. W., Septier, F. & Osborne, M. A. Spatial field reconstruction and sensor selection in heterogeneous sensor networks with stochastic energy harvesting. IEEE Trans. Signal Process. 66, 2245–2257 (2018).
Ramskill, N. P. et al. Fast imaging of laboratory core floods using 3D compressed sensing RARE MRI. J. Magn. Reson. 270, 187–197 (2016).
Fortuna, L., Graziani, S., Rizzo, A. & Xibilia, M. G. Soft Sensors for Monitoring and Control of Industrial Processes Advances in Industrial Control (Springer, 2007); http://link.springer.com/10.1007/978-1-84628-480-9
Wang, N., Zhang, N. & Wang, M. Wireless sensors in agriculture and food industry—recent development and future perspective. Comput. Electron. Agric. 50, 1–14 (2006).
Paoli, A., Neri, P., Razionale, A. V., Tamburrino, F. & Barone, S. Sensor architectures and technologies for upper limb 3D surface reconstruction: a review. Sensors 20, 6584 (2020).
Brunton, S. L. et al. Data-driven aerospace engineering: reframing the industry with machine learning. AIAA J. 59, 1–26 (2021).
Yuan, F.-G., Ashraf Zargar, S., Chen, Q., Wang Fuh-Gwo Yuan, S. & Wang, S. Machine learning for structural health monitoring: challenges and opportunities. Proc. SPIE 11379, 1137903 (2020).
Tian, G. Y., Sophian, A., Taylor, D. & Rudlin, J. Multiple sensors on pulsed eddy-current detection for 3-D subsurface crack assessment. IEEE Sens. J. 5, 90–96 (2005).
Rouet-Leduc, B., Hulbert, C. & Johnson, P. A. Continuous chatter of the Cascadia subduction zone revealed by machine learning. Nat. Geosci. 12, 75–79 (2018).
Su, H., Jiang, J., Wang, A., Zhuang, W. & Yan, X. H. Subsurface temperature reconstruction for the global ocean from 1993 to 2020 using satellite observations and deep learning. Remote Sens. 14, 3198 (2022).
Saint-Vincent, P. M. B., Sams, J. I., Hammack, R. W., Veloski, G. A. & Pekney, N. J. Identifying abandoned well sites using database records and aeromagnetic surveys. Environ. Sci. Technol. 54, 8300–8309 (2020).
Gherlone, M., Cerracchio, P., Mattone, M., Di Sciuva, M. & Tessler, A. Shape sensing of 3D frame structures using an inverse finite element method. Int. J. Solids Struct. 49, 3100–3112 (2012).
Gu, Y., Wang, L., Chen, W., Zhang, C. & He, X. Application of the meshless generalized finite difference method to inverse heat source problems. Int. Jo. Heat Mass Transf. 108, 721–729 (2017).
Das, R. A simulated annealing-based inverse computational fluid dynamics model for unknown parameter estimation in fluid flow problem. Int. J. Comput. Fluid Dyn. 26, 499–513 (2012).
Zhou, H., Soh, Y. C., Jiang, C. & Wu, X. Compressed representation learning for fluid field reconstruction from sparse sensor observations. In Proc. International Joint Conference on Neural Networks 1–6 (2015).
Loiseau, J. C., Noack, B. R. & Brunton, S. L. Sparse reduced-order modelling: sensor-based dynamics to full-state estimation. J. Fluid Mech. 844, 459–490 (2018).
Manohar, K., Brunton, B. W., Kutz, J. N. & Brunton, S. L. Data-driven sparse sensor placement for reconstruction: demonstrating the benefits of exploiting known patterns. IEEE Control Syst. 38, 63–86 (2018).
Tiwari, N. et al. Simultaneous measurement of pressure and temperature on the same surface by sensitive paints using the sensor selection method. Exp. Fluids 63, 1–13 (2022).
Callaham, J. L., Maeda, K. & Brunton, S. L. Robust flow reconstruction from limited measurements via sparse representation. Phys. Rev. Fluids 4, 103907 (2019).
Albaladejo, C., Soto, F., Torres, R., Sánchez, P. & López, J. A. A low-cost sensor buoy system for monitoring shallow marine environments. Sensors 12, 9613–9634 (2012).
Hudson, S. Three dimensional reconstruction of asteroids from radar observations. Remote Sens. Rev. 8, 195–203 (2009).
Jahanbakhsh, A. et al. Review of microfluidic devices and imaging techniques for fluid flow study in porous geomaterials. Sensors 20, 4030 (2020).
Bertalmio, M., Sapiro, G., Caselles, V. & Ballester, C. Image inpainting. In Proc. ACM SIGGRAPH Conference on Computer Graphics 417–424 (2000).
Dong, C., Loy, C. C., He, K. & Tang, X. Image Super-Resolution Using Deep Convolutional Networks. IEEE Transactions on Pattern Analysis and Machine Intelligence 38, 295–307 (2016).
Alet, F. et al. Graph element networks: adaptive, structured computation and memory. In Proc. 36th Conference on Machine Learning Research Vol. 97, 212–222 (2019).
Lagaris, I. E., Likas, A. & Fotiadis, D. I. Artificial neural networks for solving ordinary and partial differential equations. IEEE Trans. Neural Netw. 9, 987–1000 (1998).
Raissi, M., Perdikaris, P. & Karniadakis, G. E. Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 378, 686–707 (2019).
Chuang, P.-Y. & Barba, L. A. Experience report of physics-informed neural networks in fluid simulations: pitfalls and frustration. In Proc. 21st Python in Science Conference 28–36 (2022).
Güemes, A., Sanmiguel Vila, C. & Discetti, S. Super-resolution generative adversarial networks of randomly-seeded fields. Nat. Mach. Intell. 4, 1165–1173 (2022).
Fukami, K., Maulik, R., Ramachandra, N., Fukagata, K. & Taira, K. Global field reconstruction from sparse sensors with Voronoi tessellation-assisted deep learning. Nat. Mach. Intell. 3, 945–951 (2021).
Santos, J. E. et al. PoreFlow-Net: a 3D convolutional neural network to predict fluid flow through porous media. Adv. Water Resour. 138, 103539 (2020).
Vaswani, A. et al. Attention is all you need. Adv. Neural Inf. Proces. Syst. Vol 30 (eds Guyon, I. et al.) 5999–6009 (Curran Associates, Inc., 2017).
Yu, J. et al. CoCa: contrastive captioners are image-text foundation models. Preprint at http://arxiv.org/abs/2205.01917 (2022).
Chowdhery, A. et al. PaLM: scaling language modeling with pathways. Preprint at http://arxiv.org/abs/2204.02311 (2022).
Jumper, J. et al. Highly accurate protein structure prediction with AlphaFold. Nature 596, 583–589 (2021).
Liu, L., Santos, J. E., Prodanović, M. & Pyrcz, M. J. Mitigation of spatial nonstationarity with vision transformers. Comput. Geosci. 178, 105412 (2023).
Jaegle, A. et al. Perceiver: general perception with iterative attention. Preprint at http://arxiv.org/abs/2103.03206 (2021).
Yun, C., Bhojanapalli, S., Rawat, A. S., Reddi, S. J. & Kumar, S. Are transformers universal approximators of sequence-to-sequence functions? Preprint at https://arxiv.org/abs/1912.10077v2 (2019).
Jaegle, A. et al. Perceiver IO: a general architecture for structured inputs & outputs. Preprint at https://arxiv.org/abs/2107.14795v3 (2021).
Colonius, T. & Taira, K. A fast immersed boundary method using a nullspace approach and multi-domain far-field boundary conditions. Comput. Methods Appl. Mech. Eng. 197, 2131–2146 (2008).
NOAA Physical Sciences Laboratory (NOAA, 2023); https://psl.noaa.gov/
Fukagata, K., Kasagi, N. & Koumoutsakos, P. A theoretical prediction of friction drag reduction in turbulent flow by superhydrophobic surfaces. Phys. Fluids 18, 051703 (2006).
Santos, J. E. et al. MPLBM-UT: multiphase LBM library for permeable media analysis. SoftwareX 18, 101097 (2022).
Noack, B. R., Afanasiev, K., Morzyński, M., Tadmor, G. & Thiele, F. A hierarchy of low-dimensional models for the transient and post-transient cylinder wake. J. Fluid Mech. 497, 335–363 (2003).
Subel, A., Guan, Y., Chattopadhyay, A. & Hassanzadeh, P. Explaining the physics of transfer learning in data-driven turbulence modeling. PNAS Nexus 2, pgad015 (2023).
Paszke, A. et al. PyTorch: an imperative style, high-performance deep learning library. Preprint at http://arxiv.org/abs/1912.01703 (2019).
Harris, C. R. et al. Array programming with NumPy. Nature 585, 357–362 (2020).
Musy, M. et al. Vedo. Zenodo https://doi.org/10.5281/zenodo.4609336 (2021).
Hunter, J. D. Matplotlib: a 2D graphics environment. Comput. Sci. Eng. 9, 90–95 (2007).
Falcon, W. et al. PyTorch Lightning. GitHub https://github.com/PyTorchLightning/pytorch-lightning (2019).
Santos, J. E. The Senseiver dataset. https://zenodo.org/records/8290040 (2023).
Santos, J. E. The Senseiver codebase. https://github.com/OrchardLANL/Senseiver (2023).
Acknowledgements
J.E.S. and Z.R.F. gratefully acknowledge the support of the US Department of Energy through the LANL/LDRD Program and the Center for Non-Linear Studies (CNLS) for this work. H.V. gratefully acknowledges primary support from the Department of Energy, Office of Science, Office of Basic Energy Sciences, Geoscience Research programme under award number (LANLE3W1). Secondary support is from the Consortium Advancing Technology for Assessment of Lost Oil & Gas, funded by US Department of Energy, Office of Fossil Energy and Carbon Management, Office of Resource Sustainability, Methane Mitigation Technologies Division’s, Undocumented Orphan Wells Program. This paper has been co-authored by UT-Battelle, LLC under contract no. DE-AC05-00OR22725 with the US Department of Energy. J.E.S. thanks A. Jaegle and J. Carreira for their useful suggestions. Finally, we are grateful to the developers of the many software packages used throughout this project including, but not limited, to PyTorch48, Numpy49, Vedo50, Matplotlib51 and PyTorch Lightning52.
Author information
Authors and Affiliations
Contributions
J.E.S.: conceptualization, methodology, investigation, software, writing—original draft. Z.R.F.: visualization, review and editing. A.M.: investigation, funding acquisition, resources. D,O’M.: writing—review and editing, supervision. H.V.: funding acquisition, supervision, review and editing. N.L.: methodology, software, supervision, writing—original draft, writing—review and editing. All authors reviewed the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Machine Intelligence thanks the anonymous reviewers for their contribution to the peer review of this work. Primary Handling Editor: Mirko Pieropan, in collaboration with the Nature Machine Intelligence team.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary information.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Santos, J.E., Fox, Z.R., Mohan, A. et al. Development of the Senseiver for efficient field reconstruction from sparse observations. Nat Mach Intell 5, 1317–1325 (2023). https://doi.org/10.1038/s42256-023-00746-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s42256-023-00746-x