Main

The great success of graph neural networks1,2, graph convolutional networks3 and graph attention networks4 well illustrates the power of machine learning in handling graph-structured data that simultaneously characterize both objects and their relationships. As a result, graph learning5 is quickly standing out in many real-world applications such as the prediction of chemical properties of molecules for drug discovery6, recommender systems of social networks7 and combinatorial optimization for design automation8. In the era of Big Data and the Internet of Things (IoT), the size and scale of graph-structured data are exploding. For example, the social network Facebook has more than two billion users and one trillion edges representing social connections9. This imposes a critical challenge to the current graph learning paradigm that implements graph neural networks on conventional complementary metal–oxide–semiconductor (CMOS) digital circuits. Such digital hardware suffers from frequent and massive data shuttling between off-chip memory and processing units during graph learning, the so-called von Neumann bottleneck10,11,12,13,14,15,16,17,18,19. Furthermore, the technology node of transistors has reached 3 nm, the length of a few unit cells of silicon. This leads to an inevitable slowdown of Moore’s Law that has fuelled the past development of CMOS chips in the last few decades. As a result, further scaling of transistor is becoming less cost-effective. Last but not least, the training of graph neural networks is expensive, due to tedious error backpropagation for node and graph embedding. For example, the training of PinSage took 78 hours on 32 central processing unit (CPU) cores and 16 Tesla K80 graphics processing units (GPUs)20. The growing challenges in both hardware, that is, the von Neumann bottleneck and transistor scaling, as well as software, that is, tedious training, calls for a brand-new paradigm for graph learning.

Resistive memory may provide a hardware solution to these issues21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45. When these resistive elements are grouped into a crossbar array, they can naturally perform vector–matrix multiplication, one of the most expensive and frequent operations (OPs) in graph learning46,47. The matrix is stored as the conductance of the resistive memory array, where Ohm’s law and Kirchhoff’s current law physically govern multiplication and summation, respectively. As a result, the data are stored and processed in the same location. This in-memory computing concept can largely obviate the energy and time overheads incurred by expensive off-chip memory access in graph learning on conventional digital hardware. In addition, resistive memory cells have a simple, capacitor-like structure, equipping them with excellent scalability and three-dimensional (3D) stackability. However, resistive memory suffers from a series of issues when changing their resistance that can defeat the efficiency advantage of in-memory graph learning, demanding frequent updates of resistive weights. This occurs because resistive memory relies on electrochemical reactions or phase changes to adjust the conductance48,49,50,51,52,53. This mechanism results in a switching energy and duration that are orders of magnitude higher than those of transistors. In addition, the inevitable stochasticity associated with ionic or atomic motions makes precise resistance changes difficult. As a result, graph learning has not yet experimentally leveraged the advantage of resistive in-memory computing.

Here, we propose a novel hardware–software co-design, the random resisive memory-based echo state graph neural networks (ESGNN)54,55. The marriage of random resistive memory and ESGNN not only retains the boost of energy–area efficiency thanks to in-memory computing but also makes use of the intrinsic stochasticity of dielectric breakdown to provide low-cost and nanoscale hardware random weights of ESGNN. Moreover, the echo state network employs iterative random projections for node and graph embedding, which gets rid of the tedious training of conventional graph neural networks, enabling efficient and affordable real-time graph learning.

In this Article, we showcase such a co-designed ESGNN physically implemented on a 40 nm resistive computing-in-memory macro to accelerate graph learning. We demonstrate state-of-the-art graph classification results on the MUTAG and COLLAB datasets, as well as node classification on the CORA dataset. We observe 2.16×, 35.42× and 40.37× improvements in the energy efficiency of a projected random resistive memory-based hybrid analogue–digital system compared with that of a state-of-the-art GPU for classifying the MUTAG, COLLAB and CORA dataset. Furthermore, the backward pass complexity is reduced by 99.35%, 99.99% and 91.40% respectively, thanks to the representation extraction using random projections in ESGNN. Our system paves the way for efficient and fast graph learning in the future.

Hardware–software co-design: ESGNN on random resistive memory arrays

Figure 1 illustrates the hardware–software co-design scheme, where random resistive memory arrays are used to physically implement the ESGNN. Hardware-wise, the random distribution of dielectric breakdown voltages, due to inevitable process variation and motion of ions, provides a natural source of randomness (entropy) to produce large-scale random resistive memory arrays that have been validated for implementations of true random number generators56 and physically unclonable functions57 (see Supplementary Note 1 for a comparison between random resistive memory arrays and pre-computed resistor arrays). Here, we fabricated CMOS-compatible nanoscale TaN/TaOx/Ta/TiN resistive memory cells (Fig. 1a,b; see Supplementary Fig. 1 for device characteristics) in crossbar arrays (Fig. 1c) using the backend-of-line process on a 40 nm technology node tape-out (Methods). The chip is integrated on a printed circuit board with analogue–digital conversion circuitry and a Xilinx ZYNQ system-on-chip, constituting a hybrid analogue–digital computing platform (see Methods and Supplementary Fig. 2 for the system design and a photo, and Supplementary Note 2 for the system energy consumption estimation). As shown in Fig. 1c, the crossbar array is then partitioned into two sub-arrays to represent two weight matrices: \({{{{W}}}}_{{{I}}} \in {\Bbb R}^{h \times (u + 1)}\) the input matrix and \({{{{W}}}}_{{{R}}} \in {\Bbb R}^{h \times h}\) the recursive matrix, of the ESGNN, where u and h represent the input dimension and the hidden dimension of each node, respectively (see Methods on mapping resistive memory conductance to weights). Biasing all the cells of an as-deposited resistive memory to the median of their breakdown voltages, some cells will experience dielectric breakdown if their breakdown voltages are lower than the applied voltage, forming random resistor arrays as illustrated by the conductance maps of both \({{{{W}}}}_{{{I}}}\) and \({{{{W}}}}_{{{R}}}\) in Fig. 1d (see Extended Data Fig. 1 for the stochasticity of dielectric breakdown voltages). Compared with pseudo random number generation using digital systems, the source of randomness here is the stochastic redox reactions and ion migrations that arise from the compositional inhomogeneity of resistive memory cells, offering low-cost and highly scalable random resistor arrays for in-memory computing (see Supplementary Note 3 for National Institute of Standards and Technology, NIST, true randomness test results). The corresponding histogram in Fig. 1e shows a conductance gap between breakdown cells and those remain insulating. The conductance distribution of the former follows a stable, quasi-normal distribution, which can be tailored by adjusting both fabrication conditions and electrical operation parameters, offering tuneable hardware implementations of ESGNN (see Supplementary Fig. 3 for the stability of the random resistor arrays and Supplementary Fig. 4 for their tunability).

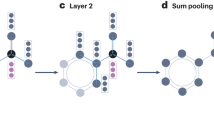
Fig. 1: Hardware–software co-design of random resistive memory-based ESGNN for graph learning.
figure 1

a, A cross-sectional transmission electron micrograph of a single resistive memory cell that works as a random resistor after dielectric breakdown. Scale bar 20 nm. b, A cross-sectional transmission electron micrograph of the resistive memory crossbar array fabricated using the backend-of-line process on a 40 nm technology node tape-out. Scale bar 500 nm. c, A schematic illustration of the partition of the random resistive memory crossbar array, where cells shadowed in blue are the weights of the recursive matrix (passing messages along edges) while those in red are the weights of the input matrix (transforming node input features). d, The corresponding conductance map of the two random resistor arrays in c. e, The conductance distribution of the random resistive memory arrays. f, The node embedding procedure of the proposed ESGNN. The internal state of each node at the next time step is co-determined by the sum of neighbouring contributions (blue arrows indicate multiplications between node internal state vectors and the recursive matrix in d), the input feature of the node after a random projection (red arrows indicate multiplications between input node feature vectors with the input matrix in d) and the node internal state in the previous time step. g, The graph embedding based on node embeddings. The graph embedding vector g is the sum pooling of all the node internal state vectors in the last time step.

Source data

Full size image

Software-wise, the echo state network (ESN) is a type of reservoir computer26,31,43,58 comprising a large number of neurons with random and recurrent interconnections, where the states of all the neurons are accessible by a simple software readout layer55,59 (see Supplementary Figs. 5 and 6 for different types of reservoir computers and their implementations). The consecutive nonlinear random projections in the high-dimensional state space produce trajectories at the edge of chaos, benefitting graph embedding extraction as reported in ref. 55. The ESGNN builds on the FDGNN model55 but differs from FDGNN in terms of a finite iteration node embedding scheme and task-dependent classification heads, which leads to better immunity to over-smoothing and improved energy efficiency on multiple tasks (see Supplementary Note 4 for the detailed differences and Supplementary Table 1 for a summary of the differences). The network parameters of ESGNN are physically embodied by the two random resistive memory arrays, where the input matrix \({{{{W}}}}_{{{I}}}\) modulates the influence of a node input feature vector on the node internal state, and the recursive matrix \({{{{W}}}}_{{{R}}}\) determines the influence of neighbouring nodes on the same node internal state (see Methods for the choice of resistance scaling factors to ensure the echo state property). This graph embedding process is schematically illustrated in Fig. 1f. For a given graph, the initial embedding of node j is a zero vector \({{{\mathbf{s}}}}_j^{\left( 0 \right)} \in {\Bbb R}^h\). The input feature of the same node \({{{\mathbf{x}}}}_i \in {\Bbb R}^{u + 1}\) will first undergo a random projection using the input matrix to produce its input projection \({{{\mathbf{u}}}}_j = {{{{W}}}}_{{{I}}}{{{\mathbf{x}}}}_j \in {\Bbb R}^h\). In each subsequent time step, a new state of the node is computed by aggregating its current state \({{{\mathbf{s}}}}_j^{\left( t \right)}\) and input projection \({{{\mathbf{u}}}}_j\), and the states of all its neighbours after random projections by the recursive matrix \(\mathop {\sum }\nolimits_{k \in {{{\mathbf{N}}}}\left(\, j \right)} {{{{W}}}}_{{{R}}}{{{\mathbf{s}}}}_k^{\left( t \right)}\) (where \({{{\mathbf{N}}}}\left( j \right)\) denotes the set of neighbouring nodes of node j). These consecutive random projections to high-dimensional space paired with nonlinear activations endow each node with a unique and discriminative representation. The final internal states of nodes, or node embeddings, will be used to create a graph embedding \({{{\mathbf{g}}}} \in {\Bbb R}^h\) by sum pooling for graph classification problems, as illustrated in Fig. 1g (see Methods for the details of node and graph embedding).

Graph classification with ESGNN

We first solve a representative graph classification task using the MUTAG molecular dataset60 with a random resistive memory-based ESGNN. MUTAG is a widely used molecular dataset that comprises 188 nitroaromatic compounds (see Fig. 2a for examples and Supplementary Fig. 7 and Supplementary Table 2 for simulation results on the large-scale organic molecule dataset QM9). These molecular compounds are essentially graphs. Their nodes stand for atoms, while edges denote chemical bonds. The molecular graphs can be divided into two categories according to their mutagenicity, that is, their ability to mutate genes of certain bacteria. Figure 2b shows the experimental input projection and evolution of node internal states of a single molecular graph according to the process shown in Fig. 1f. Internal states of nodes (columns) gradually differ from projected input features by accumulating messages from neighbouring nodes and thus encode structural information pertaining to the topology of the graph (see Extended Data Fig. 2 and Supplementary Note 5 for the initialization and storage of intermediate node embeddings). Here, the embedding process is iterated four times to achieve a balance between capturing more topological information and over-smoothing61. The final graph embeddings of the entire dataset are shown in Fig. 2c, in which embeddings of the same class are similar while those from different classes have large contrast. Figure 2d visualizes the distribution of graph embeddings by mapping them to a two-dimensional (2D) space via principal component analysis (PCA), where orange and blue dots are graphs from positive and negative classes, respectively (see Supplementary Fig. 8 for visualizing graph embedding distributions in 3D space). Although a few samples are mixed on the classification boundary, the majority of samples can be well classified by a simple linear classifier thanks to the dynamics of the echo state network. These embedding vectors will be classified by a simple software readout layer (with 102 floating-point weights) optimized by linear regression at low hardware and energy cost (see Methods for the implementation and training of the readout layer and Supplementary Table 3 for the cost of the digital readout layer). To evaluate the classification performance of the MUTAG dataset, we use ten-fold cross-validation, where the accuracy of each fold is shown in Fig. 2e. The overall performance of our implementation is approximately 92.11%, which is comparable to state-of-the-art algorithms such as deep divergence graph kernels or DDGK (91.58%)62 and Patchy-SAN (92.60%)63 running on digital computers (see Extended Data Fig. 3 for the accuracy distribution of 100 trials of ten-fold cross-validation simulation, Extended Data Fig. 4 for the simulated hyperparameter impact on accuracy, Supplementary Fig. 9 for the weight distribution and/or sparsity impact on accuracy and Supplementary Note 6, Extended Data Fig. 5 and Extended Data Table 1 for the ablation study to reveal the contribution of the echo state layer). The confusion matrices in Fig. 2f show that, on average, 5.9 out of 6.4 (12 out of 13) molecule compounds of positive (negative) mutagenicity are correctly classified, which translates to a class-wise recognition rate of 91.64% (93.35%) (see Supplementary Fig. 10 for the confusion matrices of all the folds). To verify the boost in the energy efficiency, we conducted a preliminary comparison of the energy consumption between the conventional digital hardware and our random resistive memory-based system. In Fig. 2g, the red bars show a breakdown of the number of multiply and accumulation (MAC) operations (OPs) in the ESGNN, while the light-blue and dark-blue bars show the associated estimation of the energy consumption of a state-of-the-art GPU and a projected random resistive memory-based hybrid analogue–digital system, respectively. Since multiplications with the input matrix \({{{{W}}}}_{{{I}}}\) and recursive matrix \({{{{W}}}}_{{{R}}}\) account for the majority of OPs and thus power consumption in the forward pass of the ESGNN, the overall energy of the projected random resistive memory-based hybrid analogue–digital system is approximately 34.44 μJ per forward pass of the entire dataset compared with approximately 74.32 μJ for the state-of-the-art GPU, resulting in an approximately 2.16× improvement in the inference energy efficiency (see Methods and Supplementary Fig. 11 for the impact of hyperparameters on the system energy efficiency and Supplementary Note 7 for an energy consumption comparison with a state-of-the-art GPU). As the pseudoinverse is used to train the simple readout layer of the ESGNN, the number of OPs for readout layer optimization is approximately 1.05 mega-OPs (MOPs), in contrast to approximately 160.51 MOPs per epoch of stochastic gradient descent with backpropagation for a graph neural network with the same number of weights, leading to an approximately 99.35% reduction of the backward pass complexity (see Supplementary Note 8 for details). In addition, the ESGNN on a projected random resistive memory-based hybrid analogue–digital system (34.51 μJ) offers a reduction of 53.56% in the total training energy consumption (including forward passing the echo state layer and optimizing the readout layer) compared with the software ESGNN on a state-of-the-art GPU (74.32 μJ).

Fig. 2: Classification of molecular graphs.
figure 2

a, An illustration of some samples from the MUTAG molecular dataset, where nodes of different colours represent different atoms while edges are chemical bonds. Depending on the mutagenicity, these molecules are categorized into positive and negative classes. b, An example MUTAG node embedding process. The input features of all nodes, defined as X, are first projected onto the state space using the input matrix \({{{{W}}}}_{{{I}}}\), and the hidden state of each node is updated according to the protocol shown in Fig. 1f and Methods, which leads to node embeddings that encapsulate graph information. c, The graph embedding vectors of the two categories of the MUTAG dataset. Each column vector is a graph embedding. The embeddings of the left (right) colour map are from the positive (negative) class. d, The graph embeddings are mapped to a 2D space using PCA. Pink (blue) dots represent molecules with positive (negative) mutagenicity, which can be linearly separated. e, The accuracy of each fold in a ten-fold cross-validation and the software baseline. The average accuracy is 92.11%, comparable to state-of-the-art algorithms. f, The confusion matrices of the experimental classification results. The upper matrix is a ten-fold averaged confusion matrix, which is then normalized horizontally to produce the lower matrix. g, A breakdown of the estimated MAC OPs (red bars) and associated energy (light-blue bars for a state-of-the-art GPU; dark-blue bars for a projected random resistive memory-based hybrid analogue–digital system). In a forward (backward) pass, the fully optimized model on a state-of-the-art GPU and the ESGNN on a projected random resistive memory-based hybrid analogue–digital system consume approximately 74.32 µJ (approximately 160.51 MOPs) and approximately 34.44 μJ (approximately 1.05 MOPs), respectively, revealing a >2.16 fold improvement of the inference energy efficiency (a 99.35% reduction of the backward pass complexity). BP, backpropagation.

Source data

Full size image

In addition to modelling molecules, the random resistive memory-based ESGNN has also been used to solve a representative social network classification problem using the COLLAB dataset64. As shown in Fig. 3a, each graph of the COLLAB dataset depicts a research collaboration network from one of the three branches of physics: astrophysics, high energy physics and condensed matter physics. Here, nodes are researchers while edges denote collaboration relations. We randomly pick 200 graphs from the COLLAB dataset for learning (see Supplementary Table 4 for the results on the full-scale COLLAB dataset). Nodes (or researchers) in the COLLAB dataset share a unity input feature, rendering the input projections of different nodes identical in Fig. 3b. However, thanks to the iterative message passing in ESGNN, node internal states gradually integrate graph information such as topology along iterations, yielding the unique node embeddings shown in the last time step of Fig. 3b (see Extended Data Fig. 2 and Supplementary Note 5 for the initialization and storage of intermediate node embeddings). The final graph embeddings, grouped by classes, are shown in Fig. 3c, where graphs from the condensed matter community and the high energy community are well separated from each other owing to clear differences in topology. This is also corroborated by the distribution of graph embedding vectors by mapping them to a 2D space using PCA (Fig. 3d), where blue (condensed matter physics) and purple (high energy physics) dots are linearly separable (see Supplementary Fig. 8 for visualizing graph embedding distributions in 3D space). On the other hand, graphs from the astrophysics community tend to share similar topologies with the other two, which is also revealed by the fact that pink dots (astrophysics) partially overlap with blue and purple dots. The graph embedding vectors will be classified by a simple software readout layer at small hardware and energy cost, like that used for the MUTAG dataset. Figure 3e shows the classification performance of a ten-fold cross-validation (see Supplementary Fig. 10 for the confusion matrices of all the folds). The random resistive memory-based ESGNN is able to achieve state-of-the-art accuracy of 73.00%, compared with 73.90% for graph sample and aggregate (GraphSAGE)65 and 73.76% for dynamic graph convolutional neural networks (DGCNN)66 (see Extended Data Fig. 3 for the accuracy distribution of 100 trials of ten-fold cross-validation simulation, Extended Data Fig. 4 for the simulated hyperparameter impact on accuracy, Supplementary Fig. 9 for the weight distribution and/or sparsity impact on accuracy and Supplementary Note 6, Extended Data Fig. 5 and Extended Data Table 1 for the ablation study to reveal the contribution of the echo state layer). Figure 3f shows the experimentally acquired confusion matrix of the ten-fold cross-validation (see Supplementary Fig. 10 for the confusion matrices of all the folds). The accuracy of correctly classifying astrophysics reaches 85.82%, but 31.83% and 43.48% of the samples from condensed matter physics and high energy physics tend to be misclassified as astrophysics, respectively, which is attributed to the imbalanced dataset. Figure 3g shows the breakdown of OPs in the graph learning and compares the energy consumption of a projected random resistive memory-based analogue–digital system with that of a state-of-the-art GPU. Similar to experiments on MUTAG molecular classification, the majority of the OPs are contributed by the graph embedding procedure, leading to an overall energy consumption of approximately 234.59 μJ per forward propagation of the entire dataset, considerably lower than that of the conventional implementation (approximately 8.31 mJ), achieving a 35.42 fold improvement in the inference energy efficiency (see Methods and Supplementary Fig. 11 for the impact of hyperparameters on system energy efficiency and Supplementary Note 7 for the energy consumption comparison with a state-of-the-art GPU). The number of OPs for optimizing the readout layer of the ESGNN is approximately 1.16 MOPs, compared with approximately 16.98 giga-OPs (GOPs) of one-epoch stochastic gradient descent with backpropagation for a graph neural network with the same amount of parameters, thanks to the fixed and random weights of the ESGNN, effectively reducing the backward pass complexity by approximately 99.99% (see Supplementary Note 8 for details). In addition, the ESGNN on a projected random resistive memory-based hybrid analogue–digital system (0.23 mJ) offers a reduction of 97.18% in the total training energy consumption (including forward passing the echo state layer and optimizing the readout layer) compared with the software ESGNN on a state-of-the-art GPU (8.31 mJ) (see Supplementary Note 7 for details).

Fig. 3: Classification of collaboration networks.
figure 3

a, Example collaboration network graphs from the COLLAB dataset that correspond to different branches of physics: astrophysics (AP), high energy physics (HE) and condensed matter physics (CM). Each node denotes a researcher, while an edge represents a collaboration relation. b, An example COLLAB node embedding process according to the protocol shown in Fig. 1f and Methods, which leads to node embeddings that encapsulate more graph information. c, Graph embedding vectors of the three categories of the COLLAB dataset. Each column is a graph embedding. d, Graph embeddings mapped to a 2D space using PCA. Orange, blue and purple dots denote collaboration networks from the AP, CM and HE communities, respectively, revealing a clear boundary between AP and CM. e, The accuracy of each fold in a ten-fold cross-validation and the software baseline. The average accuracy is 73.00%, comparable to state-of-the-art algorithms. f, The confusion matrices of the experimental classification results. The upper matrix is a ten-fold averaged confusion matrix, which is then normalized horizontally to produce the lower matrix. g, A breakdown of the estimated OPs (red bars) and associated energy (light-blue bars for a state-of-the-art GPU; dark-blue bars for a projected random resistive memory-based hybrid analogue–digital system). In a forward (backward) pass, the fully optimized model on a state-of-the-art GPU and ESGNN on a projected random resistive memory-based hybrid analogue–digital system consume approximately 8.31 mJ (approximately 16.98 GOPs) and approximately 234.59 μJ (approximately 1.16 MOPs), respectively, revealing a >35.42 fold improvement of the inference energy efficiency (an approximately 99.99% reduction of the backward pass complexity).

Source data

Full size image

Node classification using ESGNN

In addition to graph classification tasks, node classification tasks constitute another important category of graph learning. We simulate our ESGNN in solving a large-scale node classification problem with the CORA citation network dataset67, which is schematically illustrated in Fig. 4a (see Supplementary Table 5 for the simulation results on the large-scale social network dataset REDDIT). This graph contains 2,708 nodes, each of which represents a scientific publication and belongs to one of the seven research disciplines labelled by the node colour. Each edge of the graph represents a citation relationship between two publications. The input node features are 1,433-dimensional word vectors. The graph is then fed into the ESGNN for node embeddings (Fig. 4b). Different from the graph classification tasks that employ a trainable fully connected readout layer, a single software graph convolution layer serves as the readout layer with trainable weights to classify nodes, improving the accuracy without significantly increasing hardware and time cost (Methods). Figure 4c shows the node embeddings of the whole dataset according to Fig. 1f, grouped by node classes, where some dimensions are highly discriminative across different classes. Figure 4d shows the distribution of node embedding in a 2D space using t-distributed stochastic neighbour embedding (t-SNE) dimension reduction. Nodes from the same category are clearly clustered without any supervision (see Supplementary Fig. 8 for visualizing node embedding distributions in 3D space). To evaluate the performance, we measure the accuracy of ESGNN with different randomly initialized weights (Methods). The ten-time average test accuracy reaches 87.12% in Fig. 4e, being comparable to those of state-of-the-art algorithms such as graph convolutional networks (GCN) (86.64%)3 and graph attention networks (GAT) (88.65%)4 running on conventional digital systems (see Extended Data Fig. 3 for the accuracy distribution of 100 trials of ten-fold cross-validation simulation and Extended Data Fig. 4 for the simulated hyperparameter impact on accuracy). Figure 4f shows the simulated confusion matrix, which is dominated by diagonal elements, affirming the high classification accuracy. To benchmark the efficiency of our random resistive memory in solving this node classification problem, we count the OPs of different steps (Fig. 4g, red bars). The total number of OPs is approximately 50.05 GOPs per forward pass of the entire dataset, the majority of which (approximately 42.25 GOPs) comes from multiplications with the recurrent weight matrix \({{{{W}}}}_{{{R}}}\), while the second largest contribution (approximately 7.76 GOPs) is from multiplications with the input weight matrix \({{{{W}}}}_{{{I}}}\). The number of OPs for the backpropagation and weight updating of the readout layer is approximately 5.43 GOPs per epoch, while that for a graph neural network with the same number of parameters is approximately 63.18 GOPs per epoch, indicating a 91.40% reduction of the OPs (energy consumption) in the backpropagation and weight updating (see Supplementary Note 8 for details). The corresponding energy consumptions for inference are approximately 24.20 mJ and 599.47 μJ for a state-of-the-art GPU (light-blue bars) and a projected random resistive memory-based hybrid analogue–digital system (dark-blue bars), respectively, affirming the 40.37× large boost of energy efficiency in node classification (see Supplementary Fig. 11 for the simulated hyperparameters impact on energy efficiency). In addition, the ESGNN on a projected random resistive memory-based hybrid analogue–digital system (3.09 mJ) offers a 88.44% reduction of the training energy (including forward passing the echo state layer and optimizing the readout layer) compared with that on a state-of-the-art GPU (26.69 mJ) (see Supplementary Note 7 for details).

Fig. 4: Node classification of a citation network.
figure 4

a, An illustration of the large-scale citation network CORA. Each node in the graph is a scholarly article, while an edge indicates a citation between two papers. There are a total of seven article categories, indicated by node colours, according to their discipline. b, The node classification scheme. The input graph is first embedded using the ESGNN according to the protocol shown in Fig. 1f and Methods, followed by a graph convolution layer serving as the readout to produce a classification vector for each node. c, An illustration of simulated node embeddings. Coloured boxes on the left are the zoom-in of node embedding details. d, A node embedding mapped to a 2D spacing using t-SNE, showing clear clustering of nodes of the same categories. e, The accuracy of ten random tests for node classification and the software baseline. The average accuracy is 87.12%, comparable to state-of-the-art algorithms. f, The normalized confusion matrices of the simulated classification results. g, A breakdown of the estimated OPs (red bars) and the associated energy consumption (light-blue bars for a state-of-the-art GPU; dark-blue bars for a projected random resistive memory-based hybrid analogue–digital system). In a forward (backward) pass, the fully trainable model on a state-of-the-art GPU and ESGNN on a projected random resistive memory-based hybrid analogue–digital system consume approximately 24.20 mJ (approximately 63.18 GOPs) and approximately 599.47 μJ (approximately 5.43 GOPs), respectively, revealing a >40.37 fold improvement in the inference energy efficiency (and an approximately 91.40% reduction of the backward pass complexity).

Source data

Full size image

Discussion

In this paper, we demonstrate a hardware–software co-design scheme for graph learning. Hardware-wise, the stochasticity of resistive switching is leveraged to produce low-cost and scalable random resistive memory arrays that physically implement the weights of an ESGNN, featuring in-memory computing with large parallelism and high efficiency that overcomes the von Neumann bottleneck and slowdown of Moore’s law. Software-wise, ESGNN not only takes advantage of the physical random projections enabled by random resistive memory arrays in performing graph embedding but also substantially reduces the training complexity of traditional graph learning. The resultant system demonstrates great potential as a brand-new edge learning platform for graphs.

Methods

Fabrication of resistive memory chips

The resistive memory chip consists of a 512 × 512 crossbar array. Each of the resistive memory cells is integrated on the 40 nm standard logic platform. The resistive memory cells, including bottom electrodes, top electrodes and a transition-metal oxide dielectric layer, are built between the metal 4 and metal 5 layers of the backend-of-line process. The via of the bottom electrodes, with a diameter of 60 nm, is patterned by photolithography and etching. The via is filled with TaN by physical vapour deposition followed by chemical mechanical polishing. A buffer layer of 10 nm TaN is deposited by physical vapour deposition on the bottom electrode via. Then, 5 nm Ta is deposited and then oxidized in an oxygen ambident to form an 8 nm TaOx dielectric layer. The top electrodes comprise 3 nm Ta and 40 nm TiN, which are sequentially deposited by physical vapour deposition. After fabrication, the logic backend-of-line metal is deposited using the standard logic process. Cells in the same column share top electrode connections, while those in the same row share bottom electrode connections. Finally, the chip was post-annealed in vacuum at 400 °C for 30 min.

The hybrid analogue–digital computing platform

As shown in Supplementary Fig. 2, the platform consists of an eight-channel digital-to-analogue converter (DAC80508, 16-bit resolution; Texas Instruments) and two eight-bit shift registers (SN74HC595; Texas Instruments) to source 64-way parallel analogue voltages with eight independent voltage amplitudes in the range from 0 to 5 V. To perform vector–matrix multiplication, a DC voltage is applied to bit lines of the resistive memory chip through a four-channel analogue multiplexer (MUX, CD4051B; Texas Instruments). The results are represented by currents from source lines and converted to voltages by trans-impedance amplifiers (OPA4322-Q1; Texas Instruments). The voltages are then read by an analogue-to-digital converter (ADS8324, 14-bit resolution; Texas Instruments), which passes the readings to the Xilinx system-on-chip.

Multibit vector–matrix multiplication

To perform vector–matrix multiplication, the analogue input vector is first digitized into an m-bit binary vector where each element is an m-bit binary number (\(m = 4\) in this case). The analogue multiplication is therefore approximated by m times multiplication with binary input vectors corresponding to different significance. In each multiplication, a row is biased to a small fixed voltage (for example, 0.3 V) if it receives a bit ‘1’ or grounded if it receives a bit ‘0’. The output currents of all the columns are acquired sequentially using the column MUX. The resultant currents are multiplied with the significance and accumulated in the digital domain. Note that a larger m leads to better precision but an increased cost of energy and time.

Graph classification experiments

As shown in Fig. 1c, the crossbar array is partitioned logically into two conductance matrices \({{{{G}}}}_{{{I}}} \in {\Bbb R}^{h \times \left( {u + 1} \right)}\) and \({{{{G}}}}_{{{R}}} \in {\Bbb R}^{h \times h}\) (where u and h represent the dimension of the input feature vector and the number of hidden neurons, \(h = 50\) for both the MUTAG and COLLAB datasets) which are then mapped to the input weight matrix \({{{{W}}}}_{{{I}}} = \alpha _{I}{{{{G}}}}_{{{I}}} \in {\Bbb R}^{h \times \left( {u + 1} \right)}\) and the recursive matrix \({{{{W}}}}_{{{R}}} = \alpha _{R}{{{{G}}}}_{{{R}}} \in {\Bbb R}^{h \times h}\), respectively. Here, the scaling factors \(\alpha _{{I}}\) and \(\alpha _{R}\) are hyperparameters, which are set to 0.0016 μS−1 and 0.006 μS−1, respectively in the graph classification experiments to ensure the echo state properties of the network (spectral radius less than unity).

Given a graph \({{{\mathcal{G}}}} = ({{{\mathcal{V}}}},{{{\mathcal{E}}}})\) with n nodes \({{{\mathbf{x}}}}_i \in {{{\mathcal{V}}}}\) and edges \(({{{\mathbf{x}}}}_i,{{{\mathbf{x}}}}_j) \in \varepsilon\), we first compute the input projection of each node feature vector. For the jth node, its node input feature vector is \({{{\mathbf{x}}}}_j \in {\Bbb R}^{u + 1}\) (with a unit bias) and the input projection is \({{{\mathbf{u}}}}_j = {{{{W}}}}_{{{I}}}{{{\mathbf{x}}}}_j \in {\Bbb R}^h\), where \({{{\mathbf{x}}}}_j\) is quantized to a four-bit binary vector mapped to voltages applied to the random resistive memory array. For the MUTAG dataset, the node feature vectors are the concatenations of one-hot vectors and the bias \(\left( {{{{\mathbf{x}}}}_j \in {\Bbb R}^{7 + 1}} \right)\), denoting their atom types. For the COLLAB dataset, the node feature vectors are constant, that is, the concatenation of a unit scalar and the bias \(\left( {{{{\mathbf{x}}}}_j \in {\Bbb R}^{1 + 1}} \right)\). The node internal state vector, or its embedding, is then iteratively updated (see Extended Data Fig. 2 and Supplementary Note 5 for the initialization and storage of the intermediate node embeddings). The internal state vector of the jth node at time t + 1, denoted by \({{{\mathbf{s}}}}_j^{\left( {t + 1} \right)} \in {\Bbb R}^h\), is computed by aggregating its state \({{{\mathbf{s}}}}_j^{\left( t \right)}\) and input projection \({{{\mathbf{u}}}}_j\) and the states of all its neighbours after random projections by the recursive matrix \(\mathop {\sum }\nolimits_{k \in {{{\mathbf{N}}}}\left( j \right)} {{{{W}}}}_{{{R}}}{{{\mathbf{s}}}}_k^{\left( t \right)}\) (where \({{{\mathbf{N}}}}\left( j \right)\) denotes the set of neighbouring nodes of node j) according to equation (1).

$${{{\mathbf{s}}}}_j^{\left( {t + 1} \right)} = a{{{\mathbf{s}}}}_j^{\left( t \right)} + (1 - a)\sigma \left[ {{{{\mathbf{u}}}}_j + \mathop {\sum }\limits_{k \in {{{\mathbf{N}}}}\left( j \right)} {{{{W}}}}_{{{R}}}{{{\mathbf{s}}}}_k^{\left( t \right)}} \right],$$
(1)

where σ is the activation function (tanh, in this work), a is the leaky factor (0.2, in this work) and \({{{\mathbf{s}}}}_k^{\left( t \right)}\) is quantized to a four-bit binary vector mapped to voltages applied to the random resistive memory array. All other arithmetic OPs are performed in the digital domain.

The graph embedding is computed by sum pooling of all node embeddings of a given graph to extract a single feature vector as the representation of the graph, or mathematically \({{{\mathbf{g}}}} = \mathop {\sum }\nolimits_j {{{\mathbf{s}}}}_j^{\left( T \right)} \in {\Bbb R}^h\), where T is the total number of iterations. Unlike classical echo state networks, the node internal state in ESGNN iterates finite times (Extended Data Fig. 4), as a trade-off between accuracy, energy cost and over-smoothing.

The readout layer is a fully connected layer implemented in the digital domain. For the MUTAG (COLLAB) dataset consisting of two (three) categories, the readout layer maps graph embedding vectors g onto class vectors \({{{\mathbf{o}}}} \in {\Bbb R}^2\) (\({{{\mathbf{o}}}} \in {\Bbb R}^3\)) using 102 (153) floating-point weights with bias. It shall be noted the two-category classification can also be performed by mapping g onto class scalars \({{{\mathbf{o}}}} \in {\Bbb R}\) to further reduce the number of weights of the readout layer. During training, we first evaluate graph embeddings of the entire training set. The embeddings and the labels are then concatenated for evaluating the weights of the fully connected readout layer using linear regression.

All hyperparameters (for example, the weight scaling factors \(\alpha _{I}\) and \(\alpha _{R}\), the iteration time T and the leaky rate a) are optimized by grid searching the hyperparameter space to maximize the hardware performance in the ten-fold cross-validation tests.

Node classification simulation

For the CORA simulation, we use PyTorch 1.9.0 as the deep learning framework and Torch-geometric 1.7.2 as the graph deep learning tool. The CORA dataset visualized in Fig. 4a uses the force-directed Kamada–Kawai algorithm, where the data are grouped by classes. The coordinates of nodes have been slightly refined for better visualization. The node embedding follows the same protocol as that of graph classification tasks using 1,000 neurons. The readout layer is a single graph convolutional layer. During the training, the readout layer is optimized using stochastic gradient descent by minimizing a cross-entropy loss function. The readout layer has been trained for 200 epochs with a learning rate of 0.01, a weight decay factor of 0.005, a momentum of 0.9 and a dropout rate of 0.2. The performance of the model is assessed by training the readout layer upon different randomly initialized weights (ten sets of weights were used here).