Main

The development of materials with precisely tuned electrochemical and physical properties is critical in enabling next-generation energy technologies. One example appears in redox flow batteries (RFBs), which offer the potential to deliver low-cost and reliable energy storage at the grid scale1. Battery formulations using organic molecules as the active species are a promising alternative, as they are domestically manufacturable, are decoupled from markets for transition metals and have a lesser ecological footprint2,3,4. A wide range of organic redox couples exist and have been explored as charge carriers in flow battery applications5. Among these, persistent organic radicals are a promising class of active species with highly reversible redox processes6. These molecules have an unpaired valence electron that can be either donated or paired with an accepted electron to form a closed-shell species. However, due partly to their unique and complex chemistry, relatively few stable radical-containing materials are known to exist6,7. As a result, most studies have focused on chemical modifications of a handful of well known stable radical scaffolds8, primarily via mechanism-based approaches that identify optimal side chains to improve performance9,10,11,12,13,14,15,16,17.

The scarcity of radical scaffolds complicates the tuning of their physical and electrochemical properties to meet the strict demands of high-performance, low-cost RFBs2,3. For example, TEMPO (2,2,6,6-tetramethylpiperidine-N-oxyl) is currently a leading organic catholyte candidate (Fig. 1), but remains uneconomical due to its low oxidation potential (OP) of +0.8 V versus the standard hydrogen electrode (SHE)18,19. Viologen derivatives have similarly been explored as anolyte materials, but have a high equivalent weight (molecular weight per mole of electrons transferred)3,14,17,20. The use of separate electrolytes for the anode and cathode can result in capacity fade with chemical crossover driven by concentration gradients21. The discovery of new stable organic radical scaffolds may therefore unlock performance and cost targets unachievable with current materials. Recent work has demonstrated that the stability of organic radicals, viewed in terms of thermodynamic stabilization and kinetic persistence, can be estimated using density functional theory (DFT)22. In addition to stability, the single-electron half-reaction potentials of organic radicals can be reliably estimated via DFT from their adiabatic electron affinity and ionization energy23. Computational screening of many requirements for new redox-active moieties is therefore feasible, enabling a high-throughput search for potential candidates.

Fig. 1
figure 1

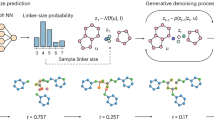
Overview of the computational strategy and molecular design criteria used for goal-directed optimization of redox-active stable radical moieties. The computational workflow (top) demonstrates how top-performing radicals were generated. The bottom panel details criteria considered in the reward function.

Full size image

The field of goal-directed molecular optimization has evolved rapidly in recent years, boosted in part by improved machine learning (ML) tools and generative algorithms24,25. Computational lead generation has been predominantly studied in pharmaceutical research, often through generating serialized molecular structures as simplified molecular-input line-entry system (SMILES) strings that resemble a given training database of compounds26,27,28,29. Techniques from reinforcement learning (RL) have shown an excellent ability to generate valid molecules with desired properties without relying on an existing database of molecular structures to learn valid structural motifs30,31. In particular, methods based on a direct tree search of molecular structures using techniques such as Monte Carlo tree search (MCTS) offer the ability to precisely control the search space of candidate molecules32,33,34,35,36,37.

In this study, we develop a complex and multi-factored objective function for organic radical charge carriers that includes radical stability, redox potential and synthesizability considerations backed by O(105) DFT calculations. We next implement a scalable RL approach based on single-player AlphaZero38 that guarantees validity and low synthetic accessibility score (SAscore)39 for optimized molecules. We seek to find a single redox-active species that can perform both the oxidation and reduction reactions, simplifying battery design and reducing capacity fade through membrane crossover40. Compared with the optimization of an asymmetric battery candidate, this requirement imposes a more complex multi-objective optimization challenge, as the quantum chemical energies of two one-electron redox processes must be balanced within a single small radical scaffold. The generative model yielded a large distribution of molecules predicted to meet the desired stability criteria while simultaneously having suitable OP and reduction potential (RP). The accuracy of these ML surrogate predictions was then validated against DFT calculations, with many radical candidates passing all criteria at the DFT level. Furthermore, we performed a post hoc analysis of the predicted retrosynthetic routes for the optimized molecules, finding many molecules with reasonable synthetic pathways41. This study demonstrates that goal-directed molecular optimization, coupled with a highly detailed ML surrogate model, can produce realistic candidates for demanding applications. Additionally, we find that stable radical scaffolds for RFBs are more abundant than the limited but well known set of experimentally characterized motifs.

Results and discussion

An overview of the computations performed in this work is shown in Fig. 1. We first define our optimization criteria and benchmark a DFT workflow against experimental data. We then construct a database of radicals using this workflow, and subsequently train and validate ML surrogate models. RL optimizes these surrogate objectives, yielding a set of candidate radicals. We perform both DFT confirmation and a post hoc synthesizability analysis on these radicals, yielding a final set of candidate results.

Computational features required for organic active species

We begin by defining the features required for organic stable radical active species to be viable candidates for RFBs (Fig. 1). For commercial viability, RFBs need to achieve a high charge density and high reversibility (that is, longevity) at low cost. Active species must therefore have a precisely tuned redox potential to take full advantage of the solvent’s electrochemical stability window, and a highly stable, long-lived radical centre to avoid reactions that might reduce the battery’s capacity over time42. We estimate standard redox potentials with adiabatic (that is, geometry-optimized) ionization potentials and electron affinities obtained from implicitly solvated DFT thermochemistry including vibrational zero-point energy. Further, we estimate radical stability using a recently developed metric that incorporates both thermodynamic and kinetic stabilization of the radical centre using three-dimensional (3D) structural features and electron spin density obtained via DFT22. Highly delocalized and sterically protected radicals are prioritized by this approach.

Radical groups must also be synthetically accessible. Synthesizability is considered by constraining the SAscore of the closed-shell R–H molecule to be less than 4.0 (refs. 39,43) and by ensuring that the R–H bond is relatively weak, with a homolytic bond dissociation enthalpy (BDE) of 60–80 kcal mol−1 (refs. 44,45). While many thermal and photochemical synthetic protocols exist to form radicals from a closed-shell parent organic compound (for example, deoxygenation, dehalogenation and so on), this BDE constraint limits our candidates to those that could be generated by a facile and selective late-stage H-atom abstraction.

Development of a fast surrogate multi-objective function

To ensure the accuracy of aqueous redox calculations, we first benchmarked a wide number of different density functional, basis set and solvation model combinations on an experimental dataset of 174 redox potentials in acetonitrile (Fig. 2a and Extended Data Fig. 1)46. The lowest mean absolute error (MAE) was achieved using M06-2X/def2-TZVP47 and the SMD solvation model48. An additional benchmark comparing calculated and experimental redox potentials in water is outlined in Extended Data Fig. 2 (refs. 49,50). We obtain an MAE of 0.25 V for 46 molecules using M06-2X/def2-TZVP with SMD solvation, with M06-2X similarly yielding the lowest error among the functionals considered.

Fig. 2: Development of a fast surrogate objective function.
figure 2

a, Prediction accuracy as a function of density functional, basis set and solvation model on an experimental database of 174 redox potentials46. b, GNN topology for predicting stability and redox potential. Two separate models are trained. The first predicts spin density and buried volume for an input molecule at each atom. The second predicts the OP and RP for an entire molecule. Input dimensions for node and edge features are n, number of atoms and r, 2 × number of bonds, respectively. c, Learning curve for redox potentials showing prediction accuracy versus number of training molecules. d, Distribution of redox prediction errors for the final trained model. e, Learning curve of the prediction of parameters governing radical stability. Error bars in c and e extend to ±1 s.d. across three replicates.

Full size image

To enable goal-directed molecular optimization, we constructed a database of 50,547 OP and 81,854 RP calculations by reoptimizing radical and charged structures from an existing database of organic radicals in an implicit water solvent51. We impose several quality checks to ensure convergence of the DFT optimization and validity of the resulting energy calculations, including checking for normal termination of the DFT method, ensuring that bonds were not broken or formed during optimization and that the optimized open-shell molecules have minimal spin contamination (Methods).

We next trained a graph neural network (GNN) model to predict both OP and RP directly from a radical’s chemical connectivity (Fig. 2b)52,53,54,55. A test set of 2,000 radicals was withheld for validation, consisting of 1,773 and 1,052 converged RP and OP calculations, respectively. Learning curves plot the models’ prediction error as a function of database size (Fig. 2c) and demonstrate that the models continue to benefit from additional data even at the full database limit. Distributions of prediction errors (in volts) for test-set compounds using the entire training dataset are shown in Fig. 2d, with an MAE of 47.4 and 37.4 mV (1.1 and 0.9 kcal mol−1) for OP and RP, respectively, close to the ‘chemical accuracy’ target of 1 kcal mol−1.

Using the same chemical connectivity inputs, we trained a second surrogate GNN model on a recently published database of radical stability scores22,56. In this dataset, radical stability is correlated with two quantum chemical descriptors: the delocalization of the radical electron’s spin, and the buried volume at the location of maximum spin57. This GNN is trained to predict local aspects of the optimized 3D geometry along with the quantum mechanical electron density (more precisely, the density difference between a- and b-spin electrons) at each atomic position. Buried volume and spin density are fractional quantities bounded between 0 and 100%. The model achieves an MAE of 1% in buried volume prediction and 0.7% in predicting quantum mechanical spin densities on each heavy (that is, non-hydrogen) atom on 5,000 radicals withheld for validation.

Stabilized radicals tend to have highly delocalized electronic structures, where substituents can potentially have a long-range influence on stability and redox potential. As demonstrated by the learning curves (Fig. 2c,e), the trained GNN models continue to benefit from additional training data even with nearly 100,000 training examples. The GNNs employed in this study use six message-passing layers and are therefore able to exchange localized chemical information within a radius of six bonds.

These two trained ML models, one for redox potential and one for radical stability, quickly and accurately predict many of the relevant parameters for organic radical viability in RFB applications, thus fulfilling the role of a viable surrogate for DFT calculations. Since RL frameworks typically operate with scalar reward functions, we converted the outputs of these two models into a single reward value as follows. First, we computed radical stability scores by combining the maximum predicted spin and the buried volume at the location of maximum spin. Stability scores range from near zero for highly unstable radicals (that is, the methyl radical) to 75 or higher for radicals known to be stable experimentally22. Second, for the redox potential score, a maximum of 100 extra points were awarded for meeting each of four separate criteria (25 points each): (1) an RP between −0.5 V and +0.2 V, (2) an OP between +0.5 V and +1.2 V, (3) a total voltage difference of at least 1 V and (4) an R–H BDE between 60 and 80 kcal mol−1. BDEs were predicted for the hydrogen-terminated radical using a previously published ML model52. We added these two scores together to obtain a single reward value. Further details on the exact structure of the reward function are provided in Methods.

After constructing an efficient surrogate objective function, we next sought to find radicals that maximize this function. Molecule optimization was posed as a search over a directed acyclic graph (DAG), beginning the search at an initial state of a lone carbon atom. In a similar fashion to previous studies, we next considered possible actions to transition between states30,31. In this study, each action adds a new bond to the molecule, either between two atoms with free valence in the original molecule (forming a ring) or between an atom in the original molecule and one of a set of possible atom additions. We considered only C, N, O or S atoms, as common elements found in organic electronic materials (Fig. 3a). To ensure that the molecules we generated were realistic, we refined the set of possible successor states from a given starting structure by (1) enumerating possible stereoisomers, (2) canonicalizing molecules to tautomer forms58 and (3) removing molecules with high SAscore values or highly constrained ring systems. To generate radical structures, additional terminal successor states were created from intermediate molecules where one atom has a hydrogen atom replaced with an unpaired electron. A more complete description of the action space, including a comparison against previous approaches, is given in Methods.

Fig. 3: Overview of the RL structure optimization strategy.
figure 3

a, An example of how molecules are constructed through the iterative addition of bonds and atoms. Percentages indicate transition probabilities between states near the end of the RL optimization (not all possible states are shown). b, Schematic of the architecture of the computational search. Molecule rollouts and policy training are performed asynchronously and coordinated by a data buffer. c, Evolution of the rewards for individual molecule rollouts (top) and losses for the policy model (bottom) versus time as the optimization proceeds. The 75th percentile of the final reward from the most recent 200 rollouts is denoted r75 (top), and is used to reshape the reward through the ranked rewards strategy61.

Full size image

Candidate optimization through RL

In this study, we limited constructed molecules to a maximum of 12 heavy atoms (approximately the size of TEMPO), as lower-molecular-weight redox-active moieties are preferred for a lower equivalent weight. Including selecting the location of the radical electron, this yields a search space of approximately 109 possible valid radicals, estimated via extrapolating from smaller maximum sizes and consistent with previous results59. The computational cost of enumerating this space grows exponentially with the maximum molecule size, motivating a more efficient strategy for finding top-performing molecules (Extended Data Fig. 3).

A framework for MCTS optimization over the defined DAGs was implemented that allows for transpositions, where the same molecule can be reached through multiple paths60. Following the approach of AlphaZero38, this framework was augmented with a policy model that replaces the simulation phase (using a random policy) of MCTS with a value score predicted from a GNN, which also initializes the prior scores for successor states from the given molecule. This policy model is trained in a concurrent process by maintaining a buffer of recent MCTS rollouts, sampling in-progress molecules and minimizing a multi-objective loss function. The loss function contains both the difference between the predicted value score and the final rollout reward and the difference between predicted prior probabilities and the actual search probabilities for each of the molecule’s successor nodes (Methods). As MCTS and the AlphaZero framework were originally designed for competitive games, the ranked reward strategy was used to enable tabula rasa self-play for the single-player combinatorial optimization problem61. In this strategy, the final reward of a rollout is rescaled to {0, 1} depending on whether the reward is greater than the 75th percentile of the last 250 results. An overview of the connectivity between the rollouts, the data buffer and the policy model is shown in Fig. 3b. In this fashion, the policy-guided rollouts evolve from an initial random walk over molecular space to a highly targeted exploration of regions likely to contain high-reward molecules.

To search for potential candidate radicals, 200 rollout workers were split across 50 compute nodes for 4 h, with a single node equipped with dual Tesla V100 graphics processing units handling the continual training of the policy model. This approach resulted in a total of 34,626 rollouts and over 3.8 million terminal state radicals evaluated with the surrogate objective function. Figure 3c plots the final reward from each molecule rollout as a function of time, along with the loss values for training the policy model to predict the final value and prior probabilities for intermediate molecule states. Using ranked rewards to rescale the final reward as a function of recent rollouts means that the policy model is forced to continually adapt to predict which intermediate states are the most likely to lead to higher-performing radicals.

Of the 3.8 million radicals evaluated during the optimization, 1,078 had a total surrogate reward greater than 195, corresponding to a minimum stability score of 95. The radical stability metric rewards molecules with highly delocalized electrons and bulky groups offering steric protection of the radical centre. As such, the stability metric tends to have a higher maximum value for larger molecules. Known stable radicals in this size range include TEMPO (with a stability score of 93.9) and the phenoxy radical (77.2). The reward function includes a maximum of 100 points for meeting all redox and bond strength criteria in addition to the radical stability score. From the radical training database, no radicals were found that had a stability score greater than 90 while satisfying the redox criteria.

Confirmation of RL-optimized candidates with DFT

All 1,078 molecules predicted to have the desired properties were subsequently analysed with DFT to verify the accuracy of the ML models. Most top-performing candidates had close to the maximum molecule size, with 960 molecules having 12 heavy atoms, 110 molecules having 11 heavy atoms, 6 atoms having 10 heavy atoms and just 2 molecules with 9 heavy atoms.

In Fig. 4a, we plot the ML-predicted redox voltages for the chosen subset, which all lie within the target triangle to permit a single radical to function as both the electron donor and acceptor in an aqueous RFB with a total voltage of at least 1 V. For radicals for which the DFT calculations converged, 80.5% fell within the desired target region (Fig. 4b). The stability scores of the radicals predicted via ML were then checked against those obtained via DFT. Figure 4c shows the distribution of stability scores for both approaches, and that stability scores obtained via DFT tended to be lower than those predicted with the surrogate objective function. Using a cutoff score of 90, well within the stability scores observed for experimentally known stable species, 41.9% of radicals were still classified as stable. As shown in Extended Data Fig. 4, while buried volume predictions for optimized radicals were highly consistent with those obtained from DFT, accurate prediction of spin density was more difficult for these highly delocalized radicals. Additional training data in this region of molecular space may improve accuracy in subsequent experiments, as the generated radicals tended to be much more stable than those found in the training data (Fig. 4c).

Fig. 4: Confirmation of top-scoring RL-generated radicals with DFT calculations.
figure 4

a, Distribution of redox potentials for radicals in the training database, highlighting the target zone for an aqueous, symmetric redox battery. Predicted redox potentials for optimized radicals are shown in blue. b, DFT-computed redox properties for RL-optimized radicals that were predicted to fall within the target zone. EA, electron affinity; IE, ionization energy. c, A comparison of ML- and DFT-derived stability estimates for optimized radicals, compared with the distribution of stability scores for radicals in the training database. A stability threshold of 90 was used as a lower bound for determining whether a radical could be classified as stable.

Full size image

Evaluation of the synthesizability of generated molecules

The synthesizability of molecules proposed by generative algorithms has been identified as an area of concern, as theoretically optimized molecules that cannot be experimentally tested are of limited practical value43. To address this concern, the ASKCOS retrosynthesis prediction web service was applied post hoc to evaluate the 1,078 top-ranked candidates (Methods)41,62. Of these, 87 returned putative synthetic routes with a median of five synthetic routes per candidate and an average depth of 7.9 steps. Following DFT validation, a total of 32 molecules were confirmed to satisfy the redox requirements while having high stability (>90). Chemical structures for a representative subset of these molecules are depicted in Fig. 5a. The RL-optimized molecules show structural variability through the varied inclusion of N, S and O heteroatoms and extended delocalized structures, frequently with unsaturated carbo- and heterocyclic (for example, cyclopentadienyl, pyrrole, furan, thiophene) cores. We notice a trend of alkoxy thiophene subunits among the chemically synthesizable RL candidates. This is in correlation with the increasing use of similar molecules in organic bioelectronic devices. Previous work has shown that the electrical properties of thiophenes can be tuned by introducing alkoxy substituents63,64. Their enrichment among the chemically synthesizable radicals may also be due to the availability of reaction templates for this chemistry, as only 104 of the 232 DFT-confirmed RL candidates possess this functional group.

Fig. 5: De novo structures generated by RL.
figure 5

a, Radical structures passing the design criteria subsequently validated with DFT. b, Visualization of the radical stability metric, consisting of both spin delocalization (top row) and buried volume at the centre of maximum spin (bottom row) for known stable radicals (left) and those generated via the RL algorithm (right). c, A possible retrosynthetic pathway for the hydrogenated form of radical 1 generated by ASKCOS. FF score is the estimated plausibility value for each reaction.

Full size image

As required by the objective function, all radicals demonstrate high spin delocalization and high steric protection of the site of highest spin density. In Fig. 5b, we visually compare spin delocalization and buried volumes for both experimentally known and RL-optimized radicals. As expected, a high predicted stability is achieved by delocalizing the radical electron density across multiple atoms and centring the location of highest spin density on an atom with a high buried volume. We note that in Fig. 5a,b the surrogate model correctly predicts that the spin is predominantly focused on the location of highest buried volume, matching DFT results, even though the radical centre is formally specified at a different atom in the SMILES string.

We next investigated the predicted retrosynthetic pathways by which the wide variety of top-performing radicals might be experimentally prepared. In Fig. 5c, we show a putative pathway from ASKCOS for the hydrogenated form of a thiophene-based radical. Thiophenes are well known fragments in organic electronics, where their semiconducting properties are exploited for high efficiency65. The retrosynthetic route consists of a minimum of two well established transformations involving a Friedel–Crafts alkylation and an acidic methyl ether cleavage, starting from commercially available 2-methoxythiophene and tert-butyl chloride (Sigma-Aldrich)66.

Error analysis of the surrogate objective function

The surrogate objective function successfully guided molecule optimization towards regions meeting the desired criteria at the DFT level. However, approximately half of the radicals predicted to meet the desired criteria ultimately failed DFT confirmation. In Fig. 6a we show optimized radicals with a DFT-calculated stability substantially lower than that predicted with the surrogate model. One reason for such failure is the incorrect prediction of the maximum spin location, with a higher fraction of spin residing on an atom that is not highly shielded by bulky substituents. This failure represents in part a weakness of the chosen stability metric, as minor differences in predicted resonance can lead to large swings in the combined score. However, erroneously predicted loci of maximum spin were chemically reasonable, generally corresponding to the location of the second-highest DFT spin density. Extended conjugated thiocarbonyl-based radicals and five-membered cyclic alkoxy thiophenes are encountered frequently in these outliers. With DFT relaxation, the maximum spin typically locates on the terminal S atom, while the surrogate objective model predicts greater spin at a or g positions, in accordance with the general principle of vinylogy67. Retraining the surrogate objective with additional examples of these systems may improve predictions in subsequent generation rounds.

Fig. 6: Sources of error in the ML surrogate model and strategies for tuning redox potential.
figure 6

a, Outliers in ML-predicted stability scores relative to DFT values. The predicted location of maximum spin is highlighted for both methods, and the resulting stability score is shown for DFT and ML. b, An example prediction error for redox potential due to lack of similar molecules present in the training database. The input radical is shown on the left, with the five closest training set radicals shown on the right. c, On the left, the distribution in redox potentials for all training set molecules is coloured according to each radical’s SOMO energy. On the right, the distribution of SOMO energies of radicals in the training database is shown, with the grey region extending from the 5th to the 95th percentile of the range observed in RL-optimized candidates. Example structures from the radical database are shown for various SOMO energies.

Full size image

Errors in redox predictions also tended to occur for functional groups absent from the training data. In Fig. 6b we show the structure of one such outlier. Using the embeddings assigned by the surrogate model’s penultimate prediction layer, we can explore which training set molecules are closest in structure to the target prediction. A nearest-neighbour search on this latent space reveals several cyclopentadienyl radicals with calculated redox potentials close to the erroneous prediction. The thioether substituent on a cyclopentadienyl, which is not found in any of the molecules in the redox potential training database, strongly influences redox behaviour in a way not captured by the surrogate model. The sulfur atom provides additional stabilization of the oxidized form through resonance and of the reduced form through inductive effects (that is, stabilization of the a-anion resonance structure). These types of prediction outlier could be remedied by augmenting the redox potential database with additional structural diversity.

Searching for a symmetric electrolyte candidate places a challenging constraint on the electronic properties of optimized molecules, as both the OP and RP must be precisely and independently tuned. To explore the strategies used by the RL algorithm, we plot the relationship between OP (derived from the ionization energy) and RP (derived from the electron affinity) in Fig. 6c. Electron-rich, more readily oxidized (for example, planar aminal) radicals are found in the lower left corner, while electron-deficient, more readily reduced (for example, heterocyclic sp2) radicals are found in the top right corner of this plot (Extended Data Fig. 5).

For open-shell molecules studied with spin-unrestricted Kohn–Sham DFT, the analogue to Koopmans’ theorem relates the energy of the highest singly occupied molecular orbital (SOMO) to the vertical ionization energy68. Similarly, the lowest unoccupied molecular orbital is linked closely to vertical electron affinity, mainly when using long-range corrected density functionals69. From our computations we observe a correlation between a radical’s SOMO energy and both redox potentials (Fig. 6c). This interdependence illustrates the challenge of independently tuning the anode and cathode half-reactions. Qualitatively, electron-poor radicals tend to be easily reduced and difficult to oxidize, while electron-rich radicals are easily oxidized and hard to reduce. However, the RL algorithm still manages to find candidates that meet both redox criteria. Radicals with the required redox properties for aqueous batteries have a SOMO energy in the range of −6.5 to −7 eV (grey region in Fig. 6c). To independently optimize OP and RP at a fixed SOMO energy, the RL policy learns to harness captodative stabilization of the radical centre70. Captodative stabilization involves the incorporation of conjugated electron-donating and electron-withdrawing groups, and provides enhanced stability to all three important redox states: the radical, oxidized and reduced states. Interestingly, this strategy mirrors the use of bipolar redox-active molecules, an emerging strategy in the development of non-aqueous RFBs such as 2-phenyl-4,4,5,5-tetramethylimidazoline-1-oxyl-3-oxide71. The algorithm thus rediscovers a fundamental concept in radical chemistry that has shown promise in the development of symmetric RFBs. However, unlike existing bipolar redox-active molecules with relatively bulky functional groups, those discovered by RL more efficiently blend all required functionality into a much lower-molecular-weight moiety.

Conclusion

In this study, we have performed a search for molecular structures that simultaneously satisfy several complex quantum chemical phenomena important in advanced energy applications. We have demonstrated that combining high-fidelity quantum chemistry simulations, ML predictive models and state-of-the-art RL strategies is an effective tool in efficiently exploring molecular space. Without being explicitly programmed on how to construct resonantly stabilized radicals with appropriate orbital energies, the RL algorithm learns a range of strategies that lead to high-performance candidates. While in this study candidates were found with reasonable efficiency (50% of optimized radicals), iterative refinement of the surrogate model with respect to the ground-truth calculations would improve the model’s accuracy. Additionally, while molecules with putative synthetic routes were found from among the top-performing candidates, more accurate and faster methods of searching synthetically accessible space are required.

Additional refinement of the top-performing candidates is also required before they are likely to be applicable in aqueous organic RFBs. Widening the redox potential ranges considered can account for applicability of additional radicals in organic RFBs, which can also allow for higher overall cell voltage. Optimizing solubility with predictive models72,73 and including charged moieties in both the training data and action space will be particularly important in achieving a high charge density. The stability metric employed also may have limitations that will need to be refined following experimental investigation. The radical stability metric was developed to capture processes sensitive to steric effects such as bimolecular recombination or disproportionation. Other fates, such as oxidative aromatization, may not be adequately predicted, requiring further refinement. Addressing these limitations to achieve holistic prediction of improved bipolar redox actives candidates remains a future goal.

Methods

Calculation and validity analysis of redox potentials

Full DFT estimation of the adiabatic (that is, including the effects of geometric relaxation and vibrational zero-point energy) ionization energy and electron affinity for a given radical takes hours per candidate, and requires three separate geometry optimizations to obtain standard-state Gibbs energies of the neutral radical and both anionic and cationic closed-shell species. We further obtain OP and RP values in volts by referencing the standard-state Gibbs energy changes to the absolute potential of the SHE74. Gaussian 16 (ref. 75) was used for all DFT calculations with a default ultrafine grid for all numerical integration. The primary database of redox potentials was built using the M06-2x/def2-TZVP level of theory by separately optimizing the neutral, oxidized and reduced radical species. The calculations were performed using the SMD solvation model with a water solvent at 298 K (ref. 48). The same initial structures were used for all three calculations and were taken from previous calculations performed in the gas phase51. Where an initial relaxed structure is not available, a single lowest-energy conformer is found using the MMFF forcefield in RDKit, as described previously51. Iodine-based molecules in the experimental redox benchmark were optimized with the LAN2DZ basis set in combination with 6-31G(d,p) and 6-31G+(d,p).

An automated workflow was developed to check optimizations for convergence by ensuring the absence of imaginary vibrational frequencies and that all bond lengths remained within 0.4 Å of the sum of their covalent radii. Additionally, molecules were inspected to see whether new bonds were formed during optimization, as this often led to difficult-to-predict redox potentials. Atom adjacency matrices were used to determine if any two atoms were closer than 1.3 times the sum of their covalent radii, and these molecules were removed from the training dataset. This primarily occurred during oxidation, as 8,566 oxidized molecules, 602 reduced molecules and 177 neutral radicals were removed from the database in this fashion.

$${{{\mathrm{Reduction}}}}\,{{{\mathrm{potential}}}}\,\left( {\mathrm{V}} \right) = \frac{{G\left( {{\mathrm{R}}\cdot } \right) - G\left( {{\mathrm{R}}^-} \right)}}{F} - E^ \ominus \left( {\frac{{{\mathrm{H}}^ + }}{{{\mathrm{H}}_2}}} \right)_{{{{\mathrm{abs}}}}}$$
$${{{\mathrm{Oxidation}}}}\,{{{\mathrm{potential}}}}\,\left( {\mathrm{V}} \right) = \frac{{G\left( {{\mathrm{R}}^ + } \right) - G\left( {{\mathrm{R}} \cdot } \right)}}{F} - E^ \ominus \left( {\frac{{{\mathrm{H}}^ + }}{{{\mathrm{H}}_2}}} \right)_{{{{\mathrm{abs}}}}}.$$

Spin contamination was checked by looking at the expectation value of the total spin, S2. Radicals were expected to have S2 = 0.75, and a handful of optimizations were discarded where spin contamination resulted in S2 > 0.8. Anions and cations were assumed to adopt a closed-shell singlet state, with S2 ~ 0. To improve the consistency of the dataset, open-shell anions and cations with S2 > 0.25 were removed.

Training the surrogate objective models

Two separate ML models were developed to predict quantum mechanical properties as a function of a candidate radical’s SMILES76 notation, that is, on the basis of only atoms and bonds without considering a specific 3D conformation. The first model predicts spin delocalization and buried volume on each heavy atom in the molecule. The second model predicts the radical’s OP and RP (V relative to SHE). SMILES strings were first converted to a graph representation using the nfp77 and RDKit78 Python libraries. Atoms and bonds were classified depending on features determined via RDKit. For atoms, this included their atomic type, chirality, presence in a ring, number of heavy atom neighbours (degree), aromaticity, number of neighbouring hydrogens and presence of a formal radical centre. For bonds, this included the atom types of the joined atoms, the bond type (single, double, aromatic), presence in a ring and Z/E stereochemistry (if present). The GNN edges are directional, and therefore two graph edges are created for each bond in the molecule, one pointing from atom A to atom B and another pointing from atom B to atom A. Each model consisted of a GNN with a similar core structure depicted in Fig. 2 and further detailed in Extended Data Fig. 6. The GNN generates representative embeddings at the atom, bond and global levels by passing the initial features through a series of message blocks79. In the stability prediction GNN, the final atom feature vector is reduced to two output predictions for each atom’s buried volume and spin density. In the redox GNN, the final global feature vector is reduced to two output predictions for the RP and OP. Both models are trained with a batch size of 128 molecules for 500 epochs over the training data, using the AdamW optimizer with an initial learning rate of 1 × 10−4, decayed by 1 × 10−5 each update step. The weight decay was set to an initial value of 1 × 10−5 (1 × 10−6 for the redox model) and was decayed by 1 × 10−5 each update step.

Learning curves were generated by restricting the training set to a random subset of examples while retaining the same validation throughout the different models. Models were trained as described above using a fixed number of gradient updates (equivalent to 500 passes over the entire training dataset), and the performance on the held-out validation set was recorded. To improve predictive performance in the region of high-reward radicals, 3,978 high-scoring molecules from previous RL runs were optimized with DFT and added to the training data for the surrogate objective functions in the final RL iteration. These molecules ranged in size between 9 and 15 heavy atoms with a maximum stability score of 109.7. DFT confirmation of the final 1,078 candidates could be used to augment this training set of high-scoring molecules in subsequent iterations.

Details of the reward function

To find radicals that meet all the desired criteria, predictions and desired ranges for multiple properties were synthesized into a scalar reward function. A continuous piecewise linear function, referred to as window below, was used to convert predictions to a score between 0 and 1, with a 1 assigned if the prediction was inside the desired range, 0 outside and a linear transition between the two scores if the prediction was near the boundary (with width equal to one sixth the width of the desired region).

The overall reward function was then composed by summing over individual scores from different properties:

$$\begin{array}{rcl} {\mathrm{reward}} & = & 50\left( {1 - \max \;s_i} \right) + 100\;{\mathrm{BV}}_j \\ && + 25\;{{{\mathrm{window}}}}\left( {R_{\mathrm{pred}},\;\left[ { - 0.5\,{\mathrm{V}},\;0.2\,{\mathrm{V}}} \right]} \right) \\ && + 25\;{{{\mathrm{window}}}}\left( {O_{\mathrm{pred}},\;\left[ {0.5\,{\mathrm{V}},\;1.2\,{\mathrm{V}}} \right]} \right) \\&& + 25\;{{{\mathrm{window}}}}\left( {R_{\mathrm{pred}} - O_{\mathrm{pred}},\;\left[ {1\,{\mathrm{V}},\;0.2\,{\mathrm{V}}} \right]} \right)\\ && + 25\;{{{\mathrm{window}}}}\left( {{\mathrm{BDE}}_{\mathrm{pred}},\;\left[ {60,\;80} \right]} \right)\\ \end{array}$$

where si represents the predicted fractional spin on atom i, and BV is a vector of predicted buried volumes. The reward function was constructed to place approximately equal weights between the stability score (including spin and buried volume contributions, typically near 100 for highly stable radicals) and the remaining BDE (kcal mol−1) and redox requirements.

Description of the molecular action space

Beginning with the initial state of a single carbon atom (that is, methane after adding implicit hydrogens), possible actions were enumerated following a series of expansion and filtering steps. First, all possible tautomers of the given starting molecule were considered as possible starting states58. From each starting state, a new bond was added between an atom in the molecule and a second atom, either one already in the molecule (forming a ring) or an unbonded C, N, O, or S atom. New molecules were generated for every possible atom pair and bond type (single, double or triple) for which valence rules were satisfied. From this set of all possible next actions, molecules were filtered according to several ring, saturation and synthetic accessibility criteria80, including restricting molecules to a maximum SAScore of 4.0. The action space was then further expanded by enumerating all possible stereochemical configurations of the starting molecule, followed by a reduction to canonical tautomer forms. Next actions were then de-duplicated by SMILES string. Additionally, we removed molecules containing moieties that differed substantially from the redox and stability training database. Hydrogen atoms were handled implicitly and filled free valence positions in each final molecule.

Our action space differs from previously described molecular ‘environments’ in several ways. Unlike the environment proposed in MolDQN31, our approach results in a DAG over possible molecules by eliminating the possibility to remove atoms and bonds from molecules under construction. This DAG property prevents cyclical searching and guarantees forward progress when building a radical. It also makes learning the value function easier by eliminating conflation and cross-contamination from cyclical paths in the search graph. Our approach is similar in this respect to the generation environment proposed by You et al.30, where atom and bond additions are guided by a policy network. Unlike You et al., we do not decompose the action into a node selection and a link selection step, and instead only evaluate policy predictions once both the atom and bond type have been chosen. This allows us to easily filter the action space on the basis of valence rules and markedly reduces the number of invalid molecules constructed by the algorithm. It additionally allows us to easily consider additional modifications of the action space, including stereochemical enumeration (for example, at tetrahedral carbon atoms and of double bonds), tautomerization and synthesizability considerations.

Details of the RL algorithm

The RL optimization was performed using the rlmolecule library81 (https://github.com/NREL/rlmolecule), which implements the AlphaZero approach for molecule and material design. In this study, the RL agent learned to select from a parametric action space, where the molecular structures resulting from possible next actions were passed through a trainable policy GNN. The policy GNN had a structure similar to that used for redox prediction (Fig. 2b), using only three message-passing layers and a feature dimension of 64. The policy model was trained with the Adam optimizer with a learning rate of 1 × 10−3 and a batch size of 32 positions. Within each batch, the policy model is presented with a molecule state and a list of potential next actions from a recently played MCTS rollout. The policy model is trained to simultaneously predict the actual visitation frequency from MCTS, as well as the outcome of the resulting molecule rollout (0 or 1 as scored via ranked rewards). Starting at the root methane state, molecule rollouts consisted of conducting 250 MCTS samples (or for a maximum of 30 s) and selecting the subsequent molecule state with probability proportional to the softmax of the visit counts. This procedure is repeated until a terminal state is selected.

The wall time limit was imposed to mitigate the effects of problematic regions of chemical space where the number of possible next actions per molecule, and therefore the time required to enumerate them, vastly outnumbered typical molecules. This was typically encountered with molecules with many possible tautomers and resulted in rollouts being added to the replay buffer that used an outdated version of the policy model.

Communication between the policy network training script and the MCTS rollout workers is handled through a shared filesystem and a PostgreSQL server. Policy checkpoints are previously written to a shared filesystem location, which is checked at the beginning of each rollout by the workers. Final statistics and molecule reward calculations are then written to the shared SQL database. The policy training script in turn selects the 256 most recent rollouts each training epoch, with each epoch consisting of 100 training steps.

Synthesizability prediction

Retrosynthetic routes are predicted using the ASKCOS web interface tool (https://askcos.mit.edu) using the tree builder module. Settings were chosen to match those used in a previous study evaluating the synthesizability of generative models43. Specifically, the maximum tree depth is limited to nine steps, the maximum branching ratio is set to 25 and the maximum wall time of each expansion is limited to 60 s, with a maximum reagent cost of US$100 g−1, 1,000 max templates and a maximum target probability of 0.999. Employing these settings along with no defined banned chemicals and reactions for radical 1 (Fig. 5a), we obtained a total of 43 routes, containing 90 chemicals and 970 reactions. Computation time for each parent molecule’s retrosynthesis tree was approximately 1 h.