Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Perspective
  • Published:

Theoretical tools for understanding the climate crisis from Hasselmann’s programme and beyond

Nature Reviews Physics volume 5, pages 744–765 (2023)Cite this article

Subjects

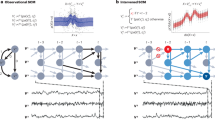
Abstract

Klaus Hasselmann’s revolutionary intuition in climate science was to use the stochasticity associated with fast weather processes to probe the slow dynamics of the climate system. Doing so led to fundamentally new ways to study the response of climate models to perturbations, and to perform detection and attribution for climate change signals. Hasselmann’s programme has been extremely influential in climate science and beyond. In this Perspective, we first summarize the main aspects of such a programme using modern concepts and tools of statistical physics and applied mathematics. We then provide an overview of some promising scientific perspectives that might clarify the science behind the climate crisis and that stem from Hasselmann’s ideas. We show how to perform rigorous and data-driven model reduction by constructing parameterizations in systems that do not necessarily feature a timescale separation between unresolved and resolved processes. We outline a general theoretical framework for explaining the relationship between climate variability and climate change, and for performing climate change projections. This framework enables us seamlessly to explain some key general aspects of climatic tipping points. Finally, we show that response theory provides a solid framework supporting optimal fingerprinting methods for detection and attribution.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: A Mitchell’s diagram depicting a qualitative representation of the climate variability across a range of scales.
Fig. 2: Example: Mori–Zwanzig decomposition without memory but with a noise term.
Fig. 3: The time evolution and standard deviation of upper-ocean potential vorticity anomalies in quasi-geostrophic turbulence and a multiscale Stuart–Landau model.
Fig. 4: Application of response theory to an Earth system model.
Fig. 5: Observation evidence of the AMOC getting closer to a tipping point.

Similar content being viewed by others

References

  1. Mitchell, J. An overview of climatic variability and its causal mechanisms. Quat. Res. 6, 481–493 (1976).

    Article  Google Scholar 

  2. Ghil, M. A century of nonlinearity in the geosciences. Earth Space Sci. 6, 1007–1042 (2019).

    Article  ADS  Google Scholar 

  3. von der Heydt, A. S. et al. Quantification and interpretation of the climate variability record. Glob. Planet. Change 197, 103399 (2021).

    Article  Google Scholar 

  4. Peixoto, J. P. & Oort, A. H. Physics of Climate (AIP, 1992).

  5. Lucarini, V. et al. Mathematical and physical ideas for climate science. Rev. Geophys. 52, 809–859 (2014).

    Article  ADS  Google Scholar 

  6. Ghil, M. & Lucarini, V. The physics of climate variability and climate change. Rev. Mod. Phys. 92, 035002 (2020).

    Article  ADS  MathSciNet  Google Scholar 

  7. Ghil, M. in Climate Change: Multidecadal and Beyond (eds Chang, C. P. et al.) 31–51 (World Scientific/Imperial College Press, 2015).

  8. Rothman, D. H. Thresholds of catastrophe in the Earth system. Sci. Adv. 3, e1700906 (2017).

    Article  ADS  Google Scholar 

  9. Arnscheidt, C. W. & Rothman, D. H. Presence or absence of stabilizing Earth system feedbacks on different time scales. Sci. Adv. 8, eadc9241 (2022).

    Article  Google Scholar 

  10. Pearl, J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference (Morgan Kaufmann, 1988).

  11. Hasselmann, K. Optimal fingerprints for the detection of time-dependent climate change. J. Clim. 6, 1957–1971 (1993).

    Article  ADS  Google Scholar 

  12. Hegerl, G. C. et al. Detecting greenhouse-gas-induced climate change with an optimal fingerprint method. J. Clim. 9, 2281–2306 (1996).

    Article  ADS  Google Scholar 

  13. Hasselmann, K. Multi-pattern fingerprint method for detection and attribution of climate change. Clim. Dyn. 13, 601–611 (1997).

    Article  Google Scholar 

  14. Bindoff, N. L. et al. Detection and Attribution of Climate Change: From Global to Regional, 867–952 (Cambridge Univ. Press, 2013).

  15. IPCC. Climate Change 2021: The Physical Science Basis (eds Masson-Delmotte, V. et al.) (Cambridge Univ. Press, 2021).

  16. IPCC. Special Report on Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation (eds Field, C. B. et al.) (Cambridge Univ. Press, 2012).

  17. Lenton, T. et al. Tipping elements in the Earth’s climate system. Proc. Natl Acad. Sci. USA 105, 1786–1793 (2008).

    Article  ADS  MATH  Google Scholar 

  18. Ashwin, P., Wieczorek, S., Vitolo, R. & Cox, P. Tipping points in open systems: bifurcation, noise-induced and rate-dependent examples in the climate system. Phil. Trans. Royal Soc. A 370, 1166–1184 (2012).

    Article  ADS  Google Scholar 

  19. Ripple, W. J. et al. World Scientists’ warning of a climate emergency 2021. BioScience 71, 894–898 (2021).

    Article  Google Scholar 

  20. Ruelle, D. General linear response formula in statistical mechanics, and the fluctuation-dissipation theorem far from equilibrium. Phys. Lett. A 245, 220–224 (1998).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  21. Ruelle, D. A review of linear response theory for general differentiable dynamical systems. Nonlinearity 22, 855–870 (2009).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  22. Hairer, M. & Majda, A. J. A simple framework to justify linear response theory. Nonlinearity 23, 909–922 (2010).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  23. Baiesi, M. & Maes, C. An update on the nonequilibrium linear response. New J. Phys. 15, 013004 (2013).

    Article  ADS  MATH  Google Scholar 

  24. Sarracino, A. & Vulpiani, A. On the fluctuation-dissipation relation in non-equilibrium and non-Hamiltonian systems. Chaos 29, 083132 (2019).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  25. Gottwald, G. A. Introduction to focus issue: linear response theory: potentials and limits. Chaos Interdiscip. J. Nonlinear Sci. 30, 20401 (2020).

    Article  Google Scholar 

  26. Santos Gutiérrez, M. & Lucarini, V. On some aspects of the response to stochastic and deterministic forcings. J. Phys. A 55, 425002 (2022).

    Article  MathSciNet  MATH  Google Scholar 

  27. Ragone, F., Lucarini, V. & Lunkeit, F. A new framework for climate sensitivity and prediction: a modelling perspective. Clim. Dyn. 46, 1459–1471 (2016).

    Article  Google Scholar 

  28. Lucarini, V., Ragone, F. & Lunkeit, F. Predicting climate change using response theory: global averages and spatial patterns. J. Stat. Phys. 166, 1036–1064 (2017).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  29. Aengenheyster, M., Feng, Q. Y., van der Ploeg, F. & Dijkstra, H. A. The point of no return for climate action: effects of climate uncertainty and risk tolerance. Earth Syst. Dyn. 9, 1085–1095 (2018).

    Article  ADS  Google Scholar 

  30. Lembo, V., Lucarini, V. & Ragone, F. Beyond forcing scenarios: predicting climate change through response operators in a coupled general circulation model. Sci. Rep. 10, 8668 (2020).

    Article  ADS  Google Scholar 

  31. Imkeller, P. & von Storch, J. S. Stochastic Climate Models (Birkhauser, 2001).

  32. von Storch, H. From Decoding Turbulence to Unveiling the Fingerprint of Climate Change (Springer, 2022).

  33. Gupta, S., Mastrantonas, N., Masoller, C. & Kurths, J. Perspectives on the importance of complex systems in understanding our climate and climate change — the Nobel Prize in Physics 2021. Chaos Interdiscip. J. Nonlinear Sci. https://doi.org/10.1063/5.0090222 (2022).

  34. Hegerl, G. C. Climate change is physics. Commun. Earth Environ. 3, 14 (2022).

    Article  ADS  Google Scholar 

  35. Hasselmann, K. Stochastic climate models Part I. Theory. Tellus 28, 473–485 (1976).

    ADS  Google Scholar 

  36. Arnold, L. in Stochastic Climate Models (eds Imkeller, P. & von Storch, J.-S.) 141–157 (Birkhäuser, 2001).

  37. Kelly, D. & Melbourne, I. Deterministic homogenization for fast–slow systems with chaotic noise. J. Funct. Anal. 272, 4063–4102 (2017).

    Article  MathSciNet  MATH  Google Scholar 

  38. Cotter, C. J., Gottwald, G. A. & Holm, D. D. Stochastic partial differential fluid equations as a diffusive limit of deterministic Lagrangian multi-time dynamics. Proc. R. Soc. A 473, 20170388 (2017).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  39. Just, W., Kantz, H., Rödenbeck, C. & Helm, M. Stochastic modelling: replacing fast degrees of freedom by noise. J. Phys. A 34, 3199–3213 (2001).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  40. Ghil, M. & Childress, S. Topics in Geophysical Fluid Dynamics: Atmospheric Dynamics, Dynamo Theory, and Climate Dynamics (Springer, 1987).

  41. Lorenz, E. The Nature and Theory of the General Circulation of the Atmosphere (World Meteorological Organization, 1967).

  42. Beck, C. Brownian motion from deterministic dynamics. Phys. A 169, 324–336 (1990).

    Article  MathSciNet  Google Scholar 

  43. Majda, A. J., Timofeyev, I. & Vanden-Eijnden, E. A mathematical framework for stochastic climate models. Comm. Pure Appl. Math 54, 891–974 (2001).

    Article  MathSciNet  MATH  Google Scholar 

  44. Pavliotis, G. A. & Stuart, A. M. Multiscale Methods (Springer, 2008).

  45. Gottwald, G. A. & Melbourne, I. Homogenization for deterministic maps and multiplicative noise. Proc. R. Soc. A 469, 20130201 (2013).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  46. Khasminsky, R. Principle of averaging for parabolic and elliptic differential equations and for Markov processes with small diffusion. Theor. Probab. Appl. 8, 1–21 (1963).

    Article  Google Scholar 

  47. Kurtz, T. A limit theorem for perturbed operator semigroups with applications to random evolutions. J. Funct. Anal. 12, 55–67 (1973).

    Article  MathSciNet  MATH  Google Scholar 

  48. Papanicolaou, G. C. & Kohler, W. Asymptotic theory of mixing stochastic ordinary differential equations. Commun. Pure Appl. Math. 27, 641–668 (1974).

    Article  MathSciNet  MATH  Google Scholar 

  49. Majda, A. J., Timofeyev, I. & Vanden-Eijnden, E. Systematic strategies for stochastic mode reduction in climate. J. Atmos. Sci. 60, 1705–1722 (2003).

    Article  ADS  MathSciNet  Google Scholar 

  50. Palmer, T. N. & Williams, P. (eds) Stochastic Physics and Climate Modelling (Cambridge Univ. Press, 2009).

  51. Berner, J. et al. Stochastic parameterization: toward a new view of weather and climate models. Bull. Am. Meteorol. Soc. 98, 565–588 (2017).

    Article  ADS  Google Scholar 

  52. Chekroun, M., Dijkstra, H., Şengül, T. & Wang, S. Transitions of zonal flows in a two-layer quasi-geostrophic ocean model. Nonlinear Dynamics 109, 1887–1904 (2022).

    Article  MATH  Google Scholar 

  53. Dijkstra, H. Nonlinear Physical Oceanography: A Dynamical Systems Approach to the Large-scale Ocean Circulation and El Niño (Springer, 2005).

  54. Dijkstra, H. A. & Ghil, M. Low-frequency variability of the large-scale ocean circulation: a dynamical systems approach. Reviews of Geophysics 43, RG3002 (2005).

    Article  ADS  Google Scholar 

  55. Chekroun, M. D., Liu, H. & Wang, S. Approximation of Stochastic Invariant Manifolds: Stochastic Manifolds for Nonlinear SPDEs I (Springer Briefs in Mathematics, 2015).

  56. Chekroun, M. D., Liu, H. & Wang, S. Stochastic Parameterizing Manifolds and Non-Markovian Reduced Equations: Stochastic Manifolds for Nonlinear SPDEs II (Springer Briefs in Mathematics, 2015).

  57. Chekroun, M., Liu, H., McWilliams, J. & Wang, S. Transitions in stochastic non-equilibrium systems: efficient reduction and analysis. J. Differ. Equ. 346, 145–204 (2023).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  58. Wouters, J. & Gottwald, G. A. Edgeworth expansions for slow–fast systems with finite time-scale separation. Proc. R. Soc. A 475, 20180358 (2019).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  59. Wouters, J. & Gottwald, G. A. Stochastic model reduction for slow–fast systems with moderate time scale separation. Multiscale Model. Simul. 17, 1172–1188 (2019).

    Article  MathSciNet  MATH  Google Scholar 

  60. Pavliotis, G. A. Stochastic Processes and Applications (Springer, 2014).

  61. Maher, N., Milinski, S. & Ludwig, R. Large ensemble climate model simulations: introduction, overview, and future prospects for utilising multiple types of large ensemble. Earth Syst. Dyn. 12, 401–418 (2021).

    Article  ADS  Google Scholar 

  62. Chekroun, M., Tantet, A., Dijkstra, H. & Neelin, J. D. Ruelle–Pollicott resonances of stochastic systems in reduced state space. Part I: Theory. J. Stat. Phys. 179, 1366–1402 (2020).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  63. Eckmann, J.-P. & Ruelle, D. Ergodic theory of chaos and strange attractors. Rev. Mod. Phys. 57, 617–656 (1985).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  64. Bojinski, S. et al. The concept of essential climate variables in support of climate research, applications, and policy. Bull. Am. Meteorol. Soc. 95, 1431–1443 (2014).

    Article  Google Scholar 

  65. Eyring, V. et al. Earth System Model Evaluation Tool (ESMValTool) v2.0 — an extended set of large-scale diagnostics for quasi-operational and comprehensive evaluation of Earth system models in CMIP. Geosci. Model Dev. 13, 3383–3438 (2020).

    Article  ADS  Google Scholar 

  66. Maier-Reimer, E. & Hasselmann, K. Transport and storage of CO2 in the ocean — an inorganic ocean-circulation carbon cycle model. Clim. Dyn. 2, 63–90 (1987).

    Article  Google Scholar 

  67. Hasselmann, K., Sausen, R., Maier-Reimer, E. & Voss, R. On the cold start problem in transient simulations with coupled atmosphere–ocean models. Clim. Dyn. 9, 53–61 (1993).

    Article  Google Scholar 

  68. Kubo, R. The fluctuation-dissipation theorem. Rep. Prog. Phys. 29, 255–284 (1966).

    Article  ADS  MATH  Google Scholar 

  69. Leith, C. Climate response and fluctuation dissipation. J. Atmos. Sci. 32, 2022–2026 (1975).

    Article  ADS  Google Scholar 

  70. Tél, T. et al. The theory of parallel climate realizations. J. Stat. Phys. 179, 1496–1530 (2020).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  71. Hannart, A., Ribes, A. & Naveau, P. Optimal fingerprinting under multiple sources of uncertainty. Geophys. Res. Lett. 41, 1261–1268 (2014).

    Article  ADS  Google Scholar 

  72. Allen, M. & Tett, S. Checking for model consistency in optimal fingerprinting. Clim. Dyn. 15, 419–434 (1999).

    Article  Google Scholar 

  73. Allen, M. & Tett, S. Estimating signal amplitudes in optimal fingerprinting, part I: theory. Clim. Dyn. 21, 477–491 (2003).

    Article  Google Scholar 

  74. Hegerl, G. & Zwiers, F. Use of models in detection and attribution of climate change. Wiley Interdiscip. Rev. Clim. Change 2, 570–591 (2011).

    Article  Google Scholar 

  75. Li, Y., Chen, K., Yan, J. & Zhang, X. Uncertainty in optimal fingerprinting is underestimated. Environ. Res. Lett. 16, 084043 (2021).

    Article  ADS  Google Scholar 

  76. McKitrick, R. Checking for model consistency in optimal fingerprinting: a comment. Clim. Dyn. 58, 405–411 (2022).

    Article  Google Scholar 

  77. Chen, H., Chen, S. X. & Mu, M. A review on the optimal fingerprinting approach in climate change studies. Preprint at https://arxiv.org/abs/2205.10508 (2022).

  78. Mori, H. Transport, collective motion, and Brownian motion. Prog. Theor. Phys. 33, 423–455 (1965).

    Article  ADS  MATH  Google Scholar 

  79. Zwanzig, R. Memory effects in irreversible thermodynamics. Phys. Rev. 124, 983–992 (1961).

    Article  ADS  MATH  Google Scholar 

  80. Chorin, A. J., Hald, O. H. & Kupferman, R. Optimal prediction with memory. Phys. D 166, 239–257 (2002).

    Article  MathSciNet  MATH  Google Scholar 

  81. Givon, D., Kupferman, R. & Stuart, A. Extracting macroscopic dynamics: model problems and algorithms. Nonlinearity 17, R55–R127 (2004).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  82. Lorenz, E. N. Attractor sets and quasi-geostrophic equilibrium. J. Atmos. Sci. 37, 1685–1699 (1980).

    Article  ADS  Google Scholar 

  83. Chekroun, M. D. & Glatt-Holtz, N. E. Invariant measures for dissipative dynamical systems: abstract results and applications. Commun. Math. Phys. 316, 723–761 (2012).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  84. Budišić, M., Mohr, R. & Mezić, I. Applied Koopmanism. Chaos 22, 047510 (2012).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  85. Ambrosio, L., Gigli, N. & Savaré, G. Gradient Flows in Metric Spaces and in the Space of Probability Measures (Springer, 2008).

  86. Chorin, A. & Hald, O. Stochastic Tools in Mathematics and Science (Springer, 2006).

  87. Vissio, G. & Lucarini, V. Evaluating a stochastic parametrization for a fast–slow system using the Wasserstein distance. Nonlinear Process. Geophys. 25, 413–427 (2018).

    Article  ADS  Google Scholar 

  88. Stinis, P. Higher order Mori–Zwanzig models for the Euler equations. Multiscale Model. Simul. 6, 741–760 (2007).

    Article  MathSciNet  MATH  Google Scholar 

  89. Li, Z., Bian, X., Li, X. & Karniadakis, G. Incorporation of memory effects in coarse-grained modeling via the Mori–Zwanzig formalism. J. Chem. Phys. 143, 243128 (2015).

    Article  ADS  Google Scholar 

  90. Lei, H., Baker, N. & Li, X. Data-driven parameterization of the generalized Langevin equation. Proc. Natl Acad. Sci. USA 113, 14183–14188 (2016).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  91. Li, Z., Lee, H., Darve, E. & Karniadakis, G. Computing the non-Markovian coarse-grained interactions derived from the Mori–Zwanzig formalism in molecular systems: application to polymer melts. J. Chem. Phys. 146, 014104 (2017).

    Article  ADS  Google Scholar 

  92. Brennan, C. & Venturi, D. Data-driven closures for stochastic dynamical systems. J. Comput. Phys. 372, 281–298 (2018).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  93. Chorin, A. J. & Lu, F. Discrete approach to stochastic parametrization and dimension reduction in nonlinear dynamics. Proc. Natl Acad. Sci. USA 112, 9804–9809 (2015).

    Article  ADS  Google Scholar 

  94. Lu, F., Lin, K. K. & Chorin, A. J. Data-based stochastic model reduction for the Kuramoto–Sivashinsky equation. Phys. D 340, 46–57 (2017).

    Article  MathSciNet  MATH  Google Scholar 

  95. Lin, K. K. & Lu, F. Data-driven model reduction, Wiener projections, and the Koopman–Mori–Zwanzig formalism. J. Comput. Phys. 424, 109864 (2021).

    Article  MathSciNet  MATH  Google Scholar 

  96. Majda, A. J. & Harlim, J. Physics constrained nonlinear regression models for time series. Nonlinearity 26, 201–217 (2013).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  97. Kondrashov, D., Chekroun, M. D. & Ghil, M. Data-driven non-Markovian closure models. Phys. D 297, 33–55 (2015).

    Article  MathSciNet  MATH  Google Scholar 

  98. Harlim, J., Jiang, S., Liang, S. & Yang, H. Machine learning for prediction with missing dynamics. J. Comput. Phys. 428, 109922 (2021).

    Article  MathSciNet  MATH  Google Scholar 

  99. Qi, D. & Harlim, J. A data-driven statistical-stochastic surrogate modeling strategy for complex nonlinear non-stationary dynamics. J. Comput. Phys. 485, 112085 (2023).

    Article  MathSciNet  MATH  Google Scholar 

  100. Gilani, F., Giannakis, D. & Harlim, J. Kernel-based prediction of non-Markovian time series. Phys. D 418, 132829 (2021).

    Article  MathSciNet  MATH  Google Scholar 

  101. Mori, H. A continued-fraction representation of the time-correlation functions. Prog. Theor. Phys. 34, 399–416 (1965).

    Article  ADS  MathSciNet  Google Scholar 

  102. Lee, M. Solutions of the generalized Langevin equation by a method of recurrence relations. Phys. Rev. B 26, 2547 (1982).

    Article  ADS  MathSciNet  Google Scholar 

  103. Florencio Jr, J. & Lee, M. H. Exact time evolution of a classical harmonic-oscillator chain. Phys. Rev. A 31, 3231 (1985).

    Article  ADS  MathSciNet  Google Scholar 

  104. Kupferman, R. Fractional kinetics in Kac–Zwanzig heat bath models. J. Stat. Phys. 114, 291–326 (2004).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  105. Chorin, A. & Stinis, P. Problem reduction, renormalization, and memory. Commun. Appl. Math. Comp. Sci. 1, 1–27 (2007).

    MathSciNet  MATH  Google Scholar 

  106. Stinis, P. A comparative study of two stochastic mode reduction methods. Phys. D 213, 197–213 (2006).

    Article  MathSciNet  MATH  Google Scholar 

  107. Götze, W. Recent tests of the mode-coupling theory for glassy dynamics. J. Phys. Condens. Matter 11, A1 (1999).

    Article  ADS  Google Scholar 

  108. Reichman, D. & Charbonneau, P. Mode-coupling theory. J. Stat. Mech. Theory Exp. 2005, P05013 (2005).

    Article  Google Scholar 

  109. Darve, E., Solomon, J. & Kia, A. Computing generalized Langevin equations and generalized Fokker–Planck equations. Proc. Natl Acad. Sci. USA 106, 10884–10889 (2009).

    Article  ADS  Google Scholar 

  110. Chen, M., Li, X. & Liu, C. Computation of the memory functions in the generalized Langevin models for collective dynamics of macromolecules. J. Chem. Phys. 141, 064112 (2014).

    Article  ADS  Google Scholar 

  111. Stinis, P. Renormalized Mori–Zwanzig-reduced models for systems without scale separation. Proc. R. Soc. A 471, 20140446 (2015).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  112. Parish, E. & Duraisamy, K. Non-Markovian closure models for large eddy simulations using the Mori–Zwanzig formalism. Phys. Rev. Fluids 2, 014604 (2017).

    Article  ADS  Google Scholar 

  113. Parish, E. J. & Duraisamy, K. A dynamic subgrid scale model for large eddy simulations based on the Mori–Zwanzig formalism. J. Comput. Phys. 349, 154–175 (2017).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  114. Zhu, Y., Dominy, J. & Venturi, D. On the estimation of the Mori–Zwanzig memory integral. J. Math. Phys. 59, 103501 (2018).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  115. Zhu, Y. & Venturi, D. Faber approximation of the Mori–Zwanzig equation. J. Comput. Phys. 372, 694–718 (2018).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  116. Venturi, D. & Karniadakis, G. Convolutionless Nakajima–Zwanzig equations for stochastic analysis in nonlinear dynamical systems. Proc. R. Soc. A 470, 20130754 (2014).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  117. Wouters, J. & Lucarini, V. Disentangling multi-level systems: averaging, correlations and memory. J. Stat. Mech. 2012, P03003 (2012).

    Article  Google Scholar 

  118. Wouters, J. & Lucarini, V. Multi-level dynamical systems: connecting the Ruelle response theory and the Mori–Zwanzig approach. J. Stat. Phys. 151, 850–860 (2013).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  119. Yoshimoto, Y. et al. Bottom-up construction of interaction models of non-Markovian dissipative particle dynamics. Phys. Rev. E 88, 043305 (2013).

    Article  ADS  Google Scholar 

  120. Hijón, C., Español, P., Vanden-Eijnden, E. & Delgado-Buscalioni, R. Mori–Zwanzig formalism as a practical computational tool. Faraday Discuss. 144, 301–322 (2010).

    Article  ADS  Google Scholar 

  121. Demaeyer, J. & Vannitsem, S. Comparison of stochastic parameterizations in the framework of a coupled ocean–atmosphere model. Nonlinear Process. Geophys. 25, 605–631 (2018).

    Article  ADS  Google Scholar 

  122. Vissio, G. & Lucarini, V. A proof of concept for scale-adaptive parametrizations: the case of the Lorenz ’96 model. Q. J. R. Meteorol. Soc. 144, 63–75 (2018).

    Article  ADS  Google Scholar 

  123. Hald, O. H. & Stinis, P. Optimal prediction and the rate of decay for solutions of the Euler equations in two and three dimensions. Proc. Natl Acad. Sci. USA 104, 6527–6532 (2007).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  124. Chekroun, M. D., Di Plinio, F., Glatt-Holtz, N. E. & Pata, V. Asymptotics of the Coleman–Gurtin model. Discrete Contin. Dyn. Syst. Ser. S 4, 351–369 (2011).

    MathSciNet  MATH  Google Scholar 

  125. Kravtsov, S., Kondrashov, D. & Ghil, M. Multilevel regression modeling of nonlinear processes: derivation and applications to climatic variability. J. Clim. 18, 4404–4424 (2005).

    Article  ADS  Google Scholar 

  126. Chekroun, M. D., Liu, H. & McWilliams, J. C. Variational approach to closure of nonlinear dynamical systems: autonomous case. J. Stat. Phys. 179, 1073–1160 (2020).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  127. Ma, C., Wang, J. & E, W. Model reduction with memory and the machine learning of dynamical systems. Commun. Comput. Phys. 25, 947–962 (2019).

    Article  MathSciNet  MATH  Google Scholar 

  128. Arnold, V. I. Geometrical Methods in the Theory of Ordinary Differential Equations 2nd edn (Springer, 1988).

  129. Chekroun, M. D., Liu, H. & McWilliams, J. C. Optimal parameterizing manifolds for anticipating tipping points and higher-order critical transitions. Preprint at https://arxiv.org/abs/2307.06537 (2023).

  130. Debussche, A. & Temam, R. Inertial manifolds and the slow manifolds in meteorology. Differ. Integral Equ. 4, 897–931 (1991).

    MathSciNet  MATH  Google Scholar 

  131. Temam, R. & Wirosoetisno, D. Slow manifolds and invariant sets of the primitive equations. J. Atmos. Sci. 68, 675–682 (2011).

    Article  ADS  Google Scholar 

  132. Zelik, S. Inertial manifolds and finite-dimensional reduction for dissipative PDEs. Proc. R. Soc. Edinb. A 144, 1245–1327 (2014).

    Article  MathSciNet  MATH  Google Scholar 

  133. Kraichnan, R. H. Eddy viscosity in two and three dimensions. J. Atmos. Sci. 33, 1521–1536 (1976).

    Article  ADS  Google Scholar 

  134. Leith, C. E. Stochastic backscatter in a subgrid-scale model: plane shear mixing layer. Phys. Fluids A 2, 297–299 (1990).

    Article  ADS  Google Scholar 

  135. Debussche, A., Dubois, T. & Temam, R. The nonlinear Galerkin method: a multiscale method applied to the simulation of homogeneous turbulent flows. Theor. Comput. Fluid Dyn. 7, 279–315 (1995).

    Article  MATH  Google Scholar 

  136. Dubois, T., Jauberteau, F. & Temam, R. Incremental unknowns, multilevel methods and the numerical simulation of turbulence. Comput. Methods Appl. Mech. Eng. 159, 123–189 (1998).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  137. Dubois, T. & Jauberteau, F. A dynamic multilevel model for the simulation of the small structures in homogeneous isotropic turbulence. J. Sci. Comput. 13, 323–367 (1998).

    Article  MathSciNet  MATH  Google Scholar 

  138. Fu, X., Chang, L.-B. & Xiu, D. Learning reduced systems via deep neural networks with memory. J. Machine Learn. Model. Comput. 1, 97–118 (2020).

    Article  Google Scholar 

  139. Wang, Q., Ripamonti, N. & Hesthaven, J. S. Recurrent neural network closure of parametric POD-Galerkin reduced-order models based on the Mori–Zwanzig formalism. J. Comput. Phys. 410, 109402 (2020).

    Article  MathSciNet  MATH  Google Scholar 

  140. Gupta, A. & Lermusiaux, P. F. J. Neural closure models for dynamical systems. Proc. R. Soc. A 477, 20201004 (2021).

    Article  ADS  MathSciNet  Google Scholar 

  141. Kraichnan, R. H. Eddy viscosity and diffusivity: exact formulas and approximations. Complex Syst. 1, 805–820 (1987).

    MathSciNet  MATH  Google Scholar 

  142. Rose, H. A. Eddy diffusivity, eddy noise and subgrid-scale modelling. J. Fluid Mech. 81, 719–734 (1977).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  143. Kondrashov, D., Kravtsov, S., Robertson, A. W. & Ghil, M. A hierarchy of data-based ENSO models. J. Clim. 18, 4425–4444 (2005).

    Article  ADS  Google Scholar 

  144. Chekroun, M. D., Kondrashov, D. & Ghil, M. Predicting stochastic systems by noise sampling, and application to the El Niño–Southern Oscillation. Proc. Natl Acad. Sci. USA 108, 11766–11771 (2011).

    Article  ADS  Google Scholar 

  145. Chen, C. et al. Diversity, nonlinearity, seasonality, and memory effect in ENSO simulation and prediction using empirical model reduction. J. Clim. 29, 1809–1830 (2016).

    Article  ADS  Google Scholar 

  146. Kondrashov, D., Kravtsov, S. & Ghil, M. Empirical mode reduction in a model of extratropical low-frequency variability. J. Atmos. Sci. 63, 1859–1877 (2006).

    Article  ADS  Google Scholar 

  147. Boers, N. et al. Inverse stochastic-dynamic models for high-resolution Greenland ice-core records. Earth Syst. Dyn. 8, 1171–1190 (2017).

    Article  ADS  Google Scholar 

  148. Kondrashov, D., Chekroun, M. D., Robertson, A. W. & Ghil, M. Low-order stochastic model and ‘past-noise forecasting’ of the Madden–Julian oscillation. Geophys. Res. Lett. 40, 5305–5310 (2013).

    Article  ADS  Google Scholar 

  149. Chen, N., Majda, A. J. & Giannakis, D. Predicting the cloud patterns of the Madden–Julian oscillation through a low-order nonlinear stochastic model. Geophys. Res. Lett. 41, 5612–5619 (2014).

    Article  ADS  Google Scholar 

  150. Chen, N. & Majda, A. J. Predicting the real-time multivariate Madden–Julian oscillation index through a low-order nonlinear stochastic model. Mon. Weather Rev. 143, 2148–2169 (2015).

    Article  ADS  Google Scholar 

  151. Santos Gutiérrez, M., Lucarini, V., Chekroun, M. D. & Ghil, M. Reduced-order models for coupled dynamical systems: data-driven methods and the Koopman operator. Chaos 31, 053116 (2021).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  152. Rowley, C. W., Mezić, I., Bagheri, S., Schlatter, P. & Henningson, D. S. Spectral analysis of nonlinear flows. J. Fluid Mech. 641, 115–127 (2009).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  153. Schmid, P. J. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28 (2010).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  154. Kutz, J., Brunton, S., Brunton, B. & Proctor, J. Dynamic Mode Decomposition: Data-Driven Modeling of Complex Systems (Society for Industrial and Applied Mathematics, 2016).

  155. Hasselmann, K. PIPs and POPs: the reduction of complex dynamical systems using principal interaction and oscillation patterns. J. Geophys. Res. 93, 11015–11021 (1988).

    Article  ADS  Google Scholar 

  156. Tu, J. H., Rowley, C. W., Luchtenburg, D. M., Brunton, S. L. & Kutz, J. N. On dynamic mode decomposition: theory and applications. J. Comput. Dyn. 1, 391–421 (2014).

    Article  MathSciNet  MATH  Google Scholar 

  157. Chekroun, M. D., Liu, H. & McWilliams, J. C. The emergence of fast oscillations in a reduced primitive equation model and its implications for closure theories. Comput. Fluids 151, 3–22 (2017).

    Article  MathSciNet  MATH  Google Scholar 

  158. Leith, C. Nonlinear normal mode initialization and quasi-geostrophic theory. J. Atmos. Sci. 37, 958–968 (1980).

    Article  ADS  MathSciNet  Google Scholar 

  159. Bolin, B. Numerical forecasting with the barotropic model. Tellus 7, 27–49 (1955).

    Article  ADS  MathSciNet  Google Scholar 

  160. Baer, F. & Tribbia, J. J. On complete filtering of gravity modes through nonlinear initialization. Mon. Weather Rev. 105, 1536–1539 (1977).

    Article  ADS  Google Scholar 

  161. Machenhauer, B. On the dynamics of gravity oscillations in a shallow water model with applications to normal mode initialization. Beitr. Phys. Atmos 50, 253–271 (1977).

    MATH  Google Scholar 

  162. Daley, R. Normal mode initialization. Rev. Geophys. 19, 450–468 (1981).

    Article  ADS  MATH  Google Scholar 

  163. Lorenz, E. N. Deterministic nonperiodic flow. J. Atmos. Sci. 20, 130–141 (1963).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  164. Chekroun, M., Liu, H. & McWilliams, J. C. The emergence of fast oscillations in a reduced primitive equation model and its implications for closure theories. Comput. Fluids 151, 3–22 (2017).

    Article  MathSciNet  MATH  Google Scholar 

  165. Plougonven, R. & Snyder, C. Inertia–gravity waves spontaneously generated by jets and fronts. Part I: Different baroclinic life cycles. J. Atmos. Sci. 64, 2502–2520 (2007).

    Article  ADS  Google Scholar 

  166. Polichtchouk, I. & Scott, R. Spontaneous inertia-gravity wave emission from a nonlinear critical layer in the stratosphere. Q. J. R. Meteorol. Soc. 146, 1516–1528 (2020).

    Article  ADS  Google Scholar 

  167. Tulich, S., Randall, D. & Mapes, B. Vertical-mode and cloud decomposition of large-scale convectively coupled gravity waves in a two-dimensional cloud-resolving model. J. Atmos. Sci. 64, 1210–1229 (2007).

    Article  ADS  Google Scholar 

  168. Lane, T. P. Convectively generated gravity waves. In Encyclopedia of Atmospheric Sciences 2nd edition, 171–179 (Elsevier, 2015).

  169. Dror, T., Chekroun, M. D., Altaratz, O. & Koren, I. Deciphering organization of GOES-16 green cumulus through the empirical orthogonal function (EOF) lens. Atmos. Chem. Phys. 21, 12261–12272 (2021).

    Article  ADS  Google Scholar 

  170. Chekroun, M., Liu, H. & McWilliams, J. Stochastic rectification of fast oscillations on slow manifold closures. Proc. Natl Acad. Sci. USA 118, e2113650118 (2021).

    Article  MathSciNet  Google Scholar 

  171. McWilliams, J. & Gent, P. Intermediate models of planetary circulations in the atmosphere and ocean. J. Atmos. Sci. 37, 1657–1678 (1980).

    Article  ADS  MathSciNet  Google Scholar 

  172. Gent, P. R. & McWilliams, J. C. Intermediate model solutions to the Lorenz equations: strange attractors and other phenomena. J. Atmos. Sci. 39, 3–13 (1982).

    Article  ADS  MathSciNet  Google Scholar 

  173. Monin, A. Change of pressure in a barotropic atmosphere. Akad. Nauk. Izv. Ser. Geofiz. 4, 76–85 (1952).

    Google Scholar 

  174. Charney, J. The use of the primitive equations of motion in numerical prediction. Tellus 7, 22–26 (1955).

    Article  ADS  MathSciNet  Google Scholar 

  175. Lorenz, E. Energy and numerical weather prediction. Tellus 12, 364–373 (1960).

    Article  ADS  Google Scholar 

  176. Chekroun, M. D. & Kondrashov, D. Data-adaptive harmonic spectra and multilayer Stuart–Landau models. Chaos 27, 093110 (2017).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  177. Zhen, Y., Chapron, B., Mémin, E. & Peng, L. Eigenvalues of autocovariance matrix: a practical method to identify the Koopman eigenfrequencies. Phys. Rev. E 105, 034205 (2022).

    Article  ADS  MathSciNet  Google Scholar 

  178. Tantet, A., Chekroun, M., Dijkstra, H. & Neelin, J. D. Ruelle–Pollicott resonances of stochastic systems in reduced state space. Part II: stochastic Hopf bifurcation. J. Stat. Phys. 179, 1403–1448 (2020).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  179. Mémin, E. Fluid flow dynamics under location uncertainty. Geophys. Astrophys. Fluid Dyn. 108, 119–146 (2014).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  180. Holm, D. D. Variational principles for stochastic fluid dynamics. Proc. R. Soc. A 471, 20140963 (2015).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  181. Cotter, C., Crisan, D., Holm, D. D., Pan, W. & Shevchenko, I. Numerically modeling stochastic lie transport in fluid dynamics. Multiscale Model. Simul. 17, 192–232 (2019).

    Article  MathSciNet  MATH  Google Scholar 

  182. Resseguier, V., Mémin, E. & Chapron, B. Geophysical flows under location uncertainty, Part I: random transport and general models. Geophys. Astrophys. Fluid Dyn. 111, 149–176 (2017).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  183. Simonnet, E., Ghil, M., Ide, K., Temam, R. & Wang, S. Low-frequency variability in shallow-water models of the wind-driven ocean circulation. Part II: time-dependent solutions. J. Phys. Oceanogr. 33, 729–752 (2003).

    Article  ADS  MathSciNet  Google Scholar 

  184. Rocha, C. B., Chereskin, T. K., Gille, S. T. & Menemenlis, D. Mesoscale to submesoscale wavenumber spectra in Drake Passage. J. Phys. Oceanogr. 46, 601–620 (2016).

    Article  ADS  Google Scholar 

  185. Young, W. R. Inertia-gravity waves and geostrophic turbulence. J. Fluid Mech. 920, F1 (2021).

    Article  MathSciNet  MATH  Google Scholar 

  186. Bolton, T. & Zanna, L. Applications of deep learning to ocean data inference and subgrid parameterization. J. Adv. Model. Earth Syst. 11, 376–399 (2019).

    Article  ADS  Google Scholar 

  187. Maulik, R., San, O., Rasheed, A. & Vedula, P. Subgrid modelling for two-dimensional turbulence using neural networks. J. Fluid Mech. 858, 122–144 (2019).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  188. Kochkov, D. et al. Machine learning–accelerated computational fluid dynamics. Proc. Natl Acad. Sci. USA 118, e2101784118 (2021).

    Article  MathSciNet  Google Scholar 

  189. Zanna, L. & Bolton, T. Data-driven equation discovery of ocean mesoscale closures. Geophys. Res. Lett. 47, e2020GL088376 (2020).

    Article  ADS  Google Scholar 

  190. Subel, A., Guan, Y., Chattopadhyay, A. & Hassanzadeh, P. Explaining the physics of transfer learning a data-driven subgrid-scale closure to a different turbulent flow. Preprint at https://doi.org/10.48550/arXiv.2206.03198 (2022).

  191. Srinivasan, K., Chekroun, M. D. & McWilliams, J. C. Turbulence closure with small, local neural networks: Forced two-dimensional and β-plane flows. Preprint at https://doi.org/10.48550/arXiv.2304.05029 (2023).

  192. Goodfellow, I., Bengio, Y. & Courville, A. Deep Learning (MIT Press, 2016).

  193. Piomelli, U., Cabot, W. H., Moin, P. & Lee, S. Subgrid-scale backscatter in turbulent and transitional flows. Phys. Fluids A 3, 1766–1771 (1991).

    Article  ADS  MATH  Google Scholar 

  194. Jansen, M. F. & Held, I. M. Parameterizing subgrid-scale eddy effects using energetically consistent backscatter. Ocean Model. 80, 36–48 (2014).

    Article  ADS  Google Scholar 

  195. Miyanawala, T. P. & Jaiman, R. K. An efficient deep learning technique for the Navier–Stokes equations: application to unsteady wake flow dynamics. Preprint at https://arxiv.org/abs/1710.09099 (2017).

  196. Foias, C., Manley, O. & Temam, R. Modeling of the interaction of small and large eddies in two-dimensional turbulent flows. RAIRO Modél. Math. Anal. Numér. 22, 93–118 (1988).

    Article  MathSciNet  MATH  Google Scholar 

  197. Foias, C., Manley, O. P. & Temam, R. Approximate inertial manifolds and effective viscosity in turbulent flows. Phys. Fluids A 3, 898–911 (1991).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  198. Pascal, F. & Basdevant, C. Nonlinear Galerkin method and subgrid-scale model for two-dimensional turbulent flows. Theor. Comput. Fluid Dyn. 3, 267–284 (1992).

    Article  MATH  Google Scholar 

  199. Lorenz, E. N. Empirical Orthogonal Functions and Statistical Weather Prediction. Scientific Report no. 1, Statistical Forecasting Project (1956).

  200. Jolliffe, I. Principal Component Analysis (Wiley Online Library, 2002).

  201. Penland, C. Random forcing and forecasting using principal oscillation pattern analysis. Mon. Weath. Rev. 117, 2165–2185 (1989).

    Article  ADS  Google Scholar 

  202. Penland, C. & Magorian, T. Prediction of Niño-3 sea surface temperatures using iinear inverse modeling 6, 1067–1076 (1993).

  203. Penland, C. & Ghil, M. Forecasting Northern Hemisphere 700-mb geopotential height anomalies using empirical normal modes. Mon. Weather Rev. 121, 2355–2372 (1993).

    Article  ADS  Google Scholar 

  204. Penland, C. & Sardeshmukh, P. D. The optimal growth of tropical sea surface temperature anomalies. J. Clim. 8, 1999–2024 (1995).

    Article  ADS  Google Scholar 

  205. Franzke, C., Majda, A. J. & Vanden-Eijnden, E. Low-order stochastic mode reduction for a realistic barotropic model climate. J. Atmos. Sci. 62, 1722–1745 (2005).

    Article  ADS  MathSciNet  Google Scholar 

  206. Franzke, C. & Majda, A. J. Low-order stochastic mode reduction for a prototype atmospheric GCM. J. Atmos. Sci. 63, 457–479 (2006).

    Article  ADS  MathSciNet  Google Scholar 

  207. Schölkopf, B., Smola, A. & Müller, K.-R. Nonlinear component analysis as a kernel eigenvalue problem. Neural comput. 10, 1299–1319 (1998).

    Article  Google Scholar 

  208. Mukhin, D., Gavrilov, A., Feigin, A., Loskutov, E. & Kurths, J. Principal nonlinear dynamical modes of climate variability. Sci. Rep.5 (2015).

  209. Tipping, M. E. & Bishop, C. M. Probabilistic principal component analysis. J. R. Stat. Soc. B 61, 611–622 (1999).

    Article  MathSciNet  MATH  Google Scholar 

  210. Schmidt, O., Mengaldo, G., Balsamo, G. & Wedi, N. Spectral empirical orthogonal function analysis of weather and climate data. Mon. Weather Rev. 147, 2979–2995 (2019).

    Article  ADS  Google Scholar 

  211. Zerenner, T., Goodfellow, M. & Ashwin, P. Harmonic cross-correlation decomposition for multivariate time series. Phys. Rev. E 103, 062213 (2021).

    Article  ADS  MathSciNet  Google Scholar 

  212. Das, S. & Giannakis, D. Delay-coordinate maps and the spectra of Koopman operators. J. Stat. Phys. 175, 1107–1145 (2019).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  213. Froyland, G., Giannakis, D., Lintner, B. R., Pike, M. & Slawinska, J. Spectral analysis of climate dynamics with operator-theoretic approaches. Nat. Commun. 12, 6570 (2021).

    Article  ADS  Google Scholar 

  214. Belkin, M. & Niyogi, P. Laplacian eigenmaps for dimensionality reduction and data representation. Neural Comput. 15, 1373–1396 (2003).

    Article  MATH  Google Scholar 

  215. Coifman, R. & Lafon, S. Diffusion maps. Appl. Comput. Harmon. Anal. 21, 5–30 (2006).

    Article  MathSciNet  MATH  Google Scholar 

  216. Giannakis, D. & Majda, A. J. Nonlinear Laplacian spectral analysis: capturing intermittent and low-frequency spatiotemporal patterns in high-dimensional data. Stat. Anal. Data Min. ASA Data Sci. J. 6, 180–194 (2013).

    Article  MathSciNet  MATH  Google Scholar 

  217. Kingma, D. & Welling, M. Auto-encoding variational Bayes. Preprint at https://arxiv.org/abs/1312.6114 (2013).

  218. Berloff, P. Dynamically consistent parameterization of mesoscale eddies. Part I: Simple model. Ocean Model. 87, 1–19 (2015).

    Article  ADS  Google Scholar 

  219. Kondrashov, D., Chekroun, M. & Berloff, P. Multiscale Stuart–Landau emulators: application to wind-driven ocean gyres. Fluids 3, 21 (2018).

    Article  ADS  Google Scholar 

  220. Rahaman, N. et al. On the spectral bias of neural networks. In International Conference on Machine Learning, 5301–5310 (PMLR, 2019).

  221. Ghil, M. et al. Advanced spectral methods for climatic time series. Rev. Geophys. 40, 1003 (2002).

    Article  ADS  Google Scholar 

  222. Kondrashov, D., Chekroun, M. D., Yuan, X. & Ghil, M. in Advances in Nonlinear Geosciences (ed. Tsonis, A.) 179–205 (Springer, 2018).

  223. Kondrashov, D., Chekroun, M. D. & Ghil, M. Data-adaptive harmonic decomposition and prediction of Arctic sea ice extent. Dyn. Stat. Clim. Syst. https://doi.org/10.1093/climsys/dzy001 (2018).

  224. Landau, L. & Lifshitz, E. M. Fluid Mechanics: Landau and Lifshitz: Course of Theoretical Physics, Vol. 6 (Elsevier, 2013).

  225. Ruelle, D. & Takens, F. On the nature of turbulence. Commun. Math. Phys 20, 167–192 (1971).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  226. Chekroun, M. D., Simonnet, E. & Ghil, M. Stochastic climate dynamics: random attractors and time-dependent invariant measures. Phys. D 240, 1685–1700 (2011).

    Article  MathSciNet  MATH  Google Scholar 

  227. Carvalho, A. N., Langa, J. A. & Robinson, J. C. Attractors for Infinite-Dimensional Non-autonomous Dynamical Systems (Springer, 2013).

  228. Tél, T. et al. The theory of parallel climate realizations. J. Stat. Phys. https://doi.org/10.1007/s10955-019-02445-7 (2019).

  229. Pierini, S. Statistical significance of small ensembles of simulations and detection of the internal climate variability: an excitable ocean system case study. J. Stat. Phys. 179, 1475–1495 (2020).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  230. Lucarini, V. Response operators for Markov processes in a finite state space: radius of convergence and link to the response theory for axiom A systems. J. Stat. Phys. 162, 312–333 (2016).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  231. Santos Gutiérrez, M. & Lucarini, V. Response and sensitivity using Markov chains. J. Stat. Phys. 179, 1572–1593 (2020).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  232. Hassanzadeh, P. & Kuang, Z. The linear response function of an idealized atmosphere. Part I: Construction using Green’s functions and applications. J. Atmos. Sci. 73, 3423–3439 (2016).

    Article  Google Scholar 

  233. Abramov, R. V. & Majda, A. J. Blended response algorithms for linear fluctuation-dissipation for complex nonlinear dynamical systems. Nonlinearity 20, 2793 (2007).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  234. North, G. R., Bell, R. E. & Hardin, J. W. Fluctuation dissipation in a general circulation model. Clim. Dyn. 8, 259–264 (1993).

    Article  Google Scholar 

  235. Cionni, I., Visconti, G. & Sassi, F. Fluctuation dissipation theorem in a general circulation model. Geophys. Res. Lett.31 (2004).

  236. Langen, P. L. & Alexeev, V. A. Estimating 2 × CO2 warming in an aquaplanet GCM using the fluctuation-dissipation theorem. Geophys. Res. Lett. https://doi.org/10.1029/2005GL024136 (2005).

  237. Gritsun, A. & Branstator, G. Climate response using a three-dimensional operator based on the fluctuation–dissipation theorem. J. Atmos. Sci. 64, 2558–2575 (2007).

    Article  ADS  Google Scholar 

  238. Hassanzadeh, P. & Kuang, Z. The linear response function of an idealized atmosphere. Part II: Implications for the practical use of the fluctuation–dissipation theorem and the role of operator’s nonnormality. J. Atmos. Sci. 73, 3441–3452 (2016).

    Google Scholar 

  239. Gritsun, A. & Lucarini, V. Fluctuations, response, and resonances in a simple atmospheric model. Phys. D 349, 62–76 (2017).

    Article  MathSciNet  MATH  Google Scholar 

  240. Dijkstra, H. A. & Ghil, M. Low-frequency variability of the large-scale ocean circulation: a dynamical systems approach. Rev. Geophys. https://doi.org/10.1029/2002RG000122 (2005).

  241. Kuhlbrodt, T. et al. On the driving processes of the Atlantic Meridional Overturning Circulation. Rev. Geophys. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/2004RG000166 (2007).

  242. Lucarini, V. Revising and extending the linear response theory for statistical mechanical systems: evaluating observables as predictors and predictands. J. Stat. Phys. 173, 1698–1721 (2018).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  243. Tomasini, U. M. & Lucarini, V. Predictors and predictands of linear response in spatially extended systems. Eur. Phys. J.: Spec. Top. 230, 2813–2832 (2021).

    Google Scholar 

  244. Antown, F., Dragičević, D. & Froyland, G. Optimal linear responses for Markov chains and stochastically perturbed dynamical systems. J. Stat. Phys. 170, 1051–1087 (2018).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  245. Antown, F., Froyland, G. & Galatolo, S. Optimal linear response for Markov Hilbert–Schmidt integral operators and stochastic dynamical systems. J. Nonlinear Sci. 32, 79 (2022).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  246. Chekroun, M. D., Kröner, A. & Liu, H. Galerkin approximations of nonlinear optimal control problems in Hilbert spaces. Electron. J. Differ. Equ. 189, 1–40 (2017).

    MathSciNet  MATH  Google Scholar 

  247. Bódai, T., Lucarini, V. & Lunkeit, F. Can we use linear response theory to assess geoengineering strategies? Chaos: Interdiscip. J. Nonlinear Sci. 30, 023124 (2020).

    Article  MathSciNet  Google Scholar 

  248. Tantet, A., Lucarini, V. & Dijkstra, H. A. Resonances in a chaotic attractor crisis of the Lorenz flow. J. Stat. Phys. 170, 584–616 (2018).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  249. Engel, K.-J. & Nagel, R. One-Parameter Semigroups for Linear Evolution Equations (Springer, 2000).

  250. Williams, M., Kevrekidis, I. & Rowley, C. A data–driven approximation of the Koopman operator: extending dynamic mode decomposition. J. Nonlinear Sci. 25, 1307–1346 (2015).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  251. Navarra, A. A new set of orthonormal modes for linearized meteorological problems. J. Atmos. Sci. 50, 2569–2583 (1993).

    Article  ADS  Google Scholar 

  252. Palmer, T. N. A nonlinear dynamical perspective on climate prediction. J. Clim. 12, 575–591 (1999).

    Article  ADS  Google Scholar 

  253. Lu, J., Liu, F., Leung, L. R. & Lei, H. Neutral modes of surface temperature and the optimal ocean thermal forcing for global cooling. NPJ Clim. Atmos. Sci. 3, 9 (2020).

    Article  ADS  Google Scholar 

  254. Chekroun, M. D., Neelin, J. D., Kondrashov, D., McWilliams, J. C. & Ghil, M. Rough parameter dependence in climate models: the role of Ruelle-Pollicott resonances. Proc. Natl Acad. Sci. USA 111, 1684–1690 (2014).

    Article  ADS  Google Scholar 

  255. Held, H. & Kleinen, T. Detection of climate system bifurcations by degenerate fingerprinting. Geophys. Res. Lett. https://doi.org/10.1029/2004GL020972 (2004).

  256. Scheffer, M. et al. Anticipating critical transitions. Science 338, 344–348 (2012).

    Article  ADS  Google Scholar 

  257. Boettner, C. & Boers, N. Critical slowing down in dynamical systems driven by nonstationary correlated noise. Phys. Rev. Res. 4, 013230 (2022).

    Article  Google Scholar 

  258. Lucarini, V. Stochastic perturbations to dynamical systems: a response theory approach. J. Stat. Phys. 146, 774–786 (2012).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  259. Rahmstorf, S. Bifurcations of the Atlantic thermohaline circulation in response to changes in the hydrological cycle. Nature 378, 145–149 (1995).

    Article  ADS  Google Scholar 

  260. Boers, N. Observation-based early-warning signals for a collapse of the Atlantic Meridional Overturning Circulation. Nat. Clim. Change 11, 680–688 (2021).

    Article  ADS  Google Scholar 

  261. Tantet, A., Chekroun, M., Neelin, J. & Dijkstra, H. Ruelle–Pollicott resonances of stochastic systems in reduced state space. Part III: Application to the Cane–Zebiak model of the El Niño–Southern Oscillation. J. Stat. Phys. 179, 1449–1474 (2020).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  262. Lucarini, V., Kuna, T., Faranda, D. & Wouters, J. Towards a general theory of extremes for observables of chaotic dynamical systems. J. Stat. Phys. 154, 723–750 (2014).

  263. Naveau, P., Hannart, A. & Ribes, A. Statistical methods for extreme event attribution in climate science. Annu. Rev. Stat. Appl. 7, 89–110 (2020).

    Article  MathSciNet  Google Scholar 

  264. Wang, Z., Jiang, Y., Wan, H., Yan, J. & Zhang, X. Toward optimal fingerprinting in detection and attribution of changes in climate extremes. J. Am. Stat. Assoc. 116, 1–13 (2021).

    Article  MathSciNet  MATH  Google Scholar 

  265. Stein, U. & Alpert, P. Factor separation in numerical simulations. J. Atmos. Sci. 50, 2107–2115 (1993).

    Article  ADS  Google Scholar 

  266. Hossain, A. et al. The impact of different atmospheric CO2 concentrations on large scale Miocene temperature signatures. Paleoceanogr. Paleoclimatol. 38, e2022PA004438 (2023).

    Article  Google Scholar 

  267. Ruelle, D. Nonequilibrium statistical mechanics near equilibrium: computing higher-order terms. Nonlinearity 11, 5–18 (1998).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  268. Chekroun, M. D., Ghil, M. & Neelin, J. D. in Advances in Nonlinear Geosciences (ed. Tsonis, A.), 1–33 (Springer, 2018).

  269. Chekroun, M. D., Koren, I., Liu, H. & Liu, H. Generic generation of noise-driven chaos in stochastic time delay systems: bridging the gap with high-end simulations. Sci. Adv. 8, eabq7137 (2022).

    Article  ADS  Google Scholar 

  270. Benzi, R., Sutera, A. & Vulpiani, A. The mechanism of stochastic resonance. J. Phys. A 14, L453–L457 (1981).

    Article  ADS  MathSciNet  Google Scholar 

  271. Nicolis, C. Solar variability and stochastic effects on climate. Sol. Phys. 74, 473–478 (1981).

    Article  ADS  Google Scholar 

  272. Benzi, R., Parisi, G., Sutera, A. & Vulpiani, A. Stochastic resonance in climatic change. Tellus 34, 10–16 (1982).

    Article  ADS  MATH  Google Scholar 

  273. Nicolis, C. Stochastic aspects of climatic transitions — response to a periodic forcing. Tellus 34, 308–308 (1982).

    ADS  MathSciNet  Google Scholar 

  274. Gammaitoni, L., Hänggi, P., Jung, P. & Marchesoni, F. Stochastic resonance. Rev. Mod. Phys. 70, 223–287 (1998).

    Article  ADS  Google Scholar 

  275. Charney, J. G. & DeVore, J. G. Multiple flow equilibria in the atmosphere and blocking. J. Atmos. Sci. 36, 1205–1216 (1979).

    Article  ADS  Google Scholar 

  276. Benzi, R., Malguzzi, P., Speranza, A. & Sutera, A. The statistical properties of general atmospheric circulation: observational evidence and a minimal theory of bimodality. Q. J. R. Meteorol. Soc. 112, 661–674 (1986).

    Article  ADS  Google Scholar 

  277. Benzi, R. & Speranza, A. Statistical properties of low-frequency variability in the Northern Hemisphere. J. Clim. 2, 367–379 (1989).

    Article  ADS  Google Scholar 

  278. Kimoto, M. & Ghil, M. Multiple flow regimes in the Northern Hemisphere winter. Part I: Methodology and hemispheric regimes. J. Atmos. Sci. 50, 2625–2643 (1993a).

    Article  ADS  Google Scholar 

  279. Itoh, H. & Kimoto, M. Multiple attractors and chaotic itinerancy in a quasigeostrophic model with realistic topography: implications for weather regimes and low-frequency variability. J. Atmos. Sci. 53, 2217–2231 (1996).

    Article  ADS  MathSciNet  Google Scholar 

  280. Arnscheidt, C. W. & Rothman, D. H. The balance of nature: a global marine perspective. Ann. Rev. Mar. Sci. 14, 49–73 (2022).

    Article  Google Scholar 

  281. Freidlin, M. I. & Wentzell, A. D. Random Perturbations of Dynamical Systems (Springer, 1998).

  282. Touchette, H. The large deviation approach to statistical mechanics. Phys. Rep. 478, 1–69 (2009).

    Article  ADS  MathSciNet  Google Scholar 

  283. Bouchet, F. & Venaille, A. Statistical mechanics of two-dimensional and geophysical flows. Phys. Rep. 515, 227–295 (2012).

    Article  ADS  MathSciNet  Google Scholar 

  284. Herbert, C. An Introduction to Large Deviations and Equilibrium Statistical Mechanics for Turbulent Flows, 53–84 (Springer International Publishing, 2015).

  285. Lucarini, V. & Bódai, T. Transitions across melancholia states in a climate model: reconciling the deterministic and stochastic points of view. Phys. Rev. Lett. 122, 158701 (2019).

    Article  ADS  Google Scholar 

  286. Lucarini, V. & Bódai, T. Global stability properties of the climate: melancholia states, invariant measures, and phase transitions. Nonlinearity 33, R59–R92 (2020).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  287. Margazoglou, G., Grafke, T., Laio, A. & Lucarini, V. Dynamical landscape and multistability of a climate model. Proc. R. Soc. A 477, 20210019 (2021).

    Article  ADS  MathSciNet  Google Scholar 

  288. Rousseau, D.-D., Bagniewski, W. & Lucarini, V. A punctuated equilibrium analysis of the climate evolution of Cenozoic exhibits a hierarchy of abrupt transitions. Sci. Rep. 13, 11290 (2023).

    Article  ADS  Google Scholar 

  289. Ditlevsen, P. D. Observation of α-stable noise induced millennial climate changes from an ice-core record. Geophys. Res. Lett. 26, 1441–1444 (1999).

    Article  ADS  Google Scholar 

  290. Penland, C. & Ewald, B. D. On modelling physical systems with stochastic models: diffusion versus Lévy processes. Phil. Trans. Roy. Soc. A 366, 2455–2474 (2008).

    Article  ADS  MATH  Google Scholar 

  291. Gottwald, G. A. A model for Dansgaard–Oeschger events and millennial-scale abrupt climate change without external forcing. Clim. Dyn. 56, 227–243 (2021).

    Article  Google Scholar 

  292. Lucarini, V., Serdukova, L. & Margazoglou, G. Lévy noise versus Gaussian-noise-induced transitions in the Ghil–Sellers energy balance model. Nonlinear Process. Geophys. 29, 183–205 (2022).

    Article  ADS  Google Scholar 

  293. Berloff, P. Dynamically consistent parameterization of mesoscale eddies — Part II: Eddy fluxes and diffusivity from transient impulses. Fluids https://doi.org/10.3390/fluids1030022 (2016).

  294. Caesar, L., Rahmstorf, S., Robinson, A., Feulner, G. & Saba, V. Observed fingerprint of a weakening Atlantic Ocean overturning circulation. Nature 556, 191–196 (2018).

    Article  ADS  Google Scholar 

  295. Saltzman, B. Dynamical Paleoclimatology: Generalized Theory of Global Climate Change (Academic, 2001).

  296. Miyadera, I. On perturbation theory for semi-groups of operators. Tohoku Math. J. Second Ser. 18, 299–310 (1966).

    MathSciNet  MATH  Google Scholar 

  297. Voigt, J. On the perturbation theory for strongly continuous semigroups. Math. Ann. 229, 163–171 (1977).

    Article  MathSciNet  MATH  Google Scholar 

  298. Givon, D., Kupferman, R. & Hald, O. Existence proof for orthogonal dynamics and the Mori–Zwanzig formalism. Isr. J. Math. 145, 221–241 (2005).

    Article  MathSciNet  MATH  Google Scholar 

  299. McWilliams, J. C. A perspective on the legacy of Edward Lorenz. Earth Space Sci. 6, 336–350 (2019).

    Article  ADS  Google Scholar 

  300. Lorenz, E. On the existence of a slow manifold. J. Atmos. Sci. 43, 1547–1558 (1986).

    Article  ADS  MathSciNet  Google Scholar 

  301. Lorenz, E. N. & Krishnamurthy, V. On the nonexistence of a slow manifold. J. Atmos. Sci. 44, 2940–2950 (1987).

    Article  ADS  Google Scholar 

  302. Vanneste, J. Exponential smallness of inertia–gravity wave generation at small Rossby number. J. Atmos. Sci. 65, 1622–1637 (2008).

    Article  ADS  Google Scholar 

  303. Vanneste, J. Balance and spontaneous wave generation in geophysical flows. Ann. Rev. Fluid Mech. 45, 147–172 (2013).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  304. IPCC. Climate Change 2013: The Physical Science Basis (eds Stocker, T. et al.) (Cambridge Univ. Press, 2014).

  305. Otto, A. et al. Energy budget constraints on climate response. Nat. Geosci. 6, 415–416 (2013).

    Article  ADS  Google Scholar 

  306. Hilborn, R. C. Einstein coefficients, cross sections, f values, dipole moments, and all that. Am. J. Phys. 50, 982–986 (1982).

    Article  ADS  Google Scholar 

  307. Lucarini, V., Saarinen, J. J., Peiponen, K.-E. & Vartiainen, E. M. Kramers–Kronig Relations in Optical Materials Research (Springer, 2005).

Download references

Acknowledgements

V.L. acknowledges support received from the European Union (EU) Horizon 2020 research and innovation programme through the projects TiPES (grant agreement no. 820970) and CriticalEarth (grant agreement no. 956170) and by the EPSRC through grant EP/T018178/1. M.D.C. acknowledges the European Research Council under the EU Horizon 2020 research and innovation programme (grant no. 810370) and the Ben May Center grant for theoretical and/or computational research. This work has been also partially supported by the Office of Naval Research (ONR) Multidisciplinary University Research Initiative (MURI) grant N00014-20-1-2023. Finally, the authors thank many close collaborators over the years without whom this review would have not been possible: O. Altaratz, P. Ashwin, P. Berloff, R. Blender, T. Bódai, N. Boers, H. Dijkstra, T. Dror, B. Dubrulle, D. Faranda, K. Fraedrich, V. M. Gálfi, G. Gallavotti, N. Glatt-Holtz, G. Gottwald, A. Gritsun, A. von der Heydt, D. Kondrashov, I. Koren, S. Kravtsov, T. Kuna, J. Kurths, H. Liu, F. Lunkeit, D. Neelin, G. Pavliotis, C. Penland, F. Ragone, L. Roques, J. Roux, M. Santos Gutiérrez, S. Schubert, E. Simonnet, A. Speranza, K. Srinivisan, A. Tantet, T. Tél, S. Vannitsem, S. Wang, J. Wouters, N. Zagli, and I. Zaliapin, with special gratitude to A. Chorin, M. Ghil, J. C. McWilliams, D. Ruelle and R. Temam for their guidance and inspirational works.

Author information

Authors and Affiliations

  1. Department of Mathematics and Statistics, University of Reading, Reading, UK

    Valerio Lucarini

  2. Centre for the Mathematics of Planet Earth, University of Reading, Reading, UK

    Valerio Lucarini

  3. Department of Earth and Planetary Sciences, Weizmann Institute of Science, Rehovot, Israel

    Mickaël D. Chekroun

  4. Department of Atmospheric and Oceanic Sciences, University of California, Los Angeles, CA, USA

    Mickaël D. Chekroun

Authors
  1. Valerio Lucarini
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mickaël D. Chekroun
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Both authors contributed to all aspects of this work.

Corresponding authors

Correspondence to Valerio Lucarini or Mickaël D. Chekroun.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Reviews Physics thanks the anonymous referees for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lucarini, V., Chekroun, M.D. Theoretical tools for understanding the climate crisis from Hasselmann’s programme and beyond. Nat Rev Phys 5, 744–765 (2023). https://doi.org/10.1038/s42254-023-00650-8

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s42254-023-00650-8

Search

Advanced search

Quick links

Nature Briefing Anthropocene

Sign up for the Nature Briefing: Anthropocene newsletter — what matters in anthropocene research, free to your inbox weekly.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing: Anthropocene