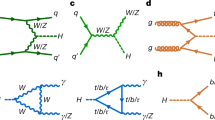
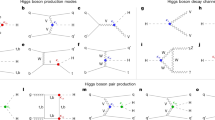
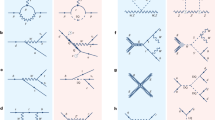
Abstract
The Higgs boson, a fundamental scalar boson with mass 125 GeV, was discovered at the Large Hadron Collider (LHC) at CERN in 2012. So far, experiments at the LHC have focused on testing the Higgs boson’s couplings to other elementary particles, precision measurements of the Higgs boson’s properties and an initial investigation of the Higgs boson’s self-interaction and shape of the Higgs potential. The Higgs boson mass of 125 GeV is a remarkable value, meaning that the underlying state of the Universe, the vacuum, sits very close to the border between stable and metastable, which may hint at deeper physics beyond the standard model. The Higgs potential also influences ideas about the cosmological constant, the dark energy that drives the accelerating expansion of the Universe, the mysterious dark matter that comprises about 80% of the matter component in the Universe and a possible phase transition in the early Universe that might be responsible for baryogenesis. A detailed study of the Higgs boson is at the centre of the European Strategy for Particle Physics update. Here we review the current understanding of the Higgs boson and discuss the insights expected from present and future experiments.
Key points
-
The discovery of the Higgs boson was a major milestone in particle physics, confirming the standard model.
-
Direct tests of the couplings of the Higgs boson to fermions confirmed the mechanism that gives mass to the W and Z bosons, thus making the electroweak interaction short range. A recent highlight is the direct observation of the Higgs boson coupling to muons.
-
The observed properties of the Higgs boson put the standard model vacuum intriguingly close to the border between stable and metastable. Further connections to the open questions pertaining to baryogenesis, the nature of dark matter and dark energy and cosmic inflation mean that the Higgs boson is central to our understanding of the Universe.
-
Precision measurements of the Higgs boson to further probe its interactions and possible deeper origin and structure are an essential part of the High-Luminosity Large Hadron Collider programme and were recently identified by the European Strategy for Particle Physics to be the highest priority for the next high-energy collider facility.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$99.00 per year
only $8.25 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout








Similar content being viewed by others
References
Aad, G. et al. Observation of a new particle in the search for the standard model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 716, 1–29 (2012).
Chatrchyan, S. et al. Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. Phys. Lett. B 716, 30–61 (2012).
Englert, F. Nobel lecture: the BEH mechanism and its scalar boson. Rev. Mod. Phys. 86, 843 (2014).
Higgs, P. W. Nobel lecture: evading the Goldstone theorem. Rev. Mod. Phys. 86, 851 (2014).
Altarelli, G. Collider physics within the standard model: a primer. Preprint at https://arxiv.org/abs/1303.2842 (2013).
Pokorski, S. Gauge Field Theories 2nd edn (Cambridge Univ. Press, 2000).
Aitchison, I. & Hey, A. Gauge Theories In Particle Physics: A Practical Introduction Vol. 2 Non-Abelian Gauge Theories: QCD and the Electroweak Theory (CRC Press, 2012).
Altarelli, G. The Higgs: so simple yet so unnatural. Phys. Scr. T 158, 014011 (2013).
Hanneke, D., Fogwell, S. & Gabrielse, G. New measurement of the electron magnetic moment and the fine structure constant. Phys. Rev. Lett. 100, 120801 (2008).
Parker, R. H., Yu, C., Zhong, W., Estey, B. & Müller, H. Measurement of the fine-structure constant as a test of the standard model. Science 360, 191–195 (2018).
Andreev, V. et al. Improved limit on the electric dipole moment of the electron. Nature 562, 355–360 (2018).
Frieman, J., Turner, M. & Huterer, D. Dark energy and the accelerating universe. Annu. Rev. Astron. Astrophys. 46, 385–432 (2008).
Dine, M. & Kusenko, A. The origin of the matter−antimatter asymmetry. Rev. Mod. Phys. 76, 1 (2003).
Baumann, D. & Peiris, H. V. Cosmological inflation: theory and observations. Adv. Sci. Lett. 2, 105–120 (2009).
Baudis, L. The search for dark matter. Eur. Rev. 26, 70–81 (2018).
Gianotti, F. & Giudice, G. A roadmap for the future. Nat. Phys. 16, 997–998 (2020).
European Strategy Group. 2020 Update of the European Strategy for Particle Physics. CERN https://cds.cern.ch/record/2721370/files/CERN-ESU-015-2020%20Update%20European%20Strategy.pdf (2020).
Higgs, P. W. Broken symmetries, massless particles and gauge fields. Phys. Lett. 12, 132–133 (1964).
Higgs, P. W. Broken symmetries and the masses of gauge bosons. Phys. Rev. Lett. 13, 508–509 (1964).
Higgs, P. W. Spontaneous symmetry breakdown without massless bosons. Phys. Rev. 145, 1156–1163 (1966).
Englert, F. & Brout, R. Broken symmetry and the mass of gauge vector mesons. Phys. Rev. Lett. 13, 321–323 (1964).
Guralnik, G., Hagen, C. & Kibble, T. Global conservation laws and massless particles. Phys. Rev. Lett. 13, 585–587 (1964).
Kibble, T. Symmetry breaking in nonAbelian gauge theories. Phys. Rev. 155, 1554–1561 (1967).
Llewellyn Smith, C. High-energy behavior and gauge symmetry. Phys. Lett. B 46, 233–236 (1973).
Bell, J. High-energy behavior of tree diagrams in gauge theories. Nucl. Phys. B 60, 427–436 (1973).
Cornwall, J. M., Levin, D. N. & Tiktopoulos, G. Uniqueness of spontaneously broken gauge theories. Phys. Rev. Lett. 30, 1268–1270 (1973).
Cornwall, J. M., Levin, D. N. & Tiktopoulos, G. Derivation of gauge invariance from high-energy unitarity bounds on the S matrix. Phys. Rev. D 10, 1145 (1974).
’t Hooft, G. Renormalizable Lagrangians for massive Yang−Mills fields. Nucl. Phys. B 35, 167–188 (1971).
’t Hooft, G. & Veltman, M. J. G. Regularization and renormalization of gauge fields. Nucl. Phys. B 44, 189–213 (1972).
Veltman, M. J. G. Perturbation theory of massive Yang−Mills fields. Nucl. Phys. B 7, 637–650 (1968).
Anderson, P. W. Plasmons, gauge invariance, and mass. Phys. Rev. 130, 439–442 (1963).
Glashow, S. L. Partial symmetries of weak interactions. Nucl. Phys. 22, 579–588 (1961).
Weinberg, S. A model of leptons. Phys. Rev. Lett. 19, 1264–1266 (1967).
Salam, A. Weak and electromagnetic interactions. In Proc. 8th Nobel Symp. C680519, 367−377 (1968).
’t Hooft, G. & Veltman, M. J. G. Regularization and renormalization of gauge fields. Nucl. Phys. B 44, 189–213 (1972).
Lykken, J. & Spiropulu, M. The future of the Higgs boson. Phys. Today 66, 28–33 (2013).
Veltman, M. J. G. Reflections on the Higgs system. CERN-YELLOW-97-05 CERN https://cds.cern.ch/record/2654857?ln=en (1997).
Carr, B. J. & Rees, M. The anthropic principle and the structure of the physical world. Nature 278, 605–612 (1979).
Chanowitz, M. S. The No-Higgs signal: strong WW scattering at the LHC. Czech. J. Phys. 55, B45–B58 (2005).
Littlewood, P. B. & Varma, C. M. Amplitude collective modes in superconductors and their coupling to charge-density waves. Phys. Rev. B 26, 4883–4893 (1982).
Sherman, D., Pracht, U. S. & Gorshunov, B. et al. The Higgs mode in disordered superconductors close to a quantum phase transition. Nat. Phys. 11, 188–197 (2015).
Anderson, P. W. Higgs, Anderson and all that. Nat. Phys. 11, 93 (2015).
Shimano, R. & Tsuji, N. Higgs mode in superconductors. Annu. Rev. Condens. Matter Phys. 11, 103–124 (2020).
Pekker, D. & Varma, C. Amplitude/Higgs modes in condensed matter physics. Annu. Rev. Condens. Matter Phys. 6, 269–297 (2015).
Bruning, O. S. et al. LHC Design Report Vol.1: the LHC Main Ring. CERN https://inspirehep.net/literature/656250 (2004).
Aad, G. et al. The ATLAS experiment at the CERN Large Hadron Collider. J. Instrum. 3, S08003 (2008).
Chatrchyan, S. et al. The CMS experiment at the CERN LHC. J. Instrum. 3, S08004 (2008).
Landau, L. On the angular momentum of a system of two photons. Dokl. Akad. Nauk SSSR 60, 207–209 (1948).
Yang, C.-N. Selection rules for the dematerialization of a particle into two photons. Phys. Rev. 77, 242–245 (1950).
Chatrchyan, S. et al. Study of the mass and spin-parity of the Higgs boson candidate via its decays to Z boson pairs. Phys. Rev. Lett. 110, 081803 (2013).
Khachatryan, V. et al. Constraints on the spin-parity and anomalous HVV couplings of the Higgs boson in proton collisions at 7 and 8 TeV. Phys. Rev. D 92, 012004 (2015).
Aad, G. et al. Evidence for the spin-0 nature of the Higgs boson using ATLAS data. Phys. Lett. B 726, 120–144 (2013).
Dawson, S., Englert, C. & Plehn, T. Higgs physics: it ain’t over till it’s over. Phys. Rep. 816, 1–85 (2019).
Heinrich, G. Collider physics at the precision frontier. Phys. Rep. 922, 1–69 (2021).
de Florian, D. et al. Handbook of LHC Higgs cross sections: 4. Deciphering the nature of the Higgs sector. Preprint at https://arxiv.org/abs/1610.07922 (2016).
de Blas, J. et al. Higgs Boson studies at future particle colliders. J. High Energy Phys. 2020 (01), 139 (2020).
Alcaraz, J. et al. A combination of preliminary electroweak measurements and constraints on the standard model. Preprint at https://arxiv.org/abs/hep-ex/0612034 (2006).
Aad, G. et al. Combined measurement of the Higgs boson mass in pp collisions at \(\sqrt{s}=7\) and 8 TeV with the ATLAS and CMS experiments. Phys. Rev. Lett. 114, 191803 (2015).
Sirunyan, A. M. et al. A measurement of the Higgs boson mass in the diphoton decay channel. Phys. Lett. B 805, 135425 (2020).
Aaboud, M. et al. Measurement of the Higgs boson mass in the H → ZZ* → 4ℓ and H → γγ channels with \(\sqrt{s}=13\) TeV pp collisions using the ATLAS detector. Phys. Lett. B 784, 345–366 (2018).
d’Enterria, D. On the (Gaussian) maximum at a mass m_H~125 GeV of the product of decay probabilities of the standard model Higgs boson. Preprint at https://arxiv.org/abs/1208.1993 (2012).
Zyla, P. et al. (Particle Data Group). Review of Particle Physics. Prog. Theor. Exp. Phys. 2020, 083C01 (2020).
Aaboud, M. et al. Observation of Higgs boson production in association with a top quark pair at the LHC with the ATLAS detector. Phys. Lett. B 784, 173–191 (2018).
Sirunyan, A. M. et al. Observation of \({\rm{t}}\bar{{\rm{t}}}\)H production. Phys. Rev. Lett. 120, 231801 (2018).
Sirunyan, A. M. et al. Measurements of \({\rm{t}}\bar{{\rm{t}}}H\) production and the CP structure of the Yukawa interaction between the Higgs boson and top quark in the diphoton decay channel. Phys. Rev. Lett. 125, 061801 (2020).
Aad, G. et al. CP properties of Higgs boson interactions with top quarks in the \(t\bar{t}H\) and tH processes using H → γγ with the ATLAS detector. Phys. Rev. Lett. 125, 061802 (2020).
Barger, V., Hagiwara, K. & Zheng, Y.-J. Probing the Higgs Yukawa coupling to the top quark at the LHC via single top+Higgs production. Phys. Rev. D 99, 031701 (2019).
Farina, M., Grojean, C., Maltoni, F., Salvioni, E. & Thamm, A. Lifting degeneracies in Higgs couplings using single top production in association with a Higgs boson. J. High Energy Phys. 2013 (05), 022 (2013).
Sirunyan, A. M. et al. Search for associated production of a Higgs boson and a single top quark in proton-proton collisions at \(\sqrt{s}=13\) TeV. Phys. Rev. D 99, 092005 (2019).
Sirunyan, A. M. et al. Measurement of the Higgs boson production rate in association with top quarks in final states with electrons, muons, and hadronically decaying tau leptons at \(\sqrt{s}=\) 13 TeV. Eur. Phys. J. C 81, 378 (2021).
Chatrchyan, S. et al. Evidence for the 125 GeV Higgs boson decaying to a pair of τ leptons. J. High Energy Phys. 2014 (05), 104 (2014).
Aad, G. et al. Evidence for the Higgs-boson Yukawa coupling to tau leptons with the ATLAS detector. J. High Energy Phys. 2015 (04), 117 (2015).
Aad, G. et al. Measurements of the Higgs boson production and decay rates and constraints on its couplings from a combined ATLAS and CMS analysis of the LHC pp collision data at \(\sqrt{s}=7\) and 8 TeV. J. High Energy Phys. 2016 (08), 045 (2016).
Sirunyan, A. M. et al. Search for the associated production of the Higgs boson and a vector boson in proton-proton collisions at \(\sqrt{s}=\) 13 TeV via Higgs boson decays to τ leptons. J. High Energy Phys. 2019 (06), 093 (2019).
Sirunyan, A. M. et al. Observation of the Higgs boson decay to a pair of τ leptons with the CMS detector. Phys. Lett. B 779, 283–316 (2018).
Aaboud, M. et al. Cross-section measurements of the Higgs boson decaying into a pair of τ-leptons in proton-proton collisions at \(\sqrt{s}=13\) TeV with the ATLAS detector. Phys. Rev. D 99, 072001 (2019).
Aaboud, M. et al. Observation of \(H\to b\bar{b}\) decays and VH production with the ATLAS detector. Phys. Lett. B 786, 59–86 (2018).
Sirunyan, A. M. et al. Observation of Higgs boson decay to bottom quarks. Phys. Rev. Lett. 121, 121801 (2018).
Sirunyan, A. M. et al. Evidence for Higgs boson decay to a pair of muons. J. High Energy Phys. 2021 (01), 148 (2021).
Aad, G. et al. A search for the dimuon decay of the standard model Higgs boson with the ATLAS detector. Phys. Lett. B 812, 135980 (2021).
Aad, G. et al. Search for the Higgs boson decays H → ee and H → eμ in pp collisions at \(\sqrt{s}=13\) TeV with the ATLAS detector. Phys. Lett. B 801, 135148 (2020).
Khachatryan, V. et al. Search for a standard model-like Higgs boson in the μ+μ− and e+e− decay channels at the LHC. Phys. Lett. B 744, 184–207 (2015).
Aaboud, M. et al. Search for the decay of the Higgs boson to charm quarks with the ATLAS experiment. Phys. Rev. Lett. 120, 211802 (2018).
Sirunyan, A. M. et al. A search for the standard model Higgs boson decaying to charm quarks. J. High Energy Phys. 2020 (03), 131 (2020).
Aaboud, M. et al. Searches for exclusive Higgs and Z boson decays into J/ψγ, ψ(2S)γ, and Υ(nS)γ at \(\sqrt{s}=13\) TeV with the ATLAS detector. Phys. Lett. B 786, 134–155 (2018).
Aad, G. et al. Search for Higgs and Z boson decays to J/ψγ and Υ(nS)γ with the ATLAS detector. Phys. Rev. Lett. 114, 121801 (2015).
Sirunyan, A. M. et al. Search for rare decays of Z and Higgs bosons to J/ψ and a photon in proton−proton collisions at \(\sqrt{s}=\) 13 TeV. Eur. Phys. J. C 79, 94 (2019).
Brivio, I., Goertz, F. & Isidori, G. Probing the charm quark Yukawa coupling in Higgs + charm production. Phys. Rev. Lett. 115, 211801 (2015).
Cepeda, M. et al. Report from Working Group 2: Higgs physics at the HL-LHC and HE-LHC. CERN Yellow Rep. Monogr. 7, 221–584 (2019).
Aaboud, M. et al. Search for exclusive Higgs and Z boson decays to ϕγ and ργ with the ATLAS detector. J. High Energy Phys. 2018 (07), 127 (2018).
Sirunyan, A. M. et al. Search for decays of the 125 GeV Higgs boson into a Z boson and a ρ or ϕ meson. J. High Energy Phys. 2020 (11), 039 (2020).
Aaboud, M. et al. Search for Higgs and Z boson decays to ϕ γ with the ATLAS detector. Phys. Rev. Lett. 117, 111802 (2016).
Aad, G. et al. Combined measurements of Higgs boson production and decay using up to 80 fb−1 of proton-proton collision data at \(\sqrt{s}=\) 13 TeV collected with the ATLAS experiment. Phys. Rev. D 101, 012002 (2020).
Sirunyan, A. M. et al. Combined measurements of Higgs boson couplings in proton–proton collisions at \(\sqrt{s}=\,13\,{\rm{Te}}{\rm{V}}\). Eur. Phys. J. C 79, 421 (2019).
Giudice, G., Grojean, C., Pomarol, A. & Rattazzi, R. The strongly-interacting light Higgs. J. High Energy Phys. 2007 (06), 045 (2007).
Grzadkowski, B., Iskrzynski, M., Misiak, M. & Rosiek, J. Dimension-six terms in the standard model Lagrangian. J. High Energy Phys. 2010 (10), 085 (2010).
Ellis, J., Sanz, V. & You, T. Complete Higgs sector constraints on dimension-6 operators. J. High Energy Phys. 2014 (07), 036 (2014).
Falkowski, A. & Riva, F. Model-independent precision constraints on dimension-6 operators. J. High Energy Phys. 2015 (02), 039 (2015).
Dawson, S., Homiller, S. & Lane, S. D. Putting standard model EFT fits to work. Phys. Rev. D 102, 055012 (2020).
Sirunyan, A. M. et al. Measurements of the Higgs boson width and anomalous HVV couplings from on-shell and off-shell production in the four-lepton final state. Phys. Rev. D 99, 112003 (2019).
Aaboud, M. et al. Constraints on off-shell Higgs boson production and the Higgs boson total width in ZZ → 4ℓ and ZZ → 2ℓ2ν final states with the ATLAS detector. Phys. Lett. B 786, 223–244 (2018).
Arcadi, G., Djouadi, A. & Raidal, M. Dark matter through the Higgs portal. Phys. Rep. 842, 1–180 (2020).
Carmona, A., Castellano Ruiz, J. & Neubert, M. A warped scalar portal to fermionic dark matter. Eur. Phys. J. C 81, 58 (2021).
Sirunyan, A. M. et al. Search for invisible decays of a Higgs boson produced through vector boson fusion in proton−proton collisions at \(\sqrt{s}=\) 13 TeV. Phys. Lett. B 793, 520–551 (2019).
Aaboud, M. et al. Combination of searches for invisible Higgs boson decays with the ATLAS experiment. Phys. Rev. Lett. 122, 231801 (2019).
Patt, B. & Wilczek, F. Higgs-field portal into hidden sectors. Preprint at https://arxiv.org/abs/hep-ph/0605188 (2006).
Eboli, O. J. & Zeppenfeld, D. Observing an invisible Higgs boson. Phys. Lett. B 495, 147–154 (2000).
Fox, P. J., Harnik, R., Kopp, J. & Tsai, Y. Missing energy signatures of dark matter at the LHC. Phys. Rev. D 85, 056011 (2012).
De Simone, A., Giudice, G. F. & Strumia, A. Benchmarks for dark matter searches at the LHC. J. High Energy Phys. 2014 (06), 081 (2014).
Carena, M., Liu, Z. & Riembau, M. Probing the electroweak phase transition via enhanced di-Higgs boson production. Phys. Rev. D 97, 095032 (2018).
Aad, G. et al. Combination of searches for Higgs boson pairs in pp collisions at \(\sqrt{s}=\)13 TeV with the ATLAS detector. Phys. Lett. B 800, 135103 (2020).
Sirunyan, A. M. et al. Combination of searches for Higgs boson pair production in proton-proton collisions at \(\sqrt{s}=\) 13 TeV. Phys. Rev. Lett. 122, 121803 (2019).
Alison, J. et al. Higgs boson potential at colliders: status and perspectives. Rev. Phys. 5, 100045 (2020).
Sirunyan, A. M. et al. Search for nonresonant Higgs boson pair production in final states with two bottom quarks and two photons in proton-proton collisions at \(\sqrt{s}=\) 13 TeV. J. High Energy Phys. 2021 (03), 257 (2021).
Aad, G. et al. Search for the \(HH\to b\bar{b}b\bar{b}\) process via vector-boson fusion production using proton-proton collisions at \(HH\to b\bar{b}b\bar{b}\) TeV with the ATLAS detector. J. High Energy Phys. 2020 (07), 108 (2020).
Di Vita, S., Grojean, C., Panico, G., Riembau, M. & Vantalon, T. A global view on the Higgs self-coupling. J. High Energy Phys. 2017 (09), 069 (2017).
Steggemann, J. Extended scalar sectors. Annu. Rev. Nucl. Part. Sci. 70, 197–223 (2020).
Brod, J., Haisch, U. & Zupan, J. Constraints on CP-violating Higgs couplings to the third generation. J. High Energy Phys. 2013 (11), 180 (2013).
Aaboud, M. et al. Measurement of the Higgs boson coupling properties in the H → ZZ* → 4ℓ decay channel at \(\sqrt{s}\) = 13 TeV with the ATLAS detector. J. High Energy Phys. 2018 (03), 095 (2018).
Aad, G. et al. Test of CP invariance in vector-boson fusion production of the Higgs boson using the optimal observable method in the ditau decay channel with the ATLAS detector. Eur. Phys. J. C 76, 658 (2016).
Sirunyan, A. M. et al. Constraints on anomalous HVV couplings from the production of Higgs bosons decaying to τ lepton pairs. Phys. Rev. D 100, 112002 (2019).
Berge, S., Bernreuther, W., Niepelt, B. & Spiesberger, H. How to pin down the CP quantum numbers of a Higgs boson in its tau decays at the LHC. Phys. Rev. D 84, 116003 (2011).
Sirunyan, A. M. et al. Search for production of four top quarks in final states with same-sign or multiple leptons in proton-proton collisions at \(\sqrt{s}=\) 13 TeV. Eur. Phys. J. C 80, 75 (2020).
Aad, G. et al. Searches for lepton-flavour-violating decays of the Higgs boson in \(\sqrt{s}=13\) TeV pp collisions with the ATLAS detector. Phys. Lett. B 800, 135069 (2020).
Sirunyan, A. M. et al. Search for lepton flavour violating decays of the Higgs boson to μτ and eτ in proton-proton collisions at \(\sqrt{s}=\) 13 TeV. J. High Energy Phys. 2018 (06), 001 (2018).
Slade, E. Towards global fits in EFT’s and new physics implications. Proc. Sci. LHCP2019, 150 (2019).
Ellis, J., Madigan, M., Mimasu, K., Sanz, V. & You, T. Top, Higgs, diboson and electroweak fit to the standard model effective field theory. J. High Energy Phys. 2021 (04), 279 (2021).
ATLAS Collaboration. Search for top quark decays t → qH with H → γγ using the ATLAS detector. J. High Energy Phys. 2014 (06), 008 (2014).
ATLAS Collaboration. Search for flavour-changing neutral current top quark decays t → Hq in pp collisions at \(\sqrt{s}=8\,{\rm{TeV}}\) with the ATLAS detector. J. High Energy Phys. 2012 (12), 061 (2015).
ATLAS Collaboration. Search for top quark decays t → qH, with H → γγ, in \(\sqrt{s}=13\,{\rm{TeV}}\) pp collisions using the ATLAS detector. J. High Energy Phys. 2017(10), 129 (2017).
ATLAS Collaboration. Search for flavor-changing neutral currents in top quark decays t → Hc and t → Hu in multilepton final states in proton–proton collisions at \(\sqrt{s}=13\,{\rm{TeV}}\) with the ATLAS detector. Phys. Rev. D 98, 032002 (2018).
ATLAS Collaboration. Search for top-quark decays t → Hq with 36 fb−1 of pp collision data at \(\sqrt{s}=13\,{\rm{TeV}}\) with the ATLAS detector. J. High Energy Phys. 2019 (05), 123 (2019).
CMS Collaboration. Search for top quark decays via Higgs-boson-mediated flavor-changing neutral currents in pp collisions at \(\sqrt{s}=8\,{\rm{TeV}}\). J. High Energy Phys. 2017 (02), 079 (2017).
CMS Collaboration. Search for the flavor-changing neutral current interactions of the top quark and the Higgs boson which decays into a pair of b quarks at \(\sqrt{s}=13\,{\rm{TeV}}\). J. High Energy Phys. 2018 (06), 102 (2018).
Baak, M. Review of electroweak fits of the SM and beyond, after the Higgs discovery — with Gfitter. Proc. Sci. EPS-HEP2013, 203 (2013).
Degrassi, G. et al. Higgs mass and vacuum stability in the standard model at NNLO. J. High Energy Phys. 2012 (08), 098 (2012).
Buttazzo, D. et al. Investigating the near-criticality of the Higgs boson. J. High Energy Phys. 2013 (12), 089 (2013).
Bezrukov, F., Kalmykov, M. Y., Kniehl, B. A. & Shaposhnikov, M. Higgs boson mass and new physics. J. High Energy Phys. 2012 (10), 140 (2012).
Alekhin, S., Djouadi, A. & Moch, S. The top quark and Higgs boson masses and the stability of the electroweak vacuum. Phys. Lett. B 716, 214–219 (2012).
Masina, I. Higgs boson and top quark masses as tests of electroweak vacuum stability. Phys. Rev. D 87, 053001 (2013).
Hamada, Y., Kawai, H. & Oda, K.-y Bare Higgs mass at Planck scale. Phys. Rev. D 87, 053009 (2013).
Jegerlehner, F. The standard model as a low-energy effective theory: what is triggering the Higgs mechanism? Acta Phys. Polon. B 45, 1167 (2014).
Bednyakov, A., Kniehl, B., Pikelner, A. & Veretin, O. Stability of the electroweak vacuum: gauge independence and advanced precision. Phys. Rev. Lett. 115, 201802 (2015).
Branchina, V. & Messina, E. Stability, Higgs boson mass and new physics. Phys. Rev. Lett. 111, 241801 (2013).
Giudice, G. F. Naturally speaking: the naturalness criterion and physics at the LHC. Preprint at https://arxiv.org/abs/0801.2562 (2008).
Wells, J. D. Lectures on Higgs boson physics in the standard model and beyond. Preprint at https://arxiv.org/abs/0909.4541 (2009).
Wess, J. & Zumino, B. A Lagrangian model invariant under supergauge transformations. Phys. Lett. B 49, 52−54 (1974).
Arkani-Hamed, N., Cohen, A. G. & Georgi, H. Electroweak symmetry breaking from dimensional deconstruction. Phys. Lett. B 513, 232–240 (2001).
Arkani-Hamed, N., Cohen, A. G., Katz, E. & Nelson, A. E. The littlest Higgs. J. High Energy Phys. 2002 (07), 034 (2002).
Chacko, Z., Goh, H.-S. & Harnik, R. The twin Higgs: natural electroweak breaking from mirror symmetry. Phys. Rev. Lett. 96, 231802 (2006).
Kaplan, D. B. Flavor at SSC energies: a new mechanism for dynamically generated fermion masses. Nucl. Phys. B 365, 259–278 (1991).
Csaki, C., Grojean, C. & Terning, J. Alternatives to an elementary Higgs. Rev. Mod. Phys. 88, 045001 (2016).
Ross, G. G. & Roberts, R. G. Minimal supersymmetric unification predictions. Nucl. Phys. B 377, 571–592 (1992).
Altarelli, G. The Higgs and the excessive success of the standard model. Frascati Phys. Ser. 58, 102 (2014).
Pokorski, S. Physics beyond the standard model in hadronic collisions. Acta Phys. Polon. B 47, 1767 (2016).
Ross, G. G. SUSY: Quo vadis? Eur. Phys. J. C 74, 2699 (2014).
Slavich, P. et al. Higgs-mass predictions in the MSSM and beyond. Preprint at https://arxiv.org/abs/2012.15629 (2020).
Jegerlehner, F. The ‘‘Ether world’’ and elementary particles. Preprint at https://arxiv.org/abs/hep-th/9803021 (1998).
Bjorken, J. Emergent gauge bosons. In Proceedings to the Workshops: What Comes Beyond The Standard Model. Vol. 1, https://doi.org/10.2172/798927 (DOE, 2001) http://www-public.slac.stanford.edu/sciDoc/docMeta.aspx?slacPubNumber=SLAC-PUB-9063.
Forster, D., Nielsen, H. B. & Ninomiya, M. Dynamical stability of local gauge symmetry: creation of light from chaos. Phys. Lett. B 94, 135–140 (1980).
Giudice, G. F. The dawn of the post-naturalness era. In From My Vast Repertoire ...: Guido Altarelli’s Legacy (eds Levy, A., Forte, S. & Ridolfi, G.) 267−292 (World Scientific, 2019).
Witten, E. Symmetry and emergence. Nat. Phys. 14, 116–119 (2018).
Bass, S. D. Emergent gauge symmetries and particle physics. Prog. Part. Nucl. Phys. 113, 103756 (2020).
Baskaran, G. & Anderson, P. W. Gauge theory of high temperature superconductors and strongly correlated Fermi systems. Phys. Rev. B 37, 580–583 (1988).
Sachdev, S. Topological order, emergent gauge fields, and Fermi surface reconstruction. Rep. Prog. Phys. 82, 014001 (2019).
Affleck, I., Zou, Z., Hsu, T. & Anderson, P. W. SU (2) gauge symmetry of the large-U limit of the Hubbard model. Phys. Rev. B 38, 745–747 (1988).
Banerjee, D. et al. Atomic quantum simulation of dynamical gauge fields coupled to fermionic matter: from string breaking to evolution after a quench. Phys. Rev. Lett. 109, 175302 (2012).
Bañuls, M. C. et al. Simulating lattice gauge theories within quantum technologies. Eur. Phys. J. D 74, 165 (2020).
Wetterich, C. Gauge symmetry from decoupling. Nucl. Phys. B 915, 135–167 (2017).
Weinberg, S. Essay: half a century of the standard model. Phys. Rev. Lett. 121, 220001 (2018).
Baha Balantekin, A. & Kayser, B. On the properties of neutrinos. Annu. Rev. Nucl. Part. Sci. 68, 313–338 (2018).
Weinberg, S. Baryon and lepton nonconserving processes. Phys. Rev. Lett. 43, 1566–1570 (1979).
Aghanim, N. et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 641, A6 (2020).
Weinberg, S. The cosmological constant problem. Rev. Mod. Phys. 61, 1–23 (1989).
Wetterich, C. The cosmon model for an asymptotically vanishing time dependent cosmological ‘constant’. Astron. Astrophys. 301, 321–328 (1995).
Sahni, V. & Starobinsky, A. A. The case for a positive cosmological lambda term. Int. J. Mod. Phys. D 9, 373–444 (2000).
Peebles, P. J. E. & Ratra, B. The cosmological constant and dark energy. Rev. Mod. Phys. 75, 559–606 (2003).
Copeland, E. J., Sami, M. & Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D15, 1753–1936 (2006).
Straumann, N. Dark energy. Lect. Notes Phys. 721, 327–397 (2007).
Bass, S. D. The cosmological constant puzzle. J. Phys. G38, 043201 (2011).
Martin, J. Everything you always wanted to know about the cosmological constant problem (but were afraid to ask). C. R. Phys. 13, 566–665 (2012).
Dvali, G. & Gomez, C. Quantum exclusion of positive cosmological constant? Ann. Phys. 528, 68–73 (2016).
Laureijs, R. et al. Euclid definition study report. Preprint at https://arxiv.org/abs/1110.3193 (2011).
Altarelli, G. Neutrino 2004: concluding talk. Nucl. Phys. Proc. Suppl. 143, 470–478 (2005).
Bass, S. D. & Krzysiak, J. The cosmological constant and Higgs mass with emergent gauge symmetries. Acta Phys. Polon. B 51, 1251 (2020).
Bass, S. D. & Krzysiak, J. Vacuum energy with mass generation and Higgs bosons. Phys. Lett. B 803, 135351 (2020).
Trodden, M. Electroweak baryogenesis. Rev. Mod. Phys. 71, 1463–1500 (1999).
Morrissey, D. E. & Ramsey-Musolf, M. J. Electroweak baryogenesis. New J. Phys. 14, 125003 (2012).
Servant, G. The serendipity of electroweak baryogenesis. Phil. Trans. R. Soc. Lond. A 376, 20170124 (2018).
Amaro-Seoane, P. et al. Laser interferometer space antenna. Preprint at https://arxiv.org/abs/1702.00786 (2017).
Caprini, C. et al. Science with the space-based interferometer eLISA. II: gravitational waves from cosmological phase transitions. J. Cosmol. Astropart. Phys. 2016, 04 (2016).
El-Neaj, Y. A. et al. AEDGE: atomic experiment for dark matter and gravity exploration in space. EPJ Quant. Technol. 7, 6 (2020).
Bezrukov, F. L. & Shaposhnikov, M. The standard model Higgs boson as the inflaton. Phys. Lett. B 659, 703–706 (2008).
Jegerlehner, F. Higgs inflation and the cosmological constant. Acta Phys. Polon. B 45, 1215 (2014).
Rubio, J. Higgs inflation. Front. Astron. Space Sci. 5, 50 (2019).
Wetterich, C. Cosmology and the fate of dilatation symmetry. Nucl. Phys. B 302, 668–696 (1988).
Peebles, P. J. E. & Ratra, B. Cosmology with a time variable cosmological constant. Astrophys. J. Lett. 325, 17 (1988).
Capozziello, S. & De Laurentis, M. Extended theories of gravity. Phys. Rep. 509, 167–321 (2011).
Brüning, O. & Rossi, L. The high-luminosity Large Hadron Collider. Nat. Rev. Phys. 1, 241–243 (2019).
Benedikt, M. & Zimmermann, F. The physics and technology of the Future Circular Collider. Nat. Rev. Phys. 1, 238–240 (2019).
Benedikt, M., Blondel, A., Janot, P., Mangano, M. & Zimmermann, F. Future circular colliders succeeding the LHC. Nat. Phys. 16, 402–407 (2020).
Stapnes, S. The compact linear collider. Nat. Rev. Phys. 1, 235–237 (2019).
Sicking, E. & Ström, R. From precision physics to the energy frontier with the compact linear collider. Nat. Phys. 16, 386–392 (2020).
Michizono, S. The international linear collider. Nat. Rev. Phys. 1, 244–245 (2019).
Lou, X. The circular electron positron collider. Nat. Rev. Phys. 1, 232–234 (2019).
Agostini, M., Benato, G. & Detwiler, J. Discovery probability of next-generation neutrinoless double-β decay experiments. Phys. Rev. D 96, 053001 (2017).
Caldwell, A., Merle, A., Schulz, O. & Totzauer, M. Global Bayesian analysis of neutrino mass data. Phys. Rev. D 96, 073001 (2017).
Kusenko, A. Are we on the brink of the Higgs abyss? APS Phys. 8, 108–110 (2015).
Petricca, F. et al. First results on low-mass dark matter from the CRESST-III experiment. J. Phys. Conf. Ser. 1342, 012076 (2020).
Akerib, D. et al. Results from a search for dark matter in the complete LUX exposure. Phys. Rev. Lett. 118, 021303 (2017).
Cui, X. et al. Dark matter results from 54-ton-day exposure of PandaX-II experiment. Phys. Rev. Lett. 119, 181302 (2017).
Aprile, E. et al. Dark matter search results from a one ton-year exposure of XENON1T. Phys. Rev. Lett. 121, 111302 (2018).
Agnes, P. et al. Low-mass dark matter search with the DarkSide-50 experiment. Phys. Rev. Lett. 121, 081307 (2018).
Kniehl, B. A., Pikelner, A. F. & Veretin, O. L. mr: a C++ library for the matching and running of the standard model parameters. Comput. Phys. Commun. 206, 84–96 (2016).
Abada, A. et al. FCC physics opportunities. Eur. Phys. J. C 79, 474 (2019).
Acknowledgements
None of the results presented in this review would have been possible without the diligent efforts of all the colleagues from the LHC accelerator group, the ATLAS and CMS experiments, the computing divisions, the theoretical community and many more, who all took part in this fantastic adventure at the energy frontier. Specifically, the authors thank M. Cepeda, F. Jegerlehner and J. Krzysiak for useful discussions during the preparation of this manuscript.
Author information
Authors and Affiliations
Contributions
The authors contributed equally to all aspects of the article.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information
Nature Reviews Physics thanks Fabio Cerutti and the other, anonymous, reviewers for their contribution to the peer review of this work.
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Glossary
- Vacuum expectation value
-
The matrix element of a field or operator in the vacuum.
- Higgs condensate
-
The Bose−Einstein condensate of Higgs bosons, which forms in the vacuum.
- Naturalness
-
The theoretical idea that dimensionless ratios of mass scales in a physical theory should be of order one. That is, without fine tuning, a mass parameter can only be much smaller than the others if setting it zero increases the symmetry of the theory.
- Gauge freedom
-
With gauge symmetry, we are free to choose the gauge symmetry parameters to make the physics look simplest, with all choices of gauge parameters being physically equivalent and degenerate.
- Radiative corrections
-
Quantum fluctuations in the intermediate state of the particle interactions.
- Barn
-
A unit that quantifies the integrated luminosity. It has the dimension of inverse area, proportional to the amount of proton−proton collisions produced by the Large Hadron Collider (LHC). One femtobarn 1 fb = 10−43 m2.One inverse attobarn 1 ab−1 = 103 fb−1. One inverse femtobarn corresponds to approximately 1014 proton−proton collisions in the LHC.
- Signal strength
-
The ratio of the signal rate divided by the predicted rate for a standard model (SM) Higgs boson at a given mass, denoted by the symbol μS. The closer μS is to one, the more it resembles a SM Higgs boson.
- Diphoton channel
-
(Higgs) particle production with two photons in the final state.
- Tree-level interference
-
A cross term in squaring the amplitude for Higgs boson production, where the Higgs particle is liberated either from a W boson or from a top quark. This is specified to distinguish the loop level interference that occurs in the diphoton decay channel.
- Decay channel
-
A collision final state involving a specific decay mode of the Higgs boson (for example, two photons, four leptons, two vector bosons, two fermions and so on).
- Production channel
-
A collision final state involving a specific production mode of the Higgs boson (for example, gluon fusion, vector boson fusion, associated production with a vector boson, a pair of top quarks and so on).
- Drell−Yan di-muon
-
A process in which a quark from one incoming proton annihilates with an antiquark from the second proton, producing a photon or Z boson that then decays into a μ+μ− pair.
- Mass shell
-
Physical particles with the correct energy−momentum relation are called on-shell or on-mass shell; otherwise, they are called off-shell or off-mass shell. Off-shell particles are virtual and can exist in interaction processes.
- Trilinear coupling
-
The interaction vertex involving three Higgs particles (and no others).
Rights and permissions
About this article
Cite this article
Bass, S.D., De Roeck, A. & Kado, M. The Higgs boson implications and prospects for future discoveries. Nat Rev Phys 3, 608–624 (2021). https://doi.org/10.1038/s42254-021-00341-2
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s42254-021-00341-2
This article is cited by
-
Quantum sensing for particle physics
Nature Reviews Physics (2024)
-
Graph neural networks at the Large Hadron Collider
Nature Reviews Physics (2023)
-
Spontaneous symmetry breaking and massive photons from a Fresnel-type potential
Pramana (2022)