Abstract
The photonic Ising machine is a new paradigm of optical computing that takes advantage of the unique properties of light wave propagation, parallel processing, and low-loss transmission. Thus, the process of solving combinatorial optimization problems can be accelerated through photonic/optoelectronic devices, but implementing photonic Ising machines that can solve arbitrary large-scale Ising problems with fast speed remains challenging. In this work, we have proposed and demonstrated the Phase Encoding and Intensity Detection Ising Annealer (PEIDIA) capable of solving arbitrary Ising problems on demand. The PEIDIA employs the heuristic algorithm and requires only one step of optical linear transformation with simplified Hamiltonian calculation by encoding the Ising spins on the phase term of the optical field and performing intensity detection during the solving process. As a proof of principle, several 20 and 30-spin Ising problems have been solved with high ground state probability (≥0.97/0.85 for the 20/30-spin Ising model).
Similar content being viewed by others
Introduction
Optimization problems1 are ubiquitous in nature and human society, such as ferromagnets2,3, phase transition4, artificial intelligence5, finance6, biology7,8, agriculture9, etc. Usually, combinatorial optimization problems (COPs) are non-deterministic polynomial hard (NP-hard) problems1, in which the required resources to find the optimal solutions grow exponentially with the problem scales on conventional von-Neumann machines. To tackle such obstacles, Ising machines as specialized hardware-sovlers are introduced to accelerate the solving process10, since any problem in the complexity class NP can be mapped to an Ising problem within polynomial complexity11,12,13. The NP-hard Ising problems can be described as finding the energy ground state corresponding to a specific Ising spin vector \({{{{{\boldsymbol{\sigma }}}}}}\), which is equivalent to searching the global minima of Hamiltonian in absence of the external field14
where \({{{{{\bf{J}}}}}}\) is the adjacent interaction matrix, \({{{{{\boldsymbol{\sigma }}}}}}\, {{{{{\boldsymbol{=}}}}}}\, {\left[{\sigma }_{1},{\sigma }_{2},\ldots ,{\sigma }_{N}\right]}^{{{{{{\rm{T}}}}}}}\) is the Ising spin vector including Ising spins \({\sigma }_{i}\in \left\{1,-1\right\}\), and the superscript T denotes the transpose. To implement Ising machines, various classical and quantum physical systems have been employed. For the quantum annealers, various systems, such as D-wave systems15, trapped atoms16,17, magnetic tunnel junctions18 and radio-frequency superconducting quantum interference devices19, have been employed to simulate the Ising model. However, the large-scale implementation and fault tolerance of the quantum system are still technically challenging, and the annealing process should be sufficiently slow to maximize the ground state probability10. In classical domain, the Ising machines mainly based on electronic devices can be divided into two categories according to the operation mechanisms. In the first category, the Ising spins are represented by the phase of coupled electronic oscillators and the system is driven to the ground state20. In the other category, electronic parallel computation schemes, such as the memristor crossbar21 or the complementary metal-oxide-semiconductor chip22,23, are utilized to accelerate the Hamiltonian calculations. Recently, advanced photonics exhibits the feasibilities to encode, transmit and process information on various spatial degrees of freedom, e.g., phase, amplitude/intensity, frequency/wavelength, time slot, and spatial profile/distribution. Thus, photonic Ising machines have emerged due to the nature of parallelism and high propagation speed of light. Likewise, there are also two types of photonic Ising machines that have been experimentally reported. The first type of photonic Ising machine is based on the nonlinear optical or optoelectronic parametric oscillators24,25,26,27,28,29, in which Ising spins are encoded on the phase terms of the time-multiplexed pulses and the ground state search relies on the spontaneous convergence of the parametric oscillators. For these Ising machines, the couplings among Ising spins have to be implemented via measurement feedback and performing vector-matrix multiplication in the electronic hardware, or aligning the oscillator pulses in the same time slot with the optical delay line. Moreover, whether Ising machines based on nonlinear parametric oscillators can solve random Ising models remains contested30. The second type of photonic Ising machine employs heuristic algorithms to solve Ising problems, in which the main computation task is to calculate the Ising Hamiltonians of different Ising spin states iteratively. Such task can be regarded as multiplying a static matrix by an ever-changing vector, which is very suitable for the optical vector-matrix multiplication (OVMM) system. Actually, the OVMM has been applied on some specific computation tasks, such as the deep diffractive neural network31,32 and the nanophotonic processor33. As shown in these works, the vector-matrix multiplications could be dramatically accelerated by photonic systems due to the parallel propagation of light. In the spatial photonic Ising machine34, numerous Ising spins are encoded on the phase terms of the light field through phase-modulation units of the spatial light modulator (SLM). However, the spins interact in the intensity distribution of the light field with a Fourier lens, hence only some specific Ising models can be solved. The on-chip array of tunable Mach-Zehnder interferometers (MZIs) network35,36, which is known as the Reck scheme37, is also employed to solve arbitrary Ising models. However, due to the complexity of the Reck scheme, only 4-spin Ising models are experimentally demonstrated36. Therefore, it is still highly desired to implement photonic Ising machines that can solve arbitrary large-scale Ising problems with fast speed.
In this work, a photonic Ising machine is proposed and demonstrated with a fully reconfigurable OVMM system and the employed heuristic algorithm is modified from simulated annealing38,39. Meanwhile, the calculation of the Hamiltonian is simplified in the optical domain where the Ising spins are encoded on the phase term of the light field and only intensity detection is required. Our proposal is named as the “Phase Encoding and Intensity Detection Ising Annealer” (PEIDIA), which will be briefly explained as follows. At the beginning, with proper treatment of the adjacent matrix \({{{{{\bf{J}}}}}}\), the calculation of Ising Hamiltonians can be modified from the quadratic form (Eq. (1)) and only one OVMM is required. Then with a simple summation of the intensities of the light field, the Hamiltonian can be readily calculated. At last, the heuristic algorithm is employed to search the ground state with the obtained Hamiltonian. Thus our proposed PEIDIA is quite helpful to simplify and speed up the calculations in the optical domain. Furthermore, the PEIDIA can serve as a kind of “on-demand” solver for arbitrary Ising models while a programmable OVMM setup is employed to perform arbitrary linear transformation of the input Ising spin vector.
In our experimental implementation, the employed OVMM scheme is based on the discrete coherent spatial (DCS) mode and SLMs, which is improved from our previous work40,41,42,43. To verify the feasibility of our proposal, we have experimentally solved an antiferromagnetic Möbius-Ladder model as well as two fully connected, randomly generated spin-glass models. For the 20-spin Möbius-Ladder model, the ground state probability reaches 0.99 (100 runs) within 400 iterations, while that of the fully connected and random model is around 0.97 (100 runs) within 600 iterations. Furthermore, the ground state probability of the 30-spin fully connected and random model is around 0.85 (100 runs) within 1200 iterations. It should be mentioned that, this proposed architecture does not rely on specific optical linear transformation schemes and heuristic algorithms. The main advantage of the PEIDIA is the simplified Hamiltonian calculation with only one OVMM so that the parallelism and fast-speed of the optical calculation may be fully exploited. Thus, the proposed PEIDIA would pave the way to achieve large-scale photonic Ising machines that can solve arbitrary Ising models on demand.
Results
Architecture and operation principles of the PEIDIA
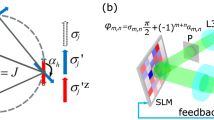
In order to accelerate the solving process of the Ising problem, we have proposed an on-demand photonic Ising machine and Fig. 1a shows the architecture design. There are three main stages in the operation of the PEIDIA: the electronic pretreatment, the optical matrix multiplication, and the electronic feedback. In the first stage of the electronic pretreatment, the parameters for the setup of the optical system are calculated and configured according to the adjacent matrix \({{{{{\bf{J}}}}}}\) of the given Ising model. In the second stage, the optical matrix multiplication system accelerates the calculation of the Hamiltonian of a certain Ising spin vector. The optical intensities obtained from the optical matrix multiplication are detected and converted to electronic signals. In the third stage, the spin vector for the next iteration will be generated and fed to the optical matrix multiplication according to the adopted heuristic algorithm. The second and the third stage will be conducted iteratively until the algorithm terminates. The details are described as follows.
a The full operation process of the PEIDIA consisting of three main stages. \({\sigma }_{i}\): the Ising spins encoded on the phase term of the light field. \({{{{{\bf{A}}}}}}\): the transformation matrix. \({E}_{i}\): the output complex amplitude. \({I}_{i}\): the output intensity. \({{{{{\bf{J}}}}}}\): the interaction matrix of the Ising model. b Detailed demonstration of the PEIDIA with arbitrary non-unitary matrix transformation of the discrete coherent spatial mode for a 9-spin Ising problem. The input field consists of 9 Gaussian beams with equal intensities. Different colors in wavefront modulation patterns and optical fields indicate different phases according to the color bar, while the black region denotes 0 phase delay for readability. In the insets of the optical fields, the brightness denotes the optical amplitude. The orange arrows denote the propagation directions of the Gaussian beams. In the shown spin-update process, one red circular region turns blue, representing a spin flip.
The main purpose of the electronic pretreatment is to simplify the calculation in the optical domain. According to Eq. (1), the Ising Hamiltonian has a quadratic form and two steps of vector-matrix multiplications are required. Actually, only one vector-matrix multiplication is needed in the optical domain with proper pretreatment. First, every real interaction matrix \({{{{{\bf{J}}}}}}\) of the given Ising model can be decomposed to a symmetric matrix \({{{{{{\bf{J}}}}}}}_{+}=({{{{{\bf{J}}}}}}+{{{{{{\bf{J}}}}}}}^{{{{{{\rm{T}}}}}}})/2\) and an anti-symmetric matrix \({{{{{{\bf{J}}}}}}}_{-}=({{{{{\bf{J}}}}}}-{{{{{{\bf{J}}}}}}}^{{{{{{\rm{T}}}}}}})/2\). Since \({{{{{{\bf{J}}}}}}}_{-}\) has no contribution to the Ising Hamiltonian in Eq. (1), we only discuss the symmetric component \({{{{{{\bf{J}}}}}}}_{+}\) and use \({{{{{\bf{J}}}}}}\) to denote \({{{{{{\bf{J}}}}}}}_{+}\) for simplicity in this article. As \({{{{{\bf{J}}}}}}\) is a real symmetric matrix, the Hamiltonian has the form as follows with eigen-decomposition44:
where \({{{{{\bf{J}}}}}}\,{{{{{\boldsymbol{=}}}}}}\,{{{{{{\bf{Q}}}}}}}^{{{{{{\rm{T}}}}}}}{{{{{\bf{D}}}}}}{{{{{\bf{Q}}}}}}\), while \({{{{{\bf{Q}}}}}}\) is the normalized orthogonal eigenvector matrix and \({{{{{\bf{D}}}}}}={{{{{\rm{diag}}}}}}\left({\lambda }_{1},{\lambda }_{2},\ldots ,{\lambda }_{N}\right)\) is the diagonal eigenvalue matrix of \({{{{{\bf{J}}}}}}\).
In our proposal, the vector-matrix multiplication of \({{{{{\bf{A}}}}}}{{{{{\boldsymbol{\sigma }}}}}}\) is performed by the OVMM. During the ground state search, the transformation matrix \({{{{{\bf{A}}}}}}\) is unchanged while the sampled spin state \({{{{{\boldsymbol{\sigma }}}}}}\) updates iteratively. Thus, each Ising spin is considered as encoded on the phase term of the optical field \({E}_{i}={E}_{0}{\sigma }_{i}={E}_{0}\exp ({{{{{\rm{i}}}}}}({\varphi }_{0}+{\varphi }_{i}))\), while \({\varphi }_{i}\) corresponds to the element of the spin vector with the value of \({\varphi }_{i}\in \left\{0,\pi \right\}.\) By neglecting the constant phase term of \(\exp ({{{{{\rm{i}}}}}}{\varphi }_{0})\), the complex amplitude of the output optical field can be written as
where \({E}_{0}\) is the constant amplitude term. By defining the output intensity vector \({{{{{\bf{I}}}}}}\) by \({I}_{i}={E}_{i}^{* }{E}_{i}\), the Hamiltonian becomes (see detailed deduction in Supplementary Note 1)
Equation (4) shows that the calculation of Hamiltonian turns into the simple summation of the optical intensities in a subtle way. Thus in our proposal, the optical computation would perform the task of encoding spin vectors on optical field, vector-matrix multiplications of \({{{{{\bf{A}}}}}}{{{{{\boldsymbol{\sigma }}}}}}\) and intensity detections as shown in Fig. 1a. It should be mentioned that although the Ising spin vector \({{{{{\boldsymbol{\sigma }}}}}}\) is encoded on the phase term of optical field, only the measurement of the output intensity vector \({{{{{\bf{I}}}}}}\) is required to obtain the Hamiltonian.
In Eq. (4), the first term in the bracket is the summation of the intensities corresponding to the negative eigenvalues, while the second term is that corresponds to the positive eigenvalues, which is due to the difference between \({E}_{i}{E}_{i}\) and \({E}_{i}^{* }{E}_{i}\) when \({\lambda }_{i} < 0\). Since there are subtracting operations, the Hamiltonian is finally calculated with Eq. (4) in the electronic domain after the intensity detection. In succession, the heuristic algorithm determines the spin vector for next iteration. Here, a modified simulated annealing algorithm is employed to search the ground state. In the iteration \(n\), a spin state \({{{{{{\boldsymbol{\sigma }}}}}}}^{(n)}\) is accepted and its Hamiltonian \({H}^{(n)}\) is calculated. Then in the next iteration \((n+1)\), \(m\) spins of the spin vector are randomly flipped, which means the spin vector \({{{{{{\boldsymbol{\sigma }}}}}}}^{(n)}\) is updated to \({{{{{{\boldsymbol{\sigma }}}}}}}^{(n+1)}\) on the optical domain via the electronic feedback. The variable \(m\) is a random integer obtained from a Cauchy random variable \(C(0,\alpha T)\), where \(\alpha\) is a scaling coefficient and \(T\) is the annealing temperature (see Supplementary Note 2). With such state-generation method, the spin state can experience long jumps occasionally and escape from local minima more easily. Then the difference between the current Hamiltonian \({H}^{(n+1)}\) and the previous one of \({H}^{(n)}\) is calculated as:
If \(\triangle H\le 0\), the generated state \({{{{{{\boldsymbol{\sigma }}}}}}}^{(n+1)}\) is accepted. If \(\triangle H \, > \, 0\), \({{{{{{\boldsymbol{\sigma }}}}}}}^{(n+1)}\) is accepted with the probability of \(\exp (-\triangle H/T)\) due to the Metropolis criterion38,39. In a single run of the algorithm, \(T\) is slowly decreased from the initial temperature of \({T}_{0}\) to zero with the increase of the iteration number. According to the annealing schedule, it can be seen that in the early stage of the annealing, the PEIDIA can perform the global search, while at the end of the annealing, it is more likely to perform the local search. Finally, a “frozen” state will be obtained, which may be the optimal ground state with high probability. Actually, other heuristic algorithms can also be adopted, such as genetic algorithm45, in which multiple-spin-flips are also desired.
Optical vector-matrix multiplication
Generally, the transformation matrix \({{{{{\bf{A}}}}}}\) in Eq. (3) is complex and non-unitary, so that the OVMM employed in our architecture should be capable of achieving such non-unitary transformation. In our previous work40,41,42,43, a matrix transformation scheme has been demonstrated with discrete coherent spatial (DCS) mode and SLMs. Such scheme can perform arbitrary complex vector-matrix multiplications for both unitary and non-unitary matrices. Based on it, the architecture of the optical computation in the PEIDIA is schematically depicted in Fig. 1b. The spin vector is encoded on the input DCS mode, which consists of a group of Gaussian beams. More specifically, the elements of the spin vector are defined as the complex amplitudes at the centers of the Gaussian beams respectively. During the annealing process, each Ising spin \({\sigma }_{i}^{(n)}\) is encoded on the input vector through the appending spin-encoding phase pattern corresponding to the phase delay of 0/\(\pi\), as depicted by the blue/red circular regions in Fig. 1b, respectively. Then the input vector passes through the meticulously designed beam-splitting and recombining phase patterns which are determined by the transformation matrix \({{{{{\bf{A}}}}}}\) (see details in Supplementary Note 3). Once generated for a given Ising problem, such two patterns are fixed during the following calculation and annealing process. The output amplitude vector \({{{{{{\bf{E}}}}}}}^{{{{{{\boldsymbol{(}}}}}}n{{{{{\boldsymbol{)}}}}}}}\) consists of the complex amplitudes at the centers of the beams in the output plane, where the output intensity vector \({{{{{{\bf{I}}}}}}}^{(n)}\) is detected. In succession, the Hamiltonian \({H}^{(n)}\) is calculated in the electronic domain and the next sampling state \({{{{{{\boldsymbol{\sigma }}}}}}}^{(n+1)}\) is generated and updated to the spin-encoding phase pattern. The spin flip can be simply achieved by adding a constant phase delay \(\pi\) to the corresponding circular region of the spin-encoding phase pattern, as depicted in the last pattern of Fig. 1b.
It should be mentioned that with our scheme, the mapping relations between the Ising model and the experimental parameters (the phase patterns corresponding to the matrix \({{{{{\bf{A}}}}}}\)) are simple and explicit. The beam-splitting and recombining scheme can directly conduct the non-unitary matrix transformation without utilizing cascaded structures40,41.
Experiment demonstration
The experimental setup of the PEIDIA with 20 spins is illustrated in Fig. 2, and the photo of the experimental setup is shown in inset (1) of Fig. 2. A Gaussian beam at 1550 nm (ORION 1550 nm Laser Module) with the fiber collimator is injected to a half-wave plate and a linear polarizer, which align the polarization according to the requirement of three phase-only reflective SLMs (Holoeye PLUTO-2.1-TELCO-013). Each SLM has 1920\(\times\)1080 pixels with the pixel pitch of 8 μm, serving as a reconfigurable wavefront modulator. SLM0 is employed to split the single incident beam with the radius of 1.63 mm into 20 Gaussian beams without overlap as the input DCS mode, and the position distribution in the transverse plane is shown in inset (2) of Fig. 2. The beams are arranged in a triangular lattice in order to encode more spins on a single SLM, and the radius of each beam is ~610 μm. The selection of the beam radius would be discussed in the section of “Discussion”. Both phase patterns for spin-encoding and beam-splitting are applied on SLM1, while the beam-recombining phase pattern is applied on SLM2. SLM1 and SLM2 perform the OVMM of \({{{{{\bf{A}}}}}}{{{{{\boldsymbol{\sigma }}}}}}\) together. The splitting ratio of each region on SLM1, which is defined as the ratio of the complex amplitudes of the beams after the splitting, is consistent with the corresponding column of \({{{{{\bf{A}}}}}}\). The recombining ratio of each region on SLM2 is an all-one vector, which sums up the incident optical complex amplitudes. For example, one of the twenty (\(N\) = 20) circular beam-recombining phase pattern is shown in inset (3) of Fig. 2. It should be mentioned that the phase pattern on SLM2 only depends on the dimensionality and the position distribution of the DCS mode, e.g., 20 beams in a triangular lattice in this work, and keeps constant during the solving process. Moreover, the radius of each beam-splitting and recombining region is set to 1175 μm that is almost twice as long as the beam radius to conveniently align each Gaussian beam with \(N\) = 20. Actually, the radius of each circular region could be reduced to about 1.5 times of the Gaussian beam radius according to our estimation while there is no significant overlap between adjacent beam spots. Thus for N = 30, each beam-splitting/recombining region on SLM is set to 950 μm (~1.55 × 610 μm). The detailed discussion about the beam radius is provided in the section of “Discussion”. After SLM2, there is a pinhole to filter out the unwanted diffraction components. Before the camera, a lens aligns the beams along the direction of the optical axis. Finally, the DCS mode is detected by the Hamamatsu InGaAs Camera C12741-03. The methods for calibrating the optical system and generating the phase patterns are provided in Supplementary Note 3. Additionally, a CPU is employed to perform the required process in the electronic domain, including the pretreatment of the adjacent matrix, generating the phase patterns on SLMs, flipping the spins, calculating the Hamiltonians, and executing other steps required in the adopted heuristic algorithm.
BPF: bandpass filter. HWP: half-wave plate. As the employed spatial light modulators (SLMs) are reflective, additional blazed gratings are applied to all SLMs to extinct the zero-order diffractions. Inset (1) is the photograph of the experimental demonstration and the detailed description is provided in Supplementary Note 3. Inset (2) shows the intensity distribution in the transverse plane surrounded by the black dashed box. Here SLM0 splits the beam into N = 20 beams, which is equal to the number of the Ising spins. The color bar denotes the incident power on each pixel. Inset (3) shows a circular beam-recombining phase pattern on SLM2 which is not superposed with the blazed grating, and the color bar shows the phase distribution. SLM1 encodes the Ising spins to the beams, and implements the optical vector-matrix multiplication together with SLM2.
Ground state search for different Ising models
To verify our proposed PEIDIA, several models with different complexities and numbers of spins have been experimentally solved. The first model is an antiferromagnetic Möbius-Ladder model with \(N\) = 20 (denoted as model 1), in which the nonzero entries are \({J}_{{ij}}=-1\) as illustrated in the inset of Fig. 3a. First, a single run of the PEIDIA is conducted, where a final accepted state is obtained after 600 iterations, and the measured experimental Hamiltonian evolution is illustrated in Fig. 3a. Figures 3b, c show the detected images and the beam intensities of the output fields of the randomly generated initial state and the final accepted state, respectively, and the positions of both states are marked in Fig. 3a. In Fig. 3b, c, the intensity of each beam is represented by the average power of central 9 pixels inferred from the grayscale. In the eigenvalue matrix \({{{{{\bf{D}}}}}}\) of the 20-dimensional Möbius-Ladder model, the first 11 eigenvalues are negative while the last 9 eigenvalues are positive. Thus, the beams with number 1–11 are marked as the “negative” beams corresponding to the negative eigenvalues, while the rest are denoted as the “positive” beams in Fig. 3b, c. In Fig. 3b, the intensity mainly concentrates on the “negative” beams, indicating that the initial state is an excited state with a high Hamiltonian (\(H\) = 11.5). Actually, Eq. (4) indicates that the optical intensities are expected to be more concentrated on the “positive” beams to achieve lower Hamiltonians. Figure 3c shows that the intensity finally concentrates on the “positive” beams 19 and 20, while there are almost no signals on the “negative” beams, which corresponds to a low value of the Hamiltonian (\(H\) = −26.0). The results in Fig. 3 indicate that the accepted spin state evolves from an initial state with a high Hamiltonian to a final state with a low Hamiltonian, thus the PEIDIA indeed minimizes the Hamiltonian.
a An experimentally measured Hamiltonian evolution curve in a single run. The inset shows the Ising model to be solved. Two arrows denote the position of the initial state in (b) and the final accepted state in (c), respectively. b The beam power of the detected image corresponding to a randomly generated initial state with a high Hamiltonian. The left inset denotes the positions of 20 beams. The color bar denotes the incident power on each pixel. c The beam power of the detected image corresponding to a final accepted state with a low Hamiltonian. The left inset denotes the positions of 20 beams. The color bar denotes the incident power on each pixel.
In the experiment, the PEIDIA has been run for 100 times, and the corresponding Hamiltonian evolutions are depicted in Fig. 4a. In each run, the initial state of the spins is randomly generated. Most of the curves converge to the low Hamiltonians within 400 iterations, and the finally obtained Hamiltonians are very close to the ground state Hamiltonian \(H\) = −26 which is denoted as the black dashed line in Fig. 4a. Such distribution may be mainly due to the systematic error and the detection noise. Actually, the target of the PEIDIA is to obtain the spin vector of the ground state, rather than the actual value of the Hamiltonian. Thus, the accepted spin vectors in each iteration corresponding to all curves in Fig. 4a are extracted to calculate the theoretical Hamiltonians with Eq. (1), and then the ground state probability is obtained by counting the proportion of the ground state Hamiltonian for each iteration within all 100 runs. The ground state probability versus the iteration number is plotted as the red curve in Fig. 4b. It can be seen that as the initial states are randomly generated, the ground state probability is almost 0 in the range of the iteration number less than 50. Then the probability would experience a rapid growth from the iteration number 50 to 300, and gradually converge in the end. The final ground state probability is around 0.99 after 400 iterations, indicating that almost all of the 100 runs can successfully obtain the ground states. For comparison, the algorithm simulation, which does not include the simulation of the entire optical system, has also been carried out for 10,000 times on a computer with the same parameters as the experimental settings, and the ground state probability versus the iteration number is plotted as the black curve in Fig. 4b. It can be seen that the experimental curve matches very well with the simulation.
a–c The 100 normalized experimental Hamiltonian evolution curves, the ground state probabilities versus the iteration number, and the fidelity distribution of the sampled output intensity vectors of model 1, respectively. d–f The 100 normalized experimental Hamiltonian evolution curves, the ground state probabilities versus the iteration number, and the fidelity distribution of the sampled output intensity vectors of model 2, respectively. g–i The 100 normalized experimental Hamiltonian evolution curves, the ground state probabilities versus the iteration number, and the fidelity distribution of the sampled output intensity vectors of model 3, respectively. The normalization method is described in Supplementary Note 5. In a, d, and g, the inset shows the spin interactions of the models where the red and blue lines denote \({J}_{{ij}}=1\) and \(-1\) respectively, and the black dashed lines indicate the theoretical ground state Hamiltonians.
As shown in Fig. 4a, the experimental Hamiltonians are distributed around the ground state Hamiltonian in the final stage of searching, indicating that the systematic error and the detection noise cannot be neglected due to the limited performance of the experimental devices. Such error and noise would cause some deviations of the actual transformation matrices, the input vectors, and the detected signals from the theoretical expectations. To quantify the influence of these two factors, the parameter of fidelity \(f\) is introduced with
In Eq. (6), \({{{{{\bf{I}}}}}}\) is the intensity vector measured by the camera and \({{{{{{\bf{I}}}}}}}_{{{{{{\rm{theo}}}}}}}\,{{{{{\boldsymbol{=}}}}}}\,{\left({{{{{\bf{A}}}}}}{{{{{\boldsymbol{\sigma }}}}}}\right)}^{{{{{{\boldsymbol{* }}}}}}}\odot {{{{{\boldsymbol{(}}}}}}{{{{{\bf{A}}}}}}{{{{{\boldsymbol{\sigma }}}}}}{{{{{\boldsymbol{)}}}}}}\) (\(\odot\) denotes the element-wise multiplication) is the theoretical output intensity vector, which is calculated by the target transformation matrix \({{{{{\bf{A}}}}}}\) and the sampled spin vector \({{{{{\boldsymbol{\sigma }}}}}}\). Thus, \(f\) could evaluate the accuracy of the output intensity vectors, since both the accuracy of the OVMM and the detection noise are involved. According to Eq. (6), \(f\) is normalized within \([0,\,1]\) and \(f=1\) represents that the two vectors are perfectly parallel to each other. The fidelities of all 6 × 104 experimental samples are calculated, and the probability distribution of \(f\) is illustrated in Fig. 4c, and the average value is 0.99978 ± 0.00039, indicating that our transformation scheme is quite accurate.
To present the “on-demand” ability of our proposal, we have considered two other randomly generated and fully connected spin-glass models with spin numbers of 20 and 30 (denoted as model 2 and 3 respectively), in which nonzero entries are uniformly distributed in \({J}_{{ij}}\in \{-{{{{\mathrm{1,1}}}}}\}\). The results of model 2 are shown in Fig. 4d–f, while those of model 3 are shown in Fig. 4g–i. The spin couplings of model 2 and 3 are shown in the insets of Fig. 4d, g respectively. The measured accepted experimental Hamiltonians for 100 runs are presented in Fig. 4d,g, where the theoretical ground state Hamiltonians are shown as the black dashed lines (\(H\)=−62 for model 2 and \(H\) = −117 for model 3). Here, the number of iterations for each run is increased to 1200 and 2000 respectively since model 2 and 3 have higher graph densities than model 1. It can be seen that most of the curves converge within 600 iterations for model 2 and 1200 iterations for model 3. The ground state probabilities versus the iteration number are also calculated and plotted in Fig. 4e, h with the final ground state probabilities of 0.97 and 0.85 for model 2 and 3, respectively. Both results indicate that our PEIDIA is capable of solving such complex and fully connected models. Furthermore, the fidelity distributions of the output vectors are also calculated and shown in Fig. 4f,i respectively. The average fidelities of the sampled output intensity vectors for model 2 and 3 are 0.99976 ± 0.00044 and 0.99942 ± 0.00131 respectively, which are very close to that in model 1. Meanwhile, the fidelities of the corresponding transformation matrices are 0.9989, 0.9994, and 0.9969 for model 1–3, respectively (see Supplementary Note 4). However, for the 30-spin demonstration, the experimental ground state probability becomes a bit lower than that in the simulation. Such result is mainly due to the decreased signal-to-noise ratio of the experimental Hamiltonian with increasing dimensionality \(N\) (see detailed discussion of the searching accuracy in Supplementary Note 6).
Discussion
According to our previous work40,41, each pattern on SLM is the superposition of a series of phase gratings, hence abundant pixels have to be employed to perform such complex pattern with enough accuracy. In this section, we would estimate the upper limit of the number of spins that can be arranged. Firstly, we refer to the Gaussian beam radius function given by
where \({w}_{0}\) is the radius of the beam waist between SLM1 and SLM2, \(\lambda\) is the wavelength and \(z\) is the axial distance relative to the beam waist. To arrange as many spins as possible for the given \(\lambda\) and distance \({L}_{12}\) between SLM1 and SLM2, it is necessary to ensure that the beam radii on both SLM1 and SLM2 are the same, which can be achieved by locating the beam waist at the midpoint between SLM1 and SLM2. For our experiment, \(\lambda\) = 1550 nm and \({z}_{{{{{{\rm{SLM}}}}}}}\) = 0.377 m (half of the distance between SLM1 and SLM2). By taking the derivative of the Gaussian beam radius function and setting \(\partial w/\partial {w}_{0}=0\), the radius of beam waist should be \({w}_{0}\) = 431 μm, which corresponds to a minimum beam radius \({w}_{{{{{{\rm{SLM}}}}}}}\) = 610 μm on SLM1 and SLM2. Thus, in our experimental setup, the beam radii on SLM1 and SLM2 are fixed and aligned to ~610 μm. Additionally, the radius of each circular pattern on SLM1 and SLM2 should be set to larger than 1.5\({w}_{{{{{{\rm{SLM}}}}}}}\) so that the beam overlap is about ~1% (estimated by the overlap integral of two Gaussian modes). Thus, for the 20-spin and 30-spin models, the radius of each beam-splitting/recombining pattern on SLM1 and SLM2 is set to 1175 μm and 950 μm, respectively. It also should be noted that, due to the paraxial approximation and the Nyquist-Shannon sampling theorem46, increasing the number of spins would not require larger beam-splitting/recombining regions. Therefore, the minimum radius of the circular pattern is ~950 μm in our current experimental setup, and the maximum number of spins is ~36. Another factor that would limit the scalability of the PEIDIA is the noise level of the experimental Hamiltonian (see detailed analysis in Supplementary Note 6). In the experiment of model 1–3, all the noise levels are less than the corresponding minimum Hamiltonian variations, thus high ground state probabilities are achieved. According to our analysis, the signal-to-noise ratio of the experimental Hamiltonian is approximately proportional to \(1/\sqrt{N}\). Such result indicates that the searching accuracy of the PEIDIA would deteriorate in high-dimensional conditions, which would lead to the failure of searching the ground state.
In the future work, the number of spins could be increased by reducing the beam radius, adjusting the distances between SLMs properly (the distances should have lower boundaries as paraxial approximation is applied), or utilizing shorter operation wavelength according to Eq. (7). For instance, if the distance between SLM1 and SLM2 is set to 0.4 m and \(\lambda\) = 800 μm, the minimum beam radii on SLM1 and 2 are ~320 μm and the minimum radius of the circular region is ~500 μm so that that ~132 beams could be processed on SLM1 and SLM2. Furthermore, if 4K SLMs (3840 × 2160 pixels) are adopted, the spin number can be increased to ~520 with the same arrangement as our present setup. Besides, the detector with lower noise and higher dynamic range would be helpful to achieve higher searching accuracy of the PEIDIA in high-dimensional conditions.
Although this work is also based on SLMs, the difference between our proposal and work of ref. 34 relies on the employed OVMM. In ref. 34, the number of the reconfigurable parameters is \(2N\), which is contributed by the amplitude modulation and the target intensity pattern. It should be noticed that an Ising interaction matrix without external field has the independent entries of \(N(N-1)/2\). Therefore, the OVMM based on a Fourier lens cannot handle arbitrary Ising models. Compared with work of ref. 34, in which each spin is encoded by a single SLM pixel, our employed OVMM utilized more pixels to form a spin for arbitrary matrix transformations, hence it can solve arbitrary Ising models — that is to say, our demonstration trades the number of implementable spins for the on-demand characteristic.
As mentioned above, our PEIDIA only requires one non-unitary OVMM with proper pretreatment. Besides, the Ising spins are encoded on the phase term of the optical field and only intensity measurement is needed to calculate the Hamiltonian. However, in the on-chip proposal of tunable MZI network, two cascaded Reck schemes are utilized to perform arbitrary OVMM since only unitary matrix transformations can be performed by the Reck scheme. Each Reck scheme requires \(N(N-1)/2\) MZIs37. For example, a 20-dimensional Reck scheme totally needs 190 MZIs, which consist of 380 beam splitters and 380 phase shifters. Such cascaded structure would impede its high-dimensional implementations. Nevertheless, the primary advantage of the proposal with tunable MZI network is the achievement of the Ising machine on a photonic chip. It should be mentioned that our architecture maybe implemented with integrated photonic devices. As shown in Fig. 2, the experimental demonstration mainly consists of lens, SLMs and camera. The functions of SLMs for OVMM and the lens could be realized with tunable metasurfaces47,48. The spin vector could be updated via high-speed phase modulators49 instead of refreshing SLMs. Besides, the high-speed photodetectors50 could be employed to measure the output intensities.
The time cost of our demonstration of the PEIDIA consists of the pretreatment cost in the electronic domain and the iteration cost during the annealing process. In the pretreatment stage, the time complexity of the eigen-decomposition is \(O({N}^{3})\)44 and the generation of the phase patterns on the SLMs is \(O({N}^{2})\). In fact, the pattern on SLM0 is a beam-splitting pattern, and that on SLM2 is a beam-recombining pattern, which could be pre-generated before the annealing process. Different beam-splitting patterns on SLM1 would correspond to different Ising problems, and the generation of each pattern takes about 11 min for the 20-spin experiment and 17 min for the 30-spin experiment. Such pre-generation could be done while solving the previous problems. During the annealing process, the beam-splitting and recombining patterns on SLM0-2 are unchanged, and only the pre-generated constant phase delay masks encoding the sampled spin state are appended to SLM1 in each iteration, as shown in Fig. 1. Therefore, the time cost is primarily determined by the optoelectronic iterations. The time cost per iteration in optical domain \({t}_{{{{{{\rm{o}}}}}}}\) depends on the propagation time of light \({t}_{{{{{{\rm{p}}}}}}}\), the updating time of SLM1 \({t}_{{{{{{\rm{u}}}}}}}\) and the detection time of the camera \({t}_{{{{{{\rm{d}}}}}}}\), leading to a total \({t}_{{{{{{\rm{o}}}}}}}={t}_{{{{{{\rm{p}}}}}}}+{t}_{{{{{{\rm{u}}}}}}}+{t}_{{{{{{\rm{d}}}}}}}\) ≈ 0.32 s. The rest operations in the electronic domain are the same as those in the algorithm simulation and the time cost \({t}_{{{{{{\rm{e}}}}}}}\) is negligible. Thus, the total time cost per iteration is \({t}_{{{{{{\rm{iter}}}}}}}={t}_{{{{{{\rm{o}}}}}}}+{t}_{{{{{{\rm{e}}}}}}}\) ≈ 0.32 s. In each iteration, the OVMM can perform \(F={2N}^{2}+2N\) floating-point operations (FLOPs)33, including \({2N}^{2}\) multiplications of \({{{{{\bf{A}}}}}}{{{{{\boldsymbol{\sigma }}}}}}\) and \(2N\) multiplications in the intensity detection process. For instance, for model 3 (\(N\)=30), the operation speed of the OVMM is \(R=F/{t}_{{{{{{\rm{iter}}}}}}}\,=\) 5.81 kFLOP/s. The total energy consumption of the optical system is \(P\)=16 W, including the power of laser and camera (see detailed analysis in Supplementary Note 7). Thus, the energy consumption is \({e}_{{ff}}=P/R\,=\) 2.75 mJ/FLOP. In the future, the PEIDIA based on integrated devices would achieve more spins, smaller size and less optical time cost, which could lead to higher computation speed and lower energy consumption.
Conclusions
In summary, our proposed PEIDIA provides an architecture that can map arbitrary Ising problems to a photonic system. The PEIDIA provides a fully reconfigurable and high-fidelity optical computation, which can accelerate the vector-matrix multiplication with the parallel propagation of light. The PEIDIA only requires one step of OVMM and intensity detection, which makes the architecture more compact and stable. As a proof of principle, two 20-dimensional and one 30-dimensional Ising problems have been successfully solved with high ground state probabilities of 0.99, 0.97, and 0.85 respectively. In the spatial-photonic implementation of the PEIDIA, the number of spins can be increased by optimizing the experimental conditions, such as employing shorter wavelength, or higher-resolution SLMs. Meanwhile, the utilization of the detector with lower noise level is significant to ensure the high searching accuracy of the PEIDIA in high-dimensional conditions. In our current experimental demonstration of the PEIDIA, the performances are severely limited by the conversion time between optical and electronic signals. We are still undergoing the corresponding work about the integrated scheme of PEIDIA, and we believe that our architecture could be further improved to achieve large-scale on-demand photonic Ising machines.
Methods
Generating the phase-only patterns on SLMs
The phase-only patterns on SLM0-2 to conduct the beam-splitting and recombining operations are iteratively optimized based on a gradient-descent method, rather than simply taking the argument pattern of the superposed weighted blazed gratings in our previous work40,41,42,43. The loss function depending on complex-valued parameters is defined as the difference between the target field and the field modulated by the pattern to be optimized. The three patterns are generated according to the actual experimental setup. More details of the method are provided in Supplementary Note 3.
Calibration of SLMs
Due to various unavoidable systematic errors such as misalignment in the OVMM system, the phase term and the beam-splitting and recombining ratios of all the patterns need to be calibrated. The calibration method is improved from our previous work42 based on homodyne detection. Such calibration significantly enhanced the fidelity of OVMM and more details are provided in Supplementary Note 3.
Annealing parameters
For model 1, the experimental parameters are: initial temperature \({\left({T}_{0}\right)}_{\exp }\) = 3000, steps per temperature stage \({n}_{{{{{{\rm{step}}}}}}}\) = 30, stages of temperature \({n}_{{{{{{\rm{temp}}}}}}}\) = 20 and annealing factor \(\eta\) = 0.9. For 100 average values of \({K}_{1}\) in Supplementary Fig. 7g, which are the Hamiltonian normalization coefficients (see Supplementary Note 5), 100 corresponding initial temperature \({\left({T}_{0}\right)}_{{{{{{\rm{simu}}}}}}}\) are obtained with \({\left({T}_{0}\right)}_{{{{{{\rm{simu}}}}}}}={\left({T}_{0}\right)}_{\exp }/{K}_{1}\). Other parameters are the same as those in experiment. For each \({\left({T}_{0}\right)}_{{{{{{\rm{simu}}}}}}}\), 100 simulations are conducted, hence totally 10000 simulations are conducted to obtained the simulation curve of ground state probability in Fig. 4b. For model 2/3, the experimental parameter is \({\left({T}_{0}\right)}_{\exp }\) = 2150/1200, \({n}_{{{{{{\rm{step}}}}}}}\) = 40/50, \({n}_{{{{{{\rm{temp}}}}}}}\) = 30/40 and \(\eta\) = 0.90/0.92, respectively. The process of obtaining the simulation curve of ground state probability in Fig. 4e, h is the same as that in model 1. The full operation process is shown in Supplementary Note 2.
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding authors upon reasonable request.
Code availability
The codes for the generation of the phase patterns on spatial light modulators in this study are available from the corresponding authors upon reasonable request.
References
Hromkovič, J. Algorithmics for Hard Problems: Introduction to Combinatorial Optimization, Randomization, Approximation, and Heuristics. (Springer Science & Business Media, 2013).
Ernst, I. Beitrag zur theorie des ferromagnetismus. Z. f.ür. Phys. A Hadrons Nucl. 31, 253–258 (1925).
Onsager, L. A two-dimensional model with an order-disorder transition (crystal statistics I). Phys. Rev. 65, 117–149 (1944).
Brilliantov, N. V. Effective magnetic Hamiltonian and Ginzburg criterion for fluids. Phys. Rev. E 58, 2628 (1998).
Hopfield, J. J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl Acad. Sci. 79, 2554–2558 (1982).
Gilli, M., Maringer, D. & Schumann, E. Numerical Methods and Optimization in Finance. (Academic Press, 2019).
Bryngelson, J. D. & Wolynes, P. G. Spin glasses and the statistical mechanics of protein folding. Proc. Natl Acad. Sci. 84, 7524–7528 (1987).
Degasperi, A., Fey, D. & Kholodenko, B. N. Performance of objective functions and optimisation procedures for parameter estimation in system biology models. NPJ Syst. Biol. Appl. 3, 1–9 (2017).
Zhang, Q., Deng, D., Dai, W., Li, J. & Jin, X. Optimization of culture conditions for differentiation of melon based on artificial neural network and genetic algorithm. Sci. Rep. 10, 1–8 (2020).
Mohseni, N., McMahon, P. L. & Byrnes, T. Ising machines as hardware solvers of combinatorial optimization problems. Nat. Rev. Phys. 4, 363–379 (2022).
Lucas, A. Ising formulations of many NP problems. Front. Phys. 2, 5 (2014).
Tanahashi, K., Takayanagi, S., Motohashi, T. & Tanaka, S. Application of Ising machines and a software development for Ising machines. J. Phys. Soc. Jpn. 88, 061010 (2019).
Karp, R. M. Reducibility among combinatorial problems. in Complexity of computer computations, 85–103 (Springer, 1972).
Brush, S. G. History of the Lenz-Ising model. Rev. Mod. Phys. 39, 883 (1967).
Cohen, E. & Tamir, B. Quantum annealing—foundations and frontiers. Eur. Phys. J. Spec. Top. 224, 89–110 (2015).
Kim, K. et al. Quantum simulation of frustrated Ising spins with trapped ions. Nature 465, 590–593 (2010).
Britton, J. W. et al. Engineered two-dimensional Ising interactions in a trapped-ion quantum simulator with hundreds of spins. Nature 484, 489–492 (2012).
Camsari, K. Y., Faria, R., Sutton, B. M. & Datta, S. Stochastic p-bits for invertible logic. Phys. Rev. X 7, 031014 (2017).
Dickson, N. G. et al. Thermally assisted quantum annealing of a 16-qubit problem. Nat. Commun. 4, 1903 (2013).
Dutta, S. et al. An Ising Hamiltonian solver based on coupled stochastic phase-transition nano-oscillators. Nat. Electron 4, 502–512 (2021).
Cai, F. et al. Power-efficient combinatorial optimization using intrinsic noise in memristor Hopfield neural networks. Nat. Electron. 3, 409–418 (2020).
Aramon, M. et al. Physics-inspired optimization for quadratic unconstrained problems using a digital annealer. Front. Phys. 7, 48 (2019).
Yamaoka, M. et al. A 20k-Spin Ising Chip to Solve Combinatorial Optimization Problems With CMOS Annealing. IEEE J. Solid-State Circuits 51, 303–309 (2016).
Wang, Z., Marandi, A., Wen, K., Byer, R. L. & Yamamoto, Y. Coherent Ising machine based on degenerate optical parametric oscillators. Phys. Rev. A 88, 063853 (2013).
Marandi, A., Wang, Z., Takata, K., Byer, R. L. & Yamamoto, Y. Network of time-multiplexed optical parametric oscillators as a coherent Ising machine. Nat. Photonics 8, 937–942 (2014).
McMahon, P. L. et al. A fully programmable 100-spin coherent Ising machine with all-to-all connections. Science 354, 614–617 (2016).
Inagaki, T. et al. A coherent Ising machine for 2000-node optimization problems. Science 354, 603–606 (2016).
Honjo, T. et al. 100,000-spin coherent Ising machine. Sci. Adv. 7, eabh0952 (2021).
Cen, Q. et al. Large-scale coherent Ising machine based on optoelectronic parametric oscillator. Light Sci. Appl. 11, 333 (2022).
Calvanese Strinati, M., Bello, L., Dalla Torre, E. G. & Pe’er, A. Can nonlinear parametric oscillators solve random Ising models? Phys. Rev. Lett. 126, 143901 (2021).
Lin, X. et al. All-optical machine learning using diffractive deep neural networks. Science 361, 1004–1008 (2018).
Zhou, T. et al. Large-scale neuromorphic optoelectronic computing with a reconfigurable diffractive processing unit. Nat. Photonics 15, 367–373 (2021).
Shen, Y. et al. Deep learning with coherent nanophotonic circuits. Nat. Photon 11, 441–446 (2017).
Pierangeli, D., Marcucci, G. & Conti, C. Large-scale photonic Ising machine by spatial light modulation. Phys. Rev. Lett. 122, 213902 (2019).
Roques-Carmes, C. et al. Heuristic recurrent algorithms for photonic Ising machines. Nat. Commun. 11, 1–8 (2020).
Prabhu, M. et al. Accelerating recurrent Ising machines in photonic integrated circuits. Optica 7, 551–558 (2020).
Reck, M., Zeilinger, A., Bernstein, H. J. & Bertani, P. Experimental realization of any discrete unitary operator. Phys. Rev. Lett. 73, 58 (1994).
Kirkpatrick, S., Gelatt, C. D. Jr & Vecchi, M. P. Optimization by simulated annealing. Science 220, 671–680 (1983).
Van Laarhoven, P. J. & Aarts, E. H. Simulated annealing. in Simulated annealing: Theory and applications 7–15 (Springer, 1987).
Wang, Y., Potoček, V., Barnett, S. M. & Feng, X. Programmable holographic technique for implementing unitary and nonunitary transformations. Phys. Rev. A 95, 033827 (2017).
Zhao, P. et al. Universal linear optical operations on discrete phase-coherent spatial modes with a fixed and non-cascaded setup. J. Opt. 21, 104003 (2019).
Li, S. et al. Programmable coherent linear quantum operations with high-dimensional optical spatial modes. Phys. Rev. Appl. 14, 024027 (2020).
Li, S. et al. All-optical image identification with programmable matrix transformation. Opt. Express 29, 26474–26485 (2021).
Abdi, H. Eigen-decomposition: eigenvalues and eigenvectors. In Encyclopedia of Measurement and Statistics (ed. Salkind, N. J.) 304–308 (Thousand Oaks: Sage Publications, 2007).
Katoch, S., Chauhan, S. S. & Kumar, V. A review on genetic algorithm: past, present, and future. Multimed. Tools Appl. 80, 8091–8126 (2021).
Shannon, C. E. Communication in the presence of noise. Proc. IRE 37, 10–21 (1949).
Li, G., Zhang, S. & Zentgraf, T. Nonlinear photonic metasurfaces. Nat. Rev. Mater. 2, 1–14 (2017).
Li, S.-Q. et al. Phase-only transmissive spatial light modulator based on tunable dielectric metasurface. Science 364, 1087–1090 (2019).
Renaud, D. et al. Sub-1 Volt and high-bandwidth visible to near-infrared electro-optic modulators. Nat. Commun. 14, 1496 (2023).
Vivien, L. et al. Zero-bias 40Gbit/s germanium waveguide photodetector on silicon. Opt. express 20, 1096–1101 (2012).
Acknowledgements
This work was supported by the National Key Research and Development Program of China (2018YFB2200402, 2017YFA0303700), the National Natural Science Foundation of China (Grant No. 61875101). This work was also supported by Beijing academy of quantum information science, Beijing National Research Center for Information Science and Technology (BNRist), Frontier Science Center for Quantum Information, Tsinghua University Initiative Scientific Research Program and Huawei Technologies Co., Ltd. The authors would like to thank Mr. Hejia Zhang, Bowen Xia and Ziyue Yang for their valuable discussions and helpful comments.
Author information
Authors and Affiliations
Contributions
J.O. and X.F. conceived the idea. J.O. designed and performed the simulations, experiments, and data analysis. Y.L. contributed significantly to the numerical simulations. Z.M. and D.K. helped to perform the experiments. J.O. and X.F. wrote the manuscript. X.Z., X.D., K.C., F.L., and W.Z. supervised the manuscript. Y.H. supervised, reviewed, and edited the manuscript. All authors read and approved the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ouyang, J., Liao, Y., Ma, Z. et al. On-demand photonic Ising machine with simplified Hamiltonian calculation by phase encoding and intensity detection. Commun Phys 7, 168 (2024). https://doi.org/10.1038/s42005-024-01658-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-024-01658-x
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.