Abstract
Recently, spatial photonic Ising machines (SPIM) have been demonstrated to compute the minima of Hamiltonians for large-scale spin systems. Here we propose to implement an antiferromagnetic model through optoelectronic correlation computing with SPIM. Also we exploit the gauge transformation which enables encoding the spins and the interaction strengths in a single phase-only spatial light modulator. With a simple setup, we experimentally show the ground-state-search acceleration of an antiferromagnetic model with 40000 spins in number-partitioning problem. Thus such an optoelectronic computing exhibits great programmability and scalability for the practical applications of studying statistical systems and combinatorial optimization problems.
Similar content being viewed by others
Introduction
The spin-glass models are widely used for investigations of interacting systems in both science and engineering1,2,3,4,5,6,7,8,9,10,11,12. In the past decades, the developments in spin machines have generated tremendous interest due to the prospects of solving a large class of NP-hard problems by searching the ground states of spin system Hamiltonians13. Optimization problem solvers with remarkable performance have been demonstrated in various systems, e.g., trapped ions14,15,16, atomic and photonic condensates17,18, superconducting circuits19, coupled parametric oscillators20,21,22,23,24,25,26,27,28,29,30, injection-locked or degenerate cavity lasers31,32,33,34, integrated nanophotonic circuits35,36,37,38,39,40, and polaritons41,42,43.
Recently, like optical analog computations exploring the spatial degrees of freedom44,45,46,47,48,49,50,51,52,53,54,55, the spatial photonic Ising machine (SPIM) has been proposed with reliable large-scale Ising spin systems, even up to thousands of spins56. With spatial light modulations, these spatial Ising spin setups benefit from the high speed and parallelism of optical signal processing56,57,58,59,60. Although the modeling of ferromagnetic and spin-glass systems has been demonstrated61, how to implement antiferromagnetic models in SPIM has not been proposed yet. In particular, the antiferromagnetic Ising models are important and extensive in research fields like oxide materials62 and giant magnetoresistance63,64. Also, the combinatorial optimization problems with antiferromagnetic Ising models have many real-world applications such as multiprocessor scheduling, minimization of circuit size and delay, cryptography, and logistics analysis65,66.
In this work, we propose to implement the antiferromagnetic model through optoelectronic correlation computing. We show that an antiferromagnetic Hamiltonian can be evaluated through the correlation between a distribution function and the measured optical intensity with SPIM, which can neither be implemented through simply adopting the gauge transformation proposed in our previous work61, nor by the target-intensity approach in the original SPIM paper56. We experimentally demonstrate the accelerated searching for optimizing the number-partitioning problem, where 40,000 spins are connected with random antiferromagnetic interaction strengths. Here we use the algorithm only to show that the SPIM with the measurement-feedback scheme efficiently accelerates the searching process with the reduced Hamiltonian, even when the system is associated with the optical aberrations and the measurement uncertainty. Our results show that the proposed antiferromagnetic model in SPIM can evolve toward the ground state, exhibiting an efficient approach by scalable degrees of freedom in spatial light modulation.
Results
Optoelectronic correlation computing for Mattis-type Ising model
We first introduce the gauge transformation for SPIM, which encodes the spins and the interaction strengths in a single phase-only spatial light modulator (SLM)61. We consider a Mattis-type spin-glass system with the Ising model Hamiltonian \(H=-{\sum}_{jh}{J}_{jh}{\sigma }_{j}{\sigma }_{h}\), where the spin configuration is \({{{{{{{\bf{S}}}}}}}}\,{{\mbox{=}}}\,\{{\sigma }_{j}\}\) (j = 1, 2, ⋯ N) and σj takes binary value of either +1 or −1, representing the spin-up or spin-down state, respectively. The interaction strengths can be expressed as Jjh = ξjξhG(j − h), where G(j − h) is the interaction strength as a function of the distance between two spins with the unit of energy, and the amplitude modulation ξj is limited as −1 ≤ ξj ≤ 1. By the gauge transformation shown in Fig. 1a, when rotating each original spin σj with the angle \({\alpha }_{j}=\arccos {\xi }_{j}\), the new spin vector \({\sigma }_{j}^{\prime}\) is projected on the z-axis to obtain the effective spin \({\sigma }_{j}^{^{\prime} z}={\xi }_{j}{\sigma }_{j}\). As a result, the gauge transformation keeps the Hamiltonian invariant \(H=-{\sum}_{jh}G(j-h){\sigma }_{j}^{^{\prime} z}{\sigma }_{h}^{^{\prime} z}\), while the interactions between the z components of gauge-transformed spins are equal to the strength G(j − h).
a Schematic of the gauge transformation. The dotted, blue and red arrows correspond to the origin spin σj, the new spin vector \({\sigma }_{j}^{\prime}\) and the effective spin vector \({\sigma }_{j}^{^{\prime} z}\), respectively. After clockwise rotating with respect to the z-axis with the angle αj, the interaction strengths Jjh are uniform and equal to J. b The experimental optical setups for SPIM: SLM, spatial light modulator; CCD: charge-coupled device; C, collimator; L, lens; P, polarizer. A collimated laser beam illuminates the SLM. By gauge transformation, the gauge-transformed effective spin configuration \({{{{{{{{\bf{S}}}}}}}}}^{^{\prime} z}=\{{\sigma }_{m,n}^{^{\prime} z}\}\) is encoded through a single phase-only SLM following Eq. (1), where φm,n is the phase modulation and \({\alpha }_{m,n}=\arccos {\xi }_{m,n}\) for each spin. The modulated light is detected by a CCD camera in the back-focus plane of lens L1.
The gauge invariance property promises that the experimental implementation only needs a single phase-only SLM, with uniform illumination by a collimated uniform laser beam (Fig. 1b). This setup circumvents the difficulty of pixel alignment in the previously proposed SPIM56,57,58,59, and therefore greatly improves the system stability and the computing fidelity. Since the spins are loaded through two-dimensional spatial modulation, the j-th spin is distributed in a square lattice at j = (m, n), where 1 ≤ m ≤ Nx, 1 ≤ n ≤ Ny. According to ref. 61 and Supplementary Note 1, after the gauge transformation, each spin is encoded by a macropixel with phase modulation φm,n such that \({\sigma }_{j}^{^{\prime} z}=\exp (i{\varphi }_{m,n})\) and
where \({\alpha }_{m,n}=\arccos {\xi }_{m,n}\). Then with lens L1 of the focal length f performing Fourier transformation, we detect the band-limited intensity distribution I(u) confined within the first diffraction order zone A on the focal plane, and \(I({{{{{{{\bf{u}}}}}}}})={\sum}_{jh}{\sigma }_{j}^{^{\prime} z}{\sigma }_{h}^{^{\prime} z}{e}^{i\frac{2\pi }{f\lambda }({{{{{{{{\bf{x}}}}}}}}}_{j}-{{{{{{{{\bf{x}}}}}}}}}_{h})\cdot {{{{{{{\bf{u}}}}}}}}}{{{\mbox{sinc}}}}^{2}(\frac{{{{{{{{\bf{u}}}}}}}}W}{f\lambda })\), where λ is the wavelength, f is the focal length of lens L1, W is the length of each macropixel, xj = Wj is the center position of the j-th pixel, u = (u, v) is the spatial coordinate in the focal plane, and \(\,{{\mbox{sinc}}}\,({{{{{{{\bf{u}}}}}}}})=\frac{\sin \pi u}{\pi u}\frac{\sin \pi v}{\pi v}\). Suppose that we preset a distribution function gc(u) and evaluate the correlation function F as
Here
that is, G(k) is the Fourier transformation of \({g}_{{{{{{{{\rm{c}}}}}}}}}\left({{{{{{{\bf{u}}}}}}}}\right){{{\mbox{sinc}}}}^{2}(\frac{W{{{{{{{\bf{u}}}}}}}}}{f\lambda })\). Indeed, Eq. (2) shows that by presetting an appropriate gc, a Mattis-type Ising Hamiltonian can be evaluated as
We note that the distribution function gc(u) is distinct from the target intensity IT(u) proposed in ref. 56. Here gc(u) can be an arbitrary real function to guarantee an even function of the interaction strength [c.f. Eq. (3)], which has either positive or negative values, while the target intensity IT always has non-negative values. In particular, for the antiferromagnetic model, all the interaction strengths Jjh < 0. In the case that ξjs are positive, G(j−h) should be negative to ensure antiferromagnetic interactions between all the spins. It leads that gc must be negative for some values of u, otherwise Eq. (3) shows G > 0 for j = h. Moreover, when gc has both positive and negative values, the Hamiltonian can be evaluated through the correlation function as Eq. (2), while it cannot be implemented by the target-intensity approach in ref. 56. Although Eq. (2) requires the numerical computation, as discussed in the last paragraph of the “Experimental ground state search” in the Results, the optical computation is dominant in our proposed spatial photonic Ising machine.
Number-partitioning problem with the antiferromagnetic Hamiltonian
The antiferromagnetic model in SPIM provides a computation platform for studying the challenging combinatorial optimization problems. As a demonstration, here we present the ground-state-search process of a combinatorial optimization problem, the NP-hard number-partitioning problem13,67: One would like to divide a set Ξ = {ξj}, containing N real numbers (j = 1, 2, ⋯ N), into two subsets Ξ1 and Ξ2, such that the difference between the summations of elements in two subsets \({\sum }_{1}={\sum}_{{\xi }_{j}\in {{{\Xi }}}_{1}}{\xi }_{j}\) and \({\sum }_{2}={\sum}_{{\xi }_{j}\in {{{\Xi }}}_{2}}{\xi }_{j}\) is as small as possible. Without loss of generality, we suppose all ξjs in the set Ξ are real numbers belonging to the range (0, 1]. Specifically, when the number set Ξ has parity symmetry, the spins of such models can be analytically zed. For instance, for the set with an even total number of ξjs, when ξj = ξN+1−j, the spin should be σj = − σN+1−j to ensure the equivalence of two subsets. In general, by labeling the elements belonging to two different subsets Ξ1 and Ξ2 with σj = 1 and −1, respectively, the optimization is equivalent to minimizing the antiferromagnetic Hamiltonian \(H={({\sum}_{j}{\xi }_{j}{\sigma }_{j})}^{2}={\sum}_{jh}{\xi }_{j}{\xi }_{h}{\sigma }_{j}{\sigma }_{h}\).
To implement such an antiferromagnetic Hamiltonian in SPIM, we explore the gauge transformation to search a spin configuration \({{{{{{{{\bf{S}}}}}}}}}^{\prime}=\{{\sigma }_{j}^{^{\prime} z}\}\) where \({\sigma }_{j}^{^{\prime} z}={\xi }_{j}{\sigma }_{j}\) while keeping the interaction strength between any two spins G(k) = −1. Due to the gauge invariance, the Hamiltonian is \(H={\sum}_{jh}{\sigma }_{j}^{^{\prime} z}{\sigma }_{h}^{^{\prime} z}\) and the optimized value of \(\left|{\sum }_{1}-{\sum }_{2}\right|\) is the total magnetization strength of the gauge-transformed spins \(\left|m^{\prime} \right|=\frac{1}{N}\left|{\sum}_{j}{\sigma }_{j}^{^{\prime} z}\right|\). During the experimental iterations, the spin configuration is updated gradually56, and the system definitely evolves to the ground states, indicating the process of solving the optimization problem.
Experimental ground state search
We experimentally demonstrate the ground-state-search acceleration with the number-partitioning problem (see the “Experimental setup” in the Methods). Here each spin is encoded by a macropixel with 2-by-2 pixels on SLM with the length of W = 16 μm. As the beam size is much larger than that of the array, we assume that light illuminates each macropixel with a uniform amplitude.
In order to evaluate the correlation function F, we first numerically calculate the distribution function gc(u) through Eq. (3). Since \(G\left({{{{{{{\bf{k}}}}}}}}\right)\) are known for specific optimization problems, \({g}_{{{{{{{{\rm{c}}}}}}}}}\left({{{{{{{\bf{u}}}}}}}}\right)\) can be numerically evaluated by the inverse Fourier transform, without numerical errors even for the discrete u. Given the interaction strength between any two spins G(k) = −1, Fig. 2a shows the calculated distribution function gc(u). We note that gc(u) have both positive and negative values, which means such a case cannot be implemented by the target-intensity approach as ref. 56. We also need to calibrate the intensity measurement such that the distribution function gc(u) has the same origin as the intensity distribution I(u). In order to reduce the impact of optical aberrations, we measure the intensity distribution on charge-coupled device (CCD) plane (Fig. 2b) by setting the SLM with uniform phase modulation. Therefore, the origin of I(u) is marked at the maximal intensity through the numerical fitting.
a Calculated distribution function gc(u) of the antiferromagnetic Mattis model, where the interaction strength between any two spins G(k) = −1. b By setting the spatial light modulator (SLM) with uniform phase modulation, we measure the intensity on the camera plane and thus determine the origin of coordinates at the maximal intensity. Imax is the maximal measured intensity, W = 16 μm, f = 100 mm, λ = 532 nm, and u = (u, v), where u and v are the spatial coordinates in the camera plane, respectively.
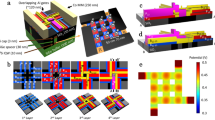
Next as an example, we demonstrate the searching process with the number-partitioning problem of a set Ξ = {ξj} with N = 40,000 elements. The set Ξ is randomly generated that each element ξj is a real number randomly chosen from (0, 1], as presented in Fig. 3a in the form of a 200-by-200 array. We start with the initial state that all spins are uniformly distributed as σj = 1 and update the spin configuration for ground state search. Here we utilize the Markov chain Monte Carlo algorithm, where σjs are tentatively updated during each iteration, and the gauge-transformed spins \({\sigma }_{j}^{^{\prime} z}={\xi }_{j}{\sigma }_{j}\) are encoded on SLM following Eq. (1). Then we measure the intensity I(u) on the CCD and evaluate the system Hamiltonian through the correlation function F as Eq. (2). The updated spin configuration is accepted only when the Hamiltonian decreases.
a The set Ξ = {ξj} containing 40,000 elements, where each ξj is chosen randomly from (0, 1] with uniform probability. b Evolutions of the Hamiltonian H and the amplitude of the gauge-transformed magnetization \(m^{\prime}\) during the iterations. Four independent trials are conducted with uniform initial spin configurations. For clear visualization, c and d, respectively, presents only a part of the final configurations of the gauge-transformed spins \(\{{\sigma }_{j}^{^{\prime} z}\}\) on the spatial light modulator and the original spins \(\left\{{\sigma }_{j}\right\}\), which correspond to the red square box in (a).
Figure 3b shows the evolution of the Hamiltonian H and the amplitude of the gauge-transformed magnetization \(\left|m^{\prime} \right|\) during the ground-state-search process. In the experiment, four independent trials are conducted with the initial state that all spins are uniformly distributed. For all the four cases, the Hamiltonian H and the magnetization \(\left|m^{\prime} \right|\) decrease rapidly at the beginning of the iteration, because the initial spin configuration strongly deviates from the ground state. As the number of iterations increases, the Hamiltonian tends to be stable, while the \(\left|m^{\prime} \right|\) starts to fluctuate. We attribute it to the too weak intensity distribution I(u), which is strongly affected by the noise during the measurement. As a result, the spin configuration may be incorrectly updated with the distribution resulting in a larger \(\left|m^{\prime} \right|\). The accuracy can be improved by using a wide dynamic-range detector for intensity measurement, or by adjusting the input light intensity in real time within a suitable range.
Here for clear visualization, corresponding to the red square in Fig. 3a, Fig. 3c and d present a part of the final configurations of the gauge-transformed spins \({{{{{{{{\bf{S}}}}}}}}}^{\prime}=\{{\sigma }_{j}^{^{\prime} z}\}\) and the resulting spin configuration \(\{{\sigma }_{j}\}\), respectively. Overall, for all these four trials, \(\left|m^{\prime} \right|\) reaches lower than 1.7 × 10−3 within 100 iterations. Thus during the ground state search, the magnetization \(\left|m^{\prime} \right|\) decreases by nearly three orders of magnitude, which indicates the validity of the gauge transformation method for antiferromagnetic model.
To evaluate the scalability of the ground state search for number-partitioning problems, we define the computing fidelity as \(\left|\frac{{\sum }_{1}\,-\,{\sum }_{2}}{{\sum }_{1}\,+\,{\sum }_{2}}\right|\), which is expected to be as small as possible like \(\left|m^{\prime} \right|\), and investigate its performance as a function of the size N of the number set. We perform experiments for sizes N varying from 1600 to 40,000. For each N, we perform 10 independent experimental trials with different sets Ξ = {ξj}, and then the averaged computing fidelity is obtained by measuring the final states after 1000 iterations. From the results in Fig. 4, we can see that fidelity remains within 6.9 × 10−3, demonstrating that the experimental setup works effectively for large-scale number sets. The good scalability of SPIM with gauge transformation on number-partitioning problems is inherited in the parallelism of the optical analog signal processing in the spatial domain.
We note that the stable variation of the fidelity with the number of spins is attributed to the background noise of CCD measurement. As the number of spins N grows, the measurement uncertainty of the Hamiltonian accumulates and the deviation between the subsets \(\left|{{{\Sigma }}}_{1}-{{{\Sigma }}}_{2}\right|\) becomes larger. At the same time, the entire set \(\left|{{{\Sigma }}}_{1}+{{{\Sigma }}}_{2}\right|\) as the denominator is also increasing, while the fidelity remains stable with N. We add the details of a numerical simulation for the fidelity in Supplementary Note 2, which also agrees well with the experimental results shown in Fig. 4. It is worth noting that by reducing the impact of the background noise, the fidelity can be improved with low-noise CCD devices or dynamic adjustment of the intensity for laser source and the corresponding \({g}_{{{{{{{{\rm{c}}}}}}}}}\left({{{{{{{\bf{u}}}}}}}}\right)\).
We further investigate the system computing acceleration and analyze the fraction of the physical process of light in the total computation. We evaluate how many real-number operations are required to simulate the physical process of light and the details are given in Supplementary Note 3, with the computational method utilized in ref. 68. As a result, we show that the optical computation is dominant in the proposed SPIM, e.g., for the condition of N = 40,000, the fraction of the total computation by the physical process of light is more than 94%. We note that the optical computation process is ultrafast, high-throughput, and low-power-consumption in comparison with the digital one. Therefore, we believe our method can greatly improve speed and efficiency of the simulation for antiferromagnetic Hamiltonian.
Conclusion
We propose to implement antiferromagnetic model in SPIM. By gauge transformation, an antiferromagnetic Hamiltonian can be evaluated through the correlation between the distribution function and the measured optical intensity with SPIM. To improve the processing speed of the system, the ultrafast SLM and CCD at gigahertz rates with the most recent technologies69,70 is helpful and practical. Also, the computing accuracy can be improved with a more sensitive CCD camera. We note that our proposed method can be applied to the ground-state-search process, e.g., adiabatic evolution and simulated annealing algorithms71,72.
In summary, we optically demonstrate the ground-state-search process of an antiferromagnetic Mattis model with thousands of spins, as well as the number-partitioning problem. With the improved accuracy resulting from gauge transformation, we successfully reduce the total magnetization strength of the gauge-transformed spins \(\left|m^{\prime} \right|\) by nearly three orders of magnitude. Thus for practical applications in modeling statistical systems and studying combinatorial optimization problems, such an optoelectronic computing exhibits great programmability and scalability in large-scale systems.
Methods
Experimental setup
As shown in Fig. 1b, a collimated Gaussian beam (wavelength λ = 532 nm) is expanded by two confocal lenses L2 (50 mm focal length) and L3 (500 mm focal length). After expansion, the waist radius of the collimated beam is about 36 mm. Then a polarizer P is used to prepare the incident beam linearly polarized along the long display axis of the SLM (Holoeye PLUTO-NIR-011). The SLM is calibrated through the two-shot method based on generalized spatial differentiator73. Lens L1 with the focal length f = 100 mm performs Fourier transformation, where a CCD beam profiler (Ophir SP620) is used to detect the optical field intensity on the back focal plane.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Code availability
The code that support the findings of this study are available from the corresponding author upon reasonable request.
References
Binder, K. & Young, A. P. Spin glasses: experimental facts, theoretical concepts, and open questions. Rev. Mod. Phys. 58, 801 (1986).
Edwards, S. F. & Anderson, P. W. Theory of spin glasses. J. Phys. F: Met. Phys. 5, 965 (1975).
Sherrington, D. & Kirkpatrick, S. Solvable model of a spin-glass. Phys. Rev. Lett. 35, 1792 (1975).
Gabay, M. & Toulouse, G. Coexistence of spin-glass and ferromagnetic orderings. Phys. Rev. Lett. 47, 201 (1981).
Reger, J. D. & Zippelius, A. Three-dimensional random-bond Ising model: phase diagram and critical properties. Phys. Rev. Lett. 57, 3225 (1986).
De las Cuevas, G., Dur, W., Briegel, H. J. & Martin-Delgado, M. A. Unifying all classical spin models in a lattice gauge theory. Phys. Rev. Lett. 102, 230502 (2009).
Bañuls, M. C. et al. Simulating lattice gauge theories within quantum technologies. Eur. Phys. J. D. 74, 165 (2020).
Hopfield, J. J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl Acad. Sci. USA 79, 2554 (1982).
Amit, D. J., Gutfreund, H. & Sompolinsky, H. Spin-glass models of neural networks. Phys. Rev. A 32, 1007 (1985).
Agliari, E., Barra, A., De Antoni, A. & Galluzzi, A. Parallel retrieval of correlated patterns: from Hopfield networks to Boltzmann machines. Neural Netw. 38, 52 (2013).
Sourlas, N. Spin-glass models as error-correcting codes. Nature 339, 693 (1989).
Nishimori, H. Statistical Physics of Spin Glasses and Information Processing: an Introduction 111 (Clarendon Press, 2001).
Lucas, A. Ising formulations of many NP problems. Front. Phys. 2, 5 (2014).
Kim, K. et al. Quantum simulation of frustrated Ising spins with trapped ions. Nature 465, 590 (2010).
Britton, J. W. et al. Engineered two-dimensional Ising interactions in a trapped-ion quantum simulator with hundreds of spins. Nature 484, 489 (2012).
Ma, X.-S., Dakic, B., Naylor, W., Zeilinger, A. & Walther, P. Quantum simulation of the wavefunction to probe frustrated Heisenberg spin systems. Nat. Phys. 7, 399 (2011).
Struck, J. et al. Engineering Ising-XY spin-models in a triangular lattice using tunable artificial gauge fields. Nat. Phys. 9, 738 (2013).
Vretenar, M., Kassenberg, B., Bissesar, S. Toebes, C., & Klaers, J. Controllable Josephson junction for photon Bose–Einstein condensates. Phys. Rev. Research 3, American Physical Society, 023167 https://doi.org/10.1103/PhysRevResearch.3.023167 (2021).
Johnson, M. W. et al. Quantum annealing with manufactured spins. Nature 473, 194 (2011).
McMahon, P. L. et al. A fully programmable 100-spin coherent Ising machine with all-to-all connections. Science 354, 614 (2016).
Inagaki, T. et al. A coherent Ising machine for 2000-node optimization problems. Science 354, 603 (2016).
Inagaki, T. et al. Large-scale Ising spin network based on degenerate optical parametric oscillators. Nat. Photonics 10, 415 (2016).
Böhm, F., Verschaffelt, G. & Van der Sande, G. A poor man’s coherent Ising machine based on opto-electronic feedback systems for solving optimization problems. Nat. Commun. 10, 3538 (2019).
Hamerly, R. et al. Experimental investigation of performance differences between coherent Ising machines and a quantum annealer. Sci. Adv. 5, eaau0823 (2019).
Bello, L., Calvanese Strinati, M., Dalla Torre, E. G. & Pe’er, A. Persistent coherent beating in coupled parametric oscillators. Phys. Rev. Lett. 123, 083901 (2019).
Böhm, F. et al. Understanding dynamics of coherent Ising machines through simulation of large-scale 2D Ising models. Nat. Commun. 9, 5020 (2018).
Tiunov, E. S., Ulanov, A. E. & Lvovsky, A. Annealing by simulating the coherent Ising machine. Opt. Express 27, 10288 (2019).
Wang, Z., Marandi, A., Wen, K., Byer, R. L. & Yamamoto, Y. Coherent Ising machine based on degenerate optical parametric oscillators. Phys. Rev. A 88, 063853 (2013).
Yamamoto, Y. et al. Coherent Ising machines optical neural networks operating at the quantum limit. npj Quantum Inf. 3, 49 (2017).
Marandi, A., Wang, Z., Takata, K., Byer, R. L. & Yamamoto, Y. Network of time-multiplexed optical parametric oscillators as a coherent Ising machine. Nat. Photonics 8, 937 (2014).
Utsunomiya, S., Takata, K. & Yamamoto, Y. Mapping of Ising models onto injection-locked laser systems. Opt. Express 19, 18091 (2011).
Takata, K., Utsunomiya, S. & Yamamoto, Y. Transient time of an Ising machine based on injection-locked laser network. N. J. Phys. 14, 013052 (2012).
Babaeian, M. et al. A single shot coherent Ising machine based on a network of injection-locked multicore fiber lasers. Nat. Commun. 10, 3516 (2019).
Tradonsky, C. et al. Rapid laser solver for the phase retrieval problem. Sci. Adv. 5, eaax4530 (2019).
Roques-Carmes, C. et al. Heuristic recurrent algorithms for photonic Ising machines. Nat. Commun. 11, 249 (2020).
Prabhu, M. et al. Accelerating recurrent Ising machines in photonic integrated circuits. Optica 7, 551 (2020).
Shen, Y. & Harris, N. C. et al. Deep learning with coherent nanophotonic circuits. Nat. Photonics 11, 441 (2017).
Wu, K., De Abajo, J. G., Soci, C., Shum, P. P. & Zheludev, N. I. An optical fiber network oracle for NP-complete problems. Light.: Sci. Appl. 3, e147 (2014).
Vázquez, M. R. et al. Optical NP problem solver on laser-written waveguide platform. Opt. Express 26, 702 (2018).
Okawachi, Y. et al. Demonstration of chip-based coupled degenerate optical parametric oscillators for realizing a nanophotonic spin-glass Nature communications 11, 1–7 Nature Publishing Group, (2020).
Berloff, N. G. et al. Realizing the classical XY Hamiltonian in polariton simulators. Nat. Mater. 16, 1120 (2017).
Kalinin, K. P. & Berloff, N. G. Simulating Ising and n-state planar Potts models and external fields with nonequilibrium condensates. Phys. Rev. Lett. 121, 235302 (2018).
Kalinin, K. P., Amo, A., Bloch, J. & Berloff, N. G. Polaritonic XY-Ising machine. Nanophotonics 9, 4127 (2020).
Silva, A. et al. Performing mathematical operations with metamaterials. Science 343, 160 (2014).
Bykov, D. A., Doskolovich, L. L., Bezus, E. A. & Soifer, V. A. Optical computation of the Laplace operator using phase-shifted Bragg grating. Opt. Express 22, 25084 (2014).
Ruan, Z. Spatial mode control of surface plasmon polariton excitation with gain medium: from spatial differentiator to integrator. Opt. Lett. 40, 601 (2015).
Youssefi, A., Zangeneh-Nejad, F., Abdollahramezani, S. & Khavasi, A. Analog computing by Brewster effect. Opt. Lett. 41, 3467 (2016).
Zhu, T. et al. Plasmonic computing of spatial differentiation. Nat. Commun. 8, 15391 (2017).
Zhang, W. et al. Implementing quantum search algorithm with metamaterials. Adv. Mater. 30, 1703986 (2018).
Guo, C., Xiao, M., Minkov, M., Shi, Y. & Fan, S. Photonic crystal slab Laplace operator for image differentiation. Optica 5, 251 (2018).
Zhu, T. et al. Generalized spatial differentiation from the spin Hall effect of light and its application in image processing of edge detection. Phys. Rev. Appl. 11, 034043 (2019).
Zhu, T., Huang, J. & Ruan, Z. Optical phase mining by adjustable spatial differentiator. Adv. Photonics 2, 016001 (2020).
Zangeneh-Nejad, F., Sounas, D. L., Alù, A. & Fleury, R. Analogue computing with metamaterials. Nat. Rev. Mater. 6, 207 (2020).
Huang, J., Zhang, J., Zhu, T. & Ruan, Z. Spatiotemporal differentiators generating optical vortices with pure transverse orbital angular momentum and detecting sharp change of pulse envelope. Preprint at https://arxiv.org/abs/2106.14420 (2021).
Zhu, T. et al. Topological optical differentiator. Nat. Commun. 12, 680 (2021).
Pierangeli, D., Marcucci, G. & Conti, C. Large-scale photonic Ising machine by spatial light modulation. Phys. Rev. Lett. 122, 213902 (2019).
Pierangeli, D., Marcucci, G., Brunner, D. & Conti, C. Noise-enhanced spatial-photonic Ising machine. Nanophotonics 9, 4109 (2020).
Pierangeli, D., Marcucci, G. & Conti, C. Adiabatic evolution on a spatial-photonic Ising machine. Optica 7, 1535 (2020b).
Pierangeli, D., Rafayelyan, M., Conti, C. & Gigan, S. Scalable spin-glass optical simulator. Phys. Rev. Appl. 15, 034087 (2021).
Kumar, S., Zhang, H. & Huang, Y.-P. Large-scale Ising emulation with four body interaction and all-to-all connections. Commun. Phys. 3, 108 (2020).
Fang, Y., Huang, J. & Ruan, Z. Experimental observation of phase transitions in spatial photonic Ising machine. Phys. Rev. Lett. 127, 043902 (2021).
Shull, C. G., Strauser, W. & Wollan, E. Neutron diffraction by paramagnetic and antiferromagnetic substances. Phys. Rev. 83, 333 (1951).
Binasch, G., Grünberg, P., Saurenbach, F. & Zinn, W. Enhanced magnetoresistance in layered magnetic structures with antiferromagnetic interlayer exchange. Phys. Rev. B 39, 4828 (1989).
Baibich, M. N. et al. Giant magnetoresistance of (001) Fe/(001) Cr magnetic superlattices. Phys. Rev. Lett. 61, 2472 (1988).
Graß, T., Raventós, D., Juliá-Díaz, B., Gogolin, C. & Lewenstein, M. Quantum annealing for the number-partitioning problem using a tunable spin glass of ions. Nat. Commun. 7, 11524 (2016).
Mertens, S. The easiest hard problem: number partitioning. Computational Complex. Stat. Phys. 125, 125 (2006).
Mertens, S. Phase transition in the number partitioning problem. Phys. Rev. Lett. 81, 4281 (1998).
Zhou, T. et al. Large-scale neuromorphic optoelectronic computing with a reconfigurable diffractive processing unit. Nat. Photonics 15, 367 (2021).
Chen, Q. et al. Ultra-broadband spatial light modulation with dual-resonance coupled epsilon-near-zero materials. Nano Res. 14, 2673 (2021).
Park, J. et al. All-solid-state spatial light modulator with independent phase and amplitude control for three-dimensional LiDAR applications. Nat. Nanotechnol. 16, 69 (2021).
Farhi, E. et al. A quantum adiabatic evolution algorithm applied to random instances of an NP-complete problem. Science 292, 472 (2001).
Kirkpatrick, S., Gelatt, C. D. & Vecchi, M. P. Optimization by simulated annealing. Science 220, 671 (1983).
Huang, J., Zhu, T. & Ruan, Z. Two-shot calibration method for phase-only spatial light modulators with generalized spatial differentiator. Phys. Rev. Appl. 14, 054040 (2020).
Acknowledgements
The authors acknowledge funding through the National Natural Science Foundation of China (NSFC Grants Nos. 12174340, 91850108, and 61675179), the National Key Research and Development Program of China (Grant No. 2017YFA0205700), the Open Foundation of the State Key Laboratory of Modern Optical Instrumentation, and the Open Research Program of Key Laboratory of 3D Micro/Nano Fabrication and Characterization of Zhejiang Province.
Author information
Authors and Affiliations
Contributions
J.H. and Y.F. carried out numerical simulations, experiments, and data analysis. All the authors contributed to write the paper. Z.R. supervised the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Communications Physics thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Huang, J., Fang, Y. & Ruan, Z. Antiferromagnetic spatial photonic Ising machine through optoelectronic correlation computing. Commun Phys 4, 242 (2021). https://doi.org/10.1038/s42005-021-00741-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-021-00741-x
This article is cited by
-
Point convolutional neural network algorithm for Ising model ground state research based on spring vibration
Scientific Reports (2024)
-
Observation of distinct phase transitions in a nonlinear optical Ising machine
Communications Physics (2023)
-
Photonic matrix multiplication lights up photonic accelerator and beyond
Light: Science & Applications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.