Abstract
Generative modeling has seen a rising interest in both classical and quantum machine learning, and it represents a promising candidate to obtain a practical quantum advantage in the near term. In this study, we build over an existing framework for evaluating the generalization performance of generative models, and we establish the first quantitative comparative race towards practical quantum advantage (PQA) between classical and quantum generative models, namely Quantum Circuit Born Machines (QCBMs), Transformers (TFs), Recurrent Neural Networks (RNNs), Variational Autoencoders (VAEs), and Wasserstein Generative Adversarial Networks (WGANs). After defining four types of PQAs scenarios, we focus on what we refer to as potential PQA, aiming to compare quantum models with the best-known classical algorithms for the task at hand. We let the models race on a well-defined and application-relevant competition setting, where we illustrate and demonstrate our framework on 20 variables (qubits) generative modeling task. Our results suggest that QCBMs are more efficient in the data-limited regime than the other state-of-the-art classical generative models. Such a feature is highly desirable in a wide range of real-world applications where the available data is scarce.
Similar content being viewed by others
Introduction
Generative modeling has become more widely popular with its remarkable success in tasks related to image generation and text synthesis, as well as machine translation1,2,3,4,5,6, making this field a promising avenue to demonstrate the power of quantum computers and to reach the paramount milestone of practical quantum advantage (PQA)7. The most desirable feature in any machine learning (ML) model is generalization, and as such, this property should be considered to assess its performance in search of PQA. However, the definition of this property in the domain of generative modeling can be cumbersome, and it is yet an unresolved question for the case of arbitrary generative tasks8. Its definition can take on different nuances depending on the area of research, such as in computational learning theory9 or other practical approaches10,11. Reference 12 defines an unambiguous framework for generalization on discrete search spaces for practical tasks. This approach puts all generative models on an equal footing since it is sample-based and does not require knowledge of the exact likelihood, therefore making it a model-agnostic and tractable evaluation framework. This reference also demonstrates footprints of a quantum-inspired advantage of Tensor Network Born Machines13 compared to Generative Adversarial Networks14.
To the best of our knowledge, in the search for PQA, a concrete quantitative comparison between quantum generative models and a broader class of classical state-of-the-art generative models is still lacking. In particular, quantum circuit Born machines (QCBMs)15 have not been compared up-to-date with other classical generative models in terms of generalization, although they have been shown recently for their ability to generalize16. In this paper, we aim to bridge this gap by providing a numerical comparison between quantum and classical state-of-the-art generative models in terms of generalization.
In this comparison, these models compete for PQA. For this ‘race’ to be well-defined, it is essential to establish its rules first. Indeed, a clear-cut definition of PQA is not present in the relevant literature so far, especially when it comes to challenging ML applications such as generative modeling, or in general, to practical ML.
Previous works emphasize either computational quantum advantage, or settings that are not relevant from a real-world perspective, or scenarios that use data sets that give an advantage to the quantum model from the start (and also bear no relevance to a real-world setting)17,18,19,20,21. One potential exception would be the case of ref. 22, which showed an advantage for a quantum ML model in a practical setting. However, besides the challenge of relying on loaded quantum data23, it is still unclear if it would be relevant to some concrete real-world and large-scale applications, although the authors mention some potential applications in the domain of quantum sensing.
We acknowledge as well previous works that have attempted or proposed ways to perform model comparisons, within generative models and beyond. For instance, a recent work24 has developed a metric for assessing the quality of variational calculations for different classical and quantum models on an equal footing. Another recent study25 proposes a detailed analysis that systematically compares generative models in terms of the quality of training to provide insights on the advantage of their adoption by quantum computing practitioners, although without addressing the question of generalization. In another recent work26, the authors propose the generic notion of quantum utility, a measure for quantifying effectiveness and practicality, as an index for PQA, but this work differs from our study in the sense that PQA is defined in a broad perspective as the ability of a quantum device to be either faster, more accurate or demanding less energy compared to classical machines with similar characteristics in a certain task of interest. Others have emphasized quantum simulation as one of the prominent opportunities for PQA27. In our paper, we share the long-term goal of identifying practical use cases for which quantum computing has the potential to bring an advantage. However, our work is focused on generative models and their generalization capabilities, which is the gold standard to measure the performance of generative ML models in real-world use cases.
In summary, the goal of this framework and of this study is to set the stage for a quantitative race between different state-of-the-art classical and quantum generative models in terms of generalization in search of PQA, uncovering the strengths and weaknesses of each model under realistic ‘race conditions’ (see Fig. 1). These competition rules are defined in advance before the fine-tuning of each model and dictated by the desired outcome from real-world motivated metrics and limitations, making our framework application and/or commercially relevant from the start. Hence, we consider this formalization to be one of the main contributions of this work. This focus is motivated by the growing interest of the scientific and business community in showcasing the value of quantum strategies compared to conventional algorithms, and provides a common ground for a fair comparison based on relevant properties. Overall, we show that QCBMs are competitive with the other classical state-of-the-art generative models and provide the best compromise for the requirements of the generalization framework we are adopting. Additionally, we demonstrate that QCBMs perform well in the low-data regime, which constitutes a bottleneck for deep learning models28,29,30 and which we believe to be a promising setting for PQA.
In (a), each runner (generative model) is characterized by (some of) its strengths and weaknesses, namely: training efficiency, sampling efficiency, and expressive power. Note that the power bars are indicative, and that is far from trivial to determine them, but some insights can be obtained from intuition from the theoretical characterization of some of the models, e.g., via computational quantum advantage papers, or known properties or highlights for each model. A complete characterization of the runner can be used to identify the odds-on favorite, independent of the specific race context. In (b), the different runners are embedded into a context (i.e., ‘the real-world application setting’) represented as a concrete instance of a hurdles race. They all run the same race, but they see the hurdles differently according to their strengths and weaknesses. The runners can compete on different tracks, for instance, on shorter or longer tracks. For the PQA race to be well defined, it is necessary to clearly state what track is taken under examination. In this study, we propose two tracks, motivated by the limitation of sampling or cost evaluation budget. Once the track is selected, we can evaluate runners using different criteria: application-driven metrics need to be defined to fully characterize the race. Our evaluation criterion is the quality-based generalization, with appropriate metrics defined in Methods Section ‘Generalization Metrics’ (see also Fig. 2 for further specific details).
Results and discussion
Defining practical quantum advantage
In this work, we refer to practical quantum advantage (PQA) as the ability of a quantum system to perform a useful task—where ‘useful’ can refer to a scientific, industrial, or societal use - with performance that is faster or better than what is enabled by any existing classical system26,31. We highlight that this concept differs from the computational quantum advantage notion (originally introduced as quantum supremacy), which refers instead to the capability of quantum machines to outperform classical computers, providing a speedup in solving a given task, which would otherwise be classically unsolvable, even using the best classical machine and algorithm18,20,22,32.
By taking inspiration from ref. 33, we define four different types of PQA. The first version, which we refer to as provable PQA (PrPQA) has the ultimate goal of demonstrating the superiority of a quantum algorithm with respect to the best classical algorithm, where the proof is backed up by complexity theory arguments34,35. An example of this would be to show a realization of Shor’s algorithm at scale. To the best of our knowledge, the equivalent of Shor’s algorithm in the context of real-world ML tasks, i.e., useful enough to be included in the definition of provable PQA provided above, is still missing. Here, we focus on the following three classes, which might be more reachable with near- and medium-term quantum devices. We define robust PQA (RPQA) as a practical advantage of a quantum algorithm compared to the best available classical algorithms. It is worth noting that an RPQA can be short-lived when a better classical algorithm is potentially developed after an RPQA has been established. On some occasions, there is no clear consensus about the status of the best available classical algorithm as it depends on each scientific community. To go around that, we can conduct a comparison with a state-of-the-art classical algorithm or a set of classical algorithms. If there is a quantum advantage in this case, we can refer to it as potential PQA (PPQA). Within this scenario, a genuine attempt to compare against the best-known classical algorithms has to be conducted with the possibility that a PPQA is short-lived with the development or discovery of more powerful and advanced classical algorithms. A weaker scenario corresponds to the case where we promote a classical algorithm to its quantum counterpart to investigate whether quantum effects are useful. A quantum advantage in this scenario is an example of limited PQA (LPQA). A potential case is a comparison between a restricted Boltzmann machine36 and a quantum Boltzmann machine37. In this study, we are pushing the search for PQA beyond the LPQA scenario to a PPQA, with the hope to include a more comprehensive list of the best available classical models in our comparison in future studies.
In this study, we consider different generative models and let them compete for PPQA. To illustrate our approach, we propose a simple sports analogy. Let us consider a hurdles race, where different runners are competing against each other. Each generative model can thus be seen as a runner in such a race. Each contender has their strengths and weaknesses, which make them see hurdles differently (see Fig. 1a). Thus, one can aim to investigate relevant model features and determine whether they constitute a strength for the model under examination. However, hurdles races take place in a specific concrete context, for instance, with given wind and track surface conditions, which affect the competition outcome significantly (see Fig. 1b). The PQA approach takes this concrete context into account when evaluating the contenders, who are analyzed not only ‘in principle’ but also embedded in a specific context. For example, the track field’s length is crucial for the evaluation since different runners can perform differently if the ‘rules of the game’ are modified. The conditions of the race affect the runners’ performance, which is equivalent to saying that generative models are affected by factors such as the type and size of the dataset, the ground truth distribution to be learned, etc. Each instance of a generative modeling task is unique, just as the conditions for every day of the competitions could be unique. As such, the tracks and the race conditions must be specified before the competition happens, to clarify the precise setting where the search for PQA (or, in our study, for PPQA) takes place.
Lastly, we argue that, when evaluating performance in a concrete instance of a race on a given track, the measure of success for an athlete might not necessarily be attributed to the maximum speed. Outside the analogy, other factors than the speedup are likely needed to be taken into account to judge if practical quantum advantage has occurred. Quality-based generalization is one of these playgrounds. This is particularly relevant when considering combinatorial optimization problems, as suggested by the generative enhanced optimization (GEO) framework38. This reference introduces a connection between generative models and optimization, which is in and of itself a new perspective on a family of commercially valuable use cases for generative models beyond large language models and image generation, but that is not fully appreciated yet by the ML community. Remarkably, quality-based generalization turns out to be paramount when the generative modeling task under examination is linked to a cost-equipped optimization problem. In this scenario, it is desirable to learn to generate solutions with the lowest possible cost, at least lower (i.e., of better quality) compared to the available costs in a training dataset. The utility, the minimum value, and the quality coverage have been introduced precisely to quantify this capability. However, these metrics can be computed in different ways according to the main features of a specific use case, i.e., as in the analogy of a track field defining the rules of the game. In Section ‘Competition details’, we propose two distinct ‘track fields’ that give us two different lenses, according to which we conduct a comparison of generative models toward PPQA in an optimization context that takes the resource bottlenecks of the specific use case into consideration.
Competition details
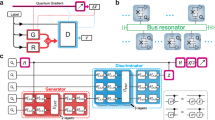
In our study, we compare several quantum and state-of-the-art classical generative models. On the quantum side, we use quantum circuit Born machines (QCBMs)15 that are trained with a gradient-free optimization technique. On the classical side, we use Recurrent Neural Networks (RNN)39, Transformers (TF)2, Variational Autoencoders (VAE)40, and Wasserstein Generative Adversarial Networks (WGAN)14. More details about these models and their characteristics along with their hyperparameters are explained in Supplementary Note 1 ‘Generative Models’.
As a test bed, and to illustrate a concrete realization of our framework, we choose a re-weighted version of the Evens (also known as parity) distribution where each bitstring with a non-zero probability has an even number of ones16. Although the cost values for the bitstrings of the Evens dataset are synthetic and used mainly to provide a simple illustration of the framework, this distribution embeds a combinatorial constraint that is relevant in marginal probabilistic inference tasks41,42, and in modular constrained optimization43, and it also has real-world applications, namely in the parity-constrained facility location problem44. For the Evens distribution, the size of the solution space, for Nvar binary variable, is given by \(| S| ={2}^{{N}_{{{{{{{{\rm{var}}}}}}}}}-1}\). Furthermore, we choose a synthetic cost, called the negative separation cost c16, which is defined as the negative of the largest separation between two 1 in a bitstring, i.e., c(x) = − (z + 1), where z is the largest number of consecutive zeros in the bitstring x. For instance, c (‘11100011’) = −4, c (‘10110011’) = −3, and c (‘11111111’) = −1. Note that the minimum of this cost function is known exactly and it is equal to − (Nvar − 1), which corresponds to the bitstring ‘100…001’.
Given this cost function, we can define our re-weighted training distribution Ptrain over the training data, such that:
with inverse temperature \(\beta \equiv \hat{\beta }/2\), where \(\hat{\beta}\) is defined as the standard deviation of the scores c in the training set. If a data point \({{{{{{{\bf{x}}}}}}}}\, \notin \, {{{{{{{{\mathcal{D}}}}}}}}}_{{{{{{{{\rm{train}}}}}}}}}\), then we assign Ptrain(x) = 0. The re-weighting procedure applied to the training data encourages our trained models to generate samples with low costs, with the hope that we sample unseen configurations that have a lower cost than the costs seen in the training set38. To achieve the latter, it is crucial that the Kullback-Leibler (KL) divergence between the generative model distribution and the training distribution does not tend to zero during the training to avoid memorizing the training data16. It is important to note that it is not mandatory to apply the re-weighting of the samples as part of the generative modeling task. However, the re-weighting procedure in Eq. (1) has been shown to help in finding high quality samples12,16,38,45. Since all the models will be evaluated in their capabilities to generate low-cost and diverse samples, as dictated by the evaluation criteria Cq, MV, and U, we used the re-weighted dataset to train all the generative models studied here. In reality, the bare training set consists of T data points with their respective cost values c, and any other transformation could be applied to facilitate the generation of high-quality samples.
In our simulations, we choose Nvar = 20 as the size of each bitstring, and we train our generative models for two training set sizes corresponding to ϵ = 0.001 and ϵ = 0.01 (see Fig. 2). We choose the training data for the two different epsilons, such that we have the same minimum cost of −12 for the two datasets. The purpose of this constraint is to rule out the effect of the minimum seen cost in our experiments. We have selected these small epsilon values to probe the model’s capabilities to successfully train and generalize in this scarce-data regime.
Given the training dataset with size ∣Dtrain∣ = ϵ∣S∣, sampled from the Evens distribution where \(| S| ={2}^{{N}_{{{{{{{{\rm{var}}}}}}}}}-1}\), we choose different generative models, and select the track we want to compare them on (i.e., select the ‘rules of the game’ used to probe the generative models). We then train and fine-tune them using the chosen dataset. After this step, we estimate the quality-based metrics Cq, MV, and U using the selected track, T1 or T2, to assess the quality of the queries generated by each model. In the first track T1, we use Q = 104 queries to estimate our metrics, whereas, for the second track T2, we require Qu = 102 unique and valid samples at most to compute our metrics. We also choose different values of the data portion ϵ to investigate its influence on the generalization of each generative model. For a fair comparison, we use the same training budget Nepochs = 1000. Additionally, we use Nseeds = 10 different initializations for each generative model to obtain error bars on metrics.
We focus our attention on evaluating quality-based generalization for the aforementioned generative models (the ‘runners’) using two different competition rules (the ‘tracks’). These two tracks described next are motivated, respectively, by the sampling budget and the difficulty of evaluating a cost function, which are common bottlenecks affecting real-world tasks. Specifically:
-
Track 1 (T1): there is a fixed budget of queries Q generated by the generative model to compute the quality coverage Cq, minimum value MV and the utility U to establish the most advantageous models (see Methods ‘Generalization Metrics’). This criterion is appropriate in the case where it is cheap to compute the cost associated with samples while only having access to a limited sampling budget. For instance, a definition of PPQA based on T1 can be used in the case of generative models requiring expensive resources for sampling, such as QCBMs executed on real-world quantum computers. Here, one aims to reduce the number of measurements as much as possible while still being able to see an advantage in the quality of the generated solutions.
-
Track 2 (T2): there is a fixed budget Qu of unique, unseen and valid samples to compute the quality coverage, the utility and the minimum value. This approach implies the ability of sampling from the trained models repeatedly to get up to Qu unique, unseen and valid queries. Note that some models might never get to the target Qu, for instance, if they suffer from mode collapse. In this case, the metrics can be computed using the reached \({\tilde{Q}}_{{{{{{{{\rm{u}}}}}}}}}\). This track is motivated by a class of optimization problems where the cost evaluation is expensive. Examples of such scenarios include molecule design and drug discovery that involve clinical trials. In these settings, the cost function is expensive to compute. This track is aimed to provide a proxy reflecting these real-world use cases. In this case, one aims to avoid excessive evaluations of the cost function, i.e., for repeated samples.
Regarding the sampling budget, we use Q = 104 configurations to estimate our quality metrics for track T1. From the perspective of track T2, we sample until we obtain Qu = 102 unique configurations that are used to compute our quality-based metrics. Note that we checked how many sample batches are needed, and we observed that Q = 104 is enough to extract Qu = 102 unique configurations for all the generative models in our study. Our metrics are averaged over 10 random seeds for each model while keeping the same data for each portion ϵ. For a fair comparison between the generative models, we conduct a hyperparameters grid search using Optuna46, and we extract the best generative model that allows obtaining the lowest utility after 100 training steps. Note that, in order to carry out the hyperparameters tuning process, one could also utilize MV, Cq, or any appropriate combination of the three metrics. Additionally, as a fair training budget, we train all our generative models for Nepochs = 1000 steps. We compute our quality-based generalization metrics for tracks T1 and T2 after each 100 training steps. We do not include this sampling cost in the evaluation budget (Q or Qu), as in this study, we are not focusing on the training efficiency of these models, so we allow potentially unlimited resources for the training process. However, for a more realistic setting, the sampling budget could be customized to keep the training requirements into account. For clarity, Fig. 2 provides a schematic representation of our methods. The hyperparameters of each architecture and the parameter count are detailed in Supplementary Table I.
Numerical experiments
We show the generalization results of the different generative models for the two levels of data availability, ϵ = 0.01, 0.001, and for the two different tracks, T1 and T2. We start our analysis with ϵ = 0.01 as illustrated in Fig. 3a. By looking at the first track T1, and focusing on the MV results, we observe that the models experience a quick drop for the first 100 training steps. It is also interesting to see that all the models produce samples with a cost lower than the minimum cost value provided in the training set samples. Furthermore, we can see that VAEs, WGANs, and QCBMs converge to the lowest minimum value of −19, whereas RNNs and TFs jump to higher minimum values with more training steps. In this case, these two models gradually overfit the training data and generalize less to the low-cost sectors. This point highlights the importance of early stopping or monitoring our models during training to obtain their best performances. The utility (T1) provides a complementary picture, where we observe the VAE providing the lowest utility throughout training, followed by the QCBM and then by the other generative models. This ranking highlights the value of QCBMs compared to the other classical generative models. One interesting feature of QCBMs compared to the other models is the monotonic decrease of the utility in addition to its competitive diversity of samples, as illustrated by the quality coverage (T1). The quality coverage also shows the ability of QCBMs, in addition to VAEs and WGANs, to generate a diverse pool of unseen solutions with a lower cost compared to the costs shown in the training data. From the point of view of the second track T2, we observe that the WGAN has the best performance in terms of the three metrics. Additionally, all the models are still generalizing to configurations with a lower cost compared to what was seen in the training data. A complementary picture of the best quality metrics throughout training is provided in Fig. 4a for clearer visibility of the ranking of generative models in our race.
Here, we plot the quality coverage, utility, and minimum value for the two tracks T1 and T2 for Nvar = 20 binary variables. Additionally, the models are trained using Nseeds = 10 random seeds, and the outcomes of the metrics are averaged over these seeds with error bars estimated as one standard deviation, which can be computed for each metric as \(\sqrt{\,{{\mbox{Variance}}}\,/{N}_{{{{{{{{\rm{seeds}}}}}}}}}}\). a Corresponds to data fraction ϵ = 0.01, hence to a size of the training dataset of 5242. Here, the VAE (Variational AutoEncoder) provides the best overall performance for T1 (a1–a3), whereas the WGAN (Wasserstein Generative Adversarial Network) is superior compared to the other models for T2 (a4–a6). b Corresponds to ϵ = 0.001, hence to a smaller size of the training dataset equal to 524. From the T1 point of view (b1–b3), we observe that the QCBM (Quantum Circuit Born Machine) obtains the lowest utility compared to the other models while having a competitive diversity of high-quality solutions. From the perspective of T2 (b4–b6), QCBMs are competitive with the VAE and ahead of the WGAN, the TF (Transformer), and the RNN (Recurrent Neural Network). These results highlight the efficiency of the QCBMs in the scarce-data regime. Note that the dashed horizontal lines correspond to the minimum cost of −12 in the training data.
The setup is the same as in Fig. 3, where the two tracks T1 and T2 for Nvar = 20 binary variables are considered, the models are trained using Nseeds = 10 random seeds. The error bars correspond to one standard deviation defined as \(\sqrt{\,{{\mbox{Variance}}}\,/{N}_{{{{{{{{\rm{seeds}}}}}}}}}}\) where the number of seeds Nseeds = 10. In (a), we represent the best quality metrics with a data fraction ϵ = 0.01, which corresponds to a size of the training dataset of 5242. Here, we observe that the VAE (Variational AutoEncoder) has the best performance for track T1, whereas the WGAN (Wasserstein Generative Adversarial Network) is the best model for track T2. In (b), we represent our best results for ϵ = 0.001, hence for a smaller size of the training dataset equal to 524. Here, we remark that the QCBM (Quantum Circuit Born Machine) has optimal performances for track T1 and is competitive with the other models on track T2 in terms of MV and U while providing a better Cq. To improve the comparison clarity, we added horizontal lines, which correspond to the largest quality coverage, the lowest minimum values, or the lowest utilities among all the models.
We now focus our attention on the results obtained for the degree of data availability corresponding to ϵ = 0.001 as illustrated in Fig. 3b. We again observe that all the models are generalizing to unseen configurations with a lower cost than the minimum cost seen in the training data. For the first track, T1, we highlight that the QCBM provides the lowest utility compared to the other models while maintaining a competitive minimum value and diversity of high-quality solutions. For the second track, T2, we observe that the QCBM is competitive with the VAE while providing the best quality coverage Cq. This point is clearer when analyzing and comparing the best quality-based metrics values in Fig. 4b.
Overall, QCBMs provide the best quality-based generalization performances compared to the other generative models in the low-data regime with the limited sampling budget, i.e., for ϵ = 0.001 and T1 with a sampling budget of Q = 104 queries. More specifically, our QCBM competes on the quality coverage and the minimum value metrics and excels in the trend of the utility. This efficiency in the low-data regime is a highly desirable feature compared to classical generative models, which are known in real-world settings to be data-hungry28,29,30. It is worthwhile to note that the used QCBM has the lowest number of parameters compared to the other generative models as outlined in Supplementary Note 1. Although using the parameters count to compare substantially different generative models is not necessarily a well-founded method (even if widespread), we highlight that the quantum models can achieve results that are competitive with classical models that have significantly more parameters, sometimes one to two order(s) of magnitude more. Overall, these findings are promising steps toward identifying scenarios where quantum models can provide a potential advantage in the scarce data regime. More details about the best results obtained by our generative models can be found in Supplementary Note 2 ‘Additional quality-based generalization results’.
Finally, we would like to note that QCBMs are also competitive with RNNs and TFs in terms of pre-generalization and validity-based generalization metrics (see Methods ‘Generalization Metrics’) for both data availability settings, ϵ = 0.001, 0.01, as outlined in Supplementary Note 3 ‘Pre-generalization and validity-based generalization results’. The VAE and the WGAN tend to sacrifice these aspects of generalization compared to quality-based generalization. Here, the QCBM provides the best balance between quality-based and validity-based generalization (see Supplementary Note 3).
Conclusions
In this paper, we have established a race between classical and quantum generative models in terms of quality-based generalization and defined four types of practical quantum advantage (PQA). Here, we focus on what we referred to as potential PQA (PPQA), which aims to compare quantum models with the best-known classical algorithms to the best of our efforts and compute capabilities for the specific task at hand. We have proposed two different competition rules for comparing different models and defining PPQA. We denote these rules as tracks based on the race analogy. We have used QCBMs, RNNs, TFs, VAEs, and WGANs to provide an instance of this comparison on the two tracks. The first track (T1) relies on assuming a fixed sampling budget at the evaluation stage while allowing for an arbitrary number of cost function evaluations. In contrast, the second track (T2) assumes we only have access to a limited number of cost function evaluations, which is the case for applications where the cost estimation is expensive. We also study the impact of the degree of data available to the models for their training. Our results have demonstrated that QCBMs are the most efficient in the scarce-data regime and, in particular, in T2. In general, QCBMs showcase a competitive diversity of solutions compared to the other state-of-the-art generative models in all the tracks and datasets considered here.
It is important to note that the two tracks we chose for this study are not comprehensive, even though they are well motivated by plausible real-world scenarios. One could also use different rules of the game where, for example, the training data can be updated for each training step, as it is customary in the generator-enhanced optimization (GEO) framework38, or where the overall budget takes into account the number of samples required during training. The two tracks introduced here serve the purpose of illustrating the possibilities ahead from this formal approach. In particular, such an approach helps to unambiguously specify the criteria for establishing PQA for generative models in real-world use cases, especially in the context of generative modeling to generate diverse and valuable solutions, which could boost in turn the solution to combinatorial optimization problems. This characterization is a long-sought-after milestone by many application scientists in the quantum information community, and we believe this framework can provide valuable insights when analyzing the suitability of the adoption of quantum or quantum-inspired models against state-of-the-art classical ones.
Despite the encouraging results obtained from our quantum-based models, we foresee a significant space for potential improvements regarding all the generative models used in this study and some not explored here. In particular, one can embed constraints into generative models such as in U(1)-symmetric tensor networks45 and U(1)-symmetric RNNs47,48. Furthermore, including other state-of-the-art generative models with different variations is vital for establishing a more comprehensive comparison, extending the list of competitors both on the classical and quantum side49,50,51,52,53. Moreover, the extension of this work to more realistic datasets is also crucial in the quest to investigate generalization-based PQA. Although for the quantum circuit layout and system sizes used here, one can have an efficient simulation with tensor networks for large system sizes through a synergistic framework between classical simulation techniques and quantum circuits54. The latter can be harnessed to provide a good starting point for quantum circuits based on tensor networks and overcome widespread trainability issues such as barren plateaus. We hope that our work will encourage more comparisons with a broader class of generative models and that it will be diversified to include more criteria for comparison into account.
Methods
Generalization metrics
The evaluation of unsupervised generative models is a challenging task, especially when one aims to compare different models in terms of generalization. In this work, we focus on discrete probability distributions of bitstrings where an unambiguous definition of generalization is possible12. Here, we start from the framework provided in ref. 12 that puts different generative models on an equal footing and allows us to assess the generalization performances of each generative model from a practical perspective.
In this framework, we assume that we are given a solution space S that corresponds to the set of bitstrings that satisfy a constraint or a set of constraints, such that \(| S| \le {2}^{{N}_{{{{{{{{\rm{var}}}}}}}}}}\) where Nvar is the number of binary variables in a bitstring. A typical example is the portfolio optimization problem, where there is a constraint on the number of assets to be included in a portfolio. Additionally, we assume that we are given a training dataset \({{{{{{{{\mathcal{D}}}}}}}}}_{{{{{{{{\rm{train}}}}}}}}}=\{{{{{{{{{\bf{x}}}}}}}}}^{(1)},{{{{{{{{\bf{x}}}}}}}}}^{(2)},\ldots ,{{{{{{{{\bf{x}}}}}}}}}^{(T)}\}\), where T = ϵ∣S∣ and ϵ is a tunable parameter that controls the size of the training dataset such that 0 < ϵ ≤ 1.
The metrics provided in ref. 12 allow probing different features of generalization. There are three main pillars of generalization: (1) pre-generalization, (2) validity-based generalization, and (3) quality-based generalization. In the main text, we focus on quality-based generalization and provide details about pre-generalization and validity-based generalization in Supplementary Note 3 ‘Pre-generalization and validity-based generalization results’.
In typical real-world applications, it is desirable to generate high-quality samples that have a low cost c compared to what has been seen in the training dataset. In the quality-based generalization framework, we can define the minimum value as:
which corresponds to the lowest cost in a given set of unseen and valid queries Gsol, which we obtain after generating a set of queries \({{{{{{{\mathcal{G}}}}}}}}=\{{{{{{{{{\bf{x}}}}}}}}}^{(1)},{{{{{{{{\bf{x}}}}}}}}}^{(2)},\ldots ,{{{{{{{{\bf{x}}}}}}}}}^{(Q)}\}\) from a generative model of interest. In our terminology, a sample x is valid if x ∈ S and it is considered unseen if x ∉ Dtrain. In the ideal scenario, MV is equal to the lowest possible cost, corresponding to the global solution of the problem of interest.
To avoid the chance effect of using the minimum, we can average over different random seeds. We can also define the utility that circumvents the use of the minimum through:
where P5 corresponds to the set of the 5% lowest-cost samples obtained from Gsol. The averaging effect allows us to ensure that a low cost was not obtained by chance. Ideally, the best quality-based generalization corresponds to U equal to the lowest possible cost in our problem of interest.
In quality-based generalization, it is also valuable to have a diverse set of samples that have high quality. To quantify this desirable feature, we define the quality coverage as
where \({g}_{{{{{{{{\rm{sol}}}}}}}}}(c < \mathop{\min }\limits_{{{{{{{{\bf{x}}}}}}}}\in {{{{{{{{\mathcal{D}}}}}}}}}_{{{{{{{{\rm{train}}}}}}}}}}c({{{{{{{\bf{x}}}}}}}}))\) corresponds to the set of unique valid and unseen samples that have a lower cost compared to the minimal cost in the training data. The choice of the values of the number of queries Q depends on the tracks/rules of comparison presented in Section ‘Defining practical quantum advantage’. Note that an ideal diversity of quality samples corresponds to Cq = 1, where all the generated queries are new, unique, and have a cost lower than the minimal training cost. Although this is the ideal case, softer upper bounds can be devised taking into account more realistic scenarios, as proposed in refs. 12,16. On the other side of the spectrum, a very bad quality diversity corresponds to Cq = 0 where all the queries are either inside the training data, are not valid, or have a cost above the minimal training cost.
Data availability
The data generated in this study is available from the corresponding author upon reasonable request.
Code availability
The code used to produce the results of this study is available from the corresponding author upon reasonable request.
References
LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436–44 (2015).
Vaswani, A. et al. Attention is all you need. Advances in Neural Information Processing Systems 30 (2017). https://proceedings.neurips.cc/paper/2017/file/3f5ee243547dee91fbd053c1c4a845aa-Paper.pdf.
Ramesh, A. et al. Zero-shot text-to-image generation. In International Conference on Machine Learning, 8821–8831 (PMLR, 2021). https://arxiv.org/abs/2102.12092.
Rombach, R., Blattmann, A., Lorenz, D., Esser, P. & Ommer, B. High-resolution image synthesis with latent diffusion models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 10684–10695 (2022). https://arxiv.org/abs/2112.10752.
Team, O. Chatgpt: Optimizing language models for dialogue. https://openai.com/blog/chatgpt (2022).
Ouyang, L. et al. Training language models to follow instructions with human feedback. In Advances in Neural Information Processing Systems, Vol. 35 (eds Koyejo, S.et al.) 27730–27744 (Curran Associates, Inc., 2022). https://proceedings.neurips.cc/paper_files/paper/2022/file/b1efde53be364a73914f58805a001731-Paper-Conference.pdf.
Perdomo-Ortiz, A., Benedetti, M., Realpe-Gómez, J. & Biswas, R. Opportunities and challenges for quantum-assisted machine learning in near-term quantum computers. Quant. Sci. Technol. 3, 030502 (2018).
Alaa, A., Van Breugel, B., Saveliev, E. S. & van der Schaar, M. How faithful is your synthetic data? Sample-level metrics for evaluating and auditing generative models. In Proceedings of the 39th International Conference on Machine Learning, Vol. 162 (eds Chaudhuri, K. et al.) 290–306 (PMLR, 2022). https://proceedings.mlr.press/v162/alaa22a.html.
Vapnik, V. N. An overview of statistical learning theory. IEEE Trans. Neural Netw. 10, 988–999 (1999).
Zhao, S. et al. Bias and generalization in deep generative models: an empirical study. Adv. Neural Inform. Process. Syst. 31. https://proceedings.neurips.cc/paper/2018/hash/5317b6799188715d5e00a638a4278901-Abstract.html (2018).
Nica, A. C. et al. Evaluating generalization in gflownets for molecule design. In ICLR2022 Machine Learning for Drug Discovery. https://openreview.net/forum?id=JFSaHKNZ35b (2022).
Gili, K., Mauri, M. & Perdomo-Ortiz, A. Generalization metrics for practical quantum advantage in generative models. arXiv:2201.08770 (2022). https://arxiv.org/abs/2201.08770.
Han, Z.-Y., Wang, J., Fan, H., Wang, L. & Zhang, P. Unsupervised generative modeling using matrix product states. PRX 8, 031012 (2018).
Goodfellow, I. Nips 2016 tutorial: Generative adversarial networks. arXiv:1701.00160 (2016). https://arxiv.org/abs/1701.00160.
Benedetti, M. et al. A generative modeling approach for benchmarking and training shallow quantum circuits. npj Quant. Inform. 5, 45 (2019).
Gili, K., Hibat-Allah, M., Mauri, M., Ballance, C. & Perdomo-Ortiz, A. Do quantum circuit born machines generalize? Quant. Sci. Technol. 8, 035021 (2023).
Havlíček, V. et al. Supervised learning with quantum-enhanced feature spaces. Nature 567, 209–212 (2019).
Boixo, S. et al. Characterizing quantum supremacy in near-term devices. Nat. Phys. 14, 595–600 (2018).
Arute, F. et al. Quantum supremacy using a programmable superconducting processor. Nature 574, 505–510 (2019).
Bouland, A., Fefferman, B., Nirkhe, C. & Vazirani, U. On the complexity and verification of quantum random circuit sampling. Nat. Phys. 15, 159–163 (2019).
Madsen, L. S. et al. Quantum computational advantage with a programmable photonic processor. Nature 606, 75–81 (2022).
Huang, H.-Y. et al. Quantum advantage in learning from experiments. Science 376, 1182–1186 (2022).
Umeano, C., Paine, A. E., Elfving, V. E. & Kyriienko, O. What can we learn from quantum convolutional neural networks? arXiv:2308.16664 (2023). https://arxiv.org/abs/2308.16664.
Wu, D. et al. Variational benchmarks for quantum many-body problems. arXiv:2302.04919 (2023). https://arxiv.org/abs/2302.04919.
Riofrío, C. A. et al. A performance characterization of quantum generative models. arXiv:2301.09363 (2023). https://arxiv.org/abs/2301.09363.
Herrmann, N. et al. Quantum utility - definition and assessment of a practical quantum advantage. In 2023 IEEE International Conference on Quantum Software (QSW), 162–174 (IEEE Computer Society, 2023). https://doi.ieeecomputersociety.org/10.1109/QSW59989.2023.00028.
Daley, A. J. et al. Practical quantum advantage in quantum simulation. Nature 607, 667–676 (2022).
Marcus, G. Deep learning: A critical appraisal. arXiv:1801.00631 (2018). https://arxiv.org/abs/1801.00631.
Zhang, Y. & Ling, C. A strategy to apply machine learning to small datasets in materials science. Npj Comput. Mater. 4, 25 (2018).
Tripp, A., Daxberger, E. & Hernández-Lobato, J. M. Sample-efficient optimization in the latent space of deep generative models via weighted retraining. In Proceedings of the 34th International Conference on Neural Information Processing Systems, NIPS 20 (2020). https://proceedings.neurips.cc/paper/2020/file/81e3225c6ad49623167a4309eb4b2e75-Paper.pdf.
Alsing, P. et al. Accelerating progress towards practical quantum advantage: A national science foundation project scoping workshop. arXiv:2210.14757 (2022). https://arxiv.org/abs/2210.14757.
Preskill, J. Quantum computing in the NISQ era and beyond. Quantum 2, 79 (2018).
Rønnow, T. F. et al. Defining and detecting quantum speedup. Science 345, 420–424 (2014).
Coyle, B., Mills, D., Danos, V. & Kashefi, E. The born supremacy: quantum advantage and training of an ising born machine. npj Quant. Inform. 6. https://www.nature.com/articles/s41534-020-00288-9 (2022).
Sweke, R., Seifert, J.-P., Hangleiter, D. & Eisert, J. On the quantum versus classical learnability of discrete distributions. Quantum 5, 417 (2021).
Hinton, G. A Practical Guide to Training Restricted Boltzmann Machines, 599–619 (Springer, 2012).
Amin, M. H., Andriyash, E., Rolfe, J., Kulchytskyy, B. & Melko, R. Quantum boltzmann machine. Phys. Rev. X 8. https://journals.aps.org/prx/abstract/10.1103/PhysRevX.8.021050 (2018).
Alcazar, J., Vakili, M. G., Kalayci, C. B. & Perdomo-Ortiz, A. Geo: enhancing combinatorial optimization with classical and quantum generative models. arXiv:2101.06250. https://arxiv.org/abs/2101.06250 (2021).
Cho, K., van Merriënboer, B., Bahdanau, D. & Bengio, Y. On the properties of neural machine translation: Encoder–decoder approaches. In Proceedings of SSST-8, Eighth Workshop on Syntax, Semantics and Structure in Statistical Translation (eds Wu, D., Carpuat, M., Carreras, X. & Vecchi, E. M.) 103–111 (Association for Computational Linguistics, 2014). https://aclanthology.org/W14-4012.
Rolfe, J. T. Discrete variational autoencoders. In International Conference on Learning Representations https://openreview.net/forum?id=ryMxXPFex (2017).
Ermon, S., Gomes, C. P., Sabharwal, A. & Selman, B. Optimization with parity constraints: From binary codes to discrete integration. In Proceedings of the Twenty-Ninth Conference on Uncertainty in Artificial Intelligence, UAI’13, 202–211 (AUAI Press, 2013).
Xue, Y., Li, Z., Ermon, S., Gomes, C. P. & Selman, B. Solving marginal map problems with np oracles and parity constraints. In Advances in Neural Information Processing Systems, vol. 29 (Curran Associates, Inc., 2016). https://proceedings.neurips.cc/paper_files/paper/2016/file/a532400ed62e772b9dc0b86f46e583ff-Paper.pdf.
Caldwell, J. R., Watson, R. A., Thies, C. & Knowles, J. D. Deep optimisation: Solving combinatorial optimisation problems using deep neural networks. arXiv:1811.00784. https://arxiv.org/abs/1811.00784 (2018).
Kim, K., Shin, Y. & An, H.-C. Constant-factor approximation algorithms for parity-constrained facility location and k-center. Algorithmica 85, 1883–1911 (2023).
Lopez-Piqueres, J., Chen, J. & Perdomo-Ortiz, A. Symmetric tensor networks for generative modeling and constrained combinatorial optimization. Machine Learning: Science and Technology 4. https://iopscience.iop.org/article/10.1088/2632-2153/ace0f5 (2022).
Akiba, T., Sano, S., Yanase, T., Ohta, T. & Koyama, M. Optuna: A next-generation hyperparameter optimization framework. In Proceedings of the 25rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (2019).
Hibat-Allah, M., Ganahl, M., Hayward, L. E., Melko, R. G. & Carrasquilla, J. Recurrent neural network wave functions. Phys. Rev. Res. 2, 023358 (2020).
Morawetz, S., De Vlugt, I. J., Carrasquilla, J. & Melko, R. G. U (1)-symmetric recurrent neural networks for quantum state reconstruction. Phys. Rev. A 104, 012401 (2021).
Ho, J., Jain, A. & Abbeel, P. Denoising diffusion probabilistic models. Adv. Neural Inform. Process. Syst. 33, 6840–6851 (2020).
Dinh, L., Sohl-Dickstein, J. & Bengio, S. Density estimation using real NVP. In International Conference on Learning Representations. https://openreview.net/forum?id=HkpbnH9lx (2017).
Kyriienko, O., Paine, A. E. & Elfving, V. E. Protocols for trainable and differentiable quantum generative modelling. arXiv:2202.08253. https://arxiv.org/abs/2202.08253 (2022).
Zoufal, C., Lucchi, A. & Woerner, S. Quantum generative adversarial networks for learning and loading random distributions. npj Quant. Inform. 5. https://doi.org/10.1038/s41534-019-0223-2 (2019).
Cong, I., Choi, S. & Lukin, M. D. Quantum convolutional neural networks. Nat. Phys. 15, 1273–1278 (2019).
Rudolph, M. S. et al. Synergistic pretraining of parametrized quantum circuits via tensor networks. Nat. Commun. 14, 8367 (2023).
Acknowledgements
We would like to thank Brian Chen for his generous comments and suggestions, which were very helpful. We also acknowledge Javier Lopez-Piqueres, Daniel Varoli, Vladimir Vargas-Calderón, Brian Dellabetta and Manuel Rudolph for insightful discussions. We also acknowledge Zofia Włoczewska for assistance in designing our figures. Our numerical simulations were performed using Orquestra™. M.H. acknowledges support from Mitacs through Mitacs Accelerate. J.C. acknowledges support from Natural Sciences and Engineering Research Council of Canada (NSERC), the Shared Hierarchical Academic Research Computing Network (SHARCNET), Compute Canada, and the Canadian Institute for Advanced Research (CIFAR) AI chair program. Research at Perimeter Institute is supported in part by the Government of Canada through the Department of Innovation, Science and Economic Development and by the Province of Ontario through the Ministry of Colleges and Universities.
Author information
Authors and Affiliations
Contributions
M.H., M.M., J.C., and A.P.-O. wrote the manuscript, designed the comparison framework, and analyzed the results. M.H., M.M., and A.P.-O. designed the numerical experiments to test the framework. M.H. ran all the simulations. A.P.-O. and M.M. co-supervised the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare the following competing interests: M.H., M.M., and A.P.-O. were employed by Zapata Computing Canada Inc. during the development of this work.
Peer review
Peer review information
Communications Physics thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hibat-Allah, M., Mauri, M., Carrasquilla, J. et al. A framework for demonstrating practical quantum advantage: comparing quantum against classical generative models. Commun Phys 7, 68 (2024). https://doi.org/10.1038/s42005-024-01552-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-024-01552-6
This article is cited by
-
Enhancing combinatorial optimization with classical and quantum generative models
Nature Communications (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.