Introduction

Over the past two decades, a lot of efforts have been devoted to the control of acoustic fields1. A strong expectation is that a wavefield should be manipulated arbitrarily with maximum power transmission efficiency. The proposal of acoustic metasurfaces has offered a feasible solution with a compact design2. Efficient wave manipulation can now be achieved passively at the sub-wavelength scale by precisely processing a microstructure3. Innovative functions such as abnormal reflection4 and refraction5, stealth6, focusing7, and acoustic holography8 have been ingeniously brought into reality. So far, various methods for metasurface design, including the generalized Snell’s law9, impedance matching techniques10,11,12, and diffractive metagrating theory13,14, have been reported and widely implemented. Nevertheless, they sometimes remain unsatisfactory in terms of efficiency, since parasitic scattering is hardly eliminated in a strict sense15.

Inspired by electromagnetism16, the recently proposed surface/interface impedance theory17 suggests a new solution that goes beyond the theoretical limit of the generalized Snell’s law. A metasurface described by the pressure-velocity relationship on a boundary or interface yields perfect control over power flow. It was demonstrated that perfect abnormal reflection can be achieved by non-local design17, while perfect abnormal refraction can be achieved simply by quadruple Helmholtz units18. Improvements were later proposed to expand both functionality and feasibility. Transverse channels inside the metasurface can be established for non-local power flow control so that the coupling between units is controlled subjectively19,20,21. Alternatively, when bent into the same shape as the power flow distribution, the metasurface is no longer required to respect the non-local power flow condition22,23. Another idea is to balance the power flow with the passive introduction of evanescent waves along the metasurface24. However, all those solutions have brought in difficulties, due to limitations on the boundary shape or to the introduction of strict requirements25. The available range of wave fields that can be contacted together under these different strategies is thus still very limited.

In this paper, a generalized acoustic impedance theory is developed. Theoretically, it is argued that any pair of wave fields at a given frequency can be contacted together through arbitrarily shaped boundaries with an impedance metasurface. Power flow conservation is no longer strictly imposed, but only loosely, through the idea of integral equivalence. Generalized impedance unit cells are then proposed. Those unit cells can be designed to approach any impedance matrix. In order to illustrate the resulting design of a metasurface, an example of beam-splitting imposing loosely the conservation of power flow is given. The results obtained in both simulation and experiment agree well and suggest that the range of functions that can be implemented is far larger than demonstrated to date.

Results

Generalized acoustic impedance theory

Consider the two disjoint regions of space A and B depicted in Fig. 1a. Inside them, we consider two harmonic sound pressure fields pA(x, y, z) and pB(x, y, z). One can obtain from them the local velocity vA(x, y, z), vB(x, y, z), and power flow distributions IA(x, y, z), IB(x, y, z), since they are non-singular exact solutions of the Helmholtz equation. Two surfaces \({\Gamma }^{A}(x,y,z)\) and \({\Gamma }^{B}(x,y,z)\) are introduced to limit the semi-infinite spaces A and B. Their normal vectors \({{{{{{{{\bf{n}}}}}}}}}^{A}(x,y,z)\) and \({{{{{{{{\bf{n}}}}}}}}}^{B}(x,y,z)\) are defined as pointing toward the interior of the regions. Multiple channels are established between the two semi-infinite spaces. It should be emphasized that the concepts of incident and transmitted fields have not been imposed in this description. Furthermore, multiple sound sources are allowed to exist simultaneously inside the two spaces.

Fig. 1: Schematic diagram of generalized acoustic impedance theory.
figure 1

a Illustration of generalized impedance metasurface. Two pressure fields \({p}^{A}\left(x,y,z\right)\) and \({p}^{B}\left(x,y,z\right)\) exist in the disjoint semi-infinite spaces A and B. Multiple channels are established between their boundaries \({\Gamma }^{A}\left(x,y,z\right)\) and \({\Gamma }^{B}\left(x,y,z\right)\), including orderly connected channels (Case 1), crosswise connected channels (Case 2) and self connected channels (Case 3). b–d Sketch of the design of a generalized impedance unit. b An impedance unit with arbitrary shape and internal structures (yellow part) connected with waveguides (gray part) on both sides. c An impedance unit with arbitrary shape and internal structures is checked by plane wave incidence with total pressure field described by one-dimension curve coordinate. d An impedance interface abstracted from the physical structure.

Full size image

In previous impedance metasurface theories, it is often required that the two boundaries have the same shape \({\Gamma }^{0}(x,y,z)\) and normal vector \({{{{{{{{\bf{n}}}}}}}}}^{0}(x,y,z)\), i.e., that they are parallel. Continuity of normal power flow is then imposed strictly24. In this paper, we consider a more general metasurface with inhomogeneous thickness between the two surfaces \({\Gamma }^{A}(x,y,z)\) and \({\Gamma }^{B}(x,y,z)\). The conservation of power flow is hence imposed only weakly. The passive and lossless connection between the two spaces is written

$${\int_{{\Gamma }^{A}}}{{{{{{{{\bf{I}}}}}}}}}^{A}\cdot {{{{{{{{\bf{n}}}}}}}}}^{A}{{{{{{{\rm{d}}}}}}}}S+{\int_{{\Gamma }^{B}}}{{{{{{{{\bf{I}}}}}}}}}^{B}\cdot {{{{{{{{\bf{n}}}}}}}}}^{B}{{{{{{{\rm{d}}}}}}}}S=0,$$
(1)

which indicates that the structures placed between regions A and B form a globally conservative system. It should be noted that there are no restrictions on the respective areas of the two surfaces, as they can be different. Then, segmentation of the two surfaces ΓA and ΓB is operated according to the following principles. First, the surfaces must be completely covered by sets of patches \({D}_{i}^{A}\) and \({D}_{i}^{B}\). Second, the maximum feature size \({\Phi }_{{D}_{i}^{\alpha }}\) for each patch \({D}_{i}^{\alpha }\) should be deeply sub-wavelength (\({\Phi }_{{D}_{i}^{\alpha }}\ll {\lambda }_{0}\)), with α = A or B. Third, the variables pα, vα, and the normal vectors nα within each patch should be slowly varying along the boundary and assume an average value approximately equal to the value at the midpoint of the patch. Fourth, for any patch \({D}_{{i}_{1}}^{{\alpha }_{1}}\), there is always a corresponding patch \({D}_{{i}_{2}}^{{\alpha }_{2}}\), satisfying

$${\int_{{D}_{{i}_{1}}^{{\alpha }_{1}}}}{{{{{{{{\bf{I}}}}}}}}}^{{\alpha }_{1}}\cdot {{{{{{{{\bf{n}}}}}}}}}^{{\alpha }_{1}}{{{{{{{\rm{d}}}}}}}}S+{\int_{{D}_{{i}_{2}}^{{\alpha }_{2}}}}{{{{{{{{\bf{I}}}}}}}}}^{{\alpha }_{2}}\cdot {{{{{{{{\bf{n}}}}}}}}}^{{\alpha }_{2}}{{{{{{{\rm{d}}}}}}}}S=0.$$
(2)

For the Cases 1 and 2 depicted in Fig. 1a, α1 = A, α2 = B, and i1 = i2; for Case 3, α1 = α2 = A or B, and i1 ≠ i2. The conservation of power flow is now established in the framework of integral equivalence. The distance between two patches is expected to remain short for practical operation, although this requirement is not essential. Then one can use a series of channels to connect patches, as illustrated in Fig. 1a. As the conditions above actually do not impose strong restrictions on the spatial location, the layout of each channel can be flexible. Two patches can be connected orderly, such as Channels 1 and 2 in Case 1. One can further establish channels crosswise if necessary, as in Channels 3 and 4 in Case 2, though this possibility may only be offered by a 3-dimensional microstructure. Channels connecting two patches of the same boundary are allowed as well, such as Channels 5 and 6 in Case 3. Such channels are termed generalized impedance units in this paper and provide functionalities beyond those of previous impedance metasurfaces. Finally, the j-th generalized impedance unit is approximately characterized by the unique impedance matrix

$$\left[\begin{array}{c}p{| }_{{D}_{{i}_{1}}^{{\alpha }_{1}}}\\ p{| }_{{D}_{{i}_{2}}^{{\alpha }_{2}}}\end{array}\right]=\left[\begin{array}{cc}{Z}_{11}^{j}&{Z}_{12}^{j}\\ {Z}_{21}^{j}&{Z}_{22}^{j}\end{array}\right]\left[\begin{array}{c}\left(-{{{{{{{{\bf{n}}}}}}}}}^{{\alpha }_{1}}\cdot {{{{{{{\bf{v}}}}}}}}\right){| }_{{D}_{{i}_{1}}^{{\alpha }_{1}}}\\ \left(-{{{{{{{{\bf{n}}}}}}}}}^{{\alpha }_{2}}\cdot {{{{{{{\bf{v}}}}}}}}\right){| }_{{D}_{{i}_{2}}^{{\alpha }_{2}}}\end{array}\right].$$
(3)

It is worth noting that the above definition of the impedance matrix is slightly different from the previous17, since the normal vectors are now selected according to the boundary of definition of the considered acoustic field.

Let us now examine what we get when the generalized impedance units exactly satisfy the objective pressure and velocity fields at the two ports. Both acoustic fields obey the governing equations inside spaces A and B and their zero and first-order boundary values are discretely related by the generalized impedance elements of Eq. (3). Meanwhile, the conservation of power flow is satisfied according to Eq. (2). The total field composed of pA and pB thus forms a single proper global wavefield solution of the second-order partial differential equation of acoustics. This result in fact indicates that two arbitrary semi-infinite sound fields can be connected only by designing generalized impedance units that meet the required impedance characteristics.

Spaces A and B are allowed to be finite as well as to include additional boundaries. Additional boundary conditions would not cause trouble since they do not occur in the discussion. Furthermore, the permissiveness of Case 2 compared to Case 1 is worthwhile for some three-dimensional scenarios. Such units may achieve the negative coupling effect, similar to topological phononic crystals26,27. They also have the potential for effective impedance modulation for extraordinary acoustic transmission28 or generation of spiral impedance patterns for acoustic vortices29,30. Along the same line, the connection of multiple sound fields is allowed as well, including with different background media, as the conclusions above would still hold. Conversely, all three cases depicted in Fig. 1a would remain the same if A and B were regarded as two different sections of the same space. Hence, both transmissive and reflective metasurfaces, and even metasurfaces with transverse channels19, can be established within a unified framework.

Finally, the proposed generalized acoustic impedance theory is naturally compatible with the conventional one. One may strictly stipulate that \({\Gamma }^{A}(x,y,z)={\Gamma }^{B}(x,y,z)+C\), where C is a constant. Then, the designed metasurface would have a uniform thickness. At this point, the generalized theory would degenerate into the conventional theory if only channels of Case 1 are adopted with \({D}_{i}^{A}\cong {D}_{i}^{B}\). As a result, a strict requirement on the power flow would be back into consideration and functionality would be greatly weakened.

Generalized acoustic impedance unit

It is essential to ensure that any target impedance matrix can be approached by an artificial unit. Generally speaking, the impedance characteristics are hardly checked directly. The design and measurement method for conventional impedance units18 is also generalized here within the framework of generalized impedance theory.

Any of the impedance units of Fig. 1a can be represented by the general geometry depicted in yellow in Fig. 1b. The impedance unit generally includes some microstructures that are added to meet the impedance requirements for actual operation; they are not illustrated here for simplicity. The two terminal ports are not required to be parallel or to connect two different spaces. The pressure field inside the generalized unit under any excitation should be unique and independent of the direction of power flow since its characteristic size is deeply sub-wavelength. Despite being possibly placed in different environments, the impedance unit exhibits a unique impedance matrix. This allows one to attach waveguides on both sides (shown as gray parts) to check its impedance. Note that the waveguides should be perpendicular to the ports of the unit but can have different cross-sectional areas as the ports do. The contribution of the generalized impedance unit to the global field is analyzed next under integral equivalence.

The impedance matrix can be examined by measuring a given set of incident, reflected, and transmitted waves with a total pressure field illustrated in Fig. 1c Still thanks to the deeply sub-wavelength characteristic size, the pressure field can be described by a one-dimensional curvilinear coordinate. This abstraction works for all three cases, as the above process does not explicitly specify the direction of power flow or of the incident wave. Therefore, we can abstract it as an impedance interface without thickness, placed at y = 0, as shown in Fig. 1d for an intuitive illustration. One needs only to launch an incident plane wave from one side to check impedance and scattering matrices, as the generalized impedance unit is linear. Considering an incident excitation pin(y) along the negative y-axis, the reflected wave \({p}^{{{{{{{{\rm{re}}}}}}}}}(y)\) and the transmitted wave \({p}^{{{{{{{{\rm{tr}}}}}}}}}(y)\) satisfy

$${\left.\left[\begin{array}{c}{p}^{{{{{{{{\rm{in}}}}}}}}}+{p}^{{{{{{{{\rm{re}}}}}}}}}\\ {p}^{{{{{{{{\rm{tr}}}}}}}}}\end{array}\right]\right\vert }_{y = 0}=\left[\begin{array}{cc}{Z}_{11}^{j}&{Z}_{12}^{j}\\ {Z}_{21}^{j}&{Z}_{22}^{j}\end{array}\right]{\left.\left[\begin{array}{c}-\left({v}^{{{{{{{{\rm{in}}}}}}}}}+{v}^{{{{{{{{\rm{re}}}}}}}}}\right)\\ {v}^{{{{{{{{\rm{tr}}}}}}}}}\end{array}\right]\right\vert }_{y = 0},$$
(4)

together with the conservation of power flow

$$\begin{array}{rcl}&&\frac{1}{2}{\left.{{{{{{{\rm{Re}}}}}}}}\left[\left({p}^{{{{{{{{\rm{in}}}}}}}}}+{p}^{{{{{{{{\rm{re}}}}}}}}}\right){\left({v}^{{{{{{{{\rm{in}}}}}}}}}+{v}^{{{{{{{{\rm{re}}}}}}}}}\right)}^{* }\right]\right\vert }_{y = 0}\cdot {A}_{1}\\ &&=\frac{1}{2}{\left.{{{{{{{\rm{Re}}}}}}}}\left[{p}^{{{{{{{{\rm{tr}}}}}}}}}{\left({v}^{{{{{{{{\rm{tr}}}}}}}}}\right)}^{* }\right]\right\vert }_{y = 0}\cdot {A}_{2},\end{array}$$
(5)

where A1 and A2 are the areas of the upper and the lower ports, respectively; Z0 = c0ρ0 is the characteristic impedance of the background medium.

For a passive and lossless system, each component of the impedance matrix Zj is imaginary (\({Z}_{ik}^{j}=\imath {X}_{ik}^{j}\), where ı2 = − 1). Solving (4) leads to

$${X}_{11}^{j}={Z}_{0}\frac{{p}_{i}\cos {\varphi }_{t}+{p}_{r}\cos \left({\varphi }_{r}-{\varphi }_{t}\right)}{{p}_{i}\sin {\varphi }_{t}+{p}_{r}\sin \left({\varphi }_{r}-{\varphi }_{t}\right)},$$
(6)
$${X}_{12}^{j}={Z}_{0}\frac{\left({p}_{i}^{2}-{p}_{r}^{2}\right)/{p}_{t}}{{p}_{i}\sin {\varphi }_{t}+{p}_{r}\sin \left({\varphi }_{r}-{\varphi }_{t}\right)},$$
(7)
$${X}_{21}^{j}={Z}_{0}\frac{{p}_{t}}{{p}_{i}\sin {\varphi }_{t}+{p}_{r}\sin \left({\varphi }_{r}-{\varphi }_{t}\right)},$$
(8)
$${X}_{22}^{j}={Z}_{0}\frac{{p}_{i}\cos {\varphi }_{t}-{p}_{r}\cos \left({\varphi }_{r}-{\varphi }_{t}\right)}{{p}_{i}\sin {\varphi }_{t}+{p}_{r}\sin \left({\varphi }_{r}-{\varphi }_{t}\right)},$$
(9)

where pi, pr, and pt are the amplitudes of incident, reflected, and transmitted waves (positive and real numbers), φr, and φt are the reflected and transmitted phases with respect to the incident phase, respectively. Notice that Eq. (5) can be simplified to

$$\left({p}_{i}^{2}-{p}_{r}^{2}\right){A}_{1}={p}_{t}^{2}{A}_{2},$$
(10)

which implies

$$\frac{{X}_{12}^{j}}{{X}_{21}^{j}}=\frac{{p}_{i}^{2}-{p}_{r}^{2}}{{p}_{t}^{2}}=\frac{{A}_{2}}{{A}_{1}}.$$
(11)

\({X}_{12}^{j}={X}_{21}^{j}\) holds if and only if the areas of the two ports are equal (A1 = A2), in which case the generalized unit degenerates into the conventional one. Besides, Eq. (11) indicates that \({X}_{12}^{j}\) and \({X}_{21}^{j}\) are not independent for a given area ratio \(\frac{{A}_{2}}{{A}_{1}}\). Hence, there are only three independent components in the impedance matrix: \({X}_{11}^{j},{X}_{12}^{j}\) and \({X}_{22}^{j}\). Assuming pi = 1, pr and pt are covariant according to Eq. (10). A complete mapping \(\left\{{X}_{11}^{j},{X}_{12}^{j},{X}_{22}^{j}\right\}\to \left\{{p}_{t},{\varphi }_{r},{\varphi }_{t}\right\}\) is hence established through Eqs. (6)–(9). There is always a unique set \(\left\{{p}_{t},{\varphi }_{r},{\varphi }_{t}\right\}\) corresponding to any impedance matrix Zj. One can construct a generalized impedance unit with a target impedance matrix by simply adjusting the transmission amplitude pt and the phase differences φr and φt. As a result, the design of the impedance matrix simplifies to a manipulation of transmission and reflection coefficients and any impedance matrix is available through an artificial generalized impedance unit.

It is generally considered that an asymmetric impedance matrix signals an active device24. However, the generalized impedance unit we just described represents a passive and lossless system as no external source is included. Because \({X}_{12}^{j} \, \ne \, {X}_{21}^{j}\) here results from different port areas, one may normalize amplitudes by the square root of the port area and the resulting impedance matrix would again be symmetric. However, the boundary conditions on both sides of the generalized impedance metasurface are still determined by the impedance matrices before normalization. Hence, normalization is not obviously beneficial overall. Though the impedance matrix is asymmetric, the generalized impedance unit is still linear, passive, and lossless. A detailed scattering analysis is proposed in the Supplementary Note 1.

Design of generalized impedance metasurface

Although the generalized impedance theory does not impose many restrictions and applies in almost all circumstances, it may seem difficult to apply in practice. It is indeed cumbersome to take into account the shapes of the two interfaces \({\Gamma }^{A}(x,y,z)\) and \({\Gamma }^{B}(x,y,z)\) together with the normal power flow distribution \({\overrightarrow{I}}^{A}\cdot {\overrightarrow{n}}^{A}\) and \({\overrightarrow{I}}^{B}\cdot {\overrightarrow{n}}^{B}\), especially for inverse design of generalized units. The practical solution illustrated in Fig. 2a is suggested herewith to provide an easier implementation of the design. A lattice with a regular shape is added as a relay between the two surfaces. For independent design of impedance units, each cell in the lattice is rigidly isolated from its neighbors. The connection between the upper and lower surfaces and the regular lattice can then be established following the principles mentioned above. Note that all connections should be fabricated with a transmittance close to 1. Consequently, the structure of the conventional impedance unit18 can be directly applied here. Only the structures inside the lattice need to be optimized to meet the target impedance requirements. The definition of the generalized impedance metasurfaces is then simplified into two independent steps: path planning and conventional impedance unit design. In this section, a generalized impedance metasurface for beam splitting is designed as a demonstration of this design strategy.

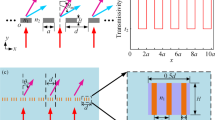
Fig. 2: Design and simulation verification of a generalized impedance metasurface.
figure 2

a Illustration of the definition of the generalized impedance metasurface. Two pressure fields, \({p}^{A}\left(x,y,z\right)\) and \({p}^{B}\left(x,y,z\right)\), are placed in the space regions A and B. A regular lattice with a particular internal structure is positioned between them. Each cell in the lattice is rigidly isolated. The connection between the sound fields and the lattice is supposed to achieve 100% transmittance to reduce the design complexity. A plane wave with an incident angle θin is split into two plane waves with transmission angles θt1 and θt2 after passing through the metasurface. b Schematic diagram of the generalized impedance unit. c Analytical determination of the required impedance matrix described by the pseudo-real expression: R11 (gray curve), X11 (orange curve), X12 (green curve), X22 (blue curve). The target impedance components (circular points) and impedance components of the practical structure are obtained through optimization (square points). d, e Verification of beam splitting based on generalized impedance theory described with d the three-layer numerical model and e the practical structure. f Mode analysis of the transmitted field for the three-layer numerical model (blue line) and the practical structure (green line).

Full size image

A feasible scheme based on conventional impedance theory to define an arbitrary beam splitter is to introduce evanescent waves on the incident side to balance the power flow24. This solution, however, implicitly restricts the output waves to be split at a large angle. Small splitting angles may thus not be achieved by conventional impedance theory. An explanation is provided in the Supplementary Note 2. Although it may be implemented using the generalized Snell’s law, parasitic scattering would inevitably occur31, resulting in efficiency below 100%17. In addition, it is almost impossible to apply if more than two plane waves are expected on the transmission side. This illustrates the restricted nature of scenarios to which conventional impedance theory can be applied.

Generalized impedance theory is employed here to solve this dilemma. The incident field pA is a plane wave with incident angle θin = 0∘. The transmitted field pB is composed of a pair of transmitted waves with transmission angles θt1 = − θt2 = 13. 5∘ and phase differences φt1 = φt2 = 60∘. An operating frequency of f0 = 3500 Hz is adopted. Such a configuration is not compatible with conventional impedance theory as presented in Supplementary Note 2.

The channels of Case 1 in Fig. 1a are adopted as generalized units. The length of the generalized units, i.e., the thickness of the metasurface, is set to tm = 13.1 cm. The unit of metasurface is composed of a trapezoidal entrance channel with a height ht = 3 cm and quadruple Helmholtz resonators with a height hh = 10.1 cm, as shown in Fig. 2b. The resonators and trapezoidal channel correspond to the regular lattice in Fig. 2a and the high transmittance connection to pA, respectively. The resonators are directly connected to the transmitted field, thus another high transmittance connection to pB is skipped. The width of the lattice is set to wo = 1.4 cm. The width of the lower port wi of each unit is then given by Eq. (11). It should be noted that there is a gap width δ = 1 mm at each side of the entrance (wi), for isolation between adjacent units.

Some walls with thickness δ = 1 mm are added to ensure intact power flow transmittance through the trapezoidal channel. The distances between the two walls on the right and the upper boundary are \({h}_{r}^{1}\) and \({h}_{r}^{2}\), and the wall lengths are \({l}_{r}^{1}\) and \({l}_{r}^{2}\), respectively. The distance from the left wall is \({h}_{l}^{1}\) and the wall length is \({l}_{l}^{1}\). A waveguide with width wa = 1 mm is connected in the middle of the upper boundary. The above six parameters \(\left\{{h}_{r}^{1},{h}_{r}^{2},{h}_{l}^{1},{l}_{r}^{1},{l}_{r}^{2},{l}_{l}^{1}\right\}\) are used as optimization variables for a genetic algorithm, so that the incident power from wi completely enters the waveguide.

Four Helmholtz resonators are then connected to the waveguide. The width and the height of the i-th resonator from top to bottom are \({w}_{r}^{i}\) and hr = 2.4 cm, respectively. The neck width is \({w}_{n}^{i}\) and the thickness δ = 1 mm. With the parameters of the trapezoidal part fixed, \({w}_{n}^{i}\) and \({w}_{r}^{i}\) together with wa are further used as optimization variables in a genetic algorithm to search for a structure with the target impedance characteristics. Detailed information on parameters and the optimization algorithm are presented in the Supplementary Note 3.

Validation via simulation and experiment

The three-layer numerical model can be referred to for verification17 of conventional impedance metasurfaces. Impedance units are numerically described by using a sequence of three impedance interfaces so as to predict the operating effect of the physical structure. However, the impedance matrices obtained from Eq. (3) are asymmetric, whereas the three-layer numerical model only describes symmetrical matrices. Considering that the behavior of generalized impedance units is similar to that of active devices, a pseudo-real expression is proposed for numerical simulations (see “Methods” section for details). The impedance matrix derived by this method possesses symmetric components, as shown in Fig. 2c. The design target and the optimization result for each generalized impedance unit are indicated with circle and square markers, respectively. The simulation of the target is then conducted through the three-layer numerical model as shown in Fig. 2d. Detailed information regarding the pseudo-real expression and the three-layer numerical model are given in the Methods section. A simulation verification of the designed generalized impedance metasurface is illustrated in Fig. 2e. Beam splitting consistent with the target design is observed, alongside some spurious scattering.

A quantitative comparison through mode analysis of the transmitted field is given in Fig. 2f. Each transmitted plane wave should theoretically transport 50% of the transmitted intensity, but for the practical structures, there is still 4% of the intensity that leaks into other modes. The major reason causing this phenomenon is the limited geometrical parameter. The 7 − 9 and 22 − 24 units are merged for the convenience of fabrication, but it makes \({w}_{o}^{{\prime} }=3{w}_{o} \, > \; {\lambda }_{0}/3\). Meanwhile, although the upper port width is determined as wo < λ0/5, the maximum width of the lower port is wi = 2wo > λ0/4. In a sense, they actually violate the deep sub-wavelength requirement (\({\Phi }_{{D}_{i}}\ll {\lambda }_{0}\)). Their impedance matrices may no longer be unique at an arbitrary incident angle. Also, the tangential dimensions of the quadruple Helmholtz resonators make it hard to refine the division of generalized impedance units. More efforts need to be made to design more efficient unit structures with thinner tangential dimensions, in order to support the requirements of generalized impedance.

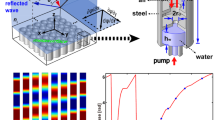
An experimental verification was carried out using 3D printing. Detailed information on the construction of the experimental platform shown in Fig. 3a is provided in the Methods Section. A photograph of one period of the fabricated generalized impedance metasurface is shown in Fig. 3b. The distributions of the real part of the sound pressure field in both simulation and experiment are shown in Fig. 3c–e. All fields have been normalized with reference to the incident wave. An ideal result is presented in Fig. 3c through simulation, for comparison purposes. The incident plane wave is split into two main steered beams after passing through the metasurface. Consistent with the expectation, the amplitudes of the steered beams are both about 0.7 Pa and the transmission angles are ± 13. 5∘. The region corresponding to the measurement area (white dashed box) is extracted as shown in Fig. 3d for a comparison with the experimental result of Fig. 3e. Good consistency can be observed visually. Some parasitic scattering can be noticed near the center of Fig. 3e. We attribute it to unsatisfactory fabrication and viscous loss. Due to heating and moisture deformation of photosensitive resins, the metasurface does not work exactly as expected. Furthermore, the connection between adjacent periodic structures is not strictly intact. The impedance of the generalized units is also affected by viscosity, resulting in a deviation from theoretical expectations regarding the interface impedance. Distortion of the sound pressure field occurs consequently. A detailed discussion of viscous loss, together with a plot of the radiation pattern, is proposed in the Supplementary Note 4. It is found that the transmitted field is generally satisfactory with the formation of two main beams with transmission angles of about + 11. 8∘ and − 9. 3∘.

Fig. 3: Experimental verification for generalized impedance metasurface.
figure 3

a Sample and experimental setup. b A period of the fabricated generalized impedance metasurface. c Simulation results given by metasurface under excitation of finite width. The acoustic field in the measuring area is given through d simulation and e experiment using the same colourbar as c.

Full size image

In summary, generalized impedance theory can theoretically transform any acoustic field. For an illustration of its functionality, an additional example of a metasurface producing multiple split beams is provided in Supplementary Note 5. The amplitude of each beam can be customized arbitrarily, even with viscosity considered. The practical design of generalized unit structures might still become a limitation in the future. Subsequent work should focus on obtaining solutions for more efficient structures and miniaturized generalized units.

Conclusions

In this paper, conventional acoustic impedance theory was extended to a more general form named generalized impedance theory. The conservation of power flow does not need to be imposed strictly in the normal direction, but only integral equivalent. A generalized impedance unit is then proposed that provides great flexibility to fulfill arbitrary impedance requirements. Taking beam splitting as an example, the construction of a generalized impedance metasurface and the design of the generalized units was demonstrated. Adopting a quadruple Helmholtz resonator together with a trapezoidal connection, the generalized unit with target impedance matrix was approached by a real model. The design based on the proposed generalized impedance theory was validated by simulation and experiment.

The proposed theory has great potential for exploitation in acoustics. Any number of acoustic fields with different signatures can be connected, as long as a conservation condition and the governing equations are obeyed. Generalized impedance theory also has a wide range of application scenarios, as the shape of the metasurface is not restricted. Sole limitations are brought about because of the lateral size of the units. Units that cannot be designed at the deep sub-wavelength scale weaken the applicability of generalized impedance theory to some extent, although this is not a drawback of the theory itself. Subsequent work will be devoted to developing more compact structures for generalized impedance units.

Methods

Pseudo-real expression for generalized impedance unit

Impedance matrices obtained from Eq. (3) are asymmetric, whereas the three-layer numerical model can only describe symmetrical matrices. A pseudo-real expression with a symmetrical impedance matrix for the generalized impedance unit is developed here.

A generalized impedance unit with \(\frac{{A}_{1}}{{A}_{2}} \, > \, 1\) visually resembles an active device, though it is passive and lossless. Since active devices encompass the passive and lossless case, the form of an active impedance matrix can be emulated. It is assumed that there is a virtual source in the channel, but that the impedance matrix remains symmetrical. If the virtual source is placed at port 1, the impedance matrix in Eq. (4) is modified to include a reactive real term \({R}_{11}^{j}\):

$${\left.\left[\begin{array}{c}{p}^{{{{{{{{\rm{in}}}}}}}}}+{p}^{{{{{{{{\rm{re}}}}}}}}}\\ {p}^{{{{{{{{\rm{tr}}}}}}}}}\end{array}\right]\right\vert }_{y = 0}=\left[\begin{array}{cc}{R}_{11}^{j}+\imath {X}_{11}^{j}&\imath {X}_{12}^{j}\\ \imath {X}_{12}^{j}&\imath {X}_{22}^{j}\end{array}\right]{\left.\left[\begin{array}{c}-\left({v}^{{{{{{{{\rm{in}}}}}}}}}+{v}^{{{{{{{{\rm{re}}}}}}}}}\right)\\ {v}^{{{{{{{{\rm{tr}}}}}}}}}\end{array}\right]\right\vert }_{y = 0}.$$
(12)

Solving for Eq. (12) taking account of Eq. (5) leads to

$${R}_{11}^{j}={Z}_{0}\frac{\left({p}_{i}^{2}-{p}_{r}^{2}\right)\left(1-\frac{{A}_{1}}{{A}_{2}}\right)}{{p}_{i}^{2}-2\cos {\varphi }_{r}{p}_{i}{p}_{r}+{p}_{r}^{2}}.$$
(13)

Hence the real part is negative (R11 < 0) and the generalized unit is equivalent to a negative resistance.

For a symmetric impedance matrix, the order of the subscripts of the impedance components can be directly reversed when ports are exchanged. But things are different for Eq. (12) when the generalized impedance unit is observed inversely. The port area ratio becomes \(\frac{{A}_{1}}{{A}_{2}} \, < \, 1\) and the virtual source moves to port 2. After exchanging subscripts 1 and 2 in Eq. (12), the real component of \({Z}_{22}^{j}\) becomes

$${R}_{22}^{j}={Z}_{0}\frac{\left({p}_{i}^{2}-{p}_{r}^{2}\right)\left(1-\frac{{A}_{1}}{{A}_{2}}\right)}{{p}_{t}^{2}}.$$
(14)

The generalized unit now is resistive since R22 > 0. This means that active units can emulate generalized units only under the condition of one-way power flow transfer. The impedance matrix of Eq. (12) is termed the pseudo-real impedance matrix in this paper.

Theoretical requirements for beam splitting

For defining a beam-splitting generalized impedance metasurface, we consider the incident and transmission pressure fields

$${p}^{A}={p}_{i}{e}^{-\imath \left({\varphi }_{i}+{k}_{0}\sin {\theta }_{in}x+{k}_{0}\cos {\theta }_{i}y\right)},$$
(15)
$${p}^{B} = \, {p}_{t1}{e}^{-\imath \left({\varphi }_{t1}+{k}_{0}\sin {\theta }_{t1}x+{k}_{0}\cos {\theta }_{t1}y\right)}\\ +\,{p}_{t2}{e}^{-\imath \left({\varphi }_{t2}+{k}_{0}\sin {\theta }_{t2}x+{k}_{0}\cos {\theta }_{t2}y\right)},$$
(16)

with the velocity fields

$${\overrightarrow{v}}^{A} = -\frac{{p}_{i}}{{Z}_{0}}{e}^{-\imath \left({\varphi }_{in}+{k}_{0}\sin {\theta }_{in}x+{k}_{0}\cos {\theta }_{in}y\right)}\\ \times \left(-\sin {\theta }_{in}{{{{{{{{\bf{e}}}}}}}}}_{x}-\cos {\theta }_{in}{{{{{{{{\bf{e}}}}}}}}}_{y}\right),$$
(17)
$${\overrightarrow{v}}^{B} = -\frac{{p}_{t1}}{{Z}_{0}}{e}^{-\imath \left({\varphi }_{t1}+{k}_{0}\sin {\theta }_{t1}x+{k}_{0}\cos {\theta }_{t1}y\right)}\\ \times \left(-\sin {\theta }_{t1}{{{{{{{{\bf{e}}}}}}}}}_{x}-\cos {\theta }_{t1}{{{{{{{{\bf{e}}}}}}}}}_{y}\right)\\ -\frac{{p}_{t2}}{{Z}_{0}}{e}^{-\imath \left({\varphi }_{t2}+{k}_{0}\sin {\theta }_{t2}x+{k}_{0}\cos {\theta }_{t2}y\right)}\\ \times \left(-\sin {\theta }_{t2}{{{{{{{{\bf{e}}}}}}}}}_{x}-\cos {\theta }_{t2}{{{{{{{{\bf{e}}}}}}}}}_{y}\right).$$
(18)

For convenience, we still adopt ΓA/B: y = 0. Although ΓA and ΓB are coincident at first, one of them can later be shifted alongside the field pA/B, in order to add sufficient space to accommodate the metasurface. Substituting Eqs. (15)–(18)) into Eq. (2), the power flow conservation condition can be solved as

$$\frac{{p}_{i}^{2}}{2{Z}_{0}}\cos {\theta }_{in}=\frac{{p}_{t1}^{2}}{2{Z}_{0}}\cos {\theta }_{t1}+\frac{{p}_{t2}^{2}}{2{Z}_{0}}\cos {\theta }_{t2}.$$
(19)

Air is still adopted as the background medium. The incident angle is set as θin = 0∘ for convenience. To ensure periodicity, transmission angles are set to θt1 = − θt2 = 13. 5∘ with the phase difference φt1/t2 − φi = 60∘. The periodicity of the metasurface is then \(C={\lambda }_{0}/\sin \left({\theta }_{t1}\right)=42\) cm.

Numerical simulation

Numerical simulations were conducted with the COMSOL Multiphysics Pressure Acoustics module. Air is described as an inviscid fluid with a sound velocity of c0 = 343 m/s and a mass density of ρ0 = 1.18 kg/m3. In consideration that beam splitting is a one-way power transfer, the pseudo-real expression was adopted for the simulations reported in Fig. 2e. The impedance relationship in Fig. 2d is given symmetrically as

$$\left[\begin{array}{c}{p}^{A}{| }_{y = 0}\\ p{| }_{{D}_{k}^{B}}\end{array}\right]=\left[\begin{array}{cc}{R}_{11}^{k}+\imath {X}_{11}^{k}&\imath {X}_{12}^{k}\\ \imath {X}_{12}^{k}&\imath {X}_{22}^{k}\end{array}\right]\left[\begin{array}{c}-\overrightarrow{n}\cdot {\overrightarrow{v}}^{A}{| }_{y = 0}\\ -\overrightarrow{n}\cdot \overrightarrow{v}{| }_{{D}_{k}^{B}}\end{array}\right].$$
(20)

The metasurface is divided equally into 30 three-layer units whose impedance components are marked as circular points. Each unit is composed of two waveguides with a length l0 = tm/2 = 6.55 cm and three interior impedance boundaries determined by

$${Z}_{1}={R}_{11}+\imath {X}_{11}+\imath {X}_{12}+\imath {Z}_{0}\cot \left({k}_{0}{l}_{0}\right),$$
(21)
$${Z}_{2}=2\imath {Z}_{0}\cot \left({k}_{0}{l}_{0}\right)-\frac{{Z}_{0}^{2}}{\imath {X}_{12}}{\sin }^{-2}\left({k}_{0}{l}_{0}\right),$$
(22)
$${Z}_{3}=\imath {X}_{22}+\imath {X}_{12}+\imath {Z}_{0}\cot \left({k}_{0}{l}_{0}\right).$$
(23)

An interior sound hard boundary is set between adjacent units for isolation. The transmitted and incident fields above and below the metasurface are of equal width to the metasurface period, with a height of 2.5λ0. The left and right edges of the model are set as periodic conditions with Floquet periodicity. The k-vector for Floquet periodicity is set as \({k}_{F}=\left(0,0\right)\) Two perfectly matched layers with a thickness of λ0/2 are connected to the upper and lower boundaries of the model to avoid reflection. The scaling factor of perfectly matched layers is set as 2 and the scaling curvature parameter is set as 1. The mesh is set with a maximum size of λ0/10 and a minimum size of λ0/40 for convergence and the discretization is set as Quadratic Lagrange. Additional refinement of the mesh is performed near the impedance boundaries. The background pressure field is set as a plane wave with unit amplitude pi = 1 Pa. The simulation in Fig. 2f uses the same simulation settings but replaces the three-layer numerical model with the practical structures.

The simulation in Fig. 3c is set according to the experimental environment in Fig. 3a. Four periods of the metasurface are included. A line source with a length of 90 cm, unit amplitude, and an operating frequency of 3500 Hz is placed in the incident field at a distance of 15 cm from the metasurface. The transmitted and incident fields above and below the metasurface are set with a width of 2 m, and a height of 0.3 m and 5 m, respectively. The other settings are the same as in Fig. 2.

Experimental apparatus

The signals generated and collected in the experiment are controlled by a B&K 3160-A-042 control module connected to a computer. The solid part is composed of a photosensitive resin which can be regarded as rigid in air. The experimental setup and fabricated sample are shown in Fig. 3a, b. Four periods of the metasurface are included and placed in a 2D single-mode waveguide with a thickness of 2 cm. A line source with a length of 90 cm and an operating frequency of 3500 Hz is placed at a distance of 15 cm from the metasurface. The whole experimental environment is surrounded by foam wedges to avoid reflection. A rectangular area with a length of 63 cm and a width of 30 cm, placed 10 cm away from the metasurface, is selected as the measuring area. There are 63 × 30 evenly distributed points with a sampling spacing of 1 cm.