Introduction

Granular systems are ubiquitously observed in daily life. Examples include sandboxes, dunes, flour, beads, and pharmaceutical powders. Despite individual particles obeying classical equations of motion, granular systems are known to exhibit complex macroscopic behavior. They can behave like a fluid, as in an hourglass, or like a solid, when they form arches or domes, clogging hoppers and pipes1,2,3,4,5. Understanding the behavior of granular systems is an important challenge for agriculture, construction, pharmaceuticals, and preparing for natural disasters such as landslides and avalanches.

It is known that forces inside dry granular systems do not propagate uniformly but in a chain-like manner. This force chain is intricately linked to their macroscopic behavior6. Although dry granular materials are well studied, it should be noted that granular materials found in nature and our daily lives often contain liquid. With the addition of even a small amount of liquid, the mechanical properties of granular materials are dramatically altered. In addition, granular materials containing water also have a large deformability. Microscopically, it is known that the liquid bridges grains (liquid adhesion or capillary bridging), and the capillary force causes an effective attractive interaction between the particles7,8,9. Then, the macroscopic shear modulus obtained by averaging the capillary forces over many grain-grain orientations is in good agreement with the experimental results10,11.

In general, the spatial distribution of water in granular materials is non-uniform since many kinds of the grains are contained, and phenomena such as evaporation and drainage also occur. In cement, the particles have a variation in particle size, which results in non-uniform hydration of the particles and then the cement becomes harder when this hydration percolates12. The mechanisms of macroscopic stiffness and deformability in heterogeneously wetted granular systems have not yet been fully elucidated experimentally. Thus, experiments in model systems of heterogeneously wetted granular systems are needed.

Sand coated with silicone oil (coated sand) is a product designed as a children’s toy13. The silicone oil is bonded directly to each grain and does not peel off. The coating allows the oil to persist stably around the sand. When the oil layers come into contact with each other, liquid adhesion occurs, causing an attractive interaction between coated particles14. Here we note that this attractive interaction remains for a long time since no evaporation and no drainage occurs. To model the spatial heterogeneity of water, this coated sand was mixed with ordinary grains with a mixing ratio of the coated sand to the total mass α. We note here that microscopy observations have confirmed that no stable liquid adhesion occurs between coated and uncoated sand, no matter how many times or how long they are mixed. Previous experiments focused on physical properties with the mixing ratio of α < 0.3, where the granular slab cannot retain its shape without a container14. It was reported that the packing fraction of random loose packing, the angle of repose, and the amount of residual material when the mixture is sieved change significantly when α is over 0.2314. This is close to the connectivity percolation value of α ~ 0.2515, suggesting that the change in physical properties may be due to percolation of clusters formed by coated sand.

Although the previous study showed that the coated sand system is an appropriate model system for the heterogeneously wetted granular materials, the mechanisms of stiffness and deformability of the wet granular materials have not been clear yet. In this study, we focus on the mechanism of the stiffness and the deformability of randomly close packed (RCP) blocks. Here we measured the α dependence of the Young’s modulus and investigated the deformability of the granular blocks by compressing. We also seek to clarify the origins of large Young’s modulus and large deformability using numerical simulations. The results show that Young’s modulus increases rapidly for α ≥ 0.6 and that the material can withstand 15% strain without cracking. Numerical simulations show that this rapid increase in Young’s modulus is due to a rigidity percolation transition, and that the recombination of the network makes the material more resistant to deformation.

Results and discussion

Young’s modulus

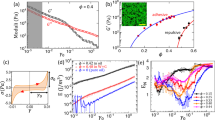
Firstly, we examined the stability of cylindrical RCP samples under their own weight. Figure 1 shows the appearance of the samples with α = 0.0, 0.3, and 0.5, 60 minutes after it was removed from a cylindrical container. When α ≤ 0.25, the sample collapses the moment it is removed from the container and forms a mound (Fig. 1a). The angle of repose is 20∘ ~ 25∘, which is almost the same as that of an ordinary sand pile2,14. On the other hand, a slab with 0.3 ≤ α ≤ 0.4 only partially collapses as shown in Fig. 1b, almost maintaining its shape. Finally, when the ratio of coated sand increases to α ≥ 0.5, the granular slab maintains its shape completely, as shown in Fig. 1c. The slab keeps its shape perfectly and does not collapse after a long time.

Fig. 1: Stability of mixed granular materials.
figure 1

Appearance of samples 60 minutes after they were removed from a cylindrical container, where (a) α = 0.0, (b) 0.3, and (c) 0.5. The scale bar corresponds to 50 mm.

Full size image

Next, we investigate response to large external forces. As shown in the experimental schematic in Fig. 2a, samples were compressed from the top surface at a constant speed by a plate, and the normal stress σ was measured. When α ≤ 0.3, the sample collapsed immediately and σ could not be measured. When α ≥ 0.4, they did not collapse under small deformations. Figure 2b shows the dependence of the normal stress σ on strain ε for α = 0.4, 0.6, 0.8 and 1.0 at a compression speed of v = 0.01 mm/s. When the strain is small ε < 0.003, the normal stress increases linearly (see the inset in Fig. 2b; as the strain is increased further, the stress increases rapidly. Here, we see that the σ-ε curve is qualitatively different for α = 0.4 and α≥0.6. Here, we measured the slope of the linear region under small strains and estimated the Young’s modulus of the grain slab, E = σ/ε, from the slope. Figure 2c shows the relationship between α and E. The Young’s modulus changes rapidly for 0.5 < α < 0.6 and then remains almost constant for α ≥ 0.6.

Fig. 2: Young’s modulus of the grain slab.
figure 2

a Schematic for the experimental setup, viewed from the side. b σ-ε curve. The inset shows the linear region of σ-ε curve. When the strain is small, the normal stress increases linearly (dashed line) and the Young’s modulus of the grain slab E can be estimated as E = σ/ε from the slope. c Young’s modulus E as a function of α. The Young’s modulus increases sharply at α ~ 0.6 for all compression rates v. The values of the Young’s modulus at α = 0.4 and 0.6 are labeled E1 and E2, respectively for each v. The error bars correspond to the standard deviations. d The Young’s modulus as a function of the compression rate v. E1 and E2 increase sharply by approximately 5 times at a transition compression rate of vt = 0.2 mm/s.

Full size image

The same experiment was conducted at different compression speeds. As shown in Fig. 2c, the Young’s modulus increases sharply at 0.5 < α < 0.6 for all v. Here we focus on the Young’s modulus at α = 0.4, E1 and α = 0.6, E2. E1 and E2 increased sharply by several times at a transition compression rate vt ~ 0.2 mm/s as shown in Fig. 2d. This suggests the existence of a relaxation time scale for the internal structure. The characteristic time may be estimated by τ ~ 〈d〉/vt ~ 1 s, where 〈d〉 is the mean size of the grains. A possible explanation for this time scale can be structural relaxation and lifetime of the attractive interaction. By the compression, the particles in contact are rearranged in the same way as T1 events in foams16 and then this liquid bridges disconnect. We measured that the time scale over which this liquid bridge disconnects is about 1 s for our coated grains and it is consistent with τ for the Young’s modulus.

Microscopic structure

Next, to clarify the origin of the change of the Young’s modulus, we compute the inner structures using a numerical simulation of packings spheres which model our mixture; details given in the Methods section. Firstly, we focus on connections between coated sand grains. Figure 3a, b shows the spatial distribution of clusters composed of coated sand grains at α = 0.2 and 0.3. The colors represent the size of each cluster. It is found that many small clusters are scattered when α = 0.2, while there is one large cluster when α = 0.3. We measured the particle number in each connected cluster Nc and defined \({N}_{c}^{max}\) as the number of particles in the largest cluster. Figure 3c shows the ratio of \({N}_{c}^{max}\) to the total number of coated sand particles βc, that is, \({\beta }_{c}={N}_{c}^{max}/N\alpha\). It is found that βc increases significantly at α = 0.3. As α increases further, βc approaches 1; this means that almost all coated sand grains are included in one large cluster. We also confirm that the large cluster percolates the system. Furthermore, the contact number Z in the maximum cluster is Z = 2.77 at α = 0.3. It has been reported previously that percolated structures are rigid when Z ≥ 2.417,18. Thus, the connectivity percolation transition corresponds to the shape-retaining property of the granular slab shown in Fig. 1. This is also consistent with the correspondence of the connectivity percolation with changes in the packing fraction of random loose packing, behavior under sieving, and the angle of repose as reported in ref. 14.

Fig. 3: Connectivity percolation.
figure 3

Spatial distribution of clusters composed of connected coated sand grains when (a) α = 0.2 and (b) 0.3. The colors correspond to the size of each cluster. It is found that many small clusters are scattered over space when α = 0.2, while one large cluster percolates the system at α = 0.3. c βc as a function of α. The maximum cluster size increases significantly at α = 0.3. The error bars correspond to the standard deviations.

Full size image

The connectivity percolation should increase the stiffness of the granular slab, but it is also known that connectivity is not enough to realize mechanical rigidity19,20,21,22,23. For example, when a particle makes contact with two particles, a linear cluster can be easily deformed by small stresses, while a triangle cluster is rigid. The rigidity connections can be determined by a mechanical test or a Pebble game algorithm24. Instead of these macroscopic methods, Maxwell’s conditions have been used to roughly determine the rigid connections. The connections is regarded as rigid when the total contact number reaches 6N-12, where N is the particle number19. Therefore, the contact number for each particles is almost 6 since N is enough large. Here we defined a rigid connection when each coated grain contacts more than 6 other coated grains. We apply this to the structures generated in our simulation and investigate the spatial distribution of rigid connections. Figure 4a and b show the distribution of rigid clusters at α = 0.5 and 0.6. Now, colors correspond to the size of rigid clusters. It is found that small rigid clusters are scattered over space at α = 0.5, even though the clusters as judged by connections are percolated. This means that the connective clusters are deformable when a large external force is applied. Meanwhile, when α = 0.6, it is clear that there is one large rigid cluster. We measured the number of particles in each rigid cluster Nr and define \({N}_{r}^{max}\) as the particle number in the largest cluster. Figure 4c shows the ratio of \({N}_{r}^{max}\) to the total number of coated particles βr, that is, \({\beta }_{r}={N}_{r}^{max}/N\alpha\). It is found that βr increases sharply at α = 0.6; the value βr = 0.3 is larger than that required for percolation (~0.25 in many model systems15). The α dependence of βr is consistent with the probability of the rigidity connections in the colloidal gels25. We also directly confirm that the rigid cluster percolates the system by checking the coordinates of the particles.

Fig. 4: Rigidity percolation.
figure 4

Spatial distribution of rigid clusters where the contact number is over 6 when (a) α = 0.5, (b) α = 0.6. The color represents the size of each rigid cluster. It is found that many small rigid clusters are scatter over space at α = 0.5, while one large rigid cluster percolates the system at α = 0.6. c βr as a function of α. Note that βr ~ 0.3 at α = 0.6; this is larger than the value required for percolation. The error bars correspond to the standard deviations. d α dependence of the Young’s modulus. It increases slightly up to α < 0.5 and increases sharply at α = 0.6. Furthermore, it is constant for α ≥ 0.6. This result is in good agreement with the experiment.

Full size image

Furthermore, we compute the Young’s modulus of the simulated system by the compression. Figure 4d shows that α dependence of the Young’s modulus. It increases slightly up to α < 0.5 and increases sharply at α = 0.6. Furthermore, it is constant for α ≥ 0.6. This result is in good agreement with the experiment. Thus, we conclude that this rigidity percolation is the reason why the Young’s modulus suddenly increases for α≥0.6.

Deformability

When the granular material is compressed more, the granular material deforms significantly. The granular material with α ≥ 0.6 can be deformed without cracking even when ε = 0.15, as shown in Fig. 5a; it is found that the width at the center of the granular material expanded more than at the base. The granular slabs with ε = 0.15 is stable at least for an hour. To investigate the reason for the large deformation, numerical simulations were performed to compress the granular material. We set that the attractive interaction is emerged after the coated particles come into contact, and disappear when the inter-particle distance becomes 1.4 times the particle diameter (see Methods section). Figure 5b shows probability distribution of the number of the attractive interaction bonds P(Z) at ε = 0, 0.10 and 0.15 at α = 0.6. It was found that P(Z) shifts in the direction of larger Z as ε increases. We also counted the number of the newly formed attractive interaction bonds and the number of the disconnect bonds by the compression. Figure 5c shows ε dependence of the ratio of the newly formed attractive interaction bonds (circle) and the disconnect bonds (triangle) to the initial total bonds p at α = 0.6. As ε increases, new bonds are created and then further increases in ε lead to an increase in the number of the disconnection. We note here that the Young’s modulus increases for ε > 0.003 in our experiment (see Fig. 2b). This is consistent with the increase of the attractive bond number in our simulation.

Fig. 5: Deformability of the granular slab.
figure 5

a Snapshots of a granular slab with α = 0.6 under different strains, ε = 0.0, 0.10, and 0.15. Dotted and dashed lines show the positions of the top surface at ε = 0.0, and 0.1, respectively. The granular slab can be deformed without cracking even though ε = 0.15 and the granular slab is stable at least for an hour. The scale bar corresponds to 50 mm. b Probability distribution of the number of the attractive interaction bonds P(Z) at ε = 0 (circle), 0.10 (triangle) and 0.15 (square) at α = 0.6. It was found that P(Z) shifts in the direction of larger Z as ε increases. c ε dependence of the ratio of the newly formed attractive interaction bonds (circle) and the disconnect bonds (triangle) to the total bonds p at α = 0.6. As ε increases, new bonds are created and then further increases in ε lead to an increase in the number of the disconnection. These results are consistent with the increase of the Young’s modulus shown as in Fig. 2b.

Full size image

We also compute the displacement of each particle. Any location dependence or dynamical heterogeneity cannot be observed. However, this may change if we include the time scale of the bond disconnect instead of quasi-static compression. It will be interesting to see if this rearrangement is related to the crack formation dynamics in the wet granular systems.

Here, we also note that normal concretes undergo brittle fracture when they are deeply compressed or a crack emerges inside. These materials are solid inside and it is hard to rearrange the bonds. Meanwhile, the bonds in the wet granular can be newly formed and be disconnected. Thus, in the context of deformation capacity, it is suggested that the importance of granular materials with structural relaxation. We also note that in this simulation, there is no time scale at which the contact breaks, and the compression is quasi-static. Therefore, we were not able to examine the velocity dependence of the Young’s modulus. In the case of the fast compression, the number of connections is expected to increase temporarily and the material may become more rigid, which is consistent with the experimental results. The transition point of the rigidity percolation is also expected to shift to lower α with increasing the compression velocity.

Here we show that the mechanical properties of mixed granular materials strongly depend on the percolation of the bonding between the coated sand particles due to attractive interactions. We note that our results at α = 1 are also consistent with previous works on wet granular, for examples by Scheel et al.9, since the liquid fraction in our experiment is quite small compared to that in their cases. We believe that this mixed granular materials are appropriate for investigating wet granular materials.

Since 60% of the coating sand is sufficient for the mechanical properties, the remaining 40% of sands can be used for other purposes. By changing the remaining 40% of sands to functional particles such as bactericidal colloids, we believe that new granular materials with high functionality can be developed. In addition, similarities with gels were observed where the percolations is formed. In the field of gels, materials such as topological gels have been developed and applied one after another26,27. Therefore, it is expected to develop materials with excellent mechanical properties by mimicking gels through improving coatings.

Finally, the rigidity percolation is commonly observed in colloidal gels and polymers and is considered an important phenomenon related to mechanical properties25,28. In the case of gels and polymers, the environment around the clusters is fluid, but in the case of granular system, it is dry grains. The dynamics of the dry grains is completely different from that of the fluids. Static properties of the rigidity percolation such as Young’s modulus are similar, however dynamical properties such as avalanches are expected to be different from those of gels. The effects of attractive interactions and the rigidity percolation in jammed systems such as glass, emulsions, and foams, as well as wet granular systems, are still largely unknown. This model system will be useful for elucidating the origin and properties of these systems.

Conclusion

To summarize, we investigated a granular material consisting of a mixture of coated and uncoated sand as a model of a wet granular system to clarify the mechanisms of stiffness and deformability. The inhomogeneity of the attractive interaction can be realized by the mass ratio α of the coated sand grains. It was found that the Young’s modulus of random close packing state suddenly increases for α ≥ 0.6. Numerical simulations were performed to investigate the relationship with the microscopic internal structure. It was found that the coated particles not only percolate via connectivity at α ≥ 0.3, but also undergo rigid percolation at α ≥ 0.6. Our results are also consistent with previous works on wet granular, since the liquid fraction in our experiment is quite small compared to that in their cases. It can be worth to emphasize that the volume fraction of the interacted particles can be easily controlled by mixing coated sands. Furthermore, the granular material with α ≥ 0.6 can be deformed without cracking even when the compression ratio ε = 0.15. Numerical simulations show that the rigidity percolation is preserved by recombination of the contact particles. Thus it is suggested that the mechanical properties of wet granular materials strongly depend on the percolation of the bonding due to attractive interactions. Those gel-like mechanism lead to develop materials with excellent mechanical properties by mimicking gels through improving coatings and by mixing highly functional particles. In addition, this system will lead to understanding the properties of jamming systems such as glasses, emulsions, and foams, where the effects of the attractive interactions and the rigidity percolation have been still unclear.

Methods

Experiment methods

For ordinary grains, we used Tohoku Silica Sand No. 5 sand (Tohoku Silica Sand Co., Ltd.). These grains have a density of 2.62 g/cm3, a short diameter of 0.08–0.35 mm, and a long diameter of 0.23–0.55 mm. Kinetic Sand (Rangs Japan) was used for silicone oil coated sand. The density is 2.62 g/cm3, the short diameter is 0.09–0.29 mm, and the long diameter is 0.16–0.41 mm. For each mass ratio α, we measured a mass of each, spread them on the same metal vat and mixed them well by hand until uniform.

We prepared the random close packed (RCP) slabs in the following way. We gently put the sand into a cylindrical container with a diameter of 74.0 mm and height of 42.0 mm, or a rectangular container with a 67.8 mm × 67.8 mm base and a height of 42.5 mm. The rate at which the sand was poured was about 10 g/s. RCP states are generated by compacting mixtures down by external pressure (~5 × 104 Pa) using a plate whose area is almost the same as the inside of the container. We then poured more sand over the top until the container is full. We repeated this process around 25 times. The packing fraction of the granular slabs becomes roughly uniform. This state can be regarded as being RCP.

We flipped the container over and extracted the RCP granular slab from the container (see Fig. 1). Next, external pressure was applied by using a slider (LT-S300, Thorlabs) equipped with a large plate (Fig. 2a). The plate is designed so that it always stays horizontal. The slider can move with a constant velocity v with a minimum v of 0.001 mm/s. The force was measured using a force gauge (DST-50N, IMADA, Japan) during the slider movement. The resolution of the force is 0.001 N. We measured this 10 times using the same experimental conditions; the error bars correspond to the maximum and minimum found during the experimental trials.

Spatial heterogeneity of mixing

The spatial distribution of α is quantified in the following way. We mixed kinetic sand colored blue (purchased from Rangs Japan) and the ordinary sands with mixing ratio α. Then we packed the grains in a container in RCP and the surface of the granular block is photographed in color. When we divided a picture of the ordinary sand (α = 0) into RGB channels, it was found that red and green have almost the same intensity. Next, the surface of a block with a mixing ratio of α is photographed, and the intensity of the red channel I(r) normalized by that of the green channel is obtained. To eliminate the effect of voids on the surface, a low pass filter is applied to average the space smaller than 6 mm × 6 mm. Here each length is 10 times larger than the mean grain size. Then we obtained the local I(r). Assuming that the blue color is proportional to the amount of the kinetic sand and that I(r) and α(r) are linearly related, the following equation is obtained.

$$\alpha (r)=\langle \alpha \rangle \frac{1-I(r)}{1-\langle I(r)\rangle },$$
(1)

where 〈〉 represents the spatial average. The spatial distribution of α(r) can be obtained from the low pass filtered image. Here, the blue color of each sand grain differs slightly, and the reflection of light causes measurement error. Therefore, we examined α = 1 and found the measurement error to be 1.5 %. Spatial inhomogeneity was examined for each α and was found to be less than 1.6 % for all α. Since this is comparable to the measurement error, we consider the mixture to be nearly homogeneous.

Simulation methods

We performed overdamped numerical simulations to investigate the internal structures of granular slabs. To simplify, we assume grains to be spherical with a diameter di for particle i. We set the particle number N = 27000 and the size distribution to be Gaussian with a polydispersity of 20 %. A two-body potential U(rij) between particles i and j is applied such that

$$U({r}_{ij})=\frac{k}{2}{\left[{r}_{ij}-({d}_{i}+{d}_{j})/2\right]}^{2},$$
(2)

if (di + dj)/2 > rij, where rij is the distance between particles i and j and k = 1. Otherwise, U(rij) = 0. Firstly, we prepared a RCP state of non-coated grains using a method reported in ref. 29,30. We used periodic boundary conditions and the system size is Lx : Ly : Lz = 64 : 64 : 64. The particles are overpacked until the packing fraction is 0.645, and then shrunk until the total potential is below 10−3. Next, we replace a certain number of non-coated sand grains with coated grains until the number ratio of coated grains becomes α. Coated grains i and j interact via an attractive potential

$$U({r}_{ij})=\frac{{k}_{att}}{2}{[{r}_{ij}-({d}_{i}+{d}_{j})/2]}^{2},$$
(3)

when (di + dj)/2 < rij < rc, where rc is a threshold for the attractive interaction. We set katt = 1.0 × 10−3 and rc = 1.1(di + dj)/2. Then, the simulation was run until the system is relaxed sufficiently. We also confirm that our results are not sensitive to the threshold value of rc. We measure 3 different particle configurations and 5 different ways to replace uncoated grains with coated grains for each data point.

We also performed numerical simulations to investigate compression of the granular slab. After the RCP state of the granular slabs are formed, Lz decreases as Lz = 64(1 − γt) where t is a simulation time, while Lx and Ly increases as 64(1−γt)−1/2 to keep the volume. γ is the compression rate and we set γ = 10−4. This rate is enough slow to relax the system to the stable state. We also set that the attractive interaction is emerged after the coated grains are contacted, while it disappears when rij > 1.4(di + dj)/2.