Abstract
In the race to curb energy and oil consumption, zeroing of wall frictional forces is highly desirable. The turbulent skin friction drag at the solid/liquid interface is responsible for substantial energy losses when conveying liquids through hydraulic networks, contributing approximately 10% to the global electric energy consumption. Despite extensive research, efficient drag reduction strategies effectively applicable in different flow regimes are still unavailable. Here, we use a wall-attached magnetic fluid film to achieve a wall drag reduction of up to 90% in channel flow. Using optical measurements supported by modelling, we find that the strong damping of wall friction emerges from the co-existence of slip and waviness at the coating interface, and the latter is a key factor to obtain almost complete wall drag reduction across laminar and turbulent flow regimes. Our magnetic fluid film is promising and ready to be applied in energy-saving and antifouling strategies in fluid transport and medical devices.
Similar content being viewed by others
Introduction
Drag reduction is an intensively researched phenomenon associated with decreased frictional forces and the consequent increase of fluid flow velocity. In wall-bounded flow through boundary layer control strategy, significant drag reduction has been achieved by modifying the wall structure using a thin chemical coating (hydrophilic or hydrophobic), or by generating micro- and nano-textures that trap microscopic gas pockets to form the Cassie–Baxter state (a superhydrophobic surfaces, riblets)1,2,3. The recent lubricant-impregnated surface approach combines and enhances the two approaches, namely coating and texture4,5. Alternatively, when the flow is turbulent, a widely adopted eddy transmission control strategy consists in manipulating the carrier fluid rheology, for example, by adding long-chained polymers6,7,8. Other solutions for decreasing drag include active control strategies, such as gas release at the wall or an oscillating wall9,10,11,12,13.
Current strategies have drawbacks that limit their range of applications. Boundary layer control1,2,3,4,5 strategies generally suffer from limitations due to the small slip length, coating detachment, and air layer failure, because their range of validity is mainly confined to the laminar regime. Strategies based on eddy transmission control6,7,8 require a continuous release of additives near the wall or into the bulk fluid. For active control9,10,11,12,13 solutions, the energy consumption of motors to generate oscillation or pumps for gas release limits the net energy gain due to drag reduction. Furthermore, although active control strategies are effective in both laminar and turbulent regimes, they nonetheless have significant constraints in the maximum achievable drag reduction and range of applicability14, for example, due to limited accessibility for the installation of an active device.
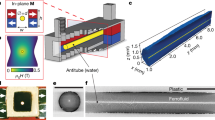
Here we present a drag-reduction technology that overcomes these limitations, offering a new opportunity for highly effective drag reduction in both laminar and turbulent regimes. Our approach relies on covering the channel wall with a magnetic fluid film (Fig. 1a), held in place by the attractive body force on the magnetite nanoparticles in the magnetic fluid colloidal structure15. The magnetic fluid coating acts as a slippery surface: indeed, slip velocities are observed at the coating interface (Fig. 1b, c), with performance that depends on the viscosity ratio between the diamagnetic fluid and the magnetic fluid. In addition to slip, the waviness of the magnetic fluid interface, a local periodic perturbation induced by the magnetic field, further reduces drag. Both slip and waviness are co-current factors that lower the velocity gradient at the coated wall, resulting in drag reduction, up to 80% in the laminar and up to 90% in the turbulent regime.
a Sketch of the working principle, where in absence of magnetic fluid film (MFF) we observe wall adherence and in the presence of MFF we observe the formation of a slippery interface with a slip velocity; (b, c) Time (denoted by the overbar) and horizontally (denoted by angular brackets) averaged velocity profiles in the diamagnetic fluid section with a magnetic fluid film at the top wall characterized by (b) low viscosity and (c) high viscosity. Experimental profiles at different Reynolds numbers, Re = U Dh /ν, where U is the mean velocity, Dh is the equivalent diameter equal to the characteristic length of the channel, and ν is the kinematic viscosity of the fluid. The shaded grey area indicates a 5% confidence interval, in accordance with the analysis presented in the Supplementary Material (Supporting Note 6).
Results
Performance: slip velocity, slip length, and drag reduction
Applying the magnetic fluid film to a channel surface results in slip velocities <ūslip > x at the interface between the coating layer and the diamagnetic fluid (Fig. 2a). Measurements using particle tracking velocimetry record the flow field inside a square channel with section 10 mm × 10 mm, where a 1 mm-thick film of magnetic fluid is held at the upper wall by a permanent magnetic field [see Methods and Supplementary Figure S1].
a Sketch of the experimental setup, where slip length bslip and slip velocity <ūslip > x are depicted; (b) Ratio between the slip velocity to the cross-sectional mean fluid velocity in the channel <ūslip > x /U, plotted as a function of Reynolds number Re. c Slip length, bslip = <ūslip > x µf/τc1 plotted as a function of the drag reduction, DR = (τw − τc)/ τw·100 [%]. Here, µf is the magnetic fluid viscosity, τc is the average shear stress at the coating interface and τw is the average shear stress at the uncoated wall. The shear stress is here estimated as the product of the diamagnetic fluid viscosity µ, and the velocity gradient at the interface, d < ū>/dy. Circles indicate experiments carried out for a viscosity ratio ηr = 6, while squares indicate experiments with ηr = 60. Unfilled symbols represent the laminar regime and filled symbols the turbulent regime.
Overall, we observe slip velocities in the range of 8–50% of the mean channel flow velocities, while varying the Reynolds number in the range of 400–4000 by changing the flow rate of the diamagnetic fluid (Fig. 2b). In addition to the slip velocity, drag reduction performance also depends on the slip length (Fig. 2a,c). Here, we achieve slip lengths, bslip1, up to values of 45 mm. For comparison, most other boundary layer control techniques, such as the superhydrophobic surfaces16 and lubricant-infused surfaces17, achieve slip lengths of the order of 30–40 µm. A performance of the same order of magnitude as that reported here is reached, for instance, by heated superhydrophobic surfaces, with a slip length of about 15 mm18. The main bottlenecks for preventing higher slip lengths in previous techniques have mainly been the micrometric thickness of the fluid layer and the detachment of the coating from the surface. Here we overcome these limitations by adopting a coating firmly attached to the wall by the attractive body force exerted by the magnetic field.
Across flow regimes spanning from laminar (390 < Re ≲ 1200) to turbulent (1200 ≲ Re < 4010) 19,20, differences in the slip velocities are mainly related to the mean velocity of the diamagnetic fluid and the viscosity ratio. An increase in the mean flow velocity causes an increase in the slip velocity (Fig. 2b), namely the velocity at the coating interface (Fig. 2a, yellow arrow). This finding is expected since a faster mean flow leads to an increase in the shear at the interface. We also observe that the viscosity ratio consistently influences the slip velocity in the turbulent regime (Re ≳ 1200). Specifically, for a similar Reynolds number but higher magnetic fluid viscosity, we obtain a lower slip velocity (filled symbols in Fig. 2b). A magnetic fluid characterized by higher magnetite concentration (higher magnetic fluid density) exhibits a higher degree of magnetization when exposed to an external magnetic field, due to the formation of stronger magnetite chains15. Consequently, it displays a higher viscosity for a given shear and magnetic field strength [see rheology curves in Supplementary Note 1, Fig. S2], which implies stronger wall attachment and resistance to motion as expressed by the wall adherence condition (see Materials and Methods section).
The magnetic fluid coating technique yields a drastic reduction in drag: up to 80% for the laminar regime and up to 90% for the turbulent regime (Fig. 2c). Magnetic fluid films characterized by high viscosity show low values of slip velocity and high values of slip length compared to the low viscosity case (Fig. 2b,c).
The underlying mechanisms for drag reduction: slip and waviness
Two concurrent factors at the fluid interface contribute to the observed drag reduction by lowering the velocity gradient at the coated wall, namely, (i) the slip caused by the shearing force and (ii) the waviness owing to the magnetic field perturbation.
The interface waviness is characterized by long waves (wavelength ~200 mm, amplitude ~0.1 mm), as shown qualitatively in the long-exposure images of the flow streamlines recorded at 500 Hz (Fig. 3a, b). The wave amplitude increases with increasing the Reynolds number, whereas the wavelength is almost constant and is controlled by the distance between individual magnets in the array. This is expected since the discrete sum of each magnetic field acts as a triggering condition for interface perturbations21. The presence of waves at the interface is associated with upwelling/downwelling regions at the coated wall, as shown by the profiles of the vertical component of the velocity: its change of sign is consistent with a transition from upwelling to downwelling behaviour of the flow associated with the undulations at the interface (Fig. 3c, e). The presence of waviness at the interface is responsible for the depletion of shear at the interface, while shear is enhanced below the interface, reaching a local maximum near the edge of the maximum wave height before decaying towards the centre of the channel (Fig. 3d, f).
a, b Long-exposure images of fluid streamlines acquired at 500 Hz. Data from experiments with coating and viscosity ratio \({\eta }_{r}\) = 6: upper row (c, d) with Re = 1335 (E1), lower row (e, f) with Re = 3038 (E2). c, e Profiles of the time-averaged vertical velocity (acquisition at 3000 Hz) for 16 locations, depicted with symbols of different colours at the bottom of (a, b–d–f) Spatial average of the mean shear rate profile. The grey rectangle depicts the area of the magnetic fluid layer. The red dashed lines in (c–d–f) show the experimental time-averaged vertical component of the velocity and the experimental shear rate profile for the case of rigid wall without coating, respectively Re = 450 in the upper row and Re = 2495 in the lower row. The velocity data presented, acquired through particle image velocimetry, is subject to a 5% confidence interval, aligning with the analysis provided in the Supplementary Material (Supporting Note 6).
A numerical simulation reproducing the wavy geometry and the slip condition at the coating interface corroborates our experimental results in terms of velocity profile and shear profile in the case of laminar flow [see Supplementary Note 2]. The results at the wavy interface show that: (i) the mean velocity profile has a lower gradient than in the case of a straight interface (Figure S2a in the Supplementary Note 2); (ii) and the mean shear profile has a maximum below the wavy surface (Figure S2b in the Supplementary Note 2).
It is worth noting that with the interface waviness, we observed the formation of a shear layer away from the interface and a velocity profile that features an inflection point near the edge of the maximum wave height. This is qualitatively similar to the observations made in flow with submerged flexible vegetation, indicating a possible analogy to canopy flow22.
The relative contributions of slip and waviness to drag reduction in laminar and turbulent regimes
In the laminar regime, the waviness of the coating interface provides the dominant contribution to drag reduction. In the turbulent regime, both slip and waviness play an important role. In this case, the dominance of one factor over the other depends mainly on the viscosity ratio.
In the laminar case, we derived the theoretical flow velocity field solution by solving the magnetohydrodynamics equations [Supplementary Note 3] assuming a flat coating interface. The velocity profile of the magnetic fluid film is characterized by a counter flow, given by the sum of a parabolic term and a linear term, as in the case of a combined Couette–Poiseuille flow. The parabolic profile is induced by the magnetic body force, while the linear term is due to the shear at the interface between the two fluids [Supplementary Note 3]. The mean velocity of the magnetic fluid film is zero. The theoretical velocity profile of the attached magnetic fluid film was validated through optical microfluidic observations [Supplementary Note 4]. In the microfluidic channel, we experimentally observed that the velocity field of the trapped volume of magnetic fluid is governed by an internal recirculation zone [Supplementary Movie 1], confirming an assumption made while performing numerical simulations in23. The theoretical solution derived in Supplementary Note 3 provides reliable estimates of the slip velocity at the interface between the diamagnetic fluid and the magnetic fluid coating, but it fails to estimate the corresponding shear rate, i.e., the velocity gradient du/dy (Fig. 4a, b).
The mean velocity profiles for experiments with magnetic fluid films of low viscosity (a, b) and high viscosity (c, d) at different Re numbers. Drag reduction due to slip through the shift upward from the reference case ΔUs+ (a–c) and due to wall shape represented by the upward shift ΔB+ in the region y+ > 30 (b–d). The mean profiles are represented in terms of y+ and U+, according to the generalized mean velocity distribution in drag-reduced flow33. The colours used in the legend correspond to experiments conducted at different Reynolds numbers. The same colour is selected for a set of experiments with different viscosities when the Reynolds number falls within a proximal range.
Indeed, the theoretical solution predicts the maximum shear at the interface (Fig. 4c), whereas the experimental data show the maximum shear rate shifted below the interface, where we observe the inflection point of the shear rate profile. The shift of the location of the maximum shear rate is responsible for the large drag reduction observed in the experiments, resulting in DR one order of magnitude higher than that predicted by the theoretical solution (Fig. 4c). The shallower velocity gradients established at the wall lead to a considerable drag reduction of 79% in the laminar regime with the low viscosity magnetic fluid. In the same regime, the theoretical solution for high-viscosity magnetic fluid still underestimated the drag reduction, although the performance is lower than that with the low-viscosity magnetic fluid (22% vs 79%, see Fig. 4c, d). It is thus the waviness of the coating interface that causes a decrease in the velocity gradient, providing the dominant contribution to drag reduction in the laminar case, regardless of the viscosity of the magnetic fluid (Fig. 4c, d).
In the turbulent regime, it is not possible to compare the wavy regime with an exact theoretical solution as in the laminar case because of the complexity of the problem. However, following24,25, we use of the fact that drag reduction leads to a shift of the velocity profile in the logarithmic layer.
That is, to evaluate the relative contribution to drag reduction at the coating interface of slip and waviness, we compare the temporally and horizontally averaged velocity profiles of our experiments with the logarithmic law of the wall. Qualitatively similar to the laminar case, the presence of waviness at the interface is responsible for a shallow velocity gradient at the wall and for a shift of the maximum value of the shear rate away from the interface (Fig. 3f, g). The shift of the maximum shear value away from the wall can be interpreted as the formation of a ‘virtual wall,’ representing a hypothetical wall located in the plane where the maximum shear stress is observed. The presence of a virtual wall implies that we set the origin of the vertical axis in that location and determine u* using the shear stress there. This provides a reasonable correspondence of the experimental data (y+ vs U+) with the theoretical reference solution (black line) (Fig. 5a, c), and a collapse of the curves for different Re when the slip velocity is subtracted (Fig. 5b, c). The mean velocity profiles show a higher velocity at any point y+ compared to the reference case (Fig. 5a, c). This evidences that drag is reduced, firstly, due to the slip through a shift of the profile upwards from the reference case ΔUs+ (Fig. 5a, c) and, secondly, due to the wall shape represented by the upward shift of the profile ΔB+ in the region y+ > 30 (Fig. 5b, d). In line with our observations, the upward shift ΔB+ was also observed in other studies, considering different wall geometries24. Similarly, an important contribution in terms of ΔB+ for the turbulent regime was also documented by25 when investigating the performance of drag reduction for streamwise travelling waves. Finally, in the turbulent regime, the low viscosity magnetic fluid shows a dominant contribution of ΔUs+ to drag reduction acting in the region close to the interface (the boundary layer), while the high viscosity magnetic fluid shows a greater contribution of ΔB+ acting in the flow region further from the interface (outside the boundary layer) (Fig. 5a-d).
a–c Comparison between the theoretical profiles (dashed lines) within the magnetic fluid FF (black) and the diamagnetic layer (green) and the experimental data (blue filled points) measured in the diamagnetic layer for laminar flow (Re = 1135) and a low viscosity magnetic fluid. a Velocity profile within the entire channel and (b) magnified view of the interface region. c Corresponding shear rate profiles. d Theoretical shear rate profile within the diamagnetic layer (green dotted line) and experimental data measured in the diamagnetic layer for laminar flow (Re = 770) and a high viscosity magnetic fluid (blue circles). The brown box in panel (a) indicates the boundaries of the magnified view of the interface region presented in panel b. The grey rectangle in panels (a–d) represents the magnetic fluid layer.
The contribution to drag reduction hence manifests in an upward shift of the velocity profile. The upward shift in the region next to the interface (boundary layer) is due to the slip condition26, while in the region further from the interface (outer layer), it is due to the waviness. In the turbulent regime, both slip and waviness play an important role. The dominance of one factor over the other depends mainly on the viscosity ratio. That is, the slip factor is dominant in a low-viscosity magnetic fluid, while the waviness factor is dominant in high-viscosity magnetic fluids (Fig. 5).
Range of applicability
The drag-reducing strategy based on a magnetic fluid-coated wall is capable of drag reduction, with better performance in the laminar regime with a low viscosity magnetic fluid (drag reduction up to 80%) and in the turbulent regime with a high viscosity magnetic fluid (drag reduction up to 90%) (Fig. 2c and Fig. 6).
a Experiments with viscosity ratio ηr = 6; (b) experiments with viscosity ratio ηr = 60. The dotted line is the theoretical solution for laminar flow f = c/Re with c = 14.22 for a square channel34,35, and the dashed line for turbulent flow f = 0.079 (cd*Re)-0.25 with cd = 1.125 for a square channel36,37. In the infographic on the right, we explain the symbols used in graphs (a, b). Data from experiments with magnetic fluid films are represented with filled symbols for the fluid interface (circles for low viscosity and squares for high viscosity experiments), and empty symbols for the bottom rigid wall. Data from experiments conducted without a magnetic fluid coating are denoted as references (indicated by the ‘x’ symbol).
To evaluate the potential range of applicability, we investigated the difference in friction factor at the coated and uncoated walls (Fig. 6). For our experiments in wall-bounded flow with a coated wall, the coated wall (filled symbols, Fig. 6) is always characterized by a lower Fanning friction factor (f = 2τ/ρU2) than the uncoated wall (open symbols, Fig. 6). The experimental data acquired in a channel without magnetic fluid (x symbols, Fig. 6) follow either the laminar (Re ≲ 1200) or the turbulent (Re ≳ 1200) solution. This holds for the uncoated wall of the magnetic fluid experiments as well. The experimental data show friction factors much lower than the laminar solution for the coated wall and fall along a slope similar to the laminar solution, but shifted substantially below the laminar curve. Although the slope of the trend indicates that the laminar regime in the magnetic fluid case might be sustained for higher Re compared to the uncoated one, we find that the flow is not laminar at Re ≳ 1200 also in the coated case. However, the magnetic fluid coating dampens turbulence, as manifested by smaller root mean squared velocity fluctuations < ūrms > and Reynolds shear stresses [Supplementary Note 5].
For the low viscosity magnetic fluid (Fig. 6a), we obtained effective drag reduction ( > 60%) in both laminar and turbulent regimes, whereas, for the higher magnetic fluid viscosity (Fig. 6b), we have pronounced drag reduction ( > 60%) only for the turbulent regime and weaker performance for the laminar regime (20–30%) (Fig. 2c). Therefore, high viscosity magnetic fluids are suitable for application in turbulent regimes due to their higher resistance to the shear force at the interface and their good performance in terms of drag reduction. Low-viscosity magnetic fluids are recommended for applications ranging from laminar to low turbulence regimes, provided that the shear does not exceed the threshold for detachment (see adherence condition in Material and Methods). However, low-viscosity magnetic fluid may also be applicable beyond the maximum Re investigated here, when using a larger length scale (i.e., larger channels) and/or lower velocity so that the shear remains in the range presented in this work.
The magnetic fluid-coating technique is a highly promising approach to achieve considerable drag reduction for applications in the transport and industrial sectors, such as navigation, pipelines, and bearings. Indeed, the results shown here were obtained with a saline solution, but they also apply to other diamagnetic fluids like freshwater, alcohol, and oil27,28. Moreover, due to the high shear resistance, the technique is also indicated for applications where slippery liquid-attached surfaces are required to achieve biofouling resistance, such as avoiding the accumulation of microorganisms, plants, or algae. The accumulation of microorganisms is indeed inhibited by creating an unfavourable hydrodynamic condition at the interface, i.e., a slip condition and a shift of the maximum value of shear rate away from the interface. Indeed, microorganisms will hardly attach and proliferate because of the continuous change/rearrangement of the surface. Leveraging biocompatible magnetic fluids29, we also envisage applications in the biomedical devices sector. This technique might represent an innovative solution for preventing thrombus formation and infection because the magnetic fluid film could prevent platelet adhesion and inhibit protein attachment30. Moreover, the magnetic fluid coating technique could mitigate the risks of combating infection (deterring attachment of bacteria and biofilm formation) and thrombosis (deterring protein adsorption and platelet adhesion) associated with biomedical devices, thereby reducing the need for pharmacological treatments with anticoagulant or antibiotic drugs, hence decreasing healthcare costs and improving outcomes.
Methods
Magnetic fluid characteristics
To generate the magnetic fluid film, we adopted two commercial products, EFH1 (dynamic viscosity 0.006 Pa s, density 1210 kg m−3) and EMG900 (dynamic viscosity 0.06 Pa s, density 1740 kg m-3) (Ferrotec USA corporate; more details about their characteristics can be found on the manufacturer’s website). These magnetic fluids are characterized by a shear-thinning rheological behaviour. We determined their rheological characteristic curves by dedicated microfluidic experiments [Supplementary Note 1].
The magnetic fluid film wall adherence is well defined by a balance equation between body force and momentum, μ0 MH » ρ U2, where μ0 is the vacuum permeability, M is the magnetic fluid magnetization, H is the magnetic field generated by permanent magnets, and ρ and U are the fluid density and mean flow velocity of the diamagnetic fluid in the channel. This defines the threshold flow condition above which we observe the detachment of the magnetic fluid layer31.
The dynamics of the trapped volume of magnetic fluid at the wall is characterized by a flow recirculation zone. This was investigated here by performing microfluidic experiments that allowed observation of the dynamics of magnetite-chain formation within the magnetic fluid flow [Supplementary Note 5].
Experimental setup
The experimental conduit consisted of a Plexiglas square channel with a section of 10 mm × 10 mm and a total length of 1.5 m. The flow in the channel was driven by a flow loop system. The flow rate could be adjusted to give a range of Re of 300–4000, for Re = U Dh/ν, where U is the mean velocity, Dh is the equivalent diameter equal to the characteristic length of the channel and ν is the kinematic viscosity of the fluid. The diamagnetic fluid pumped in the loop system was saltwater (density 1010 kg m-3). The magnetic fluid film, about 1 mm thick, was attached at the top wall. We use a diamagnetic fluid flowing in the channel, in direct contact with the magnetic fluid film at rest at the wall. We have tested different commercial fluids covering a range of viscosity ratios ηr (dynamic viscosity ratio between the coating fluid and the diamagnetic fluid). The magnetic fluid magnetization and the magnetic field can tune the shear resistance of the magnetic fluid coating, ensuring an attached magnetic fluid film in the flow regimes investigated [details in Methods Magnetic fluid characteristics]. The magnetic field was generated by an array of permanent neodymium magnets (N45, Supermagnete, with unit size 20 × 4 × 6 mm arranged in series along the channel with a gap of 2 mm between units). Each magnet functioned as a single “unit” capable of attracting a fixed volume of magnetic fluid. The array of magnets that guaranteed the adherence of the magnetic fluid film at the wall was located 8 mm above the flow channel and covered the entire channel length.
We used a high-speed video camera (Photron) to capture up to 16,000 frames per second at full resolution and record the flow field using particle tracking velocimetry (PTV) with acquisition at 3000 Hz. For these measures, the flow was seeded with neutrally buoyant anisotropic particles (average diameter 11 µm) illuminated by a vertical laser light sheet crossing the centre of the channel. The velocity field was measured 130 x Dh downstream of the flow entrance to avoid flow entrance disturbances. The PTV method was preferred over the particle image velocimetry (PIV) method due to its superior accuracy near the wall32. The accuracy of the velocity estimates (5%) was assessed by comparing data from a numerical solution in COMSOL with experimental data acquired under identical forcing conditions (Re = 1135) [Supplementary Note 6, Fig. S7].
The magnetic field H at the magnetic fluid layer was determined through a numerical simulation in COMSOL Multiphysics (Burlington, MA). We used the Magnetostatics package, which estimates a time-independent field without electric currents. Starting from the constitutive relation between magnetic flux B, magnetic field H and magnetization field M, B ≡ μ0(H + M), considering magnetostatic conditions, we have ∇B = 0 and ∇ × H = 0. It follows that the magnetic field H can be expressed as the gradient of a scalar magnetic potential, Vm, H = −∇Vm. Using this approach, at the coating layer, we estimated a mean magnetic field intensity of 7200 A m-1.
Data availability
The experimental dataset generated and analyzed during the current study is available from the authors upon request.
References
Saranadhi, D. et al. Sustained drag reduction in a turbulent flow using a low-temperature Leidenfrost surface. Sci. Adv. 2, e1600686 (2016).
Costantini, R., Mollicone, J. P. & Battista, F. Drag reduction induced by superhydrophobic surfaces in turbulent pipe flow. Phys. Fluids 30, 025102 (2018).
Dean, B. & Bhushan, B. Shark-skin surfaces for fluid-drag reduction in turbulent flow: a review. Philosophical transactions of the royal society a: mathematical. Phys. Eng. Sci. 368, 4775–4806 (2010).
Solomon, B. R., Khalil, K. S. & Varanasi, K. K. Drag reduction using lubricant-impregnated surfaces in viscous laminar flow. Langmuir 30, 10970–10976 (2014).
Kim, S. J., Kim, H. N., Lee, S. J. & Sung, H. J. A lubricant-infused slip surface for drag reduction. Phys. Fluids 32, 091901 (2020).
Hoyt, J. W. A Freeman scholar lecture: the effect of additives on fluid friction. J. Basic Eng. 94, 258–285 (1972).
Choueiri, G. H., Lopez, J. M. & Hof, B. Exceeding the asymptotic limit of polymer drag reduction. Phys. Rev. Lett. 120, 124501 (2018).
Sreenivasan, K. R. & White, C. M. The onset of drag reduction by dilute polymer additives, and the maximum drag reduction asymptote. J. Fluid Mech. 409, 149–164 (2000).
Elbing, B. R. et al. On the scaling of air layer drag reduction. J. Fluid Mech. 717, 484–513 (2013).
Roggenkamp, D., Jessen, W., Li, W., Klaas, M. & Schröder, W. Experimental investigation of turbulent boundary layers over transversal moving surfaces. CEAS Aeronaut. J. 6, 471–484 (2015).
Quadrio, M. Drag reduction in turbulent boundary layers by in-plane wall motion. Philosophical transactions of the royal society a: mathematical. Phys. Eng. Sci. 369, 1428–1442 (2011).
Józsa, T. I., Balaras, E., Kashtalyan, M., Borthwick, A. G. L. & Viola, I. M. Active and passive in-plane wall fluctuations in turbulent channel flows. J. Fluid Mech. 866, 689–720 (2019).
Tian, G., Fan, D., Feng, X. & Zhou, H. Thriving artificial underwater drag-reduction materials inspired from aquatic animals: progresses and challenges. RSC Adv. 11, 3399–3428 (2021).
Marusic, I. et al. An energy-efficient pathway to turbulent drag reduction. Nat. Commun. 12, 1–8 (2021).
Rosensweig, R. E. Ferrohydrodynamics (Cambridge University Press, 1985).
Choi, M. & Cho, K. Thermal characteristics of a multichip module using PF-5060 and water. KSME Int. J. 13, 443–450 (1999).
Vega-Sánchez, C., Peppou-Chapman, S., Zhu, L. & Neto, C. Nanobubbles explain the large slip observed on lubricant-infused surfaces. Nat. Commun. 13, 1–11 (2022).
Kühnen, J. et al. Destabilizing turbulence in pipe flow. Nat. Phys. 14, 386–390 (2018).
Khan, H. H., Anwer, S. F., Hasan, N. & Sanghi, S. Laminar to turbulent transition in a finite length square duct subjected to inlet disturbance. Phys. Fluids 33, 065128 (2021).
Owolabi, B. E., Poole, R. J. & Dennis, D. J. Experiments on low-reynolds-number turbulent flow through a square duct. J. Fluid Mech. 798, 398–410 (2016).
Zelazo, R. E. & Melcher, J. R. Dynamics and stability of ferrofluids: surface interactions. J. Fluid Mech. 39, 1–24 (1969).
Ghisalberti, M. & Nepf, H. M. Mixing layers and coherent structures in vegetated aquatic flows. J. Geophys. Res. Oceans 107, 3011 (2002).
Dunne, P. et al. Liquid flow and control without solid walls. Nature 581, 58–62 (2020).
Clauser, F. H. The turbulent boundary layer. Adv. Appl. Mech. 4, 1–51 (1956).
Hurst, E., Yang, Q. & Chung, Y. M. The effect of Reynolds number on turbulent drag reduction by streamwise travelling waves. J. Fluid Mech. 759, 28–55 (2014).
Seo, J. & Mani, A. On the scaling of the slip velocity in turbulent flows over superhydrophobic surfaces. Phys. Fluids 28, 025110 (2016).
Feng, L., He, X. Y., Zhu, J. L. & Shi, W. Y. Magnetic manipulation of diamagnetic droplet on slippery liquid-infused porous surface. Phys. Rev. Fluids 7, 053602 (2022).
Huang, J., Gray, D. D. & Edwards, B. F. Magnetic control of convection in nonconducting diamagnetic fluids. Phys. Rev. E 58, 5164 (1998).
Kose, A. R., Fischer, B., Mao, L. & Koser, H. Label-free cellular manipulation and sorting via biocompatible ferrofluids. Proc. Natl Acad. Sci. 106, 21478–21483 (2009).
Yuan, S., Luan, S., Yan, S., Shi, H. & Yin, J. Facile fabrication of lubricant-infused wrinkling surface for preventing thrombus formation and infection. ACS Appl. Mater. Inter. 7, 19466–19473 (2015).
Medvedev, V. F. & Krakov, M. S. Flow separation control by means of magnetic fluid. J. Magn. Magn. Mater. 39, 119–122 (1983).
Kähler, C. J., Scharnowski, S. & Cierpka, C. On the uncertainty of digital PIV and PTV near walls. Exp. Fluids 52, 1641–1656 (2012).
Virk, P. S. Drag reduction fundamentals. AIChE J. 21, 625–656 (1975).
Hartnett, J. P., Kwack, E. Y. & Rao, B. K. Hydrodynamic behavior of non‐Newtonian fluids in a square duct. J. Rheol. 30, S45–S59 (1986).
Kakac, S., Shah, R. K. & Aung, W. Handbook of Single-Phase Convective Heat Transfer (John Wiley and Sons, Inc., 1987).
Choi, C. H. & Kim, C. J. Large slip of aqueous liquid flow over a nanoengineered superhydrophobic surface. Phys. Rev. Lett. 96, 066001 (2006).
Jones, O. C. Jr An improvement in the calculation of turbulent friction in rectangular ducts. Asme. J. Fluids Eng. 98, 173–180 (1976).
Acknowledgements
We thank Stefano Lanzoni for insightful discussions; Roberto Pioli for providing the drawing in Fig. 1A; and Marius Halic Neamtu and Stefano Brizzolara for providing technical support for the particle velocimetry measurements. This work is part of a project that received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 841259 (to L.S. and M.H.). E.S. is supported by Swiss National Science Foundation PRIMA Grant 179834. All data are available in the main text or the supplementary materials.
Author information
Authors and Affiliations
Contributions
L.S. and M.H. designed research; L.S. performed research and analyzed data; E.S. and L.S. performed the microfluidics experiments; L.S., and M.H. wrote the paper; and all authors edited the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Stancanelli, L.M., Secchi, E. & Holzner, M. Magnetic fluid film enables almost complete drag reduction across laminar and turbulent flow regimes. Commun Phys 7, 30 (2024). https://doi.org/10.1038/s42005-023-01509-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-023-01509-1
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.