Time-resolved optical shadowgraphy of solid hydrogen jets as a testbed to benchmark particle-in-cell simulations

Abstract

Particle-in-cell (PIC) simulations are a widely-used tool to model kinetics-dominated plasmas in ultrarelativistic laser-solid interactions (dimensionless vectorpotential a₀ > 1). However, interactions approaching subrelativistic laser intensities (a₀ ≲ 1) are governed by correlated and collisional plasma physics, calling for benchmarks of available modeling capabilities and the establishment of standardized testbeds. Here, we propose such a testbed to experimentally benchmark PIC simulations of laser-solid interactions using a laser-irradiated micron-sized cryogenic hydrogen-jet target. Time-resolved optical shadowgraphy of the expanding plasma density, complemented by hydrodynamics and ray-tracing simulations, is used to determine the bulk-electron-temperature evolution after laser irradiation. We showcase our testbed by studying isochoric heating of solid hydrogen induced by laser pulses with a dimensionless vectorpotential of a₀ ≈ 1. Our testbed reveals that the initial surface-density gradient of the target is decisive to reach quantitative agreement at 1 ps after the interaction, demonstrating its suitability to benchmark controlled parameter scans at subrelativistic laser intensities.

Introduction

High-impact applications of high-intensity laser-solid interactions such as fast ignition in inertial-confinement fusion^1,2,3, laser-driven ion acceleration^4,5, the investigation of warm dense matter^6,7,8,9,10 or secondary-source development^{11,12,13,14,15,16} have developed into independent research fields over the last years. Gaining insight to the microscopic interaction picture is the domain of numerical modeling through simulations. In practice, the simulations are most often used retrospectively to guide the analysis and interpretation of exploratory experiments. Prediction making and the development of long-term strategies remains challenging. In translational research in radiation oncology^{17,18,19,20,21}, as one prominent example, the extrapolation of realized proof-of-concept studies towards future high-energy laser-driven proton accelerators^22,23 has been delayed^24,25. The technical realization of optimal laser-target interaction conditions and the further development of available simulation tools to correctly capture all occurring physical processes during the transition of the target from an initially solid state to an ultrarelativistic-plasma state represent the key aspects.

State-of-the-art modeling of ultrarelativistic laser-solid interactions with Petawatt-class lasers (peak intensity ≳ 10²¹ Wcm⁻²) includes the preexpansion of the target by the leading edge of the high-power laser²⁶, i.e., the amount of light that precedes the laser peak. Either the leading edge is limited to single picoseconds, enabling modeling by one single particle-in-cell (PIC) simulation^27,28, or it features a duration above tens of picoseconds, implying a staged approach of several numerical simulations^29,30,31. For intensities in the vicinity of the laser peak, i.e., dimensionless vectorpotentials a₀ ≳ 1, PIC simulations are optimized to compute the kinetic regime of particle motion and thermal nonequilibrium. The interaction in the subrelativistic regime (a₀ ≪ 1) during the leading edge is most often computed by radiation-hydrodynamics simulations.

However, the transition from relativistic to subrelativistic laser intensities, i.e., dimensionless vectorpotentials a₀ ≲ 1 (10¹⁶ to 10¹⁸ Wcm⁻² for 800 nm light), is currently reaching the limits of available modeling capabilities. The two most obvious approaches to cover this laser-intensity regime are being pursued; the extension of hydrodynamics-simulation tools³² and the inclusion of correlated and collisional plasma physics into PIC-simulation frameworks^25,33. These developments call for standardized theoretical and experimental benchmarks under unified interaction scenarios³⁴. As microscopic parameters are usually not directly accessible from laser-plasma interactions, such benchmarks would ideally require macroscopic observables that allow for an unambiguous allocation of specific interaction conditions.

In this work, we propose a testbed to experimentally benchmark PIC simulations of laser-solid interactions based on a laser-irradiated micron-sized cryogenic hydrogen-jet target^35,36,37. The PIC simulations benefit from the comparably low target density^{38,39,40,41,42}, the single-species composition, the negligible amount of Bremsstrahlung radiation (atomic number Z = 1) and simple ionization dynamics⁴³. Furthermore, the plasma composition of only protons and electrons enhances comparability to analytic calculations. Within the testbed, the temporal evolution of the laser-heated plasma density is visualized by time-resolved off-harmonic optical probing⁴⁴ via two spectrally separated, ultra-short laser beams. A fitting approach by pure hydrodynamics and ray-tracing simulations, excluding the laser heating of the target, completes the testbed. It enables the determination of the bulk-electron-temperature evolution after the laser energy was absorbed by the target. The bulk-electron temperature represents a specifically feasible endpoint, i.e., a macroscopic observable, to benchmark the entire modeling chain of non-thermal equilibrium that can be computed by PIC simulations. Although the bulk-electron temperature is usually measured by spatially and temporally integrating x-ray spectroscopy^{45,46,47,48,49,50,51,52}, time-resolved optical shadowgraphy is a convenient alternative for low-Z targets^53,54.

The capabilities of the testbed are showcased in an experiment studying isochoric heating of solid hydrogen when irradiated by laser pulses with 37 fs duration and a₀ ≈ 1. The focal spot of the laser is kept larger than the spatial dimensions of the target to guarantee a homogeneous interaction. Isochoric heating of solids by high-intensity lasers is a widely-used approach to generate warm dense and hot dense matter^55,56,57. Therefore, the process is particularly well suited to benchmark PIC-simulation results. During isochoric heating, the ultra-short laser pulse accelerates electrons on the laser-plasma interface up to relativistic velocities^{58,59,60,61,62}. Subsequently, the electrons traverse the target and generate a thermalized bulk-electron and bulk-ion temperature, mainly by resistive heating, drag heating or diffusion heating^45,63,64,65. Finally, the plasma undergoes an adiabatic expansion into vacuum and the electron and ion temperatures equilibrate⁶⁶. For lasers with a dimensionless vectorpotential a₀ ≲ 1, a transition from vacuum heating to resonance heating of electrons exists. It depends on the surface-density scalelength of the target^{67,68,69,70,71}. Furthermore, for a ≲ 1, the collisionality of particles increases in relevance.

By demonstrating the capability of the testbed to quantitatively benchmark PIC simulations, the showcase establishes the basis towards controlled parameter scans at laser intensities well below a₀ = 1. This transition regime from solid state to ultrarelativistic plasmas is highly relevant to all high-intensity laser-solid interaction and their applications.

Results

The testbed platform

The section is divided into two parts. The first subsection “Experiment” presents the assembly of the testbed platform and, for a specific showcase, a time-delay scan of two-color shadowgraphy in the tens-of-picosecond timeframe. The following subsections describe the determination of the corresponding electron-temperature evolution. The first subsection “Hydrodynamics simulation - HD” utilizes a homogeneous electron temperature throughout the central plane of the target and calculates the electron-density evolution via a hydrodynamics simulation. The second subsection “Ray-tracing simulation - RT” simulates the corresponding shadow diameters versus delay by ray-tracing simulations and the third subsection “χ² fit” presents a χ² fit of the simulated to the measured shadow diameters. By this we derive the best-matching electron-temperature evolution that corresponds to the bulk-electron-temperature evolution after isochoric heating and thermalization in the experiment. The combination of hydrodynamics simulations, ray-tracing simulations and the χ² fit is referred to as HD-RT fit in the following.

Experiment

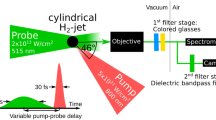
The testbed platform is established at the Draco-150 TW laser at the Helmholtz-Zentrum Dresden-Rossendorf ⁷². The top view of the experimental setup is shown in Fig. 1a. By placing a 16 mm-wide circular aperture in the collimated beam path, the pump-laser energy is reduced to a maximum value of E_laser = 160 mJ. A stepwise reduction of the energy to 10.4 mJ, 1.21 mJ, 353 μJ, and 26.6 μJ is realized by switching off specific amplifier sections of the pump laser. A pair of thin-film polarizers and a waveplate in the collimated beam path before compression (transmission between 10 and 100%) allows for an additional lowering of each energy level. The pump-laser pulses feature a central wavelength of λ_laser = 800 nm. An acousto-optic programmable dispersive filter and an optional SF6 glass block in the stretched beam path before compression enable settings of the pulse duration between τ_laser = 37 fs and 12.6 ps full width at half maximum (FWHM). The pump-laser beam is focused by an f/16 off-axis parabola (OAP) and generates an Airy-pattern focus with a spatial FWHM of 14 μm of the central disk.

Fig. 1: The testbed platform.

a Experimental setup of the testbed platform: The pump laser with a pulse energy E_laser, a pulse duration τ_laser, and a peak intensity I_laser interacts with a cylindrical hydrogen-jet target. Time-resolved high-resolution shadowgraphy utilizes a single microscope and two simultaneous backlighters with a pulse duration of 260 fs (258 nm probe) and 160 fs (515 nm probe). b Showcase with E_laser = 160 mJ, τ_laser = 37 fs, and I_laser = 1.6 × 10¹⁸ Wcm⁻²: Exemplary shadowgrams of a time-delay scan as recorded by the 258 nm probe. The pump-probe delay is given in the upper-right corner of each shadowgram and the shadow diameter ${D}_{{{{{{{{\rm{E}}}}}}}}}^{258\,{{{{{{{\rm{nm}}}}}}}}}$ is measured between the cyan arrows. For 30 ps delay, volumetric transparency is observed. The spatial extent and fluence of the parasitic plasma emission vary from shot-to shot. The colorscale and spatial scale are consistent between the images.

A continuous, self-replenishing jet of cryogenic hydrogen is used as a target^35,36. The cross-section of the target at the source is defined by a circular aperture with a diameter of (5 ± 1) μm. At the position of the laser-target interaction, the mean diameter is 4.4 μm with a standard deviation of 0.2 μm (details in “Methods” section “Measurement of the variation of the initial target diameter”). The electron density of the fully ionized target is 5.2 × 10²² cm⁻³, which corresponds to 30 times the critical plasma density of 800 nm light ${n}_{{{{{{{{\rm{c}}}}}}}}}^{800\,{{{{{{{\rm{nm}}}}}}}}}$.

The laser-target interaction is investigated by time-resolved off-harmonic optical shadowgraphy⁴⁴ at 90^∘ angle to the pump-laser propagation direction. Two copropagating backlighter pulses with the wavelengths λ of 515 nm and 258 nm are generated from a synchronized stand-alone laser system⁷³. The 258 nm probe and the 515 nm probe feature a pulse energy of approximately 0.3 μJ and 5 μJ and a pulse duration of 260 fs and 160 fs, respectively. The pump-probe delay is variable, the temporal resolution of a time-delay scan is 175 fs and the captured snapshots are blurred by the pulse duration⁴⁴. Dispersion effects in the beam path⁷⁴ cause a fixed delay of 4.6 ps between both probe-laser pulses. All delays are given with respect to the arrival of the pump-laser peak on target at 0 ps delay. To cope with the parasitic plasma emission, both probe beams are focused by an f/1 OAP.

A long-working-distance infinite-conjugate microscope objective (designed for laser wavelengths of 266 nm and 532 nm) is used to image the shadow of the target simultaneously for both wavelength, i.e., at two different ranges of plasma density. The two images are separated by a dichroic mirror and recorded by different cameras, each equipped with the corresponding color filters (more details in “Methods” section “Experimental details of the optical microscope”).

To showcase the capabilities of the testbed, all following results are derived for a pump-laser setting of E_laser = 160 mJ, τ_laser = 37 fs and a peak intensity of I_laser = 1.6 × 10¹⁸ Wcm⁻². A pump-probe time-delay scan in steps of 5 ps is performed. The inherent spatial jitter of the target is controlled by a secondary optical-probe axis³⁹. Only data from within ± 2 μm of the object plane is presented. Exemplary shadowgrams at 0 ps, 10 ps and 30 ps delay are shown in Fig. 1b. The images are recorded by the 258 nm probe and show a sideview of the target. The pump laser impinges from the left and the spatial FWHM of the focal spot is indicated by the dashed lines on the left-hand side. Plasma emission occurs mostly from within the FWHM of the focal spot and from the position of the unperturbed target-front surface. The shadow of the target features sharp edges. The shadow diameter ${D}_{{{{{{{{\rm{E}}}}}}}}}^{258\,{{{{{{{\rm{nm}}}}}}}}}$ measures the width of the shadow at the position of the pump-laser peak, as illustrated by the cyan arrows in the shadowgrams at 0 ps and 10 ps delay. Although the overall expansion of the shadow appears symmetric along the x- and y- axis, sub-micrometer-sized asymmetries on the front and on the rear side cannot be excluded due to shot-to-shot positioning jitter (compare “Methods” section “Measurement of the variation of the initial target diameter”). At 30 ps, the edges of the shadow are diffuse and prevent the measurement of ${D}_{{{{{{{{\rm{E}}}}}}}}}^{258\,{{{{{{{\rm{nm}}}}}}}}}$. Consequently, ${D}_{{{{{{{{\rm{E}}}}}}}}}^{258\,{{{{{{{\rm{nm}}}}}}}}}$ is set to zero for this delay. The shadowgram shows penetration of probe light through central parts of the target. In the following, we refer to this observation as volumetric transparency.

The whole scan of shadow diameter versus pump-probe delay is shown by the markers in Fig. 2. ${D}_{{{{{{{{\rm{E}}}}}}}}}^{258\,{{{{{{{\rm{nm}}}}}}}}}$ and ${D}_{{{{{{{{\rm{E}}}}}}}}}^{515\,{{{{{{{\rm{nm}}}}}}}}}$ both increase with pump-probe delay until volumetric transparency sets in. For the 258 nm probe and the 515 nm probe, this occurs between 20 and 25 ps and between 45 and 50 ps, respectively. For all delays greater than zero, ${D}_{{{{{{{{\rm{E}}}}}}}}}^{515\,{{{{{{{\rm{nm}}}}}}}}}$ is on average larger than ${D}_{{{{{{{{\rm{E}}}}}}}}}^{258\,{{{{{{{\rm{nm}}}}}}}}}$. This is expected, as the critical plasma density n_c drops with increasing wavelength λ according to

$${n}_{{{{{{{{\rm{c}}}}}}}}}^{\lambda }\propto \frac{1}{{\lambda }^{2}}.$$

(1)

Assuming an exponentially decreasing plasma-density surface, the difference between ${D}_{{{{{{{{\rm{E}}}}}}}}}^{258\,{{{{{{{\rm{nm}}}}}}}}}$ and ${D}_{{{{{{{{\rm{E}}}}}}}}}^{515\,{{{{{{{\rm{nm}}}}}}}}}$ enables the calculation of the corresponding scalelength L₀. For 0 ps delay, the surface scalelength calulates to values between 0 and about 0.42 μm. Figure 2 shows shot-to-shot fluctuations of the shadow diameter. They are caused by inherent shot-to-shot variations of the target and the pump laser. Target variations include local changes of diameter and aspect ratio on the submicron scale as well as bow-like deformations along the jet axis on the micron scale, which correspond to variations of the angle of incidence (details in “Methods” section “Measurement of the variation of the initial target diameter”). Furthermore, the rapid freezing of the jet introduces compositional and structural variations of the solid hydrogen⁷⁵. The main source of fluctuation of the pump-laser intensity is the peak power with a measured standard deviation of 12%. The fluctuation of the pump-laser energy is about 1% and the pointing jitter is negligible.

Fig. 2: Experimental data and result of the HD-RT fit.

Measured shadow diameter from two-color optical shadowgraphy (dots) and HD-RT fit (lines) to the experimental data (case α: T_e0 = 250 eV, D₀ = 3.5 μm). The errorbars reflect the spatial-resolution limit of the experimental diagnostic.

Hydrodynamics simulation - HD

As we will show by PIC simulations below, the density evolution of the hydrogen plasma is driven by a two-temperature adiabatic expansion, which can be modeled via hydrodynamics simulations. In the following, the simulation tool FLASH^76,77 is used to perform two-temperature hydrodynamics simulations in two-dimensional radial symmetry with the hydrogen equation of state FPEOS⁷⁸ (details in “Methods” section “Equation of state of hydrogen”). Initially, there are three free parameters of the target model: the ion temperature T_i0, the electron temperature T_e0 and the initial plasma diameter D₀. Because the evolution of the shadow diameter is sensitive to the initial plasma diameter D₀, which is subject to experimental fluctuations, we handle D₀ as a free parameter within the range of the experimental uncertainties. Compared to the effect of T_e0, the initial ion temperature T_i0 ≪ T_e0 has little effect on the evolution of the plasma density during hydrodynamic expansion, just as the consideration of an initial surface-density scalelength. As derived by PIC simulations (see later), T_i0 can be approximated by 10 eV.

Hydrodynamics simulations with different initial electron temperatures T_e0 and different initial plasma diameters D₀ are conducted. Each simulation box has a length of 50 μm and a vacuum density of 1 × 10⁻⁸ times the target density. An exemplary evolution of the electron density is shown in Fig. 3a and the corresponding evolution of ion and electron temperature is shown in Fig. 3b. The evolution of the electron density shows a transformation of the originally box-shaped profile into a smooth radial profile with an exponentially decreasing surface density. The scalelength of the surface density increases with delay. The evolution of the electron and ion temperatures show a convergence of both quantities at about 10 ps. Subsequently both temperatures jointly decrease.

Fig. 3: Hydrodynamics simulation and ray-tracing simulation of the HD-RT fit.

a Radial electron density of the hydrodynamics simulation with an initial setting of T_e0 = 300 eV and D₀ = 4 μm (case β in Fig. 4). The corresponding shadow diameters ${D}_{{{{{{{{\rm{S}}}}}}}}}^{258\,{{{{{{{\rm{nm}}}}}}}}}$ are derived by ray-tracing simulations and are given by the dashed arrows on the top. b The blue line and red dashed line show the electron and proton temperature of the target bulk at zero radius versus time (case β). c Top view of the distribution of refractive indices ${\tilde{n}}^{258{{{{{{{\rm{nm}}}}}}}}}$ (gray colorscale), which is calculated from the radial electron-density profile at 15 ps delay (case β). The distribution is placed in the object plane of the ray-tracing simulation and refraction of the 258 nm-probe rays is visualized by the purple lines. d Light distribution in the image plane of the ray-tracing simulation behind the objective. The shadow diameter ${D}_{{{{{{{{\rm{S}}}}}}}}}^{258\,{{{{{{{\rm{nm}}}}}}}}}$ is measured at half of the unperturbed background intensity.

Ray-tracing simulation - RT

To compare the evolution of the electron density in the hydrodynamics simulation with the experimentally measured shadowgraphy data, the shadow formation of each probe beam needs to be modeled. For optical shadowgraphy of solid-density plasmas, shadow formation is governed by refraction on the density gradients of the under-critical regions of the plasma⁴⁴. Each simulated density profile is transformed into a two-dimensional distribution of refractive indices $\tilde{n}$ from the local electron density n_e via the dispersion relation⁵

$$\tilde{n}=\sqrt{1-\frac{{n}_{{{{{{{{\rm{e}}}}}}}}}}{{n}_{{{{{{{{\rm{c}}}}}}}}}^{{{{{{{\lambda}}}}}}}}}\,.$$

(2)

The critical density ${n}_{{{\rm{c}}}}^{\lambda}$ depends on the wavelength and ${\tilde{n}}^{258{{{{{{{\rm{nm}}}}}}}}}$ and ${\tilde{n}}^{515{{{{{{{\rm{nm}}}}}}}}}$ are calculated separately.

The experimental imaging setup and the beam path of each probe beam are reproduced in a virtual optical setup with the software Zemax [Zemax 13 Release 2 SP6 Professional (64-bit)]. The objective features a numerical aperture of 0.55. The calculated spatial distribution of refractive indices ${\tilde{n}}^{258{{{{{{{\rm{nm}}}}}}}}}$ or ${\tilde{n}}^{515{{{{{{{\rm{nm}}}}}}}}}$ is inserted into the object plane of the corresponding setup, which is exemplary shown in Fig. 3c. The purple lines illustrate the refraction of the 258 nm-probe rays in the gradients of the refractive-index distribution. The light distribution in the image plane is calculated by Zemax and presented in Fig. 3d. The graph shows the formation of a shadow with sharp edges, similar to the experiment. Refraction leads to an increased intensity level at the rim of the shadow edges. The shadow diameter ${D}_{{{{{{{{\rm{S}}}}}}}}}^{258\,{{{{{{{\rm{nm}}}}}}}}}$ is derived at half of the unperturbed background intensity (0.5 arb. units). By utilizing the virtual setup of the 515 nm probe, ${D}_{{{{{{{{\rm{S}}}}}}}}}^{515\,{{{{{{{\rm{nm}}}}}}}}}$ is calculated accordingly.

The simulated evolution of ${D}_{{{{{{{{\rm{S}}}}}}}}}^{258\,{{{{{{{\rm{nm}}}}}}}}}$ (purple) and ${D}_{{{{{{{{\rm{S}}}}}}}}}^{515\,{{{{{{{\rm{nm}}}}}}}}}$ (green) of a hydrodynamics simulation with the initial setting T_e0 = 250 eV and D₀ = 3.5 μm (case α) is shown as solid lines in Fig. 2. Like in the experiment, D_S is set to zero at delays for which no sharp shadow edge is derived and volumetric transparency is observed instead. For the 258 nm probe and the 515 nm probe of case α, this occurs at 22.5 ps and 47.5 ps delay, respectively.

χ ² fit

To find the best-matching initial settings of the hydrodynamics simulation with respect to the experimental data, the initial electron temperature T_e0 is varied from 100 to 350 eV in steps of 50 eV. Furthermore, the initial plasma diameter D₀ is scanned from 3 to 5 μm in steps of 0.5 μm. The variance χ² of the difference between the experimental data D_E(t, λ) and the simulation data D_S(t, λ, T_e0, D₀) is

$${\chi }^{2}({T}_{{{{{{{{\rm{e}}}}}}}}0},{D}_{0})=\mathop{\sum}\limits_{t,\lambda }{\left({D}_{{{{{{{{\rm{E}}}}}}}}}(t,\lambda )-{D}_{{{{{{{{\rm{S}}}}}}}}}(t,\lambda ,{T}_{{{{{{{{\rm{e}}}}}}}}0},{D}_{0})\right)}^{2}.$$

(3)

Here, t is the pump-probe delay. The resulting χ² map is shown in Fig. 4. Minimum values of χ² are reached for case α (T_e0 = 250 eV, D₀ = 3.5 μm) and case β (T_e0 = 300 eV, D₀ = 4 μm). Case β has better agreement to the 258 nm-probing data and case α has better agreement to the 515 nm-probing data. The two cases give a lower and upper limit of the best-fitting T_e0 and D₀. A discussion of the method of the HD-RT fit is given in “Methods” section “Discussion of the HD-RT fit”.

Fig. 4: χ² fit.

The total χ² distribution between the experimental data and all HD-RT simulation data. Each grid point represents a setting of T_e0 and D₀. χ² is calculated by equation (3). α and β represent cases of minimized χ².

In summary, the HD-RT fit allows to fit a heuristic electron-temperature evolution subsequent to isochoric heating and thermalization of the bulk electrons, which constitutes the endpoint of the testbed for a comparison to PIC simulations. The HD-RT fit of the showcase with E_laser = 160 mJ, τ_laser = 37 fs and I_laser = 1.6 × 10¹⁸Wcm⁻² yields a heuristic initial bulk-electron temperature T_e0 between 250 and 300 eV at 0 ps delay.

PIC simulation

This section demonstrates a comparison of the showcase with a PIC simulation of the corresponding high-intensity laser-solid interaction. The comparable endpoint is the temporal evolution of the bulk-electron temperature. The presentation of the results of the PIC simulation details the processes of isochoric heating and thermalization of the bulk electrons (not captured by the hydrodynamics simulation of the HD-RT fit). It finally leads to the evolution of the bulk-electron temperature after thermalization, which can be compared to the hydrodynamics simulation of the HD-RT fit.

The simulation is performed with the PIC-simulation tool PIConGPU⁷⁹ in 2D3V geometry. The target is modeled by a fully ionized spherical hydrogen column. The density distribution follows the model

$$n(r)={n}_{0}\,({{\Theta }}({r}_{{{{{{{{\rm{c}}}}}}}}}-r)+{{\Theta }}(r-{r}_{{{{{{{{\rm{c}}}}}}}}})\,{e}^{-(r-{r}_{{{{{{{{\rm{c}}}}}}}}})/{L}_{0}})$$

(4)

with ${n}_{0}=30\,{n}_{{{{{{{{\rm{c}}}}}}}}}^{800\,{{{{{{{\rm{nm}}}}}}}}}$, a surface scalelength L₀ = 0.25 μm (mean of the experimental uncertainty), an unperturbed target diameter of D₀ = 4.4 μm (see “Methods” section “Measurement of the variation of the initial target diameter”), the Heaviside step function Θ and the reduced radius

$${r}_{{{{{{{{\rm{c}}}}}}}}}=\sqrt{\frac{{D}_{0}^{2}}{4}-{L}_{0}^{2}}-{L}_{0}$$

(5)

to fulfill mass conservation. The initialized total length of the surface plasma corresponds to ten times L₀ and the initial temperature of electrons and ions is 0.1 eV. The laser is incident along the y direction and polarized in x direction. It features a Gaussian shape in space and time, a pulse duration of 37 fs FWHM and a laser-spot size of 14 μm FWHM. The simulation box is 32 × 32 μm² with absorbing boundary conditions and the simulation uses a cell length of 0.8 μm/96 and 240 macro particles per cell. The simulation includes a relativistic-binary-collision mechanism.

Figure 5a shows the simulated electron-density profile for different delays. 0 ps delay corresponds to the arrival of the pump-laser peak on the front side of the target. The comparison of the blue and the orange line shows that the electron density at 0.2 ps delay does not significantly differ from the initial state at −0.1 ps. The expansion of hot electrons into the surrounding vacuum occurs at densities below about $0.1\,{n}_{{{{{{{{\rm{c}}}}}}}}}^{800\,{{{{{{{\rm{nm}}}}}}}}}$. Comparing the electron-density profiles at 0.2 ps, 1.0 ps and 2.1 ps, two characteristics are identified. The density region denoted by “1” shows a temporally increasing exponential scalelength of the plasma density. It results from adiabatic expansion, which is driven by the electron temperature T_e inside the target bulk (refer to Bulk plasma in Fig. 5b). For the electron-density profile at 1.0 ps delay, however, the exponential scalelength is overlayed by a transiently occurring step of the density profile that is denoted by “2”. It is caused by the thermal pressure of the coronal plasma that features a much higher temperature than the bulk plasma. The spatial distribution of the electron temperature T_e at 1.0 ps delay is displayed in Fig. 5b. The electrons inside the bulk plasma feature a spatially constant temperature of 450 eV while the coronal plasma features temperatures above 10 keV. For comparison of Fig. 5a, b the vertical dashed line indicates the radius of the strong increase of T_e, which coincides with the step of the electron-density profile denoted by “2”. As the hotter coronal plasma expands faster than the bulk plasma, the influence of the coronal plasma on the plasma densities in the range above $0.1\,{n}_{{{{{{{{\rm{c}}}}}}}}}^{800\,{{{{{{{\rm{nm}}}}}}}}}$ decreases with delay and adiabatic plasma expansion most likely dominates for longer delays (compare the evolution of regions “1” and “2” of the density profiles at 1.0 ps and 2.1 ps delay). Note that the hydrodynamics simulations of the HD-RT fit considers adiabatic plasma expansion only and agreement between the density profiles of the PIC simulation and the HD-RT fit to the experiment is expected at delays for which region “1” dominates the expansion process. It follows that, in the discussed case, the evolution of the electron temperature T_e in the bulk plasma is a better suited endpoint of the comparison than a direct comparison of the density profiles.

Fig. 5: PIC simulation results.

a Spatial distribution of the electron density in the PIC simulation. b The blue star markers shows the spatial distribution of the electron temperature T_e at 1 ps delay. The red dashed line marks a temperature of 450 eV. The black dashed line is a guide for the eye to enhance comparability to fig. (a). The red shaded region indicates the coronal plasma. c Temporal evolution of the equivalent temperatures T_n (equation (6)). Thermalization is reached at about 1.5 ps. d Comparison of the PIC simulation (red) and the HD-RT fit (black) to the experiment. The shaded background illustrates the transition from thermal nonequilibrium (red) to thermal equilibrium (transparent).

The temporal evolution of the bulk-electron temperature T_e and the equivalent temperatures to the average kinetic energy T_x, T_y, and T_z are displayed in Fig. 5c, d. T_n with n = x, y or z is calculated from the average kinetic energy

$${\overline{E}}_{kn}=\frac{1}{2}\,{k}_{{{{{{{{\rm{B}}}}}}}}}\,{T}_{n}$$

(6)

of the electrons within the bulk plasma (circle with a radius of 2 μm). As the laser is polarized into the x direction and propagates along the y direction, T_x and T_y include the contribution of non-thermal laser-accelerated electrons. In contrast, T_z is generated by collision of particles only. For 2D3V-PIC simulations, the bulk-electron temperature T_e is close to the temperature component T_z. Throughout this work, the quantity T_e of the PIC simulations is derived by a Maxwellian fit to the electron-velocity distribution of the bulk plasma.

The maximum of T_x and T_y of 20 keV is reached at 67 fs. Together with the approximately constant electron-density profile between −0.1 and 0.2 ps, this indicates that the heating of the plasma bulk happens isochorically. Subsequently, as the plasma starts to expand, the temperatures T_x and T_y decrease while T_z increases. The term thermalization refers to the circumstance that all electrons get the same Maxwellian temperature distribution into all spatial dimensions via collisions. As Fig. 5c shows, T_x, T_y, and T_z equal each other after about 1.5 ps, i.e., the plasma thermalized within about 1.4 ps after the termination of heating. From the analytic electron-electron collision rate of hot electrons and assuming a plasma with an electron density of $30\,{n}_{{{{{{{{\rm{c}}}}}}}}}^{800\,{{{{{{{\rm{nm}}}}}}}}}$ and a temperature of 20 keV we find a thermalization time⁸⁰

$$\tau =\frac{1}{{\nu }_{{{{{{{{\rm{ee}}}}}}}}}}=1.0\,{{{{{{{\rm{ps}}}}}}}},$$

(7)

which is in close agreement to the PIC simulation. We emphasize that the testbed utilizes a pure hydrogen target, which allows for the comparison to analytical calculations without further approximations.

Figure 5d compares the evolution of the bulk-electron temperature T_e of the PIC simulation (red line) and the electron-temperature evolution of the HD-RT fit to the experiment (black line). The lower and upper limit of the black line correspond the cases α and β. Up to 1.5 ps the PIC-simulation results show the process of isochoric heating and thermalization. Subsequently, T_e declines because of adiabatic plasma expansion. The HD-RT fit, however, shows adiabatic plasma expansion only, which artificially starts with a heuristic initial electron temperature at 0 ps delay. Both approaches are comparable only after thermalization, i.e., at delays later than 1.5 ps. Although the trend of adiabatic cooling by plasma expansion is present for both approaches, the PIC simulation overestimates the bulk-electron temperature compared to the electron temperature of the HD-RT fit. To demonstrate the feasibility of the testbed to benchmark PIC simulations, the next section discusses the disagreement by presenting systematic scans of PIC simulations.

Discussion

As exemplified, the results of the testbed are feasible to be used for quantitative comparisons to PIC simulations. In this section we discuss the effect of different parameters of the PIC simulations with respect to the chosen endpoint of the bulk-electron temperature after thermalization.

References^{67,68,69,70,71} show that resonance absorption dominates the heating of electrons for laser irradiances ${I}_{{{{{{{{\rm{laser}}}}}}}}}\,{\lambda }_{{{{{{{{\rm{laser}}}}}}}}}^{2}\,\lesssim \,1\times 1{0}^{18}\,{{{{{{{\rm{W}}}}}}}}\mu {{{{{{{{\rm{m}}}}}}}}}^{2}{{{{{{{{\rm{cm}}}}}}}}}^{-2}$ and targets with a surface-density scalelengths L₀ ≳ 0.1 λ_laser = 80 nm. Vacuum heating of electrons, however, dominates for targets with a surface scalelengths L₀ ≲ 0.1 λ_laser = 80 nm. Furthermore, ref. ⁸¹ shows that the existence of pre-plasma changes the laser-absorption efficiency. The here-utilized peak irradiance is 1.0 × 10¹⁸ Wμm²cm⁻². Consequently, we expect a dependence of the heating of electrons to the surface-density scalelength of the target.

According to the experimental uncertainties, PIC simulations with different initial scalelengths L₀ between 0 and 500 nm are conducted. Figure 6a displays the derived bulk-electron temperatures T_e at 1.8 ps delay. The two limiting cases are T_e = 1087 eV for L₀ = 0 and T_e = 353 eV for L₀ = 500 nm, which corresponds to a variation of almost a factor of 3. An exponential fit to the data (dashed line) suggests the saturation of the temperature decrease with increasing initial scalelength.

Fig. 6: Effect of pre-plasma on the electron temperature in the PIC simulation.

a Bulk-electron temperature T_e at 1.8 ps delay versus the initial surface-density scalelength of the target L₀ (markers). The dashed line is an exponential fit to the data and serve as a guide for the eye. b Electron-velocity distribution in the laser-propagation direction to the time of the maximum return current at 20 fs delay. The blue and orange line show the electron-velocity distribution of L₀ = 0 nm and 250 nm, respectively.

As explained in the following, the reduction of the bulk-electron temperature for increased surface scalelengths L₀ is caused by a change of the laser-absorption mechanism from vacuum heating at small L₀ to resonance absorption at higher L₀. Figure 6b shows the velocity distribution of electrons in laser-propagation direction in the cases of L₀ = 0 and L₀ = 250 nm at 20 fs delay. Both distributions feature a forward-moving electron current with velocities between ~0.1 c and 0.5 c. However, in the case of L₀ = 250 nm, the overall number of forward-moving electrons is decreased, which is a signature of the transition from vacuum heating to resonance absorption. A second signature of this transition is given by an increased temperature of the coronal plasma (red-shaded area in Fig. 5b) for higher L₀. The total temporal peak of the forward-moving electron current decreases from 32.4 kAμm⁻² at L₀ = 0 to 10 kAμm⁻² at L₀ = 500 nm. A temporally resolved analytic calculation of the electron-temperature increase by resistive return-current heating based on the simulated forward-moving electron current demonstrates good agreement to the increase of the bulk-electron temperature of the PIC simulations up to 70 fs delay. It follows that the decrease of the forward-moving electron current contributes to a reduction of the bulk-electron temperature as the laser-absorption mechanism changes from vacuum heating at low L₀ to resonance absorption at high L₀.

The “Methods” section of this work summarizes other parameter scans and assumptions of the PIC simulations that influence the bulk-electron temperature, each on a sub-20% level. The “Methods” section “Ionization state of the target” and “Radiative cooling” show that the assumption of an initially fully ionized target and the negligence of radiative cooling are reasonable approximations with insignificant effect on the final evolution of the bulk-electron temperature. “Methods” section “2D3V-PIC simulation versus 3D-PIC Simulation” investigates the difference of 2D3V-PIC and 3D-PIC simulations with a high number of particles per cell. The results reveal that, between 0.2 ps and 0.4 ps delay, the bulk-electron temperature of the 3D-PIC simulation is 1.7% lower than the bulk-electron temperature of the 2D3V-PIC simulation. To furthermore check the influence of the pressure gradient of hot electrons along the z axis in the experimental parameter range, “Methods” section “Lateral heat transfer” presents 3D-PIC simulations with a larger box size and lower resolution. The results demonstrate that the influence of three-dimensional effects of the hot-electron density distribution are negligible within the FWHM of the pump-laser focal spot.

PIConGPU features a Coulomb-binary-collision model, which is given by the Spitzer-resistivity model of return-current Joule heating with a constant collision-frequency cutoff at low temperatures. However, as shown in ref. ⁸², even if a constant cutoff is applied in the low-temperature regime, the Spitzer-resistivity strongly deviates from the Lee-More, Redmer, and Monte-Carlo results. Therefore, a low-temperature collision-frequency correction is needed for electron temperatures lower than the Fermi temperature³². A calculation of the relevance for the parameter range discussed here is given in “Methods” section “Low-temperature-collision correction”. During the leading edge of the laser pulse, at bulk-electron temperatures below 100 eV, slight deviations between the calculation and the results of the PIConGPU simulation are observed. However, as the collision rate remains unaffected at the hundreds-of-eV temperature level, the low-temperature collision correction has negligible influence on the bulk-electron temperature after thermalization. To furthermore test the influence of the analytic uncertainty of the Coulomb logarithm $\ln {{\Lambda }}$ of $O(\ln {{{\Lambda }}}^{-1})$, PIC simulations with different fixed Coulomb logarithms are performed in “Methods” section “Effect of the Coulomb logarithm”. A decrease of the Coulomb logarithm from 15 to 3.5 decreases the bulk-electron temperature at 1 ps delay by about 20%, which is small compared to the dependence on the initial surface-density scalelength.

In summary, systematic scans of PIC simulations show that mainly the dependence on the initial surface-density scalelength contributes to the overestimation of the bulk-electron temperature by the PIC simulation. The observed transition over different heating mechanisms of electrons confirms previous work at similar laser-intensity levels^{67,68,69,70,71}. The result underlines the importance of the exact initial distribution of the target density (beyond a simple surface-density scalelength) in PIC simulations that attempt to model experimental scenarios, which is known, for example, from laser-driven proton acceleration^29,83.

Outlook

The presented showcase of the testbed utilizes isochoric heating of solid hydrogen by an ultra-short laser pulse with a dimensionless vectorpotential a₀ ≈ 1. Considering the future prospects of the testbed, a simple reduction of the pump-laser energy directly leads to a reduction of a₀. With that, the showcase demonstrates the readiness of the testbed for controlled parameter scans in experiment and simulation at all laser intensities of a₀ ≲ 1 and varied laser-pulse duration.

By increasing the pump-laser energy in the future, the testbed is also able to investigate the transition from the thermal-driven regime of plasma expansion (a₀ < 1) to the hot-electron sheath-driven regime of plasma expansion (a₀ > 1). We expect similarities to the plasma physics of laser-heated nanoparticles^{84,85,86,87,88}. At intensities approaching 10²² Wcm⁻² (a₀ ≫ 1) similar investigations like in the presented showcase suggest that relativistically induced transparency becomes relevant⁴⁴.

In the present implementation, the testbed features probe beams at 258 nm and 515 nm wavelength. The probe beams are sensitive to plasma-density gradients around an electron density of about $0.1\,{n}_{{{{{{{{\rm{c}}}}}}}}}^{258\,{{{{{{{\rm{nm}}}}}}}}}\approx 1\,{n}_{{{{{{{{\rm{c}}}}}}}}}^{800\,{{{{{{{\rm{nm}}}}}}}}}$ and $0.1\,{n}_{{{{{{{{\rm{c}}}}}}}}}^{515\,{{{{{{{\rm{nm}}}}}}}}}\approx 0.2\,{n}_{{{{{{{{\rm{c}}}}}}}}}^{800\,{{{{{{{\rm{nm}}}}}}}}}$⁴⁴. A comparison of both densities to the density profiles of the PIC simulation in Fig. 5a shows that the shadowgraphy diagnostic does not image the density of the hot coronal plasma, which features electron densities between $0.1\,{n}_{{{{{{{{\rm{c}}}}}}}}}^{800\,{{{{{{{\rm{nm}}}}}}}}}$ and $1{0}^{-3}\,{n}_{{{{{{{{\rm{c}}}}}}}}}^{800\,{{{{{{{\rm{nm}}}}}}}}}$ (decreasing with delay). A modification of the experimental setup to probing wavelengths in the near-infrared spectral range (e.g., 2.5 μm wavelength) would allow to measure the respective densities and, by this, enable a complementary benchmark of PIC simulations with respect to non-thermal effects beyond the bulk-electron population.

Cryogenic jets of different material and composition are readily available and frequently used⁸⁹. In the future, the effect of multi-species mixtures of hydrogen and deuterium will be studied⁹⁰ and cryogenic Argon-jets will allow to benchmark ionization and recombination dynamics as well as plasma opacity, e.g., by probing with extreme-ultraviolet backlighters^91,92,93.

Finally, we would like to emphasize that the testbed is ready to be used in combination with other laser-driven secondary sources that induce isochoric heating, for example laser-accelerated ion beams⁹⁴.

Conclusions

We propose a testbed to experimentally benchmark PIC simulations based on laser-irradiated micron-sized cryogenic hydrogen-jet targets. Time-resolved optical shadowgraphy by two spectrally separated laser beams measures the temporal evolution of the plasma density. A fitting approach by hydrodynamics and ray-tracing simulations enables the determination of the bulk-electron temperature evolution after the laser energy was absorbed by the target (HD-RT fit).

A showcase studies isochoric heating of solid hydrogen by laser pulses of 37 fs duration and a dimensionless vectorpotential a₀ ≈ 1. The derived bulk-electron temperature between 250 and 300 eV is supported by systematic scans of PIC simulations.

We confirmed the universality of the testbed by further measurements of plasma expansion down to intensities of at least 10¹⁶Wcm⁻² (a₀ ≈ 0.07) and demonstrated its readiness to accompany ongoing developments of PIC simulations towards the inclusion of physics models at subrelativistic laser-intensity levels.

Methods

Experimental details of the optical microscope

For the 258 nm-probe imaging, the magnification is M = 77 and the measured spatial resolution limit is < 500 nm. The utilized camera is a PCO.ultraviolet (14bit CCD sensor with 1392 × 1040 pixels of 4.65 μm size), which results in an overall field of view (FoV) of 84 μm × 63 μm. The 515 nm-probe imaging has a magnification of M = 70 with a measured spatial resolution limit of < 1 μm. Images are recorded with a PCO.edge 4.2 camera (16bit sCMOS sensor with 2048 × 2048 pixels of 6.5 μm size each), resulting in a FoV of 190 × 190 μm².

Measurement of the variation of the initial target diameter

The HD-RT fit is sensitive to the initial diameter of the target. Experimentally, the initial target diameter is defined by the aperture of the source that ejects liquefied hydrogen into the vacuum of the target chamber³⁵. Evaporation of the liquid hydrogen causes the jet to rapidly freeze. This reduces the diameter of the frozen solid hydrogen jet. Energy conservation allows to estimate the amount of liquid hydrogen that is required to be evaporated in order to cause the residual material to freeze. Depending on the initial temperature, the evaporated material constitutes up to 25% of the initial liquid volume, resulting in a reduction of the diameter of the solid jet by up to 13.3%. Additionally, the increased density of solid hydrogen with respect to the liquid phase leads to an further reduction in diameter of about 7%. In this study, a cylindrical source aperture with a nominal diameter of 5 μm and ± 1 μm manufacturing tolerance is used. This results in an expected initial diameter of the solid hydrogen jet of about (4.0 ± 0.8) μm.

To measure the mean and the variation of the target diameter, a bright-field-microscopy image of the unperturbed target is captured by the 258 nm probe and shown in the Supplementary Fig. 1. The diameter of the target is measured at 62 positions that are evenly spaced over the full vertical FoV (blue horizontal lines). The mean target diameter is 4.4 μm with a standard deviation of 0.2 μm. Furthermore, the image shows typical target-geometry fluctuations. The target diameter varies along the jet axis and in the upper part of the image the target is bent to the right side. At y = 15 μm and between y = − 10 μm and y = − 20 μm, the target features structural differences of the bulk compared to y = 0 μm, where the target is fully transparent.

Discussion of the HD-RT fit

There are two fundamental assumptions of the HD-RT fit. The first one is a homogeneous initial temperature of the bulk-electrons as a result of isochoric heating. Details about this assumption are discussed in section “PIC simulation”. The second assumption is the utilization of hydrodynamics simulations to calculate the plasma-expansion process, which is discussed in this section. We first calculate the Knudsen number Kn. Taking the temperature T_e = 300 eV, the electron density ${n}_{{{{{{{{\rm{e}}}}}}}}}=30\,{n}_{{{{{{{{\rm{c}}}}}}}}}^{800nm}$, and the Coulomb logarithm $\ln {{\Lambda }}$ = 3.55, the electron-electron-collision rate (for thermalized temperatures T_e) calculates to

$${\tilde{\nu }}_{{{{{{{{\rm{ee}}}}}}}}}=2.91\times 1{0}^{-6}\,{n}_{{{{{{{{\rm{e}}}}}}}}}\,\ln {{\Lambda }}\,{T}_{{{{{{{{\rm{e}}}}}}}}}^{-3/2}=1.04\times 1{0}^{14}\,{{{{{{{{\rm{s}}}}}}}}}^{-1}.$$

(8)

The thermal velocity of electrons is

$${v}_{{{{{{{{\rm{the}}}}}}}}}=\sqrt{\frac{{k}_{{{{{{{{\rm{B}}}}}}}}}\,{T}_{{{{{{{{\rm{e}}}}}}}}}}{{m}_{{{{{{{{\rm{e}}}}}}}}}}}=7.26\times 1{0}^{6}{{{{{{{{\rm{ms}}}}}}}}}^{-1},$$

(9)

with Boltzmann’s constant k_B and the electron rest mass m_e. The mean free path length f of the electrons is

$$f=\frac{{v}_{{{{{{{{\rm{the}}}}}}}}}}{{\nu }_{{{{{{{{\rm{ee}}}}}}}}}}=69.8\,{{{{{{{\rm{nm}}}}}}}}.$$

(10)

With the diameter of the target L = 4.4 μm as a characteristic spatial scale of the system, the Knudsen number of the bulk plasma is

$$Kn=\frac{f}{L}\approx 0.02,$$

(11)

which is in the applicable range of hydrodynamics equations⁹⁵.

The Debye length λ_D = 1 nm gives the plasma parameter

$${{{\Lambda }}}_{{{{{{{{\rm{plasma}}}}}}}}}=4{{{{{{{\rm{\pi }}}}}}}}\,{n}_{{{{{{{{\rm{e}}}}}}}}}\,{\lambda }_{{{{{{{{\rm{D}}}}}}}}}^{3}\gg 1,$$

(12)

which shows that the plasma is weakly coupled. The PIC simulation in section “PIC simulation” yields magnetic fields B between 1 T to 100 T in the single-picosecond timeframe and the hydrodynamics simulations yield ion temperatures between 10 eV and 100 eV in the tens-of-picosecond timeframe. The characteristic Larmor radius

$$\frac{{r}_{{{{{{{{\rm{L}}}}}}}}}}{L}=\frac{{m}_{{{{{{{{\rm{i}}}}}}}}}\,{v}_{{{{{{{{\rm{thi}}}}}}}}}}{e\,B\,L}\gg 1$$

(13)

shows that the investigated plasma is weakly magnetized during all times. e is the elementary charge. We conclude that hydrodynamics simulations are feasible to calculate the plasma-expansion process.

The simulation tool FLASH is commonly used to model high-energy-density physics^96,97. Uncertainties mainly arise from the hydrogen equation of state and the assumption of two-dimensional radial symmetry. Radial symmetry is supported by the experimental observation of similar expansion in a secondary optical-probing axis antiparallel to the pump-laser axis. Lateral heat diffusion by transverse temperature gradients along the z axis is, however, not considered by two-dimensional radial symmetry. Two-dimensional cylinder-symmetric simulations in “Methods” section “Lateral heat transfer” shows that the influence is negligible in the investigated parameter range. Different equations of state are considered in “Methods” section “Equation of state of hydrogen”.

As we did not use any laser-plasma-interaction model for the HD-RT fit, the approach promises to be robust and versatile. The method does not depend on specific laser and target parameters and can be readily applied to other laser-target systems.

Equation of state of hydrogen

The equation of state (EOS) is an important input parameter of hydrodynamics simulations. Here, we test three different hydrogen EOS, which are FPEOS⁹⁸, FEOS⁹⁹, and IONMIX EOS⁷⁷. SESAME EOS¹⁰⁰ is used as a benchmark. We compare the isotherms of all EOS at temperatures of 10 eV, 100 eV, and 1000 eV, as shown in the Supplementary Fig. 2a–c. The results show that FPEOS fits SESAME EOS best. To compare the plasma-density evolution directly, a FLASH simulation with FPEOS is compared to a FLASH simulation with SESAME EOS in Supplementary Fig. 2d–f. The initial settings are T_e0 = 300 eV and D₀ = 4.4 μm. The overlapping density profiles confirm the consistency of both EOS. All other FLASH simulations of this work utilize FPEOS.

Ionization state of the target

In the PIC simulations, a two-dimensional fully ionized plasma column is assumed to resemble the target at the arrival of the laser pulse. According to Ref. ¹⁰¹, the critical field of barrier-suppression ionization of hydrogen equals a laser intensity of 8 × 10¹⁴Wcm⁻². The Supplementary Fig. 3 shows measurements of the laser contrast via a third-order autocorrelator. No measurement from the same day like the experiment of optical shadowgraphy is available. Both curves show the laser contrast several weeks before and several weeks after the day of the shadowgraphy experiment. Both laser-contrast curves shows that the intensity of 8 × 10¹⁴Wcm⁻² is already reached at about 400 fs before the laser peak. This reasons an initialization of a fully ionized hydrogen plasma at the starting point of the PIC simulations at about -100 fs delay.

Radiative cooling

The PIC simulations do not include radiative cooling of the plasma. This section estimates the energy loss by radiative cooling using analytic calculations and the non-local-thermal-equilibrium tool FLYCHK¹⁰². We find that the main mechanism of radiation loss is Bremsstrahlung radiation and, as the utilized material is hydrogen with an atomic number of Z = 1, the radiation loss per electron is negligible compared to the relevant electron temperatures of several hundred eV.

To estimate the influence of radiative cooling, we use the results of the PIC simulation (section “PIC simulation”) and calculate the corresponding energy losses from the bulk-electron-temperature evolution. There are mainly three kinds of radiation. Bound-bound radiation P_Ir accounts for the radiation that is emitted from atomic ionization, free-bound radiation accounts for the radiation by electron recombination

$${P}_{{{{{{{{\rm{Rr}}}}}}}}}[{{{{{{{{\rm{Wcm}}}}}}}}}^{-3}]=1.69\times 1{0}^{-32}\,{N}_{{{{{{{{\rm{e}}}}}}}}}\,\sqrt{{T}_{{{{{{{{\rm{e}}}}}}}}}}\,\mathop{\sum}\limits_{Z}{Z}^{2}\,N(Z)\,\frac{{E}_{\infty }^{Z-1}}{{T}_{{{{{{{{\rm{e}}}}}}}}}}.$$

(14)

Z corresponds to the ionization state. The free-free radiation P_Br accounts for Bremsstrahlung radiation by electrons. For a hydrogen-like plasma, P_Br is given by

$${P}_{{{{{{{{\rm{Br}}}}}}}}}[{{{{{{{{\rm{Wcm}}}}}}}}}^{-3}]=1.69\times 1{0}^{-32}\,{N}_{{{{{{{{\rm{e}}}}}}}}}\,\sqrt{{T}_{{{{{{{{\rm{e}}}}}}}}}}\,\mathop{\sum}\limits_{Z}{Z}^{2}\,N(Z).$$

(15)

The total radiation loss is given by the sum of all processes

$${P}_{{{{{{{{\rm{r}}}}}}}}}={P}_{{{{{{{{\rm{Ir}}}}}}}}}+{P}_{{{{{{{{\rm{Br}}}}}}}}}+{P}_{{{{{{{{\rm{Rr}}}}}}}}}.$$

(16)

Comparing equations (14) and (15), P_Rr is ${E}_{\infty }^{Z-1}/{T}_{{{{{{{{\rm{e}}}}}}}}}$ times P_Br. ${E}_{\infty }^{Z-1}$ is the ionization energy of hydrogen. As the relevant bulk-electron temperatures are in the multi-hundred-eV range, P_Rr is in the percent range of P_Br and is neglected in the following. For fully ionized hydrogen atoms, P_Ir is zero. It follows that the total emitted power is approximately equivalent to the power of Bremsstrahlung

$${P}_{{{{{{{{\rm{r}}}}}}}}}\approx {P}_{{{{{{{{\rm{Br}}}}}}}}}.$$

(17)

In the following, we calculate the total radiation loss E_r as a function of time t₀ from the temperature evolution of the PIConGPU simulation in Fig. 5d by

$${E}_{{{{{{{{\rm{r}}}}}}}}} =\int\nolimits_{0}^{{t}_{0}}{P}_{{{{{{{{\rm{r}}}}}}}}}(t)\,dt\\ =\int\nolimits_{0}^{{t}_{0}}1.69\times 1{0}^{-32}\,{N}_{{{{{{{{\rm{e}}}}}}}}}\,\sqrt{{T}_{{{{{{{{\rm{e}}}}}}}}}(t)}\mathop{\sum}\limits_{Z}{Z}^{2}\,{N}_{{{{{{{{\rm{i}}}}}}}}}(Z)\,dt.$$

(18)

With ${N}_{{{{{{{{\rm{i}}}}}}}}}={N}_{{{{{{{{\rm{e}}}}}}}}}=30\,{n}_{{{{{{{{\rm{c}}}}}}}}}^{800\,{{{{{{{\rm{nm}}}}}}}}}\times 1\,{{{{{{{{\rm{cm}}}}}}}}}^{3}$ and Z = 1, the temperature reduction by radiation ΔT = 2/3 E_r within 2 ps is 1.76 × 10³ J, which is 0.14 eV per electron. Compared to the electron temperature of the PIConGPU simulation at 2 ps, the temperature reduction amounts to 0.04% only. The temporal evolution of the radiation loss P_r(t)/N_e is shown by the black line in Fig. 7. As radiation loss scales with Z² N_eN_i, the result is in agreement with ref. ⁴⁵.

Fig. 7: Energy loss by radiative cooling.

The black line corresponds to P_r(t)/N_e in equation (18). Calculations by FLYCHK are: bound-bound (blue square), bound-free (orange dashed line), free-free (green square) and total radiation loss (yellow dashed line).

The calculation is supported by a calculation with the non-local-thermal-equilibrium tool FLYCHK¹⁰², for which we use the temperature evolution of the PIC simulation. The result is shown in Fig. 7. The bound-bound, bound-free, free-free, and total radiation energy are given by the blue squares, the orange dashed line, the green squares, and the yellow dashed line. Bound-bound and bound-free radiation contribute much less than free-free radiation, which confirms the approximation of equation (17). The total temperature reduction by radiation loss per electron as calculated by FLYCHK is 0.13 eV.

In summary, the main mechanism of radiation loss is Bremsstrahlung (free-free) radiation. Because of the low atomic number of Z = 1, the temperature reduction by radiation loss is lower than 0.1% of the relevant thermal electron energies and radiative cooling can be neglected.

2D3V-PIC simulation versus 3D-PIC Simulation

To identify possible differences between 2D3V-PIC and 3D-PIC simulations, PIConGPU simulations with a high spatial resolution are compared in the following. To account for limited computing resources, a hydrogen target with 1 μm diameter is used. The 2D3V simulation uses a box size of 32 × 32 μm² (x, y) and the 3D simulation uses a box size of 8 × 8 × 12 μm³ (x, y, z). The total length of the hydrogen target is 4 μm into the z direction. To resolve high electron densities in all dimensions, the cell size is 0.8 μm/96 and the number of macro particles per cell is 240 for both simulations. The 3D simulation is stopped at about 400 fs.

For both approaches, a Maxwell-Boltzmann distribution is fitted to the electron-velocity distribution to derive the thermal bulk-electron temperature. This eliminates the contribution of hot electrons, which is contained in the average kinetic energy. The results from a box size of 2 × 10 × 10 cells in the 3D case and 20 × 20 cells in the 2D case are shown in the Supplementary Figs. 4 and 5.

The comparison of the bulk-electron temperature between the 2D3V-PIConGPU and the 3D-PIConGPU simulation is shown in Fig. 8. Before 100 fs, there is a high agreement between the two simulations. After 100 fs, the temperature in the 3D case is increased to slightly higher absolute values. Between 200 fs and 400 fs the difference between the two cases amounts to about 1.7%.

Fig. 8: Comparison of the 2D3V and a full-3D-PIC simulations.

Bulk-electron-temperature evolution in a 3D-PIConGPU simulation (blue) and in a 2D3V-PIConGPU simulation (red).

Low-temperature-collision correction

The collision frequency of the PIC simulations does not include electron-phonon scattering, which is important at electron temperatures below the Fermi energy. However, we can use the temperature evolution as simulated by the PIC simulation, calculate the corresponding current of hot electrons, and reversibly derive the expected temperature evolution by taking the low-temperature-collision correction into account. By comparing the original temperature evolution from the PIC simulation with the artificially calculated temperature evolution, an estimate of the influence of the low-temperature-collision correction can be given.

According to the hot-electron scaling in ref. ¹⁰³, the hot-electron temperature is

$${T}_{{{{{{{{\rm{h}}}}}}}}}=\left(\sqrt{1+{a}_{0}^{2}/2}-1\right)\,{m}_{{{{{{{{\rm{e}}}}}}}}}\,{c}^{2}=90.5\,{{{{{{{\rm{keV}}}}}}}}$$

(19)

for a₀ = 0.88. Based on ref. ⁶³, the bulk-electron-temperature evolution ∂T_e/∂t by laser heating is given by

$$\frac{3}{2}{n}_{{{{{{{{\rm{e}}}}}}}}}\frac{\partial {T}_{{{{{{{{\rm{e}}}}}}}}}}{\partial t}=\frac{\partial }{\partial x}\left({K}_{{T}_{{{{{{{{\rm{e}}}}}}}}}}\frac{\partial {T}_{{{{{{{{\rm{e}}}}}}}}}}{\partial x}\right)+\frac{{j}_{{{{{{{{\rm{h}}}}}}}}}^{2}}{{\sigma }_{{T}_{{{{{{{{\rm{e}}}}}}}}}}}+\frac{3}{2}\frac{{n}_{{{{{{{{\rm{h}}}}}}}}}\,{T}_{{{{{{{{\rm{h}}}}}}}}}}{{\tau }_{e}}.$$

(20)

The three terms on the right-hand side are diffusion heating (diff), resistive return-current heating (res), and drag heating (dra). n_e is the electron density, j_h is the current density of hot electrons, n_h is the density of hot electrons, T_h is the average kinetic energy of hot electrons, ${\sigma }_{{T}_{{{{{{{{\rm{e}}}}}}}}}}$ is the electron conductivity, τ_e is the collision time of bulk electrons and ${K}_{{T}_{{{{{{{{\rm{e}}}}}}}}}}$ is the thermal conductivity of bulk electrons

$${K}_{{T}_{{{{{{{{\rm{e}}}}}}}}}}=\frac{16\sqrt{2}}{{{{{{{{{\rm{\pi }}}}}}}}}^{3/2}}\frac{{({k}_{{{{{{{{\rm{B}}}}}}}}}{T}_{{{{{{{{\rm{e}}}}}}}}})}^{5/2}}{{e}^{4}\,\sqrt{{m}_{{{{{{{{\rm{e}}}}}}}}}}\,\ln {{\Lambda }}}.$$

(21)

Here, m_e is the electron rest mass, e is the elementary charge, k_B is Boltzmann’s constant and $\ln {{\Lambda }}$ is the Coulomb logarithm.

In the PIC simulation (section “PIC simulation”), a total amount of energy of η_absorb = 25% is absorbed from the laser. The total energy of laser pulse of E_laser = 160 mJ and T_h = 90.5 keV gives the number of hot electrons N_h that is generated by the laser-target interaction

$${N}_{{{{{{{{\rm{h}}}}}}}}}\,{T}_{{{{{{{{\rm{h}}}}}}}}}={\eta }_{{{{{{{{\rm{absorb}}}}}}}}}\,{E}_{{{{{{{{\rm{laser}}}}}}}}}.$$

(22)

We assume that all the absorbed energy is converted into hot-electron energy. We derive a total number of hot electrons of N_h ≈ 2.8 × 10¹². By assuming a uniform distribution of hot electrons in the plasma column and in the laser spot, we calculate the hot electron density from the corresponding volume V by

$${n}_{{{{{{{{\rm{h}}}}}}}}}=\frac{{N}_{{{{{{{{\rm{h}}}}}}}}}}{V}\approx 7.43\,{n}_{{{{{{{{\rm{c}}}}}}}}}^{800\,{{{{{{{\rm{nm}}}}}}}}}=1.29\times 1{0}^{22}{{{{{{{{\rm{cm}}}}}}}}}^{-3}.$$

(23)

The current density of hot electrons is

$${j}_{{{{{{{{\rm{h}}}}}}}}}=e\,{n}_{{{{{{{{\rm{h}}}}}}}}}\,{v}_{{{{{{{{\rm{h}}}}}}}}}\approx 2.48\times 1{0}^{17}\,{{{{{{{{\rm{Am}}}}}}}}}^{-2}.$$

(24)

From ref. ⁶³ we derive the fraction of temperatures that are generated by resistive versus drag heating T^res/dra and resistive heating versus diffusion heating T^res/diff:

$${T}^{res/dra} \, > \, 22500\,{T}_{{{{{{{{\rm{h}}}}}}}}}^{1/3}\,{\alpha }^{2/3}\,{n}_{c,23}^{-2/3}\approx 9\times 1{0}^{6}$$

(25)

and

$${T}^{res/diff} \, > \, 600\,{\alpha }^{2/5}\,{L}_{T}^{2/5}\approx 3\times 1{0}^{3},$$

(26)

with α = 12.9, n_c,23 = 0.51 and L_T = 4.4 μm. The equations show that resistive return-current heating is dominant for the heating of bulk electrons.

Consequently, equation (20) is simplified to

$$\frac{3}{2}{n}_{{{{{{{{\rm{e}}}}}}}}}\frac{\partial {T}_{{{{{{{{\rm{e}}}}}}}}}}{\partial t}=\frac{{j}_{{{{{{{{\rm{h}}}}}}}}}^{2}}{{\sigma }_{{T}_{{{{{{{{\rm{e}}}}}}}}}}}.$$

(27)

The electron conductivity is given by

$${\sigma }_{{T}_{{{{{{{{\rm{e}}}}}}}}}}=\frac{{n}_{{{{{{{{\rm{e}}}}}}}}}\,{e}^{2}}{{m}_{{{{{{{{\rm{e}}}}}}}}}\,{\nu }_{{{{{{{{\rm{ei}}}}}}}}}}.$$

(28)

The electron-ion collision frequency ν_ei is given by Spitzer’s formula

$${\nu }_{{{{{{{{\rm{ei}}}}}}}}}=\frac{4}{3}\sqrt{2{{{{{{{\rm{\pi }}}}}}}}}\frac{{Z}_{{{{{{{{\rm{av}}}}}}}}}\,{e}^{4}\,{m}_{{{{{{{{\rm{e}}}}}}}}}\,{n}_{{{{{{{{\rm{e}}}}}}}}}}{{({m}_{{{{{{{{\rm{e}}}}}}}}}{k}_{{{{{{{{\rm{B}}}}}}}}}{T}_{{{{{{{{\rm{e}}}}}}}}})}^{3/2}}\ln {{\Lambda }}.$$

(29)

Z_av = 1 in the here considered case of a hydrogen plasma. As the mean free path length of electrons f cannot be smaller than the average ion distance r₀

$${\lambda }_{{{{{{{{\rm{e}}}}}}}}}\nless {r}_{0}={\left(\frac{1}{4{{{{{{{\rm{\pi }}}}}}}}{n}_{{{{{{{{\rm{i}}}}}}}}}}\right)}^{\!\!1/3}$$

(30)

with the ion density n_i, a cutoff at low collision frequencies is introduced

$${\nu }_{{{{{{{{\rm{cutoff}}}}}}}}}^{-1}=\frac{{r}_{0}}{\sqrt{{v}_{{{{{{{{\rm{Th}}}}}}}}}^{2}+{v}_{{{{{{{{\rm{TF}}}}}}}}}^{2}}}.$$

(31)

v_Th and v_TF are the electron thermal velocity and the Fermi-temperature velocity. The electron-ion collision frequency including the cutoff correction is

$${\nu }_{{{{{{{{\rm{ein}}}}}}}}}^{-1}={\nu }_{{{{{{{{\rm{ei}}}}}}}}}^{-1}+{\nu }_{{{{{{{{\rm{cutoff}}}}}}}}}^{-1}.$$

(32)

The low-temperature-collision correction applies to plasma temperatures lower than the Fermi temperature. Here, Spitzer’s formula of electron-ion collisions (equation (29)) is invalid, because the plasma is in a degenerate state. The collision frequency depends on the scattering of electrons with phonons. The corresponding collision frequency is given by³²

$${\nu }_{{{{{{{{\rm{ep}}}}}}}}}=2{k}_{{{{{{{{\rm{s}}}}}}}}}\frac{{e}^{2}\,{k}_{{{{{{{{\rm{B}}}}}}}}}\,{T}_{{{{{{{{\rm{i}}}}}}}}}}{{\hslash }^{2}\,{v}_{{{{{{{{\rm{TF}}}}}}}}}}.$$

(33)

k_s is a constant value that is estimated from experiments, T_i is the ion temperature, ℏ is the reduced Plank’s constant. The electron-ion collision frequency ν_eic of a plasma with a temperature smaller than the Fermi temperature is

$${\nu }_{{{{{{{{\rm{eic}}}}}}}}}^{-1}={\nu }_{{{{{{{{\rm{ein}}}}}}}}}^{-1}+{\nu }_{{{{{{{{\rm{ep}}}}}}}}}^{-1}.$$

(34)

The overall electron-ion collision frequency based on equations (29) to (34) is shown in Fig. 9a. For this graph, the Coulomb logarithm is set to 5 and the electron density is set to $30\,{n}_{{{{{{{{\rm{c}}}}}}}}}^{800\,{{{{{{{\rm{nm}}}}}}}}}$. The trend of the collision frequency is reversing for temperatures below the Fermi temperature.

Fig. 9: Low-temperature collision correction of hydrogen.

a Electron-ion collision frequency versus electron temperature with (orange dashed line) and without (blue line) low-temperature correction. Red dashed line: Fermi temperature of hydrogen. b Current density of hot electrons as calculated by equation (27) from the PIConGPU simulation with a Coulomb logarithm of 5 in Fig. 10. c Electron-temperature evolution from PIConGPU (blue dashed line) and as calculated from the current density in fig. (b) by taking into account the low-temperature-collision correction (black dashed line).

From equation (27) we derive a formula of the return-current density

$${j}_{{{{{{{{\rm{h}}}}}}}}}({t}^{i}) =\sqrt{\frac{3}{2}{n}_{{{{{{{{\rm{e}}}}}}}}}\,{\sigma }_{{T}_{{{{{{{{\rm{h}}}}}}}}}^{i}}\frac{\partial {T}_{{{{{{{{\rm{e}}}}}}}}}^{i}}{\partial {t}^{i}}}\\ \approx \sqrt{\frac{3}{2}{n}_{{{{{{{{\rm{c}}}}}}}}}\,{\sigma }_{{T}_{{{{{{{{\rm{h}}}}}}}}}^{i+1}}\frac{{T}_{{{{{{{{\rm{e}}}}}}}}}^{i+1}-{T}_{{{{{{{{\rm{e}}}}}}}}}^{i}}{{{\Delta }}t}},$$

(35)

with the temporal iteration step i of the following calculation. For each timestep, the electron temperature T_e is derived from the PIC simulation ($\ln {{\Lambda }}=5$ in Fig. 10). The upper limit of t is set to 50 fs. The retrieved current density of hot electrons is presented in Fig. 9b. From the evolution of the hot-electron current j_h, the influence of the low-temperature-collision correction on the bulk-electron temperature is calculated and compared to the PIC simulation in Fig. 9c. Minor differences are observed between -30 fs and -10 fs, i.e., before the laser peak arrives on target. After that and due to the rapid Joule heating, both approaches show the same results. It follows that the low-temperature-collision correction has negligible effect on the final bulk-electron temperature.

Fig. 10: Effect of different Coulomb logarithms.

a Bulk-electron temperatures versus time for different fixed values of the Coulomb logarithm $\ln {{\Lambda }}$. b Bulk-electron temperature at 1 ps versus $\ln {{\Lambda }}$.

Effect of the Coulomb logarithm

In the PIC simulations, the energy transfer from laser-heated hot electrons to the bulk electrons is mediated by collisions. The simulations assume a binary collision model, for which the energy transfer is proportional to the Coulomb logarithm $\ln {{\Lambda }}$. However, the Coulomb logarithm has an uncertainty of $O(\ln {{{\Lambda }}}^{-1})$. To test the influence of the Coulomb logarithm, we conduct PIConGPU simulations with different fixed values of $\ln {{\Lambda }}$ between 3.5 and 15. Figure 10a shows the resulting evolution of the bulk-electron temperature. Figure 10b compares the derived electron temperatures at 1 ps. A change of the coulomb logarithm from 3.5 to 15 changes the bulk-electron temperature from 1.25 keV to 1.5 keV, which is a variation of 20%.

Lateral heat transfer

Hot-electron pressure gradient in transverse direction

The presented 2D3V-PIC simulations simulate the temperature evolution in the x-y plane only. They ignore the dynamics caused by the hot-electron pressure gradient in the z direction (along the jet axis). Full-3D PIConGPU simulations are conducted to investigate the effect of the density gradient of hot electrons to the bulk-electron-temperature distribution within the laser-spot region. The size of the simulation box is 28 μm in z direction and 20 μm in x and y direction. The initialized target is a cylindrical hydrogen rod of 20 μm total length (z direction) and a radius of 2.2 μm. The grid size is 0.8 μm/24 in all directions and the number of macro particles per cell is 240. The initialized hydrogen plasma is fully ionized and features a density of $30\,{n}_{{{{{{{{\rm{c}}}}}}}}}^{800\,{{{{{{{\rm{nm}}}}}}}}}$ without surface scalelength. The laser parameters are equivalent to the section “PIC simulation”.

The Supplementary Fig. 6 shows sectional planes through the center of the target at 426 fs after the laser peak. The bulk electrons are already thermalized at this time. Temperature gradients are observed in all directions. The temperature is decreased from 1.7 keV in the laser-spot region to 1 keV above and below the laser spot (z axis). Along the laser-propagation direction (y axis), i.e., into the target bulk, the temperature decreases from 1.7 keV on the front to 1.6 keV on the rear side of the target. It follows that the temperature distribution in the x-y plane (Supplementary Fig. 6c) is homogeneous within 20%. This is consistent with the 2D3V-PIC simulation in section “PIC simulation”, for which a uniform temperature distribution is formed after about 500 fs.

To estimate the contribution of the hot-electron pressure gradient, we calculate the dependency of the local bulk-electron temperature on the local laser intensity and subsequently compare the calculation to the 3D-PIC-simulation result. In “Methods” section “Low-temperature-collision correction” we show that Joule heating by hot electrons is dominant for the heating of bulk electrons. The laser intensity on target is

$$I(r)={I}_{0}\,{e}^{-2{r}^{2}},$$

(36)

with the laser-spot radius r. The hot-electron temperature is denoted as T_h(r). Assuming a constant absorption coefficient η, the density of hot electrons n_h is approximated by equation (22),

$${n}_{{{{{{{{\rm{h}}}}}}}}}\,{T}_{{{{{{{{\rm{h}}}}}}}}}(r)\,dV=\eta \,I(r)\,{\tau }_{0}\,dS.$$

(37)

Here, dV and ds are the differential volume and area and τ₀ is the laser-pulse duration. It follows that

$${n}_{{{{{{{{\rm{h}}}}}}}}}\propto \frac{I(r)}{{T}_{{{{{{{{\rm{h}}}}}}}}}(r)}.$$

(38)

For v_h ≪ c, the current density of hot electrons is

$${j}_{{{{{{{{\rm{h}}}}}}}}}(r)=e\,{n}_{{{{{{{{\rm{h}}}}}}}}}\,{v}_{{{{{{{{\rm{h}}}}}}}}}(r)=c\,e\,{n}_{{{{{{{{\rm{h}}}}}}}}}\,\sqrt{\frac{2\,{k}_{{{{{{{{\rm{B}}}}}}}}}\,{T}_{{{{{{{{\rm{h}}}}}}}}}(r)}{{m}_{{{{{{{{\rm{e}}}}}}}}}\,{c}^{2}}}$$

(39)

and

$${j}_{{{{{{{{\rm{h}}}}}}}}}(r)\propto \frac{I(r)}{\sqrt{{T}_{{{{{{{{\rm{h}}}}}}}}}(r)}}.$$

(40)

Based on equations (27), (28), and (29) we have

$${T}_{{{{{{{{\rm{e}}}}}}}}}(r)\propto \frac{{j}_{{{{{{{{\rm{h}}}}}}}}}{(r)}^{2}}{{\sigma }_{{T}_{{{{{{{{\rm{e}}}}}}}}}}}\propto {j}_{{{{{{{{\rm{h}}}}}}}}}{(r)}^{2}\,{T}_{{{{{{{{\rm{e}}}}}}}}}{(r)}^{-\frac{3}{2}}$$

(41)

and

$${T}_{{{{{{{{\rm{e}}}}}}}}}(r)\propto {j}_{{{{{{{{\rm{h}}}}}}}}}{(r)}^{0.8}.$$

(42)

T_e(r) is the bulk-electron temperature. For ${a}_{0}^{2}/2\ll 1$, equation (19) gives

$${T}_{{{{{{{{\rm{h}}}}}}}}}(r)=\left(\sqrt{1+\frac{{a}_{0}^{2}}{2}}-1\right)\,{m}_{{{{{{{{\rm{e}}}}}}}}}\,{c}^{2}\approx \frac{{a}_{0}^{2}}{4}\,{m}_{{{{{{{{\rm{e}}}}}}}}}\,{c}^{2}$$

(43)

with ${a}_{0}\propto \sqrt{I(r)}$. We derive

$${T}_{{{{{{{{\rm{h}}}}}}}}}(r)\propto I(r)$$

(44)

and together with equation (40)

$${j}_{{{{{{{{\rm{h}}}}}}}}}(r)\propto \sqrt{I(r)}.$$

(45)

Finally, from equation (42) we derive the proportionality of the bulk-electron temperature and the intensity distribution of the laser

$${T}_{{{{{{{{\rm{e}}}}}}}}}(r)\propto I{(r)}^{0.4}.$$

(46)

The average bulk-electron temperature variation along the z axis of the 3D PIConGPU simulation is shown in Supplementary Fig. 7 by the blue line. It is calculated from Supplementary Fig. 6b by averaging along the x axis. The green and the orange curve in in Supplementary Fig. 7 show the intensity distribution of the laser I(r)^0.4 and I(r), each scaled to the maximum of the blue line. Within the FWHM of the laser spot (14 μm), T_e of the PIC simulation coincides with the scaling I(r)^0.4. Beyond this region, the scaling of temperature is slightly different from I(r)^0.4. This shows that the pressure gradient of hot electrons is relevant only outside the focal-spot FWHM. As the 2D3V PIC simulations refer to the central x-y plane of the interaction at z = 0, the influence three-dimensional effects of the hot-electron density distribution can be neglected.

The distribution of E_z at -18 fs and 13 fs shows that return currents on the surface of the target are negligible.

Lateral heat transfer by diffusion

Temperature gradients along the jet axis (z axis) can influence the hydrodynamic expansion of the plasma in the central x-y plane at z = 0 by lateral heat diffusion. To verify the assumption of two-dimensional radial symmetry of the hydrodynamics simulations of our experimental scenario, we conduct three-dimensional hydrodynamics simulations with different initial temperature gradients and compare the plasma density on the tens-of-picosecond timescale.

The simulations utilize FLASH and the simulation box is 20 μm in height (z axis) and 20 μm in radius. The initial diameter of the plasma column is 4.4 μm. Following the previous subsection “Hot-electron pressure gradient in transverse direction”, three different temperature gradients are initialized and shown in the Supplementary Fig. 8a. The blue line shows a uniform temperature distribution of 300 eV, the green line shows a temperature distribution proportional to the intensity distribution of the laser I(r) with a peak temperature of 300 eV and the orange line shows a temperature distribution proportional to I(r)^0.4.

The results of the simulations are presented in the Supplementary Fig. 8b–d for 10 ps, 20 ps, and 30 ps delay and at the position of the laser peak at z = 0. For comparison to the hydrodynamics simulations in section “Hydrodynamics simulation - HD”, the red-dashed line shows the results of a two-dimensional radial-symmetric simulation with T_e0 = 300 eV and D₀ = 4.4 μm. All simulations show high agreement to each other. Small deviations of the density profiles occur at densities below $0.1\,{n}_{{{{{{{{\rm{c}}}}}}}}}^{800\,{{{{{{{\rm{nm}}}}}}}}}$ only and amount to 5% at maximum for the case of an initial temperature distribution proportional to I(r). We verified that cold target regions outside the considered range have no influence on the plasma expansion at the central position.

The overall agreement of all three-dimensional cylinder-symmetric simulations to the two-dimensional radial-symmetric simulation shows the negligible influence of lateral heat diffusion in our scenario and justifies the utilization of two-dimensional radial-symmetric hydrodynamics simulations by the HD-RT fit.