High shear flow prevents bundling of bacterial flagella and induces lateral migration away from a wall

Abstract

Since the discovery of bacteria in the 17^th century, bacterial motion has been the focus of great research interest. As an example of bacterial chemotaxis, Escherichia coli exhibits run-and-tumble motion by bundling and unbundling flagella, propelling the cells along a concentration gradient. However, the behavior of bacteria in high-shear flow environments remains poorly understood. In this study, we showed experimentally that E. coli swimming is severely inhibited at shear rates above a few hundred per second. Our simulations revealed that E. coli flagellar bundling cannot occur in a high-shear regime, because the background shear flow is stronger than the flagellar-generated flow required to form a bundle. Bacteria under strong shear behave like deformable objects and exhibit lateral migration away from a wall. These results suggest that bacteria that are unable to bundle their flagella in strong shear near a wall alter their locomotion strategy to passively escape from the wall.

Introduction

Bacteria occupy a broad variety of ecological niches and constitute the bulk of the global biomass. Thus, bacteria are found in a variety of environments including soil and within animal bodies, and are closely related to environmental and health issues¹. To understand bacterial physiology and function requires an understanding of their motility^2,3,4,5. Many bacteria use helical filaments called flagella for propulsion in fluids to search for nutrients or escape from harmful substances. A helical flagellar filament is rotated by a motor complex, and the flagellar filament and motor are connected via a short, flexible hook^6,7. As the helical flagellum rotates, waves propagate from the body to the tip of the flagellum, providing thrust to swim in the direction opposite to wave propagation.

Escherichia coli (E. coli) is widely used as a model organism to study the fundamental biophysical aspects of cell motility and chemotaxis in bacteria^6,7. In the absence of physical barriers or chemical stimuli, E. coli rotates their flagella counterclockwise (CCW), resulting in a tight synchronous bundle of flagella for motility. The mechanism of flagellar bundling has been explained by a combination of flexibility and hydrodynamic interactions of flagella through simplified experimental setups^6,8,9 and detailed numerical simulation^{6,10,11,12,13,14}. Conversely, flagellar unbundling is generated by clockwise (CW) rotation of flagella in a process involving polymorphic changes of the flagellar filaments^15,16. When the flagella unbundle, forces are exerted by each flagellum in various directions, causing the cell to change orientation in a tumbling movement. When the motor switches back to CCW rotation, the filaments return to the normal shape and again form a bundle.

Bacterial swimming kinematics is strongly affected by confinement^{5,17,18,19,20} and background flow²¹. When both wall and shear flow effects are combined, E. coli near the wall tends to move in the spanwise direction and can even swim upstream along a sidewall, i.e., rheotaxis^22,23. However, previous studies were mainly conducted up to a wall shear rate of approximately 100 s⁻¹, and bacterial behavior at higher shear rates remains unclear. A microfluidics study of shear-induced spanwise drift indicated a significant decrease in the separation efficiency of bacteria at shear rates above a few hundred per second²⁴, suggesting that bacteria behave differently at such high-shear rates. High-shear rates can be found not only in such microfluidics but also in nature²⁵. For example, in our cardiovascular system, the wall shear rates in a small artery and a capillary are about 700 and 800 s^–1, respectively²⁶. In the case of sepsis, a dangerous disease, bacteria sometimes go into the bloodstream and experience such high-shear rates. While shear rates above a few hundred per second can be found in both nature and industry, the behaviors of bacteria under such high-shear flow conditions have not been elucidated.

In this study, we experimentally investigated the behavior of E. coli under high-shear flow in rectangular microchannels and revealed the mechanism of this behavior through simulations. In experiments, bacterial suspensions were pumped into the microchannel at controlled flow rates and observed through microscopy and high-speed video recording to track individual microparticles for motion analysis. We performed numerical modeling to observe flagellar bundles at high shear, as this is difficult to observe directly in experiments. The numerical simulations show that at such high-shear rates, the flagella cannot bundle because the background shear flow is stronger than the flagellar-generated flow for making a bundle. The threshold of shear rate at which the flagella cannot bundle is quantitatively consistent with the threshold of shear rate at which drift was not observed in the experiment. Furthermore, it was found that bacteria with spreading flagella behave like soft objects and migrate away from the wall. The results of this study will improve our understanding of bacterial motion and may be applicable in the research of various environmental and health issues.

Results

Spanwise drift is suppressed by high-shear rate

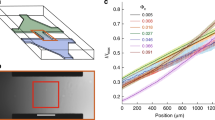
First, we examined the behavior of E. coli swimming near the bottom surface of a microfluidic slide in channel flow (Fig. 1a). A dilute suspension of E. coli was injected at flow rate Q into a microchannel of width W = 5 mm and height H = 0.2 mm, which imposed a good approximation of a planar Poiseuille flow. The observed region is at the bottom in the height direction but at the center in the spanwise direction to minimize the influence of the channel side walls; the local shear rate $\dot{\gamma }$ was calculated using Eq. (1). The trajectories of bacteria were recorded by a high-speed camera as projections in the x–y plane using a 60× objective, where x is the flow direction, y is the spanwise direction, and z is perpendicular to the bottom surface of microfluidic slide. The depth of field is about 0.17 μm.

Fig. 1: Experimental setup and spanwise drift of Escherichia coli.

a Experimental setup to examine the behavior of E. coli in a microfluidic channel (width, W = 5 mm; height, H = 0.2 mm; length, L = 50 mm) with flow controlled by a syringe. b, c Typical trajectories of E. coli at wall shear rates of 100 and 400 ${{{{{{\rm{s}}}}}}}^{-1}$, respectively. Scale bar: 25 μm. d Ratio of drifting cells with drift angles greater than ${\theta }_{{th}}$ (n = 592, 510, 514, 474, 176, and 178 for $\dot{\gamma }$ = 10, 100, 200, 300, 400, and 500, respectively).

Examples of bacterial trajectories just above the wall at wall shear rates of $\dot{\gamma }=100{{{{{{\rm{s}}}}}}}^{-1}$ and $400{{{{{{\rm{s}}}}}}}^{-1}$, are shown in Fig. 1b, c, respectively. We observed a clear drift toward the left with respect to the flow direction at $\dot{\gamma }=100{{{{{{\rm{s}}}}}}}^{-1}$. However, as shear increased to $\dot{\gamma }=400{{{{{{\rm{s}}}}}}}^{-1}$, the trajectories were mainly oriented toward the flow direction, and the spanwise drift was significantly reduced.

For quantitative analysis of the spanwise drift at different shear rates, the drift angle $\theta$ was measured (Fig. 1b). The ratio of cells with drift angles above a threshold angle ${\theta }_{{{{{{\rm{th}}}}}}}$ was determined. The relationship between the ratio of the drift velocity ${U}_{{{{{{\rm{d}}}}}}}$ to the advection velocity ${U}_{{{{{{\rm{s}}}}}}}$ and the drift angle $\theta$ was described by the equation $\tan \theta ={U}_{{{{{{\rm{d}}}}}}}/{U}_{{{{{{\rm{s}}}}}}}$. Assuming that ${U}_{{{{{{\rm{s}}}}}}}$ is proportional to shear rate $\dot{\gamma }$, we set ${\theta }_{{{{{{\rm{th}}}}}}}={\tan }^{-1}(27.5/\dot{\gamma })$, where the coefficient 27.5 had the unit s⁻¹. Figure 1d shows the drift ratio as a function of the shear rate. The drift ratio decreased significantly at shear rates exceeding 200 ${{{{{{\rm{s}}}}}}}^{-1}$. In our previous study on bacterial separation devices using the drift phenomenon²⁴, we also observed a significant decrease in the separation efficiency at shear rates above a few hundred. Particle Reynolds number using bacterial size and shear rate is sufficiently small, on the order of 10^-3, that inertial lift forces are negligible²⁷. Therefore, we hypothesized that under high-shear flow conditions, bacteria would be unable to bundle their flagella and exhibit spanwise drift. As it is difficult to experimentally observe flagellar bundling directly at high shear, we performed numerical simulations to test this hypothesis.

High-shear rates prevent flagellar bundling

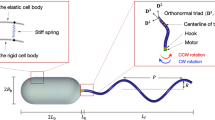
Next, we computationally investigated the behavior of a three-flagellum bacterium under simple shear flow conditions without wall boundaries (Fig. 2a). The background flow field was given as ${{{{{{\boldsymbol{u}}}}}}}^{\infty }=\left(\right.\dot{\gamma }z$,0,0), where $\dot{\gamma }$ is the shear rate, and the flagella were initially spread out as shown in Fig. 2a. The shear rate was determined by multiplying ${T}_{{{{{{\rm{m}}}}}}}/\mu {a}^{3}$ by a factor in the simulation, such that the effects of motor torque ${T}_{{{{{{\rm{m}}}}}}}$, viscosity $\mu$, and half body length $a$ could be examined simultaneously through nondimensionalization, which enables the findings of this study applicable to a variety of bacteria, not just E. coli.

Fig. 2: Model bacterium under simple shear flow conditions without a wall boundary.

a Schematic diagram of the bacterial model. The bacterium had three helical flagella connected to the body via flexible hooks. Shape parameters of the basic flagellar filament were set as follows: length ${l}_{f}=5a$, wavelength ${\lambda }_{f}=2a$, and amplitude ${h}_{f}=0.25a$. Here, $x$ represents the flow direction, $y$ the spanwise direction, and $z$ the velocity gradient direction. b Trajectories of bacteria with a shear rate of $\dot{\gamma }=0.175{T}_{{{{{{\rm{m}}}}}}}/\mu {a}^{3}$ and $0.2{T}_{{{{{{\rm{m}}}}}}}/{{{{{\rm{\mu }}}}}}{a}^{3}$. The insets show sample bacterial configurations with bundling ($\dot{\gamma }=0.175{T}_{{{{{{\rm{m}}}}}}}/\mu {a}^{3}$) and spreading ($\dot{\gamma }=0.2{T}_{{{{{{\rm{m}}}}}}}/\mu {a}^{3}$) of the flagella. c Changes of bacterial orientation over time at a shear rate of $\dot{\gamma }=0.175{T}_{{{{{{\rm{m}}}}}}}/\mu {a}^{3}$ and $0.2{T}_{{{{{{\rm{m}}}}}}}/\mu {a}^{3}$.

Bacteria with flagellar bundling or spreading

Under simple shear flow conditions at a shear rate of $\dot{\gamma }=0.175{T}_{{{{{{\rm{m}}}}}}}/\mu {a}^{3}$ (≈227.5 s⁻¹ for E. coli bacteria), the model bacteria swam in the shear flow and formed a flagellar bundle (Fig. 2b). Initially, two flagella gradually approached each other, and eventually all flagella formed a coherent bundle and pushed the cell body forward (Supplementary Movie 1). A sample trajectory at $\dot{\gamma }=0.175{T}_{{{{{{\rm{m}}}}}}}/\mu {a}^{3}$ showed spanwise drift in the positive y direction, as observed in our experimental observations (Fig. 1b) and in a previous study²⁸. The bacterium was steadily oriented in the positive y direction (Fig. 2c), and drift was caused by cell swimming, i.e., rheotaxis. The chirality of the left-handed flagellum generated a lift force along the negative y direction, while the drag force on the cell body was in the opposite direction, generating torque to orient the cell to the y direction²¹.

In contrast, when the shear rate was increased to $\dot{\gamma }=0.2{T}_{{{{{{\rm{m}}}}}}}/\mu {a}^{3}$, the bacterial flagella remained spread out and did not bundle (Fig. 2b and Supplementary Movie 2) because the background shear flow was stronger than the threshold for flagellar-generated flow for bundle formation. The bacterial orientation continued to change over time (Fig. 2c), and the cell drifted in the negative y direction. When cells were unable to swim, they drifted in the negative y direction, mainly due to the lift force exerted by the chirality of the left-handed flagella.

Threshold shear rate for flagellar bundling

To average the effects of the initial orientation of the bacteria, the orientation was varied to eight Gaussian points on two spherical triangles one quarter the area of the sphere (cf. Supplementary Fig. 1). Supplementary Fig. 2a shows the threshold shear rate for bacterial flagellar bundles with eight different initial orientations. The threshold value was $0.163{T}_{{{{{{\rm{m}}}}}}}/\mu {a}^{3}$ in three cases, $0.183{T}_{{{{{{\rm{m}}}}}}}/\mu {a}^{3}$ in three cases, and $0.213{T}_{{{{{{\rm{m}}}}}}}/\mu {a}^{3}$ in two cases, indicating that the effect of initial orientation was small. The average threshold values $\bar{{\dot{\gamma }}_{{{{{{\rm{th}}}}}}}}$ were then calculated by Gaussian integral²⁹, and the result was obtained as $\bar{{\dot{\gamma }}_{{{{{{\rm{th}}}}}}}}=0.182{T}_{{{{{{\rm{m}}}}}}}/\mu {a}^{3}$.

The effects of flagellar configuration (cf. Supplementary Fig. 3) on the threshold shear rate for bacterial bundling were also investigated. Figure 3 shows the effects of flagellar length ${l}_{f}$, flagellar wavelength ${\lambda }_{f}$, and flagellar helix amplitude on the threshold shear rate for flagellar bundling. Data points in Fig. 3 indicate the results for eight different initial orientations. Although the flagellar configuration affected the threshold shear rate $\bar{{\dot{\gamma }}_{{{{{{\rm{th}}}}}}}}$, the effect was comparable to that of initial orientation. As the flagellum rotates counterclockwise, a wave propagates from the flagellar base toward the tip, inducing a flow. As flow is generated from the flagellar base toward the tip, ambient fluid flows from the sides of the flagellum toward the flagellum to satisfy mass conservation. This flagellar-generated flow attracts the flagella to each other and causes them to bundle together. On the other hand, the background shear flow generates drag on the flagella and, depending on the configuration of the flagella, may interfere with flagellar bundling induced by the flagellar-generated flow. Therefore, flagella are bundled to the extent that the shear flow does not hinder the flagellar-generated flow. The threshold shear rate $\bar{{\dot{\gamma }}_{{{{{{\rm{th}}}}}}}}$, is the shear rate at which the effects of shear flow and flagellar-generated flow are balanced.

Fig. 3: Effects of flagellar configuration on the threshold shear rate for flagellar bundling.

Effects of a flagellar length ${l}_{f}$, b wavelength ${\lambda }_{f}$, and c amplitude ${h}_{f}$. Data points indicate the results for eight different initial orientations. Orange fork in the box plot indicates the average value of the data.

Wall-induced lift of bacteria under high-shear flow conditions

Next, we investigated the migration of bacteria perpendicular to the wall in strong Couette or Poiseuille flow. The wall boundary was located at $z$  = 0, which satisfied the no-slip boundary condition, and the bacterium was initially placed at $z$  = 7a. In Poiseuille flow, the shear gradient became nonzero.

Lift of bacteria in Couette flow

Typical trajectories of bacteria in Couette flow at different shear rates are shown in Fig. 4a, b. When $\dot{\gamma }=0.175{T}_{{{{{{\rm{m}}}}}}}/\mu {a}^{3}$, the flagella bundled and the cell oriented and drifted in the positive y direction. In contrast, at $\dot{\gamma }=0.2{T}_{{{{{{\rm{m}}}}}}}/\mu {a}^{3}$, the flagella remained spread out and did not bundle, and the cell drifted in the negative y direction. These trends were the same as those observed without the wall (Fig. 2b). The effect of the wall on the threshold shear rate for flagellar bundling $\bar{{\dot{\gamma }}_{{{{{{\rm{th}}}}}}}}$ was also not significant (see Supplementary Fig. 4).

Fig. 4: Typical trajectories of motile bacteria in Couette flow with a wall at z = 0 (l_f = 5a, λ_f = 2a, h_f = 0.25a).

a, b Trajectories in the ${xy}$ plane and ${xz}$ plane, respectively. The shear rate was given by $\dot{\gamma }=0.175{T}_{{{{{{\rm{m}}}}}}}/\mu {a}^{3}$ or $0.2{T}_{{{{{{\rm{m}}}}}}}/\mu {a}^{3}$. c Lift velocities U_lift of motile bacteria with motor-on flagella and nonmotile bacteria with motor-off flagella as functions of the shear rate $\dot{\gamma }$. d Motor-on flagella configuration during the oscillatory motion of a bacterium in Couette flow. Red color indicates the anterior part of the bacterial body, and the blue curve indicates the trajectory.

In the presence of the wall, migration in the z direction perpendicular to the wall was observed, although no such migration in the z direction was observed in the absence of the wall (see Supplementary Figs. 2b and 6b). Figure 4b shows that a bacterium with bundled flagella was trapped by the wall, and the distance from the wall gradually decreased. In contrast, a bacterium with spreading flagella drifted in the positive z direction and lifted away from the wall. As such a lift phenomenon has been reported for deformable objects in Stokes flow³⁰, it is likely that bacteria with spreading flagella behave as deformable objects due to the flexibility of their hooks.

Lift velocity in Couette flow

The final orientation of bacteria with bundled flagella was in the y direction (Fig. 2c); therefore, we present these results with initial orientation in the y direction.

Figure 4c shows the effects of bacterial motility on lift velocity in Couette flow as a function of shear rate. Nonmotile bacteria with motor-off flagella are passive objects with flexible flagella and were modeled by applying no torque to the flagella. The lift velocity of nonmotile bacteria with motor-off flagella increased monotonically with increasing shear rate.

In contrast, for a motile bacterium with motor-on flagella swimming under low shear rate conditions, the bundled flagella provided the force to push the cell toward the wall, and the negative lift velocity increased with increasing shear rate. At shear rates greater than $\bar{{\dot{\gamma }}_{{{{{{\rm{th}}}}}}}}$, motile bacteria with motor-on flagella were unable to bundle the flagella and achieve positive lift. The motor-on flagella configuration of the bacteria during the oscillatory motion is shown in Fig. 4d. The lift velocity also increased with increasing shear rate, indicating that motile bacteria under strong shear behaved as deformable objects and were subjected to lift forces due to hydrodynamic interactions with the wall.

Mechanism of lift in Poiseuille flow

To clarify the mechanism of wall-induced lift in greater detail, the behaviors of bacteria with different mechanical conditions (motor-on flagella or motor-off flagella, helical or straight flagella, flexible hook or rigid hook for motor-off flagella) were examined. The background flow was assumed to be Poiseuille flow, such that the shear rate gradient of the parabolic velocity profile was given by $\dot{\gamma }-{kz}$. The bacterium was initially placed at $z$  = 7a, and the condition $\dot{\gamma }-7{ka}=1({T}_{{{{{{\rm{m}}}}}}}/\mu {a}^{3})$ ($0\le k\le 4/7({T}_{{{{{{\rm{m}}}}}}}/\mu {a}^{4})$) was imposed (cf. details in Methods). This shear rate exceeded the threshold value $\bar{{\dot{\gamma }}_{{{{{{\rm{th}}}}}}}}$; thus, the flagella remained spread out and unable to bundle. Bacterial lift velocities under various conditions with and without a wall are shown in Fig. 5.

Fig. 5: Lift velocity U_lift of bacteria varies with different shear rate gradients k.

Without wall (a), and with wall (b), where the shear rate is given by $\dot{\gamma }-{kz}$. The bacterium was initially placed at z = 7a, and the condition $\dot{\gamma }-7{ka}=1({T}_{{{{{{\rm{m}}}}}}}/\mu {a}^{3})$ ($0\le k\le 4/7({T}_{{{{{{\rm{m}}}}}}}/\mu {a}^{4})$) was imposed. A straight flagellum shape was described by ${h}_{f}=$ 0; flexible and rigid describe the flagellar hook, where the later indicates a constant flagellar angle relative to the body.

In simple shear flow ($k=0$) without a wall, there was no net migration due to symmetry. Bacteria with straight flagella and fixed motor-off flagella with a rigid hook did not exhibit migration in the z direction regardless of the shear rate gradient ${k}$ and the presence or absence of the wall. This finding was consistent with the reversibility of Stokes flow. When a flexible hook was introduced to the straight flagella, the bacterium was deformed in shear flow, the reversibility of Stokes flow no longer held for the deformable object, and the bacterium exhibited net migration under the shear rate gradient. The lift velocity induced by the wall boundary was much higher than that induced by the shear rate gradient, and both lift velocities were positive in sign. For helical flagella, the lift velocity was even larger. Bacterial motility slightly decreased the lift velocity. These results indicated that interplay among the shear rate gradient, helical flagellum shape, and rotational torques produced migration away from the wall.

The behaviors of motile or nonmotile bacteria at shear rates below $\bar{{\dot{\gamma }}_{{{{{{\rm{th}}}}}}}}$ were also examined and the results are shown in Supplementary Fig. 5. The tendency for the lift velocity to increase with $k$ in Supplementary Fig. 5 for nonmotile bacteria with motor-off flagella was similar to that shown in Fig. 5, though motile bacteria in Supplementary Fig. 5 formed a flagellar bundle and showed negative lift velocity, i.e., swam toward the wall.

Discussion

We quantitatively compared flagellar bundle threshold shear rates $\bar{{\dot{\gamma }}_{{{{{{\rm{th}}}}}}}}$ obtained in simulations with those observed experimentally. In the simulation, the shear rate was nondimensionalized as ${\dot{\gamma }}^{* }=\dot{\gamma }\left|{{{{{{\bf{T}}}}}}}_{{{{{{\rm{mot}}}}}}}\right|/\mu {a}^{3}$. For an estimated half body length of a = 1 μm, characteristic torque of $\left|{{{{{{\bf{T}}}}}}}_{{{{{{\rm{mot}}}}}}}\right|={1.3\times 10}^{-18}$ N⋅m^31,32, and viscosity of $\mu$  = ${10}^{-3}$ Pa⋅s, the dimensionless shear rate of ${\dot{\gamma }}^{* }=0.2$ corresponded to approximately $\dot{\gamma }=$ 260 s⁻¹. In our experiments, the drift ratio decreased significantly at shear rates of >200 ${{{{{{\rm{s}}}}}}}^{-1}$ and bacteria behaved differently in the high-shear regime (Fig. 1d). Thus, we obtained quantitative agreement between simulation and experimental results.

At shear rates below the threshold $\bar{{\dot{\gamma }}_{{{{{{\rm{th}}}}}}}}$, the bacterial flagella bundled, and the cells drifted in the positive y direction. Marcos et al.²¹ explained the mechanism of rheotaxis as a hydrodynamic torque induced by the chirality of the left-handed flagellum. The same drift phenomena were also observed in this study. However, when the shear rate exceeded the threshold, the bacterial flagella remained spread out and did not bundle, and the bacterium drifted in the negative y direction. This direction is equivalent to the drift force exerted on the left-handed flagella, indicating that under strong shear conditions, bacterial drift is caused by the chirality of the flagella.

In the presence of a wall, the bacteria migrated perpendicular to the wall. In Couette flow, the lift velocity was negative when $\dot{\gamma } < \bar{{\dot{\gamma }}_{{{{{{\rm{th}}}}}}}}$ but positive when $\dot{\gamma } > \bar{{\dot{\gamma }}_{{{{{{\rm{th}}}}}}}}$. In bacteria with spreading flagella, the positive lift was induced by body deformation due to the flexible hook and the hydrodynamic interaction with the wall. The effect of the shear rate gradient on lift in bacteria with spreading flagella was examined in Poiseuille flow. The shear rate gradient generated additional lift velocity and enhanced migration away from the wall.

These results suggested that bacteria with spreading flagella under high-shear flow conditions near a wall alter their locomotion strategy to passively escape from the wall via the lift effect. These characteristics will be helpful in preventing the destruction of bacteria through excessive shear flow and retaining them within a region where they can swim. The results of this study provide a deeper understanding of bacterial swimming under high-shear flow conditions and bacterial behavior in various flow environments.

Methods

Experimental procedures

Escherichia coli strain MG1655, which has a cell body approximately 1 μm in diameter and 2 μm in length, was used in our experiments. The protocol for culturing cells was similar to that described previously²⁴. Briefly, an overnight culture was grown in tryptone broth (TB) maintained at 33 °C on a rotary shaker (200 rpm). A saturated cell culture (100 μL) was diluted in 10 mL of TB and maintained at 25 °C without shaking for 7 h. The cultured MG1655 with many motile bacteria was used in our experiments.

A rectangular microchannel (ibidi, Fitchburg, WI, USA) of height H = 0.2 mm, width W = 5 mm, and length = 50 mm was used in the experiments. A high-precision syringe pump (Chemyx Inc., Stafford, TX, USA) was used to introduce the bacterial suspension into the microchannel at controlled flow rates Q = 0.0195, 0.195, 0.39, 0.585, 0.78, and 0.975 mL/min. The corresponding wall shear rates were $\dot{\gamma }$ = 10, 100, 200, 300, 400, and 500 s⁻¹, which were calculated analytically³³.

$${u}_{x}^{{{\infty }}}\left(y,z\right)= \frac{48Q}{{\pi }^{3}{hw}}\frac{{\sum }_{n,{{{{{{\mathrm{odd}}}}}}}\,}^{{{\infty }}}\frac{1}{{n}^{3}}\left[1-\frac{\cosh \left(n\pi \frac{y}{h}\right)}{\cosh \left(n\pi \frac{w}{2h}\right)}\right]\sin \left(n\pi \frac{z}{h}\right)}{\left[1-{\sum }_{n,{{{{{{\mathrm{odd}}}}}}}\,}^{{{\infty }}}\frac{192h}{{n}^{5}{\pi }^{5}w}\tanh \left(n\pi \frac{w}{2h}\right)\right]}, \\ -\frac{w}{2} \, < \, y \, < \, \frac{w}{2},0 \, < \, z \, < \, h\,,$$

(1)

where x is the flow direction, y is the spanwise direction, and z is perpendicular to the bottom surface of the microfluidic slide.

The suspension was observed under an inverted microscope (Olympus IX71; Olympus, Tokyo, Japan) with an oil magnification objective (60×). Video recordings were taken using a high-speed camera at a frame rate of 100 fps. The recorded images were evaluated by microparticle tracking velocimetry^34,35 using the Fiji manual tracking plug-in for ImageJ (National Institutes of Health, Bethesda, MD, USA) to obtain the position and trajectory of an individual bacterium in successive images.

Simulation settings

We investigated the behavior of a bacterium under simple shear flow conditions without a wall boundary and in Couette or Poiseuille flow with wall boundaries. In Couette or Poiseuille flow, a flat wall satisfying the no-slip condition was placed at $z$  = 0. The bacterium was initially placed at $z$  = 7a in all cases, where a is the half body length. Simple shear flow and Couette flow were given as ${{{{{{\bf{u}}}}}}}^{\infty }=\left(\right.\dot{\gamma }z$,0,0), and Poiseuille flow was given as ${{{{{{\bf{u}}}}}}}^{\infty }=\left(\right.\dot{\gamma }z-k{z}^{2}/2$,0,0) with a shear rate of $\dot{\gamma }-{kz}$. The condition $\dot{\gamma }-7{ka}=1({T}_{{{{{{\rm{m}}}}}}}/\mu {a}^{3})$ ($0\le k\le 4/7({T}_{{{{{{\rm{m}}}}}}}/\mu {a}^{4})$) was imposed such that either $\dot{\gamma }$ or $k$ was the independent variable.

The body of the bacterium was modeled as an ellipsoidal cell with three helical flagella, as in our previous studies^12,36. The cell body is modeled as a prolate sphere with an axis of symmetry in the x-direction³⁷, with two minor axes to one major axis at a ratio of 0.5. The flagellum was modeled as a rigid left-handed helix, the centerline of which was given parametrically as³⁸:

$${{{{{{\bf{r}}}}}}}_{f}= \left\{s,{h}_{f}{E}_{f}\left(s\right)\cos \left(\frac{2\pi }{{\lambda }_{f}}s\right),{h}_{f}{E}_{f}\left(s\right)\sin \left(\frac{2\pi }{{\lambda }_{f}}s\right)\right\}{{{{{\rm{with}}}}}}{E}_{f}\left(s\right) \\ = 1-\exp \left(-{k}_{E}^{2}{s}^{2}\right),s\in \left[0,{l}_{f}\right],$$

(2)

where $s$ is the coordinate along the flagellar axis originating from the base of the flagellum, ${h}_{f}$ is the amplitude, ${\lambda }_{f}$ is the wavelength, and ${k}_{E}$ is a constant that determines how quickly the helix grows to its maximum amplitude. As shown in Fig. 2a, we used the following parameters to describe the basic bacterial configuration: ${\lambda }_{f}=2a$, ${h}_{f}=0.25a$, ${k}_{E}=1/a$, and flagellar length ${l}_{f}=5a$. Note that the flagellar arch length ${L}_{f}$ differed from ${l}_{f}$ in that it was measured along the curved flagellar filament.

Basic fluid mechanics equations

Consider a bacterium immersed in an infinite Newtonian liquid. Due to the small size of the bacterium, we neglected inertial effects in the flow field and assumed Stokes flow (Re«1). Therefore, fluid flow around the bacterium was governed by the boundary integral formulation of the Stokes equation. Considering the slenderness of the flagellar filament, slender body theory^37,39,40,41 can be applied to express the flow generated by the flagella. In this study, the flow field at point x located on the cell body was given by^37,41,42,43:

$${{{{{\bf{u}}}}}}\left({{{{{\bf{x}}}}}}\right)-{{{{{{\bf{u}}}}}}}^{{{\infty }}}\left({{{{{\bf{x}}}}}}\right)= -\frac{1}{8\pi \mu }{\int _{{{{{{{\mathrm{cell}}}}}}}}}\left[{{{{{\bf{J}}}}}}\left({{{{{\bf{x}}}}}},{{{{{\bf{y}}}}}}\right)+{{{{{{\bf{J}}}}}}}^{w}\left({{{{{\bf{x}}}}}},{{{{{\bf{y}}}}}}\right)\right]\cdot {{{{{\bf{q}}}}}}\left({{{{{\bf{y}}}}}}\right){dA}\left({{{{{\bf{y}}}}}}\right) \\ -\frac{1}{8\pi \mu }{\sum }_{j=1}^{N}{\int _{{{{{{{\mathrm{fla}}}}}}}}}\left[{{{{{\bf{J}}}}}}\left({{{{{\bf{x}}}}}},{{{{{\bf{y}}}}}}\right)+{{{{{{\bf{J}}}}}}}^{w}\left({{{{{\bf{x}}}}}},{{{{{\bf{y}}}}}}\right)+{{{{{\bf{W}}}}}}\left({{{{{\bf{x}}}}}},{{{{{\bf{y}}}}}}\right)\right]\cdot {{{{{\bf{f}}}}}}\left({{{{{\bf{y}}}}}}\right){d\xi }_{j}\left({{{{{\bf{y}}}}}}\right) \, ,$$

(3a)

For observation point x on the i-th flagellum, the velocity was given by:

$${{{{{\bf{u}}}}}}\left({{{{{\bf{x}}}}}}\right)-{{{{{{\bf{u}}}}}}}^{{{\infty }}}\left({{{{{\bf{x}}}}}}\right)= -\frac{1}{8\pi \mu }{\int _{{{{{{{\mathrm{cell}}}}}}}}}\left[{{{{{\bf{J}}}}}}\left({{{{{\bf{x}}}}}},{{{{{\bf{y}}}}}}\right)+{{{{{{\bf{J}}}}}}}^{w}\left({{{{{\bf{x}}}}}},{{{{{\bf{y}}}}}}\right)\right]\cdot {{{{{\bf{q}}}}}}\left({{{{{\bf{y}}}}}}\right){dA}\left({{{{{\bf{y}}}}}}\right)-\frac{1}{8\pi \mu }{{{{{\boldsymbol{\Lambda }}}}}}\left({{{{{\bf{x}}}}}}\right){{\cdot }}{{{{{\bf{f}}}}}}\left({{{{{\bf{x}}}}}}\right)\\ -\frac{1}{8\pi \mu }{\int _{{{{{{{\mathrm{fla}}}}}}}}}\left[\left\{{{{{{\bf{J}}}}}}\left({{{{{\bf{x}}}}}},{{{{{\bf{y}}}}}}\right)+{{{{{{\bf{J}}}}}}}^{w}\left({{{{{\bf{x}}}}}},{{{{{\bf{y}}}}}}\right)\right\}\cdot {{{{{\bf{f}}}}}}\left({{{{{\bf{y}}}}}}\right)+{{{{{\bf{K}}}}}}\left({{{{{\bf{x}}}}}},{{{{{\bf{y}}}}}}\right)\cdot {{{{{\bf{f}}}}}}\left({{{{{\bf{x}}}}}}\right)\right]{d\xi }_{i}\left({{{{{\bf{y}}}}}}\right)\\ -\frac{1}{8\pi \mu }{\sum }_{j\ne i}^{N}{\int _{{{{{{{\mathrm{fla}}}}}}}}}\left[{{{{{\bf{J}}}}}}\left({{{{{\bf{x}}}}}},{{{{{\bf{y}}}}}}\right)+{{{{{{\bf{J}}}}}}}^{w}\left({{{{{\bf{x}}}}}},{{{{{\bf{y}}}}}}\right)+{{{{{\bf{W}}}}}}\left({{{{{\bf{x}}}}}},{{{{{\bf{y}}}}}}\right)\right]\cdot {{{{{\bf{f}}}}}}\left({{{{{\bf{y}}}}}}\right){d\xi }_{j}\left({{{{{\bf{y}}}}}}\right),$$

(3b)

where u(x) is the velocity at position x, u^∞(x) is the background velocity, A is the surface of the cell body, ξ is the curved coordinate along the flagellum, q is the traction force on the cell body, f is the force density per unit length, and N is the total number of flagella. The first integral on the right of Eq. (3) operates over the entire ellipsoidal cell surface, and the second and third integrals operate along the curved flagellar filament. J^w is Green’s function for the half space bounded by a no-slip wall, given by⁴⁴:

$${J}_{{ij}}^{w}\left({{{{{\bf{x}}}}}}-{{{{{\bf{y}}}}}}\right)= \left(\frac{{\delta }_{{ij}}}{r}+\frac{{r}_{i}{r}_{j}}{{r}^{3}}\right)-\left(\frac{{\delta }_{{ij}}}{R}+\frac{{R}_{i}{R}_{j}}{{R}^{3}}\right) \\ +2h\left({\delta }_{j\alpha }{\delta }_{\alpha k}-{\delta }_{j3}{\delta }_{3k}\right)\frac{\partial }{\partial {R}_{k}}\left\{\frac{h{R}_{i}}{{R}^{3}}-\left(\frac{{\delta }_{i3}}{R}+\frac{{R}_{i}{R}_{3}}{{R}^{3}}\right)\right\}$$

(4)

where ${{{{{\bf{x}}}}}}=\left({x}_{1},{x}_{2},{x}_{3}\right)$, ${{{{{\bf{y}}}}}}=\left({y}_{1},{y}_{2},h\right)$, $r={\left[{\left({x}_{1}-{y}_{1}\right)}^{2}+{\left({x}_{2}-{y}_{2}\right)}^{2}{+\left({x}_{3}-h\right)}^{2}\right]}^{1/2}$, $R={\left[{\left({x}_{1}-{y}_{1}\right)}^{2}+{\left({x}_{2}-{y}_{2}\right)}^{2}{+\left({x}_{3}+h\right)}^{2}\right]}^{1/2}$, and $\alpha =1,2$.

${{{{{\bf{W}}}}}}$ is the slender body kernel, given by:

$${W}_{{ij}}\left({{{{{\bf{x}}}}}},{{{{{\bf{y}}}}}}\right)=\frac{{\left(\varepsilon {L}_{f}\right)}^{2}}{2}\left(\frac{{\delta }_{{ij}}}{{r}^{3}}-3\frac{{r}_{i}{r}_{j}}{{r}^{5}}\right)$$

(5)

In Eq. (2b), the local ${{{{{\boldsymbol{\Lambda }}}}}}$ and nonlocal ${{{{{\bf{K}}}}}}$ are the slender body theory operators, which are given by^37,41,43:

$${\varLambda }_{{ij}}\left({{{{{\bf{x}}}}}}\right)=c\left[{\delta }_{{ij}}+{t}_{i}\left({{{{{\bf{x}}}}}}\right){t}_{j}\left({{{{{\bf{x}}}}}}\right)\right]+2\left[{\delta }_{{ij}}-{t}_{i}\left({{{{{\bf{x}}}}}}\right){t}_{j}\left({{{{{\bf{x}}}}}}\right)\right],$$

(6)

and

$${K}_{{ij}}\left({{{{{\bf{x}}}}}},{{{{{\bf{y}}}}}}\right)=-\frac{{\delta }_{{ij}}+{t}_{i}\left({{{{{\bf{x}}}}}}\right){t}_{j}\left({{{{{\bf{x}}}}}}\right)}{\left|\xi \left({{{{{\bf{x}}}}}}\right)-\xi \left({{{{{\bf{y}}}}}}\right)\right|},$$

(7)

where $c=-{{{{\mathrm{ln}}}}}\left({\varepsilon }^{2}e\right)$, t is the unit tangential vector to the centerline of each flagellum, $\varepsilon ={r}_{f}/{L}_{f}$, ${r}_{f}$ is the flagellar radius, and ${L}_{f}$ is the flagellar arch length.

Force conditions and numerical methods

The bacterial model was assumed to be neutrally buoyant because the sedimentation velocity for typical aquatic bacteria is much lower than the swimming speed. Brownian motion was not considered, because the shear rate was too strong for Brownian effects to be important. The force-free and torque-free conditions were given as:

$${{{{{\bf{F}}}}}}={\int _{{{{{{{\mathrm{cell}}}}}}}}}{{{{{\bf{q}}}}}}\left({{{{{\bf{x}}}}}}\right){dA}+\mathop{\sum }\limits_{j=1}^{N}{\int _{{{{{{{\mathrm{fla}}}}}}}}}{{{{{\bf{f}}}}}}\left({{{{{\bf{x}}}}}}\right){d\xi }_{j}={{{{{\bf{0}}}}}},$$

(8)

and

$${{{{{\bf{T}}}}}}={\int _{{{{{{{\mathrm{cell}}}}}}}}}\left({{{{{\bf{x}}}}}}-{{{{{{\bf{x}}}}}}}_{{{{{{\rm{c}}}}}}}\right)\times {{{{{\bf{q}}}}}}\left({{{{{\bf{x}}}}}}\right){dA}+\mathop{\sum }\limits_{j=1}^{N}{\int _{{{{{{{\mathrm{fla}}}}}}}}}\left({{{{{\bf{x}}}}}}-{{{{{{\bf{x}}}}}}}_{{{{{{\rm{c}}}}}}}\right)\times {{{{{\bf{f}}}}}}\left({{{{{\bf{x}}}}}}\right){d\xi }_{j}=0,$$

(9)

where the integral is over the whole bacterial surface and ${{{{{{\bf{x}}}}}}}_{{{{{{\rm{c}}}}}}}$ is the center of the cell body.

Rigid body motion was assumed for the bacterial cell body and the flagella. The flagella were assumed to rotate relative to the cell body with a constant torque ${{{{{{\bf{T}}}}}}}_{{{{{{\rm{m}}}}}}}$ generated by a molecular motor in the direction of the flagellar axis. The motor torque acting on flagellum j should balance the hydrodynamic torques; thus,

$${{\int _{{{{{{{\mathrm{fla}}}}}}}}}\left({{{{{{\bf{x}}}}}}}_{j}-{{{{{{\bf{x}}}}}}}_{j,a}\right)\times {{{{{{\bf{f}}}}}}}_{j}({{{{{{\bf{x}}}}}}}_{j})}{d\xi }_{j}\;{{=}}\;-\left({{{{{{\bf{T}}}}}}}_{{{{{{\rm{m}}}}}},{{{{{\rm{j}}}}}}}{+}{{{{{{\bf{T}}}}}}}_{{{{{{\rm{bend}}}}}},j}{{+}\mathop{\sum }\limits_{i=1,i\ne j}^{N}{{{{{\bf{T}}}}}}_{{{{{{\rm{rep}}}}}},{ji}}}\right),$$

(10)

where ${{{{{{\bf{x}}}}}}}_{j,a}$ is the base position of the flagellum j (i.e., the hook position), ${{{{{{\bf{T}}}}}}}_{{{{{{\rm{bend}}}}}}}$ is the bending torque exerted by the hook, and ${{{{{{\bf{T}}}}}}}_{{{{{{\rm{rep}}}}}}}$ is the short-range repulsive torque between flagellar filaments. Bending potential $\Pi$ was applied to the hook to prevent the overlap of the body surface and the flagellum, given by¹²:

$$\Pi \left({\phi }_{j}\right)=\left\{\begin{array}{c}0\quad\qquad\quad, \quad{if}\,\cos {\phi }_{j}\ge 0\\ {-\frac{1}{2}k}_{b}{\cos }^{2}{\phi }_{j}, \,\,\,\,{{{{{{\mathrm{else}}}}}}} \hfill\,\end{array}\right.,$$

(11)

where ${\phi }_{j}$ is the angle between the orientation vector of flagellum j and the outward normal vector on the body surface, and ${k}_{b}$ was set to be sufficiently strong that the flagella and body did not overlap. This condition represents a resistance-free hook for ${\varphi }^{j}\ge 0$.

To avoid flagellar intersection, we assumed a Derjaguin–Landau–Verwey–Overbeek short-range repulsive force ${{{{{{\bf{F}}}}}}}_{{{{{{\rm{rep}}}}}}}$, given by⁴⁵:

$${{{{{{\bf{F}}}}}}}_{{{{{{\rm{rep}}}}}}}={\alpha }_{1}\frac{\exp {{{{{\rm{}}}}}}(-{\alpha }_{2}\left|{{{{{\bf{d}}}}}}\right|)}{1-\exp \left(-{\alpha }_{2}\left|{{{{{\bf{d}}}}}}\right|\right)}\frac{{{{{{\bf{d}}}}}}}{\left|{{{{{\bf{d}}}}}}\right|},$$

(12)

where ${\alpha }_{1}$ is a coefficient that controls the magnitude of the force,$\,{\alpha }_{2}$ is a coefficient to controls the decay length, $\left|{{{{{\bf{d}}}}}}\right|$ is the minimum distance between the surfaces, and ${{{{{\bf{d}}}}}}$ is the distance vector connecting two near-contact surfaces. In this study, the coefficients were set as ${\alpha }_{1}=50$ and ${\alpha }_{2}=75$.

The boundary element method was used to discretize the governing equations, similar to the approach of Ishikawa et al.⁴⁶. In total, 80 triangular elements were generated on the cell body, with 80 points along each flagellum. The surface integrals were performed on the triangular element using 28-point Gaussian polynomials, and the singularity in the integration was solved analytically⁴⁷. The line integrals were performed using 4-point Gaussian polynomials. Time marching was performed using the 4th order Adams–Bashforth method.