Polarization and multiscale structural balance in signed networks

Abstract

Polarization, or a division into mutually hostile groups, is a common feature of social systems. It is studied in Structural Balance Theory in terms of semicycles in signed networks. However, enumerating semicycles is computationally expensive, so approximations are often needed. Here we introduce the Multiscale Semiwalk Balance approach for measuring the degree of balance (DoB) in (un)directed, (un)weighted signed networks by approximating semicycles with closed semiwalks. It allows selecting the resolution of analysis appropriate for assessing DoB motivated by the Locality Principle, which posits that patterns in shorter cycles are more important than in longer ones. Our approach overcomes several limitations affecting walk-based approximations and provides methods for assessing DoB at various scales, from graphs to individual nodes, and for clustering signed networks. We demonstrate its effectiveness by applying it to real-world social systems, which leads to explainable results for networks with expected patterns (polarization in the US Congress) and a more nuanced perspective for other systems. Our work may facilitate studying polarization and structural balance in a variety of contexts and at multiple scales.

Introduction

Networks are used in many branches of science and engineering for modeling complex systems. Depending on the context, they may be undirected (ties are bidirectional) or directed and weighted (ties have weights that usually indicate strength) or unweighted¹. Moreover, some networks are signed, or have links that are either positive or negative, and thus can be used to model valenced relations such as liking and disliking, or alliances and war^2,3,4,5. Signed networks are commonly used for representing systems capable of polarization, or clustering into groups with positive in-group and negative out-group ties. As a result, they have long been important to social scientists interested in polarization and differentiation processes inherent to the formation of groups, attitudes and opinions^2,6,7,8,9. However, signed networks are also used in other disciplines for modeling diverse phenomena such as brain activation¹⁰, ecological interactions¹¹, and financial time series¹². Moreover, it is often not only the signs that matter but also the weights indicating the intensities of particular relations. Therefore, principled methods for analyzing signed networks, possibly with weights, are important for many applications.

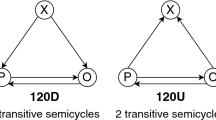
Since signed networks represent valenced relations, a fundamental question concerns the degree to which positive and negative ties are consistent with respect to notions of (anti)transitivity, and whether these microscopic patterns give rise to a polarized macroscopic organization into mutually antagonistic clusters. Both problems are studied in Structural Balance Theory (SBT)^13,14, which originated from Gestalt psychology and the work of Fritz Heider¹⁵, from which one can deduce that positive relations should be transitive (a friend of my friend is my friend) and negative relations antitransitive (an enemy of my enemy is my friend), e.g., two positively (negatively) linked nodes should have identical (opposite) signs on their ties to shared neighbors. These considerations were later formalized and generalized in graph-theoretic terms and used to demonstrate that (anti)transitivity of (negative) positive relations is directly linked to the properties of cycles and as a result to clustering and polarization. Namely, polarized systems clustered in exactly two antagonistic groups, in which in-group ties are exclusively positive and out-group ties negative, require that all cycles are positive, or that the products of the signs of their edges are positive¹³ (strong balance property; see Fig. 1 for a visual explanation and some examples). Systems clustered into b ≥ 2 antagonistic blocks require that there are no cycles with exactly one negative edge (weak balance property)¹⁶. See “Methods: Overview of Structural Balance Theory”, for the main definitions and theorems of SBT, including their general form applicable to directed networks based on the notion of semicycles.

Fig. 1: Examples of high and low polarization and its general connection to frequencies of balanced and unbalanced cycles.

The two networks depict bill co-sponsorship relations in the U.S. Senate. Positive ties (blue) link senators, who tended to promote the same bills together more often than by chance, and negative ties (red) correspond to those who collaborated less often than at random (see “Results: Polarization in the U.S. Congress” for the data description and a detailed analysis). The four triad diagrams depict four possible strongly (un)balanced undirected 3-cycles. Positive ties are marked with blue and negative with red dashed lines. a 96th Congress (1979–81, Carter administration) was a period of low polarization with frequent positive between-party and negative within-party links. b 114th Congress (2015–17, Obama administration) featured high polarization with in-group ties being almost exclusively positive and out-group ties negative. c Schematic depiction of the relationship between relative frequencies of (un)balanced cycles and low polarization, which is characterized by comparable frequencies, or more rarely by a majority, of unbalanced cycles (note that, even though only 3 cycles are depicted, the general relationship pertains to cycles of all lengths). d Relationship between (un)balanced cycles and high polarization, which implies that there is a clear majority of balanced cycles.

SBT specifies strict requirements for signed networks to be balanced (partitioned into antagonistic groups), but real-world systems are rarely organized neatly enough to satisfy them completely. This is why a lot of work in SBT is concerned with measures of the Degree of Balance (DoB), or partial balance¹⁷, which can be seen as indicators of a “distance” from the perfectly balanced state. Such measures are typically directly or indirectly related to the relative frequencies of positive and negative cycles (or cycles with exactly one negative edge in the case of weak balance).

However, measuring structural balance in practice is not trivial. While defining DoB at the level of cycles of a particular length k is simple, since in this case, the raw proportion of balanced cycles is meaningful, any global DoB measure has to integrate information across cycles of many different lengths and it is not immediately clear how this should be done. The difficulty comes from the fact that typically longer cycles will be much more numerous than shorter ones, so a simple proportion will be determined primarily by patterns found in long cycles, but this may not be a desirable property. Indeed, already Cartwright and Harrary hypothesized that shorter cycles should matter more when evaluating DoB¹³. Moreover, this intuition has been later justified empirically by demonstrating that it is easier for people to memorize the valences of ties in shorter cycles¹⁸. More recently, analyses based on counting simple cycles demonstrated that real networks often have a relatively low cycle length threshold after which DoB measures quickly decrease, indicating that structural balance is found primarily in structures at smaller scales¹⁹.

Applying SBT in practice is further complicated by the fact that enumerating and counting cycles is computationally expensive, especially for large graphs. This problem can be partially alleviated with novel algorithms and sampling methods, but exact solutions will always remain prohibitively expensive due to the nature of the problem. Moreover, the current state-of-the-art sampling methods¹⁹ are limited to “grayscale” measures which quantify DoB for cycles of particular lengths and they do not offer any principled way for aggregating them into a single global DoB index. This is an important limitation since it is typically easier and more meaningful to compare a scalar DoB value between different networks. Moreover, global measures, being scalar values, are probably more useful for designing clustering or community detection methods.

Thus, various approximations have been proposed, which can roughly be divided into two families of local and global measures. Local measures attain efficiency by focusing only on cycles of particular, usually short, lengths, such as 3-cycles (triads). They can be fast, but provide only a limited description of the real structure of a network. Hence, we argue that global measures are preferable.

Several global approaches have been proposed. Some bypass the problem of counting cycles entirely, and instead search for partitions minimizing frustration²⁰ (the number or relative weight of edges incompatible with the SBT assumptions), but they suffer from similar computational constraints due to their combinatorial nature. Others leverage spectral properties of signed graphs and are therefore computationally efficient, but measure only strong balance and quantify DoB using the smallest eigenvalue of the signed Laplacian matrix²¹, which is not normalized and can be difficult to compare between networks. The last major approach is based on approximating cycle counts with counts of closed walks which can be calculated, or at least approximated, very efficiently with standard linear algebra^4,22. Moreover, it can produce both local and global measures^4,23 as well as capture strong and weak balance properties⁵.

However, walk-based approximations can be potentially misleading as they may combine patterns found at very different cycle lengths¹⁹. On the other hand, one can put forth arguments based on the theory of dynamical consensus on signed networks and argue that closed walks provide a fuller picture of structural balance²⁴.

Here we propose Multiscale Semiwalk Balance (MSB): an approach applicable to (un)directed, (un)weighted signed networks. It is multiscale as it provides both grayscale measures approximating DoB at particular cycle lengths, as well as global indicators aggregating local measures across multiple scales in a principled manner. Namely, it enforces what we call the Locality Principle (LP) and ensures that global DoB estimates are weighted averages of estimates at specific lengths such that DoBs for shorter cycles are assigned with non-decreasing weights.

Our work builds on the Walk Balance (WB) approach proposed by Estrada and Benzi⁴, which tends to underestimate DoB, especially in large networks^19,22. We show that this is caused by too much weight being placed on long cycles and can be fixed by introducing a formal resolution parameter. Namely, we demonstrate how the inverse temperature, β, considered briefly already by Estrada and Benzi⁴, can be reinterpreted and used to determine an appropriate weighting scheme for aggregating DoB measures across different cycle lengths that satisfies LP. It also allows our MSB approach to be applicable and meaningful in the context of weighted signed networks. Additionally, we generalize the WB approach to capture both strong and weak balance, as well as define DoB measures not only at the level of entire graphs but also for particular nodes and pairs of nodes to enable the development of effective SBT-aware clustering (community detection) methods. Last but not least, by using semiwalk-based approximations our methods are more directly linked to both undirected and directed SBT theorems and therefore meaningful also for directed signed networks. We demonstrate the utility of our approach in two case studies of polarization in social systems. The first is a re-analysis of the famous Sampson’s Monks dataset²⁵, in which we show that the commonly accepted “ground truth” partition is not SBT-optimal by finding better ones, which also shed some additional light on the underlying social dynamics. In the second study, we use our methods to provide evidence for increasing polarization in the U.S. Congress based on bill co-sponsorship data⁹.

Results

Preliminaries

Before introducing the proposed framework we first introduce the notation and state the core problems our work is supposed to solve in a more formal fashion for the sake of clarity.

Notation

Here we consider weighted graphs G = (V, E, ω) with n = ∣V∣ vertices and m = ∣E∣ edges and no self-loops or multilinks, where V and E ⊆ V × V are vertex and edge sets respectively, and $\omega :E\to {\mathbb{R}}$ is a function assigning weights to edges. The weights can be negative, so the above definition captures all (un)signed, (un)weighted and (un)directed graphs.

The adjacency matrix of a graph G is given by a square n × n matrix A(G) such that A_ij = ω_ij = ω(i, j) if (i, j) ∈ E or otherwise A_ij = 0. Whenever possible without introducing ambiguity, we will drop the explicit dependence on G and prefer a simpler notation, A. We will use ∣A∣ to denote the unsigned counterpart of A such that ∣A∣_ij = ∣ω_ij∣. Additionally, P and N will denote non-negative n × n matrices corresponding to positive and negative parts of A such that A = P − N and ∣A∣ = P + N. When discussing network partitions, we will use B to denote n × b block-partition matrix such that B_iu = 1 when the ith node belongs to the uth block (group) or otherwise B_iu = 0. Matrix trace operator will be denoted by ${{{{{{{\rm{tr}}}}}}}}$. In particular, trace of the kth power of a square matrix X will be denoted by ${{{{{{{\rm{tr}}}}}}}}{{{{{{{{\bf{X}}}}}}}}}^{k}$. Hadamard (elementwise) matrix product will be denoted by ⊙.

All measures defined later in this paper will depend on a particular graph G. Thus, for the sake of simplicity, whenever possible, we will omit this general dependence in the notation.

Aggregating DoB measures

The difficulty with defining a meaningful global Degree of Balance (DoB) can be easily seen by first considering DoB measures for cycles of particular lengths. For a signed graph G we define k-balance (DoB for cycles of length k) as:

$${B}_{k}=\frac{{\mu }_{+}(k)}{{\mu }_{+}(k)+{\mu }_{-}(k)}$$

(1)

where μ₊(k) and μ₋(k) are respectively counts of balanced and unbalanced cycles of length k. This measure is easy to interpret since it is concerned with only one specific class of cycles (those of length k), so in this context, it is justified to treat every cycle equally.

However, defining a global DoB measure integrating structural balance information across different cycle lengths is more difficult, since there are infinitely many ways to do it. A reasonable solution is to assume that global DoB should be a weighted average of k-balance scores:

$$B=\mathop{\sum}\limits_{k}{\omega }_{k}{B}_{k}$$

(2)

where ω_k’s are normalized weights (ω_k ≥ 0 and ∑_kω_k = 1) assigned to different balance scores at different lengths k. However, it is not clear how the weights should be chosen in order to produce a meaningful global DoB measure.

Importantly, let us note that the above generic definitions are appropriate for both the strong and weak notions of balance. In what follows we will derive particular operationalizations of these generic formulas.

Finding clusters in signed networks

While it is useful to know the DoB of a network, which tells how close it is to being perfectly balanced and therefore clusterable, it is arguably even more useful to be able to find clusters (network communities) such that they agree with SBT to the greatest extent possible. This compatibility of a given partition of a signed network with respect to the structure theorems of SBT (see “Methods: Overview of Structural Balance Theory” for details) can be measured with frustration ratio, which can be defined as the sum of absolute weights of negative in-group and positive out-group ties relative to the sum of all absolute edge weights², which can be expressed succinctly in the matrix form as:

$$F({{{{{{{\bf{B}}}}}}}})=\frac{{{\mathbb{1}}}^{\top }\left[({{{{{{{{\bf{BB}}}}}}}}}^{\top })\odot {{{{{{{\bf{N}}}}}}}}+({\mathbb{1}}{{\mathbb{1}}}^{\top }-{{{{{{{{\bf{BB}}}}}}}}}^{\top })\odot {{{{{{{\bf{P}}}}}}}}\right]{\mathbb{1}}}{{{\mathbb{1}}}^{\top }| {{{{{{{\bf{A}}}}}}}}| {\mathbb{1}}}$$

(3)

where ${\mathbb{1}}$ is a vector of ones of an appropriate length, ${{{{{{{\bf{B}}}}}}}}\in {{\mathbb{R}}}^{n\times b}$ is a block-partition matrix and P and N are positive and negative parts of the adjacency matrix A. Note that frustration ratio can also be seen as a normalized version of frustration count, which is used to define frustration index as the minimal frustration count over all partitions of a network²⁶.

Frustration ratio is a very straightforward measure of the extent to which a given partition produces a balanced network configuration. It ranges from 0 for balanced partitions to 1 for maximally unbalanced ones (Fig. 2).

Fig. 2: Relationship between frustration ratio, F(B), and structural balance in signed networks.

Positive ties are blue and negative are red and dashed. Different groups are marked with circles.

It is important to note that the frustration ratio, while closely related to DoB, measures something different. DoB is a property of a network as such, which, thanks to the structure theorems of SBT, is informative of the extent to which a given network is clusterable. On the other hand, the frustration ratio is a property of a network and a specific partition and is directly related to how close a given partition is to being perfectly balanced. That is why we argue that it is an appropriate measure of the quality of a partition vis-à-vis the tenets of SBT. Thus, the DoB and frustration ratio are closely related but not equivalent²⁴. However, the crux is that in the limiting case of the perfect balance, DoB equal to 1 implies that there is a partition with zero frustration and vice versa. The farther a network is from this ideal case the fuzzier this relationship gets, but in general the two measures will always be related. We will use this insight to develop a clustering method utilizing DoB-like scores.

Approximating (semi)cycles with closed (semi)walks

Counting cycles is computationally very expensive, so in practice approximations are necessary. A very general and flexible approach is based on approximating cycles with closed walks, which can be counted much more efficiently using the powers of adjacency matrix. However, SBT in its most general form applicable to both directed and undirected networks is formulated in terms of closed semipaths, or semicycles¹³. A semipath is a path, in which edge directions can be ignored, but any edge can still be traversed only once. This property has an important consequence for directed networks, in which in general semicycles correspond to cycles in the associated undirected multigraph (obtained by making every link bidirectional) with the exception of 2-cycles, which require both i → j and j → i links to be present (Fig. 3).

Fig. 3: Relationship between cycles and semicycles.

a Symmetric (reciprocated) dyads generate two (semi)cycles. b Asymmetric dyads generate no (semi)cycles, since a semicycle of the form i − j − i would have to cross the directed i → j link twice. c An example of the connection between directed cycles and semicycles in signed networks. A single directed triad can generate several different balanced and unbalanced 2- and 3-semicycles (which here are marked with two-way arrows). Positive ties are blue and negative red and dashed.

Thus, we argue that semicycle counts should be approximated using semiwalks, which are simply walks on the corresponding undirected multigraph (i.e., ignoring edge directions)⁶. However, an additional correction factor should be used to account for the fact that non-reciprocated directed edges do not generate any 2-semicycles.

Multiscale semiwalk balance

Here we introduce the Multiscale Semiwalk Balance (MSB) approach which provides solutions to all of the above-mentioned problems. We first develop it without considering the role of edge weights, which, as we discuss later, appear in our approach naturally also in the context of unweighted networks. Once the core framework is established, we show that it automatically extends to weighted graphs in a meaningful way. Moreover, here we focus on the undirected version of MSB and strong balance. In “Results: Directed measures” we generalize our approach to directed signed graphs and in “Methods: Weak balance” to the weak notion of structural balance.

In what follows we will use the fact that for a graph G walks of length k between nodes i and j are counted by the elements of the k-th power of its (unsigned) adjacency matrix, ∣A∣^k (in the weighted case ∣A∣^k gives weighted counts such that each walk is assigned a weight equal to the product over its constitutive edges). Importantly, such matrix powers can be calculated and approximated easily using eigendecomposition, especially for symmetric matrices and here we will use only such.

We will be particularly interested in weighted sums of matrix powers of the following form:

$${{{{{{{\bf{W}}}}}}}}({{{{{{{\bf{A}}}}}}}},\beta ;{k}_{\min },{k}_{\max })=\mathop{\sum }\limits_{k={k}_{\min }}^{{k}_{\max }}\frac{{\beta }^{k}}{k!}{{{{{{{{\bf{A}}}}}}}}}^{k}\approx {e}^{\beta {{{{{{{\bf{A}}}}}}}}}$$

(4)

where k iterates over a sequence of consecutive non-negative integers, ${k}_{\min },\ldots ,{k}_{\max }$, and the second approximate equality is exact when ${k}_{\min }=0$ and ${k}_{\max }=\infty$. In what follows we will use a simpler notation, W(A, β), whenever it is clear from the context, or unimportant, what ${k}_{\min }$ and ${k}_{\max }$ are. Moreover, any function depending on W(…) is also implicitly parametrized by ${k}_{\min }$ and ${k}_{\max }$ but we will omit this in the notation for the sake of brevity. Note that here β is a free parameter that can be used to control the weights assigned to different powers of A. We will use this fact later. Moreover, both W(A, β) and its trace can be approximated in an accurate and efficient manner based on m leading eigenvalues of A (see “Methods: Numerical approximations and efficiency”).

Strong balance

Following Estrada and Benzi⁴, we note that powers of signed adjacency matrix, A^k, give differences between counts of positive and negative walks of a given length, while powers of unsigned adjacency matrix, ∣A∣^k, count all walks of the given length. Thus, the sum of differences between weighted counts of positive and negative walks of a lengths $k={k}_{\min },\ldots ,{k}_{\max }$ is given by W(A, β). Similarly, W(∣A∣, β) gives the corresponding sum of weighted counts of all walks.

In the case of undirected networks considered here, we have that ${k}_{\min }=3$, since 2-cycles in undirected signed networks are always trivially balanced. On the other hand, it should be that ${k}_{\max }\le n$, since no cycle can be longer than the number of nodes in a network, it is not obvious what is the proper exact choice for ${k}_{\max }$. However, any moderately large value will do, since the higher-order terms in Eq. (4) are quickly killed by the inverse factorial factor. In Supplementary Note 3, we show that typically ${k}_{\max }\ge 10$ is enough to get practically error-free results. However, to stay on the safe side in all following analyses we always use ${k}_{\max }=30$.

Counts of closed walks are given by the diagonal elements, so the overall counts are given by appropriate matrix traces. Thus, to measure structural balance in a signed network one can use Balance Index⁴, or the ratio of the difference between weighted counts of balanced (μ₊) and unbalanced (μ₋) closed walks to the weighted count of all closed walks:

$$R(\beta )=\frac{{\mu }_{+}-{\mu }_{-}}{{\mu }_{+}+{\mu }_{-}}=\frac{{{{{{{{\rm{tr}}}}}}}}{{{{{{{\bf{W}}}}}}}}({{{{{{{\bf{A}}}}}}}},\beta )}{{{{{{{{\rm{tr}}}}}}}}{{{{{{{\bf{W}}}}}}}}(| {{{{{{{\bf{A}}}}}}}}| ,\beta )}$$

(5)

A conceptually simpler measure is the Degree of Balance (DoB), proposed already by Cartwright and Harary¹³, which represents the proportion of balanced walks:

$$B(\beta )=\frac{{\mu }_{+}}{{\mu }_{+}+{\mu }_{-}}=\frac{1}{2}\left[R(G,\beta )+1\right]$$

(6)

Following Estrada and Benzi⁴ again, we can define node-level measures, also known as local balance²³, simply by calculating diagonals instead of traces:

$${r}_{i}(\beta )=\frac{{{{{{{{\bf{W}}}}}}}}{({{{{{{{\bf{A}}}}}}}},\beta )}_{ii}}{{{{{{{{\bf{W}}}}}}}}{(| {{{{{{{\bf{A}}}}}}}}| ,\beta )}_{ii}}$$

(7)

$${b}_{i}(\beta )=\frac{1}{2}\left[{r}_{i}(\beta )+1\right]$$

(8)

Note that we use lowercase letters to denote quantities describing individual nodes instead of the global properties of entire graphs. We will follow this convention also when defining other node-level measures.

Measures of k-balance (DoB at a particular length k) can also be easily defined:

$${R}_{k}=\frac{{{{{{{{\rm{tr}}}}}}}}{{{{{{{{\bf{A}}}}}}}}}^{k}}{{{{{{{{\rm{tr}}}}}}}}| {{{{{{{\bf{A}}}}}}}}{| }^{k}}$$

(9)

$${B}_{k}=\frac{1}{2}({R}_{k}+1)$$

(10)

Note that these measures do not depend on β, since, even if they did, the same weighting factor would have to appear in both the numerator and denominator. This shows that β indeed controls only the amount of weight put on different cycle lengths, but does not influence the degree of balance at particular lengths.

Contribution profiles and Locality Principle

Importantly, one can assess the contribution of closed walks of length k to the total weighted sum of closed walk counts for lengths ${k}_{\min },\ldots ,{k}_{\max }$:

$${C}_{k}(\beta )=\frac{{\beta }^{k}}{k!}\times \frac{{{{{{{{\rm{tr}}}}}}}}| {{{{{{{\bf{A}}}}}}}}{| }^{k}}{{{{{{{{\rm{tr}}}}}}}}{{{{{{{\bf{W}}}}}}}}(| {{{{{{{\bf{A}}}}}}}}| ,\beta )}$$

(11)

In other words, Eq. (11) measures the ratio of the weighted sum of closed walks of length k to the total weighted sum of closed walks over a specified range of lengths. It is normalized by construction, so C_k(β) ∈ [0, 1] and ∑_kC_k(β) = 1.

The contribution score clearly depends on β, which can be used for controlling the influence of different length scales on the overall calculations. This is a crucial feature of our approach as it allows for a straightforward operationalization of the Locality Principle (LP): shorter cycles should generally matter no less than longer ones.

Definition 1

(Locality Principle) A graph G, a resolution parameter β > 0 and a sequence of consecutive integers $2\le {k}_{\min },\ldots ,{k}_{\max }$ satisfy the Locality Principle if and only if the following set of inequalities holds:

$${C}_{{k}_{\min }}(\beta )\ge \ldots \ge {C}_{{k}_{\max }}(\beta )$$

Thus, LP allows for the identification of a range of “reasonable” values of β, which is given by a set $\left(0,{\beta }_{\max }\right]$, where ${\beta }_{\max } > 0$ is the largest value still satisfying LP. Crucially, ${\beta }_{\max }$ always exists for graphs that contain at least one closed walk for lengths ${k}_{\min },\ldots ,{k}_{\max }$.

Theorem 1

Let $2\le k={k}_{\min },\ldots ,{k}_{\max }$ be a sequence of consecutive integers and G a graph such that ${{{{{{{\rm{tr}}}}}}}}| {{{{{{{\bf{A}}}}}}}}{| }^{k} > 0$ for all k’s. Then, there exists a value ${\beta }_{\max }$ such that Def. 1 holds for values 0 < β ≤ β_max and does not hold for values $\beta \, > \, {\beta }_{\max }$.

Proof

Using Eq. (11) the condition for LP can be rewritten as:

$$\frac{{\beta }^{k}}{k!}{{{{{{{\rm{tr}}}}}}}}| {{{{{{{\bf{A}}}}}}}}{| }^{k}\ge \frac{{\beta }^{k+1}}{(k+1)!}{{{{{{{\rm{tr}}}}}}}}| {{{{{{{\bf{A}}}}}}}}{| }^{k+1}$$

which after some straightforward algebra gives the following condition for β:

$$\beta \le (k+1)\frac{{{{{{{{\rm{tr}}}}}}}}| {{{{{{{\bf{A}}}}}}}}{| }^{k}}{{{{{{{{\rm{tr}}}}}}}}| {{{{{{{\bf{A}}}}}}}}{| }^{k+1}}$$

Now we note that the right-hand side of the above inequality is always positive, so there is a maximal value ${\beta }_{\max } > 0$ satisfying all inequalities:

$${\beta }_{\max }:= \mathop{\min }\limits_{k}(k+1)\frac{{{{{{{{\rm{tr}}}}}}}}| {{{{{{{\bf{A}}}}}}}}{| }^{k}}{{{{{{{{\rm{tr}}}}}}}}| {{{{{{{\bf{A}}}}}}}}{| }^{k+1}}$$

As a result, a β value satisfies LP if and only if $\beta \in \left(0,{\beta }_{\max }\right]$, which ends the proof.

Finally, following the parsimony principle, we choose the weakest LP assumption possible and set $\beta := {\beta }_{\max }$. This is a simple heuristic and we do not make any claims regarding its optimality. We chose to use it here as developing a more principled method for selecting β is beyond the scope of this paper and we plan to address this problem in the future. However, as we later show through empirical analyses of real-world datasets, this heuristic seems to work very well in practice. Moreover, using ${\beta }_{\max }$ still yields markedly right-skewed contribution profiles, even though it can be argued that for this choice LP “barely” holds, but this is true only in the sense of the entire set of inequalities for all pairs of lengths (k, k + 1), and does not imply that contribution scores assigned to short closed walks are only marginally higher than those assigned to long walks (cf. Fig. 4).

Fig. 4: Contribution and k-balance profiles in four real-world networks.

See “Methods: Network datasets” for dataset descriptions. Measures obtained with the original Walk Balance (WB) approach of Estrada and Benzi⁴ are labeled as β = 1, and Multiscale Semiwalk Balance (MSB) measures as ${\beta }_{\max }$. Approximations based on m = 10 leading eigenvalues from both ends of the spectrum were used. Numbers of nodes are denoted by n, and DoB values according to WB and MSB approaches by B(1) and $B({\beta }_{\max })$ respectively. a Contribution scores at different closed walk lengths. In the case of the WB approach peaks of the contribution profiles are marked with stars. b Balance scores at different closed walk lengths.

Our results also explain why the original WB approach⁴ underestimates DoB in large networks. Namely, it does so because without determining the characteristic scale of a network by tuning β the contribution profile may peak over very long cycles. As Fig. 4 shows, WB places most of the weight on very long cycles (k ≈ 100) in large networks, which clearly violates LP. As a result, it produces much lower DoB estimates than MSB, since products of signs over very long closed walks are arguably mostly random. Only in the case of the directed Epinions network WB produces an estimate close to the one given by MSB. However, as balance measures at particular cycle lengths show, this happens only because of the very particular structure of the network resulting in high DoB at cycle lengths of approximately 100. Moreover, this seems to be a statistical artifact that disappears almost completely when the balance is assessed based on semiwalks (MSB) instead of ordinary walks (WB) (see “Results: Directed measures” for the generalization to directed measures based on semiwalks). Crucially, this problem is likely to affect any other walk-based methods, which do not use a well-tuned resolution parameter. Moreover, without a measure akin to Eq. (11), it is hard to know for sure whether a given method will produce correct results for a given network.

Importantly, global DoB is a weighted average of k-balance values with weights equal to the corresponding contribution scores. Thus, Eq. (6) satisfies the requirement postulated in “Results: Aggregating DoB measures”.

Theorem 2

Let G be a signed graph, β > 0 a resolution parameter and $2\le k={k}_{min},\ldots ,{k}_{\max }$ a sequence of consecutive integers. Then:

$$B(\beta )=\mathop{\sum}\limits_{k}{C}_{k}(\beta ){B}_{k}$$

Proof

It is given in Supplementary Note 1.

Node contributions

Starting from similar ideas, one can also define node-level, or local, contribution scores measuring the influence of a node i on the overall DoB calculations:

$${c}_{i}(\beta )=\frac{{{{{{{{\bf{W}}}}}}}}{(| {{{{{{{\bf{A}}}}}}}}| ,\beta )}_{ii}}{{{{{{{{\rm{tr}}}}}}}}{{{{{{{\bf{W}}}}}}}}(| {{{{{{{\bf{A}}}}}}}}| ,\beta )}$$

(12)

Note that by construction c_i(β) ∈ [0, 1] and ∑_ic_i(β) = 1, so it enjoys the same normalization property as the global contribution score. Importantly, node-level contribution scores, together with local DoB, can be useful for defining and measuring various notions of node centrality in signed networks.

Pairwise cohesion and clustering

Note that off-diagonal elements of W(A, β) also convey important information. Namely, they measure the difference between weighted counts of positive and negative walks between nodes i and j. We use this fact to define the pairwise Cohesion Index:

$${r}_{ij}(\beta )=\frac{{{{{{{{\bf{W}}}}}}}}{({{{{{{{\bf{A}}}}}}}},\beta ;{k}_{\min } = 2)}_{ij}}{{{{{{{{\bf{W}}}}}}}}{(| {{{{{{{\bf{A}}}}}}}}| ,\beta ;{k}_{\min } = 2)}_{ij}}$$

(13)

and a corresponding (pairwise) degree of cohesion measuring the fraction of positive walks between nodes i and j:

$${b}_{ij}(\beta )=\frac{1}{2}\left({r}_{ij}(\beta )+1\right)$$

(14)

Note that the cohesion index uses ${k}_{\min }=2$. This facilitates differentiating between frustrated and non-frustrated edges. If there are many positive walks between i and j, but i ~ j edge is negative, then the (i, j) pair generates many unbalanced closed walks and therefore the i ~ j edge should be considered a frustrated in-group tie rather than an out-group tie, and an analogous argument can be made for negative walks. Thus, direct links by themselves do not provide the evidence necessary for partitioning nodes and therefore should not be used for determining pairwise cohesion.

We use the same letters r and b we used to denote (local) balance measures for the sake of consistency as balance and cohesion are based on the same idea. Indeed, all balance scores can be seen as measures of “self-cohesion”. To see this, let us consider a cycle and a node i that sends a bit of information to its left neighbor, who passes it further to its left neighbor, and so on until the bit comes back to i. Moreover, let us assume that the bit is flipped when crossing negative edges. Now, it is easy to see that the bit will return to the original sender unchanged if and only if the cycle is balanced. In this sense, structural balance is measuring the consistency between sent and returning signals.

Cohesion measures are important because they allow to develop SBT-aware clustering methods. We leave a detailed study of this idea for future work. However, in what follows we combine them with standard agglomerative hierarchical clustering²⁷ (see “Methods: Hierarchical clustering with pairwise DoB measures” for details) to show that the MSB approach produces meaningful results and allows for detecting interpretable low frustration network partitions.

Weighted measures and β as average edge weight

Importantly, β can be interpreted in terms of an average edge weight. Any unweighted network can be seen as a weighted network with uniform absolute edge weights of 1. Note that in this case, the absolute product over a closed walk of any length is always equal to 1, so every walk is considered equal, and it is only β that controls and re-scales edge weights inducing nonuniform walk weights (through β^k scaling). Thus, a convenient way to handle non-unitary weights is to re-scale them, so the average absolute weight is equal to 1:

$${\omega }_{ij}^{{\prime} }=\frac{| E| {\omega }_{ij}}{{\sum }_{kl}| {\omega }_{kl}| }$$

(15)

where ω_ij is the original weight of the (i, j) edge and ∣E∣ is the number of edges.

This retains the interpretation of β in terms of an average edge weight and ensures that in a network with a completely uniformly random topology (i.e., Erdös-Rényi random graph with randomly and independently assigned signs and absolute weights) the expected absolute value of a walk weight (i.e., the product of the corresponding edge weights) gets fixed to 1 when β = 1. Results in the “Re-analysis of Sampson’s Monastery dataset” section suggest tentatively that this approach to incorporating edge weights may be indeed effective and produce better results than analogous unweighted methods (e.g., find partitions with lower frustration).

Directed measures

Here we extend all the previously defined measures to directed signed networks. To do so, we first note that the structure theorems of SBT in their most general form are formulated in terms of semipaths and semicycles (they are listed in “Methods: Overview of Structural Balance Theory”). Thus, our approach can be extended to directed networks by simply using semiwalks instead of ordinary walks.

Definition 2

(Semiwalk) A semiwalk is a sequence of adjacent edges such that for every two consecutive edges (i, j) and (k, l) it holds that k ∈ {i, j} or l ∈ {i, j}.

More intuitively, semiwalks are just ordinary walks ignoring edge directions⁶ or walks on an undirected multigraph derived from a given directed graph by making all edges bidirectional. Thus, semiwalks between all pairs of nodes in a graph G are counted by powers of its semiadjacency matrix, which is defined as the symmetric part of the adjacency matrix:

$${{{{{{{\bf{S}}}}}}}}({{{{{{{\bf{A}}}}}}}})=\frac{1}{2}\left({{{{{{{\bf{A}}}}}}}}+{{{{{{{{\bf{A}}}}}}}}}^{\top }\right)$$

(16)

Note that S is symmetric and S(A) = A when A is symmetric, which jointly means that S[S(A)] = S, so the semiadjacency operator is idempotent. In what follows, we will use a simpler notation without the explicit dependence on A and we will use S to denote S(A) and ∣S∣ to denote S(∣A∣).

Importantly, S is not a lossless representation of the adjacency matrix of the undirected multigraph underlying a given directed signed network, but it is lossy in a way that does not affect any balance-related calculations. First, reciprocal edges with opposite signs cancel each other out in S(A). However, this does not affect the difference between counts of positive and negative semiwalks, μ₊ − μ₋, since each symmetric dyad with opposite edge signs will be included in the same number of positive and negative semiwalks between i and j (Fig. 5). Second, the 1/2 factor means that S approximates the adjacency matrix of the multigraph divided by 2, but, again, this does not matter as in our approach edge weights are reweighted by the β parameter, which sets the average edge weight, anyway. The gain from using the 1/2 factor is that S is idempotent and equal to A for undirected graphs.

Fig. 5: Semiwalks in directed signed networks.

Positive and negative semiwalks passing through symmetric dyads with opposite edge signs cancel each other out. Positive ties are blue and negative red and dashed.

As a result, directed balance measures are obtained simply by substituting A with S and ∣A∣ with ∣S∣ in all the formulas. However, to account for the fact that 2-cycles in directed signed networks are not trivial (i.e., they may be both balanced and unbalanced), an additional correction is needed. As explained in “Results: Approximating (semi)cycles with closed (semi)walks”, asymmetric dyads do not span any 2-semicycles, while symmetric ones do. Thus, in the case of directed networks one needs to apply a correction to Eq. (4) to count proper 2-semicycles:

$$\overrightarrow{{{{{{{{\bf{W}}}}}}}}}({{{{{{{\bf{A}}}}}}}},\beta )=\frac{{\beta }^{2}}{2}{{{{{{{{\bf{A}}}}}}}}}^{2}+{{{{{{{\bf{W}}}}}}}}({{{{{{{\bf{S}}}}}}}},\beta )$$

(17)

where W still uses ${k}_{\min }=3$.

Re-analysis of Sampson’s Monastery dataset

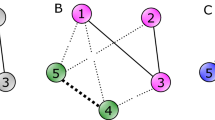
Sampson’s Monastery study²⁵ produced one of the most famous network datasets studied in Social Network Analysis (SNA) in general, and SBT in particular. It describes the evolution of the social structure in a group of postulants and novices in a monastery in New England in the 1960s. Namely, a network of liking (positive) and disliking (negative) relations was measured at five points in time. The ties are directed and weighted in the −3:3 range, with weights indicating the ordinal ranking of the preference toward or against a given person typical for sociometric studies (see “Methods: Sampson’s Monastery dataset” for details). The dataset is particularly valuable because, as the study was being conducted, the group went through a major conflict, which eventually led to either resignation or expulsion of the majority of the members of the congregation. Moreover, Sampson identified a partition into three groups, which later were independently validated with analytic SBT-motivated clustering methods², and therefore is commonly recognized as the “ground truth” solution.

The most important events happened at times t = 2, 3, 4, which correspond to a period of differentiation and polarization² that eventually led to an open conflict and disintegration of the group. At t = 2, 12 new members joined the monastery, while some older members left after t = 1, so the new group consisted of 18 men in total. This perturbation led to the emergence of two competing groups (Loyal Opposition and Young Turks) as well as a group of peripheral members, who were not fully accepted by the rest (Outcasts). The network at time t = 4 depicts the structure just before the open conflict and disintegration. At t = 5, only 7 members remained in the monastery, and those who stayed (they are marked with red labels in Fig. 6c, t = 4) belonged almost exclusively to the Loyal Opposition, which clearly “won” the conflict.

Fig. 6: Re-analysis of Sampson’s Monastery networks using Multiscale Semiwalk Balance (MSB) approach.

Full spectra were used in computations (exact results). a Signed sociograms at times t = 2, 3, 4. Left side colors denote block membership according to the “ground truth” partition and right side colors correspond to MSB partitions. Positive ties are blue and negative are red. Individuals whose “ground truth” and MSB block memberships differ (Amand, Basil and John Bosco) as well as the leaders of Young Turks (John Bosco and Gregory) are labeled. Network layout was determined with the Kamada-Kawai algorithm using only positive ties with weights (distances) on cross-block ties rescaled by a factor of 5. b Time series of strong and weak Degree of Balance (DoB) measures for t = 1, …, 5 using MSB, denoted by $B({\beta }_{\max })$ and $W({\beta }_{\max })$ respectively, as well as strong DoB based on the Walk Balance (WB) approach of Estrada and Benzi⁴, which is equivalent to MSB approach with β = 1 using ordinary adjacency matrix (denoted by B(1)). c Weak local balance expressed as z-scores relative to the overall distribution. Points are sized proportionally to local contributions and ordered first by block membership and then by balance scores. Members who remained at the monastery after the culmination of the conflict (t = 5) are marked with red labels on the subplot for t = 4. d Time series of frustration ratios for t = 1, …, 5 according to partitions obtained with MSB and WB (β = 1) approaches as well as the “ground truth” solution (which is defined only for times t = 2, 3, 4). ${F}_{{{{{{{{\rm{MSB}}}}}}}}}^{U}$ denotes frustration values using the unweighted MSB approach.

Here we use the MSB approach to demonstrate that the “ground truth” partition is not SBT-optimal, or maximally consistent with Theorem 4. This can be measured using the frustration ratio, F(B). Figure 6a shows both the “ground truth” and the MSB network partitions for times t = 2, 3, 4 (see “Methods: Hierarchical clustering with pairwise DoB measures” for details of the clustering method). They differ only in a few details, which are, nonetheless, very informative about the unfolding dynamics. First, according to the “ground truth” partition, Basil was a member of the Outcasts. However, MSB analysis indicates that initially (t = 2) he interacted mostly with the Young Turks and only later was rejected and became one of the Outcasts. Second, Amand, a member of the Loyal Opposition according to the “ground truth”, was consistently identified as one of the Outcasts by our MSB clustering procedure. Most importantly, according to MSB, John Bosco, who was considered one of the two leaders of the Young Turks (the second one was Gregory), became one of the Outcasts just before the disintegration of the monastery (t = 4). This says a lot about why the Young Turks “lost” the competition against the Loyal Opposition, of which core constituted most of the group that remained at the monastery.

As evident in Fig. 6c, the local weak balance scores of John Bosco were consistently low and at time t = 4 also Gregory, the second leader, attained low local balance (see “Methods: Weak balance” for the details of the weak balance measures). This was largely driven by the tension in their personal relationship (at t = 4 the Gregory → John Bosco tie is positive and John Bosco → Gregory is negative), which then propagated through the entire group (note that both of them had high local contribution scores, Fig. 6c) leading, probably, to its decomposition. As Fig. 6a shows, over time John Bosco established more positive connections with Outcasts and developed negative feelings toward Gregory. At the same time, the core of Loyal Opposition strengthened internal connections and became very cohesive at time t = 4, as indicated by the high weak local balance scores of most of the individuals with red labels in Fig. 6c.

Importantly, MSB measures of DoB (Fig. 6b) are clearly high during the evolution of the conflict (t = 2, 3, 4), with the maximum at t = 4, while analogous WP measures, which are not based on LP, yielded markedly lower DoB values that cannot be readily interpreted as indicative of a conflict, as they are not much greater than 1/2 (which can be expected for a random assignment of edge signs). Similarly, frustration values (Fig. 6d) obtained with MSB clustering are consistently lower than those of the “ground truth” partition, and at times t = 1, 2, 3, 4 is also lower than the ones obtained using WB. On the other hand, frustration ratios obtained when ignoring edge weights (${F}_{{{{{{{{\rm{MSB}}}}}}}}}^{U}$) are markedly higher, indicating that our approach uses edge weight information effectively leading to better results, i.e., partitions with lower frustration.

Thus, the analysis indicates that MSB can produce useful and interpretable results, including finding low frustration partitions of signed networks. Moreover, by combining global and local measures applied to time series of network snapshots, insights into the impact of microscopic changes (e.g., edge sign switching) on the meso- and macroscopic structure can be gained.

Polarization in the U.S. Congress

It is often claimed that political life in contemporary democracies has polarized significantly over the last few decades. Arguably, this debate is particularly relevant for the U.S., because of its largely two-party political system, for which the notion of (bi)polarization is particularly well-defined. Such a hypothesis is also supported by a lot of empirical evidence (cf. refs. ^9,28 and references therein).

Here we use the MSB approach to study polarization in both chambers of the U.S. Congress based on patterns of bill co-sponsorship between 1973 and 2016 (93rd to 114th Congress)⁹. The dataset consists of two sequences of undirected signed networks inferred from co-sponsorship data, where positive ties indicate a statistically significant tendency of two representatives/senators to promote the same bills and negative ties the opposite tendency to avoid promoting the same projects (see “Methods: Co-sponsorship relations in the U.S. Congress” for details).

Our analysis indicates that polarization increased markedly in both the House of Representatives. This is evident in the steadily increasing strong DoB values (Fig. 7a) meaning that co-sponsorship networks became easier to bipartition in time. The increasing trend seems to materialize during the second Congress of Carter’s administration and be stable, notwithstanding some transient perturbations. Interestingly, and consistently with our previous analysis of the importance of the Locality Principle, the WB approach yielded almost exclusively very low DoB values, and thus would not capture the true trend. This is, of course, the consequence of the violation of LP.

Fig. 7: Polarization in the U.S. Congress between 93rd and 114th Congress (1973–2016).

Panels are divided into regions corresponding to subsequent White House administrations with colors denoting Republican (red) and Democratic (blue) presidents. Approximations based on m = 10 leading eigenpairs from both ends of the spectrum were used. All results are reported for both the House of Representatives and the Senate. a Degree of Balance time series based on the Multiscale Semiwalk Balance approach, $B({\beta }_{\max })$, and Walk Balance of Estrada and Benzi⁴, B(1). b Frustration ratios computed for best partitions into 2 clusters, F(2), general partitions into k clusters, F(B), and partitions based on partisan affiliations, F(P). c Similarity between party-based partitions and best bipartitions, AMI(2, P), as well as best partitions into k clusters, AMI(B, P), using Adjusted Mutual Information (AMI) score²⁹. The closer a value is to 1, the better the match between two clustering solutions. d Numbers of clusters in the solutions minimizing F(B) (left y-axis), as well as the fraction of nodes within the two largest clusters (right y-axis).

In both chambers frustration ratios clearly converge (Fig. 7b) meaning that best bipartitions and clusterings (in k groups) based on the MSB approach (“Methods: Hierarchical clustering with pairwise DoB measures”), as well as partitions following partisan affiliations are becoming more and more consistent with the SBT theorems and therefore also similar. This is evident in the time series of the similarity between MSB and partisan partitions measured with Adjusted Mutual Information (AMI) score²⁹ (Fig. 7c). Moreover, even in k-clusterings with k large, most of the nodes tend to belong to the two largest clusters, indicating, again, an increasingly bipolar structure organized along the party lines. Note that even in the extreme case of the House of Representatives during the 96th Congress (the second congress of Carter’s administration), where we found 147 distinct “clusters”, 271 or around 61% of the representatives belong to the two largest blocks, meaning that the rest of the clusters correspond to the other 171 representatives, for whom the average cluster size was about 1.18. Thus, in this period many members of the congress were effectively functioning in-between the two main blocks, and from the perspective of the clustering procedure, they were outliers forming many small clusters, very often composed of only one node. This result is consistent with the fact that this was a period of the lowest polarization, for which the partisan cleavage should not be very pronounced.

To sum up, the results point to a strong consistency between global DoB measures and the quality of optimal partitions. Namely, the higher the DoB the lower the frustration of optimal partitions found by our clustering algorithm. Moreover, the fact that in time all empirical partitions become more and more similar to the partisan affiliations and the majority of nodes always belong to the two largest clusters jointly means that the MSB partitions we obtained are meaningful and consistent with the partisan polarization hypothesis. In other words, we indeed find that in time it becomes easier to find low frustration network partitions that largely overlap with partisan affiliations. Thus, the patterns of cooperation between the senators and representatives become more and more constrained by their party membership.

Discussion

Polarization is often considered a salient, and perhaps worrying, feature of contemporary societies^8,9,28,30. It can result in a sharp divergence of popular beliefs or attitudes (ideological polarization) as well as in-group favoritism and out-group hostility (affective polarization)²⁸. Crucially, the latter implies clustering of social networks into 2 or more groups with primarily positive in-group and negative out-group ties. This structural aspect of polarization is studied in Structural Balance Theory (SBT), which links it to properties of semicycles in signed networks and provides strict criteria for measuring polarization^13,16.

Here we introduced the Multiscale Semiwalk Balance (MSB) approach for measuring both strong and weak degrees of balance (DoB), which is applicable to any kind of (simple) signed networks, including directed and weighted ones. MSB is computationally efficient by approximating semicycles with semiwalks, which can be counted using standard linear algebra, and defines DoB measures not only for entire graphs but also specific nodes and pairs of nodes, which in turn allows for implementing effective signed community detection methods motivated by SBT. Crucially, MSB is multiscale in the three following senses:

• 1. It proposes a principled way of aggregating multiple k-balance scores for particular cycle lengths to produce a single global DoB estimate motivated by the Locality Principle (LP). The resolution of analysis, or the weighting scheme for aggregating k-balance scores, is controlled by a single parameter, β, which can be tuned based on first principles to capture the characteristic scale of a network at which its DoB should be assessed. This is a crucial feature of our framework, as even though many other approaches apply some decaying weights to longer cycles, typically the decay rate is fixed or controlled by a free parameter with no principled way of selecting an appropriate value^4,5,17,19,22.

• 2. It provides methods for measuring strong and weak DoB for entire graphs, closed walks of particular lengths, individual nodes and pairs of nodes.

• 3. Thanks to the pairwise measures it facilitates the development of methods for finding mesoscopic structures in signed networks, i.e., clusters or groups of nodes with primarily positive in-group and negative out-group ties.

Unlike many other approaches to SBT^4,5,22, MSB is formulated explicitly in terms of semiwalks as an approximation to semipaths and semicycles. This connects it more directly to the structure theorems^13,16, and as a result, facilitates meaningful analyses of directed networks. Crucially, semiwalk-based k-balance scores tend to be similar to values produced by cycle-based k-balance measures introduced by Giscard et al.¹⁹ (see “Methods: Accuracy of semiwalk-based approximations” for details). Thus, the fundamental approximation on which our approach is based seems to introduce little extra noise relative to cycle-based measures. Similarly, the error introduced by using only leading eigenvalues and eigenvectors is also typically very small (Supplementary Note 3). On the other hand, being based on (semi)walks that can be counted easily using standard linear algebra, MSB computations can be remarkably fast (Supplementary Note 5).

Furthermore, there are also theoretical reasons for preferring walk-based over cycle-based DoB measures. First, let us note that in a signed graph all cycles are balanced if and only if all closed walks are balanced, so for measuring perfect structural balance walk- and cycle-based DoB measures are equivalent. Furthermore, in opinion dynamics (diffusion) on a signed graph two groups can reach different consensus states if and only if the graph is balanced, but the diffusion process depends not only on purely cyclic structures but also on acyclic ones, as well as “artificial cycles” produced by backtracking walks²⁴. Thus, it can be argued that partial DoB measures defined in terms of (semi)walks paint a fuller picture of structural balance, especially as far as the interplay between network structure and diffusion dynamics is considered.

Thus, our perspective is different from other works on the multilevel assessment of structural balance³¹, which are focused exclusively on strong balance, and in which microlevel DoB analysis is equated with the triad-level DoB, mesolevel with the cohesiveness of the network partitions as such (which is fully compatible with our framework), and finally, macrolevel is equated with the line index (or frustration index), but computed only for partitions into two groups. Furthermore, our approach tries to follow the structure theorems of SBT as closely as possible given its approximate walk-based nature. Directed MSB measures are based on semiwalks, and thus they ignore edge directions, except for the special case of dyads (2-cycles), in which directions of both edges are considered (this is accounted for by corrections defined in Eqs. (17) and (20)). This design choice follows directly from the fact that SBT was formulated in terms of semicycles, which are simply cycles in which edge directions are ignored as long as each edge is traversed at most once. On the other hand, other directed approaches³¹ often use edge direction information in a more complex fashion, which, of course, may be insightful but is not necessary from the vantage point of SBT theorems and the problem of network partitioning.

Locality Principle is justified not only by its usefulness as a heuristic guiding DoB methods, but also by a long history of social and psychological research. In particular, experimental research on the perception of structural balance in social networks indicates that people pay more attention to small-scale structures¹⁸. This is in line with other seminal results stressing the importance of proximity (both physical and social) for social phenomena such as social impact theory³² and Dunbar’s numbers³³, which are closely related to the fact that social networks tend to be sparse and composed of ties that are localized within some physical and/or social space³⁴. Moreover, studies of structural balance using alternative cycle-based methods show that real-world networks tend to have a cycle length threshold after which k-balance scores suddenly decrease to random-like values (around 0.5)¹⁹. In other words, structural balance typically manifests itself at the level of small- and medium-sized structures, so DoB measures should account for that. This is exactly what LP does.

Importantly, β can be endowed with a physical interpretation, which helps to explain its role as a resolution parameter. Note that the cohesion index defined in Eq. (13), from which all other MSB measures may be derived, can be approximated by a ratio of elements of two matrix exponentials, ${r}_{ij}(\beta )\approx {({e}^{\beta {{{{{{{\bf{A}}}}}}}}})}_{ij}/{({e}^{\beta | {{{{{{{\bf{A}}}}}}}}| })}_{ij}$, and the exponential of a rescaled adjacency matrix, such as βA, is known as communicability, which is a general measure of connectedness defined in terms of the weighted sums of walks of different lengths between pairs of nodes³⁵. In this context, β can be interpreted as the inverse temperature of a thermal bath in which a network is submerged. More generally, the thermal bath may represent an “external situation”, e.g., the level of agitation of the system, which manifests itself by rescaling edge weights with the β factor. As a result, when β → 0 (hot regime), there is no communicability between nodes, and when β → ∞ (cold regime), then there is infinite communicability between all pairs of nodes³⁶. Note that in both cases the actual network topology ceases to matter. Thus, network structure is accounted for in DoB calculations only for appropriately chosen intermediate values of β, and in this context, LP provides an effective heuristic for fine-tuning β and finding the most relevant range of cycle lengths at which DoB should be assessed.

This stresses the importance of multiscale approaches to SBT and network science more generally. By linking structural balance to communicability^35,36, our results suggest that, perhaps, other network descriptors defined in terms of walks, or powers of adjacency matrices, such as multiscale network entanglement³⁷, can be informed by the Locality Principle. Note that contribution scores defined in Eq. (11), and used for operationalizing LP, can be calculated for any, also unsigned, network. Thus, LP is a heuristic for determining the characteristic intensity and length of internode correlations, and this determines the appropriate weighting scheme for aggregating walk-based measures across multiple scales. More generally, our results also contribute to the research on the importance of local structures in networks^38,39,40.

Our work, of course, does not come without limitations. First, even though cohesion measures are defined in Eqs. (13) and (14) seem to open up new possibilities for designing clustering or community detection methods for signed networks, the actual clustering algorithm we used here is rather naive. Developing more mature methods derived from first principles will not be an easy task and we leave it for future work. Moreover, it can be argued that an even better approach for tuning β could be based on setting it to a value that minimizes the frustration of the best partition. However, a proper solution to this problem would require a solid theory-driven clustering method parametrized by β, which we do not currently have, so the choice $\beta := {\beta }_{\max }$ should be considered the best working heuristic for selecting an optimal value for β for now, but it should be replaced with more mature solutions as they arrive. Furthermore, even though some in-depth insights regarding similarities and differences between cycle- and walk-based DoB measures vis-à-vis the tenets of SBT have been offered by Estrada²⁴, one can argue that the debate on whether the former or the latter should be preferred is not yet settled. Perhaps, an interesting “middle ground” perspective could be gained by studying DoB measures based on non-backtracking (Hashimoto) matrices⁴¹?

Methods

Overview of Structural Balance Theory

Here we state the main definitions and theorems of SBT concerned with bi-clusterability as formulated by Cartwright and Harrary¹³. We use the general formulation based on semipaths and semicycles, so the theorems are applicable to both undirected and directed graphs. Thus, we first define semipaths and semicycles.

Definition 3

(Semipath) A semipath is a walk in which each (directed) edge can be traversed both ways but only once and each node is visited exactly once.

Definition 4

(Semicycle) A semipath starting and ending at the same node (which in this case is allowed to appear twice).

Corollary

Notions of paths/cycles and semipaths/semicycles are equivalent in undirected graphs since an undirected edge is treated in this context as two directed edges pointing in opposite directions.

Definition 5

(Strong balance property) A signed graph is balanced if and only if every semicycle it contains is positive (the product over all edge signs is positive).

Theorem 3

(Strong structure theorem) A signed graph is balanced if and only if its vertices can be partitioned into two subsets such that positive edges connect vertices from the same subset and negative ones link vertices from different subsets.

The above results were later generalized by Davis¹⁶, who provided necessary and sufficient conditions for b-clusterability (where b ≥ 2 is an unknown integer).

Definition 6

(Weak balance property) A signed graph is weakly balanced if and only if no semicycle contains exactly one negative edge.

Theorem 4

(Weak structure theorem) A signed graph is weakly balanced if and only if its vertices can be partitioned into b subsets such that positive edges connect vertices from the same subset and negative ones link vertices from different subsets.

Weak balance

Following Kirkley et al.⁵, we define non-negative matrices P(A) and N(A) corresponding to positive and negative parts of the signed adjacency matrix such that A = P − N and ∣A∣ = P + N. In what follows we will use the simpler notation without the explicit dependence on A, but it is important to remember that P and N are functions of A.

Weak balance is defined in terms of the extent to which a network is free of cycles with exactly one negative edge. This single negative link can be placed anywhere along a path starting at node i. Hence, we first define a matrix counting weakly unbalanced walks of length k between nodes i and j in a signed graph G as:

$${{{{{{{{\bf{V}}}}}}}}}_{k}({{{{{{{\bf{A}}}}}}}}) =\mathop{\sum }\limits_{l=1}^{k}{{{{{{{{\bf{P}}}}}}}}}^{l-1}{{{{{{{{\bf{NP}}}}}}}}}^{k-l}\\ =\mathop{\sum }\limits_{l=1}^{k}{{{{{{{\bf{Q}}}}}}}}{{{{{{{{\boldsymbol{\Lambda }}}}}}}}}^{l-1}{{{{{{{{\bf{Q}}}}}}}}}^{\top }{{{{{{{\bf{NQ}}}}}}}}{{{{{{{{\boldsymbol{\Lambda }}}}}}}}}^{k-l}{{{{{{{{\bf{Q}}}}}}}}}^{\top }\\ ={{{{{{{\bf{Q}}}}}}}}\left[\left(\mathop{\sum }\limits_{l=1}^{k}{{{{{{{\bf{L}}}}}}}}(k,l)\right)\odot {{{{{{{\bf{M}}}}}}}}\right]{{{{{{{{\bf{Q}}}}}}}}}^{\top }$$

(18)

where QΛQ^⊤ is the eigendecomposition of P, M is a shorthand for the product Q^⊤NQ that appears in the middle of the second line, and ${{{{{{{\bf{L}}}}}}}}{(k,l)}_{ij}={\lambda }_{i}^{l-1}{\lambda }_{j}^{k-l}$. Moreover, we used the fact that Λ^l−1MΛ^k−l = L(k, l) ⊙ M.

Now, a matrix with weighted sums of counts of walks of lengths $k={k}_{\min },\ldots ,{k}_{\max }$ joining nodes i and j is given by:

$${{{{{{{\bf{V}}}}}}}}({{{{{{{\bf{A}}}}}}}},\beta ) =\mathop{\sum}\limits_{k}\frac{{\beta }^{k}}{k!}{{{{{{{{\bf{V}}}}}}}}}_{k}({{{{{{{\bf{A}}}}}}}})\\ ={{{{{{{\bf{Q}}}}}}}}\left\{\left[\mathop{\sum}\limits_{k}\frac{{\beta }^{k}}{k!}\mathop{\sum }\limits_{l=1}^{k}{{{{{{{\bf{L}}}}}}}}(k,l)\right]\odot {{{{{{{\bf{M}}}}}}}}\right\}{{{{{{{{\bf{Q}}}}}}}}}^{\top }$$

(19)

In the directed case we also apply the correction discussed in “Results: Directed measures” leading to:

$$\overrightarrow{{{{{{{{\bf{V}}}}}}}}}({{{{{{{\bf{A}}}}}}}},\beta )=\frac{{\beta }^{2}}{2}\left({{{{{{{\bf{PN}}}}}}}}+{{{{{{{\bf{NP}}}}}}}}\right)+{{{{{{{\bf{V}}}}}}}}({{{{{{{\bf{S}}}}}}}},\beta )$$

(20)

Next, we can use Eq. (19) to calculate the overall weighted sums of counts of unbalanced closed walks from appropriate traces:

$${{{{{{{\rm{tr}}}}}}}}{{{{{{{\bf{V}}}}}}}}({{{{{{{\bf{A}}}}}}}},\beta )=\mathop{\sum}\limits_{k}\frac{{\beta }^{k}}{k!}{{{{{{{\rm{tr}}}}}}}}{{{{{{{{\bf{V}}}}}}}}}_{k}({{{{{{{\bf{A}}}}}}}})$$

(21)

$${{{{{{{\rm{tr}}}}}}}}{{{{{{{{\bf{V}}}}}}}}}_{k}({{{{{{{\bf{A}}}}}}}})=k\mathop{\sum }\limits_{i=1}^{m}{\lambda }_{i}^{k-1}{{{{{{{{\bf{M}}}}}}}}}_{ii}$$

(22)

where we used the fact that trace is invariant under cyclic permutations and Q is orthonormal. The weighted sum of counts of closed walks at a node i is similarly given by the diagonal elements, V(A, β)_ii.

Now, Eqs. (4) and (21) can be used to define the measure of the overall weak balance:

$$W(\beta )=1-\frac{{\mu }_{W}}{{\mu }_{+}+{\mu }_{-}}=1-\frac{{{{{{{{\rm{tr}}}}}}}}{{{{{{{\bf{V}}}}}}}}({{{{{{{\bf{A}}}}}}}},\beta )}{{{{{{{{\rm{tr}}}}}}}}{{{{{{{\bf{W}}}}}}}}(| {{{{{{{\bf{A}}}}}}}}| ,\beta )}$$

(23)

where μ_W is the sum of weighted counts of weakly unbalanced closed walks. Weak pairwise cohesion scores are given by ratios of individual matrix elements:

$${w}_{ij}(\beta )=1-\frac{{{{{{{{\bf{V}}}}}}}}{({{{{{{{\bf{A}}}}}}}},\beta ;{k}_{\min } = 2)}_{ij}}{{{{{{{{\bf{W}}}}}}}}{(| {{{{{{{\bf{A}}}}}}}}| ,\beta ,{k}_{\min } = 2)}_{ij}}$$

(24)

with local (node-level) weak DoB given by the diagonal elements, ${w}_{ii}(\beta ;{k}_{\min }=3)$. Similarly, weak k-balance is given by considering only closed walks of a particular length k:

$${W}_{k}=1-\frac{{{{{{{{\rm{tr}}}}}}}}{{{{{{{{\bf{V}}}}}}}}}_{k}({{{{{{{\bf{A}}}}}}}})}{{{{{{{{\rm{tr}}}}}}}}| {{{{{{{\bf{A}}}}}}}}{| }^{k}}$$

(25)

Importantly, as in the case of strong balance, global weak DoB can be expressed as a weighted average of weak k-balance with weights given by the corresponding contribution scores (see Supplementary Note 2 for the proof).

Last but not least, the trace of the matrix series defined in Eq. (19) used for counting unbalanced closed walks always converges, so it is well-defined. Note that:

$$0\le \mathop{\sum}\limits_{k}\frac{{\beta }^{k}}{k!}\mathop{\sum }\limits_{l=1}^{k}{{{{{{{\rm{tr}}}}}}}}{{{{{{{{\bf{P}}}}}}}}}^{l-1}{{{{{{{\bf{N}}}}}}}}{{{{{{{{\bf{P}}}}}}}}}^{k-l}\le \mathop{\sum }\limits_{k=0}^{\infty }\frac{{\beta }^{k}}{k!}{{{{{{{\rm{tr}}}}}}}}{\left({{{{{{{\bf{P}}}}}}}}+{{{{{{{\bf{N}}}}}}}}\right)}^{k}={{{{{{{\rm{tr}}}}}}}}{e}^{\beta | {{{{{{{\bf{A}}}}}}}}| }$$

(26)

where it is known that the rightmost matrix exponential and its trace always converge, so the middle part of the inequality must converge too.

Hierarchical clustering with pairwise DoB measures

Here we will use the following naive, yet effective, clustering procedure for signed networks based on pairwise cohesion measures (see “Results: Pairwise cohesion and clustering” and “Methods: Weak balance”). Let ${{{{{{{{\bf{D}}}}}}}}}_{ij}^{S}=1-{b}_{ij}({\beta }_{\max })$ and ${{{{{{{{\bf{D}}}}}}}}}_{ij}^{W}=1-{w}_{ij}({\beta }_{\max })$ be pairwise dissimilarity matrices (so ${{{{{{{{\bf{D}}}}}}}}}_{ii}^{S}={{{{{{{{\bf{D}}}}}}}}}_{ii}^{W}:= 0$) based on the notions of strong and weak balance respectively, and let N_b be the maximum number of clusters one is willing to consider. Then, for b = 1, …, N_b:

• 1. Run Hierarchical Clustering (HC)²⁷ algorithm for b clusters using D^S as input and calculate frustration index according to Eq. (3) for the obtained block-partition matrix B.

• 2. Run HC for b clusters using D^W as input and calculate the corresponding frustration index.

• 3. Store the lower of the two frustration indices and its corresponding block partition.

Finally, choose the partition with the lowest frustration index.

Accuracy of semiwalk-based approximations

MSB approach approximates semicycles with closed semiwalks. This is a fundamental design decision ensuring high computational efficiency, but it comes at the price of introducing a discrepancy relative to cycle-based methods. Here we present a comparison of k-balance methods provided by MSB and the cycle-based approach of Giscard et al.¹⁹ based on several small and mid-sized networks. The results indicate a strong similarity between the walk-based and the cycle-based DoB estimates (Fig. 8). Thus, it seems that the error introduced by walk-based approximations relative to cycle-based estimates is typically small. This should not come as a surprise as, thanks to the Locality Principle, our MSB approach ensures that DoB measures are driven primarily by patterns found in short closed walks, which coincide with cycles much more often than long walks (e.g., closed walks of length 3 are equivalent to 3-cycles).

Fig. 8: Accuracy of semiwalk-based approximations relative to cycle-based Degree of Balance (DoB) estimates.

Cycle-based DoB scores were computed using methods from ref. ¹⁹, and congruence was assessed based on Pearson correlation coefficients, r, and relative error $\bar{\epsilon }=\left\langle \left\vert \frac{x-y}{y}\right\vert \right\rangle$. a “Grayscale” (k-balance) measures based on semiwalks (MSB) and proper cycles in small networks studied in this paper (see “Methods: New Guinea Highlands tribes” and “Sampson’s Monastery dataset”). In this case, DoB values are reported for all possible cycle lengths and both MSB and cycle-based estimates are exact. b Pearson correlations and relative errors for different cycle lengths calculated over co-sponsorship networks from the U.S. Congress (“Methods: Co-sponsorship relations in the U.S. Congress”). In this case, MSB approximations are based on m = 10 leading eigenvalues, and cycle-based estimates are approximated using sampling based on 10,000 samples. Only cycles of length up to 15 were considered.

Numerical approximations and efficiency

All computations of MSB can be implemented in a computationally efficient and accurate manner using approximations based on m leading eigenvalues and eigenvectors from both ends of the spectrum. Leading eigenpairs can be found very efficiently using modern linear algebra routines such as implicitly restarted Arnoldi method^42,43. Moreover, numerical stability can be guaranteed by conducting all computations in the log-space and using log-sum-exp trick (to avoid overflow when counting closed walks). This requires a bit of extra care as some eigenvalues may be non-positive. However, zero eigenvalues can be ignored altogether, since no measure defined here depends on the zeroth powers of adjacency matrices, so the calculations can be done over the field of complex numbers, where the logarithm of any number with non-zero modulus is well-defined, and cast back to real values only at the very end. As a result, MSB methods can be remarkably efficient, even when applied to very large systems. Supplementary Notes 3 and 5 present empirical analyses of the accuracy and efficiency of our implementation. Supplementary Note 4 discusses the theoretical basis for approximations based on leading eigenvalues and eigenvectors.

A more in-depth discussion of implementation details is beyond the scope of this paper, but we invite the interested reader to study our source code (see: Code availability).

Network datasets

New Guinea Highlands tribes

An undirected unweighted signed network of friendships among tribes of the Gahuku-Gama alliance structure of the Eastern Central Highlands region in New Guinea⁴⁴. Edge sign indicates either friendship or enmity. Accessed from: https://networks.skewed.de/net/new_guinea_tribes.

Epinions trust network

This is a who-trust-whom online social network (directed, unweighted and signed) of a general consumer review site Epinions.com. Members of the site can decide whether to “trust” each other. All the trust relationships interact and form the Web of Trust which is then combined with review ratings to determine which reviews are shown to the user⁴⁵. Accessed from: https://snap.stanford.edu/data/soc-Epinions1.html.

Wikipedia adminship vote

A directed unweighted signed network of votes on Request for Adminship (RfA) elections from a 2008 snapshot of Wikipedia⁴⁶. Nodes represent editors, and a directed edge (i, j) indicates that editor i voted on editor j. Edge sign indicates the direction of the vote: positive = for, and negative = against. Edges are timestamped. Accessed from: https://networks.skewed.de/net/elec.

Slashdot Zoo network

A directed unweighted signed network of interactions among users on Slashdot (slashdot.org), a technology news website⁴⁷. Users name each other as friends (positive tie) or foe (negative tie). The friend label increases the scores of post, and the foe label decreases the score. Accessed from: https://networks.skewed.de/net/slashdot_zoo.

Sampson’s Monastery dataset

Time series of 5 signed directed weighted networks measuring positive and negative relations between postulants and novices in a New England monastery in 1960s²⁵. We used a version of the dataset studied in ref. ² in which edges have weights between −3 and 3 corresponding to the ranking of the least and most (dis)liked/(dis)esteemed colleagues. Accessed from: http://vlado.fmf.uni-lj.si/pub/networks/data/esna/sampson.htm.

Co-sponsorship relations in the U.S. Congress

Series of undirected unweighted signed networks inferred from the data on bill co-sponsorships in both chambers of the U.S. Congress (House of Representatives and Senate) using Stochastic Degree Sequence Model^9,48. The data covers the period from 1973 (93rd Congress) to 2016 (114th Congress). Edges are signed, indicating the presence of a significant tendency to co-sponsor, or tendency to not co-sponsor, bills. See Supplementary Table 1 for descriptive statistics. Accessed from: https://figshare.com/articles/dataset/A_Sign_of_the_Times/8096429.