Introduction

Mn3Sn is a noncollinear antiferromagnet (AF) and a Weyl semimetal (WSM). It crystallises in a hexagonal P63/mmc structure. Below the Néel temperature (TN ≈ 420 K for bulk Mn3Sn1) the geometrical frustration of the Mn atoms in the a–b plane of the Kagome lattice leads to an inverse triangular spin structure, with 120° ordering1,2,3,4,5. Despite a vanishingly small net magnetisation, Mn3Sn displays phenomena that conventionally occur in ferromagnets, such as a large anomalous Hall effect6,7,8, anomalous Nernst effect9, and magneto-optical Kerr effect10. This is possible due to the unique material topology and a nonzero Berry curvature resulting from the inverse triangular spin structure1,8. Ab-initio band structure calculations have reported the existence of multiple Weyl points in the bulk and corresponding Fermi arcs on the surface of Mn3Sn3. An effect associated with WSMs is the presence of helicity-dependent photocurrents arising from non-linear optical effects. These have been observed using both electrical and THz techniques11, and have been linked to the topological charge of the Weyl nodes12, via the circular photogalvanic effect.

In this work, we present the observation of helicity-dependent ultrafast photocurrents in an 80 nm Mn3Sn film at room temperature (RT) using optical pump-THz emisison spectroscopy. The experimental results obtained at different measurement geometries, temperatures, and external magnetic fields are cross-examined with theoretical predictions, allowing us to carefully verify specific mechanisms responsible for the generation of ultrafast photocurrents.

The magnitude and direction of the photocurrents depend on the polarisation of the pump pulse and the direction of its wavevector relative to the surface of the film, but have no dependence on magnetic field. These currents cannot be attributed to a bulk photogalvanic effect as this requires the breaking of inversion symmetry13. Mn3Sn, however, respects inversion symmetry even when accounting for the magnetic ordering. This suggests that our signal originates either from a different bulk mechanism such as the inverse spin Hall effect14 or photon-drag effect15,16, or from a surface photogalvanic effect17. Our symmetry analysis of response tensors suggests that the helicity-dependent photocurrents arise predominantly due to the circular photon drag effect.

Results

Experimental layout

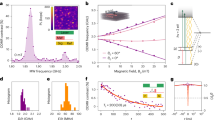
The subject of the study is an MgO(111)(0.5 mm)/Ru(5 nm)/Mn3Sn(80 nm)/Si(3 nm) sample. In Fig. 1a, we show the optical pump-THz emission geometries used in our experiments. When presenting a data set we will refer to the experiment geometry in which this data was collected as configuration 1, 2 or 3. To indicate different directions we introduce two Cartesian coordinate systems, also indicated in Fig. 1(a): (x, y, z)—fixed with respect to the experimental setup; (a, b, c)—fixed with respect to the sample. Laser pulses of 50 fs duration with a central wavelength of 800 nm propagate along the z-axis. A quarter-wave plate (QWP) placed in the pump path is used to control the polarisation and helicity of the pulses. In-plane rotations of the QWP by an angle φ allow changing between linear (φ = 0° ± nπ/2), left-handed circular (LHCP) (φ = 45° ± nπ), right-handed circular (RHCP) (φ = − 45° ± nπ), and intermediate elliptical polarisations. The angle between the laser beam and the sample surface can be varied by rotating the sample away from normal incidence about the x-axis (configuration 2) or y-axis (configuration 3). We define the tilting angles as θx and θy respectively. Additionally, the sample can be rotated in-plane, about the c-axis by an angle defined as θc. An external magnetic field up to μ0Hx ≈ 860 mT can be applied along the x direction. Unless stated otherwise, the experiments presented in the main body of the paper were performed at room temperature (RT).

Fig. 1: Optical pump-THz emission from Mn3Sn.
figure 1

a Experiment schemes in different geometries. Ultrafast laser pulses travelling along z-axis are incident on the sample, leading to the emission of broadband THz electro-dipole emission si(t) with integrated peak amplitude Si. In the experiments, we resolve the two orthogonal components of the transient THz signals: sx(t) and sy(t). θx, θy and θz label the rotation angles around the x, y and z axis respectively. Configuration 1 corresponds to a measurement in the standard geometry with normal laser incidence, in which θx = 0 and θy = 0. In configuration 2 and configuration 3 the sample is rotated about the x (θx ≠ 0 and θy = 0) or y (θx = 0 and θy ≠ 0) axes respectively. Please note that the scheme of configuration 2 is presented in a different perspective than configuration 1 and 3. b shows THz signals detected along y, emitted from Mn3Sn optically pumped with laser pulses of different polarisations. The measurements were performed in configuration 1 without an external magnetic field. The experimental data set is fitted with function introduced in Eq. (1) to find Hy, Ly, and By. Here, \({H}_{i}(\varphi )={h}_{i}\sin (2\varphi +{\varphi }_{1})\) is the magnitude of the circular polarisation helicity-dependent component with a phase shift \({\varphi }_{1},{L}_{i}(\varphi )={l}_{i}\sin (4\varphi +{\varphi }_{2})\) is the linear polarisation-dependent component with a phase shift φ2, and Bi is the polarisation-independent background component. These are presented in (c) with the extracted values of the amplitudes ∣hy∣, ∣ly∣, and By.

Full size image

THz emission from Mn3Sn

The optically induced charge currents Ji(t) result in broadband THz electro-dipole emission si(t). The subscript i indicates the polarisation components i = x or i = y, along the two axes of the experimental setup x and y. As shown in Fig. S2 in Supplementary Note 2, THz transients detected from the Mn3Sn sample switch the polarity upon changing the pump helicity from RHCP (right-hand circular polarisation) to LHCP (left-hand circular polarisation). This behaviour indicates the presence of pump-polarisation-dependent photocurrent generation mechanisms.

We define Si as the integrated peak amplitude of the emitted THz pulse (we refer the reader to Fig. S2, S3 and S4 in Supplementary Notes 2 to 4 for a more precise definition in the different measurement configurations). Figure 1b shows the φ-dependence of Sy, measured at zero magnetic field (μ0Hx = 0) and at normal pump incidence (configuration 1). The different polarisations of the pump pulse that correspond to the different values of φ are also indicated to facilitate the reading. The data is decomposed into different harmonics by fitting with the equation18:

$${S}_{i}(\varphi )={H}_{i}(\varphi )+{L}_{i}(\varphi )+{B}_{i}$$
(1)

Here, \({H}_{i}(\varphi )={h}_{i}\sin (2\varphi +{\varphi }_{1})\) is the magnitude of the circular polarisation helicity-dependent component with a phase shift \({\varphi }_{1},{L}_{i}(\varphi )={l}_{i}\sin (4\varphi +{\varphi }_{2})\) is the linear polarisation-dependent component with a phase shift φ2, and Bi is the polarisation-independent background component. As displayed in Fig. 1(c), the decomposition of Sy shows that Hy(φ), Ly(φ), and By all contribute to the measured signal. For comparison, Sx measured in the same experimental geometry (configuration 1) displays a relatively smaller contribution from the helicity-dependent Hx(φ) component, and is dominated by Lx(φ) (Supplementary Note 5). We attribute this difference to a small unintentional rotation around the y-axis, as it will be further justified in the analysis that follows. In our set-up, the sample’s mount orientation can be freely adjusted around the y-axis, but not around the x-axis, so an unintentional tilting around the y-axis is more likely. In the following considerations, we focus on polarisation-dependent components of the signal, Hy(φ), Ly(φ). The remaining contribution, Bi does not have any dependence on optical polarisation, and can therefore be correlated to heating19. When the optical pump hits the sample surface its energy is absorbed by the electron bath and induces gradients in the electron temperature distribution at sub-picosecond timescales. The asymmetric diffusion of carriers along the gradient direction can lead to photo-currents. In our measurement layout, only the photo-currents generated parallel to the sample surface are radiative and can be detected. This is possible in the lateral photo-Dember effect20, if the pump hits the sample close to one edge (we need to consider that the pump beam diameter is 1 mm, comparable to the sample size). This is also validated by the fact that the background value does not have any clear correlation with sample rotation angle, as shown in Table S1 in the Supplementary Note 6. We also exclude any magnetic field dependent effect such as the anomalous Hall effect because we do not observe any dependence on magnetic field or flipping of the sign when the magnetic field direction is flipped (please refer to the section Magnetic field dependence below and Supplementary Note 8).

The effect of experiment geometry

Here we study how both polarisation and amplitude of the photocurrent-generated THz emission depend on the direction of the optical wavevector qz relative to the sample surface. For this purpose we tilt the sample whilst leaving the direction of the pump wavevector qz unchanged with respect to the laboratory frame of reference, along the z-direction. For θx (configuration 2) or θy (configuration 3) different from zero, qz has a non-zero projection along the b and a directions on the plane of the Mn3Sn film, which we label qb and qa respectively. Consequently, the components of the wavevector relative to the sample frame are [0, qb, qc] in configuration 2 and and [qa, 0, qc] in configuration 3.

Figure 2a and b show the components of the THz emission polarised along the x and the y directions as a function of φ, measured in configuration 2 (a) and configuration 3 (b). Sx(φ) and Sy(φ) are fitted with Eq. (1) to extract the coefficients hx and hy. While in Fig. 2a hx ≫ hy, in Fig. 2b the trend is inverted and hx ≪ hy. This suggests that the direction of the helicity-dependent photocurrent, and therefore of the THz polarisation, depends on the projection of the pump wavevector on the sample plane and is perpendicular to it. Due to finer control of θy in comparison to θx in our setup, we restrict the following analysis to configuration 3 only. In Fig. 2c we show that the THz emission amplitude increases with tilting angle θy. We now study the symmetry of the THz emission for opposite tilting angles by decomposing Si(φ) into even and odd contributions as:

$${S}_{i}{(\varphi )}_{even}({\theta }_{y}=\pm \! 1{5}^{\circ })={S}_{i}(\varphi )({\theta }_{y}=+1{5}^{\circ })+{S}_{i}(\varphi )({\theta }_{y}=-1{5}^{\circ })$$
(2)
$${S}_{i}{(\varphi )}_{{{\mbox{odd}}}}({\theta }_{y}=\pm \! 1{5}^{\circ })={S}_{i}(\varphi )({\theta }_{y}=+1{5}^{\circ })-{S}_{i}(\varphi )({\theta }_{y}=-1{5}^{\circ })$$
(3)
Fig. 2: Study of various experiment geometries in optical pump-THz emission from Mn3Sn.
figure 2

Normalised THz emission amplitude Sx(φ) and Sy(φ) data sets measured in configuration 2 and configuration 3 are plotted in (a, b) respectively. The sample was rotated around the x-axis by θx = + 25° ± 5° or θy = + 15° ± 2° respectively. c shows THz signals measured along y in configuration 3 for tilting angles θy between 0 and 30°. The data sets were fitted with Eq. (1) to extract the values of ∣hy∣ and ∣ly∣ parameters, respectively the magnitude of the circular polarisation helicity-dependent component and the near polarisation-dependent component. d shows even (see Eq. (2)) and odd (see Eq. (3)) responses with respect to θy, the rotation angle around the y-axis. The figure displays normalised THz signals measured along y in configuration 3. All measurements in (a–d) were performed at room temperature with no magnetic field. Data sets shown in (a, b–d) were fitted with Eq. (1) prior to normalisation to subtract the polarisation-independent backgrounds, Bi.

Full size image

In Fig. 2d we observe that the odd component of Sy is dominant. Analogous behaviour is presented in Supplementary Note 7 for Sx. Our observations suggest that the helicity-dependent photocurrents are generated in the direction perpendicular to the in-plane projection of the pump wavevector and are proportional to it.

Magnetic field dependence

In this section we want to understand whether the photocurrents have a magnetic origin and depend on the magnetic phase of Mn3Sn. Figure 3a shows Sy measured for two opposite directions of the magnetic field ±0.860 mT. According to Reichlova et al.21, 0.860 mT may be too low to switch the magnetic ordering in Mn3Sn thin films at RT, while it is sufficient to reverse the spins at temperatures close to TN. Hence, for these measurements we followed a cool down procedure with the magnetic field continuously applied from 420 K to 380 K, at which the experiment was performed. No significant dependence on magnetic field is measured. We also do not observe a qualitative difference in the time-domain THz transients measured at different fields as shown in the SI.

Fig. 3: Magnetic field dependence of THz emission from Mn3Sn.
figure 3

a THz signals measured at 380 K in configuration 3 after field-cooling from 420 K with opposite directions of external magnetic field continuously applied along x. b Normalised THz emission amplitude Sx(φ) and Sy(φ) data sets obtained prior, and after an in-plane rotation of the film by 90°. Prior to the measurements the sample was cooled down from 420 K to room temperature with the magnetic field of +860 mT. The field was switched off at room temperature, and Si(φ)(θc = 0) were measured. Without repeating the field-cooling procedure and at zero magnetic field, the film was rotated in plane by +90° to obtain Si(φ)(θc = + 90°). The experiment was performed in configuration 3. The plots show normalised signal values. Prior to normalisation the data sets were fitted with Eq. (1) to subtract the polarisation-independent backgrounds, Bi.

Full size image

We further confirm that the polarisation and amplitude of the emitted THz pulse is not correlated with the magnetic phase of Mn3Sn by repeating the measurement after rotating the sample by 90° around the c-axis. Figure 3b shows Sx(φ) and Sy(φ) prior and after the rotation by θc = + 90°. If the direction of the photoinduced currents, hence the polarisation of the THz emission, were correlated with the orientation of the spins we would have expected a rotation of the THz polarisation plane by 90°, which we do not observe. Instead, the two graphs of Sx(φ) and Sy(φ) overlap, as is discussed further in the SI.

Theoretical analysis

Nonlinear optical effects

In this section, we investigate nonlinear optical effects in Mn3Sn as an explanation of the observed signal. Other possible sources of helicity-dependent photocurrents are discussed in the subsequent section.

We consider a phenomenological expression for the induced photocurrent Ji that in turn generates THz emission via electro-dipole interaction. Using the notation from ref. 22 and expanding to second order in the light wave amplitude E(ω) for a frequency ω we write:

$${J}_{i}={\chi }_{ijk}^{(2)}{E}_{j}{E}_{k}^{* }+{\chi }_{ijkl}^{(3)}{q}_{j}{E}_{k}{E}_{l}^{* }$$
(4)

where all indices run over the Cartesian coordinates of the sample i, j, k, l ∈ (a, b, c) and q is the momentum of the incoming light. At normal incidence (configuration 1), only qc, Ea and Eb are non-zero. The first term describes the photogalvanic effect (PGE), whereas the second term describes the photon-drag effect (PDE). We further decompose each of these tensors into symmetric and antisymmetric components with respect to the light wave amplitude which respectively give rise to the linear photogalvanic/photon drag effect (LPGE/LPDE) and the circular photogalvanic/photon drag effect (CPGE/CPDE)23. Note that all quantitative features of these effects depend crucially on the details of the band structure. We show the ab-initio bulk and surface band structures in Fig. 4, for an energy-window of ℏω ≈ 1.55 eV, corresponding to the central wavelength of the laser pulses. Due to the large number of bands involved, we focus on a qualitative phenomenological symmetry analysis of the tensors in Eq. (4).

Fig. 4: Bulk and surface band structure for Mn3Sn.
figure 4

In (a), we show the bulk band structure, for an energy window corresponding to the frequency of the laser. In (b), we show the same plot, but with the colour and opacity of the bands indicating the value of \(\mathop{\min }\limits_{m}\{{E}_{n}({{{{{{{\boldsymbol{k}}}}}}}})-({E}_{m}({{{{{{{\boldsymbol{k}}}}}}}})\pm \hslash \omega )\}\) for band n, with ± indicating whether the band is above/below the Fermi surface. This is a rough indicator of the possibility of a vertical transition from band n occurring. The flat bands around K may also allow non-vertical transitions. In (c, d), we show the surface band structure for the c-directed top and bottom surface respectively, with the colour indicating how well-localised the states are on the surface.

Full size image

Symmetry-constrained model

The spatial symmetries of the material constrain the tensors in Eq. (4) and topology24,25. Mn3Sn has space-group symmetry P63/mmc when ignoring magnetism and magnetic space-group symmetry \({{{{{{{\rm{C}}}}}}}}{m}^{{\prime} }{{{{{{{\rm{c}}}}}}}}{m}^{{\prime} }\) when including the AFM ordering2. For the tensor symmetry analysis, we focus on the unitary point-group symmetries as detailed in the SI, where also complete expressions for the symmetry-allowed forms of the PGE/PDE tensors in Eq. (4) are given. Here, we only summarise the number of independent coefficients for the various symmetry settings as shown in Table 1. In general, there are too many possible terms, making a quantitative model infeasible. However, by carefully comparing with our experimental results, it is possible to identify effects are the most relevant as detailed in the next section and in the Supplementary Note.

Table 1 Number of independent elements for the linear/circular photogalvanic effect (LPGE/CPGE) and the linear/circular photon drag effect (LPDE/CPDE), for various unitary point-group (PG) symmetries relevant to the non-magnetic/magnetic (NM/M) bulk/surface of the material.
Full size table

Interpretation of results

We begin by considering the effect of magnetism. As shown in Fig. 3a our results are insensitive to the direction and magnitude of the external magnetic field, as well as to the intrinsic spin ordering of the material [see Fig. 3b]. This suggests that the generated photocurrents do not arise as a result of the magnetic ordering in the material. We therefore focus on the non-magnetic symmetry analysis in what follows. Because the bulk of the sample respects inversion symmetry we should not expect any bulk contribution from the PGE in this case.

We address here the result of tilting the sample away from the normal pump incidence, as shown in Fig. 2. As discussed in detail in Supplementary Note 10, the tilting changes both what currents are generated in the material, and which part of the resultant THz radiation is measured at the detector. Tilting in θx (configuration 2) or θy (configuration 3) changes the geometry of the sample relative to the detector. In particular, we are able to resolve currents generated in the c-direction26. Thus, the detected integrated amplitude of the THz transient pulse in configuration 2 is given by:

$$\begin{array}{l}\begin{array}{c}{S}_{x}\propto {J}_{a}({\theta }_{x})\\ {S}_{y}\propto {J}_{b}({\theta }_{x})\cos {\theta }_{x}+{J}_{c}({\theta }_{x})\sin {\theta }_{x}\end{array}\end{array}$$
(5)

And in configuration 3:

$$\begin{array}{l}\begin{array}{c}{S}_{x}\propto {J}_{a}({\theta }_{y})\cos {\theta }_{y}+{J}_{c}({\theta }_{y})\sin {\theta }_{y}\\ {S}_{y}\propto {J}_{b}({\theta }_{y})\end{array}\end{array}$$
(6)

Where the expressions for Ji(θk) arising from PGE/PDE are give in Supplementary Note 11. When considering the contribution from the bulk photon drag effect and the surface photogalvanic effect to J, we find that all terms in the detected amplitude Si arising from a bulk photon-drag effect are odd under tilting in both θx and θy, whereas the linear surface photogalvanic effect contains lowest-order terms that are even under tilting. We do not exclude the potential presence of the surface CPGE, which could be responsible for the even component of the signal. However, as the odd components make a significant contribution to our results (see e.g. Fig. 1c), we interpret our signal to arise predominantly from the bulk photon drag effect.

As discussed in Supplementary Note 11, we further find that the circular photon drag contribution to Si normal to the rotation axis is suppressed, in agreement with the experimental results, and that only the bulk non-magnetic photon drag contribution is invariant under in-plane rotation [see Fig. 3b]. These observations indicate that the bulk photon drag effect is the main mechanism responsible for our signal.

In the photon drag effect, both angular and translational momenta are transferred from photons to the excited carriers. Therefore, this effect is linked to non-vertical transitions in momentum space27,28. As shown in Fig. 4b, Mn3Sn has a flat bulk band below the Fermi energy around the K-point, with a corresponding band at a distance of ℏω corresponding to the energies of the optical excitation. This may lead to a large joint density of states, and allow for non-vertical transitions with finite q. Hence, we note that the photon drag effect is also appealing from a bulk band-structure perspective.

Other possible sources of photocurrent

Another way in which helicity-dependent photocurrents can be generated is through a combination of the inverse Faraday effect (IFE) and inverse spin Hall effect (ISHE), as described recently for Bismuth thin-films in ref. 14. This could be an important mechanism in Mn3Sn, where effects related to the nonzero Berry curvature are significant8 and may result in strong responses of the Faraday effect29. Furthermore, Mn3Sn has been shown to have a large spin Hall angle30. However, we believe this mechanism does not play a significant role in our experimental results. Firstly, for an efficient conversion of IFE-induced spin currents into charge currents and THz electric fields the spins must travel relatively long distances14. This is not the case in Mn3Sn, where the reported spin propagation length is below 1 nm31. Secondly, a Berry curvature related effect, such as the IFE, would show a strong dependence on the magnetic phase of Mn3Sn. We do not observe this behaviour in our temperature measurements reported in Fig. S8 in Supplementary Note 9. Previous studies have reported that at temperatures above 420 K Mn3Sn becomes paramagnetic and that upon cooling below RT the material can undergo transitions into the spiral and spin glass phases1. Our investigation in the temperature range of 50 − 400 K does not reveal any abrupt changes in the magnitude of THz signals that could indicate the role of magnetic phase-dependent mechanisms. We do not, however, rule out that our sample remains in the same magnetic state over the entire investigated temperature range. Finally, the mechanism relying on the IFE and ISHE could only explain the helicity-dependent photocurrents and cannot account for the generation of photocurrents that show linear dependence on the pump polarisation. As shown in Fig. 1c, the magnitudes of Hy and Ly are comparable, and therefore we suggest their main contributions originate from related mechanisms, namely the CPDE and LPDE.

Conclusions

In conclusion, using optical pump-THz emission spectroscopy we present the generation of helicity-dependent ultrafast photocurrents in a Mn3Sn thin film. The magnitude and direction of these can be fully controlled by the polarisation and incidence angle of the optical pump and are not affected by external magnetic fields. We combine the experimental results with theoretical analysis to suggest that the bulk photon drag effect is the main mechanism responsible for the generation of the helicity-dependent photocurrents.

Methods

The sample

Epitaxial Mn3Sn films were grown using magnetron sputtering in a BESTEC ultra-high vacuum (UHV) system with a base pressure of <2 × 10−9 mbar and a process gas (Ar 5 N) pressure of 3 × 10−3 mbar. The target to substrate distance was fixed at 20 cm and the substrates were rotated during deposition to ensure homogeneous growth. The underlayer was deposited using a Ru (5.08 cm) target by applying 40 W DC power with the substrate held at 400 °C. Following cooling back to room temperature, Mn3Sn was grown from Mn (7.62 cm) and Sn (5.08 cm) sources in confocal geometry, using 47 W and 11 W DC power respectively. The stack was then annealed in-situ under UHV at 350 °C for 10 min. The stoichiometry is Mn75Sn25 (±2 at. %), estimated by using energy dispersive x-ray spectroscopy (see Fig. S1 in Supplementary Note 1). Finally, a Si capping layer was deposited at room temperature using an Si (5.08 cm) target at 60 W RF power to protect the film from oxidation. Magnetotransport studies on films grown under the same conditions and with comparable crystal quality are presented in ref. 32 and show a large anomalous Hall effect at room temperature and a transition to topological Hall effect below 50 K.

Density-functional calculations

The electronic band structure was calculated using density-functional theory (DFT) as implemented in Quantum Espresso33,34 with a fully-relativistic norm-conserving pseudopotential, generated using the ONCVPSP package35. We used the experimental crystal parameters a = b = 5.67 Å and c = 4.53 Å, with an 8 × 8 × 8 k-grid and a kinetic-energy cutoff of 870 eV. The magnetic structure was relaxed by constraining the total direction of the magnetization. The bands were then Wannierised using Wannier9036, with all d-orbitals of Mn considered in the projector. Finally, the slab band structure was computed using WannierTools37.