Intertype superconductivity in ferromagnetic superconductors

Abstract

In many pnictides the superconductivity coexists with ferromagnetism in an accessible range of temperatures and compositions. Recent experiments revealed that when the temperature of magnetic ordering T_m is below the superconducting transition temperature T_c, highly non-trivial physical phenomena occur. In this work we demonstrate the existence of a temperature window, situated between T_m and T_c, where these intrinsically type-II superconductors are in the intertype regime. We explore analytically and numerically its rich phase diagram characterized by exotic spatial flux configurations—vortex clusters, chains, giant vortices and vortex liquid droplets—which are absent in both type-I and type-II bulk superconductors. We find that the intertype regime is almost independent of microscopic parameters, and can be achieved by simply varying the temperature. This opens the route for experimental studies of the intertype superconductivity scarcely investigated to date.

Introduction

Substantial advances in studying ferromagnetic superconductors have introduced many truly fascinating aspects of superconductivity physics, in particular, concerning magnetic properties of superconductors. Coexistence of superconductivity and magnetism in such materials depends crucially on the way these two subsystems are coupled. The most important is which of the two subsystems is the “strongest", i.e., which of the two critical temperatures is the largest: the Curie temperature of the magnetic ordering T_m or the superconducting critical temperature T_c. In uranium based compounds, such as UGe₂, URhGe, or UCoGe, as well as in Ho_1.2Mo₆S₈, ErRh₄B₄, and ZrZn₂, the interaction between magnetic moments and free electron spins is controlled by the exchange mechanism and T_c ≪ T_m^1,2,3,4,5,6. In this case the singlet pairing is suppressed, and the superconductivity with the triplet pairing provides only marginal corrections to a predominantly ferromagnetic state^{1,2,3,7,8,9,10}.

Iron pnictides are the opposite example, where the coupling between superconducting and weak magnetic subsystems (T_m ≲ T_c) is mediated by the electromagnetic field (via the orbital effects). The weak ferromagnetism in those materials does not suppress the conventional singlet pairing. In particular, this takes place in ${{{{{{{{\rm{EuFe}}}}}}}}}_{2}{({{{{{{{{\rm{As}}}}}}}}}_{1-{{{{{{{\rm{x}}}}}}}}}{{{{{{{{\rm{P}}}}}}}}}_{{{{{{{{\rm{x}}}}}}}}})}_{2}$ compounds for a large interval of the P-doping parameter x. In those materials, the superconductivity is associated with the Fe-3d electrons, while the ferromagnetic ordering is created by the Eu-4f spins. For example, at x = 0.21 one finds T_m = 19K and T_c = 24.2K^11,12,13,14.

Coexistence of the two order parameters at T < T_m in such iron pnictides results in a plethora of physical phenomena not observed in conventional superconductors and ferromagnets^14,15,16. In particular, recent measurements of the magnetization spatial profile^14,17,18,19 revealed a large variety of exotic patterns that are very sensitive to changes in the temperature, applied magnetic field and current. These structures are new representatives of the family of the self-organized spontaneous patterns, emerging in many systems in nature, ranging from geological superstructures and vegetation patterns in semiarid regions to skin pigmentation spots and stripes of animals/fishes, and even to spatiotemporal patterns in ecology and epidemiology^{20,21,22,23,24}. A prominent and distinctive feature of such exotic structures in ferromagnetic superconductors is a nontrivial involvement of topological excitations, such as vortex-antivortex pairs embedded in striped and dendrite-like patterns in ${{{{{{{{\rm{EuFe}}}}}}}}}_{2}{({{{{{{{{\rm{As}}}}}}}}}_{1-{{{{{{{\rm{x}}}}}}}}}{{{{{{{{\rm{P}}}}}}}}}_{{{{{{{{\rm{x}}}}}}}}})}_{2}$^14,17,18,19, or skirmions coupled to vortices in ferromagnet-superconductor hybrids²⁵.

In contrast, the interval of intermediate temperatures T_m < T < T_c has attracted much less attention. The reason is that in this case, the magnetic ordering does not exist of its own, acting as a perturbation to the superconducting state. However, even here the influence of the magnetic subsystem can be significant because the paramagnetic response of spins can strongly modify superconducting characteristics. This follows already from the London superconductivity theory when coupling to an additional magnetic subsystem is taken into account. This theory predicts that the vortex-vortex interaction, being initially repulsive, becomes attractive at low temperatures^26,27,28, pointing to the crossover from type-II to type-I superconductivity⁹.

The mechanism behind this type-II/type-I crossover is explained by the evolution of the magnetic penetration depth λ. This quantity defines the radius of the area S ~ λ² around an isolated Abrikosov vortex, where the supercurrents circulating around the vortex core generate the magnetic flux equal to the superconductive flux quantum $\int\,{{{{{{{\bf{B}}}}}}}}\cdot d{{{{{{{\bf{S}}}}}}}}=h{\mathbb{c}}/2e={{{\Phi }}}_{0}$. In ferromagnetic superconductors with a linear response of the magnetic subsystem, the induction B created by the vortex supercurrents is proportional to the magnetic permeability μ (reflecting the contribution of the magnetic subsystem to B). Since the total flux Φ₀ is fixed, the effective vortex area S scales as 1/μ. In this way λ of the superconducting subsystem decoupled from the magnetic one is multiplied by the factor $1/\sqrt{\mu }$ and so is the Ginzburg-Landau (GL) parameter κ = λ/ξ (the superconducting coherence length ξ remains the same). The permeability μ increases when T drops and approaches T_m, diverging in the limit T → T_m. It is, therefore, expected that the GL parameter of a ferromagnetic pnictide, which is a type-II superconductor at T → T_c, decreases when the temperature is lowered towards T_m and the material eventually becomes a type-I superconductor⁹.

Here we demonstrate that in ferromagnetic superconductors with T_m < T_c, the crossover from type II to type I passes through the entire interval of the intertype (IT) superconductivity, and that all parts of its phase diagram can be accessed simply by tuning the temperature. Thus, to date, iron pnictides with T_m < T_c represent a unique class of emerging materials that offers a universal testing ground to probe details of the IT regime and its exotic intermediate mixed state (IMS). This yields a promising perspective for technological applications, where a controlled change of the superconductive magnetic response can be used to design sensing devices for the field, current, and temperature.

Results and discussion

IT superconductivity

Before discussing the IT domain in ferromagnetic superconductors, we describe the physics behind IT superconductivity, which is often referred to as type-II/1. It is related to the presence of two characteristic length scales that control the interaction between areas of the penetrating magnetic flux (vortices) in the mixed state of superconductors.

The character of this interaction is controlled by the balance between two opposing tendencies. Domains of depleted condensate around vortex cores attract one another, whereas penetrating magnetic field gives rise to repulsion. Depending on which of the two characteristic lengths - λ or ξ - is larger, one of the tendencies dominates, making superconductor type-II, where vortices are totally repulsive, or type-I, where they are attractive. If these lengths are comparable ($\kappa \simeq {\kappa }_{0}=1/\sqrt{2}$), the interaction becomes more complex, demonstrating nonmonotonic spatial dependence^29,30,31 and significant multi-vortex contributions³². These properties are main prerequisites for the appearance of exotic spatial flux configurations in the IT domain. They lead to the magnetic response with characteristics of both type I and type II and also with configurations found in neither of these conventional types^{33,34,35,36,37,38,39,40,41,42}.

The IT regime can also be viewed as a result of lifting the degeneracy of the BCS theory at the Bogomolnyi point (κ₀, T_c) [B-point]. When approaching the B-point, the BCS theory becomes degenerate at the thermodynamic critical field as an infinite number of its solutions have the same Gibbs free energy. This means that positions of vortices can be arbitrary (vortices do not interact) and, consequently, the energy of an Abrikosov lattice and of the state with lamellas are exactly equal. Departing from the B-point, by either changing the GL parameter κ or by lowering T, removes this degeneracy but the removal differs for different flux configurations. This difference has well-known consequences when the system is far from the B-point: deep in type I (κ ≪ 1) the vortex matter fails while deep in type II (κ ≫ 1) a vortex lattice forms the mixed state. However, the results of the degeneracy removal are much less trivial when κ ≃ κ₀, leading to the IT superconductivity with various stable IMS configurations shaping the internal structure of the IT domain.

In conventional superconductors, the GL parameter κ, which controls the superconductivity type, is fixed by microscopic parameters of the material and does not depend on T. In this case, the superconductivity type generally cannot be changed by varying the temperature. An exception is the low-κ superconductors with κ ≃ κ₀^{43,44,45,46,47,48,49}, where lowering the temperature can drive an initially type-I (type-II) material into the IT regime.

As we show below, the situation changes in ferromagnetic superconductors like ${{{{{{{{\rm{EuFe}}}}}}}}}_{2}{({{{{{{{{\rm{As}}}}}}}}}_{1-{{{{{{{\rm{x}}}}}}}}}{{{{{{{{\rm{P}}}}}}}}}_{{{{{{{{\rm{x}}}}}}}}})}_{2}$, where coupling to the magnetic subsystem effectively screens the field-mediated repulsive component of the vortex interaction. The screening increases when the temperature decreases from T_c to T_m. Such materials, when being initially in type II, demonstrate the crossover from type II to type I with the IT regime in a finite interval T_l < T < T_u between T_m and T_c. The lower T_l and upper T_u boundaries of this interval depend on the material parameters. However, the internal structure of the IT domain together with the characteristic flux-condensate distributions remain qualitatively similar.

Model

Properties of a ferromagnetic superconductor will be described by using an approach that combines the BCS theory with a phenomenological model of the ferromagnetic subsystem. The free energy density of this model has three components

$$f={f}_{{{{{{{{\rm{s}}}}}}}}}+{f}_{{{{{{{{\rm{m}}}}}}}}}+{f}_{{{{{{{{\rm{int}}}}}}}}},$$

(1)

where f_s is the BCS superconductor contribution which depends on the gap function Δ and magnetic field B, f_m is the free energy density of the ferromagnetic subsystem

$$\begin{array}{r}{f}_{{{{{{{{\rm{m}}}}}}}}}=\frac{{a}_{{{{{{{{\rm{m}}}}}}}}}}{2}{{{{{{{{\bf{M}}}}}}}}}^{2}+\frac{{b}_{{{{{{{{\rm{m}}}}}}}}}}{4}{({{{{{{{{\bf{M}}}}}}}}}^{2})}^{2}+\frac{{{{{{{{{\mathcal{K}}}}}}}}}_{m}}{2}\mathop{\sum}\limits_{i}{({\nabla }_{i}{{{{{{{\bf{M}}}}}}}})}^{2},\end{array}$$

(2)

where M is a three-component magnetization vector, ∇_i is the partial derivative with respect to the i-spatial coordinate (i = x, y, z), a_m, b_m, and ${{{{{{{{\mathcal{K}}}}}}}}}_{{{{{{{{\rm{m}}}}}}}}}$ are the relevant parameters, and the interaction between the two components of the system is controlled by

$${f}_{{{{{{{{\rm{int}}}}}}}}}=\gamma {{{{{{{{\bf{M}}}}}}}}}^{2}| {{\Delta }}{| }^{2}-{{{{{{{\bf{M}}}}}}}}\cdot {{{{{{{\bf{B}}}}}}}},$$

(3)

with the coupling constant γ. The Curie transition in this model is governed by the temperature dependence of a_m. A minimum of the free energy functional determines stationary configurations of Δ, B and M⁵⁰. In this work we obtain the minimum using the perturbative approach, briefly outlined below, see Supplementary Note 1. For illustration, both superconductive and ferromagnetic subsystems are chosen isotropic.

A small parameter for the perturbation expansion is the proximity to the superconductive critical temperature τ = 1 − T/T_c. The derivation is similar to the earlier works^{37,51,52,53,54}, which is, however, adapted to the situation where the system has an additional order parameter to describe the spins of the magnetic subsystem. The calculation is done under the assumption that the Curie temperature T_m is lower then the critical superconductive temperature T_c. In other words, the “weak" magnetic subsystem is driven by the “strong" superconducting one, so that the magnetic order parameter M is zero when the coupling between the subsystems is absent.

In the perturbation formalism the solution to the pertinent physical quantities is sought in the form of the following series expansions:

$${{\Delta }} ={\tau }^{1/2}{{\Psi }}+{\tau }^{3/2}\psi +\ldots ,\,{{{{{{{\bf{M}}}}}}}}=\tau {{{{{{{\boldsymbol{{{{{{{{\mathcal{M}}}}}}}}}}}}}}}}+{\tau }^{2}{\mathfrak{m}}+\ldots ,\\ {{{{{{{\bf{B}}}}}}}} =\tau {{{{{{{\boldsymbol{{{{{{{{\mathcal{B}}}}}}}}}}}}}}}}+{\tau }^{2}{\mathfrak{b}}+\ldots ,{{{{{{{\bf{A}}}}}}}}={\tau }^{1/2}{{{{{{{\boldsymbol{{{{{{{{\mathcal{A}}}}}}}}}}}}}}}}+{\tau }^{3/2}{\mathfrak{a}}+\ldots .$$

(4)

Furthermore, the formalism takes into account that in the vicinity of T_c, the superconductor characteristic lengths are divergent as λ, ξ ∝ τ^−1/2. Introducing the spatial scaling r → τ^1/2r, one obtains the scaling factor for the spatial gradients as ∇ → τ^−1/2∇. Finally, all the temperature dependent coefficients in the free energy functional are also represented as the series expansions in τ. However, in order to describe the behavior of the system close to the ferromagnetic transition, we keep the original temperature dependence of the coefficient a_m, which is then considered as a system parameter. The reason for this is that the expansion of this parameter close to T_c yields a poor approximation when only two lowest order contributions in the perturbation series over τ are taken into account, see Supplementary Note 1.

GL theory and crossover between types I and II

The crossover between the conventional superconductivity types can be described already in the lowest order of the perturbation expansion of the free energy (1), where the contributions of the order ${{{{{{{\mathcal{O}}}}}}}}({\tau }^{2})$ are kept. Notice, that the order ${{{{{{{\mathcal{O}}}}}}}}(\tau )$ disappears due to the equation for T_c. The order ${{{{{{{\mathcal{O}}}}}}}}({\tau }^{2})$ yields the superconductor GL theory modified by the linear coupling to the magnetic subsystem. The corresponding GL equations read as

$$(a+b| {{\Psi }}{| }^{2}){{\Psi }}-{{{{{{{\mathcal{K}}}}}}}}{{{{{{{{\boldsymbol{{{{{{{{\mathcal{D}}}}}}}}}}}}}}}}}^{2}{{\Psi }}=0,$$

(5a)

$${{{{{{{\rm{rot}}}}}}}}\left[{{{{{{{\boldsymbol{{{{{{{{\mathcal{B}}}}}}}}}}}}}}}}-4\pi {{{{{{{\boldsymbol{{{{{{{{\mathcal{M}}}}}}}}}}}}}}}}\right]=\frac{4\pi }{{\mathbb{c}}}{\mathfrak{j}},$$

(5b)

$${a}_{{{{{{{{\rm{m}}}}}}}}}{{{{{{{\boldsymbol{{{{{{{{\mathcal{M}}}}}}}}}}}}}}}}={{{{{{{\boldsymbol{{{{{{{{\mathcal{B}}}}}}}}}}}}}}}},$$

(5c)

where ${{{{{{{\boldsymbol{{{{{{{{\mathcal{D}}}}}}}}}}}}}}}}$ is the gauge invariant derivative with the leading order contribution ${{{{{{{\boldsymbol{{{{{{{{\mathcal{A}}}}}}}}}}}}}}}}$ to the vector potential, the coefficients ${{{{{{{\mathcal{K}}}}}}}},a$ (< 0), and b are obtained from the microscopic model of the charge carrier states in the BCS theory⁵⁵, and the leading order contribution to the supercurrent density is given by ${\mathfrak{j}}={{{{{{{\mathcal{K}}}}}}}}{\mathbb{c}}{\mathfrak{i}}$, with ${\mathfrak{i}}=4e{{{{{{{\rm{Im}}}}}}}}[{{{\Psi }}}^{* }{{{{{{{\boldsymbol{{{{{{{{\mathcal{D}}}}}}}}}}}}}}}}{{\Psi }}]/\hslash {\mathbb{c}}$. Equations (5) describe a superconductor, placed in a magnetic medium (made of the magnetic subsystem spins) and having the effective (stationary) GL free energy density given by

$$\begin{array}{r}{f}^{(0)}=\frac{{{{{{{{{\boldsymbol{{{{{{{{\mathcal{B}}}}}}}}}}}}}}}}}^{2}}{8\pi \mu }+{{{{{{{\mathcal{K}}}}}}}}{\left\vert {{{{{{{\boldsymbol{{{{{{{{\mathcal{D}}}}}}}}}}}}}}}}{{\Psi }}\right\vert }^{2}+a| {{\Psi }}{| }^{2}+\frac{b}{2}| {{\Psi }}{| }^{4},\end{array}$$

(6)

where

$$\begin{array}{r}\mu ={\left(1-\frac{4\pi }{{a}_{{{{{{{{\rm{m}}}}}}}}}}\right)}^{-1}\end{array}$$

(7)

is magnetic permeability diverging at the Curie critical temperature T_m, given as a_m(T_m) = 4π. We assume a_m(T) = α_m(T − θ), where θ is the bare Curie temperature related to T_m via θ = T_m − 4π/α_m. Notice that the real Curie temperature is shifted from its bare value due to coupling to the superconductive subsystem⁵⁶. This shift, however, is not significant for conclusions of our work.

The next step in our analysis is introducing the dimensionless quantities

$$\begin{array}{rc}&\tilde{{{{{{{{\bf{r}}}}}}}}}=\frac{{{{{{{{\bf{r}}}}}}}}}{{\lambda }_{\mu }\sqrt{2}},\,\tilde{{{{{{{{\boldsymbol{{{{{{{{\mathcal{B}}}}}}}}}}}}}}}}}=\frac{{\kappa }_{\mu }\sqrt{2}}{\mu {H}_{{{{{{{{\rm{c}}}}}}}}}^{(0)}}{{{{{{{\boldsymbol{{{{{{{{\mathcal{B}}}}}}}}}}}}}}}},\,\tilde{{{{{{{{\boldsymbol{{{{{{{{\mathcal{A}}}}}}}}}}}}}}}}}=\frac{{\kappa }_{\mu }}{\mu {H}_{{{{{{{{\rm{c}}}}}}}}}^{(0)}{\lambda }_{\mu }}{{{{{{{\boldsymbol{{{{{{{{\mathcal{A}}}}}}}}}}}}}}}},\\ &\tilde{{{\Psi }}}=\frac{{{\Psi }}}{{{{\Psi }}}_{0}},\tilde{f}=\frac{4\pi \,f}{\mu {H}_{{{{{{{{\rm{c}}}}}}}}}^{(0)2}},\end{array}$$

(8)

where ${{{\Psi }}}_{0}=\sqrt{-a/b}$ is the uniform solution to the GL equations (5), ${H}_{{{{{{{{\rm{c}}}}}}}}}^{(0)}=\sqrt{4\pi {a}^{2}/b\mu }$ stands for the GL thermodynamic critical field [strictly speaking, up to the factor τ, see the τ-expansion in Eq. (4)], and the effective magnetic penetration depth λ_μ and the effective GL parameter κ_μ are defined as (see also the paper⁹)

$$\begin{array}{r}{\lambda }_{\mu }=\frac{\lambda }{\sqrt{\mu }},\quad {\kappa }_{\mu }=\frac{\kappa }{\sqrt{\mu }},\end{array}$$

(9)

where λ and κ are the magnetic depth and GL parameter of the superconducting subsystem taken separately. We note that due to the spatial scaling r → τ^1/2r [see the discussion after Eq. (4)], all the characteristic lengths are multiplied by τ^1/2. Using Eqs. (8) and (9), one writes the GL free energy density in the dimensionless form as

$${f}^{(0)}=\frac{{{{{{{{{\boldsymbol{{{{{{{{\mathcal{B}}}}}}}}}}}}}}}}}^{2}}{4{\kappa }_{\mu }^{2}}+\frac{1}{2{\kappa }_{\mu }^{2}}| {{{{{{{\boldsymbol{{{{{{{{\mathcal{D}}}}}}}}}}}}}}}}{{\Psi }}{| }^{2}-| {{\Psi }}{| }^{2}+\frac{1}{2}| {{\Psi }}{| }^{4},$$

(10)

where ${{{{{{{\boldsymbol{{{{{{{{\mathcal{D}}}}}}}}}}}}}}}}={{{{{{{\boldsymbol{\nabla }}}}}}}}+{{{{{{{\rm{i}}}}}}}}{{{{{{{\boldsymbol{{{{{{{{\mathcal{A}}}}}}}}}}}}}}}}$ and we omit tilde for the dimensionless quantities. One can see that the stationary GL free energy functional of the ferromagnetic superconductor is reduced to the standard superconductive GL free energy with the effective GL parameter κ_μ.

The effective magnetic penetration depth λ_μ and GL parameter κ_μ given by Eq. (9) become smaller when μ increases. Taking into account that μ increases with decreasing T, one concludes that the material, which is a type-II superconductor for T ≃ T_c, moves towards type I for lower temperatures. Switching between types I and II occurs when κ_μ crosses κ₀. Together with Eqs. (7) and (9), this condition defines the crossover line κ^*(T) on the κ-T plane that separates type I and type II and is given by

$$\begin{array}{r}{\kappa }^{* }={\kappa }_{0}\sqrt{\frac{T-\theta }{T-{T}_{{{{{{{{\rm{m}}}}}}}}}}}.\end{array}$$

(11)

One notes that in general one has κ^* > κ₀, even for T → T_c the crossover line is situated above the critical GL parameter κ₀ that separates types I and II in the GL theory of the conventional superconductors. It means that the inequality κ > κ₀ does not guarantee that the ferromagnetic superconductors with T_m < T_c are in type II near the superconducting critical temperature. Now the type-II criterion for T → T_c reads as

$$\begin{array}{r}\kappa \, > \, {\kappa }^{* }({T}_{{{{{{{{\rm{c}}}}}}}}})={\kappa }_{0}\sqrt{\frac{{T}_{{{{{{{{\rm{c}}}}}}}}}-\theta }{{T}_{{{{{{{{\rm{c}}}}}}}}}-{T}_{{{{{{{{\rm{m}}}}}}}}}}},\end{array}$$

(12)

where the right-hand side of the inequality can be significantly larger than κ₀ when T_c is close to T_m. One can see that for T_c → T_m the system is always in the type-I regime irrespective of a particular value of the GL parameter κ. We remark that the difference T_c − θ is always larger than T_c − T_m and, hence, remains finite when T_c approaches T_m. Notice that the ratio T_m/T_c can be significantly varied in e.g., EuFe₂(As_1−xP_x)₂ by changing the P-doping value x¹⁹. As is mentioned above, at x = 0.21 one finds T_c = 24.2K and T_m = 19K in this material^11,12,13,14 while T_c and T_m are nearly the same at x = 0.25¹⁹.

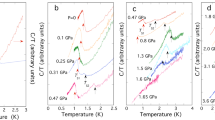
Figure 1a and b show an example of the crossover line κ^*(T), given by the dashed orange line and calculated for the set of the microscopic parameters corresponding to T_m/T_c = 0.65 and α_mT_c = 200. For T → T_c we obtain κ^* = 0.77, which is larger than κ₀ = 0.71, in agreement with the discussion of the previous paragraph. It is important that the line κ^*(T) goes upward when T decreases irrespective of a particular parametric choice. To the right of this line, at κ > κ^*, the superconductivity is of type II, while at κ < κ^* it is of type I.

Fig. 1: Intertype (IT) domain in the κ-T phase diagram, with κ the Ginzburg-Landau parameter and T the temperature.

a, b show the upper κ_u and lower κ_l boundaries of the IT domain for a ferromagnetic superconductor with the s-wave pairing and the Curie temperature smaller than the superconducting one. κ^* separates types I and II in the GL theory, κ_s is the line of the zero surface tension of a normal-superconducting domain wall. Panel c illustrates examples of the pairwise vortex interaction potential V(R) as a function of the intervortex distance R/ξ (with ξ the Ginzburg-Landau coherence length) together with the corresponding vortex configurations at low magnetic fields (red - Meissner domains, green - vortices) for different points on the phase diagram marked by colored circles.

Thus, one finds that a ferromagnetic superconductor that is of type II at T ≃ T_c [κ obeys Eq. (12)], inevitably crosses the line separating superconductivity types I and II when decreasing the temperature, in agreement with the conclusions of previous works, see⁹. This occurs at the temperature

$$\begin{array}{r}{T}^{* }={T}_{{{{{{{{\rm{m}}}}}}}}}+\frac{{\kappa }_{0}^{2}({T}_{{{{{{{{\rm{m}}}}}}}}}-\theta )}{{\kappa }^{2}-{\kappa }_{0}^{2}},\end{array}$$

(13)

which is above the Curie temperature T_m. One can see that T^* − T_m is proportional to the difference between the Curie temperature T_m and the bare Curie temperature θ. The stronger is the effect of the superconductive subsystem on the Curie temperature, the larger the difference (T^* − T_m)/T_c, controlled by the parameter α_mT_c. When α_mT_c ≫ 4π, T^* is close to T_m (see Fig. 1, where α_mT_c = 200). However, when α_mT_c ≳ 4π, T^* can significantly deviate from T_m.

Beyond the GL theory

Within the GL theory the switching between types I and II takes place exactly at κ = κ^*. However, the situation changes when one considers contributions beyond the GL theory. In conventional superconductors these contributions give rise to a finite domain of the IT superconductivity in the κ-T plane. We now demonstrate that this takes place also in ferromagnetic superconductors when the temperature decreases from T_c to T_m. Furthermore, such ferromagnetic superconductors have a finite IT temperature interval around T^* almost irrespective of the initial GL parameter in the vicinity of T_c. The crossover is always present if the superconductor demonstrates the type-II behavior near the superconducting critical temperature, i.e., if the inequality of Eq. (12) is satisfied.

The analysis is done by recalling that IT superconductivity is determined by the possibility of developing IMS with unusual field-condensate configurations with exotic properties, for example, non-monotonic vortex interactions. The stability of such IMS configurations is investigated by comparing their Gibbs free energy with that of the Meissner state, calculated at the thermodynamic critical field H_c. The difference between the Gibbs free energies of the two states is written as (see details in the papers^{40, 41,49,57})

$$\begin{array}{r}G=\int\,g\,{d}^{2}{{{{{{{\bf{r}}}}}}}},\quad g=f+\frac{{H}_{{{{{{{{\rm{c}}}}}}}}}^{2}}{2}-\frac{{H}_{{{{{{{{\rm{c}}}}}}}}}B}{\sqrt{2}{\kappa }_{\mu }},\end{array}$$

(14)

where we assume that the external field H_c = (0, 0, H_c) is parallel to B = (0, 0, B) and g and G are given in units of $\mu {H}_{{{{{{{{\rm{c}}}}}}}}}^{(0)2}/4\pi$ and $\mu {H}_{{{{{{{{\rm{c}}}}}}}}}^{(0)2}{\lambda }_{\mu }^{2}L/2\pi$, respectively (L is the sample size in the z-direction). This energy difference is to be calculated by using relevant solutions for the stationary point equations (5) which do not depend on z, i.e., the integration is performed in the x-y plane.

Using the perturbation approach, we represent G in the form of the series expansion in τ, and keep only the leading and next-to-leading order contributions, see Supplementary Note 1. In addition, we also apply the expansion procedure with respect to the small deviation δκ_μ = κ_μ − κ₀, because we are focused on the IT domain, where κ_μ is close to the critical value κ₀. Then, the perturbation expansion yields

$$\begin{array}{r}G={\tau }^{2}\left({G}^{(0)}+\frac{d{G}^{(0)}}{d{\kappa }_{\mu }}\,\delta {\kappa }_{\mu }+{G}^{(1)}\,\tau \right),\end{array}$$

(15)

where G⁽⁰⁾ is the GL contribution obtained by integrating the functional of Eq. (10), dG⁽⁰⁾/dκ_μ is its derivative with respect to κ_μ, and the last term represents the leading correction to the GL theory in τ. All these terms are calculated at κ_μ = κ₀.

The GL contribution G⁽⁰⁾ vanishes^40,41,49,57 for all solutions of the GL equations (5). This degeneracy of the GL theory is closely related to its self-duality at the B-point κ_μ = κ₀. Then, the Gibbs free energy difference is obtained in the form

$$\frac{G}{{\tau }^{2}}= -\sqrt{2}\,{{{{{{{\mathcal{I}}}}}}}}\,\delta {\kappa }_{\mu }+\tau \,\left\{\left[1-c+2{{{{{{{\mathcal{Q}}}}}}}}+\gamma \right]\,{{{{{{{\mathcal{I}}}}}}}}\right.\\ \left.+\left[2\,{{{{{{{\mathcal{L}}}}}}}}-c-\frac{5{{{{{{{\mathcal{Q}}}}}}}}}{3}-\gamma +\mu {{{{{{{{\mathcal{K}}}}}}}}}_{{{{{{{{\rm{m}}}}}}}}}\right]{{{{{{{\mathcal{J}}}}}}}}\right\}.$$

(16)

where ${{{{{{{\mathcal{Q}}}}}}}},{{{{{{{\mathcal{L}}}}}}}},c$ are the dimensionless coefficients calculated from an appropriate microscopic model of the single-particle states (for the details of the relevant calculations, see the papers^40,41,49,57) and γ and ${{{{{{{{\mathcal{K}}}}}}}}}_{{{{{{{{\rm{m}}}}}}}}}$ are also given in the dimensionless units as

$$\begin{array}{r}\gamma \to -\,\frac{\gamma a{{{\Phi }}}_{0}^{2}}{4 \pi^2{a}_{{{{{{{{\rm{m}}}}}}}}}^{2}{{{{{{{{\mathcal{K}}}}}}}}}^{2}},{{{{{{{{\mathcal{K}}}}}}}}}_{m}\to -\frac{2\pi {{{{{{{{\mathcal{K}}}}}}}}}_{{{{{{{{\rm{m}}}}}}}}}a}{{a}_{{{{{{{{\rm{m}}}}}}}}}^{2}{{{{{{{\mathcal{K}}}}}}}}},\end{array}$$

(17)

where Φ₀ is the magnetic superconducting flux quantum, see Supplementary Note 1. ${{{{{{{\mathcal{I}}}}}}}}$ and ${{{{{{{\mathcal{J}}}}}}}}$ in Eq. (16) are given by the integrals

$$\begin{array}{r}{{{{{{{\mathcal{I}}}}}}}}=\int| {{\Psi }}{| }^{2}\left(1-| {{\Psi }}{| }^{2}\right){d}^{2}{{{{{{{\bf{r}}}}}}}},\,{{{{{{{\mathcal{J}}}}}}}}=\int| {{\Psi }}{| }^{4}\left(1-| {{\Psi }}{| }^{2}\right){d}^{2}{{{{{{{\bf{r}}}}}}}},\end{array}$$

(18)

where Ψ is a solution of the GL theory given by Eq. (5) at κ_μ = κ₀. Notice, that the leading corrections to the order parameter ψ and the field ${\mathfrak{b}}$ (${\mathfrak{a}}$) are not required to get the leading-order correction to the GL contribution in the Gibbs free energy difference.

IT domain boundaries - analytical results

Using the Gibbs free energy difference (16), one can investigate stability of the IMS vortex configurations and establish boundaries of the IT domain, as it has been previously done for conventional BCS superconductors and multiband superconducting systems^40,41,49,57. However, it is to be noted that Eq. (16) differs from the earlier result^40,41,49,57. First, there are two additional contributions including the scaled parameters γ and ${{{{{{{{\mathcal{K}}}}}}}}}_{{{{{{{{\rm{m}}}}}}}}}$ and related to the magnetic subsystem. Second, the small quantities δκ_μ and τ are not independent in the present case because κ_μ is temperature dependent. It is important, however, that the appearance of the Gibbs free energy difference (16) is the same as for a standalone BCS superconductor. This makes sure that the mechanism underlying the IT superconductivity regime - lifting the degeneracy of the system at the B point - remains also similar, and one can use the same criteria to determine the IT domain boundaries in the κ-T plane^40,41,49,57.

The boundary between the IT and type-I superconductivity (the lower boundary of the IT domain) is obtained from the condition of the IMS appearance/disappearance expressed by the equality of the thermodynamic and upper critical fields, H_c = H_c2. It is equivalent⁴⁰ to the condition G = 0 defining the point at which a non-homogeneous solution Ψ ≠ 0 becomes energetically favorable at H = H_c. As Ψ → 0, one obtains ${{{{{{{\mathcal{J}}}}}}}}\ll {{{{{{{\mathcal{I}}}}}}}}$, which yields the lower boundary as

$$\begin{array}{r}\frac{{\kappa }_{l}}{{\kappa }_{0}\sqrt{\mu }}=1+\tau \left(1-c+2{{{{{{{\mathcal{Q}}}}}}}}+\gamma \right),\end{array}$$

(19)

where it is taken into account that $\delta {\kappa }_{\mu }=\kappa /\sqrt{\mu }-{\kappa }_{0}$.

The boundary between IT and type II (the upper boundary of the IT domain) is defined by the onset of the long-range vortex-vortex attraction, which makes the mixed state with a vortex lattice unstable at low magnetic fields. The vortex-vortex interaction potential is calculated from G, where one employs the two-vortex solution of the GL equations and keep only the contribution depending on the distance between vortices. Then, changing the sign of the long-range interaction potential is obtained from the condition G = 0 when using the asymptote of the two-vortex solution of the GL equations at large distance R between vortices. As a result, one gets⁴⁰${{{{{{{\mathcal{J}}}}}}}}(R\to \infty )=2{{{{{{{\mathcal{I}}}}}}}}(R\to \infty )$. Substituting this relation into Eq. (16) yields the upper boundary of the IT domain as

$$\begin{array}{r}\frac{{\kappa }_{{{{{{{{\rm{u}}}}}}}}}}{{\kappa }_{0}\sqrt{\mu }}=1+\tau \left(1-3c+4{{{{{{{\mathcal{L}}}}}}}}-\frac{4{{{{{{{\mathcal{Q}}}}}}}}}{3}-\gamma +2\mu {{{{{{{{\mathcal{K}}}}}}}}}_{{{{{{{{\rm{m}}}}}}}}}\right).\end{array}$$

(20)

Finally, we calculate another important critical parameter which divides the IT domain into the part where the energy of the domain wall between the superconductive and normal states is positive and the part where it is negative. The line, separating these parts is found by resolving the equation G = 0, with Ψ corresponding to the domain-wall solution. In this case one gets

$$\frac{{\kappa }_{{{{{{{{\rm{s}}}}}}}}}}{{\kappa }_{0}\sqrt{\mu }}= \,1+\tau \left(1-1.56c+1.12{{{{{{{\mathcal{L}}}}}}}}+1.07{{{{{{{\mathcal{Q}}}}}}}}\right. \\ \left. +0.44\gamma +0.56\mu {{{{{{{{\mathcal{K}}}}}}}}}_{{{{{{{{\rm{m}}}}}}}}}\right),$$

(21)

when using⁴⁰${{{{{{{\mathcal{J}}}}}}}}=0.56{{{{{{{\mathcal{I}}}}}}}}$. Thus, κ_l(T), κ_u(T), and κ_s(T) control all important boundaries of the IT domain in ferromagnetic superconductors under consideration. The presence of the magnetic subsystem is reflected in the fact that these boundaries are dependent on the permeability μ.

IT domain boundaries - numerical results

Numerical results for the IT-domain boundaries are calculated using the model where the superconductivity is created by pairing in a single band with the spherically symmetric Fermi surface and the quadratic dispersion. In this case, the coefficients of the superconducting subsystem are given by the universal constants⁴⁰

$$\begin{array}{r}c=-0.227,\quad {{{{{{{\mathcal{L}}}}}}}}=-0.454,\quad {{{{{{{\mathcal{Q}}}}}}}}=-0.817\end{array}$$

(22)

independent of microscopic parameters such as the band mass or the Fermi velocity. The coefficients in Eqs. (19), (20), and (21) related to the magnetic subsystem are not given by universal constants and depend on the microscopic characteristics of both the superconducting and magnetic subsystems. However, our qualitative results are general and not sensitive to a particular choice of these coefficients. For illustration we choose the dimensionless parameters in Eqs. (19), (20), and (21) as γ = 0 and ${{{{{{{{\mathcal{K}}}}}}}}}_{{{{{{{{\rm{m}}}}}}}}}=1$. Further, we take θ/T_c = 0.5 and α_mT_c = 200, which gives the Curie temperature T_m/T_c = 0.65, as in the GL case discussed above.

Using these parameters we calculate the upper κ_u and lower κ_l boundaries of the IT domain and plot the results in Fig. 1a. In addition, Fig. 1b represents the zoomed part of Fig. 1a. The figures also show the line κ_s with zero surface energy (tension) of the N-S interface and demonstrate the line κ^* that separates the two conventional superconductivity types within the GL theory.

All of the critical lines originate (cross each other) at the B-point given by T = T_c and κ = κ^*(T_c). As is discussed previously, κ^*(T_c) ≠ κ₀ due to the coupling to the magnetic subsystem. At small τ, the qualitative behavior of the IT boundaries are close to that of the conventional BCS superconductors. In particular, κ_l increases, κ_u decreases and κ_s remains almost the same when the temperature is lowered. However, when approaching T_m, all the critical lines bend upwards. However, the internal structure of the IT domain, i.e., the mutual arrangement of the critical lines κ_l < κ_s < κ_u, remains intact. It is defined by the solutions of the GL theory that control the integrals ${{{{{{{\mathcal{I}}}}}}}}$ and ${{{{{{{\mathcal{J}}}}}}}}$ and is qualitatively independent of the parameters in Eq. (16).

Temperature-controlled changes of IMS configurations

Results in Fig. 1 demonstrate that lowering the temperature for κ > κ^*(T_c) [κ^*(T_c) > κ₀] drives the system from type II, when T is close to T_c, to type I, when T approaches T_m. On this way, the whole interval of the IT superconductivity is crossed. As discussed above, the IT domain is characterized by the appearance of the IMS with the vortex structure determined by non-monotonic vortex interactions combining attraction and repulsion. Changes in the relevant vortex configurations and the pairwise interaction are illustrated in Fig. 1c, for more details, see Supplementary Note 2. The interaction potential is calculated by using the GL solution for two vortices at the distance R and extracting the R-dependent part of the Gibbs free energy difference (16). Vortex configurations given in Fig. 1c are also calculated from Eq. (16), where the multi-vortex solution Ψ is combined with the Monte-Carlo simulations to find the lowest energy configurations of vortices, see the previous work⁴¹. This configuration is obtained by keeping the total magnetic flux constant (i.e., the number of vortices is fixed while the temperature is lowered).

Figure 1c demonstrates that crossing the IT interval is accompanied by a universal sequence of transformations of the vortex matter, the same as for conventional BCS superconductors in the IT regime⁴¹. When the line κ_u, separating type II and IT, is crossed, the interaction between vortices changes from fully repulsive to spatially non-monotonic, being attractive at large and repulsive at small distances. This implies rearrangement of vortex configurations at low magnetic fields. They change from the standard hexagonal Abrikosov lattice to the IMS states with vortex clusters having the hexagonal lattice inside.

At lower temperatures, deeper in the IT domain, vortices form the chain-like structures, while the mean distance between them decreases. This is accompanied by the corresponding change in the vortex-vortex interaction potential: its local minimum shifts to smaller inter-vortex distances [Fig. 1c]. In the second part of the IT interval, when κ is below κ_s, the internal structure of vortex clusters changes from the solid to the liquid state. In this case the pairwise vortex interaction becomes fully attractive and the vortex clusters-droplets are stabilized by the many-vortex interactions³².

Conclusions

The interaction between superconducting and magnetic subsystems in superconducting ferromagnetic pnictides gives rise to a temperature dependent crossover from type II to type I. The physics underlying this crossover is related to the paramagnetic response of the magnetic subsystem spins that reduces the magnetic penetration depth of the superconducting condensate. It opens a fascinating possibility to drive the system through the regime of the IT superconductivity simply by varying the temperature, which provides a well-controlled access to unconventional configurations of the IT vortex matter, including vortex clusters, vortex chains, giant vortices, and liquid vortex droplets. This gives an unmatched opportunity to systematically investigate details of the entire IT regime, which has not been yet achieved to date.

In contrast to earlier works, where the IT regime was ascribed only to low-κ superconductors such as Nb^31,39 or ZrB₁₂^58,59, here we demonstrate that in ferromagnetic superconducting pnictides it takes place whenever the material is a type-II superconductor in the vicinity of T_c and the latter exceeds the Curie temperature T_m of the magnetic subsystem. The first condition is satisfied for most superconducting compounds, including pnictides. The second condition can be fulfilled by tuning microscopical structure of the material, e.g., by varying the P-doping parameter x in ${{{{{{{{\rm{EuFe}}}}}}}}}_{2}{({{{{{{{{\rm{As}}}}}}}}}_{1-{{{{{{{\rm{x}}}}}}}}}{{{{{{{{\rm{P}}}}}}}}}_{{{{{{{{\rm{x}}}}}}}}})}_{2}$^11,12,13,14.

One notes (see Fig. 1) that the IT temperature interval shrinks with the rising κ and becomes rather narrow when κ ≫ κ₀. However, the decrease is relatively slow such that the IT domain remains accessible experimentally even at large κ. For example, for the parameters used in Fig. 1, one estimates the temperature IT interval as ΔT = T_u − T_l ≃ 0.01T_c at κ = 10. Given that T_c ≃ 20K for ${{{{{{{{\rm{EuFe}}}}}}}}}_{2}{({{{{{{{{\rm{As}}}}}}}}}_{1-{{{{{{{\rm{x}}}}}}}}}{{{{{{{{\rm{P}}}}}}}}}_{{{{{{{{\rm{x}}}}}}}}})}_{2}$¹⁴, one obtains ΔT ≃ 0.2K, which is well accessible experimentally. For smaller values of κ the IT interval ΔT is larger by an order of magnitude. Even at κ = 100, we find ΔT ≃ 0.01K, which can be still scanned experimentally. We stress that up to date, the vortex states are scarcely investigated in the temperature interval T_m < T < T_c. In order to detect the IT signals above T_m, one needs to scan this interval using fairly small temperature increments.

An important question not addressed in the calculations is the effect of disorder. It is known that the IT domain shrinks significantly in disordered single-band superconductors.³⁷. However, as is expected³⁷, in this case, the IT physics manifests itself in the first-order transition at the upper critical field³⁷, which can be observed experimentally. Furthermore, there is experimental evidence⁶⁰ that many ferromagnetic superconducting pnictides are multiband superconductors, where the aggregate superconducting condensate comprises several partial band-dependent condensates. Until now the IT physics for dirty multiband superconductors remains unexplored. However, based on recent results that the IT domain in clean multiband superconductors tends to expand as compared to the single-band case⁴⁰, one can anticipate the same trend in disordered materials. One way or the other, one can expect that the IT regime can be observed in ferromagnetic superconducting pnictides.

Notice that the IT superconductivity in multiband superconductors is sometimes called the type-1.5 superconductivity, following the article⁶¹. Though some researchers believe that type 1.5 is a unique superconductivity type of multiband systems, this point has long been debated, see e.g., the papers^31,62,63,64. The physics that governs properties of the vortex matter is very much the same in the IT regime of single-band superconductors and in what is attributed to the type-1.5 superconductivity in multiband materials³¹. In both cases, the key characteristics are the nonmonotonic spatial dependence of the vortex-vortex interactions and a significant contribution of the many-vortex component to it. As an example of this similarity, one can compare IT vortex configurations obtained using the models with one and two contributing bands^41,65. The present single-band results and our preliminary calculations for the multiband case demonstrate that irrespective of the number of the available bands, there is the interval of temperatures above T_m, where the system of interest develops the IMS with exotic vortex patterns.

We also note that the calculations are done within the mean field theory and do not take into account magnetic fluctuations, which could become significant close to the Curie temperature T_m. However, it has been recently demonstrated, however, that those fluctuations additionally reduce the magnetic penetration depth, driving the system towards the type-I regime even further⁶⁶. It is, therefore, expected that although the fluctuations will likely shift values of all pertinent quantities, they can hardly change the main conclusion of the work that by reducing the temperature in superconducting ferromagnetic pnictides, one can study details of the IT regime together with its exotic intermediate mixed state configurations.

Finally, it is worth noting that the crossover between superconductivity types and the IT regime can be achieved also in hybrid systems made of alternating superconducting and ferromagnetic layers. The superconducting and magnetic properties of such artificial systems are expected to be similar to those of ${{{{{{{{\rm{EuFe}}}}}}}}}_{2}{({{{{{{{{\rm{As}}}}}}}}}_{1-{{{{{{{\rm{x}}}}}}}}}{{{{{{{{\rm{P}}}}}}}}}_{{{{{{{{\rm{x}}}}}}}}})}_{2}$^11,12,13,14. In the latter, superconductivity and ferromagnetism occur in different atomic layers: the superconducting condensate is facilitated by Fe-3d electrons, while the ferromagnetism appears due to Eu-4f spins. In a hybrid material, the thickness of superconducting layers can serve as an additional tuning parameter to shift the boundaries of the IT domain, e.g., due to the influence of stray magnetic fields outside the sample^67,68. However, the crucial challenge in constructing hybrid systems is to find a quasi-two-dimensional ferromagnetic material with the sufficiently low Curie temperature. Such materials can possibly be fabricated by nano-engineering of artificial van der Waals heterostructures⁶⁹.