Introduction

Optomechanical sensors1,2,3 are widely applicable to high-precision measurements of force4, acceleration5 and magnetic fields6. Recently, they have also shown great value in the study of fundamental physics and the Universe7,8,9,10,11,12,13,14,15,16. For example, the Laser Interferometer Gravitational-Wave Observatory (LIGO), one of the most sophisticated optomechanical sensors humans have built so far, has revealed important information about how black hole binaries merge7. Moreover, optomechanical sensors have found another important application to fundamental physics—the search for Dark Matter (DM)8,9,10,11,12,13,14,15,16, one of the most pressing quests for modern physics.

A key advantage of optomechanical sensors is the ability to read out the displacement of macroscopic mechanical oscillators at the thermal noise limit, with a precision limited by optical shot noise—including, more recently, radiation pressure shot noise (quantum backaction)17. Squeezed light has moreover been used to overcome shot noise and backaction limits, finding application in Advanced LIGO18, chip-scale magnetometry19, and thermometry20.

Looking forward, an emerging set of proposals envisions arrays of optomechanical sensors for detecting weak distributed forces11,21,22. As with the LIGO, these proposals are largely driven by extreme applications such as searching for DM, however, they might also find application in a variety of precision distributed force sensing tasks, such as gravity-based subterranean imaging, ultrasound, and magnetic resonance force imaging. These proposals reveal the benefits of coherent post-processing with an optomechanical array operating at the standard quantum limit (SQL), but explicit details—as well as potential advantages from entanglement-enhanced readout—remain largely unexplored. For instance, in the backaction region, it is unclear whether an optomechanical array can enjoy the entanglement advantages that has been experimentally shown recently outside the backaction region23.

In this work, we propose entanglement-enhanced readout of an array of optomechanical sensors (see Fig. 1), exploiting recently developed techniques in distributed quantum sensing (DQS)24,25,26,27. Building upon the quantum theory of optomechanics28,29,30, we show that, by coherently operating an array of mechanical sensors and utilizing continuous-variable multi-partite entanglement between the optical fields, entanglement enhancement and advantageous scaling with the number of sensors are simultaneously achievable.

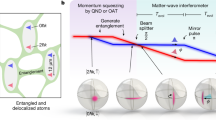
Fig. 1: Illustration of our distributed quantum sensing (DQS) proposal.
figure 1

A stochastic field (e.g., DM field; background cloud) faintly drives an array of mechanical oscillators, in a correlated manner, leading to feeble vibrations of the oscillators' positions. To interrogate the oscillators, squeezed laser light is distributed to the array via passive elements (beam-splitters; glass boxes), which generates an entangled state (represented by purple wiggly lines). The impinging radiation reflects off the oscillators and is detected with homodyne detectors. The measurement results are jointly combined in post-processing, from which the signal is inferred. Inset shows details of homodyne detection. Signal light interferes with a local oscillator (L.O.) on a 50:50 beamsplitter. Photocurrents are measured at the output ports and subtracted to infer the amplitude of the signal.

Full size image

We apply the entanglement-enhanced design to a previously proposed detector based on an array of acoustic-frequency optomechanical accelerometers functionalized to search for ultralight dark photon DM9. As an example, we show that entanglement-enhancement in a network of ten sensors can, in principle, help realize the sensitivities required to exceed existing constraints from MICROSCOPE31,32, Eöt-Wash33, and LIGO/VIRGO34. Our theory applies to a recent proof-of-principle experiment23 and futuristic optomechanical arrays, such as the proposed Windchime project for DM search21,22, and may be relevant to other proposals based on arrays of optical magnetometers35 and atom interferometers36. We note that there exists many possible architectures—including cantilevers, pendula, levitated particles, and high-Q membrane resonators—that can be functionalized to search for DM, as reviewed in Ref. 11, and are furthermore compatible with our proposed entanglement-enhanced readout scheme.

Results and discussions

Our main result is a readout scheme for optomechanical sensor arrays that achieves global noise reduction from distributed squeezing. As sketched in Fig. 1, an array of M sensors jointly measures global properties of the force field. To suppress the measurement noise of the optical readout, a single-mode bright squeezed beam is distributed between each sensor using a passive beamsplitter array. The resultant multi-partite entanglement enables noise correlations and improved sensitivity to global properties of the force (e.g., a weighted average force), equivalent to probing each sensor with an independent single-mode squeezed state but with dramatically reduced overhead. We subsequently apply this approach to an optomechanical accelerometer array designed to search for ultralight DM and project what advantages entanglement offers in concrete constraint space.

Our work extends the paradigm of distributed quantum sensing to optomechanical sensors and shows that entanglement’s advantage can still be achieved despite the presence of backaction and other noise sources. While the basic working principle has been recently demonstrated in Ref. 23 in the low power limit with two sensors, our full modeling of arbitrary M sensors with backaction and thermal noise pave the way towards pushing the experimental systems23 to the back-action limited regime where the best precision can be achieved.

Our analysis on the application to DM search is also parallel to recent efforts in applying quantum sensing technique to microwave-cavity based DM searches. Besides squeezing enhanced microwave search37,38, arrays of microwave cavities have been recently proposed39,40,41,42. In particular, Ref. 42 applies DQS to design an entangled array of microwave cavities for DM search. Our work further extends the paradigm to optomechanical based DM searches.

The results section is organized as the following. We begin by introducing the well-established model of optomechanical force sensing to facilitate our analyses. Then we introduce the performance metric suitable for benchmarking a quantum advantage. Our major results of entangled optomechanical sensor array is presented following the performance metric. Finally, we apply our results to dark matter search scenarios and conclude with experimental projections.

Optomechanical force sensing

For clarity, we start our discussion with a simplified model for optomechanical sensors and then proceed to the full cavity model28,29,30, which includes simplified model in the bad cavity limit. As shown in Fig. 1, each optomechanical sensor is composed of a mirror-like mechanical oscillator which couples dispersively to a free electromagnetic field. DM hypothetically couples to the mechanics and drives the oscillator’s motion.

To detect the motion of the oscillator, one stimulates an input light field \({\hat{E}}^{{{{{{{{\rm{in}}}}}}}}}(t)\), which impinges on the mechanical element, and interferes with the output field \({\hat{E}}^{{{{{{{{\rm{out}}}}}}}}}(t)\) post-interaction. The mechanics completely reflects the input field and induces a small phase shift, \(\zeta \hat{q}(t)\ll 1\), such that \({\hat{E}}^{{{{{{{{\rm{in}}}}}}}}}(t)\to {e}^{{{{{{{{\rm{i}}}}}}}}\zeta \hat{q}(t)}{\hat{E}}^{{{{{{{{\rm{in}}}}}}}}}(t)\), where ζ = 2ΩL/c and \(\hat{q}\) is the position operator of the mechanics. Setting the carrier frequency as zero, we can write out the strong laser mean field E0 explicitly as \({\hat{E}}^{{{{{{{{\rm{in}}}}}}}}}(t)\approx {E}_{0}+\hat{E}(t)\); therefore, the output (including, e.g., detector efficiency, 0 ≤ η2 ≤ 1) can be expressed to leading order as \({\hat{E}}^{{{{{{{{\rm{out}}}}}}}}}(t)\approx \eta \left[{E}_{0}\left(1+{{{{{{{\rm{i}}}}}}}}\zeta \hat{q}(t)\right)+\hat{E}(t)\right],\) where loss-induced vacuum terms are omitted for simplicity. From here, we immediately see that the motion of the oscillator leads to a detectable optical displacement on the field \(i\eta \zeta {E}_{0}\hat{q}(t)\). Going to the Fourier domain, the phase quadrature of the field has the input-output relation (see Supplementary Notes 1 and 3)

$${\hat{Y}}^{{{{{{{{\rm{out}}}}}}}}}(\omega )=\eta \left[{\hat{Y}}^{{{{{{{{\rm{in}}}}}}}}}(\omega )+\sqrt{2}{E}_{0}\zeta \hat{q}(\omega )\right],$$
(1)

while the amplitude quadrature \({\hat{X}}^{{{{{{{{\rm{out}}}}}}}}}(\omega )\) does not pick up the signal.

In order to analyze the setup in a more complete fashion, we present a full optomechanical cavity model28,29,30. We utilize linear input-output theory to describe radiation coupling to an optical cavity with one vibrating mirror (the mechanics). In this theory, the intra-cavity field and the mechanical motion of the mirror are dissipatively coupled to ingoing “bath-modes”—\(({\hat{X}}^{{{{{{{{\rm{in}}}}}}}}},{\hat{Y}}^{{{{{{{{\rm{in}}}}}}}}})\) and \(({\hat{Q}}^{{{{{{{{\rm{in}}}}}}}}},{\hat{P}}^{{{{{{{{\rm{in}}}}}}}}})\)—at dissipation rates κ and γ, respectively. Physically, the bath-modes of the mechanics \(({\hat{Q}}^{{{{{{{{\rm{in}}}}}}}}},{\hat{P}}^{{{{{{{{\rm{in}}}}}}}}})\) describe a thermal bath (at temperature T) that randomly drives the mechanics and leads to random Brownian motion. For the optical cavity, we assume over-coupling at a rate γ and, thus, the ingoing optical bath-modes \(({\hat{X}}^{{{{{{{{\rm{in}}}}}}}}},{\hat{Y}}^{{{{{{{{\rm{in}}}}}}}}})\) describe the photons that are actually sent into (and later emerge from) the optical cavity. The equations of motion for the open quantum system leads to a set of coupled first-order differential equations in the time domain for the intra-cavity modes and the mechanics (\(\hat{X},\hat{Y},\hat{Q}\), and \(\hat{P}\)) in terms of the coupling rates and the ingoing bath modes, which can be analytically solved in the frequency domain. Here, \(\hat{Q}=\hat{q}/\sqrt{2}{q}_{{{{{{{{\rm{zp}}}}}}}}}\) is the normalized position operator, where \({q}_{{{{{{{{\rm{zp}}}}}}}}}\equiv \sqrt{\hslash /2m{{\Omega }}}\) is the zero-point motion, and \(\hat{P}\) is the conjugate momentum. The outgoing fluxes—denoted by the operators \(({\hat{X}}^{{{{{{{{\rm{out}}}}}}}}},{\hat{Y}}^{{{{{{{{\rm{out}}}}}}}}})\) and \(({\hat{Q}}^{{{{{{{{\rm{out}}}}}}}}},{\hat{P}}^{{{{{{{{\rm{out}}}}}}}}})\)—are then determined via the input-output relations \({\hat{X}}^{{{{{{{{\rm{out}}}}}}}}}={\hat{X}}^{{{{{{{{\rm{in}}}}}}}}}-\sqrt{\gamma }\hat{X}\) etc.; see Refs. 28,29 and Supplementary Notes 4 for further details.

An exact output relation for the spectral amplitude of the phase quadrature can be found28,29,

$${\hat{Y}}^{{{{{{{{\rm{out}}}}}}}}}(\omega )=-{{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}{\varphi }_{\omega }}{\hat{Y}}^{{{{{{{{\rm{in}}}}}}}}}(\omega )+2\sqrt{2\gamma {C}_{\omega }}\hat{Q}(\omega ),$$
(2)

where the phase φω and the optomechanical cooperativity Cω are defined via

$$\begin{array}{r}{{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}{\varphi }_{\omega }}\equiv \left(\frac{\kappa /2+{{{{{{{\rm{i}}}}}}}}\omega }{\kappa /2-{{{{{{{\rm{i}}}}}}}}\omega }\right),{C}_{\omega }\equiv \frac{2{G}^{2}/\gamma \kappa }{{(1-2{{{{{{{\rm{i}}}}}}}}\omega /\kappa )}^{2}}=\left\vert {C}_{\omega }\right\vert {{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{i}}}}}}}}{\varphi }_{\omega }}.\end{array}$$
(3)

Here G ≡ EG0 is the cavity-enhanced optomechanical coupling-rate, G0 is the vacuum optomechanical coupling rate, and E is the intra-cavity field (taken to be real). The intra-cavity field, E, is related to the amplitude of the input field, E0, via \({E}^{2}=(4{\kappa }_{r}/{\kappa }^{2}){E}_{0}^{2}\), where κ is the total dissipation-rate of the cavity and κr is the dissipation-rate to the readout port. Here, the spectral amplitude of the oscillator’s position, \(\hat{Q}(\omega )\), is given as,

$$\hat{Q}(\omega )=2\sqrt{\gamma }{\chi }_{\omega }\left({\hat{P}}^{{{{{{{{\rm{in}}}}}}}}}(\omega )-\sqrt{2{C}_{\omega }}{\hat{X}}^{{{{{{{{\rm{in}}}}}}}}}(\omega )\right)+{Q}_{{{{{{{{\rm{dr}}}}}}}}}(\omega ),$$
(4)

where Qdr(ω) is the diplacement induced by the driving force, Fdr, and is related via \({F}_{{{{{{{{\rm{dr}}}}}}}}}(\omega )\equiv (\sqrt{\hslash m{{\Omega }}}/{\chi }_{\omega }){Q}_{{{{{{{{\rm{dr}}}}}}}}}(\omega )\) and χω = Ω/(Ω2 − ω2 − i2γω) is the mechanical susceptibility. The term proportional to the amplitude quadrature, \({\hat{X}}^{{{{{{{{\rm{in}}}}}}}}}\), represents the fluctuation of the oscillator’s position due to radiation pressure.

With the complete cavity optomechanics model, we recover the mechanical motion induced quadrature displacement identified in Eq. (1) in the simplified model. The relation can be made quantitative by treating the output mirror in the cavity model as a transparent window, see Supplementary Notes 3 and 4 for further comparisons.

We estimate the force impressed on the mechanics from homodyne measurements on the phase-quadrature via

$$\hat{F}(\omega )\equiv \frac{{{{{{{{{\rm{e}}}}}}}}}^{-{{{{{{{\rm{i}}}}}}}}{\varphi }_{\omega }/2}}{{\chi }_{\omega }}\sqrt{\frac{\hslash m{{\Omega }}}{8\gamma \left\vert {C}_{\omega }\right\vert }}{\hat{Y}}^{{{{{{{{\rm{out}}}}}}}}}(\omega ),$$
(5)

which has units N\(\cdot {{{{{{{{\rm{Hz}}}}}}}}}^{-\frac{1}{2}}\). We are often interested in the power spectral density (PSD) of the force, as force can be random. For any time-dependent operators \(\hat{O},{\hat{O}}^{{\prime} }\) with stationary statistics, the PSD is defined as

$${S}_{\hat{O}{\hat{O}}^{{\prime} }}(\omega )=\frac{1}{2\pi }\int\nolimits_{-\infty }^{+\infty }{{{{{{{\rm{d}}}}}}}}{\omega }^{{\prime} }\left\langle {\hat{O}}^{{{{\dagger}}} }(-\omega )\hat{{O}^{{\prime} }}({\omega }^{{\prime} })\right\rangle ,$$
(6)

where \({\hat{O}}^{{{{\dagger}}} }(\omega )\) is the Fourier transform of the time-domain operator. We also define a symmetrized PSD, \({\bar{S}}_{\hat{O}{\hat{O}}^{{\prime} }}(\omega )\equiv [{S}_{\hat{O}{\hat{O}}^{{\prime} }}(\omega )+{S}_{\hat{O}{\hat{O}}^{{\prime} }}(-\omega )]/2\). When \(\hat{O}={\hat{O}}^{{\prime} }\), we simplify the notation as \({S}_{\hat{O}}(\omega )\). With the above definition, a general expression for the noise PSD (in units of N2 ⋅ Hz−1) can also be derived,

$${\hskip -1pt}{\bar{S}}_{{F}_{{{{{{{{\rm{noise}}}}}}}}}}(\omega )\, =\, \frac{\hslash m{{\Omega }}}{8\gamma \left\vert {C}_{\omega }\right\vert {\left\vert {\chi }_{\omega }\right\vert }^{2}}{\bar{S}}_{{\hat{Y}}^{{{{{{{{\rm{in}}}}}}}}}}(\omega )+8\hslash m\gamma {{\Omega }}\left\vert {C}_{\omega }\right\vert {\bar{S}}_{{\hat{X}}^{{{{{{{{\rm{in}}}}}}}}}}(\omega )\\ +\frac{2\hslash m{{\Omega }}}{\left\vert {\chi }_{\omega }\right\vert }{{{{{\mathrm{Re}}}}}} \left(\frac{{\chi }_{\omega }}{\left\vert {\chi }_{\omega }\right\vert }{\tilde{S}}_{{\hat{X}}^{{{{{{{{\rm{in}}}}}}}}}{\hat{Y}}^{{{{{{{{\rm{in}}}}}}}}}}(\omega )\right)+4\hslash m\gamma {{\Omega }}{\bar{S}}_{{\hat{P}}^{{{{{{{{\rm{in}}}}}}}}}}(\omega ),$$
(7)

where we have defined,

$${\tilde{S}}_{{\hat{X}}^{{{{{{{{\rm{in}}}}}}}}}{\hat{Y}}^{{{{{{{{\rm{in}}}}}}}}}}(\omega )\equiv \frac{{S}_{{\hat{X}}^{{{{{{{{\rm{in}}}}}}}}}{\hat{Y}}^{{{{{{{{\rm{in}}}}}}}}}}(\omega )+{S}_{{\hat{X}}^{{{{{{{{\rm{in}}}}}}}}}{\hat{Y}}^{{{{{{{{\rm{in}}}}}}}}}}^{* }(-\omega )}{2}.$$
(8)

The first term in Eq. (7) is the shot noise, the second term is the back-action noise due to radiation pressure, the third term encodes the quadrature correlations, and the fourth term consists of mechanical fluctuations—e.g., \({\bar{S}}_{{P}^{{{{{{{{\rm{in}}}}}}}}}}\approx {K}_{B}T/\hslash {{\Omega }}\) for thermally dominated fluctuations. The SQL can be obtained by assuming initial vacuum fluctuations (\({\bar{S}}_{{\hat{Y}}^{{{{{{{{\rm{in}}}}}}}}}}={\bar{S}}_{{\hat{X}}^{{{{{{{{\rm{in}}}}}}}}}}=1/2\) and \({\tilde{S}}_{{\hat{X}}^{{{{{{{{\rm{in}}}}}}}}}{\hat{Y}}^{{{{{{{{\rm{in}}}}}}}}}}=0\)) and choosing \(\left\vert {C}_{\omega }\right\vert =1/8\gamma \left\vert {\chi }_{\omega }\right\vert\), then (ignoring mechanical noise) the noise at the SQL is \({\bar{S}}_{{F}_{{{{{{{{\rm{noise}}}}}}}}}}^{{{{{{{{\rm{SQL}}}}}}}}}\equiv \hslash m{{\Omega }}/\left\vert {\chi }_{\omega }\right\vert\). We can also incorporate detection loss 1 − η2 in the cavity model via the simple substitution \({\bar{S}}_{{F}_{{{{{{{{\rm{noise}}}}}}}}}}\to {\bar{S}}_{{F}_{{{{{{{{\rm{noise}}}}}}}}}}+\frac{1-{\eta }^{2}}{{\eta }^{2}}(\hslash m{{\Omega }}/16\gamma \left\vert {C}_{\omega }\right\vert {\left\vert {\chi }_{\omega }\right\vert }^{2})\); see Supplementary Notes 4 for more discussion on loss.

Quantifying performance

Since the mass of the DM signal is a priori unknown, one must integrate over many frequencies to rule out a range of potential masses for DM43,44,45,46,47,48,49,50. Hence, detection bandwidth of the setup is paramount, however sensitivity is equally important, as such is needed to quickly build statistical confidence in our measurements. A general figure of merit for broadband sensing of an incoherent force, which takes both sensitivity and bandwidth into account, is the integrated sensitivity,

$${{{{{{{{\mathcal{I}}}}}}}}}_{{{\Omega }}}\equiv \int\nolimits_{0}^{\infty }{\left(\frac{{\bar{S}}_{{F}_{{{{{{{{\rm{dr}}}}}}}}}}(\omega )}{{\bar{S}}_{{F}_{{{{{{{{\rm{noise}}}}}}}}}}(\omega )}\right)}^{2}\frac{{{{{{{{\rm{d}}}}}}}}\omega }{\pi }.$$
(9)

For a thorough discussion about the integrated sensitivity being a good figure of merit in DM searches, see Refs. 51,52 and Supplementary Note 2 for further discussion. Later, we evaluate the integrated sensitivity for an array of M sensors and denote the quantity as \({{{{{{{{\mathcal{I}}}}}}}}}_{{{\Omega }}}^{(M)}\).

With regards to a DM search, the hypothetical DM signal is sharply peaked around some frequency, the value of which is unknown. We assume no prior knowledge about where the DM signal may be in frequency space, and thus, each frequency bin is equiprobable to contain a signal. We can thus characterize the signal with a flat spectrum. The principal figure of merit is then the detector response over a large band of frequencies. Assuming \({\bar{S}}_{{F}_{{{{{{{{\rm{dr}}}}}}}}}}\) is approximately flat over the integration range, we find the integrated sensitivity for the SQL, \({{{{{{{{\mathcal{I}}}}}}}}}_{{{\Omega }}}^{{{{{{{{\rm{SQL}}}}}}}}}/{\bar{S}}_{{F}_{{{{{{{{\rm{dr}}}}}}}}}}^{2}=4\gamma /{(\hslash m{{\Omega }}\gamma )}^{2}\), which is the ratio of the mechanical linewidth, γ, and the on-resonance PSD at the SQL, \({\bar{S}}_{{F}_{{{{{{{{\rm{noise}}}}}}}}}}^{{{{{{{{\rm{SQL}}}}}}}}}({{\Omega }})=\hslash m{{\Omega }}\gamma /2\). Without quantum resources, this sets the ultimate classical limit in broadband detection for a given set of mechanical parameters m,  γ,  and Ω, which in turn imposes limits on a DM search with a mechanical system.

Entangled optomechanical sensor array

Squeezing the input radiation is known to increase the effective bandwidth in optomechanical sensing while leaving the peak sensitivity (set by the SQL) the same19,53,54,55,56,57,58,59,60, thus resulting in squeezing-enhanced broadband sensing. Here, we extend the results on squeezing-enhanced broadband sensitivity to entanglement-enhanced broadband sensitivity with an array of M mechanical sensors. In our setup, the optomechanics are not directly coupled across the array; rather, we allow for mixing of the input and output optical fields via linear optical elements (Fig. 1). We further suppose that the stochastic drive force (e.g., the DM field) impresses a correlated displacement on the sensors. We show that, by utilizing entangled optical fields to measure the mechanics, the squeezing-enhancement demonstrated for a single sensor19,53,54,55,56,57,58,59,60 naturally extends to a sensor-array with the same amount of squeezed photons.

Consider M input modes, \({\{{\hat{a}}_{n}^{{{{{{{{\rm{in}}}}}}}}}\}}_{n = 0}^{M-1}\), and a strong laser field at center frequency ΩL on the \({\hat{a}}_{0}^{{{{{{{{\rm{in}}}}}}}}}\) mode, with frequency-dependent squeezed sidebands that lowers noise around the mechanical frequency. This mode is mixed with the idling input-modes (consisting of uncorrelated vacuum fluctuations) of the remaining M − 1 inputs via linear optical elements described by the dividing-weights {wn0}, with \({w}_{n0}\in {\mathbb{C}}\). After interaction with the mechanics, we measure the outgoing phase quadrature at each sensor, \({\hat{Y}}_{n}^{{{{{{{{\rm{out}}}}}}}}}\), via homodyne detection (see Supplementary Note 5). In post-processing, we convert the measurement result at the nth sensor to a force measurement via the relation (5) and write the resulting value as \({\hat{F}}_{n}\). We then statistically combine the signals from each sensor with combining-weights {W0n}, with \({W}_{0n}\in {\mathbb{C}}\), and construct a weighted average force estimator,

$$\hat{\overline{F}}(\omega )\equiv \mathop{\sum }\limits_{n=0}^{M-1}{W}_{0n}{\hat{F}}_{n}(\omega ).$$
(10)

In this manner, we capitalize on the correlations of the stochastic drive field (e.g., the spatial-uniformity of the DM field) across the array to achieve favorable scaling with the size of the array.

Suppose that the drive force obeys the following statistics, \(\langle {\hat{F}}_{{{{{{{{\rm{dr}}}}}}}},n}{\hat{F}}_{{{{{{{{\rm{dr}}}}}}}},{n}^{{\prime} }}\rangle ={{{{{{{{\mathcal{M}}}}}}}}}_{n}{{{{{{{{\mathcal{M}}}}}}}}}_{{n}^{{\prime} }}{f}^{2}\), where f is common to each sensor and \({{{{{{{{\mathcal{M}}}}}}}}}_{n}\) is a sensor dependent pre-factor. The signal PSD of the force is then,

$${\bar{S}}_{{\hat{F}}_{{{{{{{{\rm{dr}}}}}}}}}}^{(M)}(\omega )={\left\vert \mathop{\sum }\limits_{n = 0}^{M-1}{W}_{0n}{{{{{{{{\mathcal{M}}}}}}}}}_{n}\right\vert }^{2}{f}^{2}.$$
(11)

Consider the ideal scenario where all the sensors are identical. In this case, the dividing- and combining-weights are chosen to satisfy \({\sum }_{k}{W}_{0n}^{* }{w}_{k0}={\delta }_{nk}\) and \(\left\vert {w}_{k0}\right\vert =\left\vert {W}_{k0}\right\vert =1/\sqrt{M}\). In words, since the performance of each sensor is identical and the response of each sensor to the drive force is identical, the best strategy is to distribute the input radiation uniformly to each sensor and then uniformly combine the signals. The signal PSD in the ideal setting is M times the single-sensor signal PSD (\({\bar{S}}_{{\hat{F}}_{{{{{{{{\rm{dr}}}}}}}}}}^{(M)}=M{\bar{S}}_{{\hat{F}}_{{{{{{{{\rm{dr}}}}}}}}}}\)) which follows directly from Eq. (11). This is due to the classical correlations of the drive field across the array which we take advantage of via coherent post-processing.

Let us now consider the noise PSD. If we scale the laser power with the number of sensors, \({E}_{0}^{2}\to M{E}_{0}^{2}\), such that the power per sensor is held fixed as we increase the number of sensors, then the multi-sensor force noise (see Supplementary Note 5 for details) reduces to the single-sensor force noise of Eq. (7). Therefore, it follows that we can use an equal amount of squeezing in a multi-sensor setup as in a single-sensor setup to achieve an equivalent noise reduction; this comes along with an M-factor boost to the signal due to coherent post-processing as previously mentioned.

Our results are captured in Fig. 2, where we plot the integrated sensitivity for an array of identical sensors versus the number of sensors. To generate the data, we assume the mechanical sensors have similar parameters with Refs. 9—resonance frequencies at Ω = 2 kHz, mechanical quality factors of Q = 109, and masses of m = 6 mg with each operating at T = 10mK. The sensors act end mirrors for high-finesse optical cavities of 1 mm lengths with κ = . 94 GHz (corresponding to a finesse \({{{{{{{\mathcal{F}}}}}}}} \sim 1000\)). The input light has wavelength of 1.06 μm, and the power per sensor is chosen to be P = 2 mW.

Fig. 2: Scaling of the integrated sensitivity versus the number of mechanical sensors M.
figure 2

Red curve represents a distributed quantum sensing (DQS) scheme with 10 dB input squeezing uniformly distributed across the array (M2 scaling). Blue curve represents a classical scheme with coherent post-processing (M2 scaling). Black dotted curve represents a classical scheme that operates each sensor independently (M scaling). DQS scheme permits a constant factor improvement (factor of 100 here) for all M that depends on the amount of squeezing (10 dB here).

Full size image

For the DQS setup (red curve), a bright squeezed beam, with 10 dB squeezing (Ns = 2.03 squeezed photons) and frequency dependent squeezing angle \(\theta ={\theta }_{\omega }^{\star }\), is distributed uniformly across the array; see Refs. 56,57,58,59, where tunability of the squeezing angle in optomechanical systems is addressed (see Supplementary Notes 4 and 5). We observe scaling enhancements for the DQS setup as well as for the classical setup with coherent processing (blue curve). The classical setup and the DQS setup enjoy a quadratic scaling enhancement over the independent sensor setup [Classical (Incoh.); black dotted] by leveraging spatial correlations of the drive field. On top of the scaling advantage, our DQS setup achieves a constant factor improvement over the classical scheme for all values of M, due to compounding the benefits of classical correlations from the drive field that boosts the signal and quantum correlations between the optical fields that results in a broadband reduction of the noise.

We stress that independent sensors cannot achieve the performance of our proposed DQS array with the same amount of squeezing—no matter the input laser power. Moreover, if we allow for joint post-processing but do not allow for entanglement between the modes, then M independent bright squeezed beams—each with Ns number of squeezed photons—must be utilized in order to achieve the same performance as our DQS setup. This implies that the improvement in our DQS scheme is not necessarily due to the amount of squeezed light that impinges on a single mechanical oscillator but, rather, is a consequence of the quantum correlations between the optical fields that impacts the mechanics as a collective.

DQS versus separable schemes

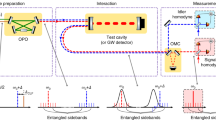
Here, we elaborate on the differences between distributed quantum sensing (DQS) and distributed classical sensing (DCS) schemes; see Fig. 3. In the DQS scheme (Fig. 3a), an input entangled state of M modes is prepared by splitting a bright squeezed beam of Ns squeezed photons (and \(M{E}_{0}^{2}\) total laser power) between the modes. The entangled radiation is then distributed to an array of M mechanical oscillators, after which the signals are jointly post-processed. In the DCS scheme with squeezed light (Fig. 3b), M bright squeezed beams—each with Ns number of photons (and power \({E}_{0}^{2}\) per beam)—are generated and independently distributed to M mechanical oscillators; likewise, the signals are jointly post-processed. These two schemes are equivalent in terms of their performance (quantified via, e.g., the SNR or the integrated sensitivity), however the former DQS scheme demands only Ns squeezed photons whereas the DCS scheme requires MNs squeezed photons. For a local sensor array where distributing the squeezing is easy, this represents a significant quantum resource reduction. The conceptual difference between these two setups is that the former utilizes multi-partite entanglement to correlate the shot-noise and radiation pressure fluctuations across the sensor array—therefore alleviating the total measurement noise.

Fig. 3: Illustration depicting distributed quantum sensing (DQS) and distributed classical sensing (DCS) schemes.
figure 3

a A DQS scheme, where a bright squeezed beam with laser power \(M{E}_{0}^{2}\) and Ns squeezed photons is distributed through a passive linear network—generating an entangled state—to an array of M mechanical oscillators. b A DCS scheme, where M bright squeezed beams—each with laser power \({E}_{0}^{2}\) and Ns squeezed photons—impinge on an array of M mechanical oscillators. These two setups have equal performance, but the DQS scheme requires only ns = Ns/M squeezed photons per sensor while the DCS scheme requires ns = Ns squeezed photons per sensor. In dB, the squeezing per sensor is \({s}_{{{{{{{{\rm{dB}}}}}}}}}:=20{\log }_{10}\left((\sqrt{{n}_{s}+1}+\sqrt{{n}_{s}})/2\right)\).

Full size image

Dark matter searches as force sensing

A particular application of our results is in DM search. The evidence for the existence of DM are ubiquitous—such as the cosmic microwave background survey61,62, gravitational lensing63 and rotation curves of spiral galaxies64,65,66,67—with a consistent DM mass ranging over eighty orders of magnitude. Depending on the DM model, various types of DM sensors have been designed. In models where DM consists of axions, DM can be converted to photons in a background magnetic field; therefore microwave cavities immersed in a powerful magnetic field are leveraged for a DM search37,38,43,44,45,46,47,48,49,50,68. In other models, DM induces forces on normal matter; therefore mechanical sensors good at sensing weak forces can be used for a DM search8,9,10,11,12,13,14,15,16,68.

Optomechanical sensor arrays have seen a resurgence of interest in the context of DM searches11, spurred by the possibility of direct gravitational detection of DM particles21 and various theories which posit coupling of DM to the size or position of atoms69,70. Wavelike ultralight DM (ULDM)—particles whose deBroglie wavelength λDM exceeds the spacing predicted by the local DM energy density, implying condensation into a wavelike fluid—has received particular attention, since it may manifest as a coherent force field. Indeed, for particle masses mDM = 10−14 − 10−8 eV/c2, ULDM could produce a force oscillating at the Compton frequency ΩDM = mDMc2/ℏ = 2π × (1 Hz − 1 MHz) with a wavelength λDM = h/(mDMνDM) = 10 km − 1 mm, and a doppler-broadened linewidth of \({{\Delta }}{\Omega }_{{{\mbox{DM}}}}={{{\Omega }}}_{{{\mbox{DM}}}}{({{\Delta }}{\nu }_{{{\mbox{DM}}}}/c)}^{2}\approx 1{0}^{-6}{\omega }_{{{\mbox{DM}}}}\), respectively (where νDM ≈ 10−3c is average particle speed, coinciding with the orbital velocity of solar system). These values fortuitously coincide with the frequency, size/distribution, and Q factor of terrestrial mechanical oscillators, ranging from the earth iself70 to micromechanical resonators8,9.

Two types of ULDM forces are typically considered: scalar (body) forces, which couple to breathing-mode mechanical resonators (e.g. bulk acoustic wave resonators)8,70, and vector forces, which couple to center-of-mass-mode resonators (e.g. cantilevers)9,69. Without loss of generality, we specialize to vector ULDM.

Vector ULDM produces a force field oscillating at ΩDM with coherence time τDM ~ 1/ΔΩDM69. On timescales less than τDM, the force can be expressed as

$$\begin{array}{r}{F}_{{{{{{{{\rm{dr}}}}}}}}}(t)\simeq {F}_{{{{{{{{\rm{DM}}}}}}}}}\cos ({{{\Omega }}}_{{{{{{{{\rm{DM}}}}}}}}}t+\varphi ),\end{array}$$
(12)

where \({F}_{{{{{{{{\rm{DM}}}}}}}}}=g\sqrt{2{e}^{2}{\rho }_{{{{{{{{\rm{DM}}}}}}}}}/3{\epsilon }_{0}}{{{{{{{\mathcal{M}}}}}}}}\) is the average amplitude (including the effect of random polarization)10,11,69. Here, g quantifies the coupling between DM and normal matter, e is the elementary charge, ρDM is the DM mass density, ϵ0 is the vacuum permittivity, and \({{{{{{{\mathcal{M}}}}}}}}\, \lesssim \, 1\) is a correction factor that depends on material and geometrical properties of the sensor. On timescales greater than τDM, the force can be described as stationary process with PSD \({S}_{{F}_{{{{{{{{\rm{dr}}}}}}}}}}[{{{\Omega }}}_{{{\mbox{DM}}}}] \sim {F}_{{{{{{{{\rm{DM}}}}}}}}}^{2}/{{\Delta }}{\Omega }_{{{\mbox{DM}}}}\).

We re-emphasize that for frequencies under consideration ΩDM ~ kHz the DM field’s de Broglie wavelength is λDM ~ 105 km; this length-scale is pertinent for detector arrays that wish to take advantage of the signal correlations over the extent of the array.

Example: entanglement-enhanced accelerometer array to search for vector B − L dark matter

Broadly speaking, all optomechanical inertial force sensors (sensitive to changes in the center-of-mass of the device platform) can be functionalized to search for vector ULDM9. A recent review enumerates possible architectures11, focusing on nano- to centimeter-scale mechanical resonators, which are simultaneously arrayable and cryogenics-compatible. These include cantilevers, pendula, levitated particles, and high-Q membrane resonators. The latter two are leading platforms in contemporary quantum optomechanics and have been probed at the SQL at cryogenic temperatures71,72.

To illustrate the potential benefits of entanglement-enhaced readout with a concrete system in mind, we consider a recently proposed vector ULDM detector based on an array of membrane-based optomechanical accelerometers9,16, similar in design and operation to the dual-membrane sensor employed in a recent demonstration of entanglement-enhanced optomechanical sensing23. In brief, each membrane, made of Si3N4, acts as an end-mirror in a finesse ~ 100 optical cavity made of neutron dense Be, rendering it sensitive to a vector force proportional to the Baryon-Lepton (i.e., neutron) charge—a well-motivated DM coupling mechanism69. The membranes are centimeter-scale, support flexural modes in the 1–10 kHz band, are assumed to have quality factors Q ~ 109, and are housed in a 10 mK dilution refrigerator to minimize thermal noise.

Figure 4 gives projections for the minimum detectable DM coupling strength gB-L9 using an array of membrane-based optomechanical accelerometers probed with and without entanglement enhancement. Optical and mechanical properties of each sensor are the same as in Fig. 2 (deliberately chosen to coincide with the parameters in9), corresponding to a 20 cm membrane with a 2 kHz resonance frequency. For a single sensor, the probe strength is chosen to give a backaction-limited acceleration sensitivity of ~ 10−11ms−2Hz−1/2 on resonance, yielding a minimum detectable DM coupling strength of gB-L ~ 10−25 after an averaging time of 1 year (light blue curve, M = 1). For comparison, we also show leading constraints from MICROSCOPE31,32 (green shaded region), Eöt-Wash33 (gray shaded), and LIGO/VIRGO34 (purple shaded) experiments.

Fig. 4: Projections for minimum detectable coupling strength gB−L.
figure 4

Shaded regions in the main plot indicate existing experimental constraints on coupling strength gB−L from MICROSCOPE (green)31,32, Eöt-Wash (gray)33, and LIGO/VIRGO (purple)34. For comparison, we show the single-sensor (M = 1) classical setup and M = 10 independently operated sensors. A classical scheme implementing coherent post-processing but no quantum resources is also shown as well as our proposed distributed quantum sensing (DQS) scheme. The standard quantum limit (SQL) and DQS limit are highlighted (dashed blue and dashed red curves, respectively). Inset shows the spectrum around the mechanical resonance frequency. Classical sensing schemes lie strictly above the blue shaded region (determined by the SQL) while the DQS scheme can dip below the SQL but is ultimately limited by the amount of squeezing (10 dB of squeezing here).

Full size image

The progression of blue and red curves in Fig. 4 explores the advantage of coherently and incoherently processed M = 10 sensor arrays, with and without entanglement. Arrays probed with a coherent (classical) state still have improved sensitivity over a single sensor, by \(\root 4 \of {M}\) and \(\sqrt{M}\) (in gB−L units), respectively, for incoherent and coherent signal processing (darker blue curves). Assuming no loss, arrays probed with a distributed 10 dB bright squeezed beam achieves a further \(\sqrt{10}\) improvement (red curve), yielding a \(\sqrt{10M}\)-fold improvement over a single classical sensor and beating the SQL for a classical sensor array (blue dotted). One could further increase the power per sensor (in this case to P = 10 mW) to reach the DQS limit (red dotted) in the shot-noise-dominated region (10−2-100 kHz), giving access to a broader range of unexplored coupling strengths and frequencies.

We note that while the single sensor parameters in our example9 are rooted in state-of-the-art membrane optomechanics experiments (with the exception of 10 cm membranes, which more likely will be realized by equivalent mass-loading73,74), the challenge of array based optomechanical sensing—classical and entangled—remains largely unexplored. A key challenge will be the identification of platforms which permit sufficiently low optical loss to take advantage of entanglement. As a reference, the recent demonstration23 of an entanglement-enhanced M = 2 optomechanical sensor array had an overall loss of 51% (18% due to the sensor itself), sufficient to degrade 5 dB of squeezing to an effective 2.4 dB. As with gravitational wave interferometry, the time horizon and perceived importance of DM searches may be expected to drive future performance improvements.

Conclusions

In this work, we propose an entangled network of optomechanical sensors for force sensing. The joint coherent processing of the sensors enable an improved scaling of integrated sensitivity versus the number of sensors. By entangled optical inputs, a single bright squeezed beam can enable simultaneous global noise reduction of M sensors when jointly processing the readout. In comparison, to achieve the same performance, separable sensor networks will require M bright squeezed beams, leading to a large overhead in the required quantum resources. Such a protocol is in particularly suitable for dark matter search, as the goal is to search for feeble force across a large possible bandwidth. We provide projected performance of such an entangled network of optomechanical sensors in dark matter search, showing promising improvement in the minimum detectable coupling strength of dark matter. Our theory proposal is recently demonstrated23 and paves the way towards ultra-precise broadband force sensing for different applications.

Before we end, we clarify the connections to previous works of some of the authors. Ref. 9 addresses a single classical opto-mechanical sensor for DM search, without any quantum effect such as squeezing or entanglement; Ref. 23 is an experiment demonstration of opto-mechanical force sensing performed in the low power limit, where backaction is not manifested and no DM scan is performed to provide benchmark. Ref. 42 considers entangled microwave cavities for DM search, where the physical system is entirely different from the current work (e.g., one does not usually discuss radiation pressure noise in the cavity systems).

Methods

Details on experimental projections

As a concrete example of entanglement-enhanced readout of DM-detectors, we consider the detector proposed in9: a membrane-based optomechanical accelerometer deployed as a resonant sensor for vector ultralight dark matter (ULDM), specifically, B − L (“baryon minus lepton”) ULDM. Vector ULDM—a field-like DM-candidate expected to produce material-dependent acceleration signals oscillating at the DM Compton frequency—could produce center-of-mass motion in membranes by driving their highly sensitive flexural modes. Cavity-enhanced readout of membrane motion can be further boosted by using a DQS scheme over an array of membrane accelerometers.

In the presence of vector B-L ULDM, different materials would experience an oscillating acceleration with amplitude determined by the B-L charge density of the material. Over timescales less than the ULDM coherence time, an atom or molecule with Zi protons, Ai nucleons, and total mass mi would experience an approximately sinusoidal acceleration69

$${a}_{i}(t)\simeq {g}_{{{\mbox{B-L}}}}\left(\frac{{A}_{i}-{Z}_{i}}{{m}_{i}}\right)\sqrt{\frac{2{e}^{2}{\rho }_{{{\mbox{DM}}}}}{{\epsilon }_{0}}}\cos ({{{\Omega }}}_{{{{{{{{\rm{DM}}}}}}}}}t+\varphi )$$
(13)

where gB-L quantifies the coupling between vector DM and B-L charge, ρDM is the local DM energy density, ΩDM is the ULDM Compton frequency, φ is a random and unknown phase, e is the elementary charge, and ϵ0 is the vacuum permittivity. Integrating this acceleration over the entire detector, one can express the vector ULDM signal simply as a driving force \({F}_{{{{{{{{\rm{dr}}}}}}}}}(t)\simeq {F}_{{{{{{{{\rm{DM}}}}}}}}}\cos ({{{\Omega }}}_{{{{{{{{\rm{DM}}}}}}}}}t+\varphi )\) on a mechanical oscillator where

$${F}_{{{{{{{{\rm{DM}}}}}}}}}=g\sqrt{2{e}^{2}{\rho }_{{{{{{{{\rm{DM}}}}}}}}}/3{\epsilon }_{0}}{{{{{{{\mathcal{M}}}}}}}}.$$
(14)

Here, \({{{{{{{\mathcal{M}}}}}}}}\) is a geometrical and material-dependent parameter that characterizes the coupling between the vector ULDM field and the detector, and the factor 3 in the denominator is introduced to account for the average projection of the ULDM field polarization along the detector’s axis69 (see also the Supplemental Material from Ref. 9).

The ULDM accelerometers proposed in9 employ cm-scale stoichiometric silicon nitride (Si3N4) nanomembranes as test masses. Their fundamental flexural modes resonate at 1–10 kHz frequencies, corresponding to 1–100 peV DM mass. Higher-order flexural modes acting as independent test masses and spanning decades of frequency up to ~ 1 MHz are simultaneously accessible, though we analyze only the fundamental mode here. On resonance, acceleration signals would be amplified by the mechanical quality (Q) factor; Q’s exceeding 1 billion are achievable in membrane-based silicon nitride structures75,76. For readout, the membranes would serve as highly reflective (after photonic patterning77,78) end-mirrors in optical cavities.

To create Fig. 4 of the main text, we consider the detector to be a mg-scale square membrane with a side length of 20 cm and a thickness of 200 nm, resulting in a fundamental resonance frequency around 2 kHz, whose motion is monitored with an averaging time of 1 year. Following Ref. 9, the membrane is assumed to be fixed to a beryllium substrate in order to gain sensitivity to the material-dependent acceleration produced by vector ULDM. For this detector design, \({{{{{{{\mathcal{M}}}}}}}}=\left\vert \frac{{Z}_{{{{\rm SiN}}}}}{{m}_{{{{\rm SiN}}}}}-\frac{{Z}_{{{{\rm Be}}}}}{{m}_{{{{\rm Be}}}}}\right\vert m{\left(4/\pi \right)}^{2}\), where mSiN (mBe) and ZSiN (ZBe) are the total mass and number of protons within the membrane (substrate) and m is the effective mass of the membrane’s fundamental mode. At an operating temperature of 10 mK and a mechanical quality factor of Q = 109, this system can achieve a thermal-noise-equivalent acceleration resolution of 10−12 ms\({}^{-2}/\sqrt{{{{{{{{\rm{Hz}}}}}}}}}\) (see Supplementary Figure 2), corresponding to a minimum detectable DM coupling strength of gB-L = 4 × 10−25. In this example, the membrane serves as an end-mirror in an optical cavity of length L = 1 mm with finesse \({{{{{{{\mathcal{F}}}}}}}}=\pi c/L\kappa =1000\). Optical readout of the membrane’s displacement would be performed using a laser with wavelength λ = 1 μm and input power 2 mW, resulting in a shot-noise-limited displacement sensitivity of 9 × 10−19 m\(/\sqrt{{{{{{{{\rm{Hz}}}}}}}}}\).

As depicted in Fig. 4 of the main text, a mechanical resonator achieves the best acceleration sensitivity at its resonance frequency. While shot noise limits the detector’s off-resonance sensitivity, the dominant noise source on resonance is expected to be radiation pressure backaction at P = 2 mW input power, with an acceleration noise floor of 2 × 10−11 ms\({}^{-2}/\sqrt{\,{{\mbox{Hz}}}}\) (gB-L = 7 × 10−24). The figure includes additional curves for both classical and DQS schemes, highlighting the potential improvement that can be attained by using multiple (M = 10) sensors and an entangled light source. The SQL of a classical array (blue dotted) is included, where the laser power is tuned at each frequency to minimize the optical measurement noise. A similar limit is plotted for a DQS setup (red dotted)—where a squeezed vacuum state is distributed uniformly across the sensor array—illustrating the best achievable sensitivity with a fixed squeezing of 10 dB.