Introduction

The many-body interaction of dipoles is crucial to understanding a diverse range of phenomena across physics, with its long-range anisotropic nature yielding a wealth of fascinating phenomena. For example, dipolar interactions can yield novel vortex stripes in an ultracold quantum gas1, a low temperature residual entropy in frustrated condensed matter systems2 and Rosensweig instabilities in ferrofluids3, yielding self-organised surface structures. The pioneering work of Luttinger and Tisza4 provided a foundation for understanding dipolar ordering in simple lattice geometries, but this was only extended recently to arbitrary geometries5. To date, the experimental placement of dipoles into complex 3D arrangements has been lacking, with scientists mainly relying upon arrangements provided by condensed matter systems. One such model system, known as spin-ice6, has been studied intensively and has allowed systematic study of frustration and associated emergence7. These systems consist of rare earth moments on corner sharing tetrahedra. The Hamiltonian consists of dipolar and exchange terms and the ~10 Bohr magneton moment means that dipolar interactions are important in determining the nature of the ground state. Since all pairwise interactions within a single tetrahedra cannot be simultaneously satisfied, the system is geometrically frustrated. This yields a local ordering principle known as the ice-rule, in which two spins point into the centre of a tetrahedron and two spins point out, yielding a macroscopically degenerate ground state and a residual entropy measured at low temperature. Interestingly, Monte-Carlo (MC) simulations which encompass sufficient dynamics via a loop algorithm find an ordered phase in spin-ice at very low temperatures, which consists of stripes of anti-parallel spins8 but so far this has not been measured experimentally.

A new framework to understand the physics of spin-ice was later proposed which treated each spin as a dimer consisting of equal and opposite charges9,10. Within this framework local excitations above the ice-manifold are magnetic monopoles in the vector fields M and H, since once the chemical potential has been surpassed, they interact via a magnetic equivalent of Coulomb’s law. Subsequent studies provided experimental evidence of magnetic charge transport in bulk spin-ice materials11,12. The ground state of spin-ice and the associated dynamic route can then be considered within the framework of magnetic charge, where the ratio of the chemical potential to the magnetic Coulomb energy of a nucleated pair is an important quantity13. When this effective chemical potential approaches a value of half the Madelung constant (M/2 = 0.819 for a diamond lattice), a magnetic charge crystal is expected, whereby charges of alternating polarity are tiled throughout the structure13. For the canonical spin-ice materials, the effective chemical potential is 1.42, suggesting the monopoles are free to propagate through the system, yielding a disordered spin-ice phase. To observe charge-ordered states in bulk solid-state systems, one needs to find systems with specific material properties. One example, the spin-ice candidate Nd2Zr2O7 has recently shown charge crystal behaviour, combined with disordered spin background, a signature of magnetic fragmentation whereby the local magnetic moment splits into divergence-full and divergence-free parts14. A tuneable, engineered system has the capability to explore this phase space systematically.

Artificial spin-ice materials are arrays of lithographically patterned single-domain nanomagnets15,16. As such they are a powerful means to explore ordering in dipolar systems by design. Initial studies focussed upon simple square15 and Kagome arrays17, which has subsequently been extended to a wide range of 2D geometries providing a means to explore a variety of model spin systems in statistical physics and more exotic phenomenon such as topological frustration in the Shatki lattice18 and superferromagnetism in pinwheel lattices19. To date most ASI studies have focussed upon 2D systems due to ease of fabrication but interest has spanned into layered systems20,21 with both theoretical and experimental studies investigating how these can be used to realise a range of ground states including model vertex systems22 and superlattice structures23.

The advent of three-dimensional lithography now allows the creation of lattices that directly mimic bulk spin-ice geometries24,25,26,27, but with tunability to control factors such as magnetic moment and lattice spacing. Such 3D artificial spin-ice (3DASI) systems within a diamond-bond geometry and which have a Hamiltonian governed purely by dipolar energetics, have been the focus of nanofabrication efforts using focussed electron beam induced deposition (FEBID)27 and using two-photon lithography (TPL)24. Recent work with the TPL methodology has produced systems with the required geometry and degeneracy and through simple linear field driving protocols, magnetic charge has been directly observed across the 3DASI surface24. Theoretical work upon 3DASI geometries has further demonstrated tensionless Dirac strings and mobile magnetic monopoles that can be steered using an applied magnetic field28. Another novel 3D structure which has relevance to frustration and ASI is the buckyball29, which has been fabricated using TPL and theoretical work indicates tuneable magnonic properties30.

In this article we first use finite temperature MC simulations to carry out a detailed mapping of ordering in idealised 3DASI systems within a diamond-bond lattice geometry. We find a rich phase diagram consisting of a double-charged monopole crystal, single-charged monopole crystal and a spin-ice phase. We move on to measure the demagnetised state in an experimental 3DASI system and find evidence of an out-of-equilibrium state, whereby crystallites of magnetic charge are superimposed upon an ice background.

Results and discussion

Simulating the phase diagram of an idealised 3D artificial spin-ice

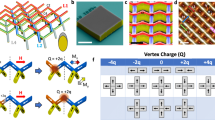
Figure 1a,b shows a schematic of the simulated unit-cell geometry. Compass needle dipoles are placed upon a diamond-bond lattice, which has a lateral extent of 15 × 15 unit cells and a thickness of a single-unit-cell. To aid in discussion, we define a series of sub-lattices which are labelled L1–L4. The upper surface terminates in coordination-two vertices (L1), below which two layers of coordination-four vertices are found (L2, L3). Finally, the lower lattice surface again terminates in coordination-two vertices (L4). This geometry matches our experimental 3DASI system. The compass needle model (see Methods), is equivalent to treating magnetic dipoles as two magnetic monopoles with a small variable separation. We use a metropolis algorithm to determine the ground state of the system as a function of the dipole length (b), with a fixed lattice spacing (a = 1), over a range of temperatures. We note that in experimental systems, previous work24 has shown that complex domain walls form at vertices in order to minimise the total micro-magnetic energy, consisting of magnetostatic and exchange contributions. The net result of this is a reduction in the uniform, Ising-like part of the nanowire to some fraction of the lattice spacing. Hence, even in connected 3DASI systems it is appropriate to explore the phase diagram for b < 1.

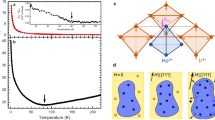
Fig. 1: Simulating the phase diagram in a 3D artificial spin-ice.
figure 1

a A unit-cell of the simulated geometry. Spins are placed onto the bonds of a diamond-bond lattice. Magnetic charges are represented as spheres of different colour according to legend. b View of unit-cell along [001] direction. Arrows are coloured according to layer with cream denoting the surface termination (L1) with coordination-two vertices, yellow (L2), brown (L3) denoting coordination-four vertices and dark red denoting lower surface termination (L4) with coordination-two vertices. c Phase diagram of 3D artificial spin-ice showing charge crystal order parameter (Mc) as a function of reduced dipole length, b and temperature, T. d The phase diagram now showing variation of ice-rule vertices with reduced dipole length, b and temperature, T. Overall, three main phases are observed. e The specific heat Cv and f the entropy per site for four b values with a = 1. Entropies were normalised to the high-temperature paramagnetic value. At low temperature for b = 1 the residual entropy matches the analytical prediction (see Methods). g The ice phase, observed for high b and low to intermediate temperatures. h The magnetic structure factor of the ice phase, showing the typical pinch points associated with a Coulomb phase. i The double-charge monopole crystal, consisting of ±2q upon the surface terminations, ±4q at L1/L2 and L3/L4 junctions with a neutral layer at L2/L3 vertices. j The magnetic structure factor associated with the double-charge monopole crystal. k Phase observed for lower b and intermediate temperatures, showing a single-charged monopole crystal and l its associated structure factor. Colour scales represents intensity.

Full size image

Figure 1c,d show an overview of the phase diagram as a function of b over a range of temperatures, whilst Fig. 1e,f show the specific heat Cv and corresponding entropy per site s for four values of b. To facilitate interpretation, we define an order parameter (Mc, see Methods) which quantifies the extent to which a magnetic charge crystal has formed. For lower temperatures, a high b lattice yields strong local Coulomb interactions upon vertices, forcing charge neutrality and a spin-ice ground state as can be seen in Fig. 1c,d. A representative arrow map of the spin-ice state is shown in Fig. 1g. Ice vertices dominate the microstate occurring at frequencies reflecting underlying vertex probabilities (ergodic balance). The surface L1 layer forms short ferromagnetic strings as seen in previous theoretical studies31. The magnetic structure factor (Fig. 1h) shows pinch points associated with a Coulomb phase and signatures of short-range magnetic strings with diagonal lines seen along q = [1,1] and q = [−1,−1]. At b = 1, low temperature, the ground state entropy s0 of spin-ice is evident (Fig. 1f). In the Methods we calculate s0 analytically using two models: first, using Pauling’s method of independent tetrahedra which is well tested in bulk spin-ice. Second, by assuming that the surfaces order first and constrain subsequent layers. Figure 1f shows a closer agreement with the latter model, a fundamental difference between the bulk and slab geometries. As b decreases, the frustration and ground state entropy disappear.

Reducing b lowers the chemical potential and in the low temperature regime this yields a phase transition to a double-charge crystal (CII). Of particular interest is how such a crystal forms whilst constrained to an odd number of charge layers. The state is characterised by ±2q charges upon surface coordination-two vertices (L1 and L4) and ±4q charges upon L1/L2 and L3/L4 coordination-four vertices, as portrayed in Fig. 1i,d. The order parameter (Mc) of this CII state is found to be greater than 0.8, as seen by the yellow region in Fig. 1c. A neutral layer is found in the centre, consisting of type I vertices. Notably, the sheet geometry produces a coarse-grained field that is approximately constant with respect to distance. This makes the inclusion of a neutral spacing layer more negligible. The magnetic structure factor (Fig. 1j) shows clear Bragg peaks due to anti-ferromagnetic order and associated charge ordering. With intermediate values of b, and at higher temperature, one of the coordination-four double-charged sheets “spreads” into the neutral layer, creating two consecutive single charge sheets, as depicted in Fig. 1k, cross-sectional view shown in Fig. 1d, right-panel and the associated structure factor shown in Fig. 1l. This state is named CI. This increases the entropy of the system while maintaining a relatively favourable environment for charges. As temperature is further increased, a peak in specific heat (Fig. 1e), corresponding increase in entropy (Fig. 1f) and decrease in Mc (Fig. 1c) indicates a phase transition to a paramagnetic state. Overall, the phase diagram described by MC simulations is also captured analytically with a simple mean field analysis (See Methods).

Exploring the ordering in experimental 3D artificial spin-ice systems

A 3DASI system was fabricated to explore the extent to which the idealised theoretical phase diagram can be captured experimentally. The system was fabricated using a combination of two-photon lithography and evaporation (See Methods)24,32. Figure 2a shows a scanning electron microscopy (SEM) image of the array which takes a diamond-bond lattice geometry and has a lateral extent of 50 μm × 50 μm. Figure 2b shows a zoomed top-view, false-colour SEM image with the upper four sub-lattices labelled (L1–L4). As in the simulated systems, the lattice terminates in coordination-two vertices upon the surface, with typical coordination-four vertices found below at the L1/L2 and L2/L3 junctions. The lower L4 sub-lattice, again terminates in coordination-two vertices.

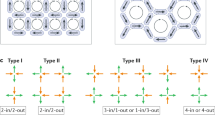
Fig. 2: Experimental vertex states and measured magnetic force microscopy contrast.
figure 2

a A scanning electron microscope (SEM) image of the 3D artificial spin-ice lattice, scale bar is 20 µm. b Top-view, false-colour SEM image of the 3DASI lattice with the individual sub-lattices labelled. Scale bar is 1 µm. c Magnetic force microscopy (MFM) contrast of the vertex types found upon the L1 coordination-two vertices. d Contrast for vertex types measured at the L1/L2 vertex. Here, both ice-rule (Type I, Type II) and single-charged vertices (Type III) are observed. e Contrast for vertex types measured at the L2/L3 vertex, which shows a mixture of ice vertices as well as those with single and double magnetic charge (Type IV). Colour scale represents normalised MFM phase.

Full size image

Our previous work has shown that individual nanowires are single-domain and magnetic force microscopy (MFM) can be used to determine the contrast for different vertex types24,32. We now exploit this to determine the demagnetised configuration obtained in 3DASI systems. Note, due to the limited resolution of MFM with lift height, we are only able to measure contrast upon the upper three layers, L1–L3. MFM was performed over large portions of the lattice after planar demagnetisation protocols (See Methods). All vertex types observed in previous experiments24, including ice-rule vertices with zero magnetic charge and monopole states with magnetic charge Q = ±2q are again observed (Fig. 2c, d). The demagnetised array also contains previously unseen monopole states of charge Q = ±4q, as can be seen in Fig. 2e.

Figure 3a shows an experimental magnetic charge map of a 30 μm × 30 μm region of the lattice, determined by MFM, with experimental images shown in Supplementary Fig. 1. Three distinct phases are measured and can be readily identified in the charge map with detailed configuration shown in Fig. 3b–d. Magnetic charge crystallites can be seen with ±2q tiling, as highlighted by the green box in Fig. 3a. An arrow map of a typical charge crystallite region is shown in Fig. 3b, which shows that it arises due to two types of distinct ordering. The L1 sub-lattice that consists of alternating coordination two and coordination-four vertices is found to order into ferromagnetic stripes (MFM contrast shown in Supplementary Fig. 1a). Analysis of the L1 sub-lattice, shows that this is the case for the entire measured area, with coordination-two monopoles being very rare and only observed upon <1% of vertices consistent with previous work24. Over large regions of the measured area (~20 %), including in the charge crystallite regions, the L2 sub-lattice is found to host anti-ferromagnetic ordering. Typical MFM contrast of such anti-ferromagnetic ordering is shown in Supplementary Fig. 1b. Experimental MFM images of the three different phases are shown in Supplementary Fig. 1c–f, with example charge crystal patches from additional samples shown in Supplementary Fig. 1g–j. Arrow maps depicting L1 and L2 magnetisation separately are shown in Supplementary Fig. 2a, b. Breaks in the anti-ferromagnetic ordering upon L2, via short ferromagnetic strings occurs frequently, with frequency decaying with string length (Supplementary Fig. 2c, d). Interestingly, we find that breaks in the anti-ferromagnetic ordering often occurs to mitigate the formation of ±4q charges. We note that since the configuration of the charge crystallites observed experimentally (CIE) has ferromagnetic stripes on L1, it is distinct to the CI charge crystal seen in simulations.

Fig. 3: Measuring the experimental demagnetised state of a 3D artificial spin-ice.
figure 3

a Global magnetic charge map of the measured sample region. Charged regions are represented by colour as according to legend. The map shows examples of single-charge crystallite (green outline), the ice phase (orange outline) and the double-charge crystal (purple). Colour scale represents magnetic charge (q). b More detailed arrow map of the experimental single-charge crystallite. It can be seen to consist of ferromagnetic stripes on the surface L1 layer with anti-ferromagnetic ordering upon L2. c Ice phase with type II tiling and d double-charge crystallite, which only occurs at breaks in the L1 ferromagnetic ordering. Arrows represent the magnetisation of the L1, L2, and L3 sublattices. Here, the distinction between surface coordination two, and sub-surface coordination-four vertices can be seen. All sublattices are shaded to guide the eye. Magnetic charges are represented by circles of different colour, superimposed upon vertices.

Full size image

Between areas of magnetic charge crystallite, large patches of the ice phase are observed, as shown by the orange region in Fig. 3a, with full representative arrow map shown in Fig. 3c. These ice regions are largely composed of type II vertices, which due to a subtle broken symmetry in 3D geometry, are the lowest energy vertex type according to micro-magnetic simulations24. Finally, only very small regions of the double-charge (CII) crystallite are observed as shown by purple region in Fig. 3a and associated arrow map in Fig. 3d. The full measured region is shown in Supplementary Fig 3a, with associated vertex types shown in Supplementary Fig. 3b and vertex charge shown in Supplementary Fig. 3c. The vertex statistics show a strong preference for type III vertices (61.2%), followed by type II vertices (29.8%). Both low energy type I vertices and high energy type IV vertices are only observed occasionally at 5.3% and 3.6% respectively. As would be expected, our measurements indicate charge neutrality, within error as shown in Supplementary Fig. 3c. Overall, the charge order parameter as calculated for simulations takes a value of 0.31, for this experimental system (See Methods).

The magnetic structure factor of the entire measured data is shown in Fig. 4a, with sub-sets corresponding to individual sub-lattices shown in Fig. 4(b–d). Focussing upon the data for all layers (Fig. 4a), the presence of intense Bragg peaks can be seen, superimposed upon weaker diagonal lines along q = [1,1]. In order to further interpret this data, we deconvolve the layers. The L1 structure factor (Fig. 4b) consists of a peak upon q = [0,0], indicative of ferromagnetic order on the surface. Weaker split peaks about q = [1/2,1/2] come about due to presence of longer period domains upon L1, as demonstrated in Supplementary Fig. 4. The L2 structure factor (Fig. 4c) shows peaks due to both type II tiling as well as the magnetic charge crystallite regions as demonstrated in Supplementary Fig. 5. Finally, the L3 structure factor (Fig. 4d) shows a diffuse signal, with weak Bragg peaks superimposed. This is consistent with the full arrow map (Supplementary Fig. 3a), which shows a mixture of charge ordered and ice states upon L3. Further breakdown of the structure factor via layer and region can be found in Supplementary Fig. 6.

Fig. 4: Experimental magnetic structure factors.
figure 4

a The magnetic structure factor of all sub-lattices superimposed. Clear Bragg peaks can be seen with periodicity in two dimensions. b The magnetic structure factor of the L1 sub-lattice. Peaks can be seen at q = [0,0], corresponding to the ferromagnetic ordering upon the surface. The split peaks about q = [1/2, 1/2], are due to domains on L1 with larger periodicity as demonstrated in Supplementary Fig. 4. c The structure factor for the L2 sub-lattice. Bragg peaks can be seen, resulting from both type II vertices and charge crystallites d The structure factor for the L3 sub-lattice. Bragg peaks are again seen and match the periodicity seen for L2 sub-lattice, superimposed upon a diffuse background. Colour scale represents intensity (I).

Full size image

Magnetic charge crystallite formation

We now discuss the observed experimental configuration in terms of the states predicted by MC simulations. For the real experimental systems studied here, the scaled needle length (b) depends upon the vertex type (Supplementary Fig. 7), due to the presence of domain walls close to the vertex. When considering all ice-rule vertices, an average b of 0.89 is obtained, suggesting a Q = ±4q monopole crystal would be expected as the ground state. However, a set of Q = ±2q crystallites form, superimposed upon an ice background. A number of factors may account for this discrepancy. Previous work has suggested that in experimental 3DASI systems, magnetic charges upon surface coordination-two vertices are very unfavourable with micro-magnetic calculations of single vertices suggesting such excitations cost a factor of three larger than coordination-four monopoles24. The immediate implication of this is that ferromagnetic stripes upon L1 will forbid the formation of a Q = ±4q monopole crystal, apart from regions with local disorder. This is reinforced by the deterministic demagnetisation protocol which favours the formation of ferromagnetic stripes upon the surface. Given this constraint, the system can only form a single charge crystal. However, the formation of a charge crystallite via a demagnetisation routine remains surprising and has not been seen previously in either pristine, traditional 2DASI or more exotic layered 2.5D systems. In the former case, charge crystals can be formed in modified square ASI by utilising an MFM tip to selectively switch islands33 but demagnetisation of conventional square systems yields a low magnetisation, disordered ice phase with low frequencies of monopole excitations15. An interesting question is whether conventional (planar) square ASI has some region of parameter space where charge ordering may occur naturally after demagnetisation or thermalisation. We note that in our system, it is the 3D geometry of the vertex that allows like charges to separate sufficiently, reducing the monopole energy and allowing the stable formation of charge crystallites. Furthermore, the charge crystal in the 3DASI lattice yields 3D shells of attractive charges, with a reduced average separation, lowering the energy. It is possible, that within a connected regime that such charge ordering may be accessed by designing the vertex geometry so as to control degeneracy and monopole energy. However, we note that previous extensive work has not found any evidence of this34,35. For pristine Kagome systems, demagnetisation yields a 2-in/1-out ice-rule throughout the lattice17 with only thermally annealed systems yielding some degree of charge ordering36. Modifications of the Kagome geometry, either by tuning island lengths within a single-unit-cell37, or by placing exotic nano-bridges at vertices, can also yield charge ordering38.

Considering the dynamics of the demagnetising protocol and starting in saturating fields, the system becomes uniformly tiled in type II vertices. Though these are the lowest energy state for single vertices24, the net magnetisation makes these less favourable globally. The effective chemical potential upon L124 as modified by surface energetics (μ* = 1.22) means that deconfined monopoles nucleate and propagate for each 180° rotation of the field. At threshold fields, nucleation events upon L1 become less likely, leaving long ferromagnetic strings as observed in the experimental data. The effective chemical potential upon the L2 sub-lattice24, within a simple dipolar approximation is lower (μ* = 1.03) and favours the local production of correlated charge pairs (type III vertices). Quenched disorder in the lattice, means that this will occur more favourably at positions where an L2 nanowire has a slightly reduced coercive field, with respect to the mean. Such initial nucleation events seed the formation of charge crystallites. It is interesting to note that type III vertices have a slightly lower b value (0.78) due to the complex 3D distribution of magnetic charge around the vertex. Specifically, the equilibrium distance between like charges across the vertex is increased, whilst the distance between opposing charges on the nanowire are decreased. When taking this into account, the effective chemical potential is reduced and has value (See methods) of μ* = 0.91, approaching the critical value of M/2 = 0.819. The implication of this is that nucleated monopole pairs on L2 are particularly stable, as supported by previous experiments24.Once a single monopole pair is formed, it is energetically favourable for a charge crystallite to grow by minimising local vertex-vertex Coulomb interactions and tiling charges of opposing sign. The residual ice-rule regions reflect regions which have not yet equilibrated. It is possible that longer or more complex 3D demagnetisation protocols will promote more efficient exploration of the energy landscape, allowing such ice regions to be further minimised.

In summary, returning artificial spin-ice to its three-dimensional origins unlocks previously inaccessible exploration of phase space. We anticipate that fine control of 3D vertex geometry and NiFe thickness will allow suppression of surface energetics and together with an exploration of more complex demagnetisation protocols, or thermal relaxation will allow a realisation of the double-charged crystal. It is also expected that more sophisticated synchrotron techniques39 may allow imaging of systems greater than one-unit-cell in thickness.

Methods

Entropy calculations

In this section we provide the details of our analytical calculation of the ground state entropy of our spin-ice model. We employ the following conventions.

  • We adopt the graph theory terminology of vertices connected by edges. In our system each edge hosts a single, Ising-like magnetisation.

  • Two edges meet at each vertex in layers L1 and L5. Four edges meet at each vertex in layers L2, L3, L4 ; each of these vertices shares two edges with vertices in each of its neighbouring layers.

  • There are the same number of vertices, N, in each layer.

  • Let Sn be the entropy in layer n, in units where KB = 1, and sn = Sn/N is the entropy per vertex in layer n.

  • Let S be the total entropy of the system, and s = S/(5 N).

Paramagnet

we use the high-temperature paramagnetic phase to constrain the entropy in our numerical calculations. Each domain’s orientation is independent. In layers 1 and 5 there are two edges per vertex, giving s1,5 = log 22, and in the other layers there are 4 edges per vertex giving s2,3,4 = log 24 . Therefore,

$$s=(16/5){{\log }}(2)\approx 2.22$$
(1)

Spin-ice

for the ice state without field annealing (the physically relevant case around b/a≈1) we have a net charge of zero at every vertex. Each L1 vertex therefore has a net magnetisation (1-in 1-out means both domains align). It appears the L1 vertices are completely uncorrelated, even along a single L1 line. Therefore, there are 2 choices per vertex, and s1 = s5 = (1/5) log(2) . Each L2 vertex now has two of its domains fixed by L1 vertices, giving no freedom in these two domains. There are two remaining independent choices per vertex, giving s2,4 = (1/5)log(2). L3 is then completely constrained by L2 and L4 . Therefore S3 = 0 . Overall,

$$s=(4/5){{\log }}(2)\approx 0.55$$
(2)

This agrees with our numerically calculated result to within standard error. The value differs from the Pauling estimate in bulk spin-ice; this is because surface energetics dominate in our single-unit-cell slabs.

Monte-Carlo simulations

The interaction energy between two artificial nanomagnets may accurately account for their finite size through the compass needle model. That is, the energy, \({E}_{{ij}}\), between magnets \(i\) and \(j\) is approximated by considering two point charges at the end of each nanomagnet that interact with Coulomb attraction or repulsion:

$${E}_{{{{{{{\rm{ij}}}}}}}}\,={\alpha }_{{{{{{{\rm{ij}}}}}}}}\,\frac{{\mu }_{0}{m}^{2}}{4\pi {L}^{2}}\,\left[\frac{1}{\left|{{{{{{\boldsymbol{r}}}}}}}_{{{{{{{\rm{ai}}}}}}}}-{{{{{{\boldsymbol{r}}}}}}}_{{{{{{{\rm{aj}}}}}}}}\right|}-\,\frac{1}{\left|{{{{{{\boldsymbol{r}}}}}}}_{{{{{{{\rm{ai}}}}}}}}-{{{{{{\boldsymbol{r}}}}}}}_{{{{{{{\rm{bj}}}}}}}}\right|}-\frac{1}{\left|{{{{{{\boldsymbol{r}}}}}}}_{{{{{{{\rm{bi}}}}}}}}-{{{{{{\boldsymbol{r}}}}}}}_{{{{{{{\rm{aj}}}}}}}}\right|}\,+\frac{1}{\left|{{{{{{\boldsymbol{r}}}}}}}_{{{{{{{\rm{bi}}}}}}}}-{{{{{{\boldsymbol{r}}}}}}}_{{{{{{{\rm{bj}}}}}}}}\right|}\,\right]$$
(3)

Here \({\mu }_{0}\) is the permeability of free space, \(m\) is the nanomagnet’s magnetic moment, and \(L\) is the nanomagnet length. \({{{{{{\boldsymbol{r}}}}}}}_{{{{{{{\rm{ai}}}}}}}}\) is the position of a magnetic charge, the first index \(a\) referring to it being positive and the second index \(i\) denoting to which magnet it belongs. \({\alpha }_{{{{{{{\rm{ij}}}}}}}}\) is the surface energy factor, which for data presented in this publication was set to 1. Since nanomagnet length wildly influences energy scales, all computational energies were normalised by their strongest interactions, such that \({\widetilde{E}}_{{{{{{{\rm{ij}}}}}}}}={E}_{{{{{{{\rm{ij}}}}}}}}/{E}_{\max }\,\).

From this energy we can see that increasing length of the magnets increases nearest neighbour dominance. It’s worth noting that the exact distribution of charge and, therefore, precisely what the “length” of the magnets is, depends largely on the details of the nanomagnet’s geometry and domain wall arrangement. In this study, this energy is used in the evaluation of a metropolis method Monte-Carlo analysis.

Effective chemical potential calculations

The chemical potential of a coordination-four vertex, upon a diamond-bond geometry has previously been calculated within a dipolar framework. The energy between any pair of dipoles can be written as:

$${E}_{12=}\frac{u}{4}\frac{\left|{\hat{m}}_{1}\cdot {\hat{m}}_{2}-3({\hat{m}}_{1}\cdot \hat{r})({\hat{m}}_{2}\cdot \hat{r})\right|}{{\left|\frac{r}{a}\right|}^{3}}$$
(4)

Where m represents the magnetic moment unit vector, r is the moment separation, a is the lattice constant and u is the Coulomb energy between charges:

$$u=\frac{{\mu }_{0}{Q}^{2}}{4\pi a}$$
(5)

with \(Q=2m/a\) . One can then simply write the chemical potential as the energy difference between a monopole and an ice-rule state, offset by the magnetic Coulomb interaction, between created charges:

$$\mu =({E}_{{{{{{{\rm{monopole}}}}}}}}-{E}_{{{{{{{\rm{lr}}}}}}}}-{E}_{{{{{{{\rm{ice}}}}}}}})$$
(6)

with

$${E}_{{lr}}=\frac{u}{\frac{{r}_{{{{{{{\rm{charge}}}}}}}}}{a}}$$
(7)

Assuming a perfect dipolar model whereby the charges are separated by a single-lattice spacing yields a chemical potential \(\mu\) of 1.03 u. The effective chemical potential is therefore \({\mu }^{* }=\frac{\mu }{u}=1.03\)

However, in our real experimental system the charge separation in the monopole state is reduced, with \({r}_{{charge}}\approx\)0.8a, yielding a reduced \({\mu }^{* }=0.91\). This locally promotes the formation of charge crystallites.

Magnetic charge crystal order parameter

In charge-ordered systems, twofold degenerate patterns emerge as the ground states. To measure similarity to these states, we can calculate a charge crystal order parameter defined as:

$${M}_{c}=\left|{\sum }_{i}{\triangle }_{i}\,{Q}_{i}\,\right|$$
(8)

\({\triangle }_{i}\) is a template of +1’s, −1’s, and 0’s representing a ground state. This was used to calculate the order parameter for both Monte-Carlo simulations, as shown in Fig. 1c and for experiments.

Magnetic structure factor

In the canonical spin-ice materials, spin-flip neutron scattering12 provides what is probably the clearest evidence of spin-ice behaviour. Neutron scattering probes the magnetic structure factor projected along the direction of neutron propagation. In artificial spin-ice there is a similar tradition of calculating the structure factors, although neutron scattering is not used as a probe. Instead, the structure factor can be inferred directly by Fourier transforming the MFM image16,40. In this work we calculated the magnetic structure factor for spin configurations modelling those in our real lattices, as well as those generated in our Monte-Carlo simulations. We calculated the full 3D structure factors before taking the qZ = 0 slice, suitable for modelling what would be seen when Fourier transforming a surface MFM arrow map.

Mean field analysis

Considering the system in the dumbbell model approximation,

$$E=\frac{1}{2}\,{\sum }_{i\ne j}{K}_{{ij}}{Q}_{i}{Q}_{j}\,+\mu {\sum }_{i}{Q}_{i}^{2}$$
(9)

where Qi = ±2, ±1, 0 is the value of the charge on the ith vertex, \({K}_{{ij}}\) is the interaction strength between charges, and \(\mu\) is the chemical potential of a charge. We can calculate the Maxwell-Boltzmann distribution in the mean field approximation and motivate how charge ordering differs from spin-ice ground states. Taking the change of variables Qi = Δi Xi, where \({\Delta }_{i}\) is a general charge-ordered ground state, and introducing a perturbative “field” to this variable \(h\) which will later be set to zero,

$$E=\,\frac{1}{2}\,{\sum }_{{ij}}{K}_{{ij}}\,{\Delta }_{i}\,{\Delta }_{j}\,{X}_{i}\,{X}_{j}\,\,+\mu \,{\sum }_{i}{X}_{i}^{2}-\,h\,{\sum }_{i}\,{X}_{i}.$$
(10)

The variable is approximated by deviations from its mean value, \({X}_{i}=\langle X\rangle +\delta {X}_{i}\). The energy gained by a charge-ordered state is called the Madelung constant, which can be written as \(\alpha =-\frac{1}{N}{\sum }_{{ij}}{K}_{{ij}}\,{\Delta }_{i}\,{\Delta }_{j}\) and \(\alpha =-{\sum }_{j}{K}_{{ij}}{\Delta }_{i}{\Delta }_{j}\). Substituting then yields

$$E\,=\,N{\left\langle X\right\rangle }^{2}\left(\frac{\alpha }{2}\,-\mu \right)\,+\,\left[\left(-\alpha +2\mu \right)\left\langle X\right\rangle -h\right]{\sum }_{i}{X}_{i}$$
(11)

from this we can calculate the partition function of a single variable and, because they are independent, \(Z={\left({Z}_{1}\right)}^{N}\). For a pyrochlore lattice, \({Q}_{i}=\pm 2\,(\Omega =1)\), \(\pm 1\,(\Omega =4)\), and \(0\,(\Omega =6)\) where \(\Omega\) is the degeneracy. Substituting \(k=\beta (-\alpha +2\mu )\),

$$Z={{\exp }}\,\left[-N{\langle X\rangle }^{2}\frac{k}{2}\right]\,\{2{{\cosh }}\,[2k\langle X\rangle -2h\beta ]+8{{\cosh }}\,[k\langle X\rangle -h\beta ]+6\}$$
(12)

the expectation value of the charge ordering variable is then obtained self consistently from the partition function:

$${{\langle }}X{{\rangle }}=-2{{\tanh }}\left(k\frac{\left\langle X\right\rangle }{2}\right)$$
(13)

This self-consistency equation is relatively standard for mean field theories. At high values of \(-k\), effectively equivalent to low temperatures, \(\left\langle X\right\rangle =\pm 2\). As \(-k\) becomes closer to zero, these values gradually drop until the system is no longer ordered. This ordering transition may be characterised for small \(k\left\langle X\right\rangle\) through the first term of the Taylor series:

$$\left\langle X\right\rangle =-k\left\langle X\right\rangle$$
(14)

This is true when \(\left\langle X\right\rangle =\,0\) and \(k\le -1\), meaning below a critical temperature, the system will transition to a nonzero order parameter, corresponding to a charge crystal. That critical temperature is

$${T}_{c}=\frac{\alpha -2\mu }{{k}_{B}}$$
(15)

This agrees with the previous experimental results that found a spin-ice ground state in systems with a reduced chemical potential greater than \(\frac{\alpha }{2}\) and a lack of discrete transition in this regime. The critical temperature also decreases with chemical potential as previously observed. Also, since as temperature approaches zero, the order parameter approaches 2, a double-charged crystal is the anticipated ground state. One can justify this by considering the lower entropy of the doubly charged state. Since the experimental system is limited to single charges on the surface, the maximum order parameter we predict for the charge crystal ground state of the pyrochlore thin film with 5 charge sites is \({M}_{c}^{s}=1.5\).

Fabrication of 3DASI lattices

Three-dimensional artificial spin-ice lattices were fabricated using two-photon lithography followed by thermal evaporation of Ni81Fe19. The coverslips were cleaned in acetone in an ultrasonic cleaner and then washed by isopropyl alcohol (IPA), after which samples were gently dried using compressed air. The coverslip was prepared for TPL with a droplet of immersion oil on one side and Nanoscribe negative-tone photoresist (IPL-780) on the reverse side. The coverslip was then loaded into a Nanoscribe TPL apparatus, and a fabrication script created a number of diamond-bond lattice geometries, each with varying power and scan speed settings. The dimensions of each created lattice are 50 μm × 50 μm × 10 μm. The completed sample was developed in propyl glycol monomethyl ether acetate (PGMEA) and then rinsed in IPA. An air gun was then again used to remove excess IPA. The sample was then subject to a 50 nm Ni81Fe19 evaporation, at a base pressure of 1 × 10−6 mBar. Approximately 0.06 g of evaporated permalloy was used to achieve this thickness based on previous depositions. A crystal quartz monitor (QCM) present during evaporation measured the deposited thickness; this was later confirmed with atomic force microscopy measurements. The resultant structure has a diamond-bond geometry polymer scaffold with magnetic material upon the upper surface of nanowires forming a crescent-shaped cross-sectional geometry. Due to line-of-sight deposition, the magnetic coating creates a 3DASI lattice which is one-unit-cell in thickness, as described previously28. Individual nanowires are single domain and have a crescent-shaped cross-section with effective width of 200 nm and length of 866 nm.

Experimental demagnetisation of lattices

We used a demagnetising protocol akin to method 1 in a previous publication41 with a sample rotating at ~1000 revolutions per minute, with axis perpendicular to substrate plane. This effectively yields a rotating magnetic field in the substrate plane. The magnetic field starts at 0 mT and ramps up to 75 mT at 2.5 Ts−1 where it is held for 1 s. After this, the field ramps down at 2.5 T s−1 to −75 mT and is held for a second. The field then oscillates, whilst the magnitude decreases stepwise to zero over a period of five days.

Magnetic force microscopy (MFM)

MFM data was captured using a Bruker (Dimension Icon) scanning probe microscope in tapping mode. Ultra-low moment probes were magnetised along the tip axis using a 0.5 T permanent magnet. The samples were placed with the L1 sub-lattice parallel to the probe cantilever with a 45-degree scan angle to the L1 sub-lattice. MFM data were captured using a 65 nm lift-height. Separate scans with reversed tip magnetisation were performed to verify consistency of the contrast, and separate scans with the sample rotated 180 degrees were performed to control for artefacts in the scans. Nominally identical behaviour with charge crystallites superimposed upon a type II ice background have been observed in four independent samples.