Abstract
The quasi-1D chiral edge states in a quantum anomalous Hall insulator are dissipationless, while the 2D helical surface states in a topological insulator are insensitive to spin-independent scatterings due to the topological protection. Both serve as essential ingredients for topological electronics. Here, we integrate these states into a single device using selective area epitaxy based on the molecular beam epitaxy technique. The chiral edge state comes from the quantum anomalous Hall insulator Cr:(Bi,Sb)2Te3, while the helical surface state comes from the intrinsic topological insulator (Bi,Sb)2Te3 which only interfaces with a partial edge of the former, forming a selective-area heterostructure. At the heterointerface, the chiral state in Cr:(Bi,Sb)2Te3 is allowed to be scattered into (Bi,Sb)2Te3 so that the incoming current will be redistributed according to the coordination between the chirality and helicity. Our device enables the collaboration between chiral and helical states for low-dissipative transport with tunable current dimension.
Similar content being viewed by others
Introduction
The time-reversal (\({{{{{\mathcal{T}}}}}}\)) invariant 3D topological insulator (TI), such as (Bi,Sb)2Te3 (BST), has insulating bulk states but gapless surface states1,2,3,4,5,6,7. These surface states are helical, whose eigenstates \({| \uppsi \rangle}\) with opposite spins are Kramers degenerate as a consequence of \({{{{{\mathcal{T}}}}}}\)-invariance. Therefore, the counterpropagating helical states are \({{{{{\mathcal{T}}}}}}\)-partners of each other, \({|{\uppsi }}_{{{{{{\mathcal{T}}}}}}}\rangle ={{{{{\mathcal{T}}}}}}|\uppsi \rangle\), with the same energy but opposite spins. Since they are orthogonal to each other, \(\left\langle \Psi {{{{{\rm{|}}}}}}{\Psi }_{{{{{{\mathcal{T}}}}}}}\right\rangle =0\), the \({{{{{\mathcal{T}}}}}}\)-invariant backscattering between them is prohibited but only moves the energy of degeneracy, forming the Kramers pair. When the TI is magnetically doped, such as Cr:(Bi,Sb)2Te3 (CBST), to break \({{{{{\mathcal{T}}}}}}\)-symmetry, one spin splitting of the pair is enhanced while the other penetrates deeper into the bulk and eventually disappears, leaving only one spin-polarized states propagating along the edge8,9,10,11. Such edge states thus propagate unidirectionally, i.e., chiral, which enables dissipationless transport. This is the formation of the quantum anomalous Hall (QAH) insulator.
In the QAH insulator, the bulk electrons are localized, and the edge electrons propagate in either a clockwise or counterclockwise fashion since there is no other possible state for the edge electrons to be scattered into. Although this enables a unidirectional transport without dissipation, the chiral state is only quasi-1D, while the degrees of freedom in controlling the electron’s propagation and current distribution are low. We propose to improve this by connecting the chiral state with the helical one, via which the chiral state becomes allowed to be scattered into one of the constituents in the helical state depending on the relative direction of their spins. In this way, while the transport remains topological with low dissipation, the space for the chiral state could be populated from quasi-1D, i.e., the edge, to 2D, i.e., the surface, or vice versa, which allows for a tunable dimension for current propagation. This is achieved by fabricating an epitaxial selective-area heterostructure (SAH) based on the molecular beam epitaxy technique, which integrates the chiral and helical transports from QAH insulator CBST and TI BST, respectively, into a single device. The heterointerface allows the transformation between the chiral state and helical state back and forth, during which the transport current will be redistributed according to the coordination between the chirality and helicity.
Results and discussion
A device with SAH
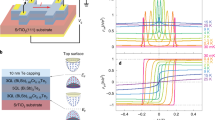
Experiments were conducted on two Hall bars, which are patterned from a piece of QAH insulator on areas with and without SAH, respectively, so that CBSTs in both Hall bars are essentially the same. The detailed process is provided in Methods. The Fermi level of BST was tuned to around the Dirac point by optimizing the composition ratio of Bi/Sb. This is reflected by the fact that, while keeping this Bi/Sb ratio, Cr atoms were doped into BST to open a gap around the Dirac point12,13, via which the QAH effect is realized in our CBST. As shown in Fig. 1a, b, the width of BST in the transverse direction is about 2/3 of the Hall bar width as w1 ~2d/3, leaving CBST without being covered by any BST as w2 ~d/3 (d ~500 μm). Transmission electron microscope images taken from the areas without and with SAH are shown in Fig. 1c, d, respectively. The van der Waals layers stacked in both can be clearly identified, and, importantly, the BST film has a similar crystalline quality to that of the underneath CBST in SAH, which indicates our in situ stencil lithography does not interrupt the epitaxy of BST.
a Schematic of the SAH device. BST: (Bi,Sb)2Te3, CBST: Cr-doped (Bi,Sb)2Te3. b Optical image of the device. The width of the Hall bar is d ~500 μm. The width of the region covered by BST is w1 ~2d/3, leaving CBST without any BST as w2 ~d/3. c, d Transmission electron microscope images in areas without and with SAH. The dashed line at the interface is determined according to the thickness of each layer. e–g Transport results of Hall resistance Rxy, longitudinal resistance Rxx, and Hall conductance σxy as functions of perpendicular magnetic fields B using Hall bars without and with SAH. The cyan curve/areas in (g) is the difference between the other two.
Additional plateau-transition
Transport measurements were performed at 20 mK under a perpendicular magnetic field B, and the results are summarized in Fig. 1e–g. Without SAH, the CBST film shows the QAH effect with quantized Hall resistance \({R}_{{xy}}=\pm h/{e}^{2}\) and vanishing magnetoresistance \({R}_{{xx}} \sim 0\). When a 6-nm-thick BST layer is partially deposited on top of CBST, since the helical channel in BST is more dissipative than the chiral transport in CBST, BST will be essentially shunted by CBST and does not affect the QAH plateaus. Strikingly, a pair of additional Hall plateaus \({R}_{{xy}}^{{\prime} }\) appears between \(\left|{B}_{c1}\right|\) ~ 0.05 T and \(\left|{B}_{c2}\right|\) ~ 0.15 T. In contrast to QAH plateaus, \({R}_{{xy}}^{{\prime} }\) is not quantized to any value but varies between 0.73 ~ 0.86\(h/{e}^{2}\) and −0.67 ~−0.86\(h/{e}^{2}\) during multiple measurements (Supplementary Fig. 1) being sensitive to the magnetic field sweep rate (Supplementary Fig. 2). The value of \({R}_{{xy}}^{{\prime} }\) also exhibits time-dependent random variations when the field sweep is stopped in the range between \(\left|{B}_{c1}\right|\) and \(\left|{B}_{c2}\right|\) (Supplementary Fig. 3). These observations imply that the origin of \({R}_{{xy}}^{{\prime} }\) is of a metastable magnetic structure and exhibits the stochastic nature in domain switching. The appearance of \({R}_{{xy}}^{{\prime} }\) correlates with the behavior of \({R}_{{xx}}\) as the range of \(\left|{B}_{c1}\right|\) ~ \(\left|{B}_{c2}\right|\) precisely marks the position of the finite \({R}_{{xx}}\). \({R}_{{xx}}\) measured from the BST side is essentially similar to that from the CBST side, implying a homogenous quantization. Their remnant \({R}_{{xx}}\) under 0.3 T are ~4.7 × 10−3\(h/{e}^{2}\) and ~5.9 × 10−5\(h/{e}^{2}\), respectively. Although the remnant \({R}_{{xx}}\) of the BST side is slightly larger than that of the CBST side, such a tiny difference may come from the measurement uncertainty of the lock-in amplifier and vary according to the sample condition and measurement environment, which thus may not act as an evidence to the dissipative nature of the helical state in BST. It is worth mentioning that \({R}_{{xx}}\) in devices with and without SAH exhibit step-like features between ± 0.05 T and ± 0.1 T. This behavior indeed has been widely observed in different CBST samples14,15,16,17,18 which may be ascribed to the temperature increment when sweeping the magnetic field across zero and/or the complex microscopic magnetic structure in the sample that responses to the small magnetic field after switching the field polarity. After converting to Hall conductance σxy in Fig. 1g, the Hall bar with SAH exhibits a rise in σxy within the same B-range, which is in contrast to the quantized \({\sigma }_{{xy}}=\pm {e}^{2}/h\) in the one without SAH. This rise can be identified by the cyan areas, which are obtained by subtracting σxy in the Hall bar without SAH from the one with. We regard, intuitively, that the SAH introduces extra conductive channels to the QAH insulator during the plateau transition.
Chiral current redistribution
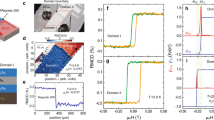
To get further insights, the current distribution is investigated. Two measurement configurations in Fig. 2a–f are used respectively, in which a current of I = 10 nA is applied to CBST (Lead 1) and SAH (Lead 2), respectively, to measure the current flowing out from other leads (Ii, i = 1, 2, 3, …, 6) which are all grounded19. In the first configuration, for a positively magnetized state under +B, the clockwise chiral current propagates along the boundary of CBST without dissipation in Fig. 2a. Hence, as shown in Fig. 2c, the lead nearest to the source in the clockwise direction, i.e., Lead 6, drains all the applied current to the ground. This is shown by the \({I}_{6}\) = 10 nA-plateau under \(+B\) whereas the currents from other leads are all zero, \({I}_{{{{{\mathrm{2,3,4,5}}}}}}\) = 0. For the negatively magnetized state under \(-B\), in principle, the counterclockwise antichiral current should now propagate along the opposite boundary without dissipation, and likewise, Lead 2 should drain all the applied current. However, we detected similar amounts of currents flowing out from Leads 2 to 4 as \({I}_{{{{{\mathrm{2,3,4}}}}}} \sim I/3\), but careful inspection finds that \({I}_{2} \, > {I}_{3} \, > {I}_{4}\) although the differences are very small. Considering that the distances between Leads 2 and 4 and the current source 1 increase successively, this result strongly supports that the transport in BST of the SAH region is dissipative in nature, whose resistance is proportional to the SAH geometry, i.e., length and shape. No current flows out from Leads 5 or 6 as \({I}_{{{{{\mathrm{5,6}}}}}}\) = 0. It is thus likely that SAH serves as a current divider that redistributes the incoming current to the three leads, as displayed in Fig. 2b. This implication is supported by the results from the second configuration. In the clockwise chirality of Fig. 2d, the applied current should be all drained by Lead 1. Surprisingly, as shown by Fig. 2f, only ~\(0.87I\) flows out from Lead 1, and the remaining current ~0.13I is out from Lead 3. This looks elusive since the current flowing from Lead 2 to 3 is against the chirality and should be prohibited. Multiple tests on this current distribution have been performed, which will repeat this result (Supplementary Fig. 4), although these quantization values are not universal. When reversing to the counterclockwise antichirality in Fig. 2e, we found not only Lead 3 but also Lead 4 drains the applied current with similar amounts as \({I}_{{{{{\mathrm{3,4}}}}}}\) ~ I⁄ 2, no matter Lead 3 should be the only lead that drains all the applied current. Consistent with the results of \({I}_{2} \, > {I}_{3} \, > {I}_{4}\) in Fig. 2c, because the distance between Lead 3 and the current source 2 is shorter than that between Leads 4 and 2, we could still distinguish that \({I}_{3} \, > {I}_{4}\). From the results in both configurations, it is recognized that, depending on the (anti)chirality, SAH can actually provide extra channels for guiding the incoming current toward either direction within the TI surface. Specifically, if this channel conforms with the (anti)chirality, like Fig. 2b and e, the incoming current will be redistributed according to the channel length, no matter whether the current is applied from the CBST or SAH. If it is against the (anti)chirality, like Fig. 2d, most of the current will still follow the (anti)chiral direction, whereas a small portion goes to the opposite direction, no matter whether propagating to such a direction should be prohibited. This nature underlines the role played by the counterpropagating helical state on the top surface of the TI BST, which can accommodate any incoming (anti)chiral state from the QAH insulator before redistribution. In summary, an electron incident to the SAH would have a SAH-geometry-dependent probability to be scattered into any helical channel as long as the channel(s) conforms with the (anti)chirality in the QAH insulator. According to Fig. 2f, this probability will be weighted by ~87% if there exists an additional helical channel that is against the (anti)chirality, whereas the electron could be scattered to such an unfavorable channel by weight of ~13%. Obviously, although being against the (anti)chirality, this channel should produce quite low dissipation comparable to that of chiral transport. Otherwise, the current will be simply shunted by the chiral state.
a, b, d, e Two measurement configurations. The solid lines represent the chiral currents, while the dashed lines are the redistributed currents due to helical surface states. c, f The corresponding measured results of current distributions. \({I}_{i}\left(i={{{{\mathrm{1,2}}}}},\ldots ,6\right)\) represents the current flowing out from Lead i.
Possible mechanism
Based on the above results, which are from the QAH states, we below explore how the helical state induces \({R}_{{xy}}^{{\prime} }\) during the plateau transition between the QAH states. This transition was known to have a percolative nature19,20, similar to the plateau-to-plateau transition in QH system21,22,23,24. By plotting the longitudinal conductivity \({\sigma}_{{xx}}\) under −0.08 ~0 T as a function of \({T}^{-1/3}\) in Fig. 3(a), we found that all of the data show linear regimes which can be fitted using the 2D variable range hopping (VRH) model \({\sigma}_{{xx}}={\sigma}_{0} \, {{\exp }}\left[-{\left({T}_{0}/T\right)}^{1/3}\right]\) where \({\sigma }_{0}\) and \({T}_{0}\) are fitting parameters15,25. This implies that, within the \(T\)-ranges for fittings, there exist a number of extra states for hopping in the exchange gap15,26. At lower temperatures, the tails of the data deviate from this model and saturate to different constants, which is a signature of ground states after freezing the in-gap states. The tails under 0 ~ \(-{B}_{c1}\), i.e. 0, −0.02, and −0.04 T, converge to a single constant of ~3.5 × 10−3\({e}^{2}/h\), while those inside the range of \(-{B}_{c1}\) ~ \(-{B}_{c2}\), i.e. −0.06, −0.07, and −0.08 T, gradually increase to ~2.4 × 10−1\({e}^{2}/h\). While the former corresponds to the QAH state, the latter enters the range of \({R}_{{xy}}^{{\prime} }\). During this transition, the VRH behavior allows us to evaluate the effective localization length \(\xi\) of the edge state (see Supplementary Note 1: Estimations to the localization length)15,25. The resulted \(B\)-dependent \(\xi\) is plotted in Fig. 3b. \(\xi\) within the QAH state under 0 ~ \(-{B}_{c1}\) is ~1.78 μm, consistent with the previous report15,27,28. Within \(-{B}_{c1}\) ~ \(-{B}_{c2}\), \(\xi\) quickly increases by one order of magnitude to ~17.77 μm under −0.08 T. This agrees with the band evolution of the QAH insulator that the exchange gap will gradually shrink and ultimately close at the coercivity due to the destruction of the net magnetization by multidomain29. Correspondingly, \(\xi\) from opposite edges will expand towards the bulk and merge together to hybridize a trivial state. \({\sigma }_{{xx}}\) further out of this range (\(B\)< −0.08 T) becomes unstable and does not allow conducting a meaningful estimation to \(\xi\). According to the percolation theory, \(\xi\) diverges as a power law by \(\xi \sim {\left(B-{B}_{c}\right)}^{-v}\) where \({B}_{c}\) is the coercive field and \(v\) is a universal critical exponent22,30,31,32. Using \({B}_{c}\)= −0.1 T and v = 2.38 according to previous reports24,33, the data could be well fitted by the percolation model, except for a slight deviation around 0 ~ \(-{B}_{c1}\). This deviation is reasonable because the measured \(\xi\) of this range are within the QAH state that should depart from the clean limit with \(\xi\)~100 nm34,35 owing to the VRH mechanism15. By extrapolating the fitting curve to evaluate \(\xi\) around the center of \({R}_{{xy}}^{{\prime} }\)-plateau, as shown by the inset of Fig. 3b, we found that \(\xi\) reaches to \({w}_{2}/2\) ~ 83 μm under −0.09 T and fully covers \({w}_{2}\) ~ 166 μm under −0.093 T. Such a prompt expansion of \(\xi\) within the tiny \(B\)-range is likely to result in a join between the chiral state from opposite edges, which may closely relate to the origin of \({R}_{{xy}}^{{\prime} }\). To explore this, a second SAH hall bar was fabricated, whose \({w}_{1}\) is narrowed down to d/3, as shown in Fig. 3(c). Likewise, a control Hall bar was also fabricated from the area without any SAH. Both resulted \({R}_{{xy}}\) are plotted in Fig. 3d. Consistent with previous results in Fig. 1e, the pair of \({R}_{{xy}}^{{\prime} }\)-plateaus appear near coercivity and also exhibits stochastic nature (Supplementary Fig. 6), but now they are much narrower than the previous ones. If the appearance of \({R}_{{xy}}^{{\prime} }\) is initiated by the join between the chiral states, this narrowing could be understood as a retardation for accomplishing the join since \({w}_{2}\) in this Hall bar is doubled, which requires further sweeping \(B\) before \(\xi\) fully covers \({w}_{2}\).
a The temperature (T)-dependent longitudinal conductance (σxx) for the selective-area heterostructure (SAH) device plotted as a function of \({T}^{-1/3}\) under different magnetic fields. Black lines are fitted to the data. b Magnetic field (B)-dependent localization length (ξ) data fitted using the percolation theory. Inset extrapolates the fitting to the coercivity compared to the CBST width without covered by BST, w2. c Optical image of another selective-area heterostructure device [BST: (Bi,Sb)2Te3, CBST: Cr-doped (Bi,Sb)2Te3], and d its Hall resistance Rxy measurement as a function of external magnetic field B. The width of the Hall bar is d ~ 500 μm. e Proposed spin-Hall effect and spin-orbit torque mechanism. \({{{{{{\boldsymbol{\tau }}}}}}}_{{{{{{\rm{SO}}}}}}}\): spin–orbit torque, \({{{{{{\bf{B}}}}}}}_{{{{{{\rm{SO}}}}}}}\): spin–orbit field, and M: magnetization.
The microscopic interaction between the chiral and helical states as well as how this affects the gap evolution, is the key to understanding these results. Since \({R}_{{xy}}\) serves as a probe to the topological invariant, which is \(\pm 1\) for QAH states, \({R}_{{xy}}^{{\prime} }\) implies the coexistence of opposite QAH states along the transverse direction that deducts from the quantized \({R}_{{xy}}\)27. Intuitively, after being covered by BST, the CBST may have a different gap evolution respective to \(B\)36 so that the gap closing/reopening points of the CBSTs covered with and without SAH are unsynchronized. When the applied current propagates along the chiral channel in the QAH insulator and arrives at the SAH, the spin-polarized chiral current is allowed to be scattered into one of the constituents of the helical state depending on the relative direction of their spins. Note that the helical state at the SAH interface may not be formed due to the topological nature between CBST and BST, whereas the helical state on the top surface of BST, which is away from the interface, remains intact. In this sense, the SAH is similar to the semi-magnetic TI in ref. 13, i.e., a CBST (2 nm)/BST (8 nm) heterostructure, in which both the chiral edge state and helical surface state were found to contribute. Detailed discussion on the results from such a semi-magnetic TI13 and the present study is provided in Supplementary Note 2: Discussion on the transport contributions in semi-magnetic topological insulators.
Below we provide one of the possible mechanisms to understand the appearance of \({R}_{{xy}}^{{\prime} }\). Because of the spin-momentum locking in the helical state and/or the spin Hall effect of the BST, the helical current then results in the accumulation of non-equilibrium polarized spins on the surfaces of TI, as shown in Fig. 3e37. Thanks to the clean and atomically flat heterointerface, these accumulated spins can couple to the adjacent CBST and results in a flow of spin angular momentum, which exerts a spin-orbit torque (SOT) on the magnetization of CBST as \({{{{{{\boldsymbol{\tau }}}}}}}_{{{{{{\rm{SO}}}}}}}=-\gamma {{{{{\bf{M}}}}}}\times {{{{{{\bf{B}}}}}}}_{{{{{{\rm{SO}}}}}}}\), where \(\gamma\) the gyromagnetic ratio, \({{{{{{\bf{B}}}}}}}_{{{{{{\rm{SO}}}}}}}=I{\lambda }_{{{{{{\rm{SO}}}}}}}{{{{{\bf{M}}}}}}\times \hat{y}\) the effective SO field, and \({\lambda }_{{{{{{\rm{SO}}}}}}}\) the coefficient proportional to the strength of SO coupling38,39,40,41,42. In Ref. 43, a similar CBST/BST heterostructure has the parameters of \({h}_{{DL}}/j\) = 4.8 ~ 14.6 \(\mu {{{{{\rm{T}}}}}}/\left({{{{{\rm{A}}}}}}\cdot {{{{{{\rm{cm}}}}}}}^{-2}\right)\) and \({M}_{s}\) = 16 \({{{{{\rm{emu}}}}}}/{{{{{{\rm{cm}}}}}}}^{-3}\) where \({h}_{{DL}}\) the effective DL-field and j are the current density. In the present study, \(j=I/{wt}\) where the applied current I = 10 nA, the SAH width w = 2d/3 ~ 333 μm, and the thickness t = 6 nm. Thus \({h}_{{DL}}\) = 2.4 ~ 7.3 μT. Note that this value is underestimated because this evaluation is based on the results at 1.9 K and the assumption of a uniform conductivity as used in ref. 43, whereas in the present study, the temperature is 20 mK, while the bulk of the sample is insulating, and the edge conduction dominates the transport. The precise evaluation to \({h}_{{DL}}\) is challenging as the current distribution in SAH is unclear. Therefore, we could not judge the role played by SOT, and the present experimental results do not allow us to precisely evaluate the contribution of SOT. Although the lack of an in-plane B does not allow a deterministic reversal of M, the induced \({{{{{{\bf{B}}}}}}}_{{{{{{\rm{SO}}}}}}}\) already cants M of CBST towards the in-plane direction. This advances the magnetization reversal in SAH and hence leads to the unsynchronized gap closings/reopenings29. In this situation, there arise chiral states along the SAH boundary, which may contribute extra \({\sigma }_{{xy}}\) and corresponding finite \({R}_{xx}\), as observed in Fig. 1g and f. Besides the SOT, we notice that the unsynchronized gap closings/reopenings might also be possible if the magnetic anisotropy of CBST is modified after being covered by BST and/or Cr dopants interdiffusion from CBST into the BST in the SAH region. Although the Cr interdiffusion in CBST/BST heterostructure was found to be unlikely44, the validation of these possible explanations requires further experimental investigations.
Theoretical model
To describe the unsynchronized gap closings/reopenings that emerge under \({B}_{c1}\) ~ \({B}_{c2}\), without losing the generality, we assume the mass terms \({m}_{1}=-m\) for the QAH insulator within SAH and \({m}_{2}=-1+\sqrt{4-{\left(m+1\right)}^{2}}\) for the one outside SAH, where \(m\in \left[-{{{{\mathrm{1,1}}}}}\right]\), as shown in Fig. 4a. The Hamiltonian of the SAH is
where \({\Psi }_{p}^{{{\dagger}} }=\left[{a}_{\uparrow }^{{{\dagger}} },{a}_{\downarrow }^{{{\dagger}} },{b}_{\uparrow }^{{{\dagger}} },{b}_{\downarrow }^{{{\dagger}} }\right]\) with a(b) are the surface states of TI and ↑(↓) are the spins, \({h}_{{{{{{\rm{QAH}}}}}}1}\left(p\right)={{\hslash}}{v}_{F}{p}_{1}{\sigma}_{1}+{{\hslash}}{v}_{F}{p}_{2}{\sigma}_{2}+{m}_{1}{\sigma}_{3}\) and \({h}_{{{{{{\rm{TI}}}}}}}\left(p\right)={{\hslash }}{v}_{F}^{{\prime}}\left({p}_{1}{\sigma}_{2}-{p}_{2}{\sigma}_{1}\right)\) are the Hamiltonians for the QAH insulator and the TI in the SAH respectively, \({v}_{F}\) and \({v}_{F}^{{\prime} }\) are the Fermi velocities for the chiral and helical states respectively, \({\sigma }_{0,1,2,3}\) are the unit matrix and the Pauli matrices acting on the spins, and \(T=t{\sigma }_{0}\) describes the interfacial coupling. The Hamiltonian for the QAH insulator outside of SAH is
where \({h}_{{{{{{\rm{QAH}}}}}}2}\left(p\right)={{\hslash}}{v}_{F}{p}_{1}{\sigma}_{1}+{{\hslash }}{v}_{F}{p}_{2}{\sigma}_{2}+{m}_{2}{\sigma}_{3}\). To calculate the transport of the whole system, we use the following tight-biding Hamiltonian45
where the former four terms describe the entire QAH insulator, the fifth term for the TI, and the last term for the coupling between them \(({{\hslash }}{v}_{F}={{\hslash }}{v}_{F}^{{\prime}}=1)\). We establish a similar Hall bar (d = 60a where a is the lattice constant) to calculate \({R}_{{xy}}\) using nonequilibrium Green’s function technique (see Supplementary Note 3: Nonequilibrium Green’s function calculation for details) as shown in Fig. 4(b), which essentially reproduces the unquantized \({R}_{{xy}}^{{\prime} }\) near coercivity. We found three regimes divided by two critical masses, \({m}_{c1}=0\) and \({m}_{c2}=\sqrt{3}-1\). When \(m \, > \, {m}_{c2}\) so that \({m}_{{{{{\mathrm{1,2}}}}}} \, < \, 0\), such as m = 1 in Fig. 4c, the band inversion and chiral states only occur around k = 0 (denoted as \(k={0}^{\pm }\) for a positive Fermi level), which is the QAH state with \({R}_{{xy}}=h/{e}^{2}\). \(\xi\) at this state, as quantified by the participation ratio \(p\) color-plotted in Fig. 4(c) and the square of wavefunction in transverse direction \({\left|{\uppsi }_{y}\right|}^{2}\) in Fig. 4d, is as narrow as ~2a along outer edges. However, when entering the intermediate regime with \({m}_{c1} \le m\le {m}_{c2}\) so that \({m}_{1} \, < \, 0\) but \({m}_{2} \, > \, 0\), such as \(m=0.15\) in Fig. 4e, f where \({R}_{{xy}}^{{\prime} }\) locates, the QAH state within SAH switches sign ahead of others due to the SOT. In this way, the band inversion around \(k=\pi\) is initiated, which forms new chiral states along SAH edges, \({\pi }^{\pm }\), with opposite chirality to \({0}^{\pm }\). States \({0}^{\pm }\) still remain but move out from SAH. Since \({m}_{1}\) is now close to zero, \({\left|{\uppsi }_{y}\right|}^{2}\) is dramatically enlarged to ~15a that covers \({w}_{2}/2\), which allows the join between \({0}^{\pm }\) across the \({w}_{2}\)-bulk. Hence, it is because of such join results in \({R}_{{xy}}^{{\prime} }\). This explains the result that, the larger \({w}_{2}\), the narrower \({R}_{{xy}}^{{\prime} }\)-plateau width will be. Finally, when \(m \, < \, {m}_{c1}\) so that \({m}_{{{{{\mathrm{1,2}}}}}} \, > \, 0\), such as \(m=-0.5\) in Fig. 4g, h, the band inversion and chiral states then only occur around \(k=\pi\), which enters another QAH state with \({R}_{{xy}}=-h/{e}^{2}\). Note that the contribution from the helical state in TI is crucial for the value of \({R}_{{xy}}^{{\prime} }\), without which \({R}_{{xy}}^{{\prime} }\) will be quantized to zero due to the cancelation from opposite QAH states27 as shown in Fig. 4b.
a Assumed masses evolutions for areas with and without SAH, m1, and m2. b Calculated Rxy as a function of m with and without topological insulator (TI). c Calculated band structure for m = 1 with the color representing the participation ratio p and d the corresponding square of the wavefunction in transverse direction \({\left|{\psi }_{y}\right|}^{2}\). e–h Similar plots for various m. Insets show the schematics of the current distributions of the SAH devices. Red and blue areas indicate the layers covered with and without (Bi,Sb)2Te3, respectively.
Conclusions
To summarize, we have demonstrated the integration between the chiral and helical states using SAH, whose outcome is unveiled by the current redistribution and additional Hall plateaus. Our results support that constructing versatile structures using SAH is a route toward low-dissipative topological electronics.
Methods
SAH growth and device fabrication
Films growths were conducted in an MBE system. The QAH insulator, which consists of a 6-nm-thick Cr:(Bi,Sb)2Te3 (CBST) film, was epitaxially grown on the entire surface of a GaAs(111)B substrate19,46,47. During this growth, the substrate was held at 200 °C with high-purity materials (Bi, Sb, Te, and Cr) co-evaporated from Knudsen cells. The film thickness was controlled by the reflection high-energy electron diffraction (RHEED) that was used to count the number of quintuple layers until 6 quintuple layers (corresponding to 6 nm) of CBST had been deposited. Details of the growth can be found in refs. 19,47,48. After this, the film was transferred into the mask chamber, which is vacuum-connected with the MBE chamber, to stack a stencil mask contacting with the film surface. This substrate/film/mask stack was then transferred back to the MBE chamber for the deposition of TI, which consists of a 6-nm-thick (Bi,Sb)2Te3 (BST) film, through the opening in the stencil mask. Such stencil lithography allows the BST film to grow only on a part of the CBST surface. In the growth of BST, RHEED cannot be used due to the stencil mask. Instead, we deposited the BST layer according to the pre-calibrated time that corresponds to six quintuple layers of BST. During the transfer, the vacuum is maintained around 2 × 10−9 mbar. Hall bars are patterned from the areas with and without SAH, respectively, by stencil masks using the reactive ion etching technique. The contacts were made by Al wires attached to the sample with indium.
Data availability
The datasets generated during and/or analyzed during the current study are available from the corresponding author upon reasonable request.
Code availability
The computer codes that support the findings presented in the main text are available from the corresponding authors upon reasonable request.
References
Kane, C. L. & Mele, E. J. Z2 topological order and the quantum spin Hall effect. Phys. Rev. Lett. 95, 146802 (2005).
Fu, L. & Kane, C. L. Time reversal polarization and aZ2adiabatic spin pump. Phys. Rev. B 74, 195312 (2006).
Fu, L. & Kane, C. L. Topological insulators with inversion symmetry. Phys. Rev. B 76, 045302 (2007).
Fu, L., Kane, C. L. & Mele, E. J. Topological insulators in three dimensions. Phys. Rev. Lett. 98, 106803 (2007).
Moore, J. E. & Balents, L. Topological invariants of time-reversal-invariant band structures. Phys. Rev. B 75, 121306 (2007).
Qi, X.-L., Hughes, T. L. & Zhang, S.-C. Topological field theory of time-reversal invariant insulators. Phys. Rev. B 78, 195424 (2008).
Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Liu, C.-X., Qi, X.-L., Dai, X., Fang, Z. & Zhang, S.-C. Quantum anomalous hall effect in Hg1−yMnyTe quantum wells. Phys. Rev. Lett. 101, 146802 (2008).
Yu, R. et al. Quantized anomalous Hall effect in magnetic topological insulators. Science 329, 61–64 (2010).
Nomura, K. & Nagaosa, N. Surface-quantized anomalous Hall current and the magnetoelectric effect in magnetically disordered topological insulators. Phys. Rev. Lett. 106, 166802 (2011).
Tokura, Y., Yasuda, K. & Tsukazaki, A. Magnetic topological insulators. Nat. Rev. Phys. 1, 126–143 (2019).
Mogi, M. et al. Magnetic modulation doping in topological insulators toward higher-temperature quantum anomalous Hall effect. Appl. Phys. Lett. 107, 182401 (2015).
Mogi, M. et al. Experimental signature of the parity anomaly in a semi-magnetic topological insulator. Nat. Phys. 18, 390–394 (2022).
Bestwick, A. J. et al. Precise quantization of the anomalous hall effect near zero magnetic field. Phys. Rev. Lett. 114, 187201 (2015).
Kawamura, M. et al. Current-driven instability of the quantum anomalous hall effect in ferromagnetic topological insulators. Phys. Rev. Lett. 119, 016803 (2017).
Pan, L. et al. Observation of quantum anomalous hall effect and exchange interaction in topological insulator/antiferromagnet heterostructure. Adv. Mater. 32, e2001460 (2020).
Luan, J. et al. Controlling the zero hall plateau in a quantum anomalous hall insulator by in-plane magnetic field. Phys. Rev. Lett. 130, 186201 (2023).
Ji, Y. et al. Thickness-driven quantum anomalous hall phase transition in magnetic topological insulator thin films. ACS Nano 16, 1134–1141 (2022).
Huang, Y. et al. Bias-modulated switching in Chern insulator. N. J. Phys. 24, 083036 (2022).
Wu, X. et al. Scaling behavior of the quantum phase transition from a quantum-anomalous-Hall insulator to an axion insulator. Nat. Commun. 11, 4532 (2020).
Wei, H. P., Tsui, D. C., Paalanen, M. A. & Pruisken, A. M. M. Experiments on delocalization and university in the integral quantum Hall effect. Phys. Rev. Lett. 61, 1294–1296 (1988).
Pruisken, A. M. M. Universal singularities in the integral quantum Hall effect. Phys. Rev. Lett. 61, 1297–1300 (1988).
Li, W., Csáthy, G. A., Tsui, D. C., Pfeiffer, L. N. & West, K. W. Scaling and universality of integer quantum Hall plateau-to-plateau transitions. Phys. Rev. Lett. 94, 206807 (2005).
Li, W. et al. Scaling in plateau-to-plateau transition: a direct connection of quantum hall systems with the Anderson localization model. Phys. Rev. Lett. 102, 216801 (2009).
Furlan, M. Electronic transport and the localization length in the quantum Hall effect. Phys. Rev. B 57, 14818–14828 (1998).
Pan, L. et al. Probing the low-temperature limit of the quantum anomalous Hall effect. Sci. Adv. 6, eaaz3595 (2020).
Yasuda, K. et al. Quantized chiral edge conduction on domain walls of a magnetic topological insulator. Science 358, 1311–1314 (2017).
Allen, M. et al. Visualization of an axion insulating state at the transition between 2 chiral quantum anomalous Hall states. Proc. Natl Acad. Sci. USA 116, 14511–14515 (2019).
He, Q. L. et al. Topological transitions induced by antiferromagnetism in a thin-film topological insulator. Phys. Rev. Lett. 121, 096802 (2018).
Huckestein, B. & Kramer, B. One-parameter scaling in the lowest Landau band: Precise determination of the critical behavior of the localization length. Phys. Rev. Lett. 64, 1437–1440 (1990).
Huo, Y. & Bhatt, R. N. Current carrying states in the lowest Landau level. Phys. Rev. Lett. 68, 1375–1378 (1992).
Wang, J., Lian, B. & Zhang, S.-C. Universal scaling of the quantum anomalous Hall plateau transition. Phys. Rev. B 89, 085106 (2014).
Koch, S., Haug, R. J., Klitzing, K. & Ploog, K. Size-dependent analysis of the metal-insulator transition in the integral quantum Hall effect. Phys. Rev. Lett. 67, 883–886 (1991).
Zhou, B., Lu, H.-Z., Chu, R.-L., Shen, S.-Q. & Niu, Q. Finite size effects on helical edge states in a quantum spin-Hall system. Phys. Rev. Lett. 101, 246807 (2008).
Chen, C.-Z., Xie, Y.-M., Liu, J., Lee, P. A. & Law, K. T. Quasi-one-dimensional quantum anomalous Hall systems as new platforms for scalable topological quantum computation. Phys. Rev. B 97, 104504 (2018).
Mogi, M. et al. A magnetic heterostructure of topological insulators as a candidate for an axion insulator. Nat. Mater. 16, 516–521 (2017).
Mellnik, A. R. et al. Spin-transfer torque generated by a topological insulator. Nature 511, 449–451 (2014).
Liu, L., Lee, O. J., Gudmundsen, T. J., Ralph, D. C. & Buhrman, R. A. Current-induced switching of perpendicularly magnetized magnetic layers using spin torque from the spin Hall effect. Phys. Rev. Lett. 109, 096602 (2012).
Liu, L. et al. Spin-torque switching with the giant spin Hall effect of tantalum. Science 336, 555–558 (2012).
Garello, K. et al. Symmetry and magnitude of spin–orbit torques in ferromagnetic heterostructures. Nat. Nanotechnol. 8, 587–593 (2013).
Miron, I. M. et al. Perpendicular switching of a single ferromagnetic layer induced by in-plane current injection. Nature 476, 189–193 (2011).
Manchon, A. et al. Current-induced spin-orbit torques in ferromagnetic and antiferromagnetic systems. Rev. Mod. Phys. 91, 035004 (2019).
Fan, Y. et al. Magnetization switching through giant spin-orbit torque in a magnetically doped topological insulator heterostructure. Nat. Mater. 13, 699–704 (2014).
Yoshimi, R. et al. Quantum Hall states stabilized in semi-magnetic bilayers of topological insulators. Nat. Commun. 6, 8530 (2015).
Qi, X.-L., Wu, Y.-S. & Zhang, S.-C. Topological quantization of the spin Hall effect in two-dimensional paramagnetic semiconductors. Phys. Rev. B 74, 085308 (2006).
Kou, X. et al. Metal-to-insulator switching in quantum anomalous Hall states. Nat. Commun. 6, 8474 (2015).
Sun, H. et al. Topological transitions in the presence of random magnetic domains. Commun. Phys. 5, 217 (2022).
He, M. et al. Quantum anomalous Hall interferometer. J. Appl. Phys. 133, 084401 (2023).
Acknowledgements
The authors thank Wenlu Lin for assisting with the experiments. This research is supported by the National Key RD Program of China (Grants No. 2020YFA0308900 and No. 2018YFA0305601), the National Natural Science Foundation of China (Grant No. 11874070), and the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB28000000). C.W. thanks for the support from Tianjin University.
Author information
Authors and Affiliations
Contributions
Q.L.H. and H.S. conceived and designed the experiments. H.S. and Y.H. grew the films. H.S. fabricated the devices and performed the measurements. S.Z. and B.Z. performed the transmission electron microscope experiments. C.W. performed the theoretical calculation and analysis. H.S. and Q.L.H. processed and analyzed the data. Q.L.H. wrote the paper with contributions from H.S., Y.H., M.H., Y.F., S.Z., B.Z., and C.W..
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sun, H., Huang, Y., He, M. et al. Chiral and helical states in selective-area epitaxial heterostructure. Commun Phys 6, 204 (2023). https://doi.org/10.1038/s42005-023-01328-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-023-01328-4
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.