Mixed orbital states and modulated crystal structures in La_1−xCa_xMnO₃ deduced from synchrotron X-ray diffraction

Abstract

In the model manganese perovskites La_1−xCa_xMnO₃, several important phenomena have been observed, including ferromagnetic metallic/insulating states, colossal magnetoresistance effects, and charge- and orbital-ordered states. In the past, only compounds with x = 1/2, 2/3 and 3/4 and an insulating ground/antiferromagnetic state have been studied. To fully understand the crystal and electronic structures of these materials, it is important to study compounds with doping levels in the range of 0.5 < x < 2/3. Here we study the crystal structure in a series of compounds with 0.5 < x ≤ 0.6 using ultrahigh-resolution synchrotron X-ray diffraction. The experimental results reveal that all compounds undergo a structural transition at T < T_CO(x) ≈ 200 − 220 K with the concomitant emergence of superlattice Bragg peaks, which can be indexed assuming a superstructure with a modulation propagation vector, τ. At the base temperature of 5 K, the modulation vector of the superstructure τ = [τ_a, 0, 0] is parallel to the a-axis, with τ_a varying linearly with x, as τ_a ≈ 1 − x. Our results may aid attempts to understand more deeply phenomena related to spin, charge, and orbital ordering, as well as colossal magnetoresistance and symmetry breaking and emergent order in quantum states.

Introduction

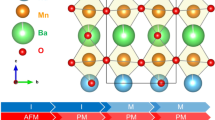
An important unresolved issue in understanding the physics of La_1−xCa_xMnO₃ relates to the physical mechanism responsible for the change in the ground state from ferromagnetic metallic for 0.23 < x < 0.5 to antiferromagnetic insulating for 0.5 < x ≤ 1 (for reviews see refs. ^1,2). Early and recent studies have explained this dichotomy using the charge and orbital ordering model (CO-OO) adopted, especially when x is equal to a simple fraction, e.g., x = n/(n + 1) with n = 1, 2, and 3. This model was first proposed in the 1950s by Wollan, Kohler³ and Goodenough⁴ in order to interpret the two distinct sets of magnetic Bragg peaks observed in the $x=\frac{1}{2}$ compound. For $x=\frac{1}{2}$, charge neutrality necessitates an average charge of 3.5 per Mn atom due to the difference in charge between La³⁺ and Ca²⁺. This charge state can be realized by considering a random distribution of an equal number of Mn³⁺ and Mn⁴⁺ ions at the lattice points. As the sample is cooled below the so-called charge-ordering temperature (T_CO), minimization of the electrostatic energy generates long-range ordering of Mn³⁺ and Mn⁴⁺ onto specific sites (Fig. 1a). Since Mn³⁺ is a Jahn-Teller–active ion, the e_g orbital degeneracy is lifted, inducing a distortion of the Mn³⁺O₆ octahedra. Minimization of the strain energy induces long-range orbital ordering (essentially strain ordering) concomitant with the charge ordering. In the case of $x=\frac{1}{2}$, it is believed that the elongated Mn³⁺-O bond is directly related with the $3{d}_{z}^{2}$ orbital, which is oriented along this bond (Fig. 1a).

Fig. 1: Schematic projection of the crystal and modulated structures of La_1−xCa_xMnO₃ compound.

a Schematic projection of the crystal and magnetic structures of La_1−xCa_xMnO₃ (x = 1/2) along the b-axis in the charge and orbital-ordered model. b Modulated crystal structure of La_1−xCa_xMnO₃ (x = 0.6). For clarity, only the Mn and O atoms are shown. u(r_x) represents the displacement of the atoms from average crystal structure positions along the c-axis as a function of r_x. Λ is the wavelength of the modulation.

The magnetic structure of La_1/2Ca_1/2MnO₃ includes antiferromagnetic and ferromagnetic interactions. In the ac-plane (Pnmn description), the magnetic structure can be considered as consisting of ferromagnetic zigzag chains (see Fig. 1a). These chains are coupled antiferromagnetically along the c-axis. In a chain (see Fig. 1a), the occupied e_g orbitals of two Mn³⁺ ions are directed toward the intermediate Mn⁴⁺ ion (where the e_g orbital is unoccupied). Virtual hopping of these e_g-electrons onto empty Mn⁴⁺-e_g orbitals produces a ferromagnetic exchange interaction along the chain². Antiferromagnetic interaction between zigzags and along the b-axis can be through the antiferromagnetic exchange of the occupied t_2g-electrons^2,5. This model has been widely accepted in the mid-1990s because of the discovery of satellite Bragg peaks in X-ray and transmission electron microscopy (TEM) diffraction data below the charge-ordering temperature (T_CO)^6,7,8,9. The commensurate wave vector used to index the satellite Bragg peaks when $x=\frac{1}{2}$ can be attributed to a layer-type ABAB ⋯ arrangement of Mn-O layers located perpendicular to the a-axis and consisting exclusively of Mn³⁺(A) and Mn⁴⁺(B). Essentially, in this model, Mn³⁺ and Mn⁴⁺ ions order along the diagonal directions of the Mn-O square lattice of the parent perovskite structure (Fig. 1). The same interpretation is applicable to the compositions with $x=\frac{2}{3}$ and $\frac{3}{4}$, simply by changing the layer sequence to ABBABB ⋯ and ABBBABBB ⋯, respectively. For $x\approx \frac{4}{5}$ and T < T_CO, the crystal structure becomes monoclinic with two manganese sites without modulation, while the magnetic structure can be described with only one propagation vector, ${{{{{{{{\bf{k}}}}}}}}}_{{{{{{{{\rm{C}}}}}}}}}=[\frac{1}{2},0,\frac{1}{2}]$ (C-structure). The ground state at this particular concentration regime displays only orbital ordering without charge ordering^10,11.

Although this plausible physical picture interprets the majority of the experimental data, especially for the compositions with $x=\frac{1}{2},\frac{2}{3}$, and $\frac{3}{4}$, there are however some experimental issues which are not compatible with it^{12,13,14,15,16}. The most significant problem for the charge-ordered model is that it is not able to predict the commensurate-to-incommensurate modulation observed in the interval [T_N, T_CO] for $x=\frac{1}{2},\frac{2}{3}$, and $\frac{3}{4}$ and the incommensurate superstructure for $\frac{1}{2} < x < \frac{2}{3}$ and $\frac{2}{3} < x < \frac{3}{4}$. Finally, and most importantly, the wave vector, τ = (1 − x)a^* = [1 − x, 0, 0] needed to index the satellite Bragg peaks observed in TEM images by Loudon et al.¹⁶ for La_1−xCa_xMnO₃ compositions with x > 0.5 is not compatible with the simple charge-ordered arrangement of manganese ions employed for $x=\frac{1}{2},\frac{2}{3}$, and $\frac{3}{4}$. In addition, it has been demonstrated¹⁶ that the particular variation of the wave vector with x contradicts the interpretation that there exist only four distinct phases (at $x=\frac{1}{2}$, $\frac{2}{3}$, $\frac{3}{4}$, and $\frac{4}{5}$) with miscibility gaps at values of x in between^17,18,19.

In this article, we present a crystallographic study using high-resolution synchrotron X-ray diffraction (SXRD) data in carefully prepared powder La_1−xCa_xMnO₃ samples with 0.51 ≤ x ≤ 0.6 aiming at the elucidation of the crystal structure below the charge-ordering temperature. In this particular calcium concentration regime, the diffraction patterns at 5 K clearly display satellite Bragg peaks—here, we use a site displacive modulation model and attempt a quantitative analysis of the modulation. First, we present the refinement of the SXRD data based on the average crystal structure and the anisotropic microstrain broadening of the Bragg peaks. Next, modeling of the satellite peaks as function of x and temperature is attempted. The Rietveld refinement results, together with the description of the satellite peaks, show that all the samples in the present study are single-phase materials above and below the charge-ordering temperature. The superstructure arises from a displacive modulation of the average structure with a propagation vector, τ_a, along the a-axis varying with x as τ_a = 1 − x. The amplitude of the modulation wave is transverse to the modulation vector, parallel to the c-axis.

Results and discussion

Average crystal structure

The average orthorhombic structural model (space group Pnma) of the La_1−xCa_xMnO₃ compound was successfully used for the refinement of the SXRD patterns of all samples at the studied temperatures. To account for the axial divergence effects and the anisotropic broadening of the Bragg peaks, the profile function #7 and the strain model #3 are used (see Fullprof manual for more details²⁰).

The first refinement steps were dedicated to refining the scale factor, the background coefficients, the unit cell parameters, the zero-shift errors, and the full width at half maximum (FWHM) peak profile coefficients, U, V, W, X, and Y. During this procedure, we found that the Gaussian contribution to the peak shape is very small, U = V = 0, W ~ 10⁻⁴(deg.)² together with negligible Lorentzian Scherrer size broadening, Y < 10⁻⁴ deg. both at 295 and 5 K. The peak shape appears to be dominated by the Lorentzian contribution, X ≈ 0.1817 and 0.1879 deg. at 295 and 5 K, respectively, possibly due to strain fluctuation effects.

Owing to the ultrahigh resolution of the diffractometer, we ascertained that the diffraction peaks are characterized by selective peak broadening, which is closely related to the orbital ordering occurring on cooling below the CO transition (T < T_CO). This effect is clearly evident when one inspects the (n, 0, n)/(0, 2n, 0) family of diffraction lines. Such type of broadening can be phenomenologically reproduced by assuming that the lattice metrics vector, α = (A, B, C, D, E, F), encountered in the expression of the lattice plane spacings, ${M}_{hkl}=1/{d}_{hkl}^{2}=A{h}^{2}+B{k}^{2}+C{l}^{2}+Dkl+Ehl+Fhk$ is a stochastic vector, which follows a multidimensional Gaussian distribution characterized by the mean value vector and the variance-covariance matrix, C_ij = E[(α_i − 〈α_i〉)(α_j − 〈α_j〉)] (Stephens’ model)²¹. The centroid position of the Bragg peaks is calculated from the average values of the metric parameters, while their broadening from the variance, σ²(M_hkl) = ∑_i,jC_ij(∂M/∂α_i)(∂M/∂α_j). In an orthorhombic system, the variance of σ²(M_hkl) can be expressed in terms of six independent parameters²¹ (S₄₀₀, S₀₄₀, S₀₀₄, S₂₂₀, S₂₀₂, S₀₂₂) through the relation σ²(M_hkl) = S₄₀₀h⁴ + S₀₄₀k⁴ + S₀₀₄l⁴ + S₂₂₀h²k² + S₂₀₂h²l² + S₀₂₂k²l², which can be estimated from the results of the Rietveld refinements. In order to simplify the refinements, we kept the isotropic Gaussian U, V, W and Lorentzian X, Y FWHM parameters at zero. Instead, we used the parameter, ξ which ‘shares’ the anisotropic FWHM in the Gaussian ${H}_{G}^{2}={(1-\xi )}^{2}{D}^{2}{\tan }^{2}\theta$ and the Lorentzian ${H}_{L}=\xi D\tan \theta$ parts with ${D}^{2}=1{0}^{-8}8\ln 2{(180/\pi )}^{2}{\sigma }^{2}({M}_{hkl})/{M}_{hkl}^{2}$ (see ref. ²⁰ for more details).

The use of Stephens’ model led to smoothly proceeding Rietveld refinements of the diffraction data with the reliability factors reduced approximately by a factor of two in comparison to the results of the analysis using isotropic lineshape parameters. A similar methodology was used before in the analysis of the SXRD patterns of the Bi_0.15Ca_0.85MnO₃ manganite measured with the same diffractometer²². At the final stages of the refinement, the atomic coordinates and isotropic temperature factors were freely refined. The occupancy factors were kept fixed at the nominal values. After several refinement cycles, we succeeded in achieving very good Rietveld refinement results of the average crystal structure. As an example, the Rietveld plots of the x = 0.6 sample at 5 and 295 K are shown in Fig. 2. Tables 1 and 2 summarize the refined structural and microstructural parameters for all samples at 295 and 5 K. For the sample with nominal Ca doping level, x = 0.51, the Gaussian distribution of the cell parameters does not reproduce well the experimental Bragg peak shapes in the diffraction profile at T = 5 K. In particular, this is especially prominent for the (2n, 0, 2n) and (0, 4n, 0) reflections related to the charge-ordering transition below T_CO that appear strongly asymmetric. This results in a very high value of the agreement factor, χ². No such issues are evident in the room temperature diffraction data, as can be seen from the low χ² value.

Fig. 2: Rietveld plots of La_0.4Ca_0.6MnO₃ compound based on the average crystal structure.

Results of the Rietveld refinement of the average structure (Pnma space group) of the La_1−xCa_xMnO₃ (x = 0.6) composition to synchrotron X-ray powder diffraction data (λ = 0.50008 Å) at a 295 and b 5 K. The observed data points are indicated by open circles, while the calculated and difference patterns are shown as solid lines. The positions of the reflections are indicated by vertical lines below the patterns. The insets show enlarged views of a selected area of the profiles near the background level. A number of superlattice peaks present in the measured profile at 5 K (black color) are not accounted for by the average structural model in the calculated profile (red color). These are not present in the measured profile at 295 K.

Table 1 Refined average crystal-structure parameters at 295 K.

Table 2 Refined average crystal-structure parameters at 5 K.

Figure 3 shows the variation of the lattice parameters at T = 5 K with increasing Ca²⁺ concentration, x. The reduction of all lattice parameters with increasing x can be accounted for by the smaller ionic radius of Ca²⁺ than that of La³⁺. Here we point out that the monotonic variation of the lattice parameters with x at 5 K (as well as at 295 K) indicates that the average calcium concentration varies from sample to sample in a controlled way.

Fig. 3: Unit cell constants of the average crystal structure of La_1−xCa_xMnO₃ (0.5≺ x ≤ 0.6) at 5 K.

Variation of the unit cell constants of La_1−xCa_xMnO₃ (0.5 ≤ x ≤ 0.6) with changing x at 5 K. Error bars are smaller than the data points.

Analysis of the satellite peaks

Having successfully described the SXRD patterns with the Pnma space group structural model for all samples, a careful inspection of the profile near the background level (inset of Fig. 2b) revealed several weak peaks not predicted by the average-structure model. These peaks can be indexed using fractional Miller indices. Equivalently, they can be reproduced with a modulation wave vector, τ_s = [τ_a, 0, 0] with τ_a = 1 − x. They are all satellites of the strongest Bragg peaks originating from the aristotype cubic perovskite structure. In all cases, La/Ca and Mn contribute constructively to the structure factor, while the Miller index, ℓ is non-zero [e.g., (1 ± τ_a, 2, 1), (τ_a, 0, 2) (unresolved) (τ_a, 2, 2), (2 ± τ_a, 0, 2), (1 ± τ_a, 2, 3)] with the satellite-peak intensity increasing as ℓ increases.

These observations can be nicely explained by (Eq. 7, in Supplementary Note 1) because the most intense first-order satellites are expected to be connected with fundamental Bragg peaks of the highest structure factors (e.g., the peaks deriving from the cubic perovskite structure (1, 2, 1), (2, 0, 2), and (1, 2, 3) reflections) and the highest ℓ index. This is observable up to a certain Bragg angle where the reduction of the atomic scattering factors is not overcome by the increase in ℓ. Recalling that the structure factor of the satellite peaks is $\sim {{{{{{{\bf{{u}}}}}}}_{i}^{0}}}\cdot ({{{{{{{\bf{Q}}}}}}}}-{{{{{{{\boldsymbol{\tau }}}}}}}})$ (see Supplementary Note 1), we can conclude that the polarization of the modulation is along the c-axis. Similar satellite peaks but with a-components of the structural modulation vector equal to $\frac{1}{2}$, $\frac{1}{3}$, and $\frac{1}{4}$ were observed in La_1−xCa_xMnO₃ with $x=\frac{1}{2}$, $x=\frac{2}{3}$, and $x=\frac{3}{4}$, respectively^6,7,8 and provided the diffraction signatures of the so-called 2a, 3a, and 4a superstructures. In order to analyze the structural modulation quantitatively, we simulated the SXRD patterns using the atomic displacement model described in Supplementary Note 1 (Eq. 4, Supplementary Note 1), assuming that below T_CO, the crystal structure is harmonically modulated. It was immediately apparent that second- and higher-order satellites made negligible contributions to the calculated patterns. Consequently, for simplicity, we consider only first-order satellites. The zeroth-order, m = 0 Bragg peaks (Eq. 6, in Supplementary Note 1) are reproduced by the refined average-structure and microstructure model described earlier. A simple inspection of the satellite Bragg peaks also revealed that they had larger linewidths than those of the zeroth-order ones. We accounted for this broadening by employing as a profile function a Lorentzian curve with a FWHM varying by a Scherrer-type equation, $\Delta 2\theta \sim L/\cos \theta$. Figure 4 shows the experimental and calculated SXRD patterns of the samples La_1−xCa_xMnO₃ (0.5 < x ≤ 0.6) at 5 K.

Fig. 4: Experimental and simulated X-ray diffraction patterns of the La_1−xCa_xMnO₃ (0.5 < x ≤ 0.6) compositions at 5 K.

The black, red, and blue lines correspond to the experimental, to the calculated using the average crystal structure model, and to the calculated using the first-order satellites model, respectively. The well-resolved superlattice peaks are highlighted in yellow. Superlattice peaks with appreciable intensity have k = 2n.

The following conclusions were reached after performing a series of trial-and-error simulations by varying the amplitude and the phase of the modulation for each atom. (1) The very good data statistics show that only first harmonics are observed, implying that the structural modulation in La_1−xCa_xMnO₃ (x ≥ 0.5) is harmonic, with a single modulation vector. (2) The modulation vector, τ ≈ (1 − x)a^*, is along the a-axis and varies continuously with x. (3) The polarization of the modulation is parallel to the c-axis (${{{{{{{{\boldsymbol{u}}}}}}}}}_{i}^{0}\parallel c$-axis, see Fig. 1b). (4) The displacements of all atoms are in-phase. (5) The best agreement between observed and calculated patterns is obtained when the modulation amplitudes of (La,Ca), (Mn, O1), and O2 atoms are ≈0.016, ≈0.012, and ≈0.016 fractional units, respectively (e.g., for (La,Ca) the amplitude is estimated to be u = 0.016c ≈ 0.09 Å). (6) Finally, the effective size of the diffraction domains contributing to the satellite peaks is estimated to be about 200–300 Å for all samples at 5 K. Here, we also note that one cannot exclude a small c-component of the wave modulation vector [τ_a, 0, τ_c ≈ 0.003] in accounting for the extra broadening of the satellite Bragg peaks. In TEM studies, such an extra component has been attributed^23,24 to anti-phase domains.

Figure 5 shows the concentration dependence of the a-component, τ_a of the modulation vector deduced from the location of the satellite peaks in the SXRD patterns. Although the experimental points slightly deviate from the τ_a = 1 − x line, it appears reasonable to deduce a linear variation in the ideal case. The deviation of the observed points from the ideal curve could be attributed to a systematic error in the value of real calcium concentration (i.e., there may be a small constant error in x when compared with the nominal values). The obtained results are in good agreement with the data of Loudon et al.¹⁶.

Fig. 5: Concentration variation of a-component of the modulation vector at 5 K.

Variation of the a-component, τ_a of the modulation vector with concentration, x in La_1−xCa_xMnO₃ at 5 K.

Results of variable temperature diffraction data

Let us continue by next examining the temperature variation of the SXRD patterns. Figure 6 depicts the temperature variation of the unit cell parameters for samples with x = 0.53, 0.57, and 0.6. The lattice metrics respond sensitively to temperature on cooling, with a and c increasing abruptly and $b/\sqrt{2}$ undergoing a step-like decrease. The temperature range at which the changes occur depends on the Ca concentration, x. This variation corresponds to a structural transition, which has been attributed for $x=\frac{1}{2}$, $x=\frac{2}{3}$, and $x=\frac{3}{4}$ to the so-called charge-ordering transition at temperatures, T_CO. We would like to point out that the terms “charge-ordering temperature” or “charge-ordering transition” are used here to denote the temperature where the zero-field-cooled magnetization curves show a local maximum, the average crystal-structure lattice parameters change abruptly, and satellite Bragg peaks are observed both in TEM and SXRD measurements. This transition does not necessarily mean ordering of the electric charges.

Fig. 6: Temperature variation of the unit cell parameters of La_1−xCa_xMnO₃ compound with x = 0.53, 0.57, and 0.6.

The arrows denote the charge-ordering transitions located at the temperatures where the slope of each b(T) curve is at a maximum. Error bars are smaller than the data points (the standard deviations have been calculated by fullprof program as described in the fullprof manual page 43).

We define the transition temperature as the temperature at which the db(T)/dT curves show a maximum, as indicated by arrows in Fig. 6. This coincides with the temperature at which a peak is observed in the bulk magnetization data^25,26. The changes observed in the temperature variation of the unit cell parameters at T_CO are accompanied by the appearance of the satellite Bragg peaks, a fact signaling that two distortion mechanisms start to operate simultaneously. The first is related to the ordering of the deformation of the Mn-O₆ octahedral units and the second with the development of the superstructure. The changes in the unit cell parameters at T_CO correlate with the shortening of the Mn-O1 apical bond length to ~1.91 Å, compared with the value of ~1.93 Å at T > T_CO. This bond is roughly parallel to the b-axis, and consequently, its decrease is directly related to the temperature variation of the b-axis. At the same time, the in-plane Mn-O2 bonds increase slightly for T < T_CO. It is interesting to note that the magnitude of these changes is much smaller than the amplitude of the ion displacements of ≈0.09 Å. Based on the correlation of the Mn-O₆ octahedral deformations with the Jahn-Teller effect, the average distortion is of the apically compressed type, implying that the ${d}_{z}^{2}$ orbital lies in the a–c plane. Therefore, in the structural transition occurring at T < T_CO, the ${d}_{z}^{2}$ orbitals are brought into the a–c plane, while the harmonic modulation with amplitude along the c-axis may be related to the charge localization.

Panels (a1, b1, c1) of Fig. 7 depict the temperature evolution of selected areas of the SXRD patterns in which satellite peaks (1 ± τ_a, 2, 3) with maximal intensity are present for samples with x = 0.53, 0.57, and 0.6, respectively. The (1 − τ_a, 2, 3) Bragg peak is displaced toward higher angles on heating, whereas the (1 + τ_a, 2, 3) to lower angles, implying that τ_a is temperature dependent. The satellite peaks eventually disappear above T_CO. Given their weak intensity, it is difficult to conclude with certainty whether the satellites disappear suddenly or gradually, a fact related to the character of the phase transition. By invoking the information from the magnetic measurements, the disappearance of the satellites is most likely sudden, corresponding to a first-order transition.

Fig. 7: Satellite Bragg peaks for the samples with x = 0.53, 0.57, and 0.6.

a1, b1, c1 Selected regions of the synchrotron X-ray powder diffraction patterns showing the temperature evolution of the satellite Bragg peaks with Miller indices (1 ± τ_a, 2, 3) for the x = 0.53, 0.57, and 0.6 samples. a2, b2, c2 Temperature variation of the a-component of the modulation wave vector (left axis) and of the normalized integrated intensity of the (1 − τ_a, 2, 3) satellite Bragg peak (right axis) for each composition. The dashed and continuous lines through the τ_a(T) and I(1 − τ_a, 2, 3)/I₀ points are guides to the eye.

Panels (a2, b2, c2) of Fig. 7 show the temperature variation of the non-zero a-component of the modulation vector, τ_a, together with that of the integrated intensity of the (1 − τ_a, 2, 3) satellite Bragg peak. Within standard deviation, for T < T_N, τ_a(T) is temperature independent, while for T > T_N, τ_a decreases markedly with temperature, meaning that the wavelength of the modulation becomes larger. This particular temperature dependence of τ_a agrees well with the predictions of Milward, Calderon, and Littlewood (see Fig. 1b of ref. ²⁷).

Figure 8 shows the temperature dependence of the S_HKL parameters for the x = 0.57 sample. Similar results are obtained for all the other samples. The temperature variation of the S_HKL parameters changes drastically at charge-ordering temperature. The largest values of the variance of the unit cell parameters, especially for the b-axis, are observed at T_CO. The unusual Bragg peak broadening essentially originates from the peak in the standard deviation of the b parameter (Fig. 8) at T_CO, which in turn is related to the orbital ordering of the ${d}_{z}^{2}$ orbital in the a–c plane. It is tempting to associate the observed selective peak broadening with the remarkable softening of the shear modulus observed²⁸ on approaching the charge-ordering temperature, T_CO. As the shear modulus reaches its minimum value, the crystal structure becomes unstable to strains, and it changes to a more distorted, lower-symmetry structure.

Fig. 8: Temperature variation of the variance and covariance coefficients.

Temperature variation of the variance and covariance coefficients of the unit lattice parameters of the La_1−xCa_xMnO₃, x = 0.57 composition. Error bars are smaller than in some data points (the standard deviations have been calculated by fullprof program as described in the fullprof manual page 43).

This type of anisotropic peak broadening is observable because of the ultrahigh resolution of the present diffractometer, and it is inherent in the structural phase transition at T_CO in the polycrystalline samples. All studied samples display single-phase X-ray diffraction patterns (absence of macroscopic phase segregation) both above T_CO and at 5 K. Clear phase separation (in the sense of multiple diffraction pattern contributions) has been observed in La_0.25Ca_0.75MnO₃⁸ and Bi_0.15Ca_0.85MnO₃²² samples, measured with the same diffractometer.

It is also interesting to note that although the SXRD pattern of the sample with x = 0.6 at 5 K can be reproduced here with a single modulated phase, the neutron diffraction pattern at 5 K contains magnetic Bragg peaks²⁶, related to the x = 1/2 and 2/3 phases. This is an unusual result implying that either the magnetic structure originates from a single phase consisting of three Fourier components, or the phase separation cannot be resolved in the SXRD patterns.

Comparison with other studies

Experimental and theoretical studies to date have proposed that the so-called charge-ordered state (or stripe phase) in the La_1−xCa_xMnO₃ (0.5 ≤ x ≤ 0.75) series may be related to the formation of charge density waves (CDW)^{16,27,29,30,31,32,33,34}—namely, lattice-distortion waves and their associated conduction-electron density waves, accompanied by the opening of a gap in the one-electron excitation spectrum at the Fermi level^35,36. The idea of a CDW wave has its origin in Peierls^37,38, who proved that an ideal one-dimensional crystal with a partially occupied conduction band is unstable to the formation of a CDW state at low temperatures.

The CDW scenario, as appropriately modified for manganites²⁷, reproduces some of the aspects of the experimental data of the La_1−xCa_xMnO₃ (x > 0.5) compounds. However, there are two key issues needing more detailed experimental verification in order to reach a final resolution of this fundamental issue. (1) Above the Peierls transition, T_p (T_p ≡ T_CO), the compounds are insulators (the resistivity has an activated temperature dependence), not conductors. Cox et al.³³ have explained this issue by invoking the role of large impurity density to account for the insulating behavior well above T_CO. (2) The Peierls transition is energetically favorable only for materials with a quasi-one-dimensional band structure or with certain Fermi surface topologies with parallel parts of the Fermi surface connected by a reciprocal lattice vector (i.e., nesting)³⁹. Obviously, these issues need to be addressed by a clear theoretical and experimental study.

It is interesting to refer here to the conclusions^40,41,42,43 from THz spectroscopy studies in manganites samples with similar calcium (x > 0.5) concentration as CDWs are expected to give low-energy excitations in the THz frequency range. Frequency-domain THz spectroscopic data⁴¹ in a sample with x = 3/4 and for samples⁴⁰ with 0.5 ≤ x ≤ 1 do not show any feature that can be connected with a collective response (charge density wave) of the spatially charge-ordered state. Instead, the observed THz resonances have been interpreted by Goshunov et al.⁴⁰ and Shukova et al.⁴¹ as “acoustical lattice vibrations that acquire optical activity when the Brillouin zone is folded due to the superstructure in the CO state”.

Neutron diffraction measurements^25,26 of some older as well as the same samples used in the present work revealed that the samples with 1/2 < x ≤ 0.56 display magnetic Bragg peaks similar to those observed for $x=\frac{1}{2}$, the so-called charge exchange (CE) magnetic structure. The CE magnetic Bragg peaks for $x=\frac{1}{2}$ have been successfully interpreted by a layer-type ordering of Mn³⁺ and Mn⁴⁺ ions (stacked along the a-axis), forming ferromagnetic zigzag chains coupled antiferromagnetically. The two families of magnetic Bragg peaks have been directly connected with the two charge states. Specifically, the propagation vector, ${{{{{{{{\bf{k}}}}}}}}}_{{{{{{{{\rm{C}}}}}}}}}=[\frac{1}{2},0,\frac{1}{2}]$ has been attributed to “Mn⁴⁺”-like ions, while the ${{{{{{{{\bf{k}}}}}}}}}_{{{{{{{{\rm{E}}}}}}}}}=[0,0,\frac{1}{2}]$ one (see ref. ⁶) to “Mn³⁺”-like ions. When we tried to apply this model to the samples with 1/2 < x ≤ 0.56, we discovered several key features, which put in doubt the validity of the classical Goodenough CE model when x > 0.5 in agreement with the present SXRD data. The most spectacular observation is that the calculated E-type $(1,1,\frac{1}{2})$ magnetic Bragg peaks are located at slightly higher angles in comparison to the experimental ones. In addition, the same peaks display a pronounced broadening. These experimental findings advocate that the simple CE model is inappropriate for compositions with Ca concentrations, 1/2 < x ≤ 0.56. In order to index the E-type magnetic peaks, we have to use an incommensurate propagation vector, k_E = [ε_E, 0, 1/2], instead of the commensurate one, k_E = [0, 0, 1/2] used for x = 1/2. The incommensurate component, ε_E, is directly connected with the a-component of the structural modulation vector through the relationship, ε_E = 1/2 − τ_a.

Since the difference of the charge between the Mn sites is not so large to produce measurable scattering intensity, the satellite intensities in the SXRD patterns arise mainly from the displacement of the cations and the coordinated oxygen atoms. One may speculate that the modulation is related to a mixed-orbital state of the Mn e_g levels. Such an orbital state could be related to the mixed-orbital state, $[\cos (\theta /2){d}_{3{z}^{2}-{r}^{2}}-\sin (\theta /2){d}_{{x}^{2}-{y}^{2}},\sin (\theta /2){d}_{3{z}^{2}-{r}^{2}}+\cos (\theta /2){d}_{{x}^{2}-{y}^{2}}]$ proposed by Tao and co-workers⁴⁴. The mixing angle, θ, changes continuously along the a-axis leading to a transverse displacive modulation with the τ_a(x) wave number changing continuously with x. At the x = 1/2, 2/3, and 3/4 compositions, the modulation becomes commensurate, and therefore, it can be interpreted with the classical Goodenough charge and orbital model.

The temperature dependence of the modulation vector, [τ_a(x, T), 0, 0], can be attributed to phase defects of the displacement field, ${{{{{{{\bf{u}}}}}}}}({{{{{{{\bf{x}}}}}}}})={{{{{{{{\bf{u}}}}}}}}}_{0}({{{{{{{\bf{x}}}}}}}})\exp [i{{{{{{{\boldsymbol{\tau }}}}}}}}\cdot {{{{{{{\bf{r}}}}}}}}+\phi ({{{{{{{\bf{r}}}}}}}})]$. The average value of the random jumps of the phase can be effectively described by a phase gradient, 〈ϕ(x)〉 = Δτ ⋅ x, which leads to a change in the modulation vector, ${{{{{{{{\boldsymbol{\tau }}}}}}}}}^{{\prime} }={{{{{{{\boldsymbol{\tau }}}}}}}}+\Delta {{{{{{{\boldsymbol{\tau }}}}}}}}$. This model has been proposed by Baggari et al.^45,46 in order to interpret the evolution of scanning transmission electron contrasts measured in a τ = [1/3, 0, 0] Bi_1−xSr_x−yCa_yMnO₃ (x = 0.65, y = 0.47) compound. This phase inhomogeneity is absent at low temperatures and spreads in the sample as the charge-ordering temperature is approached. A similar explanation for the temperature dependence of τ_a(x, T) below and near the charge-ordering temperature has been proposed by Tao and co-workers^44,47. The temperature change of τ_a(x, T) has been attributed to defects (dislocations) of the electronic superstructure mainly arising from orbital degrees of freedom, not necessarily connected with the crystal-structure defects. Finally, we note that the observed structural incommensurability may be related to the short-range structure, comprising a superposition of charge-disordered Mn^3.5+ and orbital-ordered Mn³⁺ layers, recently proposed by Chen et al.⁴⁸.

Conclusions

Thanks to the ultrahigh resolution of the synchrotron X-ray diffraction data, we have established that all studied La_1−xCa_xMnO₃ (x = 0.51, 0.53, 0.545, 0.56, 0.57, 0.58, and 0.6) compositions are single phase in the entire temperature range of the present work (from room temperature down to 5 K). At the same time, all samples adopt a modulated crystal structure at temperatures T < T_CO. The modulated structure can be modeled by an atomic displacement model, which incorporates a harmonic modulation, ${{{{{{{{\bf{u}}}}}}}}}_{j}({{{{{{{\bf{R}}}}}}}})={{{{{{{{\bf{u}}}}}}}}}_{j}^{0}\cos [2\pi {{{{{{{\boldsymbol{\tau }}}}}}}}\cdot ({{{{{{{\bf{R}}}}}}}}+{{{{{{{{\bf{r}}}}}}}}}_{i})+{\phi }_{i}]$ with a modulation wave vector, which obeys roughly the empirical relation, τ = (1 − x)a^*, and with polarization along the c-axis. The observed temperature variation of τ may be related to phase defects of the order parameter that describes the lattice displacements, arising either from charge or orbital ordering. Our results here on the model La_1−xCa_xMnO₃ manganite phases may aid attempts at a deeper understanding of the currently debated condensed matter physics topics regarding spin, charge, and orbital ordering, as well as symmetry breaking and emergent order in quantum states.

Methods

Samples with nominal stoichiometry La_1−xCa_xMnO₃ (x = 0.51, 0.53. 0.545, 0.56, 0.57, 0.58, and 0.60) were synthesized by thoroughly mixing high-purity stoichiometric amounts of CaCO₃, La₂O₃, and MnO₂. The mixed powders were reacted in air at temperatures up to 1400 °C for several days with intermediate grindings. In the final reaction step, the samples were cooled slowly to 25 °C. High-resolution SXRD powder diffraction patterns were measured with the multi-detector powder diffractometer on the ID31 beamline (now ID22) at the ESRF (Grenoble, France). Powder samples were sealed in thin-wall borosilicate glass capillaries (d = 0.5 mm), inserted in a continuous-flow cryostat and rotated during data collection. Data were collected in Debye-Scherrer (transmission) configuration with λ = 0.50008 Å. Next, they were rebinned to a 0.002° step in the range of 4–60°. Average crystal-structure models were refined to the SXRD data using the Rietveld method with the FULLPROF suite of programs²⁰. In order to analyze the superlattice peaks qualitatively, we consider that the average Pnma crystal structure is harmonically modulated. Simulations of the SXRD patterns are made by a purpose-written FORTRAN program, taking into account only first-order satellites. Based on this program, we estimated the modulation wave vector as a function of calcium concentration and temperature. In addition, based on the best agreement between theoretical and experimental satellite-peak intensities, we also estimated the polarization and the amplitude of the modulation vector for each atom.