Many-body quantum chaos in stroboscopically-driven cold atoms

Abstract

In quantum chaotic systems, the spectral form factor (SFF), defined as the Fourier transform of two-level spectral correlation function, is known to follow random matrix theory (RMT), namely a ‘ramp’ followed by a ‘plateau’ in late times. Recently, a generic early-time deviation from RMT, so-called the ‘bump’, was shown to exist in random quantum circuits as toy models for many-body quantum systems. We demonstrate the existence of ‘bump-ramp-plateau’ behavior in the SFF for a number of paradigmatic and stroboscopically-driven 1D cold-atom models: spinless and spin-1/2 Bose-Hubbard models, and nonintegrable spin-1 condensate with contact or dipolar interactions. We find that the scaling of the many-body Thouless time t_Th —the onset of RMT—, and the bump amplitude are more sensitive to variations in atom number than the lattice size regardless of the hyperfine structure, the symmetry classes, or the choice of driving protocol. Moreover, t_Th scaling and the increase of the bump amplitude in atom number are significantly slower in spinor gases than interacting bosons in 1D optical lattices, demonstrating the role of locality. We obtain universal scaling functions of SFF which suggest power-law behavior for the bump regime in quantum chaotic cold-atom systems, and propose an interference measurement protocol.

Introduction

Quantum chaos is historically diagnosed with level repulsion: A quantum system is considered chaotic if it exhibits spectral statistics given by the random matrix theory (RMT), in sufficiently small energy scales¹. Such signatures have been found in a plethora of disciplines including nuclear resonance spectra^2,3, mesoscopic physics^4,5,6, quantum chaos^7,8,9, black hole physics^10,11,12, and quantum chromodynamics^13,14. With their unprecedented degree of controllability^15,16, trapped cold atoms^{17,18,19,20,21,22,23} are excellent platforms to study many-body phenomena, including signatures of quantum chaos in spectral statistics, and for large-scale simulations of quantum systems^{15,16,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38}.

A particularly intriguing objective of quantum simulations so far has been to understand the underlying mechanisms which lead to thermalization, as in eigenstate thermalization hypothesis (ETH)^28,39,40, or its absence via many-body localization (MBL)^{32,37,41,42,43}, the existence of quantum many-body scars^34,44,45, and Hilbert space fragmentation^46,47. In this vein, as a probe for quantum chaos and ergodicity^{48,49,50,51,52,53,54,55,56,57,58,59,60}, observables such as entanglement entropy and out-of-time-order correlators (OTOCs) have been intensively studied, and measured with quantum simulators^{31,33,54,61,62,63,64,65,66}. However, the OTOCs could be susceptible to quantum criticality and order as found by refs. ^67,68,69,70, even in nonintegrable quantum many-body models at infinite temperature⁷¹. Moreover, it was demonstrated by refs. ^72,73 that exponentially fast scrambling detected by OTOCs could be induced at the fixed points in phase space, and is not necessarily the signature of quantum chaos. Alternatively, the metrics of spectral statistics can be defined in the energy domain, e.g. spacing distribution and ratio^1,74,75,76, as well as number variance^7,77. While the spacing distribution can be experimentally obtained for few particles^3,6, it is particularly challenging for many-body systems: One must access an exponentially large number of energy levels, and resolve exponentially small many-body energy gaps. Consequently, a direct experimental probe of level repulsion and, more generally, of spectral correlations in a many-body spectrum remains elusive.

To circumvent this issue, we consider the spectral form factor (SFF), a time-domain observable defined as the Fourier transform of the two-level spectral correlation function^78,79. For a physical system, the appearance of the RMT-like “ramp” and subsequent “plateau” in SFF, Fig. 1a, is a signature of quantum chaos. In particular, the SFF behavior around the Heisenberg time t_H that separates ramp and plateau, is a manifestation of the energy level repulsion, which is often probed with reference to the Wigner-Dyson level spacing distribution⁸⁰ (Fig. 1c). SFF has been instrumental in the discovery of a number of novel and universal signatures of many-body quantum chaotic systems in both condensed matter^{8,9,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104}, and in high energy physics^{11,12,105,106,107,108,109,110,111}. Black holes have been shown to display RMT behavior in late times with SFF^11,110, and the SFF has been utilized to investigate the ergodic-to-MBL transition in 1D spin chains^85,86,95,97.

Fig. 1: Spectral Form Factor (SFF).

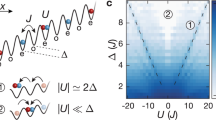
a Representative behavior of the SFF $K(t)=\langle | {{{{{{{\rm{Tr}}}}}}}}\hat{U}(t){| }^{2}\rangle$ for a many-body driven quantum chaotic spin-1/2 Bose-Hubbard system with time evolution operator $\hat{U}(t)$, e.g., with u_↑ = u_↓ = u_↑↓ = J where J_↑ = J_↓ ≡ J_↑↓ = J = 1 is the characteristic energy scale in Eq. (3). Here 〈… 〉 denotes averaging over an ensemble of statistically similar systems. Interacting spin-1/2 bosons in a lattice with unit filling factor ν = 1, atom number N = 4, and lattice size L = 4, are subjected to a two- (red symbols) or three-step (purple symbols) driving protocols where the driving periods are T = 1 and T = 3, respectively. The two- and three-step protocols approach the respective RMT behaviors given by circular orthogonal ensemble (COE) shown with green dashed, and circular unitary ensemble (CUE) shown with orange dotted. On the other hand, spin-1/2 atoms in a driven single well, L = 1 (blue line), follows the Poisson statistics given by the flat line (pink), K_Poi(t) = D, where D is the Hilbert space dimension. This is a signature of integrability. The Thouless times t_Th, denoted by stars, and the Heisenberg time t_H determines the onset of the random matrix theory (RMT) behavior and the appearance of the plateaus respectively. b K(t) following the three-step driving protocol in a spin-1/2 setting with ν = 1/4, N = 3, L = 12. The bump (t < t_Th) is a signature of many-body quantum chaotic systems. c The nearest-neighbour spacing distribution P(δ) of a spin − 1/2 many-body system with N = 9 atoms trapped in M = 3 wells and driven according to two-step protocol with a period of T = 1 (blue) coincides with the one for the random matrix ensemble (red), and displays level repulsion, which is also captured by the SFF at t_H in (a). Error bars in (a) and (b) are found by calculating ${\sigma }_{{{{{{{{\mathcal{K}}}}}}}}}(t)/\sqrt{{{{{{{{\mathcal{A}}}}}}}}}$ where ${\sigma }_{{{{{{{{\mathcal{K}}}}}}}}}(t)\equiv {[\langle {{{{{{{{\mathcal{K}}}}}}}}}^{2}\rangle -{\langle {{{{{{{\mathcal{K}}}}}}}}\rangle }^{2}]}^{1/2}$ is the variance of ${{{{{{{\mathcal{K}}}}}}}}\equiv | \,{{\mbox{Tr}}}\,[\hat{U}(t)]{| }^{2}$ over an ensemble of ${{{{{{{\mathcal{A}}}}}}}}$ statistically similar systems.

For many-body spin models and local random quantum circuits, it has been shown that SFF could deviate from RMT. Specifically a “bump” appears at early times t ≪ t_H (see Fig. 1a, b), and RMT is recovered only after the many-body Thouless time t_Th^{8,9,83,85,89,91,102,105}, as illustrated by star markers in Fig. 1. Thouless time is an intrinsic timescale that generically grows with the system size – with the exception of quantum circuits satisfying the dual unitarity condition^81,92 – and can be characterized by a set of Lyapunov exponents⁹⁰. For systems without conserved quantities, this behavior of t_Th originates from the domain walls in emergent statistical mechanical models that separates growing RMT-like regions^8,93,95. For systems with conserved quantities and constraints, the origin of the t_Th scaling can be traced back to the diffusive and sub-diffusive modes of the charges^83,91. The extension of such results to cold atom systems is nontrivial, since only an approximate mapping between spin and cold atom models could be established for the Mott insulating regime, where spinful atoms are confined to lattice sites¹¹².

A central result of our work is the existence of the “bump-ramp-plateau” behavior in the SFF of stroboscopically-driven interacting (spinless and spin-1/2) bosons in optical lattices beyond the Mott insulator regime, as well as spin − 1 condensates with either short-range contact or long-range dipolar interactions. We account for the trapped atoms’ motional degree of freedom in addition to spin degree of freedom. Our focus on SFF in driven atomic systems complements the investigations of chaos in atomic models utilizing time-independent setups^113,114,115, Rydberg interactions^116,117, highly long-range interactions^89,102 or tools such as dynamical fidelity^118,119 and nearest-neighbor energy level statistics^{58,76,120,121,122,123,124,125,126,127,128}. Recent studies^116,117 have proposed schemes to measure SFF, numerically implement spin-1/2 chains and study the SFF in dipole-blockaded Rydberg atoms, with an emphasis on t_H and the ramp-plateau behavior. In this work, we argue that t_Th is not only experimentally more accessible for large systems, because t_Th ≪ t_H and probing t_Th does not require resolving the many-body level spacing, but it is also physically more appealing — t_Th and the bump regime emerge in many-body chaotic systems. The onset of the RMT ramp, as quantified by t_Th, provides us with another physically meaningful timescale in quantum many-body systems.

To investigate the dependence of t_Th on the locality of the underlying Hamiltonian, we employ spatially-extended Bose-Hubbard (BH) chains¹²⁹ (Fig. 2a), as opposed to a chaotic spin − 1 condensate under single-mode approximation (SMA)¹³⁰ (Fig. 2b). The latter refers to an ensemble of pairwise interacting spin − 1 atoms, and hence effectively a zero-dimensional model^{62,131,132,133}. We find that the Thouless time increases significantly more slowly as a function of atom number in the case of chaotic spin − 1 condensates as compared to the lattice confined interacting bosons. Furthermore, we reveal that both the bump amplitude and t_Th scaling are more sensitive to the atom number than the lattice size. This strong dependence on the atom number is not affected by the atomic hyperfine structure, e.g., single- or two-states; the symmetry class, and the choice of driving protocol. Our choice of quantum many-body models is experimentally motivated. The BH model describes the physics of cold atoms trapped in optical lattices²⁴, as experimentally demonstrated in²⁶, while different hyperfine states of bosonic atoms can be routinely used to realize Bose mixtures^134,135. The spinor condensates constitute yet another atom-based platform to simulate many-body physics^{136,137,138,139}. We utilize Floquet driving, because the stroboscopically-driven setups have the advantage to produce a uniform density of states, i.e., no unfolding¹⁴⁰ or filtering¹⁰⁵ procedures are required for the computation of the spectral statistics, unlike in time-independent Hamiltonian systems. Floquet driving of cold atom systems have been realized^141,142,143. We also empirically obtain a power-law scaling function for the bump regime. This suggests a power-law correction to the SFF “ramp-plateau” in cold atom lattices. The deduced scaling function for the bump, in turn, proves to be practically useful to statistically differentiate the bump from ramp in an experiment. In addition, we establish a relation between the SFF and the survival probability thus corroborating the experimental detectability of the former. The latter has been theoretically studied to probe quantum chaos^113,114,144 and measured in picosecond spectroscopy of molecular dissociation^145,146,147. We devise a read-out protocol for the SFF through many-body state interference¹⁴⁸, which measures survival probability and is a state-of-the-art measurement scheme for cold atoms in optical lattices³¹.

Fig. 2: Schematics of the model setups.

a, b Schematic representation of periodically driven 1D lattice trapped and interacting spin − 1/2 bosons and a spin − 1 condensate in a harmonic potential. The tunnelling (J_↑, J_↓) and the spin-mixing J_↑↓ (e.g. facilitated by Raman-assisted tunneling with a certain Rabi frequency, see the dashed line) are depicted. u_↑, u_↓ (u_↑↓) refer to the on-site interactions, while the induced on-site disorder is illustrated with the irregular wells.

Results and discussion

SFF is the Fourier transform of the two-level spectral function, and can be defined directly in the time domain as

$$K(t)=\left\langle {\left\vert {{{{{{{\rm{Tr}}}}}}}}\left[\hat{U}(t)\right]\right\vert }^{2}\right\rangle =\left\langle \mathop{\sum}\limits_{m,n}{e}^{i({E}_{m}-{E}_{n})t}\right\rangle ,$$

(1)

where $\hat{U}(t)$ is the time evolution operator of a given system with spectrum {E_m}, and 〈… 〉 denotes averaging over certain ensemble of statistically-similar systems. Hence, we can define error bars around K(t) at each t through ${\sigma }_{{{{{{{{\mathcal{K}}}}}}}}}(t)/\sqrt{{{{{{{{\mathcal{A}}}}}}}}}$ where ${\sigma }_{{{{{{{{\mathcal{K}}}}}}}}}(t)\equiv {[\langle {{{{{{{{\mathcal{K}}}}}}}}}^{2}\rangle -{\langle {{{{{{{\mathcal{K}}}}}}}}\rangle }^{2}]}^{1/2}$ is the variance of ${{{{{{{\mathcal{K}}}}}}}}\equiv | \,{{\mbox{Tr}}}\,[\hat{U}(t)]{| }^{2}$ over an ensemble of ${{{{{{{\mathcal{A}}}}}}}}$ statistically similar systems. The error bars in all figures on SFF in this Manuscript are found by calculating ${\sigma }_{{{{{{{{\mathcal{K}}}}}}}}}(t)/\sqrt{{{{{{{{\mathcal{A}}}}}}}}}$. Our results discussed below are based on ${{{{{{{\mathcal{A}}}}}}}}\in [10000,50000]$ realizations of $\hat{U}$.

To understand the basic features of SFF for quantum chaotic systems, consider the circular unitary ensemble (CUE) and the circular orthogonal ensemble (COE) in RMT^78,79. CUE is the ensemble of n-by-n matrices uniformly distributed in the unitary group $\hat{U}(n)$ according to the Haar measure, and can be used to model quantum chaotic systems without symmetries. In this case, the SFF is given by K_CUE(t) = t for t ≤ t_H and K_CUE(t) = D for t > t_H, where the Heisenberg time t_H = O(Δ⁻¹) = O(D) is proportional to the inverse energy level spacing Δ and hence to the size of the Hilbert space D. COE is the ensemble of uniformly-distributed unitary symmetric matrices, and can be utilized to model systems with time-reversal symmetry with the antiunitary time reversal operator ${{{{{{{\mathcal{T}}}}}}}}$ satisfying ${{{{{{{{\mathcal{T}}}}}}}}}^{2}=1$⁷⁹. The corresponding SFF behavior is ${K}_{{{{{{{{\rm{COE}}}}}}}}}(t)=2t-t\log (1+2t/{t}_{{{{{{{{\rm{H}}}}}}}}})$ for t ≤ t_H = D and ${K}_{{{{{{{{\rm{COE}}}}}}}}}(t)=2{t}_{{{{{{{{\rm{H}}}}}}}}}-t\log [(2t+{t}_{{{{{{{{\rm{H}}}}}}}}})/(2t-{t}_{{{{{{{{\rm{H}}}}}}}}})]$ for t > t_H = D. The RMT-like ramp in a spin − 1/2 BH model can be seen in Fig. 1a for both symmetry classes. A deviation from RMT behavior in SFF, the “bump”, has been demonstrated to exist at times earlier than the many-body Thouless time t_Th in generic many-body quantum systems (see Fig. 1a, b). The temporal region t < t_Th of SFF (Fig. 1b) will be referred to as the bump regime throughout the text.

The driving protocol is expressed via the unitary operator $\hat{U}({t}^{{\prime} })\equiv {\hat{U}}^{{t}^{{\prime} }}$. This refers to the repeated application of the (i) two-step (with period T = τ) and (ii) three-step (alternating from τ₁ to τ₂ and having a period T = (2τ₁ + τ₂)/2) periodic driving scheme defined by the Floquet operator

$$\hat{U}=\left\{\begin{array}{ll}{e}^{-i{\hat{H}}_{2}\tau }{e}^{-i{\hat{H}}_{1}\tau }\hfill\quad &\,{{\mbox{two-step}}}\,\\ {e}^{-i{\hat{H}}_{1}{\tau }_{1}}{e}^{-i{\hat{H}}_{2}{\tau }_{2}}{e}^{-i{\hat{H}}_{1}{\tau }_{1}}\quad &\,{{\mbox{three-step}}}\,\end{array}\right.,$$

(2)

with τ₁ ≠ τ₂ ≠ 0 which breaks the time-reversal symmetry for the three-step protocol.

Dependence of the bump regime and Thouless time on atom number and lattice size

The simplest tight-binding model for interacting bosons, the BH model¹²⁹, can be effectively realized by loading bosonic cold atoms into a one-dimensional optical lattice²⁴. Such a geometry can be readily implemented in an experiment with tightly confined transversal directions so that the excitations along the latter are highly suppressed, and hence the system corresponds to a series of independent 1D tubes across the x direction³⁷. We employ a setup where the interacting bosonic atoms have two hyperfine states described by a spin − 1/2 BH Hamiltonian (Fig. 2a),

$${\hat{H}}_{{{{{{{{\rm{BH}}}}}}}}} = \, \mathop{\sum}\limits_{r}\left(\mathop{\sum}\limits_{\sigma }{J}_{\sigma }{\hat{b}}_{\sigma ,r}^{{{{\dagger}}} }{\hat{b}}_{\sigma ,r+1}+{J}_{\uparrow \downarrow ,r}{\hat{b}}_{\uparrow ,r}^{{{{\dagger}}} }{\hat{b}}_{\downarrow ,r}+\,{{\mbox{h.c.}}}\,\right)\\ + \frac{1}{2}\mathop{\sum}\limits_{\sigma ,r}{u}_{\sigma }{\hat{n}}_{\sigma ,r}({\hat{n}}_{\sigma ,r}-1)+{u}_{\uparrow \downarrow }\mathop{\sum}\limits_{r}{\hat{n}}_{\uparrow ,r}{\hat{n}}_{\downarrow ,r}\\ + \mathop{\sum}\limits_{\sigma ,r}{\mu }_{\sigma ,r}{\hat{n}}_{\sigma ,r}.$$

(3)

Here σ =  ↑, ↓ is the spin index. J_σ, u_σ and u_↑↓ denote the tunneling and on-site interaction strengths, that can be experimentally tuned through the laser fields generating the lattice potential^24,112. Additionally, J_↑↓ refers to the spin-mixing coupling between two hyperfine states. It can be created and adjusted using Raman assisted tunneling²⁵ or the radio-frequency fields¹⁴⁹. The position-dependent random potential μ_σ,r can be realized with the aid of digital micromirror devices^37,150,151.

In the absence of spin-mixing coupling J_↑↓ = 0, the projection to a spin-preserving subspace could be achieved through transferring all atoms to one hyperfine state. This is effectively modeled by the spinless BH model¹²⁹. The Hamiltonian of this spinless model could be written in the form of Eq. (3) with the constraint that all atoms are, for instance, in the spin-↓ state. Namely, we consider the parameters J_↑↓ = u_↑↓ = J_↑ = u_↑ = μ_r,↑ = 0, and assume that N = N_↓. The remaining parameters are denoted by J_↓ = J, u_↓ = u and μ_r,↓ = μ_r. Exploring how to induce chaotic behavior in the spinless BH model and comparing the predictions with the spin-1/2 case enable us to determine how the bump regime and the Thouless time depend on the hyperfine structure of the atoms.

The size of the Hilbert space in BH models is determined by two parameters: the chain size L and the atom number N. These parameters dictate the size of the Hilbert space as D = (N + αL − 1)!/(N! × (αL − 1)!), where α is the number of hyperfine levels. Therefore, we can explore the dependence of the bump regime and t_Th scaling not only on L but also on N, and hence the filling factor ν of the lattice. We confirm that the bump-ramp-plateau behavior persists in the Mott insulator regime, where u ≫ J holds for the spin − 1/2 bosonic system (Supplementary Note 6), and further explore the bump and the emergence of RMT beyond the Mott insulator regime below.

Figure 3a, b demonstrate that the early time behavior of SFF in a spin − 1/2 BH model, converges to the CUE behavior, as a function of L (N) with fixed N = 3 (L = 3). Figure 3c, on the other hand, shows the presence of the bump when the system is driven according to the two-step protocol, and thus exhibits COE statistics as a function of L with three atoms. The amplitude of the bump increases with L at fixed N for both protocols that simulate CUE and COE symmetry classes as illustrated in Fig. 3a, c. The model-specific details of the Floquet protocol are given in Eq. (13).

Fig. 3: Early time Spectral Form Factor (SFF) for the spin-1/2 Bose-Hubbard (BH) model.

The bump behavior of spin-1/2 BH model is visible when driven according to (a, b) three-step and (c) two-step protocols. a SFF for N = 3 following circular unitary ensemble (CUE), which is denoted with green-solid, for a driving period T = 3 with lattice sizes L ∈ [4, 12] which is encoded in the shading from yellow to red, respectively. Inset: Thouless time t_Th increases with L, however its function cannot be unambiguously determined with the available data. Solid- and dashed-red lines are fit models for power-law and logarithmic, respectively. b SFF for a triple well L = 3 following CUE (green-solid) for a driving period of T = 1.5 with atom numbers N ∈ [3, 10] from yellow to red, respectively. Inset: t_Th scaling is fitted to a power-law with t_Th(N = 3, L) ∝ N² (red-solid). c SFF of three atoms N = 3 following circular orthogonal ensemble (COE) for a driving period T = 1 with lattice sizes L ∈ [4, 13] from yellow to red, respectively. The green-solid denote the COE for largest D in the data set. Inset: t_Th scaling with L is fitted to a power-law with t_Th(N = 3, L) ∝ L^0.78 (red-solid). For all cases, the bumps generally increase with L and N. Error bars in all panels are found by calculating ${\sigma }_{{{{{{{{\mathcal{K}}}}}}}}}(t)/\sqrt{{{{{{{{\mathcal{A}}}}}}}}}$ for an ensemble of ${{{{{{{\mathcal{A}}}}}}}}$ statistically similar systems.

An increase of L (N) while keeping all other parameters fixed results in a more dilute (denser) lattice trapped gas. Interestingly, the bump is significantly enhanced for a denser gas as seen by comparing Fig. 3b, a. In all cases of spin − 1/2 BH model, t_Th increases either as a function of L or N, but it is difficult to determine the functional form of t_Th(N, L) based on the accessible finite-size data. To compare the scaling behavior among different cases, power-law fits are provided in the insets of Fig. 3. We observe that the scaling exponent of t_Th is larger in N for filling factors ν → ∞ (N → ∞, fixed L) e.g., t_Th(N, L = 3) ∝ N², than in L for ν → 0 (L → ∞, fixed N) e.g., t_Th(N = 3, L) ∝ L^0.44.

For the two-step protocol simulating COE symmetry class presented in Fig. 3c, the bump is more pronounced in L compared to the three-step protocol simulating CUE class shown in Fig. 3a. Consistently, t_Th(N = 3, L) ∝ L^0.78 scaling is slightly faster. For the corresponding scaling behavior at N > 3 or L > 3, see Supplementary Note 4. A similar stark difference between the scaling in N and L persists also for the two-step protocol under COE symmetry class with t_Th(N, L = 3) ∝ N^1.95 and t_Th(N = 3, L) ∝ L^0.78, respectively.

These observations suggest that t_Th(N, L) is more sensitive to N than to L for spin − 1/2 interacting bosons in optical lattices. This dependence on atom number, in turn could be traced back to the interactions between lattice confined atoms. In fact, increasing the interaction strengths u = u_↑ = u_↓ = u_↑↓ so that the system transitions to a Mott insulator, increases the Thouless time and results in a larger bump amplitude (see Supplementary Note 6).

To further test the generality of the argument given above, we compare the SFF of the spinless BH model with three different filling factor regimes, namely ν → 0, ν = 1 and ν → ∞ as D increases. As depicted in Fig. 4c, the bump signature is more pronounced for increasing ν, and t_Th scales faster (t_Th(N, L = 5) ∝ N^2.16) than in Fig. 4b, where ν = 1 holds (t_Th(N, L = N) ∝ N^1.12). We observe that this difference also depends on the choice of the driving protocol: The t_Th(N, L) scaling turns out to be the same for the filling factors ν = 1 and ν → ∞ both leading to a scaling t_Th(N, L) ∝ N⁴ when the stroboscopic driving scheme is set to be an alternative driving protocol, the VE-protocol (see Sec. Methods). The comparison of the SFF obtained with VE-protocol suggests that the onset of RMT behavior in cold atoms occurs earlier in the three-step protocol described by Eq. (2). Nevertheless, for both protocols we observe a significant difference in the bump regimes and t_Th scaling between ν → ∞ and ν → 0. This manifests again the sensitivity of t_Th(N, L) to N.

Fig. 4: Early time Spectral Form Factor (SFF) for the spinless Bose-Hubbard (BH) model.

Bump behavior of spinless BH model is visible in different filling factor regimes with three-step circular unitary ensemble (CUE) protocol and a driving period of T = 3. The filling factors are a ν → 0, b ν = 1 and c ν → ∞ as the Hilbert space dimension increases. a The atom number is N = 5 and lattice size changes, L ∈ [5, 11] which is encoded in the shading from yellow to red, respectively. Inset: Thouless time t_Th(N = 5, L) fluctuates with L. b N and L both change, L = N ∈ [4, 8] from yellow to red, respectively. Inset: t_Th(N = L, L) increases either linearly 1.3L − 1 (dotted-red) or close to linear ∝ L^1.12 (solid-red). c L = 5 and N ∈ [5, 13] from yellow to red, respectively. Inset: The power-law fit to t_Th scaling is t_Th(N, L = 5) ∝ N^2.16 (solid-red). Error bars in all panels are found by calculating ${\sigma }_{{{{{{{{\mathcal{K}}}}}}}}}(t)/\sqrt{{{{{{{{\mathcal{A}}}}}}}}}$ for an ensemble of ${{{{{{{\mathcal{A}}}}}}}}$ statistically similar systems. The solid-green line in all panels denote CUE.

For the spinless BH model, t_Th fluctuates around a fixed value instead of exhibiting a monotonic increase with L for ν → 0 as illustrated in the inset of Fig. 4a. We confirm the independency of this behavior from the protocol choice (see Supplementary Note 1). In Supplementary Note 4, we show a slowly increasing trend in L with fluctuations for t_Th(N = 4, L), so that we can simulate up to L = 15. Therefore, observing no scaling for t_Th(N = 5, L) in L might be a finite-size effect.

To summarize this subsection, we find that the bump regime and t_Th scaling are more sensitive to variations in the atom number than in the chain size, regardless of the hyperfine structure, symmetry class and the protocol choice.

Role of locality in the bump regime and Thouless time

For a many-body system that does not extend spatially in a 1D chain, the Thouless time scaling is significantly slower due to lack of locality^82,105. As we show in Fig. 1a, a spin−1/2 gas trapped in a single well does not exhibit RMT statistics (blue markers). Since we aim to identify the role of spatial extendedness in the bump regime of the cold atom models, we employ an s−wave interacting spin−1 Bose gas within the single-mode approximation (SMA)^{130,152,153,154} which assumes a separation of the spin and spatial degrees of freedom. In particular, the wave functions for each hyperfine state are described by the same spatial mode ϕ_m=0,±1(x) = ϕ(x) and different spin wave functions such that the decomposition ${\hat{\psi }}_{m}({{{{{{{\bf{r}}}}}}}})={\hat{a}}_{m}\phi ({{{{{{{\bf{r}}}}}}}})$ holds where ${\hat{a}}_{m}$ is the annihilation operator acting on the spin-m. SMA is valid for atom numbers as small as N = 100 when the condensate is prepared in a tight laser trap¹³⁹, and it could break down for long evolution times either due to the build-up of spatial correlations^136,154 as well as atom loss related processes from the condensate^136,138,155. There is no spatial-extendedness in this model due to the SMA. All atoms, regardless of the physical distance between them, could interact with one another equally likely through contact interaction, i.e. such a spinor Hamiltonian is effectively zero-dimensional.

The SMA Hamiltonian for the spin−1 condensate, with both linear and quadratic Zeeman fields along the x−and z−spin directions, reads

$${\hat{H}}_{{{{{{{{\rm{SC}}}}}}}}}=\frac{{c}_{1}}{2N}{\hat{{{{{{{{\bf{F}}}}}}}}}}^{2}+\mathop{\sum}\limits_{i=x,z}\left({p}_{i}{\hat{F}}_{i}+{q}_{i}{\hat{F}}_{i}^{2}\right).$$

(4)

Here ${\hat{{{{{{{{\bf{F}}}}}}}}}}^{2}={\hat{F}}_{x}^{2}+{\hat{F}}_{y}^{2}+{\hat{F}}_{z}^{2}$ denotes the spin operator, while c₁ > 0 is assumed corresponding to a ferromagnetic spinor gas¹³⁶. A magnetic field across the z − direction, embodied in the quadratic Zeeman term ${q}_{z}{\hat{F}}_{z}^{2}$, breaks the rotational symmetry of the spinor gas¹³⁶. ${c}_{1}{\hat{{{{{{{{\bf{F}}}}}}}}}}^{2}/2N+{q}_{z}{\hat{F}}_{z}^{2}$ is still an integrable model^156,157, however, the addition of a linear Zeeman field in the x − direction has been recently shown to break its integrability^127,139. This is because the ${p}_{x}{\hat{F}}_{x}$ term breaks the SO(2) symmetry of the spinor condensate, giving rise to signatures of level repulsion which are captured by the Brody distribution². We find that spin − 1 condensates with ${p}_{x}{\hat{F}}_{x}$ term display stronger level repulsion and spectral rigidity, i.e., an extended RMT ramp in SFF, only when a quadratic Zeeman shift in the x − direction ${q}_{x}{\hat{F}}_{x}^{2}$ or a linear Zeeman shift in the z − direction ${p}_{z}{\hat{F}}_{z}$ are introduced to the system (see Supplementary Note 5).

Figure 5 a shows the presence of the bump regime for H_SC driven according to the three-step protocol Eq. (15), and projected to even parity subspace when p_z = 0 and q_x = 2 hold, (see Sec. Methods for symmetry subspace projection). Although this spin−1 gas is a zero-dimensional model, we observe a bump in the SFF whose amplitude increases with N, i.e. the bump feature is not a finite-size effect. However, t_Th scaling with N is significantly slower compared to 1D BH models. For instance, assuming a power-law scaling function, we obtain t_Th(N) ∝ N^0.3N/∣c₁∣ ∝ N^0.63 when we take N dependence of c₁ into account (see Sec. Methods).

Fig. 5: Early time Spectral Form Factor (SFF) for the chaotic spinor condensate.

a Projected SFF of the spinor condensate H_SC on even parity sector driven according to three-step protocol and with p_z = 0, q_x = 2. The atom number changes between N ∈ [30 − 100] which is encoded in the shading from yellow to red, respectively. Inset: The Thouless timescales with the atom number, either in a slow power-law ( ∝ N^0.3N/∣c₁∣ ∝ N^0.63, solid-red) or logarithmic ($\propto \log (N)$, dashed-red). b SFF of the entire Hilbert space of the spinor condensate H_SC driven according to three-step protocol, with p_z = 2, q_x = 0 and the atom number changing between N ∈ [30, 80] from yellow to red, respectively. Inset: The Thouless timescales with the atom number in a slow power-law ∝ N^0.63N/∣c₁∣ ∝ N^0.96 (solid-red). c Projected SFF of the spinor condensate with dipolar interactions H_DC on even parity sector driven according to three-step protocol and with χ = 2. The dipolar interaction strength is χ = 2 for atom numbers N ∈ [30, 110] from yellow to red, respectively. Inset: The Thouless time fluctuates with the atom number, resulting in t_Th(N) ∝ N/∣c₁∣ ∝ N^1/3 scaling in atom number. In all panels, we set the driving period as T = 3, and error bars are found by calculating ${\sigma }_{{{{{{{{\mathcal{K}}}}}}}}}(t)/\sqrt{{{{{{{{\mathcal{A}}}}}}}}}$ for an ensemble of ${{{{{{{\mathcal{A}}}}}}}}$ statistically similar systems. The solid-green line in all panels denote CUE.

An experimental operation to achieve the subspace projection is through introducing a linear Zeeman term along the spin z − direction, i.e., p_z ≠ 0 breaking the inversion symmetry. The resulting SFF when taking into account the entire Hilbert space is presented in Fig. 5(b), where p_z = 2 and q_x = 0 were set. The bump gets sharper with increasing atom number, and t_Th scaling can be described with a power-law increase in N with an exponent γ ~ 1 that is still smaller than the spatially extended BH models.

In order to generalize our results beyond the short-range s − wave interactions, we consider the effect of long-range interactions in the spin−1 condensate and study the bump regime in the even parity subspace when there are dipolar magnetic interactions between the spinor atoms^136,158. For an anisotropic harmonic trap, it is possible to arrive at the so-called two-axis counter-twisting (TACT) Hamiltonian¹⁵⁹, namely

$${\hat{H}}_{{{{{{{{\rm{TACT}}}}}}}}}=\chi \left({\hat{F}}_{x}^{2}-{\hat{F}}_{y}^{2}-{\hat{D}}_{xy}\right),$$

(5)

The latter term in Eq. (5) is one of the eight SU(3) Lie algebra operators ${\hat{D}}_{xy}={\hat{a}}_{1}^{{{{\dagger}}} }{\hat{a}}_{-1}+\,{{\mbox{h.c.}}}\,$ where ${\hat{a}}_{\nu }$ (${\hat{a}}_{\nu }^{{{{\dagger}}} }$) refers to the annihilation (creation) operators of an atom occupying the spin − ν hyperfine level. Accordingly, we write the Hamiltonian for the dipolar spin − 1 condensate as

$${\hat{H}}_{{{{{{{{\rm{DC}}}}}}}}}=\frac{{c}_{1}}{2N}{\hat{{{{{{{{\bf{F}}}}}}}}}}^{2}+{p}_{x}{\hat{F}}_{x}+{q}_{z}{\hat{F}}_{z}^{2}+{\hat{H}}_{{{{{{{{\rm{TACT}}}}}}}}}.$$

(6)

Here, we fix χ = 2 in Eq. (6), and drive it according to the three-step protocol. The projected SFF on the even parity sector is presented in Fig. 5c. A tendency for suppression in the amplitude of the bump takes place compared to Fig. 5a, while t_Th does not exhibit any clear scaling trend with N. When N/∣c₁∣ rescaling is taken into account, we find t_Th(N) ∝ N^1/3. Therefore, our findings corroborate the idea that the locality of the underlying Hamiltonian is indeed reflected on the bump regime and t_Th scaling.

To summarize this subsection, we observe that interacting bosons trapped in a single well display RMT behavior in SFF much faster than the bosonic system in spatially extended potentials.

Universal scaling of the bump regime

Figures 3, 4 and 5 suggest the existence of rescaling parameters in both t − and y − axes where K(t) for different D could collapse on each other in the bump region. We rescale time with t_Th and K(t) with the analytical ramp expression to spotlight the bump region: K(t)/K_rmt(t) which should saturate at unity for t > t_Th. To determine how the bump approaches unity and whether there is a universal behavior for all D, we plot K(t)/K_rmt(t) − 1. This rescaling analysis reveals a collapse of data around t_Th. The data collapses well in the RMT regime t/t_th ≳ 1 as expected, and in the bump region t < t_Th. We observe no data collapse for t/t_Th → 0. Interestingly for all models, a collapse in the rescaled SFF K(t)/K_rmt(t) − 1 for sufficiently large D is present, and K(t)/K_rmt(t) − 1 approaches the saturation value ~ 0 as a power-law in the rescaled time t/t_Th. We notice that this power-law approach to RMT in fact describes the region where K(t) decreases from certain time that we call t_b, reaches a minimum and increases towards RMT. We can then write the following empirical expression for the SFF which also characterizes the bump region,

$$K({t}_{{{{{{{{\rm{b}}}}}}}}} \, < \, t \, < \, {t}_{{{{{{{{\rm{H}}}}}}}}})\approx {K}_{{{{{{{{\rm{RMT}}}}}}}}}(t)\left[\beta {\left(\frac{t}{{t}_{{{{{{{{\rm{Th}}}}}}}}}}\right)}^{\xi }+1\right],$$

(7)

where β and ξ < 0 are scalar. Based on our analysis, we observe β ≪ 1 is a small parameter, and the exact value of ξ could depend on the microscopics, e.g., − 4 < ξ < − 1.4. We note that t_b coincides with time where the bump exhibits a local peak before reaching a local minimum for all cases.

We depict two cases of spin − 1/2 BH chain in a triple well with different atom numbers in Fig. 6a, b where (a) data is for CUE and (b) for COE. The associated bump region and t_Th scaling of (a) are already given in Fig. 3b. Hence Fig. 6b suggests that the physics discussed earlier also holds for COE. We plot the rescaled SFF in Fig. 6c for the spinless BH model of five atoms trapped in optical lattices of varying sizes. The associated bump region is given in Fig. 4a whose inset actually shows no t_Th scaling with lattice size. Nevertheless the bump regime is present, and consistently with the rest of the observations, it introduces a power-law correction to the RMT. Finally in Fig. 6d, we demonstrate the bump scaling for a chaotic spinor condensate and again find that the expression in Eq. (7) holds.

Fig. 6: Universality of the bump regime through the collapse of data around Thouless time t_Th.

a Spin − 1/2 Bose-Hubbard (BH) model for atom numbers ranging between N ∈ [6, 10] from yellow to red in a triple well following the circular unitary ensemble (CUE) statistics and giving ξ = − 1.75 in Eq. (7) shown with solid-green. b Spin − 1/2 BH model for atom numbers ranging between N ∈ [4, 9] from yellow to red in a triple well following the circular orthogonal ensemble statistics and giving ξ = − 1.75 shown with solid-green. c Spinless BH model of five atoms for lattice sizes ranging between L ∈ [9, 11] from yellow to red in a triple well following the CUE statistics and giving ξ = − 3.25 shown with solid-green. d Spinor condensate with p_z = 2 and q_x = 0 for atom numbers ranging between N ∈ [30, 80] from yellow to red following the CUE statistics and giving ξ = − 1.6 shown with solid-green. The x − axes are scaled with the numerically extracted t_Th. The y − axes are scaled with the corresponding random matrix theory behavior. Error bars in all panels are found by calculating ${\sigma }_{{{{{{{{\mathcal{K}}}}}}}}}(t)/\sqrt{{{{{{{{\mathcal{A}}}}}}}}}$ for an ensemble of ${{{{{{{\mathcal{A}}}}}}}}$ statistically similar systems.

The observation that a consistent scaling, Eq. (7), exists for the different atomic systems and parameter values suggests universality beyond the RMT regime. This means that the physical signature of quantum chaos in many-body systems precedes the ramp and the Thouless time, and includes the bump region t_b < t < t_Th. An indirect physical evidence in support of this argument can be found in the heating times of local observables¹²⁶. For the considered lattice sizes, we find that the heating times of density populations in the BH models are less than the corresponding t_Th, and in fact sometimes comparable to t_b, i.e. the time when the bump regime collapse starts (see Supplementary Note 7). Hence, the knowledge of relevant timescales of quantum chaos in an experiment may have practical consequences for information acquisition.

Experimental protocol

Next we discuss an experimental protocol applicable to cold atoms trapped in optical lattices. For concreteness, we will focus on the BH model, however the arguments are valid for the spin − 1/2 BH model which requires an additional hyperfine state. Later, we comment on the case of spin − 1 condensates.

SFF is defined through a trace operation (see Eq. (1)) meaning that the system should be initialized in an infinite-temperature state whose controlled preparation in an experiment is not a simple task. On the other hand, the BH model in an optical lattice can be routinely initialized in the Mott insulator regime, i.e., a product state³¹. The VE-protocol could be utilized to generate a random state $\left\vert \psi \right\rangle$ from a Mott insulating product state $\left\vert {{{{{{{\bf{1}}}}}}}}\right\rangle$, as a variant of this protocol has been shown to generate unitary−2 design¹⁶⁰.

An important ingredient underlying our protocol is the relation between the survival probability and SFF. The survival probability for an initial state $\left\vert \psi \right\rangle$ reads,

$$P(t,\{U,\left\vert \psi \right\rangle \})={\left\vert \left\langle \psi \right\vert \hat{U}(t)\left\vert \psi \right\rangle \right\vert }^{2}.$$

(8)

Consider replicating the system with the pure initial state $\left\vert \psi \right\rangle$, so that the density matrix of both systems is $\rho =(\vert \psi \rangle \otimes \vert \psi \rangle )(\langle \psi \vert \otimes \langle \psi \vert )$. Defining the swap operator ${\hat{V}}_{2}$ by the action ${\hat{V}}_{2}\left\vert {\psi }_{1}\right\rangle \otimes \left\vert {\psi }_{2}\right\rangle =\left\vert {\psi }_{2}\right\rangle \otimes \left\vert {\psi }_{1}\right\rangle$, it is possible to express the survival probability in the form

$$P(t)=\,{{\mbox{Tr}}}\,\left[\left(\hat{U}(t)\otimes {\mathbb{1}}\right)\rho \left({\hat{U}}^{{{{\dagger}}} }(t)\otimes {\mathbb{1}}\right){\hat{V}}_{2}\right],$$

(9)

which has a diagrammatical tensor network representation shown in Fig. 7(a).

Fig. 7: Circuit for the experimental proposal.

Diagrammatical tensor network representation of (a) the survival probability, which is a quantum circuit of a pair of replicated systems, a time evolution operation on system 1 and a swap operator; and (b) the SFF, in terms of survival probability with initial state chosen to be a certain pure state, e.g. a Mott insulating product state $\left\vert {{{{{{{\bf{1}}}}}}}}\right\rangle$, and a set of global rotations W which form a 2-design.

SFF can be expressed as the survival probability for certain initial states. For instance, $P(t,\{\hat{U},\left\vert \psi \right\rangle \})=K(t)$ if $\left\vert \psi \right\rangle ={D}^{-1}{\sum }_{a}\left\vert {E}_{a}\right\rangle$ is chosen to be the equal-amplitude superposition of the eigenstates $\left\vert {E}_{a}\right\rangle$ of $\hat{U}$ or $\hat{H}$ with Hilbert space dimension D. Here, instead, we use an experimentally realizable initial state given by

$${\left\vert \psi \right\rangle }_{{{{{{{{\rm{CUE}}}}}}}}}=\hat{W}\left\vert {{{{{{{\bf{1}}}}}}}}\right\rangle ,\quad \hat{W}\in \,{{\mbox{CUE}}}\,(D).$$

(10)

so that

$${K}^{{{{{{{{\rm{ex}}}}}}}}}(t)=\left\langle {\mathbb{E}}{\left[P(\{{\left\vert \psi \right\rangle }_{{{{{{{{\rm{CUE}}}}}}}}},\hat{U}(t)\})\right]}_{W}\right\rangle D(D+1)-D.$$

(11)

where we have used ${\mathbb{E}}{[\ldots ]}_{W}$ to denote averages over W. See Methods Section for the derivation of Eq. (11). The circuit to measure K(t) in terms of P(t) is sketched in Fig. 7(b).

Now we show that the survival probability and consequently, the SFF of a many-body system can be experimentally measured utilizing Eq. (9). A feasible read-out protocol for probing SFF of cold atoms in optical lattices is the interference measurement through the measurement of swap operator ${\hat{V}}_{2}$^31,148 which is outlined below:

• (i) Initiate two BH chains in a Mott insulator state and apply VE-protocol to both copies with global rotations $\hat{W}$ to obtain the same random state $\left\vert \psi \right\rangle$. In other words, $\hat{W}=\mathop{\prod }\nolimits_{m}^{M}{e}^{-i{\hat{H}}_{m}\tau }$ where M should be chosen M ≥ 6 (see Supplementary Note 1).

• (ii) Freeze one of the copies, and evolve the other one with the Floquet unitary of either two-step or three-step protocol, $\hat{U}$ for an evolution time t.

• (iii) Switch off the hoping parameters across the 1D chains, and subsequently lower the potential between the two chains to interfere the respective many-body states. This corresponds to beam-splitting operation³¹.

• (iv) Measure the parity of each site in the first chain, e.g., system 1 in Fig. 7a with a quantum gas microscope²³, and compute $P(t)={\prod }_{j\in R}{e}^{i\pi {n}_{j}}$ where R is the entire chain.

• (v) Repeat steps (i)-(iv) for a number of different realizations of $\hat{U}$ and $\hat{W}$ at each time t to compute $\big\langle {\mathbb{E}}{[P(\{{\big| \psi \big\rangle }_{{{{{{{{\rm{CUE}}}}}}}}},\hat{U}(t)\})]}_{\hat{W}}\big\rangle$.

• (vi) Compute SFF via Eq. (11).

An alternative proposal for the experimental detection of SFF has been recently introduced in ref. ¹¹⁶, using interferometry with a control atom^161,162 for Rydberg gases in tweezer arrays which realize spin models. We comment on the application of interferometry to our systems in the Supplementary Note 2, which could be realized by introducing a cavity to implement the controlled coupling of the auxiliary atom to the many-body quantum simulator¹⁶³. Another alternative protocol is proposed for Rydberg gases by utilizing the so-called randomized measurement toolbox in ref. ¹¹⁷ where measurements are performed on the system of interest after a time evolution and random on-site rotations. Our interference measurement complements this randomized measurement circuit described in ref. ¹¹⁷: By introducing a replica of the chain and many-body interfering the copies, we remove the requirement of applying ${\hat{W}}^{{{{\dagger}}} }$ before read-out. This potentially helps with reducing the total time of a single experimental run.

We emphasize that it is important to measure the SFF with its standard normalization, e.g. Eq. (11), instead of a normalization as 0 < K^ex(t)/D² ≤ 1 as in refs. ^116,117. This ensures a sufficient resolution for the bump regime and not to inadvertently suppress the bump amplitude as D increases.

An experimental implication of our results concerns the resolution of K(t_b < t ≲ t_Th) where we would aim to differentiate the bump from the ramp. Eq. (7) provides the difference between bump and ramp amplitudes as $K({t}_{{{{{{{{\rm{b}}}}}}}}} \, < \, t \, < \, {t}_{{{{{{{{\rm{H}}}}}}}}})-K(t\ge {t}_{{{{{{{{\rm{Th}}}}}}}}}) \sim \beta {t}^{1+\xi }{t}_{{{{{{{{\rm{Th}}}}}}}}}^{| \xi | }$. For the bump to be measured, this difference should be greater than the standard deviation of ${{{{{{{\mathcal{A}}}}}}}}$ measurements. Hence, an upper bound for the variance ${\sigma }_{{{{{{{{\mathcal{K}}}}}}}}}(t)$ (see Methods Section) must read

$$\frac{{\sigma }_{{{{{{{{\mathcal{K}}}}}}}}}(t)}{\sqrt{{{{{{{{\mathcal{A}}}}}}}}}} \, < \, \beta {t}^{1+\xi }{t}_{{{{{{{{\rm{Th}}}}}}}}}^{| \xi | }=\beta {t}^{1+\xi }{N}^{\gamma | \xi | }.$$

(12)

The equality follows from assuming a power-law form for the Thouless time scaling in atom number, N^γ. For spatially extended models γ > 1, whereas for spinor condensates γ < 1, and ξ < − 1 based on our analysis in the previous subsections resulting in γ∣ξ∣ > 1. Although setting D sufficiently small is crucial to be able to resolve t_H and recover the ramp-plateau behavior, we observe that larger atom numbers increase the upper bound for the error in measuring the bump. For the data set depicted in Fig. 8 for ν = 1, Eq. (12) requires ${{{{{{{\mathcal{A}}}}}}}} \sim 5000$ runs of the experiment for a single time point to differentiate the bump from ramp. On the other hand, ${{{{{{{\mathcal{A}}}}}}}} \sim 2000$ is sufficient for the same system with N = 8 and L = 5, which has a similar Hilbert space dimension and t_Th = 10.

Fig. 8: Benchmarking the experimental proposal.

Eq. (11), interference measurement result, (blue, dotted-crosses) is compared to Eq. (1), the theoretical prediction (yellow-solid) for a three-step protocol applied to spinless Bose-Hubbard model at N = L = 6. To prepare W operators, we used the VE-protocol with M = 8. a Focus on the early-time spectral form factor (SFF) where the experimental protocol with ${{{{{{{\mathcal{A}}}}}}}}=50000$ realization number captures Thouless time t_Th = 8 and most of early-time SFF well except t≤3. The green line is the circular unitary ensemble. b The experimental protocol captures the ramp and plateau well. Error bars in both panels are found by calculating ${\sigma }_{{{{{{{{\mathcal{K}}}}}}}}}(t)/\sqrt{{{{{{{{\mathcal{A}}}}}}}}}$ for an ensemble of ${{{{{{{\mathcal{A}}}}}}}}$ statistically similar systems.

Atomic systems in optical lattices are highly flexible platforms¹⁵. Indeed, their parameters, including the on-site interaction and hopping terms, can be readily tuned in the experiment over a wide range of values. For instance, it is possible to adjust the hopping parameter J from J/h ∝ 2 Hz preparing a shallow lattice to J/h ∝ 150 Hz constructing a deep lattice¹⁶⁴ where h is the Planck’s constant. By considering a hopping amplitude of the order of 100 Hz for the spin − 1/2 BH model with N = L = 4 as depicted in Fig. 1a, typical total evolution times correspond to ∝ 10 s [ ∝ 30 s] for two [three] step driving protocol. For this system, Thouless time is around t_Th ∝ 0.6 s in both driving protocols which should be experimentally feasible to monitor. This is in contrast to the respective Heisenberg times that are attained for t_H ∝ 6.6 s [t_H ∝ 19.8 s] in the case of a two-[three-]step driving protocol.

Turning to the short-range interacting spin − 1 condensate and using a spin-spin interaction coefficient c₁ = − 2π × 9 Hz¹³⁶ the Thouless time for a three-step driving protocol corresponds to t_Th ≈ 3.93 s and t_Th ≈ 2.17 s in the case of N = 100 and N = 40 respectively. Along the same lines, the Thouless time for a dipolar spin − 1 bosonic gas is t_Th ≈ 4.43 s [t_Th ≈ 2.54 s] for N = 100 [N = 40]. For a spinor condensate trapped in a single well, a single copy randomized measurement¹¹⁷ might be more feasible than two-copy beam-splitting operation. The condensate could be initialized in a state where all atoms occupy the spin-0 hyperfine level and a measurement on the number of atoms in each hyperfine level can be made at the end of the protocol to estimate Eq. (8).

Conclusions

We investigated signatures of quantum many-body chaos in various stroboscopically-driven atomic setups ranging from lattice trapped spinless or spin − 1/2 bosons to harmonically confined spin − 1 condensates. A particular focus is placed on the behavior of the spectral form factor which was found to feature a universal bump regime and for longer evolution times, the ramp and plateau regimes. The latter is a measure of spectral rigidity, and hence quantum chaos. Our many-body cold atom models, regardless of the locality of the underlying Hamiltonian, hyperfine structure, driving protocols or the symmetry classes, exhibit a universal bump, and suggest a power-law correction to the RMT prediction of the SFF at early experimentally accessible times. Extension of universality from the RMT to the bump regime and the observation that heating times of density populations are significantly shorter than the corresponding t_Th highlight the role of t_b, the start time of the bump regime collapse. The practical consequences of such a separation in the early timescales in many-body quantum chaos, e.g., for information retrieval from a heating system, is an intriguing endeavor.

We study t_Th scaling with respect to relevant system parameters, the atom number and chain size. The Thouless time scaling with atom number is significantly slower in spin − 1 gases trapped in a single well than the 1D-lattice trapped BH models with L ≥ 3. This suggests that the spatially-extended cold atom systems take longer to exhibit RMT. Consequently, the locality of the underlying Hamiltonian is a key condition for the Thouless time scaling and the bump amplitude. Importantly, we find that t_Th of spatially-extended systems is more sensitive to the atom number than the lattice size. Namely, the scaling in atom number is larger than in lattice size, and subsequently it takes a denser gas longer to reach RMT. These conclusions highlight the role of atom number for determining the onset of RMT in many-body systems, and therefore the impact of interactions. Consistently, the bump regime is enhanced as the lattice-trapped gas becomes denser. These observations hold true regardless of the hyperfine structure, symmetry classes or the choice of driving protocol.

Our results suggest the existence of a universal scaling function for the Thouless time depending on both the lattice size and the atom number t_Th(N, L). Determining the exact form of this scaling function is an important next step to better understand the nature of many-body quantum chaos in experimentally realizable systems. Constructing dual cold atom circuits for this purpose could be a fruitful direction. Alternatively, one could utilize advanced numerical techniques such as time-dependent density matrix renormalization group¹⁶⁵ or multiconfiguration approaches¹⁶⁶ in order to access larger lattice sizes and atom numbers while taking into account relevant many-body correlation effects.

As proposed, the bump regime and Thouless time can be measured with cold atoms in optical lattices with quantum gas microscopy. How the bump regime changes as one deviates from random initial states is an intriguing and potentially useful prospect for experiments. Exploring the signatures of the bump regime and the Thouless time in infinite-temperature correlators and entanglement entropy is an interesting future direction, and can provide a route to understand connections between spectral and spatio-temporal correlations. Finally, devising spectroscopic probes of the bump and the Thouless energy in many-body systems is also a fruitful direction, as these features do not require resolving the many-body level spacing.

Methods

Throughout the study t_Th is numerically defined as a time at which an error function ϵ(t) = ∣K(t) − K_RMT(t)∣/K_RMT(t) is smaller than a threshold of choice, where K_RMT is the SFF behavior for RMT of an appropriate symmetry class.

Models

Here we discuss the system-specific ingredients of the Floquet protocols, and further details of our models, the spatially extended spinless and spin − 1/2 BH models and chaotic spin − 1 condensates.

The spin − 1/2 BH Hamiltonians in the Floquet unitaries are characterized by the fixed parameters J_↑ = u_↑ = u_↓ = u_↑↓ = u = J, while the remaining parameters alternate according to

$$\begin{array}{l}{\hat{H}}_{1}\to {\hat{H}}_{{{{{{{{\rm{BH}}}}}}}}}\,\,{{\mbox{with}}}\,\,{J}_{\downarrow }=J,{J}_{\uparrow \downarrow }=0,{\mu }_{\uparrow ,r}\in [-J,J],\\ {\hat{H}}_{2}\to {\hat{H}}_{{{{{{{{\rm{BH}}}}}}}}}\,\,{{\mbox{with}}}\,\,{J}_{\downarrow }=0,{J}_{\uparrow \downarrow ,r}\in [-J,J],\mu =0,\end{array}$$

(13)

with the constraint μ_↑,r = − μ_↓,r. As such, within the first step, a random potential is turned on across the chain where the notation [ − J, J] means that we randomly choose the site-dependent potential values from a uniform distribution. However let us note that the strength of the disorder does not affect the physics so long as it is larger than J. Subsequently, in the second step, we switch off this random potential, while the tunneling of the atoms confined in $\left\vert \downarrow \right\rangle$ hyperfine state vanishes and an onsite random spin-mixing tunneling amplitude between different hyperfine states is turned on. The driving frequency should not be on resonance with the spin-mixing coupling J_↑↓ not to inadvertently polarize the time-dependent state.

Evolution times for the BH Hamiltonians, e.g., τ, are expressed in units of inverse tunneling 1/J, and to compute ${\hat{U}}^{{t}^{{\prime} }}$ we apply trotterization. When τ ≫ 0.1 holds, the application of the two-step scheme reproduces COE spectral statistics for the spin-1/2 bosonic system. In contrast, by following the three-step periodic scheme the system transitions from exhibiting COE to CUE spectral statistics as τ₁ and τ₂ increase, and has persistent CUE statistics for τ₁, τ₂ ≫ 0.1. For convenience, throughout, we define a dimensionless normalized time $t={t}^{{\prime} }/T$ such that our many-body simulations are directly comparable to the analytic predictions of RMT.

Although our results, presented above, are based on the stroboscopically-driven protocol discussed above, there is flexibility in the choice of parameters for establishing a chaotic behavior in the spin-1/2 setting. Here, we briefly summarize the range of this flexibility and refer to the Supplementary Note 3 for numerical evidence. (i) If desired, the number of simultaneous pulses can be further decreased. (ii) Randomizing either ${\hat{H}}_{1}$ or ${\hat{H}}_{2}$ is sufficient, e.g. J_↑↓,r does not have to be randomized. (iii) The interaction or tunneling strengths do not need to be equal to each other and one of the three interaction parameters could be set to zero. We observe that the two-step driven Floquet system moves away from COE statistics when the atoms with either spin components transition deep into the superfluid regime, e.g., J_↑ = 20 J. Overall, we find that the necessary parameter to simulate RMT statistics in the spin − 1/2 BH model is the onsite spin-mixing tunneling J_↑↓. The underlying reason can be traced back to the fact that the spin-mixing tunneling term breaks the SU(2) symmetry of the system^149,167. In the presence of this symmetry and two-step driving, the chaotic behavior described by COE statistics is not apparent to the SFF of the entire Hilbert space (i.e., unprojected SFF) as shown in Supplementary Note 3.

The periodically driven spinless BH model exhibits chaotic behavior when the Hamiltonians of the Floquet unitary are given by ${\hat{H}}_{1}={\hat{H}}_{{{{{{{{\rm{BH}}}}}}}}}$ with {J = 1, u = J, μ_r ∈ [ − J, J]}, and ${\hat{H}}_{2}={\hat{H}}_{{{{{{{{\rm{BH}}}}}}}}}$ with {J = 0, u = 1, μ_r = 0}. Note that the first two guidelines stated above, (i) and (ii), for the parameter selection that could lead to RMT behavior, are also valid for the spinless BH model.

The spinor Hamiltonian described in Eq. (4) can also be expressed in the Fock basis $\left\vert {n}_{-1},{n}_{0},{n}_{1}\right\rangle$, where n_i is the population in each hyperfine state. By utilizing the SU(3) Lie algebra operators¹⁶⁸,

$${\hat{H}}_{{{{{{{{\rm{SC}}}}}}}}} = \, \frac{{c}_{1}}{2N}\left[{\hat{a}}_{0}^{{{{\dagger}}} }{\hat{a}}_{0}^{{{{\dagger}}} }{\hat{a}}_{1}{\hat{a}}_{-1}+\,{{\mbox{h.c.}}}\,+{\hat{N}}_{0}({\hat{N}}_{1}+{\hat{N}}_{-1})\right. + \left.\frac{1}{2}{\left({\hat{N}}_{1}-{\hat{N}}_{-1}\right)}^{2}\right]\\ +\frac{{p}_{x}}{\sqrt{2}}\left[({\hat{a}}_{1}^{{{{\dagger}}} }+{\hat{a}}_{-1}^{{{{\dagger}}} }){\hat{a}}_{0}+\,{{\mbox{h.c.}}}\,\right]\\ + {p}_{z}\left({\hat{N}}_{1}-{\hat{N}}_{-1}\right)+\frac{{q}_{x}}{2}\left[{\hat{a}}_{1}^{{{{\dagger}}} }{\hat{a}}_{-1}+\,{{\mbox{h.c.}}}\,\right]-{q}_{z}{\hat{N}}_{0},$$

(14)

where ${\hat{a}}_{\nu }$ (${\hat{a}}_{\nu }^{{{{\dagger}}} }$) and ${\hat{N}}_{\nu }$ refer to the annihilation (creation) and the number operators of an atom occupying the spin − ν hyperfine level, respectively. Note the presence of spin-mixing collision interactions¹³⁰ in the first two terms of Eq. (14). Similarly the TACT Hamiltonian defined in Role of locality in the bump regime and Thouless time Section, can be written in the Fock basis,

$${\hat{H}}_{{{{{{{{\rm{TACT}}}}}}}}}=\chi \left[2{\hat{N}}_{0}{\hat{a}}_{-1}^{{{{\dagger}}} }{\hat{a}}_{1}+{\hat{a}}_{0}^{{{{\dagger}}} }{\hat{a}}_{0}^{{{{\dagger}}} }({\hat{a}}_{1}^{2}+{\hat{a}}_{-1}^{2})+\,{{\mbox{h.c.}}}\,\right].$$

We construct the Floquet unitaries of both the BH models and the spinor condensates in the Fock basis.

Let us emphasize that without ${p}_{z}{\hat{F}}_{z}$ term in Eq. (14), the condensate preserves the inversion symmetry $\hat{{{{{{{{\mathcal{P}}}}}}}}}={e}^{i\pi {\hat{F}}_{x}}$ which separates the Hilbert space into two independent symmetry sectors. For a Fock basis representation $\vert {N}_{0},{{{{{{{\mathcal{M}}}}}}}}\rangle$ where ${{{{{{{\mathcal{M}}}}}}}}={N}_{1}-{N}_{-1}$ is the magnetization, the parity operator acts on the states as $\hat{{{{{{{{\mathcal{P}}}}}}}}}\vert {N}_{0},{{{{{{{\mathcal{M}}}}}}}}\rangle =\vert {N}_{0},-{{{{{{{\mathcal{M}}}}}}}}\rangle$. Hence a more convenient basis choice is in terms of even and odd parity sectors, where the even parity sector consists of states that are even under the application of $\hat{{{{{{{{\mathcal{P}}}}}}}}}$, e.g., $\vert {N}_{0},0\rangle$ and $(\vert {N}_{0},{{{{{{{\mathcal{M}}}}}}}}\rangle +\vert {N}_{0},-{{{{{{{\mathcal{M}}}}}}}}\rangle )/\sqrt{2}$, and the odd parity sector consists of states $(\vert {N}_{0},{{{{{{{\mathcal{M}}}}}}}}\rangle -\vert {N}_{0},-{{{{{{{\mathcal{M}}}}}}}}\rangle )/\sqrt{2}$. Therefore, in order to capture the bump-ramp-plateau behavior in SFF, we either perform projection onto the symmetry subspace with even parity $\vert {N}_{0},{{{{{{{\mathcal{M}}}}}}}}\rangle \to (\vert {N}_{0},{{{{{{{\mathcal{M}}}}}}}}\rangle +\vert {N}_{0},-{{{{{{{\mathcal{M}}}}}}}}\rangle )/\sqrt{2}$, or we add linear Zeeman field in the z − direction, as in Eq. (14), and compute the unprojected SFF. The latter approach is experimentally feasible.

Similar to the BH model protocols described above, the two- and three-step stroboscopic protocols of Eq. (2) lead to COE and CUE statistics with the following Hamiltonians in the Floquet unitary,

$$\begin{array}{l}{\hat{H}}_{1}\to {\hat{H}}_{{{{{{{{\rm{SC}}}}}}}}/{{{{{{{\rm{DC}}}}}}}}}\,\,{{\mbox{with}}}\,\,{q}_{z}\in \left[0,\frac{{c}_{1}}{N}\right],{p}_{x}=\frac{{c}_{1}}{N},\hfill\\ {\hat{H}}_{2}\to {\hat{H}}_{{{{{{{{\rm{SC}}}}}}}}/{{{{{{{\rm{DC}}}}}}}}}\,\,{{\mbox{with}}}\,\,{q}_{z}\in \left[-\frac{{c}_{1}}{N},0\right],{p}_{x}=-\frac{{c}_{1}}{N}.\end{array}$$

(15)

For concreteness throughout the text, we assume a spinor condensate in the Thomas-Fermi limit and confined in a 1D trap¹⁶⁹, such that c₁/N ∝ N^−1/3 holds.

VE-protocol

We utilize an alternative protocol, which we refer to as the VE-protocol, based on refs. ^160,170 to test whether, and if so how, t_Th depends on the choice of the driving protocol. The VE protocol is defined by the Floquet unitary, ${\hat{U}}_{{{{{{{{\rm{V\; E}}}}}}}}}=\mathop{\prod }\nolimits_{m}^{M}{e}^{-i{\hat{H}}_{m}\tau }$ where ${\hat{H}}_{m}$ is a spinless BH Hamiltonian with a different random potential landscape at each Floquet step μ_r,m ∈ [ − J, J] for J = 1 and u = J. This protocol reproduces COE symmetry class for a two-step M = 2 Floquet unitary and smoothly transitions to simulating CUE symmetry class as the number of steps in the Floquet unitary increases to M > 5 (Supplementary Note 1).

Survival probability and spectral form factor

In this section, we discuss the relationship between survival probability and spectral form factor, and investigate the survival probability of randomly sampled initial states. The survival probability for the system of interest with initial state $\left\vert \psi \right\rangle$ and time evolution operator $\hat{U}$ is given by Eq. (8). When the state $\left\vert \psi \right\rangle$ is chosen to be the equal-amplitude superposition of all eigenstates of ${\hat{U}}$, then

$$P\left(\left\{\left\vert \psi \right\rangle =\mathop{\sum}\limits_{n}\left\vert {\theta }_{n}\right\rangle ,\hat{U}\right\},t\right)={K}_{\hat{U}}(t).$$

(16)

Next, we consider the survival probability of two randomly sampled initial states, namely,

• 1. Globally randomly rotated states, i.e.

  $$\left\vert \psi \right\rangle =\hat{W}\left\vert \Psi \right\rangle ,\quad \hat{V}\in {{{{{{{\rm{CUE}}}}}}}}(D)={{{{{{{\rm{CUE}}}}}}}}({q}^{L})$$

  (17)

  where $\hat{W}$ is a random unitary drawn from the D-by-D CUE, D and q are the Hilbert space dimension and the on-site Hilbert space dimension respectively. $\left\vert \Psi \right\rangle$ is any pure state including product states.

• 2. Locally randomly rotated states, i.e.

  $$\left\vert \psi \right\rangle =\left(\mathop{\bigotimes}\limits_{i}^{L} {\hat{v}}_{i}\right)\left\vert \Psi \right\rangle ,\quad {\hat{v}}_{i}\in {{{{{{{\rm{CUE}}}}}}}}(q).$$

  (18)

Using the two-design formula for m-by-m random unitaries $\hat{W}$ from CUE,

$$\begin{array}{l}{\mathbb{E}}{\left[{\hat{W}}_{{a}_{1}{a}_{1}^{{\prime} }}{\hat{W}}_{{a}_{2}{a}_{2}^{{\prime} }}{\hat{W}}_{{b}_{1}{b}_{1}^{{\prime} }}^{* }{\hat{W}}_{{b}_{2}{b}_{2}^{{\prime} }}^{* }\right]}_{\hat{W}}=\\ \frac{1}{{m}^{2}-1} \left({\delta }_{{a}_{1}{b}_{1}}{\delta }_{{a}_{1}^{{\prime} }{b}_{1}^{{\prime} }}{\delta }_{{a}_{2}{b}_{2}}{\delta }_{{a}_{2}^{{\prime} }{b}_{2}^{{\prime} }}+{\delta }_{{a}_{1}{b}_{2}}{\delta }_{{a}_{1}^{{\prime} }{b}_{2}^{{\prime} }}{\delta }_{{a}_{2}{b}_{1}}{\delta }_{{a}_{2}^{{\prime} }{b}_{1}^{{\prime} }}\right)-\\ \frac{1}{m({m}^{2}-1)}\left({\delta }_{{a}_{1}{b}_{2}}{\delta }_{{a}_{1}^{{\prime} }{b}_{1}^{{\prime} }}{\delta }_{{a}_{2}{b}_{1}}{\delta }_{{a}_{2}^{{\prime} }{b}_{2}^{{\prime} }}+{\delta }_{{a}_{1}{b}_{1}}{\delta }_{{a}_{1}^{{\prime} }{b}_{2}^{{\prime} }}{\delta }_{{a}_{2}{b}_{2}}{\delta }_{{a}_{2}^{{\prime} }{b}_{1}^{{\prime} }}\right),\end{array}$$

(19)

one can compute Eq. (11) for both cases in Eqs. (17) and (18).