Abstract
Particle track fitting is crucial for understanding particle kinematics. In this article, we use artificial intelligence algorithms to show how to enhance the resolution of the elementary particle track fitting in dense detectors, such as plastic scintillators. We use deep learning to replace more traditional Bayesian filtering methods, drastically improving the reconstruction of the interacting particle kinematics. We show that a specific form of neural network, inherited from the field of natural language processing, is very close to the concept of a Bayesian filter that adopts a hyper-informative prior. Such a paradigm change can influence the design of future particle physics experiments and their data exploitation.
Similar content being viewed by others
Introduction
Understanding the behaviour of subatomic particles traversing dense materials, often immersed in magnetic fields, has been crucial to their discovery, detection, identification and reconstruction, and it is a critical component for exploiting any particle detector1,2,3,4,5,6. Modern radiation detectors have evolved towards 'imaging detectors', in which elementary particles leave individual traces called 'tracks'7,8,9,10,11. These imaging detectors require a 'particle flow' reconstruction: particle signatures are precisely reconstructed in three dimensions, and the kinematics (energy and momentum vector) of the primary particle can be measured track-by-track. It also means that a more significant amount of details can be obtained on each particle. These features open the question of which methods are best suited to handle the 'images' created by the subatomic particles.
Common Monte Carlo (MC) based methods used in the track fitting flow belong to the family of Bayesian filters and, more specifically, they are extensions to the standard Kalman filter12 or particle filter algorithms, with special mention to the Sequential Importance Resampling particle filter (SIR-PF)13. The knowledge about how an electrically charged subatomic particle propagates through a medium (i.e. the energy loss, the effect of multiple scattering, and the curvature due to magnetic field) can be embedded into a prior (often in the form of a covariance matrix for Kalman filters). In particle filters, the nodes of the track are fitted sequentially: given a node state, the following node in the particle track is obtained by throwing random samples—known as 'particles'—and making a guess of the following state by applying a likelihood between the sampled particles and the data (which could be, for instance, the signatures obtained from the detector readout channels). The result can be the position of the fitted nodes of a particle track or directly its momentum vector and its electric charge. Usually, the problem is simplified using a prior that follows a Gaussian distribution, like in the Kalman filter, which also considers a simplified version of the detector geometry. Examples can be found in refs. 14,15,16. However, the filtering is not trivial since both the particle energy loss and multiple scattering angles depend on the momentum, which changes fast in dense materials, and approximations are often necessary. Moreover, it is hard to incorporate finer details of a realistic detector geometry and response (e.g. signal crosstalk between channels, air gaps in the detector active volume, presence of different materials, or non-uniformities in the detector response as a function of the particle position, inhomogeneous magnetic field) or to deal with deviations in the particle trajectory due to the emission of high-energy δ-rays, with photon Bremsstrahlung emission, with the Bragg peak of a stopping particle, or with inelastic interactions. All these pieces of information are available in the simulation of a particle physics experiment17,18,19,20,21 and can be validated or tuned with data, but it is not straightforward to use them in the reconstruction of the particle interaction. Hence, developing new reconstruction methods capable of analysing all the information available becomes essential.
The most promising solution is given by artificial intelligence and, more specifically, by deep learning, a sub-field of machine learning based on artificial neural networks22,23,24,25,26,27. Initially inspired by how the human brain functions, these mathematical algorithms can efficiently extract complex features in a multi-dimensional space after appropriate training. Neural networks (NNs) have been found to be particularly successful in the reconstruction and analysis of particle physics experiments28,29,30,31. Thus far, deep learning has been used in high-energy physics (HEP) for tasks such as classification29,32,33,34, semantic segmentation35,36, or regression37,38,39. Typically, the raw detector signal is analysed to extract the physics information. This approach is quite common in experiments studying neutrinos, for example, to classify the flavour of the interaction (νμ, νe or ντ) by using convolutional neural networks (CNNs)29,32,40, or the different types of signatures observed in the detector35,36. These methods have been shown to outperform more traditional ones, such as likelihood inference or decision trees. However, asking a neural network to extract high-level physics information directly from the raw signatures left in the detector by the charged particles produced by a neutrino interaction is conceivable as challenging. An example is the neutrino flavour identification (as mentioned before), which incorporates diverse contributions, from the modelling of the neutrino interaction cross-section to the propagation of the particles in matter and, finally, the particular response of the detector. Expecting a neural network to learn and parametrise all these contributions could become unrealistic and lead to potential deficiencies.
An alternative and promising approach is to use deep learning to assist the more traditional particle flow methods in reconstructing particle propagation, which consists of a chain of different analysis steps that can include the three-dimensional matching of the voxelised signatures in the detector readout 2D views, the definition of more complex objects such as tracks and, finally, the fit of the track in order to reconstruct the particle kinematics. As described above, the last step is critical and is usually performed by a Bayesian filter that has to contain as much information as possible in its multi-dimensional prior. It becomes clear that, overall, the reconstruction performance depends on the detector design (e.g., granularity or detection efficiency) and on the a priori knowledge of the particle propagation in the detector, the prior. Although prohibitive for traditional Bayesian filters, the problem of parameterising a high-dimensional space can be overcome with deep learning since neural networks can be explicitly designed for it.
Even though the generic idea of using deep learning as an alternative to Bayesian filtering has already been explored41, common applications focus on tasks such as enhancing and predicting vehicle trajectories42,43. Furthermore, the closest application we can currently find in HEP and other fields like biology is to use deep learning to perform “particle tracking”44,45,46, which relies on connecting detected hits to form and select particles, distinct from the idea of fitting the detected hits to obtain a good approximation to the actual particle trajectory.
In this article, we propose the design of a recurrent neural network (RNN) and a Transformer to fit particle trajectories. We found that these neural nets, inherited from the field of natural language processing, are very close to the concept of a Bayesian filter that adopts a hyper-informative prior. Hence, they become excellent tools for drastically improving the accuracy and resolution of elementary particle trajectories.
Results
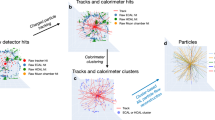
In this section, we discuss the performance of a recurrent neural network (RNN)47,48,49 and a transformer50, comparing their results with the ones from a custom SIR-PF (as described in the 'Introduction' section). The developed methods, described in detail in the 'Methods' section, were run on a test dataset of simulated elementary particles (statistically independent of the dataset used for training) from a three-dimensional fine-grain plastic scintillator detector, consisting of 1,759,491 particles (412,092 protons, 432,807 pions π±, 447,003 μ± and 467,589 e±). For each simulated particle, the goal was to use the reconstructed hits to predict the actual track trajectory and then to analyse its physics impact on the detector performance, as described later in this section. The output of the different methods was a list of fitted nodes, i.e. the predicted 3D positions of the elementary particle in the detector. A visual example of the particle trajectory fitting using the different techniques is shown in Fig. 1.
From left to right, the diagram shows the steps from the particle simulation/detection until the particle is fitted using the different algorithms: recurrent neural network (RNN), transformer, and sequential importance resampling particle filter (SIR-PF). First, the detector response in the form of 2D projections is reconstructed into a 3D event, where target particle(s) can be extracted; then, the fitting algorithms (already trained or designed using a simulated dataset) are applied to a target particle to output its trajectory accurately. The right-hand side of the figure shows the true muon track trajectory in green, together with the predicted trajectories using the three algorithms. Part of the track is zoomed in for visualisation reasons.
Fitting of the particle trajectory
For the SIR-PF, we have considered two different scenarios that vary in the reconstructed input information to the filter: (1) all the reconstructed 3D hits are used as input; (2) only real track hits (hits from cubes the actual particle has passed through) are used as input, which is unavailable information for actual data (and represents a nonphysical scenario) but allows us to test the ideal performance for the current filter. The input for the RNN and transformer always consisted of all the reconstructed 3D hits. Figure 2 shows a comparison of the performance for the three methods (considering the SIR-PF variant with all the reconstructed hits as input). The results indicate that the Transformer outperforms the other techniques (even for the case with only track hits). Besides, the RNN reports significantly better results than the SIR-PF with only track hits used as input and slightly better fittings concerning the SIR-PF with all hits used as input, which demonstrates not only that the NN-based approaches can handle crosstalk hits but also go beyond and accomplish spatial determination <1.5 mm far (on average) from the real physical case.
a The distribution of the three-dimensional Euclidean distance between the actual elementary particle position and the corresponding fitted node predicted by the transformer, the recurrent neural network (RNN), and the sequential importance resampling particle filter (SIR-PF, with only track hits and all hits as input). The sample used to generate the histograms contains all the simulated particles. Results show the distributions for a log-scale density, as well as the one-sided area ranges, representing 68 and 95% of the distributions. b Same results for a standard-scale density and a maximum distance cropped at 5 mm.
A more exhaustive analysis of the performance of both methods is presented in Table 1, which reveals the effectiveness of the NNs compared to the SIR-PF variants. The table also confirms that the track fitting becomes more manageable when the crosstalk hits are removed from the input and more precise information is given to the filter (the SIR-PF version with only track hits outperforms the one with all hits as input). This last fact also evidences the power of deep learning, which is, on average, able to predict more accurately the node positions and thus the true track trajectory, even if its input consists of all the reconstructed hits without any type of pre-processing (e.g., removal of crosstalk hits), meaning that it could understand the relations between hits internally, confirming the ability to discard the crosstalk hits during the fitting calculation. The measured spatial resolution can depend on multiple factors, including the particle type. We expect electrons, muons, pions and protons to exhibit slightly different resolutions. For instance, the electron spatial resolution can be affected by multiple scattering (for example, the way they scatter via the Bhabha process) and Bremsstrahlung (enhanced for electrons with respect to other particles of the same momenta). Besides, particles escaping the detector exhibit a better spatial resolution primarily due to higher momenta than particles that stop in the detector, typically more energetic and collimated. Moreover, escaping particles are generally longer, meaning they have more points on average available for trajectory reconstruction. In order to compare the Transformer and the RNN, it is worth looking at the muon fitting in Table 1: the Transformer reports the best results for fitting muon particles (for both mean and standard deviation) in contrast to the RNN, which reports an atypically large std dev. for muon tracks contained in the detector. The explanation relies on the length of the particles and the properties of the algorithms: since muons tend to have the most extended track length among the simulated stopping particles (protons and pions tend to have more secondary interactions and electrons produce electromagnetic showers), and the RNN depends on its memory mechanisms to bring features from faraway hits to fit a particular reconstructed hit (see Supplementary Note 1, for more details), it is habitual to omit some information from remote hits during the fitting; on the other hand, the Transformer reduces its mistakes by having a complete picture of the particle thanks to its capacity to learn the correlations among all reconstructed hits.
To understand the behaviour of the fittings for the different physical structures of the particles, we have calculated the mean-squared error (MSE, which is the loss function used during the neural network trainings) between each fitted and true node and visualised the information in Fig. 3. The MSE loss, which penalises outliers by construction, seems flatter for the RNN and Transformer than for the SIR-PF, indicating more stability in the fitting. Besides, it is notorious for highlighting the tendency for particular negative ΔE values to report high losses in the NN cases, caused mainly due to the low charge of crosstalk compared to track hits. Besides, Fig. 3, as expected, also reveals that the three algorithms report worse fittings when getting closer to cluster hits connected to the track. For instance, in the case of muon particles, these clusters are typically due to the ejection of δ-rays, i.e. orbiting electrons knocked out of atoms, often causing a kink on the muon track; however, both NNs seem to deal much better with this attribute.
a MSE loss concerning \(\parallel (\Delta x,\overrightarrow{\Delta y},\Delta z)\parallel\) (the magnitude of the vector resulting from the differences in position between consecutive nodes) and ΔE (differences in energy deposition between successive nodes) for the three algorithms (from left to right): Sequential Importance Resampling particle filter (SIR-PF) with all hits, recurrent neural network (RNN), and transformer. After standardisation, each bin corresponds to the average mean-squared error (MSE) loss applied to the pair (true node, fitted/predicted node). All fitted nodes are considered. b MSE loss concerning the distance from each fitted node to the closest cluster hit and ∣clusterE − nodeE∣ (absolute difference between the energy depositions of the fitted node and the nearest cluster hit) for the three algorithms (from left to right): SIR-PF with all hits, RNN, and transformer. After standardisation, each bin corresponds to the average mean-squared error (MSE) loss applied to the pair (true node, fitted/predicted node). Only nodes from muon (μ±) particles are considered.
Even if the primary goal of this article is to show the performance of the fitting from a physics perspective, it is worth comparing the different algorithms in terms of computing time. Table 2 manifests the average time it takes for each algorithm to run the fitting on a single particle. The results exhibit a considerable speedup for both the RNN and the Transformer models (with speedups of ~× 4 and ~× 35, respectively) with a single thread on the CPU. The table does not show the SIR-PF results for the distributed computing scenarios since it would require some time to parallelise the SIR-PF code to run it with multiple threads or to adapt it to GPU computation, which is clearly beyond the scope of the study; that being said, the table shows the parallel results for the RNN and Transformer cases since these are features available in the PyTorch framework, which show how inexpensive it would be to achieve significant speedups for an ordinary user.
Finally, if we look at the size of the histogram used to calculate the likelihood, it consists of 3,948,724 bins with non-zero values, compared to the 213,553 learnt parameters of the RNN (~18 times fewer parameters) and the 167,875 parameters of the Transformer (~23 times fewer parameters than the SIR-PF histogram). Of course, it would be possible to design a more efficient version of the histogram (which is also out of the scope of the article) to reduce the difference in parameters among the methods. Nevertheless, this first approximation already gives insights into how compact the information is encoded in the neural network cases in contrast to the Bayesian filter scenario with a physics-based likelihood calculation.
Impact on the detector physics performance
The reconstruction of the primary particle kinematics provides diverse information: the electric charge (negative or positive); the identification of the particle type (protons, pions, muons, electrons), which mainly depends on the particle stopping power as a function of its momentum; the momentum, either from the track range of the particle that stops and releases all its energy in the detector active volume or from the curvature of its track if the detector is immersed in a magnetic volume; the direction. An improved resolution on the spatial coordinate and, consequently, of the particle stopping power impacts the accuracy and precision of the physics measurement. This section compares the performance of the reconstruction of particle interactions provided by the Transformer and RNN to the one using the SIR-PF.
The charge identification (charge ID) is performed by reconstructing the curvature of the particle track in the detector immersed in the 0.5 T magnetic field. The charge ID performance was studied for muons (resp. electrons) with momenta between 0 and 2.5 GeV/c (resp. 0 and 3.5 GeV/c) and isotropic direction distribution. From Fig. 4, it is evident that the NNs outperform the SIR-PF. For instance, the muon charge can be identified with an accuracy better than 90% if the track has a length projected on the plane transverse to the magnetic field of ~33 and ~36 cm for the transformer and RNN, respectively. Instead, the SIR-PF (with all the hits, the version with the same input as the neural network cases) requires a track of at least ~42 cm in order to achieve the same performance. Similar conclusions can be derived from the charge ID study on electrons and positrons.
a Charge ID probability for muons and antimuons (μ±) as a function of the track length projected on the plane perpendicular to the 0.5 T magnetic field. An equal number of particles and antiparticles are considered. The error is less than 6 × 10−3 for all data points (charge ID prob.). b Charge ID probability for electrons and positrons (e±) as a function of the track length projected on the plane perpendicular to the 0.5 T magnetic field. An equal number of particles and antiparticles are considered. The error is less than 5 × 10−3 for all data points (charge ID prob.). c A muon example of 0.6 GeV/c with a 0.5 T magnetic field is considered to show the momentum-by-curvature resolution as a function of the track length projected on the plane perpendicular to the magnetic field. The average Euclidean distance (between true and fitted nodes) per muon particle was considered. d A muon example of 0.6 GeV/c with a 0.5 T magnetic field is considered to show the angular resolution as a function of the particle length in the detector. The average Euclidean distance (between true and fitted nodes) per muon particle was considered. The results in this figure are presented for the different fitting techniques: Transformer, recurrent neural network (RNN), and sequential importance resampling particle filter (SIR-PF) with all hits and only track hits as input.
In Fig. 4, the case of a 0.6 GeV/c muon was also studied, showing the node positions fitted with the NNs and SIR-PF, with the Transformer better capturing the curvature due to the magnetic field. It was found that if the tracking resolution is accurate, it is possible to either improve the detector performance beyond its design or to aim for a more compact design of the scintillator detector deployed in a magnetic field. For instance, the spatial resolution achieved with the NNs in a magnetic field of 0.5 T allows measuring the momentum of a 0.6 GeV/c muon from its curvature with a resolution of about 15% with a length of the track projected on the plane transverse to the magnetic field of almost 40 cm, shorter by about 20 cm than the length needed by the SIR-PF with all the hits. Such an improvement implies the possibility of accurately reconstructing the momentum of muons escaping the detector for a larger sample of data. At the same time, improved methods for the reconstruction of particle interactions could become a new tool in the design of future particle physics experiments, for example leading to more compact detectors, thus lower costs. Similar conclusions can be achieved about the particle angular resolution, improved by about a factor of two and, simultaneously, requiring a track length three times shorter than the one obtained with traditional methods.
The transformer outperforms the SIR-PF also in the reconstruction of the particle momentum, both by range and curvature. For instance, the momentum-by-range resolution for protons stopping in the detector between 0.9 and 1.3 GeV/c is improved by a factor of ~15%, as shown in Fig. 5. Since protons typically have a much stronger stopping power towards the end of the track (Bragg peak), the total amount of energy leaked to the adjacent cubes is more significant. We observe that the fitting near the Bragg peak becomes more challenging for protons (for example, compared to muons) and less precise due to the presence of more crosstalk hits. This becomes particularly relevant for low momentum (true initial momentum from 0.4 to 0.8 GeV/c)—hence short—protons. However, the transformer seems to deal well with this difficulty, whilst the RNN reports worse resolutions for this particular case, as shown in Fig. 5.
a Energy deposit measured by stopping protons at each fitted node as a function of its distance from the last fitted node for the transformer. b Energy deposit measured stopping protons at each fitted node as a function of its distance from the last fitted node for the recurrent neural network (RNN). c Energy deposit measured by stopping protons at each fitted node as a function of its distance from the last fitted node for the sequential importance resampling particle filter (SIR-PF) with all hits as input. Note that we chose a different binning for the SIR-PF than the one used for the NN versions for visualisation reasons since the former algorithm reports fewer fitted nodes per particle on average. d The reconstructed momentum bias, in percentage, for stopping protons as a function of real initial proton momentum is shown for the different fitting algorithms. The error bars show the resolution.
The particle identification performance depends on the capability of reconstructing the particle stopping power along its path as a function of its initial momentum. The resolution to the particle dE/dx is shown in Fig. 5, where one can see that the energy deposited by protons as a function of the fitted node position is neater and more refined for the NNs compared to the SIR-PF (with all hits as input), in particular for the Transformer that shows the most accurate Bragg peak. Automatically, this translates into a more performing particle identification capability, as shown in Table 3 for different particles such as muons, pions, protons and electrons for a wide range of energies.
Discussion
Deep learning is starting to play a more relevant role in the design and exploitation of particle physics experiments, although it is still in a gestation phase within the high-energy physics community. If the optimal neural network is optimised, deep learning has the unique capability of building a non-linear multi-dimensional MC-based prior probability function with many degrees of freedom (d.o.f.) that can efficiently and accurately model all the information acquired in a particle physics experiment and enhance the performance of the particle track fitting and, consequently, its kinematics reconstruction. Such a level of detail is, otherwise, nearly impossible to incorporate “by hand” in the form of, for example, a covariance matrix to be used in a traditional particle filter. In this work, we show that a Transformer and an RNN can efficiently learn the details of the particle propagation in matter mixed with the detector response and lead to a significantly improved reconstruction of the interacting particle kinematics. We observed that the NNs capture better the details of the particle propagation even when its complexity increases, which is the case near the presence of clusters of hits, for example, due to δ-rays.
It is worth noting that, as mentioned in the “Results” section, this work does not aim to report on the performance of the simulated particle detector but rather to show the added value provided by an NN-based fitting. Moreover, the proposed method does not replace the entire chain of algorithms traditionally adopted in a particle flow analysis (e.g. minimum spanning tree, vertex fitting, etc.) but is meant to assist and complement them as a more performing fitter. For instance, a possibility could be to apply SIR-PF several times with 'ad-hoc' manipulation of the data between each step. However, this would be an unfair comparison as one could also implement multiple deep learning methods and focus on their optimisation.
We believe this approach is a milestone in artificial intelligence applications in HEP and can play the role of a game changer by shifting the paradigm in reconstructing particle interactions in the detectors. The prior, which is consciously built from the modelling of the underlying physics from data external to the experiment, becomes as essential as the real data collected for the physics measurement. De facto, the prior provides a strong constraint to the 'interpretation' of the data, helping to remove outliers introduced by detector effects, such as from the smearing introduced by the point spread function and improving the spatial resolution well below the actual granularity of the detector.
Its accuracy also depends on the quality of the training sample, i.e. on the capability of the MC simulation to correctly reproduce the data. Although this is true for most of the charged particles, a careful characterisation of the detector response will be crucial to validate and, if necessary, tune the simulation (e.g. electromagnetic shower development or hadronic secondary interactions) used to generate the training sample.
This study requires that, first, the signatures observed in the detector are analysed, and the three-dimensional hits that compose tracks belonging to primary particles (directly produced at the primary interaction vertex) are distinguished and analysed independently. This approach is typical of particle flow analyses.
This work is focused on physics exploitation in particle physics experiments. However, the developed AI-based methods can also fulfil the requirements in applications outside of HEP, as long as one has a valid training dataset. One example is proton computed tomography51,52,53,54 used in cancer therapy, where scintillator detectors are used to measure the proton stopping power along its track in the Bragg peak region to precisely predict the stopping position of the proton in the human body. This measurement is analogous to the momentum regression described in the 'Computation of particle kinematics' subsection of the 'Methods' section, given the nearly complete correlation between the particle range and momentum.
Future improvements to the developed NNs may involve investigating the effects of varying noise levels and multiple tracks in the detector volume, as well as the direct computation of the node stopping power from the track, i.e. the combined fitting of both the node particle position and energy loss. In this context, we would also like to highlight some previous work on event reconstruction with track overlaps, where the effectiveness of a graph neural network was demonstrated to identify ambiguities and boost reconstruction performance in the presence of high multiplicity signatures and signal leakage between neighbouring active detector volumes36. These insights could be further extended to more general scenarios of overlapping or intersecting particle tracks in dense detectors.
Methods
Proof-of-principle
In order to train and test the developed neural networks and compare their performance with a more classical Bayesian filter, an idealised three-dimensional fine-grain plastic scintillator detector was taken as a case study. We simulated a cubic detector composed of a homogeneous plastic scintillator with a size of 2 × 2 × 2 m3. A uniform magnetic field is applied, aligned to one axis of the detector (X-axis) and its strength is chosen to be 0.5 T. The detector is divided into small cubes of size 1 cm3, summing 200 × 200 × 200 cubes in total. Each cube is assumed to be equipped with a sensor that collects the scintillation light produced when a particle traverses it. We simulate the signals read from each sensor and reconstruct the event based on these signals. The track input to the fitters will be extracted from event reconstruction.
Overall, the simulation and reconstruction are divided into three steps:
-
1.
Energy deposition simulation: this step uses the Geant4 toolkit17,18,19 to simulate particle trajectories in the detector and their energy deposition along the path.
-
2.
Detector response simulation: this step simulates detector effects and converts the energy deposition into signals the detector can receive. The current detector effect being considered is the light leakage from one cube to the adjacent one (named crosstalk). The leakage probability per face is assumed to be 3%. The energy deposition is converted from the physics unit (MeV) into the ‘signal unit’ (depending on the detector) by using a constant factor, which is fixed to be 100/MeV for this analysis. Besides, a threshold is also implemented on the sensor, requiring that at least one signal unit be received to activate the sensor.
-
3.
Reconstruction: This step takes the signals generated from the former steps and reconstructs objects, such as tracks, that can be input to the fitter. Starting from 3D 'cube hits' (what we have after the detector response simulation), we then apply the following two methods to find track segments from the whole event: (1) the density-based spatial clustering of applications with noise (DBSCAN)55, which groups hit into large clusters that, in each cluster, all hits are adjacent to each other; (2) the minimum spanning tree (MST)56 for each cluster to order hits and break the cluster into smaller track segments at each junction point. Afterwards, the primary track segment will be selected for track fitter input.
The simulation and reconstruction processes produced single-charged particles (protons, pions π±, muons μ± and electrons e±) starting at random positions in the detector active volume with isotropic directions and uniform distributions of their initial momentum: between 0 and 1.5 GeV/c (protons), 0 and 1.5 GeV/c (pions), 0 and 2.5 GeV/c (muons) and 0 and 3.5 GeV/c (electrons). Each particle consisted of a number of reconstructed 3D hits belonging to the track, where each hit is represented by a three-dimensional spatial position and an energy deposition in an arbitrary signal unit. For each reconstructed hit in a particle, there is a true node (to be learnt during the supervised training) which represents the closest 3D point to the hit in the actual particle trajectory; in that way, there is a 1-to-1 correspondence between reconstructed hits (even for crosstalk) and true nodes. We refer in the rest of the article to the output of the algorithms developed as fitted nodes, which form the fitted trajectory for each particle.
Description of the fitting algorithms
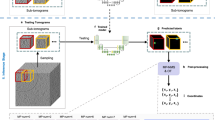
To test the capability of deep learning to fit particle trajectories using reconstructed hits as input, we developed two neural networks that represent the state-of-the-art in the field of natural language processing (NLP, as detailed in Supplementary Note 1): the recurrent neural network (RNN)47,48,49 and the Transformer50 (see Fig. 6 for a full picture of the architectures). We chose RNNs and Transformers for their ability to handle sequential data with variable lengths, which is crucial for particle trajectory fitting where the number of hits in a track can vary. Both algorithms learn from input sequences, each of these sequences being, for instance, a succession of words forming a sentence in the NLP case; or reconstructed hits representing a detected elementary particle in our scenario. Their power relies on their capacity to learn relations between all elements of a sequence. In general terms, RNNs count with memory mechanisms to use information from the 'past' (previous items in the sequence) and the 'future' (following items in the sequence) to make predictions. Thus, RNNs assume the input sequences to be ordered. Transformers do not necessarily need sequences to be ordered: the correlations among different items in the sequence are learnt throughout the training process. In contrast, other architectures, such as CNNs, require fixed-length inputs, which would be difficult to achieve for our application, and would not account for hard scatterings and crosstalk in the detector.
a Recurrent neural network (RNN). In high-level terms, the RNN consists of five bi-directional GRU layers, followed by a linear layer that projects the sum of the outputs of the GRU layers into a vector of length three. b Transformer encoder. It consists of five encoder layers, followed by a linear layer that projects the sum of the outputs of the encoder layers into a vector of length three. For both models, the input hit position (xi, yi, zi) is summed to the network’s output, allowing it only to learn the 'residuals' of the reconstructed hits concerning the true node states (\({\overrightarrow{S}}_{{{{{{\mathrm{in}}}}}}}\to {\overrightarrow{S}}_{{{{{{\mathrm{out}}}}}}}\)).
Both RNNs and transformers can efficiently capture long-range dependencies in the input data and are well-suited for regression tasks like particle trajectory fitting. We carefully optimised our implementation to achieve high performance, but we also acknowledge that hyper-parameter optimisation is an important consideration for timing studies. We would like to clarify that while the choice of algorithm is important, the performance is ultimately determined by the quality of the input data, the complexity of the physics model used for simulation, and the training procedure. Our approach turns the track-fitting problem into a regression task, and the resolution performance is not limited by the algorithm but by the inherent resolution of the detector and the quality of the input data. However, the choice of algorithm can still have a significant impact on the computational efficiency and the ability to handle variable-length inputs.
We implemented a bi-directional RNN, and the memory mechanism used is the gated recurrent unit (GRU)57. Our RNN consists of five bi-directional GRU layers with 50 hidden units each. The output of each GRU layer is the concatenation of the forward and backward modules of the layer and is given as input for the following layer (except for the last layer). Instead of propagating only the output of the last GRU layer to the final dense layer, the outputs of all layers are summed together, replicating the concept of “skipped connections” in a similar way to what the ResNet or DenseNet model do58. As regularisation, a dropout of 0.1 is applied to the output of each GRU layer (except for the last GRU layer) and to the summed output of the GRU layers, which is then projected through a final dense layer to have fitted nodes of size 3, representing the coordinates in a three-dimensional (x, y and z). The implemented RNN has a total of 213,553 trainable parameters.
The Transformer model designed consists of five-stacked transformer-encoder layers, with eight heads per layer and a dimension of 128 for the hidden dense layer. The input hits are embedded into vectors of size 64. A dropout of 0.1 is applied in each encoder layer and also to the output of the encoder layers to be further projected through a final dense layer (analogously to the RNN), making each fitted node have a length of three. There is no positional encoding since the goal is to make the network learn the relative ordering of the hits based on the 3D positions. The network has a total of 167,875 trainable parameters.
We implemented both networks in Python v3.10.459 using PyTorch version 1.11.060, and trained them on a dataset of simulated elementary particles consisting of 1,762,327 particles (414,824 protons, 432,855 pions, 446,858 muons and antimuons and 467,790 electrons and positrons). Each particle consists of a sequence of reconstructed hits with their known positions (centre of the matching cubes) and energy depositions (in an arbitrary signal unit) represented for each hit with the tuple \({\overrightarrow{S}}_{{{{{{\mathrm{in}}}}}}}=({x}_{i},{y}_{i},{z}_{i},{E}_{i})\) and truth node position to be learnt \({\overrightarrow{S}}_{{{{{{\mathrm{out}}}}}}}=({x}_{i},{y}_{i},{z}_{i})\). Each variable is normalised to the range [0, 1]. We used 80% of the particles from this sample for training and 20% for validation, ignoring particles with either less than 10 reconstructed hits or less than 2 track hits, both representing less than 1% of the total particles. Note that this dataset is statistically independent of the one used for producing the results shown in the “Results” section. Mean-squared error and Adam (batch size of 128, learning rate of 10−4, β1 = 0.9 and β2 = 0.98) are the loss function (typical for regression) and optimiser, respectively, chosen for both networks. We performed a grid search to identify the best-performing hyper-parameters. We trained the models on an NVIDIA A100 GPU for an indefinite number of epochs but with early stopping after 30 epochs, meaning that the training terminates when the loss on the validation set does not improve for 30 epochs. We trained the models on an NVIDIA A100 GPU for an indefinite number of epochs but with an early stopping of 30, meaning that the training terminates when the loss on the validation set does not improve for 30 epochs. The training and validation losses are shown in Fig. 7.
a Recurrent neural network (RNN). b Transformer. For both models, the loss function used is the mean-squared error (MSE). The dashed-vertical lines represent the epoch that minimises the loss and, thus, the model weights used for the subsequent analysis. The Transformer network converges much faster than the RNN, presumably because the former can learn the correlations among unordered reconstructed hits, and the latter assumes the reconstructed hits are ordered, which can lead to confusion due to the inherent flaws of the ordering provided (impossibility of arranging an optimal order from reconstructed information).
It is necessary to mention that for both the RNN and the transformer, we sum together (position-wise) the output of the models for each fitted node and the 3D position of the corresponding reconstructed hit given as input. In that way, we force the networks to learn the residuals between reconstructed hits and fitted nodes (in other words, what is learnt is how to adjust each reconstructed hit to a node position that matches the actual particle trajectory).
Regarding the sequential importance resampling particle filter (SIR-PF), for each particle, we use the first reconstructed hit as prior (hits are reordered with respect to the axis the particle is travelling through the furthest; if there are several candidates for the first position, we chose the one with the highest energy deposition), meaning we use it to sample the first random particles inside that cube, and the energy deposition of each particle happens to be the one of the hitting cube. In each step, the random particles are propagated through the next 15 hits (we make sure the random particles are sampled inside the available reconstructed hits, starting with counting from the position of the current state). For each random particle, the algorithm calculates the variation in x, y, z, θ (elevation angle defined from the XY-plane, in spherical coordinates), and energy deposition (in an arbitrary signal unit) between the particle and the current state and assigns a likelihood based on the value of the selected bin in a five-dimensional histogram (used for the likelihood calculation of the SIR-PF, filled with the variation between consecutive true nodes in x, y, z, θ, and energy deposition, named: Δx, Δy, Δz, Δθ and ΔE, respectively, and with 100 bins per dimension), pre-filled using the same dataset used to train the RNN and the Transformer. In that way, the next state ends up being the weighted average (using the pre-computed likelihood) of the positions of the different sampled particles available. The filter is run from the start to the end of the particle (forward fitting) and from the end to the start (backwards fitting); the results of the forward and backward fittings are averaged in a weighted manner, giving more relevance to nodes fitted last in both cases. The total number of random particles sampled in each step is 10,000.
Computation of particle kinematics
The RNN, Transformer, and SIR-PF outputs are analysed to extract the kinematics from the fitted tracks. The performance of the methods depends on the accuracy of the fitted nodes compared to the true track trajectories. The same procedure has been applied to the nodes fitted with the different algorithms for a fair comparison.
The following steps have been followed to perform the physics analysis, that is, particle identification (PID), momentum reconstruction and charge identification (charge ID):
-
1.
Extract 'track' nodes: the input 3D hits can be divided into two categories: (1) track hits, directly crossed by the charged particle, (2) crosstalk hits, caused by the leakage of scintillation light from the cube containing the charged particle. After the track is fitted, the 3D hits are identified as track-like if there is a scintillator cube with a particular energy deposition that contains the fitted node. The remaining nodes are classified as non-track, and they include crosstalk hits. The scintillation light observed in a non-track hit is summed to the nearest track hit. The position of the fitted node is then used to compute the stopping power (dE/dx).
-
2.
Node energy smoothing: the energy of the remaining 'track' nodes is smoothed in order to eliminate fluctuations due, for example, to the different path lengths travelled by the particle in the adjacent cubes (the scintillation light in a cube is nearly proportional to the distance travelled by the particle). The smoothing of an energy node is performed by applying an average over the energy of nearby nodes weighted by a Gaussian distribution function of the respective distance.
-
3.
Particle identification and momentum regression: a gradient-boosted decision tree (GBDT)61, available in the TMVA package of the CERN ROOT analysis software (https://root.cern.ch/), was used to perform the particle identification and the momentum regression. The GBDT input parameters were chosen as (1) the first 5 and the last ten fitted node energies along the track; (2) the neighbouring node distances of those 15 nodes; (3) the track total length and energy deposition. Two independent GBDTs with the same structure were trained to reconstruct the primary particle type (muon, proton, pion or electron, classification) and its initial momentum (regression).
The electric charge of the particle was identified by measuring the deflection of the track projected to the plane perpendicular to the magnetic field. The convex or concave deflection implies either a positive or a negative charge, where the positions of the fitted nodes were used.
The momentum reconstruction from the track curvature produced by the magnetic field was estimated for the resolutions provided by different track fitters and studied for different configurations by using parameterised formulas that incorporate the spatial resolution from tracking in a magnetic field as well as the multiple scattering in dense material62,63, that have been shown to reproduce data well enough for sensitivity studies.
Data availability
The datasets used to train and test our models are publicly available at https://doi.org/10.5281/zenodo.7347563.
Code availability
All code used to implement the methods and reproduce the findings presented in this paper is publicly available at https://github.com/saulam/trajectory_fitting.
References
Hasert, F. et al. Search for elastic muon-neutrino electron scattering. Phys. Lett. B 46, 121–124 (1973).
Hasert, F. et al. Observation of neutrino-like interactions without muon or electron in the Gargamelle neutrino experiment. Nucl. Phys. B 73, 1–22 (1974).
Chatrchyan, S. et al. Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. Phys. Lett. B 716, 30–61 (2012).
Aad, G. et al. Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 716, 1–29 (2012).
Abe, F. et al. Observation of top quark production in \(\overline{{p}}{p}\) collisions with the Collider Detector at Fermilab. Phys. Rev. Lett. 74, 2626–2631 (1995).
Gruber, L. LHCb SciFi — upgrading LHCb with a scintillating fibre tracker. Nucl. Instrum. Methods Phys. Res. A 958, 162025 (2020).
Amerio, S. et al. Design, construction and tests of the ICARUS T600 detector. Nucl. Instrum. Methods Phys. Res. A. 527, 329–410 (2004).
Abi, B. et al. Deep underground Neutrino Experiment (DUNE), far detector technical design report, volume II DUNE physics. Preprint at arXiv:2002.03005 (2020).
Acciarri, R. et al. Design and construction of the MicroBooNE detector. J. Instrum. 12, P02017 (2017).
Blondel, A. et al. A fully-active fine-grained detector with three readout views. J. Instrum. 13, P02006–P02006 (2018).
Andreev, V. et al. A high-granularity plastic scintillator tile hadronic calorimeter with APD readout for a linear collider detector. Nucl. Instrum. Methods A 564, 144–154 (2006).
Kalman, R. E. A new approach to linear filtering and prediction problems. J. Basic Eng. 82, 35–45 (1960).
Gordon, N., Salmond, D. & Smith, A. Novel approach to nonlinear/non-gaussian bayesian state estimation. IEE Proc. F 140, 107–113(6) (1993).
Innocente, V., Maire, M. & Nagy, E. GEANE: average tracking and error propagation package. In Workshop on Detector and Event Simulation in High-energy Physics (MC ’91) 58–78 (CERN Program Library W5013-E, 1991).
Innocente, V. & Nagy, E. Trajectory fit in presence of dense materials. Nucl. Instrum. Method A 324, 297–306 (1993).
Cervera-Villanueva, A., Gomez-Cadenas, J. J. & Hernando, J. A. ’RecPack’ a reconstruction toolkit. Nucl. Instrum. Method A 534, 180–183 (2004).
Agostinelli, S. et al. Geant4—a simulation toolkit. Nucl. Instrum. Methods Phys. Res. A. 506, 250–303 (2003).
Allison, J. et al. Geant4 developments and applications. IEEE Trans. Nucl. Sci. 53, 270–278 (2006).
Allison, J. et al. Recent developments in Geant4. Nucl. Instrum. Methods Phys. Res. A 835, 186–225 (2016).
Ahdida, C. et al. New capabilities of the FLUKA multi-purpose code. Front. Phys. 9, 788253 (2022).
Battistoni, G. et al. Overview of the FLUKA code. Ann. Nucl. Energy 82, 10–18 (2015).
de Oliveira, L., Paganini, M. & Nachman, B. Learning particle physics by example: location-aware generative adversarial networks for physics synthesis. Comput. Software Big Sci. 1, 1–24 (2017).
Radovic, A. et al. Machine learning at the energy and intensity frontiers of particle physics. Nature 560, 41–48 (2018).
Guest, D., Cranmer, K. & Whiteson, D. Deep learning and its application to LHC physics. Ann. Rev. Nucl. Part. Sci. 68, 161–181 (2018).
Carleo, G. et al. Machine learning and the physical sciences. Rev. Mod. Phys. 91, 045002 (2019).
Albertsson, K. et al. Machine learning in high energy physics community white paper. J. Phys. Conf. Ser. 1085, 022008 (2018).
Bourilkov, D. Machine and deep learning applications in particle physics. Int. J. Mod. Phys. A 34, 1930019 (2020).
Baldi, P., Sadowski, P. & Whiteson, D. Searching for exotic particles in high-energy physics with deep learning. Nat. Commun. 5, 1–9 (2014).
Abi, B. et al. Neutrino interaction classification with a convolutional neural network in the DUNE far detector. Phys. Rev. D https://doi.org/10.1103/PhysRevD.102.092003 (2020).
Drielsma, F., Terao, K., Dominé, L. & Koh, D. H. Scalable, end-to-end, deep-learning-based data reconstruction chain for particle imaging detectors. Preprint at https://arxiv.org/abs/2102.01033 (2021).
Andrews, M., Paulini, M., Gleyzer, S. & Poczos, B. End-to-end physics event classification with cms open data: Applying image-based deep learning to detector data for the direct classification of collision events at the LHC. Comput. Software Big Sci. 4, 1–14 (2020).
Aurisano, A. et al. A convolutional neural network neutrino event classifier. J. Instrum. 11, P09001 (2016).
Nguyen, T. Q. et al. Topology classification with deep learning to improve real-time event selection at the LHC. Comput. Software Big Sci. 3, 1–14 (2019).
Bhattacharya, S., Nandi, S., Patra, S. K. & Sahoo, S. ’deep’ dive into b → c anomalies: standardized and future-proof model selection using self-normalizing neural networks. Preprint at arxiv https://arxiv.org/abs/2008.04316 (2020).
Abratenko, P. et al. Semantic segmentation with a sparse convolutional neural network for event reconstruction in MicroBooNE. Phys. Rev. D 103, 052012 (2021).
Alonso-Monsalve, S. et al. Graph neural network for 3D classification of ambiguities and optical crosstalk in scintillator-based neutrino detectors. Phys. Rev. D 103, 032005 (2021).
Cheong, S., Cukierman, A., Nachman, B., Safdari, M. & Schwartzman, A. Parametrizing the detector response with neural networks. J. Instrum. 15, P01030–P01030 (2020).
Qian, Z. et al. Vertex and energy reconstruction in juno with machine learning methods. Nucl. Instrum. Methods Phys. Res. A 1010, 165527 (2021).
Carloni, K., Kamp, N. W., Schneider, A. & Conrad, J. M. Convolutional neural networks for shower energy prediction in liquid argon time projection chambers. J. Instrum. 17, P02022 (2022).
Acciarri, R. et al. Convolutional neural networks applied to neutrino events in a liquid argon time projection chamber. J. Instrum. 12, P03011 (2017).
Gao, C., Yan, J., Zhou, S., Varshney, P. K. & Liu, H. Long short-term memory-based deep recurrent neural networks for target tracking. Inform. Sci. 502, 279–296 (2019).
Suo, Y., Chen, W., Claramunt, C. & Yang, S. A ship trajectory prediction framework based on a recurrent neural network. Sensorshttps://www.mdpi.com/1424-8220/20/18/5133 (2020).
Zyner, A., Worrall, S. & Nebot, E. Naturalistic driver intention and path prediction using recurrent neural networks. IEEE Trans. Intell. Transport. Syst. 21, 1584–1594 (2020).
DeZoort, G. et al. Charged particle tracking via edge-classifying interaction networks. Comput. Software Big Sci. 5, 1–13 (2021).
Yao, Y., Smal, I., Grigoriev, I., Akhmanova, A. & Meijering, E. Deep-learning method for data association in particle tracking. Bioinformatics 36, 4935–4941 (2020).
Tsaris, A. et al. The HEP.TrkX project: deep learning for particle tracking. J. Phys. Conference Series 1085, 042023 (2018).
Jordan, M. I. Chapter 25 - serial order: a parallel distributed processing approach. Adv. Psychol. 121, 471–495 (1997).
Jain, L. C. & Medsker, L. R.Recurrent Neural Networks: Design and Applications 1st edn (CRC Press, 1999).
Sherstinsky, A. Fundamentals of recurrent neural network (RNN) and long short-term memory (LSTM) network. Physica D 404, 132306 (2020).
Vaswani, A. et al. Attention is all you need. Preprint at arxiv https://arxiv.org/abs/1706.03762 (2017).
Schulte, R. W. et al. Density resolution of proton computed tomography. Med. Phys. 32, 1035–1046 (2005).
Poludniowski, G., Allinson, N. M. & Evans, P. M. Proton radiography and tomography with application to proton therapy. Br. J. Radiol. 88, 20150134 (2015).
Johnson, R. P. Review of medical radiography and tomography with proton beams. Rep. Prog. Phys. 81, 016701 (2018).
Pettersen, H. et al. Proton tracking in a high-granularity digital tracking calorimeter for proton ct purposes. Nucl. Instrum. Methods Phys. Res. A 860, 51–61 (2017).
Ester, M., Kriegel, H.-P., Sander, J. & Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proc. Second International Conference on Knowledge Discovery and Data Mining, KDD’96 226–231 (AAAI Press, 1996).
Kruskal, J. B. On the shortest spanning subtree of a graph and the traveling salesman problem. Proc. Am. Math. Soc. 7, 48–50 (1956).
Cho, K., van Merriënboer, B., Bahdanau, D. & Bengio, Y. On the properties of neural machine translation: Encoder–decoder approaches. In Proc. SSST-8, Eighth Workshop on Syntax, Semantics and Structure in Statistical Translation 103–111 (Association for Computational Linguistics, 2014).
He, K., Zhang, X., Ren, S. & Sun, J. Deep residual learning for image recognition. Preprint at arxiv http://arxiv.org/abs/1512.03385 (2015).
Rossum, Van, G & Drake, F. L. Python 3 Reference Manual (CreateSpace, 2009).
Paszke, A. et al. PyTorch: An imperative style, high-performance deep learning library. In Proc. 33rd International Conference on Neural Information Processing Systems 8024–8035 (Curran Associates, Inc., 2019).
Hastie, T., Tibshirani, R. & Friedman, J. in The Elements of Statistical Learning Ch. 10 (Springer, 2009). https://doi.org/10.1007/978-0-387-84858-7.
Gluckstern, R. Uncertainties in track momentum and direction, due to multiple scattering and measurement errors. Nucl. Instrum. Meth. 24, 381–389 (1963).
Sperduti, A. & Starita, A. Supervised neural networks for the classification of structures. IEEE Trans. Neural Netw. 8, 714–735 (1997).
Acknowledgements
Part of this work was supported by the SNF grant PCEFP2_203261, Switzerland.
Author information
Authors and Affiliations
Contributions
X.Z. and C.M. implemented the code needed for the simulation. X.Z. generated the datasets, and S.A.-M. preprocessed them. S.A.-M. designed, implemented, trained (when applicable), and tested the different algorithms. D.S., X.Z. and S.A.-M. performed the analysis. A.R. and D.S. supervised the entire process. All authors wrote, discussed and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks Dimitri Bourilkov and Nhan Tran for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Alonso-Monsalve, S., Sgalaberna, D., Zhao, X. et al. Artificial intelligence for improved fitting of trajectories of elementary particles in dense materials immersed in a magnetic field. Commun Phys 6, 119 (2023). https://doi.org/10.1038/s42005-023-01239-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-023-01239-4
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.