Introduction

The efficient detection of single photons is an important capability with wide-ranging uses1. Tremendous progress has been made in the development of devices that can attain high efficiency while also achieving minimal dark counts and jitter2,3,4,5,6,7,8. Recent work has also focused on imparting new functionality, such as photon-number resolution9,10,11. One functionality that is highly desirable for many applications is the ability to resolve the frequency/wavelength of the detected photon. For example, a high efficiency single photon detector with frequency resolution would be useful for hyperspectral imaging12, identification of remote galaxies13, and confocal microscopy14.

For detection of light in the classical limit, frequency resolution is straightforward; A typical device operating in this regime comprises a few detectors covering different but overlapping energy bands, so that the frequency can be inferred from the relative intensity reported by each detector element. For example, the human eye uses three types of photoreceptors to span the visible spectrum giving us the ability to distinguish on the order of 10 million colors15. However, since this is ultimately a statistical procedure relying on a signal with many photons, this scheme fails in the single photon limit, and an entirely new approach to frequency resolution is required.

The simplest approach for single photon frequency resolution is to spatially guide the photon to different single photon detectors based on its frequency16, but this becomes more challenging as the number of frequency bins increases. These detectors have achieved frequency resolution δω ≈ 2 meV over bandwidths Δω ≈ 10 meV, timing jitter less than 50 ps, dark count rates less than 10 Hz, at count rates that could attain 100 MHz. For such platforms, the overall detection efficiency is about 19%. Further progress has recently been made by using compact on-chip wavelength dispersion with signal timing information in a meandering superconducting nanowire detector17 where δω ≈ 2 meV over bandwidths Δω ≈ 3 eV, timing jitter of 41 ps, dark count rates less than 30 Hz, at count rates that could attain 10 MHz. Overall detection efficiency is less than 0.3%. Other approaches have used tunable electromagnetically induced transmission to perform single photon spectrometry18.

An alternative approach is for one detector to be directly sensitive to the photon frequency. For example, transition edge sensors are sensitive to the total energy of an incoming photon pulse9,19,20, a phenomenon that can be used to extract the photon energy provided there is only one photon in the pulse. Such systems have achieved detection efficiencies greater than 95%, and could operate at 1 MHz, with an energy resolution ≈0.2 eV. Recent work21 has improved the energy resolution to 67 meV, at the cost of a lower detection efficiency of 60%.

While overcoming a number of engineering challenges could further improve the performance of existing energy-resolving detectors, the above experimental results illustrate the difficulty in achieving high performance across detection metrics. An interesting scientific question is whether it is possible for a detector architecture to simultaneously achieve high performance in all metrics, and if not, what tradeoffs exist between metrics.

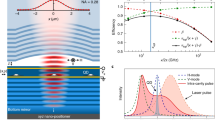
In this work we propose a different approach for a photodetector, schematically shown in Fig. 1, that is capable of accurately determining the frequency of a single photon while also maintaining high efficiency and low jitter. Critical to achieving this performance is the engineered cooperative coherent behavior of detector elements. (We use the term cooperative to refer to the simultaneous interaction of subwavelength detector elements with a common electromagnetic field. Such a situation can lead to superabsorption, but this is not the effect that we will take advantage of in this work).We discuss the requirements on the general architecture, the resulting performance limits and tradeoffs, and propose a physical realization based on nanoscale materials.

Fig. 1: Illustration of the proposed frequency-resolving single photon detector.
figure 1

A photon of wavelength λ is guided into a single mode waveguide. The subwavelength detector comprises groups of elements, represented by the colored squares, interacting with the photon field and capable of generating a signal when a photon is absorbed (green trace). The elements are coupled not only to the photon but to each other via the field mode, resulting in a collective absorption process.

Full size image

Results and discussion

Design

Figure 2 shows a schematic of our photodetector design and a corresponding energy level diagram. A single photon of frequency ω propagates in a waveguide that supports a single mode for frequencies around ω0. The photon is incident on a detector composed of a collection of sub-wavelength objects arranged hierarchically. The system is divided into N subsystems (N = 4 hexagons in Fig. 2); the ith subsystem is made up of ni elements that interact with the photon and an amplifier that produces a signal if one of the subsystem elements absorbs a photon. Each element (represented by colored squares in Fig. 2) couples to the photon field with strength γ. Absorption of the photon excites the element from the ground state 0 to an excited state 1im, where m indexes the elements in subsystem i. The excitation energies ωim of the elements in subsystem i (which are rendered in the same color in Fig. 2) are centered on a frequency ωi associated with the subsystem; the mth element’s detuning from this frequency will be designated as δim. We will assume in all cases that the frequencies ωi are evenly spaced over the desired range of frequency resolution Ω. It is important to note that the entire range Ω must lie within the single-mode regime of the waveguide; i.e., the width of Ω must be less than the cutoff frequency of the waveguide. These excited states undergo incoherent decay at rate Γ2 to long-lived states Cim, which once populated remain so indefinitely. These states are monitored and amplified by an output channel (indicated by hexagons in Fig. 2) at rate χ into a classical signal indicating that the photon was absorbed by system i. Thus, the subsystems correspond to frequency bins into which the photon is sorted. For detection of single monochromatic photons, the absorption and incoherent rates of a single subsystem can be optimized to yield ideal detection22.

Fig. 2: Internal architecture of the photodetector.
figure 2

a Illustration of the detector structure for the case of N = 4. A photon (blue wavepacket) propagating from top to bottom is guided into a single mode waveguide. The detector comprises absorbing elements (squares) and amplifiers (hexagons), which are grouped into subsystems containing multiple absorbing elements that are (near-)degenerate with subsystem-specific transition frequency. The absorbing elements in all subsystems interact with the photon (as indicated by the dashed lines), which is ultimately absorbed by a single element (filled square), modulating the signal in the associated amplifier (filled hexagon). b Energy diagram for the detector. The elements are divided into groups characterized by near-degenerate transitions of different energies. Optical excitation is from the ground state 0 to the excited state 1, followed by incoherent decay to dark states C monitored by amplifiers; each dark state corresponding to elements of different transition frequency are associated with distinct amplifiers allowing for discrimination of the incoming photon frequency. Dots between lines marking energy states are used to indicate that many more states are present than are drawn explicitly. Here Γ is the incoherent transition rate, γ is the optical transition rate, and χ is the measurement rate.

Full size image

Due to the sub-wavelength size of the system, it will exhibit cooperativity23,24—the interaction of all the elements with the incident photon is collective (through the field-mediated inter-element interactions). This type of detector is thus best described as a quantum detector whereby the photon field, the absorption process, and the measurement process are treated as part of one quantum system22. This can be done using techniques from quantum optics and quantum information as we now discuss.

Formalism

To calculate the properties of the detector we employ a recently developed formalism for modeling quantum photodetection of arbitrary light states22.

The matter-field system that composes the detector is treated as an open quantum system whose density matrix \({\hat{\rho }}_{{{{{{{{\rm{TOT}}}}}}}}}\) evolves according to a quantum master equation. As shown in ref. 25, for a monochromatic, single-mode wavepacket containing n-photons with temporal profile ε(t) and frequency ω0, the field degrees of freedom can be eliminated and the matter system density matrix \(\hat{\rho }(t)={{{{{{{{\rm{Tr}}}}}}}}}_{{{{{{{{\rm{LIGHT}}}}}}}}}[{\hat{\rho }}_{{{{{{{{\rm{TOT}}}}}}}}}(t)]\) can be evolved according to a hierarchy of equations evolving auxiliary density matrices depending on the initial field state. We shall confine ourselves to the single photon case with a stable initial state \(\hat{\rho }({t}_{0})\), in which case these can be written using a single auxiliary density matrix \(\hat{\varrho }\) as26

$$\dot{\hat{\rho }}(t) = {{{{{{{{\mathcal{V}}}}}}}}}_{{{{{{{{\rm{M}}}}}}}}}(\hat{\rho }(t))+\varepsilon (t){{{{{{{{\rm{e}}}}}}}}}^{-i{\omega }_{0}t}[\hat{\varrho }(t),{\hat{L}}^{{{{\dagger}}} }]\\ + {\varepsilon }^{* }(t){{{{{{{{\rm{e}}}}}}}}}^{i\omega t}[\hat{L},\hat{\varrho }^{{{{\dagger}}} }(t)]+{{{{{{{{\mathcal{V}}}}}}}}}_{{{{{{{{\rm{L-M,Coop}}}}}}}}}(\hat{\rho }(t))\\ \dot{\hat{\varrho }}(t) = {{{{{{{{\mathcal{V}}}}}}}}}_{{{{{{{{\rm{M}}}}}}}}}(\hat{\rho }(t))+{\varepsilon }^{* }(t){{{{{{{{\rm{e}}}}}}}}}^{i{\omega }_{0}t}[\hat{L},\hat{\rho }({t}_{0})]\\ + {{{{{{{{\mathcal{V}}}}}}}}}_{{{{{{{{\rm{L-M,Coop}}}}}}}}}(\hat{\varrho }(t))$$
(1)

where

$${{{{{{{{\mathcal{V}}}}}}}}}_{{{{{{{{\rm{M}}}}}}}}}(\hat{\rho }(t)) = -i[\hat{H},\hat{\rho }(t)] + \mathop{\sum }\limits_{im}^{{{{{{{{\rm{BATHS}}}}}}}}}{{{{{{{\mathcal{D}}}}}}}}[{\hat{Y}}_{im}]\hat{\rho }(t)\\ + \mathop{\sum }\limits_{i}^{{{{{{{{\rm{AMPS}}}}}}}}}{{{{{{{\mathcal{D}}}}}}}}[{(2{k}_{i})}^{1/2}{\hat{X}}_{i}]\hat{\rho }(t)\\ {{{{{{{{\mathcal{V}}}}}}}}}_{{{{{{{{\rm{L-M,Coop}}}}}}}}}(\hat{\rho }(t)) = \, {{{{{{{\mathcal{D}}}}}}}}[\hat{L}]\hat{\rho }(t).$$
(2)

Here \({{{{{{{\mathcal{D}}}}}}}}\) represents the Lindblad superoperator \({{{{{{{\mathcal{D}}}}}}}}[\hat{O}]\hat{\rho }=\hat{O}\hat{\rho }\hat{O}^{{{{\dagger}}} }-\frac{1}{2}\{\hat{O}^{{{{\dagger}}} }\hat{O},\hat{\rho }\}\) and we have assumed ℏ = 1. The matter system is thus governed by an internal Hamiltonian \(\hat{H}\), its coupling to the optical field captured by the operator \(\hat{L}\), its coupling to external reservoir(s) (BATHS) captured by operator(s) \({\hat{Y}}_{im}\), and the dynamics induced by the measurement/output channels (AMPS) which couple into the system with rate(s) 2ki and operator(s) \({\hat{X}}_{i}\). We note that the cooperative interactions are captured by the term \({{{{{{{{\mathcal{V}}}}}}}}}_{{{{{{{{\rm{L-M,Coop}}}}}}}}}\) and are furnished by the \(\hat{L}\) operator via the Lindbladian term; \(\hat{L}^{{{{\dagger}}} }\hat{L}\) contains, in addition to diagonal matrix elements corresponding to single system element spontaneous emission, off-diagonal matrix elements that couple system elements. As shown previously22,27, cooperative interactions can play a crucial role in single photon detection and must be accounted for in optimizing detector parameters. In particular, the distributed absorption over detector elements allows for longer overall collection and measurement processes and sharply defined detection bandwidths that are crucial to high performance frequency resolution. For our design these operators are:

$$\hat{H} = \mathop{\sum }\limits_{i}^{N}\mathop{\sum }\limits_{m}^{{n}_{i}}\left({\omega }_{i}+{\delta }_{im}\right)\left\vert {1}_{im}\right\rangle \left\langle {1}_{im}\right\vert \\ \hat{L} = \mathop{\sum }\limits_{i}^{N}\mathop{\sum }\limits_{m}^{{n}_{i}}\gamma \left\vert 0\right\rangle \left\langle {1}_{im}\right\vert \\ {\hat{Y}}_{im}= {{\Gamma }}\left\vert {C}_{im}\right\rangle \left\langle {1}_{im}\right\vert \\ {\hat{X}}_{i} = \mathop{\sum }\limits_{m}^{{n}_{i}}\chi \left\vert {C}_{im}\right\rangle \left\langle {C}_{im}\right\vert .$$
(3)

The ω quantities have units of energy, while γ, Γ, and χ have units of square root energy and are associated with rates. The initial state of the detector, \({\hat{\rho }}_{{{{{{{{\rm{M}}}}}}}}}({t}_{0})\), is assumed to be the ground state of all absorbing elements and the photon wavepacket is assumed to contain a single photon (n = 1). We note that practically there will be element-wise variations in parameters as well as additional processes present due to impurities, disorder, and other non-idealities. However, for the sake of numerical tractability and clarity we restrict ourselves to this simplified model. We also neglect spatial variations of the photon mode in the waveguide; the optimization approach described below could include this detail. In this model we omit the decay from the C state to the ground state as it was previously shown that such a system can be engineered for high performance monochromatic single photon detection.

In general one can write measurement outcomes Π(t) as

$${{\Pi }}(t)={{{{{{{\rm{Tr}}}}}}}}\left[{{{{{{{\mathcal{K}}}}}}}}(t,{t}_{0}){\hat{\rho }}_{{{{{{{{\rm{TOT}}}}}}}}}({t}_{0})\right],$$
(4)

where \({{{{{{{\mathcal{K}}}}}}}}\) is an operator that accounts for both the detector state evolution and measurement output collection and processing, which can be used to determine detector performance22. In cases such as the present one, where the C states are stable (there is no population transfer to other states), this takes a simple form and we can write the probability that a single incident photon of frequency ω0 registers as a hit in output channel i at time t as11,22

$${{{\Pi }}}_{i}(t;{\varepsilon }_{{\omega }_{0}})={{{{{{{\rm{Tr}}}}}}}}\left[{\hat{x}}_{i}\hat{\rho }(t;{\varepsilon }_{{\omega }_{0}})\right]$$
(5)

where \({\hat{x}}_{i}\) is a projection matrix such that \(\chi {\hat{x}}_{i}={\hat{X}}_{i}\).

From this formalism we can determine a number of key metrics, of which the following are presently of interest:

Efficiency

Efficiency is the probability of having detected the photon after it has passed the detector; i.e., at t → ∞. For a given channel this probability is directly given by \({{{\Pi }}}_{i}(\infty ;{\varepsilon }_{{\omega }_{0}})\), for which we use the simplified notation \({{{\Pi }}}_{i}({\varepsilon }_{{\omega }_{0}})\) while for the overall efficiency we write \(P({\varepsilon }_{{\omega }_{0}})={\sum }_{i}{{{\Pi }}}_{i}({\varepsilon }_{{\omega }_{0}})\). In the present work we assume ε(t) to be infinitely broad, corresponding to a delta function in frequency space at ω0. We have previously shown that this is a good approximation even for pulses that are short in a practical sense26. In this case these quantities become functions of the frequency ω0 only. Furthermore, since \({\hat{Y}}_{im}{\hat{Y}}_{jk}={\hat{Y}}_{im}\hat{L}={\hat{Y}}_{im}{\hat{X}}_{i}=0\,\forall i,j,k,m\)11, we obtain from Eq. (5):

$${\Pi}_{i}(\omega_0) = \mathop{\sum}\limits_{m=1}^{n_i}|{\langle{C_{im}}|{\hat{Y}}_{im}\left[i(\omega_0-{\hat{H}}-{\hat{H}}_D)\right]^{-1} {\hat{L}}^{{{\dagger}}}|{0}\rangle}|^{2} \\ {{\hat{H}}_D} = \,i{\frac{1}{2}}\left(\mathop{\sum}\limits_{im}^{{{{{\rm{BATHS}}}}}}{\hat{Y}}_{im}\,{{\,\!}^{{{\dagger}}}{\hat{Y}}_{im}}+{\hat{L}}{\,\!}^{{{\dagger}}}{\hat{L}}\right)$$
(6)

as the long-time or steady-state probability that output channel i registers the photon.

Jitter

Since \(\dot{{{\Pi }}}(t;{\varepsilon }_{{\omega }_{0}})\) gives a distribution of detection times, the jitter for channel i is

$${\sigma }_{i}({\varepsilon }_{{\omega }_{0}})=\sqrt{\int\nolimits_{{t}_{0}}^{\infty }dt\,{t}^{2}\frac{{\dot{{{\Pi }}}}_{i}(t;{\varepsilon }_{{\omega }_{0}})}{{{{\Pi }}}_{i}({\varepsilon }_{{\omega }_{0}})}-{\left(\int\nolimits_{{t}_{0}}^{\infty }dtt\frac{{\dot{{{\Pi }}}}_{i}(t;{\varepsilon }_{{\omega }_{0}})}{{{{\Pi }}}_{i}({\varepsilon }_{{\omega }_{0}})}\right)}^{2}}$$
(7)

with the total jitter obtainable by replacing Πi in the above with P. Since the overall jitter strongly depends on the pulse characteristics, we define σSYS as the total jitter minus the temporal width of the pulse

$${\sigma }_{{{{{{{{\rm{SYS}}}}}}}}}({\varepsilon }_{{\omega }_{0}})=\sqrt{{(\sigma ({\varepsilon }_{{\omega }_{0}}))}^{2}-{\left({\sigma }_{0}\right)}^{2}}$$
(8)

with

$${\sigma }_{0}=\sqrt{\int\nolimits_{{t}_{0}}^{\infty }dt\,{t}^{2}{\left\vert \varepsilon (t)\right\vert }^{2}-{\left(\int\nolimits_{{t}_{0}}^{\infty }dtt{\left\vert \varepsilon (t)\right\vert }^{2}\right)}^{2}}.$$
(9)

The regime of infinitely broad ε(t) under consideration corresponds to the limit σ0 → ∞, in which \(\sigma ({\varepsilon }_{{\omega }_{0}})\) goes to infinity as well. However, \({\sigma }_{{{{{{{{\rm{SYS}}}}}}}}}({\varepsilon }_{{\omega }_{0}})\) remains finite and converges to a fixed value which can be obtained numerically; we will thus report the jitter defined as

$${\sigma }_{{{{{{{{\rm{SYS}}}}}}}}}({\omega }_{0})=\mathop{\lim }\limits_{{\sigma }_{0}\to \infty }\sqrt{{\left(\sigma ({\varepsilon }_{{\omega }_{0}})\right)}^{2}-{\left({\sigma }_{0}\right)}^{2}}.$$
(10)

Frequency resolution

The Πi furnish a set of probabilities that an incident photon of frequency ω0 will be recorded as photons of frequency ωi. We can thus write the expected measurement frequency and standard deviation as

$${\omega }_{\mu }({\omega }_{0}) = \mathop{\sum}\limits_{i}{\omega }_{i}{{{\Pi }}}_{i}({\omega }_{0})/P({\omega }_{0})\\ {\omega }_{\varsigma }({\omega }_{0}) = \mathop{\sum}\limits_{i}{({\omega }_{i}-{\omega }_{\mu })}^{2}{{{\Pi }}}_{i}({\omega }_{0})/P({\omega }_{0}).$$
(11)

We will use the latter to define frequency resolution.

Theoretical performance

Given the above design and model, we now optimize the parameters in the model (Eq. (3)) to achieve optimal tradeoff between efficiency, frequency resolution, and jitter. Both the parameters and device metrics can be defined in terms of the width of Ω, which sets a frequency scale for the model. For simplicity we will set Ω to be the range (1.9, 2.9) eV, covering the bulk of the visible spectrum. For a given set of parameters N, γ, and Γ, we take ni—the number of elements in subsystem i—to be optimization parameters. These must be optimized for performance due to their collective interaction with the field. While for some systems analytical expressions for this optimization are available22, in the present case it must be done numerically. In what follows we will use the set of ni such that \(\mathop{\max }\nolimits_{-{{\Omega }}/2 < {\omega }_{0} < {{\Omega }}/2}[1-P({\omega }_{0})]\) is minimized, i.e. the worst case inefficiency over the detector bandwidth is minimized. This minimization was performed using the L-BFGS-B algorithm28. We note that under the described conditions the results are independent of the parameter χ as discussed in previous work26.

The results are shown in Fig. 3a, b for N = 12, with the ωi equally spaced from 1.9 eV to 2.9 eV (the results can be extended to larger N but become computationally more demanding. However we note that the efficiency and jitter are essentially independent of N, so that the main role of N is to impact the frequency resolution). Figure 3a shows that the optimized ni (scaled by γ2/Ω to remove the dependence on parameters γ and Ω) for each subsystem follow a non-uniform distribution across the detection range. This distribution with peaks at the end of the range is reminescent of the density of states in quasi-one-dimensional systems which was previously shown to ensure optimal efficiency over a broad frequency range in non-frequency-resolving detectors11. As shown in Fig. 3b the efficiency of detecting the photon is at least 99% over the target range, with relatively narrow distributions; the ως for the three sample frequencies are 133 meV, 145 meV, and 112 meV.

Fig. 3: Performance of photodetector.
figure 3

a, b Implementation for N = 12 frequency bins when all the absorbers are monitored. Here the incoherent transition rate Γ2 = 0.085eV. c, d. N = 12 system where end subsystems that do not decay to monitored dark states are added. Here the incoherent transition rate Γ2 = 0.082eV. e, f A version of the design of c, d where the incoherent decay rate Γ2 is reduced by half, resulting in higher frequency resolution but reduced overall efficiency. For each configuration, photons of three frequencies ω0 are considered, denoted by different colors and marked by dashed lines. In b, d, f the colored bars indicate the probability of a photon of that frequency ω0 being detected at each bin, the characteristic frequencies of which are marked by the x-axis ticks.

Full size image

One non-ideal aspect of Fig. 3a is the excess absorption at the ends, especially for frequencies outside the desired spectral range. For example, the blue photon with frequency outside the detection range still gives an apparent peak in one of the detection channels, with a 57% probability of being detected at ωμ = 2.872 eV. This arises from the large ni necessary at the ends to obtain uniformly high efficiency11. To combat this effect we include elements uncoupled to decay channels and amplifiers at 1.81 eV and 2.99 eV. This modulates the field coupling of the overall detector while substantially reducing the absorption outside the desired band (Fig. 3c, d) and removes the need for large ni in highest and lowest frequency bins. As a result, the purple photon no longer appears with a high probability in detection bins, being detected only 10% of the time. This effect highlights the cooperative nature of the detection; absorptive elements outside the frequency range of desired detection can be exploited to shape the detection frequency window.

The system can also be engineered to improve the frequency resolution. In Fig. 3e, f we show a system with an incoherent decay rate Γ2 reduced by half which leads to a narrower distribution of detection probabilities around the target bin. This arises because the slower decay rate leads to a reduced broadening of the absorption spectrum. However, this reduced broadening prevents full coverage of the detection window, leading to a reduced overall detection efficiency. Larger N can reduce the frequency spacing of subsystems, allowing more complete coverage of the frequency range Ω, but at the cost of increased device complexity. Thus, for this particular architecture there appears to be a trade-off between efficiency and frequency resolution for a given N.

An alternative approach to improve frequency resolution is to introduce dispersion in the transition energies of subsystem elements. We will take this dispersion to be flat over a range Δω, such that δim ∈ ( − Δω/2, Δω/2). In Fig. 4a–d we show results for the case where the subsystem elements were given transition energies spread over Δω = 88.6 meV—slightly less than the bin frequency spacing—and Γ was optimized to ensure ≥99% efficiency over the specified frequency range.

Fig. 4: Simultaneous high performance across metrics.
figure 4

a, b Performance of the system with the absorption of each subsystem elements uniformly spread over a range of 88.6meV, reflected in the width of the grey bars in a. In b the response for photons of three differencies ω0 is shown, indicating very narrow frequency resolution while maintaining high efficiency. c σSYS and ως that result from the slowest Γ2 that maintains greater than 99% efficiency for a given Δωi. d σSYS plotted against ως from b on a log/log scale.

Full size image

The result is improved frequency resolution as evidenced by the higher central peaks in each bin. The impact of the absorption spread on frequency resolution is plotted in Fig. 4c, showing how it is minimized with increasing Δω until it reaches the bin frequency spacing. This result was obtained by choosing Γ for each Δω to be as slow as possible while achieving efficiency ≥99%.

Thus, the tradeoff between efficiency and resolution has been essentially eliminated. In addition this design also gives low jitter. Indeed, Fig. 4c shows the relationship between frequency resolution and jitter as a function of the bin width. For small bin widths, the jitter is as low as 50 fs with a frequency resolution of 115 meV. As the bin width increases, the jitter remains low as the frequency resolution improves and starts to increase as further improvements in frequency resolution are obtained for larger bin widths. This constitutes a trade-off between jitter and frequency resolution, as shown in Fig. 4d. In practice this is not particularly onerous since a 35 meV frequency resolution still only has 500 fs of jitter. The tradeoff arises because on the one hand Γ determines the jitter (with higher values of Γ giving lower jitter), while small values of Γ are required to reduce broadening and maximize the frequency resolution. We also note that a non-uniform distribution of states over the bin energy (e.g. gaussian) will generally worsen the frequency resolution, as it is akin to improperly assigning elements near the edges of one bin to the adjacent one. Additionally, depending on the distribution, it may increase the corrugations in the overal efficiency. The later could be compensated for by increasing the incoherent rate Γ, though at the expense of some additional jitter.

In order to highlight the importance of cooperativity on detector performance, first consider the case of fully independent detectors. Previously26, we showed that an engineered two-level system could function as a perfect narrowband single photon detector, and therefore it should be possible to realize a high performance frequency-resolving detector by sequentially organizing such detectors in a waveguide and separating them by more than a wavelength. The challenge in this case is the large number of detectors needed to cover the detection bandwidth of interest; indeed, as discussed below, the absorbtion width for two-level systems is on the order of μeV so a large number of detectors would be needed to achieve uniform coverage over a bandwidth of interest. For example, a 1 eV bandwidth would require one million detectors which would occupy at least 50 cm for light in the visible range. Cooperative effects allow us to engineer the light-matter interaction in the detector in order to circumvent these limitations. This is possible because even non-resonant elements influence the interaction of the resonant elements with the field.

To further illustrate the role of cooperativity, we also performed simulations for the case where the absorbing elements for the different frequency bins are confined to different planes, with the frequency planes separated by more than the photon wavelength (Fig. 5a–d). Thus, the system consists of independently absorbing planes, within which cooperative effects exist. The subsystems are taken to interact with the photon in sequence, starting from the lowest frequency bin; the photon interacts with a given subsystem only if it is not detected by the prior subsystems. If the subsystems from Fig. 4 are used then the frequency resolution is nearly as good, but the overall efficiency away from the center frequency of the bins suffers, falling below 90% at the midpoints between bins (Fig. 5b). On the other hand, if Γ2 is increased to satisfy the ≥99% efficiency condition over the whole frequency range, then frequency resolution is significantly compromised (Fig. 5d). In addition, the absorption strength niγ2 of each bin must be higher. It might be possible to re-engineer the density of states within each independent bin to re-establish high performance, but this would essentially rely on cooperative effects. Thus, cooperativity provides clear advantage over independently interacting systems.

Fig. 5: Performance of photodetectors without cooperativity.
figure 5

Performance of detectors comprising independent subsystems interacting with the photon in sequence, starting from the lowest frequency bin. Under these conditions the nonabsorbing lowest and highest frequency subsystems have no impact on the detector performance and are omitted. a, b The subsystem compositions are the same as the optimal detector when cooperativity is included. c, d The subsystems are calibrated to satisfy the condition of efficiency ≥99% over the detector frequency range. In b, d the colored bars indicate the probability of a photon of that frequency ω0 being detected at each bin, the characteristic frequencies of which are marked by the x-axis ticks.

Full size image

Ultimately, this analysis reveals that an appropriately designed and constructed detector can achieve high efficiency, low jitter, and arbitrarily fine frequency resolution, with tradeoffs appearing only at performance extrema. The main challenge that remains is to choose materials and methods allowing for sufficiently precise fabrication for the desired performance regime.

Physical realization

In this section, we discuss how the optimal design of Fig. 4 can be physically realized. We consider components confined in a single-mode waveguide like the one in Fig. 1 with detector elements arranged in multiple layers (Fig. 6a–d). For the basic components, we focus on carbon nanotubes (CNTs) functionalized with quantum dots (QDs), since this approach has been experimentally shown to give ultrahigh responsivity at room temperature29,30 for classical light fields. In addition, approaches have been demonstrated for controlling the density of QDs around the CNTs31 and for integrating CNTs functionalized with different QDs in the same electronic platform32. Furthermore, detailed non-equilibrium quantum transport simulations have been employed for in-depth simulations of functionalized CNT devices for detection of monochromatic single photons29,33,34, and their connection to the formalism employed here has been presented26.

Fig. 6: Physical realization of photodetector.
figure 6

a The device as situated in the waveguide. The teal region is the active area of the device containing absorbing and measuring components. The dark grey region represents a mirror at the end of the waveguide. The vertical plane with a dotted outline shows the cross section taken for depiction of the two device configurations shown in b, c. In these the quantum dots (QDs) are shown as colored squares, with the carbon nanotube (CNT) measurement channel cross section shown as a black circle. λ is the wavelength of the incoming photon. b The most direct realization of the design. The incoherent process in this case (depicted in the inset with rate Γ) is the separation of the QD exciton, depicted as a solid gray circle for the electron and a dotted line circle for the hole, with a carrier (in this case the hole) migrating into the CNT. The field due the remaining carrier alters the conductivity of the CNT (indicated by the black filling), which is detected as an absorption event. c A transduction process comprising multiple steps. The first part of the incoherent decay is the separation of the exciton (rate Γ), followed by migration to adjacent quantum dots (rate \({{\Gamma }}^{\prime}\)). A field near the carbon nanotube drives the carriers apart, with one arriving at a dot adjacent to the tube, where it modulates the CNT conductivity. d A more detailed representation of the CNTs with the QD functionalization is shown.

Full size image

In the implementation considered here, the photon is absorbed by a QD, with the QD exciton state serving as the excited state of the two-level system in our model. We assume that the QD shape is nearly spherical so that the sensitivity to the photon polarization is minimal, or that the QDs are oriented to maximize the absorption for the propagating mode in the waveguide. The incoherent decay pathway is furnished by exciton dissociation, with either the free electron or free hole being transferred to the CNT and conducted away, while the remaining charge modulates the electronic transport in the CNT. Frequency resolution is enabled by having multiple CNT devices in the waveguide, each functionalized with QDs of different exciton absorption energies. The CNT devices are stacked in the waveguide to improve absorption and frequency coverage. Above and below these planes, unmonitored layers of QDs are added to control the absorption outside of the range of interest. We note that in this case, depicted in Fig. 6c, it is necessary for QDs to be adjacent to CNTs, and for QDs adjacent to different CNTs to be electronically uncoupled, preventing carrier transfer to other QDs. In the case of the unmonitored layers, all QDs must be uncoupled. The degree of coupling—or lack thereof—can be controlled by tuning the distance and level of contact between the quantum dots35.

The use of QD exciton states constrains the range Ω over which detection can occur: in order to behave properly as two level systems, the exciton absorption energy corresponding to the lowest energy bin must be separated from the continuum absorption edge of the dot by more than Ω at least. This difference is constrained by the binding energy of the exciton, which may in some cases be as high as 1eV, but can be lower depending on the QD size. We will consider Ω = 0.4 eV in the following for frequencies between 2.2 eV and 2.6 eV which is typical of QD systems such as CdSe36. In this case the QD diameter varies between 3–5 nm.

A waveguide cross-section for this frequency band is about 400 nm × 200 nm in size; assuming that the CNT spans the whole waveguide with the electrodes outside of the waveguide, the full 200 nm of the CNT length is available for functionalization. For the average QD diameter of 4nm, each CNT would have 200 QDs if the QDs are densily packed around the CNT. Each CNT device would occupy about 8 nm × 8 nm in cross section, implying that 50 devices could fit across the length of the waveguide, and that a layer of functionalized CNTs would be about 9-10nm thick including spacing for isolation and contain about 10000 QDs. If each layer is assigned to a specific wavelength, then all the CNTs in the layer can be connected to the same source/drain electrodes, which can be 10 nm in thickness with 15 nm pitch. The condition that the stack thickness fall well within a wavelength (<1/3λ) implies that N = 8 is roughly the number of frequency bins that the detector could support, assuming that two unmonitored layers are added above and below.

In this case, each subsystem requires a narrow absorption peak of width ωi = Ω/8 = 50 meV. To determine if this arrangement can achieve high performance, we need to estimate the quantity niγ2/Ω and compare with the values ni ≈ 0.05 in the top panel of Fig. 4a. The value of γ for QDs in the waveguide is on the order of the free-space spontaneous emission11; QD radiative lifetimes have been measured to be as short as 200ps37, giving γ2 = 3.2 μeV. Thus, for the above design we obtain niγ2/Ω = 0.08, suggesting that the basic design could attain high performance.

One limitation of the basic design is the need for each QD to be in contact with a CNT. In addition to limiting the number of QDs due to inefficient packing, this also demands many CNT channels and precise fabrication. This may be ameloriated by introducing additional QDs that are not in direct contact with the CNT, but that can transfer their excitation to another QD adjacent to the CNT. In this scenario, shown in Fig. 6c, the carrier is blocked from migrating into the CNT channel, and multiple shell of QDs may be associated with a single nanotube; a layer of the system will take the form of layers of QDs with CNTs running through the center. A layer about five dots thick (~20 nm) would then contain around 3ni dots (assuming ~ 20% tighter packing than the first case); partitioning this layer into three subsystems would require four layers, or 90 nm including spacing between subsystem layers. In this case we could take Ω = 0.6 eV and N = 12, with the unmonitored bins above and below requiring around 50 nm, and remain under our depth budget. Thus the more flexible transduction process allows greater QD density—and ultimately greater frequency range—as well as simpler fabrication. This comes, however, at the cost of increased jitter due to a varying number of additional steps associated with the carrier migration.

Fabrication of the proposed design is challenging, but several fundamental demonstrations make it plausible. As mentioned above, photodetectors with QD-functionalized CNTs have been demonstrated. In addition, waveguide-integrated CNT photodetectors have been realized38 including with dense arrays of CNTs in the waveguide39. In terms of addressing individual devices at high density, nanometer size low-resistance contacts to CNTs have been demonstrated40, while e-beam lithography has been extended to 10 nm pitch41. Other approaches could also be employed to control the absorption frequency of each element, such as putting molecules or atoms in electric field gradients.

Conclusion

We propose a design for a single photon detector capable of intrinsically resolving frequency while maintaining high efficiency and low jitter. The challenge of doing so is distinctly greater than for generic light, since averages over many photons are not available. Our theoretical analysis clarifies the technical challenges that must be overcome in order to realize such a device, as well as fundamental limitations, and highlights the critical role of cooperativity in achieving optimal performance. As a specific example, we find that frequency resolution of tens of meV over a 1 eV bandwidth is possible while achieving near perfect detection efficiency and jitter of hundreds of femtoseconds. The required design is shown to require a non-trivial distribution of absorbing elements in each frequency bin, reminescent of the density of states in quasi-one-dimensional systems. Our design dictates the need for precision nanoscale engineering capabilities in order to exploit cooperativity and ensure consistent and reliable frequency discrimination in addition to efficient detection. While the precision needed to realize our detector design is demanding, it is not out of reach of modern nanoscale engineering technologies. Moreover, our design represents a benchmark to aim for, and evidence that simultaneous optimization of efficiency, jitter and frequency resolution is possible in photodetection. It also demonstrates the utility of quantum optics and quantum information formalisms to understand the ultimate limits of photodetection, and opens up a path for studying even more complex detectors, such as those that could simultaneously perform photon number resolution and frequency resolution.