Abstract
Optomechanics deals with the control and applications of mechanical effects of light that stems from the redistribution of photon momenta in light scattering. As an example, light-induced levitation of an infinitesimally small dipolar particle is expected in front of epsilon-near-zero (ENZ) metamaterials. However, a theoretical understanding of these effects on single-material and multi-material larger particles is still lacking. Here, we investigate, analytically and numerically, optical forces on polarizable particles with size ranging from 20 nm to a 1 μm in proximity of ENZ metamaterials. We look at the general features of the repulsive-attractive optomechanics from the nano to the microscale exploiting different theoretical methods (dipole approximation, finite elements calculations, transition (T-)matrix). We discuss the role of realistic layered materials, as our ENZ substrate, on optical forces and analyze the influence of composition and shape by studying a range of complex particles (dielectric, core-shell, plasmonic ellipsoids). Physical insights into the results are discussed and future research directions are forecasted. Our results provide possibilities in exploiting engineered materials and surfaces for the manipulation and tailoring of light-induced forces in optomechanics.
Similar content being viewed by others
Introduction
Recent developments in the field of metamaterials and metasurfaces have provided useful platforms for manipulating and tailoring light–matter interaction with numerous applications ranging from cloaking1,2, enhanced spontaneous emission3, sensing4, signal processing and information handling5,6, and nonreciprocity7, just to name a few. Among various classes of metamaterials, the epsilon-near-zero (ENZ) and near-zero-index (NZI) structures have attracted increasing attention due to their unique features in light–matter interaction8,9,10,11. In such structures, relative permittivity and/or relative permeability attain values near zero, thus making the effective refractive index of the structure near zero. Consequently, at the operating frequency, the wavelength in these media is “stretched”, making the phase of the signal approximately uniform across this structure12. As a result, the waves exhibit “static-like” spatial distributions, while temporally they are dynamic. This has led to numerous exciting wave phenomena, with several potential applications8,9,10,11,13. One such feature is the possibility of levitation of electrically polarized nanoparticles in the vicinity of ENZ substrates14. In our earlier work, we theoretically showed that an infinitesimally small nanoparticle, when electrically polarized at a given frequency, could be levitated when placed near an ENZ substrate. This phenomenon, which was inspired as a classical analog to the Meissner effect (levitated magnets in the proximity of superconductors), can provide an approach in optomechanics when manipulation of electrically polarizable particles is desired in the presence of optical fields15,16,17,18,19.
Careful manipulation of particles with light, which has a long history dating back to the pioneering work of Ashkin in 1970s20,21, has played important roles in various areas, from biology22 to nanoscience and nanotechnology23. At the nanoscale, various methodologies have been used for such optical manipulation, including trapping24,25, pushing26,27, and binding28,29, with different materials such as dielectrics, semiconductors, plasmonic, and biological30. The surrounding media can be vacuum, air, or liquid. Optical tweezing30,31 is usually achieved using optical beam shaping to generate desired potential traps32. Recently, new approaches to optical manipulation of objects without beam shaping were proposed. Soljacic and co-workers33 proposed that the motion of a Janus particle with spatially asymmetric absorption can be controlled by changing the incident wavelength. Ilic and Atwater34 proposed self-stabilizing optical manipulation of macroscopic objects by controlling the anisotropy of the scattered light from the structured object’s surface. Both approaches, however, rely on structuring the object in lieu of the incident light.
In this work, we merge the two fields of ENZ metamaterials and of optical trapping, providing a platform, which we name ENZ-based optomechanics, for manipulating and controlling mechanical motion of particles in vicinity of ENZ structures. We explore, numerically and analytically, how various parameters, such as the size, shape, and composition of the particle and its distance to the ENZ substrate affect the optomechanical forces on such particles. We consider both homogeneous and layered structures as our ENZ substrates. In recent years, researchers have been able to tailor the effective permeability and permittivity of composite media by engineering the electric and magnetic resonances of nanostructures. Together with related developments in nanophotonics, metamaterials provide unprecedented freedom to define and sculpt electromagnetic modes. Metamaterials allow to alter the topology of photonic isofrequency surfaces—which govern the momentum and energy of optical modes inside a medium—contrarily to conventional bounded spherical and ellipsoidal isofrequency surfaces in natural dielectrics35. Among many other extreme optical features, unbounded isofrequency surfaces in hyperbolic dispersion metamaterials36 and point-like vanishing surfaces in ENZ media37 constitutes two examples of advanced modal engineering. In particular, epsilon-near-zero metamaterials provide extended modes with uniform phase over micrometer length scales inducing profound effects on nanoscopic light–matter interactions. These deeply subwavelength structured surfaces support unique electromagnetic modes that can be used in sub-diffraction imaging,38 and waveguiding8, spontaneous emission engineering39 and biosensing40.
In the following, we introduce the geometry of the problem, and discuss the electromagnetic modeling for the structure, along with the dipole approximation. We also present extensive numerical results, based on the finite-element method (using the commercial software COMSOL Multiphysics®) and on the T-matrix methods. We also present a series of results for various parameters involved in the problem. Physical insights into the results are presented and future directions are discussed.
Results and discussion
Geometry of the problem
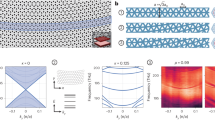
Figure 1a presents the geometry of our problem. A polarizable particle, made of a single nonmagnetic material (or multilayered materials), surrounded by an external medium (e.g., water) of refractive index nm, is located at an edge-to-edge distance h above a metamaterial substrate. The particle can be spherical (or other shapes as will be discussed later in the manuscript), and it is made of a (dielectric or metallic) material with a relative permittivity εp. The substrate can be considered as a homogenized nonmagnetic medium with relative permittivity near zero at the frequency of operation, or a layered structure engineered to function as ENZ.
a Sketch of the geometry. We consider a generic particle, in principle of any shape and composition, in front of a metamaterial surface at an edge-to-edge distance, h, immersed in an external medium (e.g., water) of refractive index nm. The origin of the coordinate system is placed on the surface so that the z axis is positive in the semi-infinite space where the particle resides. A monochromatic optical wave illuminates the particle and surface at normal incidence so that the total field is the superposition of incident (EI), reflected (ER) and scattered fields (ES, ESR). The resulting optical force can be either attractive (negative) or repulsive (positive). b Near-field force (R, ϕ) map. We explore the range of reflectivity, R, and phase, ϕ, related to the reflection of the incident wave on a generic surface. The ideal ENZ surface (R = 1, ϕ = 0)) is in the top right corner of the map and shows a repulsive force. Here, the near-field force component is calculated in the dipole approximation for a polystyrene (dielectric constant εp = 2.543 at 560 nm)) particle of radius a = 20 nm at a fixed edge-to-edge distance of h = 10 nm in water. c Curves of (R, ϕ) for different substrates consisting of alternating metal and dielectric layers, in the thin layer limit where effective medium theory is valid. The color of each curve indicates the metal filling fraction. The zero-force lines from panels d and e are superimposed as dashed lines. d–f Total force (R, ϕ) maps as calculated from T-matrix methods for a dielectric particle size of a = 20 nm (d), a = 220 nm (e), and a = 1000 nm (f), respectively, and at a fixed h = 10 nm. The total force maps have a structure that is strongly dependent on particle size. This is due to the increase of the scattering force component that, for large particles, overcomes any other gradient-like force component that is dominant for nanoparticles.
A monochromatic optical wave is illuminating this structure at normal incidence. The goal is to evaluate the optical force on the particle and to investigate how various parameters, radius a, edge-to-edge distance h, particle’s permittivity, and signal frequency affect the optical force’s magnitude and direction, i.e. whether it is a repulsive (positive) or an attractive (negative) force. In the next section, in order to gain some physical insight we start by assuming the polarizable particle to be represented by an infinitesimally small electric dipole, and discuss the analytical approach for evaluating the force acting on this particle. In the subsequent sections, we will expand our approach to include the full-wave numerical simulations of the problem, allowing to consider realistic sizes and shapes for this particle.
Dipole approximation
We first consider a particle size much smaller than the light wavelength (a < < λ) so that optical forces can be calculated analytically within the dipole approximation (DA)30,41,42. Due to its simplicity, the dipole approximation can provide useful results that can be compared with more complex light scattering approaches (T-matrix, finite-elements methods) at the nanoscale43.
We start our analysis from the near-field force component. It has been shown14 that in front of an ENZ surface an emitting point dipole source is subjected to a near-field repulsive force, reminiscent of the Meissner effect in superconductors14. This portion of the force, which we refer to as the “near-field” force, is due to the interaction of the emitting dipole with the substrate (excluding the force due to the presence of the incident and reflected waves). When all forces are considered (including the forces caused by the incident and reflected waves), the forces are called “total force”. We can extend the result of ref. 14 to a finite-sized polarizable particle illuminated by an incident field by considering the radiated power upon scattering, Prad = σscatI(z), in terms of the scattering cross section, σscat, and light intensity, I(z). Thus, the near-field force component is (see Section S1.1: Optical forces in the dipole approximation in front of epsilon-near-zero materials in the Supplementary Methods):
where z is the axial coordinate (z = h + a, a is the radius of the particle, h is the edge-to-edge distance of the particle from the surface), c is the vacuum speed of light, \({\varepsilon }_{{{{{{{{\rm{m}}}}}}}}}={\varepsilon }_{0}{n}_{{{{{{{{\rm{m}}}}}}}}}^{2}\) is the permittivity of the surrounding medium, nm is the refractive index of the medium, and εs is the complex dielectric permittivity of the ENZ surface. In Supplementary Fig. S2 a panel summarizing the results of the calculation of the near-field force (d–f) on a 20 nm dielectric bead in water is shown. Three different surfaces are considered: lossless (Im(εs/ε0) = 0), with medium loss (Im(εs/ε0) = 0.5), and with high loss (Im(εs/ε0) = 0.8). The comparison with the results obtained for a point dipole in vacuum14 shows that in this work the presence of a medium (water) broadens the repulsive near-field force region from − 1 < εs/ε0 < 1 to − 1.77 < εs/ε0 < 1.77; moreover, as already observed14, even in surfaces with high loss there is still a repulsive near-field force. It must be noted here that, as pointed out in ref. 16, the condition for the force to be repulsive in Eq. (1) can be algebraically simplified to ∣εs∣ < ∣εm∣. This defines a disk of radius ∣εm∣ in the complex plane of permittivities ∣εs∣. Moreover, this inequality also explains the effect of use of water in expanding the repulsion region, and also the robustness to losses.
In order to explore how the ENZ surface can influence the near-field and total forces on the particle, we evaluate such effects in terms of the amplitude ρ and phase ϕ of the complex reflection coefficient of an incident wave from this surface. In Fig. 1b, the near-field force on a a = 20 nm radius dielectric bead at h = 10 nm from the surface has been calculated as a function of the surface reflectivity R = \({\left\vert \rho {e}^{i\phi }\right\vert }^{2}={\rho }^{2}\) and phase angle ϕ which are connected to the surface complex refractive index \(\tilde{n}={n}_{{{{{{{{\rm{s}}}}}}}}}+i{k}_{{{{{{{{\rm{s}}}}}}}}}\) by44:
Here, we use e−iωt as our time harmonic convention. The calculated near-field force can reach a fraction of femtonewton for an incident intensity of ~5.6 × 108 W/m2 (corresponding to a typical experimental configuration, see Section S1.1.1: Plane wave illumination of the Supplementary Methods) and changes character from attractive to repulsive when the reflection phase angle changes from ϕ = –π to ϕ = 0. Metals such as Au or Ag, having a certain amount of absorption (ks in Eq. (2)), are in the attractive region of the near-field force (compare Fig. 1b, c). On the contrary, in front of an ideal ENZ surface, having R = 1 and ϕ = 0, the near-field force is repulsive. Substrates of alternating metal and dielectric layers can span a broader range of ϕ and R values. In the limit of layers much smaller than the incident wavelength, where effective medium theory (EMT) is valid, we show the (R, ϕ) results for four different metal / dielectric mixtures in Fig. 1c (see Section S1.4: Layered metamaterial calculations in the Supplementary Methods for more details on the EMT calculation). The metal filling fraction is indicated by the color of the curve. Depending on the fraction, we can switch the sign of the force from attractive to repulsive and vice versa. If we go beyond EMT and take into account the finite thickness of layers in real structures using an exact transfer matrix approach, we can achieve an even wider range of ϕ and R values.
We now consider the total optical force from an incident field on a nanoparticle calculated in DA. This is the sum of two main components: a gradient force, \({{{{{{{{\rm{F}}}}}}}}}_{{{{{{{{\rm{grad}}}}}}}}}\), and a scattering force, Fscat30. For plane wave illumination (for Gaussian beams see Section S1.1.2: Gaussian beams in Supplementary Methods) impinging normally to the ENZ surface, the force components are influenced by incident and reflected fields. Thus, considering only the axial direction z, they are written as:
where α is the particle complex polarizability45,
α0 is the Clausius–Mossotti polarizability and \({\sigma }_{{{{{{{{\rm{ext}}}}}}}}}=\frac{k}{{\varepsilon }_{{{{{{{{\rm{m}}}}}}}}}}{{{{{{{\rm{Im}}}}}}}}(\alpha )\) is the extinction cross section, related to the particle absorption and scattering30,42, with k = 2πnm/λ the wave number and λ the wavelength.
The gradient force, \({{{{{{{{\rm{F}}}}}}}}}_{{{{{{{{\rm{grad}}}}}}}}}\), drives the particle towards the maximum (minimum) of the modulated light intensity profile for positive (negative) real part of the polarizability. On the other hand, the scattering force, Fscat, is constant with respect z, and it always pushes the particle along the beam propagation direction.
In Fig. 1d, the (R, ϕ) map of calculated total axial force on a polystyrene a = 20 nm bead (dielectric constant εp = 2.543 at 560 nm) at h = 10 nm from the surface is shown. The total force is one order of magnitude larger than the near-field force (Fig. 1b) and shows a change in the repulsive–attractive character when the phase angle changes from − π to 0, respectively. This is due to the gradient force (see also Fig. 2a, short dots) that dominates the optomechanical response and drives the particle toward the high-field intensity regions. The change of the phase of the reflection coefficient shifts the intensity modulation resulting from the interference between the incident and reflected wave. Thus, the high-intensity points shift accordingly and the sign of the force changes around ϕ ~ − π/4.
Total optical force as a function of edge-to-edge distance, h, for polystyrene particles of different size: a a = 20 nm), b a = 220 nm, and c a = 1 μm. Different approaches for the calculation of the force are compared: dipole approximation (short dots), COMSOL (circles) and T-matrix (continuous lines). Different surfaces, glass (red), silver (magenta), ENZ (blue), yield very different optomechanical interactions in terms of force amplitude, modulation with respect to h, and phase shifts. Arrows indicate self-binding points, where particles are stably trapped in front of the surface. d, e Size dependence of the total optical force for fixed edge-to-edge distance, h = 10 nm. For small particles the gradient force component of the partially reflected plane wave dominates, resulting in a dependence with particle size, while for large particles radiation pressure has a major contribution resulting in a negative force pushing the particle towards the surface.
We now calculate the total optical force on the dielectric bead in front of glass, Ag and ENZ surfaces as a function of distance, h. The ENZ material is chosen so that ns ≈ 0.476 and ks ≈ 0.511, in order to obtain a real part of complex permittivity close to zero and an imaginary part close to 0.5 to include unavoidable losses of realistic systems. This choice leads to values of R and ϕ similar to those in the experimentally fabricated layered substrates described below, corresponding to the point marked with a red star in Fig. 3. The strong modulation resulting from the standing wave is clearly visible. The points with zero force and negative slope are trapping points that correspond to equilibrium positions for the particle dynamics (arrows in Fig. 2a). For the case of the ENZ surface the equilibrium point closest to the surface occurs at h ~ 10 nm, while for the glass and Ag surface they occur at h ~ 85 nm and h ~ 60 nm, respectively. By linearizing the force at the equilibrium points, F(z) ≈ − κz, a trap spring constant κ can be calculated. The trap spring constants κENZ and κAg calculated in front of ENZ and Ag surfaces can be compared to the spring constant κS calculated, in a standard single-beam optical tweezers setup, with the same particle, and at the same light intensity (see Section S1.1.1: Plane wave illumination in the Supplementary methods). The spring constants are κENZ = 15 fN μm−1 and κAg = 27 fN μm−1, while the trap spring constant κS in a standard optical tweezers setup is two order of magnitude lower, κS = 0.24 fN μm−1. The beneficial effect of the ENZ and Ag reflective surfaces on the trapping is evident. The increasing size of the particles corresponds to larger optical forces and different trapping points (see Supplementary Fig. S1 in Section S1.1.1: Plane wave illumination in the Supplementary Methods for DA calculations on larger-size nanoparticles at 50 and 100 nm).
R versus ϕ is illustrated for light at normal incidence with wavelength λ = 560 nm reflected from the surface of a thin-film stack. The thick curves of varying color are exact transfer matrix numerical calculations labeled n × d, where n refers to the number of bilayers in the stack, and d the thickness of each bilayer. The total thickness nd = 500 nm is kept constant. The bilayers consist of individual Ag and Al2O3 layers, with the fraction of Ag in the bilayer indicated by the metal filling fraction color. The red n × d labels correspond to systems where the dielectric is the upper layer in each bilayer (the one closest to the surface), while the blue labels are the ones where the metal is on top. The curve labeled EMT is the isotropic effective medium approximation to the system, which corresponds to n → ∞, d → 0 with nd = 500 nm. In all the above cases the superstrate is water and the substrate is glass. For comparison we show points indicating the R and ϕ values for a simple interface between a water superstrate and a pure material substrate (Ag, Au, Ge, TiO2, Al2O3, and an ideal ENZ). We also show experimental results (green stars, details in the Supplementary Information) involving a water superstrate and five trilayers (Al2O3/Ag/Ge from top to bottom, where Ge is present as a thin wetting layer to ensure fabrication quality). The dotted green trend line corresponds to keeping the Ag and Ge layer thicknesses fixed at 15 nm and 2.5 nm, respectively, while varying Al2O3 thickness from 80 nm to 20 nm (left to right). In order to compare the transfer matrix calculation with the full-wave analysis, COMSOL is used (black diamonds) to calculate R and ϕ for four different layered structure configurations, with the results showing good agreement with the corresponding transfer matrix curves.
Full-wave simulations
In order to calculate optical forces on larger particles, we use two different full-wave modeling approaches based on the transition (T-)matrix formalism46,47 and on finite-elements methods using the commercial software COMSOL Multiphysics®, respectively (see Section S1.2: Electromagnetic scattering theory and T-matrix formalism in front of epsilon-near-zero materials and Section S1.3: Finite-elements methods in the Supplementary Methods for details). In particular, electromagnetic scattering from particles near to or deposited on a plane surface that separates two homogeneous media of different optical properties in the T-matrix formalism47,48,49,50 can give an account on the role of the different multipoles in the particle-surface interaction. Indeed, the presence of the surface can have a striking effect on the scattering pattern from the particles, because the field that illuminates the particle is partly or totally reflected by the surface, and the reflected fields contribute both to the exciting and to the observed field. Moreover, the field scattered by the particle is reflected by the interface and thus contributes to the exciting field. In other words, there are multiple scattering processes between the particles and the interface. As a result, the field in the accessible half-space includes the incident field EI, the reflected field from the interface ER (as we would have if no particle were present), the scattered field from the particle ES and, finally, the field that after scattering by the particle is reflected by the surface, ESR, related to ES by the reflection condition (see Fig. 1a). Thus, the observed field, superposition of ES and ESR, includes all the scattered and scattered-reflected multipole contributions (see Section S1.2: Electromagnetic scattering theory and T-matrix formalism in front of epsilon-near-zero materials in the Supplementary Methods for more details).
It is possible to define the T-matrix for particles in the presence of the interface that is the starting point to calculate optical forces and torques either by direct integration of the Maxwell stress tensor (MST) over a closed surface containing the particle30 or by exploiting the general expressions of optical force and torque in terms of multiple expansion51,52,53. The optical force is obtained in COMSOL by direct integration of the MST that is calculated based on the total electric field and magnetic field which include the incident fields, the scattered fields by the particle, and all the reflected fields by the surface (see Section S1.3: Finite-elements methods in the Supplementary Methods).
The results obtained in DA from the different surfaces are compared in Fig. 2a with those obtained by using full electromagnetic calculations based on COMSOL (circles), and T-matrix methods (continuous lines). A very good agreement is clearly observed. In all approaches, the total optical force on small particles is modulated by the sinusoidal term of the gradient force. Its magnitude is larger (in the fN range) on more reflective surfaces and its phase changes sign going from a Ag to an ENZ substrate, leading to the formation of optical trapping points at different distances (arrows in Fig. 2a). In brief, the gradient force dominates the ENZ-optomechanics for small particles even in the proximity of the surface.
T-matrix and COMSOL allow the calculation of optical forces for larger particles than in DA. In Fig. 1e, f, the (R, ϕ) map of total axial force calculated with the T-matrix approach on a a = 220 nm bead (Fig. 1e) and a = 1 μm bead (Fig. 1f), at h = 10 nm from the surface, are shown. The comparison with Fig. 1d highlights the strong dependence of the total optical force on the bead size. The repulsive–attractive behavior is driven by the competition between gradient force and scattering force, which may give repulsive behavior, for intermediate-size beads, in surfaces having large reflectivity (see Fig. 1e); however, at large bead size (Fig. 1f), scattering force overcomes gradient force, and the total optical force is attractive in front of every type of surface.
In Fig. 2b, c, the T-matrix calculations of the total optical force on larger particles are shown as a function of the edge-to-edge distance from ENZ, Ag and glass surfaces. The larger size of these particles with respect to the nanosized bead in Fig. 2a highlights the increased contribution of the scattering force on the gradient force. The scattering force is detrimental towards stable equilibrium positions in front of glass surface for the 220 nm radius bead and in front of both ENZ and glass surfaces for 1 μm radius bead. The lower reflectivity of these surfaces as compared to the reflection from the Ag surface does not allow an efficient balance between scattering force from incoming and reflected beams, increasing the scattering force contribution with respect gradient force and hindering the trapping.
In Fig. 2d, e, the results are reported for increasing bead size at fixed distance, h = 10 nm, from the ENZ, Ag or glass surfaces. It is shown that at small bead size (below ~300 nm radius), the gradient force modulates the total force. At increasing bead size, the particle extinction cross section increases, consequently the scattering force is predominant on the gradient force, inhibiting equilibrium points and inducing an effective attractive force directed toward the surfaces.
Epsilon-near-zero metamaterials
Regarding layered ENZ materials, we have demonstrated experimentally that it is possible to control the optical topology and to induce the ENZ behavior by designing and fabricating subwavelength-layered lattice structures as a result of interlocking noble metals and dielectric thin films54. Upon selecting metal-dielectric bilayers, the thickness of each layer, the filling fraction and the number of bilayers, the frequency of the optical topological transition in the isofrequency surface leading to the epsilon-near-zero behavior can be tailored. The lattice structure is fabricated as a five tri-layer system using \({{{{{{{{\rm{A{l}}}}}}}_{2}O}}}_{{{{{{{{\rm{3}}}}}}}}}\), Ag, and Ge from top to bottom. The Ag layer thicknesses were in the range of 10–25 nm, with a thin Ge layer (1–3 nm) underneath to ensure surface wetting. The \({{{{{{{{\rm{A{l}}}}}}}_{2}O}}}_{{{{{{{{\rm{3}}}}}}}}}\) layer thicknesses were systematically varied between roughly 20 nm and 80 nm across different material systems (Fig. 3), subsequently tuning the frequency of the topological transition. In previous studies, we used effective medium theory to calculate the dielectric permittivity of the entire structure, as opposed to more recent inverse design approaches to account for a wider material parameters space. We perform spectroscopic ellipsometry measurements to evaluate the dielectric tensor components and the dispersive behavior of the layered structure. By fitting the measured angular reflectance and the ellipsometry parameters ψ and Δ, we can directly obtain the effective optical constants of the multilayer slab. Using the transfer matrix method, we can then predict the magnitude and phase of reflection at normal incidence with a water superstrate. The green stars in Fig. 3 represent these predicted values from 6 samples consisting of a five-bilayer Al2O3/Ag thin-film stack with a Ge seed layer to ensure the uniformity of the Ag films. By varying the thickness of the \({{{{{{{{\rm{A{l}}}}}}}_{2}O}}}_{{{{{{{{\rm{3}}}}}}}}}\) layers, we covered a phase range of ΔΦ ≈ 180∘ and reflectance range of ΔR ≈ 0.5. The full range of accessible R and ϕ values is even larger if we expand the design space of the substrate to include different numbers of bilayers and metal filling fractions. The thick curves in Fig. 3 show transfer matrix calculations of (R, ϕ) for Al2O3/Ag stacks with different structural parameters indicated by the labels. In all cases the total thickness of the stack was kept fixed at 500 nm. The color at each point along the curves corresponds to the metal filling fraction. In the limit of many thin bilayers, we approach the EMT result of Fig. 1c, which is also reproduced here for comparison. Note that actual layered materials can achieve positive values of ϕ, while homogeneous materials (for example, those described by EMT) are confined to the ϕ < 0 subspace. Fig. S11 shows how ϕ varies with wavelength for a subset of the layer configurations in Fig. 3.
Complex particles (core–shell, ellipsoids, ENZ)
In addition to spherical beads, we evaluate the optical forces on different types of particles in front of dielectric, metallic or ENZ surfaces. We consider spherical core–shell particles based on SiO2 and Ag, an Ag prolate spheroid and a spherical particle made by an ENZ material.
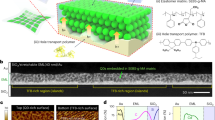
We first used COMSOL simulation to calculate the forces on core–shell structures in front of layered ENZ material at 560 nm illumination. The total particle radius atot is fixed at 20 nm. The particles had alternatively SiO2 or Ag as the core, with the other material as the shell. In Fig. 4a, the total force on the core–shell particles as a function of the distance from the ENZ surface is shown. It is clearly observed that the presence of Ag in the outer shell enhances the total force with respect of the inverse structure having SiO2 as the shell, but also with respect to the pure Ag sphere (Fig. 4b). The highest value of the force is found (red curve in Fig. 4a) for a SiO2–Ag core–shell structure having a core radius of a1 = 16.1 nm and an Ag shell 3.9 nm thick which, as shown in Fig. 4c, is at the resonance condition at the ENZ wavelength.
a COMSOL calculation of total optical force on core–shell particles based on SiO2 and Ag as a function of the distance from the metamaterial surface. Different ratios between core radius a1 and total particle radius atot = 20 nm have been considered. Moreover, both materials have been considered as a core. b Maximum force found in each core–shell structure considered, as pointed out by the dashed blue line in (a). c Extinction spectrum of the SiO2-Ag core–shell particle (total radius atot = 20 nm and core radius a1 = 16.1 nm) in water. d (R, ϕ) contour plot of the total optical force for the core–shell particle at h = 10 nm from the surface. The ENZ and Ag surfaces used for the calculation of the optical forces in DA approximation are shown as circles. e Extinction spectra of Ag prolate ellipsoid in water oriented with the long axis parallel to the field (black solid line) and oriented with the short axis parallel to the field (red dashed line). The resonances relative to the long and short axes are indicated. f (R, ϕ) contour plot of the total optical force on the Ag ellipsoid at h = 10 nm distance from the surface. In the calculation, the spheroid is aligned with the long axis in the direction of the wave polarization. The ENZ and Ag surfaces used for the calculation of the optical forces in DA approximation are shown as circles. The optical force is in the order of tens of pN in front of ENZ (repulsive) and Ag (attractive). The force can be close to 200 pN if the spheroid is in front of an ideal ENZ surface, having R = 1 and ϕ = 0.
As shown in Fig. 4d and Supplementary Fig. S5d, e, the particle resonance at 560 nm enhances the optical force to the piconewton range (Supplementary Fig. S4d) but only at very short distances from the surfaces, being repulsive in the ENZ case (Supplementary Fig. S4d) and attractive in the Ag case (Supplementary Fig. S5e). Otherwise, the total optical force is at the fN range.
Specifically, at the resonance Fenz is in the piconewton range close to the ENZ surface (from h = 0 nm to roughly 10 nm). The gradient force, \({{{{{{{{\rm{F}}}}}}}}}_{{{{{{{{\rm{grad}}}}}}}}}\), has an oscillating character, but its amplitude is smaller ( ≈ 1 fN) than Fenz, due to the small real part of the polarizability at resonance (Re(α) = 0.04 × 10−32 Fm2). On the contrary, Fscatt is large (tens of femtonewton), because of the large extinction cross section at resonance. Thus, at 560 nm (black curve in Supplementary Fig. S6a), the total force is repulsive and in the piconewton range close to the surface, but becomes attractive and approximately constant as the Fenz contribution fades off with distance.
The behavior of the forces on the core–shell particle can also be studied for wavelengths smaller and larger than the particle plasmon resonance (see Supplementary Fig. S6a, b in the Supplementary Methods). The calculation has been made for 552 nm, on the blue side of the plasmon resonance, and at 566 nm, on its red side. At these wavelengths, the scattering force is slightly lower than at resonance, while \({{{{{{{{\rm{F}}}}}}}}}_{{{{{{{{\rm{grad}}}}}}}}}\) increases by at least one order of magnitude. For this reason, its oscillating character shows up in the total force (Supplementary Fig. S6a, blue and red curves). Moreover, as the polarizability changes sign from one side to the other of the resonance, also the gradient force inverts its phase from the blue to the red side of the resonance. Similar discussions hold for the optical forces in front of Ag surface (Supplementary Fig. S6b); however, in this case, the Fenz is attractive close to the surface.
We now consider an Ag prolate spheroid as a prototypical non-spherical particle. This is chosen with a long axis a1 = 56.8 nm and short axes a2 = a3 = 20 nm. As shown in Fig. 4e, the particle has, in water, a long axis resonance at 560 nm and a short axis resonance at 360 nm. For the calculation of the total optical forces we considered the case in which the spheroid has the long axis aligned with the wave polarization, and the short semiaxis as the size parameter in Eq. (1). We obtain a further enhancement of the total optical force (tens of piconewton, Fig. 4f) which, as in the core–shell structure, is repulsive in front of ENZ surface and attractive in front of Ag surface. In Fig. 4f, a contour plot of the total optical force, calculated as a function of the surface reflectivity R and phase shift ϕ, namely, in front of all possible surfaces, is shown. We clearly see that the repulsive force can be close to 200 pN in front of an “ideal" ENZ surface, having the maximum reflectivity and a vanishing phase shift.
In the case of ENZ particles, we do not consider any multilayered structure but we wanted to make a comparison between a dielectric particle (Fig. 1) and a particle with the same size (or even larger) but with ENZ properties. For the calculations we simply consider an effective medium with n and k chosen so that np = 0.476 and kp = 0.511, in order to obtain a real part of complex permittivity close to zero and an imaginary part close to 0.5. We calculated optical forces in front of glass, Ag or ENZ surfaces. The calculation has been made for ENZ beads having radii a = 20, 50, and 100 nm. As shown in Supplementary Fig. S4, the forces are about five times larger than the ones observed in dielectric bead counterparts. The larger scattering force of ENZ particle hinders its trapping in front of glass surface, for all radii. Moreover, the 100-nm-radius ENZ particle cannot be trapped also in front of ENZ surface (Supplementary Fig. S4c). Results are shown in Section S.1.1.1: Plane wave illumination of the Supplementary Methods.
We have also studied the total optical force in case of a focused (NA = 1.3) Gaussian beam, typical of optical tweezers experiments (Section S1.1.2: Gaussian beams in the Supplementary Methods). The calculations, made for a 20 nm radius polystyrene bead, show that, both in front of ENZ (Supplementary Fig. S8a) and Ag (Supplementary Fig. S8b) surfaces, the beam focusing induces a fading of the total force with the distance h (see Supplementary Fig. S8). The extension of the calculations for beads with larger radius (contour plots of the total optical force in front of ENZ, Supplementary Fig. S8c, and Ag, Supplementary Fig. S8d, surfaces) shows that the total force increases at increasing bead radius, reaching the range of tens of femtonewton in front of ENZ and hundreds of femtonewton in front of Ag surface. The modulation induced by the gradient force is clearly visible. Note that when Gaussian beams are used, for a direct comparison, the beam power is reduced with respect to the plane wave case in order to maintain the intensity at the beam focus similar to the plane wave intensity.
It is worth noting that the assumption of a lossless surrounding medium (such as air or water) is crucial for the correct calculations of optical forces on polarizable particles. This is generally valid in the visible and near-infrared where typical optical tweezers experiments are performed. Considering a medium with losses would make the optical force spatially dependent and any calculation would require to be specific for a given geometry. This is indeed an interesting problem that it is also challenging as one has to modify the electromagnetic scattering theory equations that are also the starting point for the semi-analytical calculation of optical forces in the T-matrix formalism. A starting point can be considered ref. 55, where scattering theory is re-formulated for spherical particles in an absorbing medium. From this starting point a T-matrix framework and the use of the locally defined Maxwell stress tensor can be used to calculate the spatially dependent optical forces.
Finally, we add some few considerations about the Casimir effect that is observed between two metallic surfaces (or a particle and a surface) at very short distances. Usually, μm-size particles are used56,57,58. In the case of a small dielectric bead, as the one in our paper, the Casimir effect is weaker59 but, when dielectric–metallic core–shell spheres or silver ellipsoids are in front of silver and ENZ surfaces, it could give a contribution. However, all our calculations consider particles and surfaces in water, and this fact does further reduce the Casimir force. A quantitative estimation of the Casimir force on our particles based on the results given in refs. 56,57,58,59 shows (see Section S2.1: Casimir effect in the Supplementary Discussion) that in our case Casimir effect can be safely neglected. However, it is not excluded that forces due to thermal fluctuation effects, which are considered Casimir forces in a broader sense, may induce a sticking of these small particles to the surfaces, limiting the practical exploitation of the ENZ-related optomechanical forces.
Conclusions
In conclusion, ENZ-based optomechanics may provide a way to manipulate and tailor mechanical effects of light exploiting flat surfaces. We focused our study on the repulsive–attractive optomechanics for particles in front of an ENZ surface in realistic conditions for a wide range of parameters (particle size and shape, ENZ surface structure, etc.) in the axial direction. Combining the unique optical properties of ENZ metamaterials with patterning capabilities will also enable further manipulation and control in the transverse direction towards a full dynamical engineering of ENZ-based optical forces. Various potential applications for future study include particle sorting due to the strong dependence of ENZ-based optical forces on the size and material composition of particles, biomolecular trapping and sensing, wavelength multiplexing of optical forces, and chiral optical sorting, just to name a few.
Methods
The calculation of optical forces on particles having size ≤100 nm has been made by using DA in front of dielectric, Ag and ENZ surfaces (see Section S1.1: Optical forces in the dipole approximation in front of epsilon-near-zero materials of the Supplementary Methods). Dielectric, ENZ, core–shell particles, and Ag prolate spheroids under plane wave illumination have been considered (see Section S1.1.1: Plane wave illumination of the Supplementary Methods). Illumination under Gaussian beams has also been discussed (Section S1.1.2: Gaussian beams of the Supplementary Methods). The calculation of optical forces on larger-size particles has been carried out by using the transition (T-)matrix formalism (Section S1.2: Electromagnetic scattering theory and T-matrix formalism in front of epsilon-near-zero materials of the Supplementary Methods) and by using finite-elements methods (COMSOL), which was also used to calculate forces on core–shell structures in front of layered ENZ metamaterials (Section S1.3: Finite-elements methods of the Supplementary Methods). The optical properties of layered ENZ structures have been calculated by transfer matrix calculations (Section S1.4: Layered metamaterial calculations in the Supplementary Methods).
Data availability
Data that support the findings of this study are available from the corresponding authors upon reasonable request.
Code availability
The Fortran code and MatLab scripts for the T-matrix approach, the MathCad scripts for the dipole approximation calculation of the forces, and the COMSOL scripts for the FEM calculations are available from the authors on reasonable request.
References
Alù, A. & Engheta, N. Achieving transparency with plasmonic and metamaterial coatings. Phys. Rev. E 72, 016623 (2005).
Schurig, D. et al. Metamaterial electromagnetic cloak at microwave frequencies. Science 314, 977–980 (2006).
Alù, A. & Engheta, N. Boosting molecular fluorescence with a plasmonic nanolauncher. Phys. Rev. Lett. 103, 043902 (2009).
Alù, A. & Engheta, N. Cloaking a sensor. Phys. Rev. Lett. 102, 233901 (2009).
Silva, A. et al. Performing mathematical operations with metamaterials. Science 343, 160–163 (2014).
Estakhri, N. M., Edwards, B. & Engheta, N. Inverse-designed metastructures that solve equations. Science 363, 1333–1338 (2019).
Coulais, C., Sounas, D. & Alu, A. Static non-reciprocity in mechanical metamaterials. Nature 542, 461–464 (2017).
Silveirinha, M. & Engheta, N. Tunneling of electromagnetic energy through subwavelength channels and bends using ε-near-zero materials. Phys. Rev. Lett. 97, 157403 (2006).
Liberal, I. & Engheta, N. Near-zero refractive index photonics. Nat. Photon. 11, 149–158 (2017).
Reshef, O., De Leon, I., Alam, M. Z. & Boyd, R. W. Nonlinear optical effects in epsilon-near-zero media. Nat. Rev. Mater. 4, 535–551 (2019).
Kinsey, N., DeVault, C., Boltasseva, A. & Shalaev, V. M. Near-zero-index materials for photonics. Nat. Rev. Mater. 4, 742–760 (2019).
Engheta, N. Pursuing near-zero response. Science 340, 286–287 (2013).
Liberal, I. & Engheta, N. The rise of near-zero-index technologies. Science 358, 1540–1541 (2017).
Rodríguez-Fortuño, F. J., Vakil, A. & Engheta, N. Electric levitation using epsilon-near-zero metamaterials. Phys. Rev. Lett. 112, 033902 (2014).
Krasikov, S., Iorsh, I. V., Shalin, A. & Belov, P. A. Levitation of finite-size electric dipole over epsilon-near-zero metamaterial. Physica Status Solidi (RRL)–Rapid Res. Lett. 8, 1015–1018 (2014).
Rodríguez-Fortuño, F. J. & Zayats, A. V. Repulsion of polarised particles from anisotropic materials with a near-zero permittivity component. Light Sci. Appl. 5, e16022–e16022 (2016).
Ivinskaya, A. et al. Optomechanical manipulation with hyperbolic metasurfaces. ACS Photon. 5, 4371–4377 (2018).
Kingsley-Smith, J. J., Picardi, M. F. & Rodríguez-Fortuño, F. J. Optical magnetic dipole levitation using a plasmonic surface. Nano Lett. 20, 7094–7099 (2020).
Rodríguez-Fortuño, F. J., Picardi, M. F. & Zayats, A. V. Repulsion of polarized particles from two-dimensional materials. Phys. Rev. B 97, 205401 (2018).
Ashkin, A. Acceleration and trapping of particles by radiation pressure. Phys. Rev. Lett. 24, 156–159 (1970).
Ashkin, A. & Dziedzic, J. M. Optical levitation by radiation pressure. Appl. Phys. Lett. 19, 283–285 (1971).
Fazal, F. M. & Block, S. M. Optical tweezers study life under tension. Nat. Photon. 5, 318–321 (2011).
Maragò, O. M., Jones, P. H., Gucciardi, P. G., Volpe, G. & Ferrari, A. C. Optical trapping and manipulation of nanostructures. Nat. Nanotechnol. 8, 807–819 (2013).
Spesyvtseva, S. E. S. & Dholakia, K. Trapping in a material world. ACS Photon. 3, 719–736 (2016).
Juan, M. L., Righini, M. & Quidant, R. Plasmon nano-optical tweezers. Nat. Photon. 5, 349–356 (2011).
Gargiulo, J., Cerrota, S., Cortes, E., Violi, I. L. & Stefani, F. D. Connecting metallic nanoparticles by optical printing. Nano Lett. 16, 1224–1229 (2016).
Donato, M. G. et al. Optical trapping and optical force positioning of two-dimensional materials. Nanoscale 10, 1245–1255 (2018).
Demergis, V. & Florin, E.-L. Ultrastrong optical binding of metallic nanoparticles. Nano Lett. 12, 5756–5760 (2012).
Donato, M. G. et al. Optical trapping, optical binding, and rotational dynamics of silicon nanowires in counter-propagating beams. Nano Lett. 19, 342–352 (2019).
Jones, P. H., Maragò, O. M. & Volpe, G. Optical Tweezers: Principles and Applications (Cambridge University Press, 2015).
Ashkin, A., Dziedzic, J., Bjorkholm, J. & Chu, S. Observation of a single-beam gradient optical trap for dielectric particles. Optics Lett. 11, 288–290 (1986).
Dholakia, K. & Čižmár, T. Shaping the future of manipulation. Nat. Photon. 5, 335–342 (2011).
Ilic, O. et al. Topologically enabled optical nanomotors. Sci. Adv. 3, e1602738 (2017).
Ilic, O. & Atwater, H. A. Self-stabilizing photonic levitation and propulsion of nanostructured macroscopic objects. Nat. Photon. 13, 289–295 (2019).
Krishnamoorthy, H. N., Jacob, Z., Narimanov, E., Kretzschmar, I. & Menon, V. M. Topological transitions in metamaterials. Science 336, 205–209 (2012).
Poddubny, A., Iorsh, I., Belov, P. & Kivshar, Y. Hyperbolic metamaterials. Nat. Photon. 7, 948 (2013).
Mahmoud, A. M. & Engheta, N. Wave–matter interactions in epsilon-and-mu-near-zero structures. Nat. Commun. 5, 1–7 (2014).
Jacob, Z., Alekseyev, L. V. & Narimanov, E. Optical hyperlens: far-field imaging beyond the diffraction limit. Opt. Express 14, 8247–8256 (2006).
Cortes, C., Newman, W., Molesky, S. & Jacob, Z. Quantum nanophotonics using hyperbolic metamaterials. J. Opt. 14, 063001 (2012).
Sreekanth, K. V. et al. Extreme sensitivity biosensing platform based on hyperbolic metamaterials. Nat. Mater. 15, 621–627 (2016).
Chaumet, P. C. & Nieto-Vesperinas, M. Time-averaged total force on a dipolar sphere in an electromagnetic field. Opt. Lett. 25, 1065–1067 (2000).
Arias-González, J. & Nieto-Vesperinas, M. Optical forces on small particles: attractive and repulsive nature and plasmon-resonance conditions. J. Opt. Soc. Am. A 20, 1201–1209 (2003).
Polimeno, P. et al. Optical tweezers and their applications. J. Quant. Spectrosc. Radiat. Transf. 218, 131–150 (2018).
Born, M. & Wolf, E. Principles of Optics, 6th edn. (Pergamon, 1980).
Draine, B. & Goodman, J. Beyond Clausius-Mossotti: wave propagation on a polarizable point lattice and the discrete dipole approximation. Astrophys. J. 405, 685–697 (1994).
Waterman, P. Symmetry, unitarity, and geometry in electromagnetic scattering. Phys. Rev. D 3, 825 (1971).
Borghese, F., Denti, P. & Saija, R. Scattering from Model Nonspherical Particles (Springer, 2007).
Borghese, F., Denti, P., Saija, R., Fucile, E. & Sindoni, O. Optical properties of model anisotropic particles on or near a perfectly reflecting surface. J. Opt. Soc. Am. A 12, 530–540 (1995).
Denti, P., Borghese, F., Saija, R., Fucile, E. & Sindoni, O. Optical properties of aggregated spheres in the vicinity of a plane surface. J. Opt. Soc. Am. A 16, 167–175 (1999).
Denti, P., Borghese, F., Saija, R., Iati, M. A. & Sindoni, O. I. Optical properties of a dispersion of randomly oriented identical aggregates of spheres deposited on a plane surface. Appl. Opt. 38, 6421–6430 (1999).
Saija, R., Iatì, M. A., Giusto, A., Denti, P. & Borghese, F. Transverse components of the radiation force on nonspherical particles in the t-matrix formalism. J. Quant. Spectrosc. Radiat. Transf. 94, 163–179 (2005).
Borghese, F., Denti, P., Saija, R. & Iatì, M. A. Radiation torque on nonspherical particles in the transition matrix formalism. Opt. Express 14, 9508–9521 (2006).
Borghese, F., Denti, P., Saija, R. & Iatì, M. A. Optical trapping of nonspherical particles in the T-matrix formalism. Opt. Express 15, 11984–11998 (2007).
Sreekanth, K. V., De Luca, A. & Strangi, G. Experimental demonstration of surface and bulk plasmon polaritons in hypergratings. Sci. Rep. 3, 3291 (2013).
Mishchenko, M. I. & Dlugach, J. M. Scattering and extinction by spherical particles immersed in an absorbing host medium. J. Quant. Spectrosc. Radiat. Transf. 211, 179–187 (2018).
Munday, J., Capasso, F., Parsegian, V. A. & Bezrukov, S. M. Measurements of the Casimir-Lifshitz force in fluids: the effect of electrostatic forces and debye screening. Phys. Rev. A 78, 032109 (2008).
Munday, J. N., Capasso, F. & Parsegian, V. A. Measured long-range repulsive Casimir-Lifshitz forces. Nature 457, 170–173 (2009).
Le Cunuder, A., Petrosyan, A., Palasantzas, G., Svetovoy, V. & Ciliberto, S. Measurement of the Casimir force in a gas and in a liquid. Phys. Rev. B 98, 201408 (2018).
Pires, L. B. et al. Probing the screening of the Casimir interaction with optical tweezers. Phys. Rev. Res. 3, 033037 (2021).
Acknowledgements
The authors thank Professor Jeremy Munday (UC Davis) for the fruitful discussion during the preparation of the revised manuscript. M.G.D., R.S., and O.M.M. acknowledge financial support from the agreement ASI-INAF n.2018-16-HH.0, Project “SPACE Tweezers”. N.E. acknowledges partial support from the Vannevar Bush Faculty Fellowship program sponsored by the Basic Research Office of the Assistant Secretary of Defense for Research and Engineering, funded by the Office of Naval Research through Grant No. N00014-16-1-2029. G.S. acknowledges financial support from the Ohio Third Frontier Program and the National Science Foundation—DMR Grant No. 1708742.
Author information
Authors and Affiliations
Contributions
Y.K., M.G.D., and R.S. performed the calculation of optical forces. M.H., M.E., and T.L. performed the simulation of the optical properties of ENZ material. R.S. provided the theoretical foundations for the T-Matrix approach. N.E., G.S., and O.M.M. conceived the idea and supervised the project. All the authors discussed and commented on the results and on the manuscript text.
Corresponding authors
Ethics declarations
Competing interests
N.E. is a strategic scientific advisor/consultant to Meta Materials, Inc. The remaining authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks Francisco Rodríguez-Fortuño, Lyuba Kuznetsova and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kiasat, Y., Donato, M.G., Hinczewski, M. et al. Epsilon-near-zero (ENZ)-based optomechanics. Commun Phys 6, 69 (2023). https://doi.org/10.1038/s42005-023-01186-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-023-01186-0
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.