Introduction

Back-action limited weak measurements are essential for advancing quantum technologies, enable new probes of quantum systems, and offer new ways to understand the measurement process. Most quantum technologies simultaneously require quantum limited measurements and feedback control to establish and maintain quantum coherence and entanglement, with applications ranging from quantum state preparation1,2 to quantum error correction3. Even without feedback, system dynamics combined with weak measurements can lead to entangled states in the thermodynamic limit4,5,6,7. Large-scale applications of these capabilities hinge on understanding system-reservoir dynamics of many-body quantum systems, whose Hilbert space grows exponentially with system size. Ultracold atoms, a workhorse for quantum simulation8,9, are an ideal platform for studying the system-reservoir dynamics of large-scale many-body systems.

Weakly measured quantum systems can be understood using the robust framework of quantum trajectories10,11. In these descriptions, the system and a larger reservoir interact and become weakly entangled, at which point the reservoir is projectively measured. This destroys the system-reservoir (SR) entanglement and leads to a change in the system’s wavefunction. We develop such a measurement model to study the interplay between the system-reservoir interaction, the scattered light, and the post-measurement system state.

Very far from atomic resonance light Rayleigh-scatters from atomic ensembles, changing the incident light’s wavevector in proportion to the Fourier transform of the atomic density distribution. The straightforward interpretation of back-action resulting from scattered photons makes quantum trajectories an ideal tool for both intuitively and quantitatively understanding the system-reservoir interaction. When the reservoir-measurement outcomes are rejected, quantum trajectories methods form a specific physically motivated “unraveling” of the master equation11. In the quantum problem, light scattering gives information both about the expectation value of the density—essentially classical scattering—as well as quantum fluctuations, which contribute to spontaneous emission. Quite recently a trio of papers observed the predicted suppression of light-scattering from deeply degenerate Fermi gases12,13,14 as well as amplification from ultracold Bose gases15; these effects result from scattering atoms into occupied quantum states.

Ultracold atoms have multiple well-established “non-destructive” measurement techniques16,17,18,19,20,21. While backaction-induced heating of a single motional degree of freedom of a BEC was observed in a single-mode optical cavity22, previous demonstrations of such methods with spatial resolution did not quantify quantum back-action.

Here we characterize measurement back-action in atomic Bose-Einstein condensates (BECs), weakly interacting with a far-from resonant laser beam. The information extracted by light-scattering can be treated as a quantum measurement process where the scattered light is detected by the environment (Fig. 1a, b), and we—the observer—detect only the resulting back-action on the system. The wavefunction change is quantified by the phase shift and contrast of a Ramsey interferometer. In our Ramsey interferometer (Fig. 1c), spontaneously scattered light measures atoms to be in the detected spin state, thereby breaking its coherence and reducing the interferometer contrast. We further distinguish between non-destructive measurements (where the system is apparently undisturbed) and back-action limited measurements (where observed quantum projection noise dominates the change in the post-measurement state). We systematically control for two stray effects that otherwise lead to excess excitation or loss: inhomogeneities in the probe beam, and a weak optical lattice from weak back-reflections of the probe beam. We explore a third systematic effect: light-induced collisions—intrinsic atomic processes—that were found to have limited impact on our Ramsey data. We demonstrate that these technical artifacts can be eliminated, bringing the observed back-action into agreement with our measurement model.

Fig. 1: Photodetection measurement model and Ramsey interferometry.
figure 1

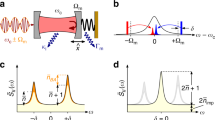
a Interaction. A Bose-Einstein condensate (BEC) illustrated in blue, is illuminated with far-detuned laser light (red) for a time tm and scatters light (wiggly lines) into both occupied (red) and reservoir (orange) modes. b Measurement. The reservoir modes are projectively measured by an array of photo-detectors encompassing 4π steradians yielding the outgoing wavevector and polarization. c Level diagram. d Time sequence for Ramsey interferometry. An initial π/2 microwave pulse (light blue) is followed by a 15 μs evolution period; then the tm = 20 μs off-resonant light pulse (red) is applied, and after a 5 μs delay (giving a total T = 40 μs free evolution time) the Ramsey sequence is completed with a second π/2 pulse (light blue). The optical dipole trap (ODT), denoted by the orange dashed line, is extinguished immediately following the Ramsey sequence. A Stern-Gerlach (SG) gradient (gray) is applied during time-of-flight (TOF) and the final density is detected using absorption imaging (purple). e Bloch sphere depiction of Ramsey interferometry. The dark blue arrows depict the axes of rotation for each microwave pulse and the light blue arrows mark the associated trajectories. The green circles show the coherent evolution during each step of our sequence. Red arrows depict evolution associated with the measurement pulse with the solid curve resulting from the Stark shift and dashed curves resulting from measurement back-action. The red circles are the states that were measured to be in |g2〉. Translucent (solid) symbols indicate the initial (final) state.

Full size image

Results

Quantum trajectories model

We consider a weakly interacting atomic BEC (the system) dispersively coupled to the optical electric field \(\hat{{{{{{\bf{E}}}}}}}\left({{{{{\bf{x}}}}}},t\right)\) (the reservoir) by the ac Stark shift with interaction picture Hamiltonian

$${\hat{H}}_{{{{{{\rm{SR}}}}}}}\left(t\right) = \int \frac{{d}^{3}{{{{{\bf{x}}}}}}}{{{\hslash }}\Delta }{\hat{n}}_{{{{{{\rm{g}}}}}}}\left({{{{{\bf{x}}}}}}\right)\otimes \left[\hat{{{{{{\bf{E}}}}}}}\left({{{{{\bf{x}}}}}},t\right)\cdot {{{{{{\bf{d}}}}}}}_{{{{{{\rm{ge}}}}}}}\right]\left[{{{{{{\bf{d}}}}}}}_{{{{{{\rm{ge}}}}}}}^{* }\cdot {\hat{{{{{{\bf{E}}}}}}}}^{{{\dagger}} }\left({{{{{\bf{x}}}}}},t\right)\right].$$
(1)

Here \({\hat{n}}_{{{{{{\rm{g}}}}}}}\left({{{{{\bf{x}}}}}}\right)={\hat{b}}_{{{{{{\rm{g}}}}}}}^{{{\dagger}} }\left({{{{{\bf{x}}}}}}\right){\hat{b}}_{{{{{{\rm{g}}}}}}}\left({{{{{\bf{x}}}}}}\right)\) is the atomic density operator in terms of the bosonic field operators \({\hat{b}}_{{{{{{\rm{g}}}}}}}\left({{{{{\bf{x}}}}}}\right)\) for ground state atoms at position \({{{{{\bf{x}}}}}}\); \({{{{{{\bf{d}}}}}}}_{{{{{{\rm{ge}}}}}}}\) is the dipole matrix element for transitions between ground and excited state atoms with energy difference \({{\hslash }}{\omega }_{{{{{{\rm{ge}}}}}}}\); lastly, \(\Delta ={\omega }_{0}-{\omega }_{{{{{{\rm{ge}}}}}}}\) is the detuning from atomic resonance of a probe laser with frequency \({\omega }_{0}\).

For \(\left|\Delta \right|\ll {\omega }_{{{{{{\rm{ge}}}}}}}\), the optical electric field operator is

$$\hat{{{{{{\bf{E}}}}}}}\left({{{{{\bf{x}}}}}},t\right) =i\sqrt{\frac{{{\hslash }}{\omega }_{{{{{{\rm{ge}}}}}}}}{2{\epsilon }_{0}}}\mathop{\sum}\limits_{\sigma }\int \frac{{d}^{3}{{{{{\bf{k}}}}}}}{{\left(2\pi \right)}^{3}}{\hat{a}}_{\sigma }\left({{{{{\bf{k}}}}}}\right){{{{{{\boldsymbol{\epsilon }}}}}}}_{\sigma }\left({{{{{\bf{k}}}}}}\right){e}^{i\left({{{{{\bf{k}}}}}}\cdot {{{{{\bf{x}}}}}}-c\left|{{{{{\bf{k}}}}}}\right|t\right)},$$
(2)

expressed in terms of field operators \({\hat{a}}_{\sigma }\left({{{{{\bf{k}}}}}}\right)\) describing states with wavevector k and polarization σ. Here, c is the speed of light; ϵ0 is the electric constant; and ϵσ(k) are a pair orthogonal polarization vectors transverse to k, labeled by σ = ±. Figure 1a depicts the full system-reservoir coupling scheme with the BEC interacting with outgoing transverse modes and a probe laser in mode (k0, σ0) for a duration tm.

During this time the atomic ensemble scatters monochromatic light into outgoing modes of wavevector k⊥ with coupling strength

$${g}_{\sigma }\left({{{{{{\bf{k}}}}}}}_{\perp }\right) \equiv -i{\left(\frac{{\omega }_{{{{{{\rm{ge}}}}}}}}{2{{\hslash }}{\epsilon }_{0}}\right)}^{1/2}\left[{{{{{{\bf{d}}}}}}}_{{{{{{\rm{ge}}}}}}}\cdot {{{{{{\boldsymbol{\epsilon }}}}}}}_{\sigma }\left({{{{{{\bf{k}}}}}}}_{\perp }\right)\right].$$
(3)

Since each outgoing mode is in a specific polarization state ϵ(k⊥) the polarization subscript is redundant.

Assuming that the probe laser of wavelength λ occupies a single optical mode (k0, σ0) with k0 ≡ |k0| = 2π/λ, we make the replacement \({\hat{a}}_{\sigma }\left({{{{{\bf{k}}}}}}\right)\to \delta \left({{{{{\bf{k}}}}}}-{{{{{{\bf{k}}}}}}}_{0}\right){\delta }_{\sigma ,{\sigma }_{0}}{\alpha }_{0}+{\hat{a}}_{\sigma }\left({{{{{\bf{k}}}}}}\right)\), which describes a coherent driving field with amplitude α0. In this expression the modes \({\hat{a}}_{\sigma }\left({{{{{\bf{k}}}}}}\right)\) are initially empty. This replacement allows us to expand Eq. (1) in decreasing powers of the large parameter α0. The leading term describes the ac Stark shift, and the next term

$${\hat{H}}_{\rm eff}=\frac{{{\hslash }}{P}_{{{{{{\rm{e}}}}}}}^{1/2}}{{\left(c{t}_{{{{{{\rm{m}}}}}}}\right)}^{1/2}}{\oint }_{{k}_{0}}\frac{{d}^{2}{{{{{{\bf{k}}}}}}}_{\perp }}{{\left(2\pi \right)}^{2}}{g}^{* }\left({{{{{{\bf{k}}}}}}}_{\perp }\right){\hat{n}}_{{{{{{\mathcal{F}}}}}}}\left({{{{{{\bf{k}}}}}}}_{\perp }-{{{{{{\bf{k}}}}}}}_{0}\right){\hat{a}}^{{{\dagger}} }\left({{{{{{\bf{k}}}}}}}_{\perp }\right)+{{{{{\rm{H}}}}}}.{{{{{\rm{c}}}}}},$$

describes scattering from the probe field into outgoing modes by any structure in the atomic density, with Fourier components

$${\hat{n}}_{{{{{{\mathcal{F}}}}}}}\left({{{{{{\bf{k}}}}}}}_{\perp }-{{{{{{\bf{k}}}}}}}_{0}\right)=\int \frac{{d}^{3}{{{{{\bf{k}}}}}}}{{\left(2\pi \right)}^{3}}{\hat{b}}^{{{\dagger}} }\left[{{{{{\bf{k}}}}}}-\left({{{{{{\bf{k}}}}}}}_{\perp }-{{{{{{\bf{k}}}}}}}_{0}\right)\right]\hat{b}\left({{{{{\bf{k}}}}}}\right).$$

Here \({P}_{{{{{{\rm{e}}}}}}}={|{\alpha }_{0}{g}_{{\sigma }_{0}}({{{{{{\bf{k}}}}}}}_{0})|}^{2}/{\varDelta }^{2}\) is the excited state occupation probability. In the far-detuned limit, the outgoing wavenumber is fixed at k0 leading to the surface integral over the sphere of radius k0.

We model the larger environment as performing measurements on the outgoing light in the far-field with an ideal photo detection process, a strong measurement of the photon density \({\hat{a}}^{{{\dagger}} }\left({{{{{{\bf{k}}}}}}}_{\perp }\right)\hat{a}\left({{{{{{\bf{k}}}}}}}_{\perp }\right)\) (Fig. 1b). In the abstract, this process begins with the combined system reservoir state \({{{{{\rm{|}}}}}}0{{\rangle }}\otimes {{{{{\rm{|}}}}}}{\Psi }_{{{{{S}}}}}{{\rangle }}\), describing a reservoir with no photons but with the system in an arbitrary state. This state evolves briefly for a time tm via the time evolution operator \({\hat{U}}_{{SR}}\left({t}_{{{{{{\rm{m}}}}}}}\right)\,{{{{{\mathscr{=}}}}}}\,{{{{{\mathcal{T}}}}}}{{\exp }}[-i{\int }_{-{t}_{{{{{{\rm{m}}}}}}}/2}^{{t}_{{{{{{\rm{m}}}}}}}/2}{\hat{H}}_{{{{{{\rm{eff}}}}}}}\left(t\right){dt}/{{\hslash }}]\). This entangles the system and reservoir; as depicted in Fig. 1a amplitude can be present in every reservoir mode prior to measurement by the environment.

Photodetection

We turn to the photodetection model shown in Fig. 1b. In this case, the measurement of the reservoir collapses the superposition by measuring either no photons or a single photon in final state |k⊥〉. The back-action of this measurement is described by a conditional change in the system wavefunction \({{{{{\rm{|}}}}}}{\Psi }_{S}^{{\prime} }{{\rangle }}=\hat{M}\left({{{{{{\bf{k}}}}}}}_{\perp }\right){{{{{\rm{|}}}}}}{\Psi }_{S}{{\rangle }}\), an operation described by Kraus operator \(\hat{M}\left({{{{{{\bf{k}}}}}}}_{\perp }\right)={{\langle }}{{{{{{\bf{k}}}}}}}_{\perp }{{{{{\rm{|}}}}}}{\hat{U}}_{{SR}}\left({t}_{{{{{{\rm{m}}}}}}}\right){{{{{\rm{|}}}}}}0{{\rangle }}\). Taken together this schema is a generalized measurement of the system effected by projective measurements on the reservoir.

In the limit of small tm, such that at most one photon is scattered, we obtain the Kraus operator

$$\hat{M}\left({{{{{{\bf{k}}}}}}}_{\perp }\right) =-i{P}_{{{{{{\rm{e}}}}}}}^{1/2}{\left(\frac{{t}_{{{{{{\rm{m}}}}}}}}{c}\right)}^{1/2}{g}^{* }\left({{{{{{\bf{k}}}}}}}_{\perp }\right){\hat{n}}_{{{{{{\mathcal{F}}}}}}}\left({{{{{{\bf{k}}}}}}}_{\perp }-{{{{{{\bf{k}}}}}}}_{0}\right)$$
(4)

describing the recoil of the system from momentum-conserving scattering out of every occupied state.

The Kraus operator contains information both about the change in the system as well as the probability density

$$P\left({{{{{{\bf{k}}}}}}}_{\perp }\right) \equiv {{\langle }}{\varPsi }_{S}{{{{{\rm{|}}}}}}{\hat{M}}^{{{\dagger}} }\left({{{{{{\bf{k}}}}}}}_{\perp }\right)\hat{M}\left({{{{{{\bf{k}}}}}}}_{\perp }\right){{{{{\rm{|}}}}}}{\varPsi }_{S}{{\rangle }}\\ =\frac{{t}_{{{{{{\rm{m}}}}}}}{P}_{{{{{{\rm{e}}}}}}}}{c}{\left|g\left({{{{{{\bf{k}}}}}}}_{\perp }\right)\right|}^{2}{{\langle }}{\varPsi }_{S}{{{{{\rm{|}}}}}}{\left|{\hat{n}}_{{{{{{\mathcal{F}}}}}}}\left({{{{{{\bf{k}}}}}}}_{0}-{{{{{{\bf{k}}}}}}}_{\perp }\right)\right|}^{2}{{{{{\rm{|}}}}}}{\varPsi }_{S}{{\rangle }}$$
(5)

that this change occurred. Bringing \({\left|{\hat{n}}_{{{{{{\mathcal{F}}}}}}}\right|}^{2}\) into a normal-ordered form shows that the scattering probability has two contributions. For a BEC with condensate mode \(\widetilde{\psi }\left({{{{{\bf{k}}}}}}\right)\) the scattering probability is

$$P\left({{{{{{\bf{k}}}}}}}_{\perp }\right) =\frac{{t}_{{{{{{\rm{m}}}}}}}{P}_{{{{{{\rm{e}}}}}}}}{c}{\left|g\left({{{{{{\bf{k}}}}}}}_{\perp }\right)\right|}^{2}N\left[\left(N-1\right){\left|{n}_{{{{{{\mathcal{F}}}}}}}\left({{{{{{\bf{k}}}}}}}_{0}-{{{{{{\bf{k}}}}}}}_{\perp }\right)\right|}^{2}+1\right],$$

where in analogy with the operator expression, \({n}_{{{{{{\mathcal{F}}}}}}}\left({{{{{{\bf{k}}}}}}}_{0}-{{{{{{\bf{k}}}}}}}_{\perp }\right)\) describes the Fourier components of the probability-density. The first term describes collective scattering from the overall density profile (including thermal fluctuations), a.k.a. classical scattering23, while the second results from scattering from quantum fluctuations, here giving rise to spontaneous emission. For extended systems such as our BEC, the collective term is dominated by small angle forward scattering while the spontaneous term is nominally isotropic. Notably, this result illustrates that the ratio between collective and spontaneous scattering depends on N but not the measurement parameters.

Integrating over the final k⊥ states gives \({P}_{{{\rm{tot}}}}={P}_{{{\rm{col}}}}+{P}_{{{\rm{sp}}}}\) with the spontaneous scattering probability \({P}_{{{\rm{sp}}}}=\varGamma {t}_{{{{{{\rm{m}}}}}}}{P}_{{{{{{\rm{e}}}}}}}={g}^{2}/8\). We introduced an overall measurement strength \(g=\sqrt{{\bar{t}}_{{{{{{\rm{m}}}}}}}\bar{I}}/\bar{\delta }\) in terms of dimensionless: time \({\bar{t}}_{{{{{{\rm{m}}}}}}}=\varGamma {t}_{{{{{{\rm{m}}}}}}}\) scaled by the natural linewidth Γ; detuning \(\bar{\delta }=\varDelta /\varGamma\) in units of Γ; and laser intensity \(\bar{I}=I/{I}_{{{\rm{sat}}}}\) in units of the saturation intensity Isat. Thus when \(g=\sqrt{8}\) each atom will have on average spontaneously scattered a single photon (The relation between g and the signal to noise ratio of a measurement outcome is briefly discussed in Supplementary Note 1.).

In experiment, a single measurement pulse can lead to thousands of photodetection events, each described by a Kraus operator. The concatenation of many such Kraus operators—one for each scattering event—describes the evolution of our system. By contrast with master equation methods that trace out the environment, quantum trajectories approaches predict individual measurement outcomes and the associated back-action, drawn from a suitable statistical distribution. Thus, the final post-measurement state can be predicted given an experimentally observed measurement record. For ensemble averaged predictions, our technique and standard methods such as those used in Appel et al.24 give the same results. We compare the predictions of this theoretical description with an observable, contrast in a Ramsey interferometer, that does not rely on knowledge of the specific quantum trajectory that the system followed.

Experimental system

Our experiments started with highly elongated 87Rb BECs prepared in a crossed optical dipole trap (ODT) with frequencies \(({\omega }_{x},{\omega }_{y},{\omega }_{z})=2\pi \times [9.61(3),113.9(3),163.2(3)]\ {\rm Hz}\) in the \({{{{{\rm{|}}}}}}{g}_{1}{{\rangle }}\equiv |F=1,{m}_{F}=1\rangle\) electronic ground state (All uncertainties herein reflect the uncorrelated combination of single-sigma statistical and systematic uncertainties). This trap configuration yielded condensates with Nc = 0.70(15) × 105 atoms25,26, condensate fraction Rc = 78(3)%, and chemical potential \(\mu=h\times0.76(6)\ {\rm kHz}\). We drove transitions between |g1〉 and \({{{{{\rm{|}}}}}}{g}_{2}{{\rangle }}\equiv {{{{{\rm{|}}}}}}F=2,{m}_{F}=2{{\rangle }}\) using an ≈ 6.8 GHz microwave magnetic field with Rabi frequency ≈ 7.5 kHz.

In our experiments we illuminated the BEC in situ with an off-resonant probe laser beam that drove the |g2〉 to \({{{{{\rm{|}}}}}}e{{\rangle }}\equiv {{{{{\rm{|}}}}}}{F}^{{\prime} }=3,{m}_{F}^{{\prime} }=3{{\rangle }}\) ground to excited state transition. This probe laser was blue detuned by \(0 \, < \, \bar\delta \, < \, 317\), and had intensity \(\bar I \, \lesssim \, 10\). We theoretically describe the light scattered at large angle as being subsequently projectively measured by the environment, as described above. We then detected the post-measurement density distribution using absorption imaging after a longer 20 ms TOF during which a Stern-Gerlach gradient spatially separated the |g1〉 and |g2〉 components.

Detecting wavefunction change via Ramsey interferometry

We characterize the light matter interaction, as well as back-action, predicted by our quantum trajectories model using Ramsey interferometry (RI). Our Ramsey interferometer (Fig. 1d, e) commenced with a resonant microwave pulse driving a π/2 rotation about ey, taking the atoms from −ez (in |g1〉) to ex. Then during the free evolution time we applied the probe laser detuned by \(\bar{\delta }\) from the |g2〉 to |e〉 transition for a time tm; the resulting ac Stark shift drove a rotation about ez by ϕ (solid red arc). A second microwave pulse drove a π/2 rotation about an axis rotated by δϕP at which time we measured the final populations N1 and N2 in |g1〉 and |g2〉 respectively in TOF, giving the fraction in |g2〉 as R2 = N2/(N1 + N2). The black data (squares) in Fig. 2a, taken with the probe laser off, shows that the resulting fractional population R2 is cosinusoidal, and the red data (circles), with the probe on, is phase shifted (from the ac Stark shift on |g2〉). We obtain the phase shift ϕ, contrast A, and center shift b with fits to \({R}_{2}=\left[1+A{{\cos }}\left(\delta {\phi }_{P}+\phi \right)\right]/2+b\).

Fig. 2: Ramsey interferometry data.
figure 2

a Ramsey oscillation without (black squares) and with the light pulse at \(\bar{\delta }=63.4\) and \(\bar{I}\approx 2\) (red circles) and \(\bar{I}\approx 7\) (blue triangles), taken in situ as the phase jump δϕP between the two pulses is varied. Solid curves are fits to the equation given in the text. Blue Ramsey data δϕP values are deliberately shifted by 2π to visualize the reduction in contrast and the larger phase shift. b Optically induced phase shift ϕ as a function \(\bar{I}\) at \(\bar{\delta }=63.4\) (red circles) and \(\bar{\delta }=116.2\) (green squares). The same-color lines are fits to \(-V_{\rm ac} t_{\rm m} / \hbar\ {\rm mod}\ 2\pi\). Shaded regions indicate the ±1σ statistical uncertainty range.

Full size image

The RI phase shift is a direct measure of the differential phase acquired during free evolution, here \(-V_{\rm ac} t_{\rm m} / \hbar\) from the ac Stark shift of |g2〉 due to the probe beam, with \({V}_{{{{{{\rm{ac}}}}}}}=\varGamma \bar{I}/\left(8\bar{\delta }\right)\). The Stark shift of |g1〉 is a small contribution that we do not include in our fits. The data in Fig. 2b was taken at \(\bar{\delta }=63.4\) and 116.2 (circles and squares respectively). As expected the slope is larger for smaller \(\bar{\delta }\), but in both cases the acquired phase can exceed 2π at which point it wraps back to zero. The intensity of the probe laser is difficult to obtain in vacuo27,28; however, fitting tmVac to these data gives a direct calibration of the laser intensity, providing a conversion between our camera signal and Isat with <5% fractional uncertainty. We imaged the in situ probe beam (with no atoms present) on a charge coupled device camera to obtain the local probe intensity (in arbitrary camera units) at the location of the BEC. Further details are described in Altuntas et al.29. The solid lines in Fig. 2b are the result of this fitting process.

Figure 2a shows a second effect of increasing measurement strength (blue data): the Ramsey contrast decreases with increasing measurement strength, implying that the post-measurement many-body wave function is not described by a coherent superposition of |g1〉 and |g2〉.

Our measurement model predicts this effect: as illustrated in the middle Bloch sphere in Fig. 1e, each time a photon is spontaneously scattered and detected by the environment, the wavefunction of a single atom collapses into |g2〉 (along ez), losing any coherence with |g1〉 (red dashed arrows). The second π/2 pulse always returns that atom to the equator of the Bloch sphere, reducing the contrast by 1/N. In this situation, the per-atom probability of scattering a single photon at large angle is g2/16 (see Supplementary Note 2 for the complete calculation). By contrast for collective scattering (generally at small-angle), a detected photon scattered off of the global density distribution yields Mössbauer-like collective back-action and no reduction in contrast. As a result, the change in contrast measures the number of spontaneously scattered photons24.

The ideal Ramsey interferometry scheme presented in Fig. 1d is sensitive to additional systematic effects leading to contrast reduction. In the following sections we identify such factors, and develop an enhanced RI scheme that detects the post-measurement wavefunction change in agreement with the theoretical prediction.

Spin-echo Ramsey interferometer

Spatial inhomogeneities in the probe beam as well as near-dc magnetic field noise can reduce the RI contrast. In the first case, the resulting position-dependent ac Stark shift imprints spatial structure to the RI phase ϕ, thereby reducing the spatially averaged contrast. Second, because the |g1〉-|g2〉 transition is first-order sensitive to the external magnetic field, the RI contrast is reduced when field noise randomly shifts the resonance condition between different repetitions of the experiment.

We added a spin-echo pulse to our interferometer (Fig. 3a) to compensate for both of these parasitic effects. As Fig. 3c shows, the noise in the spin-echo signal (circles) is reduced compared to the standard RI measurement (squares). Although the measurement noise is reduced, the contrast with spin echo is unchanged (Fig. 4a, b), leaving the substantial disagreement with our theory prediction (black curve) due to the systematic factor we report next.

Fig. 3: Improved Ramsey interferometers.
figure 3

a, b Pulse sequences for spin-echo (SE) and pulse-evolve-pulse with spin-echo (PEP-SE) Ramsey interferometers. The red blocks denote the dispersive measurement pulses, and blue bars indicate the microwave pulses. c Interferometer signal measured using: a conventional Ramsey sequence (blue squares), a spin-echo Ramsey sequence (green circles), and a pulse-evolve-pulse with spin-echo sequence (magenta diamonds). All measurements were performed in situ at \(\bar{\delta }=63.4\) with \(\bar{I}\approx 7\) yielding g ≈ 1.

Full size image
Fig. 4: Ramsey interferometer contrast A dependence on the measurement strength g for different schemes.
figure 4

a In situ Ramsey interferometry measurements. b In situ Ramsey interferometry with spin-echo measurements. c In situ Pulse-evolve-pulse with spin-echo Ramsey interferometry measurements. d Pulse-evolve-pulse with spin-echo sequence after 2 ms TOF measurements. The horizontal blue lines show the RI contrast observed without the measurement pulse with the shaded regions indicating the ±1σ statistical uncertainty range. The black curves plot the prediction of our photodetection model. The pink curves depict a fit of the \(\bar{\delta }=63.4\) data to A = A0 − αg2 with each best-fit alpha value quoted on the respective figure.

Full size image

Ramsey interferometer with split measurement pulses

Contrary to our predictions, Fig. 4a, b show that the contrast depends on probe detuning (green squares versus red circles). This difference signifies the presence of the second parasitic effect: a weak optical lattice generated by the probe beam interfering with its retro-reflections off subsequent optical elements. The probe beam is nearly perfectly concentric with our imaging system and intersects each optical element at normal incidence. While it is common practice in optical setups to slightly tilt optical elements to eliminate back-reflections, in the high-resolution imaging context optimized alignment is a necessary condition for minimizing optical aberrations.

As a result, each probe pulse corresponds to the sudden application of a lattice potential. Weak lattices create populations in matter-wave diffraction orders with momentum ±2ℏk0. In principle a suitable spin-echo sequence could remedy this, nonetheless, the rapidly moving diffracted atoms experience different lattice potentials during our first and second pulses precluding effective cancellation.

Instead we extended the ideas in Wu et al.30 and Herold et al.31 by splitting each probe pulse into two pulses of duration tp = 8.2 μs spaced in time by a carefully chosen td = 25.6 μs of free evolution, essentially unwinding the phase imprinted by the lattice (see Supplementary Note 3). Figure 3b shows such a pulse-evolve-pulse with spin-echo (PEP-SE) sequence. The near-full contrast magenta Ramsey fringe in Fig. 3c results from this PEP-SE sequence applied in situ for g ≈ 1. As seen in Fig. 4c, there is negligible difference in the extracted contrast between measurements at the same g value but with different probe detunings (squares and circles), further confirming control over systematic effects. The PEP-SE Ramsey contrast is in good agreement with our theoretical model (black curve) and provides a mechanism for identifying the regime of back-action limited measurements of ultracold gases. In order to obtain a quantitative metric for comparison with theoretical prediction, we fit the \(\bar{\delta }=63.4\) data in g ≤ 1 to A = A0 − αg2, where A0 describes a small overall reduction in contrast. PEP-SE scheme measurements yield α = 0.083(10), which is in good agreement with the theoretical prediction αth = 1/16 ≈ 0.063.

Light-induced collisions

We used the post-measurement atom number as an auxiliary probe of measurement back-action and found that, although photoassociation (PA) is suppressed at blue detuning, at our high in situ atomic densities of 1 × 1014 cm−3, light-induced collisions lead to rampant atom loss15. We quantify the importance of these losses by preparing BECs with N0 total atoms in |g2〉 and measuring fractional change in total atom number Nt/N0 and in uncondensed number Nnc/N0. Nnc/N0 counts both thermal atoms as well as atoms that have undergone large-angle light scattering.

Figure 5a confirms that this is a 2-body process by reducing the atomic density with a short TOF. We find that the losses rapidly drop starting at tTOF ≈ 0.5 ms (when mean-field driven expansion becomes significant) and vanish after 3 ms (at which time the density has dropped by a factor of nearly 20). We also investigated another potential loss mechanism due to two-color PA resulting from the combination of the intense dipole trapping beam and the probe beam. Data taken just before (star symbols at negative time for clarity) and just after the ODT turn-off have no difference in loss, confirming the absence of any two-color PA effects.

Fig. 5: Light-induced collisions.
figure 5

Fractional total number of atoms (green squares) and number of atoms outside the BEC but within a 1 recoil momentum circle (blue circles) following measurement. The symbols mark experimental data while the curves are the result of our 2-body model. In all cases, the opacity of the points reflects the detuning. a Dispersive measurements at two different probe detunings (\(\bar{\delta }=84.5\) and \(\bar{\delta }=126.7\)) after a variable short time-of-flight (TOF). All measurements were at measurement strength g ≈ 1, which was attained by adjusting intensity to \(\bar{I}\approx 9.5\) and \(\bar{I}\approx 21\) respectively. Star symbols mark in situ measurements with the optical dipole trap on (plotted at negative TOF for display purposes). b In situ measurements at different \(\bar{\delta }\) all with g ≈ 1. Measurement time was tm = 25 μs in a and b. c, d Loss as a function of g2 for measurements made in situ in c and with a 2 ms TOF in d. The red dashed line in d plots the expected g2/8 light-scattering behavior. Both cases were at \(\bar{\delta }=84.5\) and \(\bar{I}\approx 9.5\) with tm varied from 4 to 36 μs.

Full size image

Panel b, taken in situ, shows that the fractional number is independent of \(\bar{\delta }\). These data were taken at constant Pe (achieved by tuning \(\bar{I}\)) and demonstrate that there are no PA resonances. Figure 5c shows that in situ the total number drops rapidly with increasing g2 while the number outside the BEC remains constant. This verifies that the high-density BEC experiences light-induced collisions while the low density thermal cloud is left mostly unchanged. Lastly Fig. 5d plots these quantities following a 2 ms TOF, confirming the same reduced losses found in Fig. 5a. Furthermore Nnc increases linearly with slope g2/8 (red dashed curve) as expected from photon scattering.

All of these data are well described by a 2-body loss model (solid curves), however, these simulations require a 2-body coefficient that is about 20 × in excess of the PA loss coefficient found in Fuhrmanek et al.32. In fact these observations reflect different processes: in the blue-detuned case light-induced collision leads to rapidly accelerated atom pairs rather than PA33.

Lastly, we note that light traversing the BEC acquires a phase shift causing the atomic cloud to act as a lens. When the phase shift is in excess of about 1 radian the scattering is no longer described by our model and atomic cloud experiences excess compression, potentially enhancing 3-body loss. The absence of \(\bar{\delta }\) dependence in Fig. 5b affirms that effects such as this arising from the ac Stark shift do not contribute to loss.

As light-assisted collisions precipitate atom loss, we added a short TOF to the spin-echo pulse-evolve-pulse Ramsey sequence to study the impact of light-assisted collisions on RI contrast. As shown in Fig. 4d, the contrast is modestly reduced, and as with Fig. 4a, b, data taken at larger detuning are impacted more significantly. We attribute this reduction to the changing optical intensity profile that the falling BEC experiences as it traverses different regions of the probe beam during the pulse sequence; this compromises the PEP-SE sequence.

Discussion

Even though RI contrast is a direct measure of the overall wavefunction change, our light-assisted collision data show that RI contrast alone is insufficient to identify back-action dominated measurement regimes. For our in situ results—with rampant light-induced losses—photon scattering from the measurement process does not fully explain the change of the system’s state. Consequently such measurements are not back-action limited, even in principle. An interesting question that we did not touch on, is how light-induced collisions are able to remove atoms while leaving the Ramsey contrast largely unchanged.

For the modest range of detuning explored here, the two-body loss rate scales as the excited state probability Pe ∝ g2; this implies that for a target measurement strength, light-induced collisions are not reduced until vastly larger detuning when this scaling breaks down34. In our experiment, data taken with g ≲ 0.3 (with per-atom spontaneous scattering probability \({P}_{{{{{{\rm{sp}}}}}}} \, \lesssim \,0.01\)) had no discernible loss in Ramsey contrast or reduction in atom number: functionally non-destructive16. However, our results demonstrate that such functionally non-destructive measurements can be far from quantum back-action limited. As a consequence, back-action limited measurements of BECs can be achieved either by managing the atom density, or by careful control of molecular resonances35. In degenerate Fermi gases the Pauli pressure leads to much lower densities36, typically diluted by an order of magnitude or more compared to BECs, making two-body losses less significant.

Employing the strategies identified here is necessary to achieve back-action limited measurements, and as a next step the scattered light must actually be detected. There are multiple imaging techniques for quantum gases based on the dispersive light-matter interaction16,20,37,38 that in principle can give back-action limited measurement outcomes. Implementing these requires an imaging system with minimal losses and large numerical aperture in conjunction with a high efficiency detector, as any scattered light that is not detected is effectively measured by the environment and its information lost. Furthermore, the captured signal must lead to a faithful representation of the atomic ensemble, necessitating an imaging system with minimal or well-calibrated aberrations as we demonstrated previously21. Lastly, the initial optical field must be well known, for which techniques such as outlined here and described in more detail in Altuntas et al.29, are essential. These physical considerations do not touch on technical matters such as calibrating the response and hardware specific noise properties of the physical detector, i.e., a charge coupled device (CCD) or complementary metal oxide semiconductor (CMOS) camera. Future work needs to account for these sources of technical noise.

Looking forward, back-action limited weak measurements coupled with real-time control are enabling tools for quantum technology. Feedback cooling is one application of closed loop quantum control, and the interplay between measurement back-action and the actual information extracted from the system limits the achievable temperature39,40,41. In addition to simply cooling into established quantum states (both weakly and strongly correlated), closed-loop feedback enables the engineering of artificial, non-local, and non-Markovian, reservoirs. Existing proposals with engineered reservoirs show that suitable quantum jumps lead to equilibration into strongly correlated states42; and schemes using feedback can generate new Mott insulating phases43 and squeezed states44,45. In the latter case a single measurement locally creates conditional squeezing that requires a second spatially resolved control pulse—conditioned on the measurement outcome—to obtain useful unconditional squeezing. Metrological implementations would also require atoms individually confined in the sites of an optical lattice to prevent spatial diffusion and clock shifts.

In addition, weak measurements offer new ways to explore fundamental concepts in quantum mechanics. For example, a weak measurement of strength g can be decomposed into a series of N sub-measurements46,47 each with strength \(g/\sqrt{N}\). In this configuration, the total outcome of these measurements recovers an individual measurement of strength g, but the quantum back-action of earlier sub-measurements correlates with the outcome of later sub-measurements, giving information that is erased in a single stronger measurement. For example, correlating the outcome of two sub-measurements can isolate the measurement back-action of the first measurement.

Methods

Magnetic field lock

Our interferometry measurements operate on the magnetic field sensitive \({{{{{\rm{|}}}}}}F=1,{m}_{F}=1{{\rangle }}\) to \({{{{{\rm{|}}}}}}F=2,{m}_{F}=2{{\rangle }}\) transition, and as a result are negatively impacted by magnetic field noise. To minimize any effect on contrast, we monitored the field shifts using a microwave based monitoring scheme first implemented in LeBlanc et al.48.

Our two level system is well described by the Hamiltonian

$$\begin{array}{cc}{\hat{H}}_{{{{{{\rm{\mu }}}}}}} & =\frac{{{\hslash }}}{2}\left(\begin{array}{cc}{\varDelta }_{\mu }+{\delta }_{\mu } & {\varOmega }_{\mu }\\ {\varOmega }_{\mu } & -\left({\varDelta }_{\mu }+{\delta }_{\mu }\right)\end{array}\right),\end{array}$$

where Δμ describes an unknown detuning from resonance, δμ is an adjustable detuning, and Ωμ is the microwave Rabi frequency.

Our protocol began with optically trapped atoms just above Tc in the \({{{{{\rm{|}}}}}}F=1,{m}_{F}=1{{\rangle }}\) hyperfine state. We applied a microwave pulse of duration \({t}_{\mu }=100\,\mu {{{{{\rm{s}}}}}}\) and Rabi frequency \({\varOmega }_{\mu }/\left(2\pi \right)\approx 0.1/{t}_{\mu }\) detuned by \(\delta_\mu/(2\pi) = 1/(2t_{\mu}) = 5\ {\rm kHz}\) from resonance and absorption-imaged the atoms transferred to \({{{{{\rm{|}}}}}}F=2,{m}_{F}=2{{\rangle }}\) in-situ (≈ 10% fractional transfer) leaving \({{{{{\rm{|}}}}}}F=1,{m}_{F}=1{{\rangle }}\) state atoms undisturbed. We used these data to obtain the transferred atom number N+. Then after a ≈ 34 ms delay, we repeated the processes with \(\delta \to -\delta\), giving N−. The delay between the transfer pulses was selected to be an integer multiple of the \(T_{\rm line} = (60\ {\rm Hz})^{-1} \approx 17\ {\rm ms}\) line period.

The fractional imbalance between the transferred numbers

$$\begin{array}{cc}\varepsilon & =\frac{{N}_{+}-{N}_{-}}{{N}_{+}+{N}_{-}}\approx -4{t}_{\mu }\frac{{\varDelta }_{\mu }}{2\pi },\end{array}$$
(6)

provides an error signal that can be related to any overall shift in detuning Δμ (see Supplementary Fig. 2 in Supplementary Note 4). For example ϵ = 0.5 corresponds to a detuning of just \(\Delta_\mu/ 2\pi \approx 1.25\ {\rm kHz}\).

We employed a two step procedure to minimize the impact of field noise during interferometry experiments. First, prior to any measurement sequence we optimized the bias field to minimize δB. Second, we post-selected data to exclude cases with |ϵ| > 0.5; this value was determined empirically to retain most of the data while notably removing outliers in measured contrast.

Lattice pulse sequence

An intuitive picture of our scheme for mitigating the effect of the optical lattice begins with a three-state truncation30,31 of the full lattice Hamiltonian

$$\begin{array}{cc}\frac{\hat{H}\left(k\right)}{{E}_{0}} & = \left(\begin{array}{ccc}{\left(k+2{k}_{0}\right)}^{2} & s/4 & 0\\ s/4 & {k}^{2} & s/4\\ 0 & s/4 & {\left(k-2{k}_{0}\right)}^{2}\end{array}\right),\end{array}$$
(7)

describing a lattice of depth sE0, with single photon recoil momentum \({{\hslash }}{k}_{0}=2\pi {{\hslash }}/\lambda\), energy \({E}_{0}={{{\hslash }}}^{2}{k}_{0}^{2}/\left(2m\right)\), and time \({T}_{0}={2\pi {{\hslash }}}/{{E}_{0}}\approx 265\ \mu{{{{{\rm{s}}}}}}\). For atoms initially at rest, i.e. k = 0, this is a resonant lambda coupling scheme with bright state subspace spanned by \({{{{{\rm{|}}}}}}{b}_{0}{{\rangle }}={{{{{\rm{|}}}}}}k=0{{\rangle }}\) and \({{{{{\rm{|}}}}}}{b}_{1}{{\rangle }}=\left({{{{{\rm{|}}}}}}k=+2{k}_{0}{{\rangle }}+{{{{{\rm{|}}}}}}k=-2{k}_{0}{{{{\rangle}}}}\right)/\sqrt{2}\) and an uncoupled dark state \({{{{{\rm{|}}}}}}d{{\rangle }}=\left({{{{{\rm{|}}}}}}k=+2{k}_{0}{{\rangle }}-{{{{{\rm{|}}}}}}k=-2{k}_{0}{{\rangle }}\right)/\sqrt{2}\).

Since our initial state |k = 0〉 is in the bright state manifold, we focus on the bright state Hamiltonian

$$\frac{{\hat{H}}_{{{{{{\rm{b}}}}}}}\left(0\right)}{{E}_{0}} =\left(\begin{array}{cc}0 & s/\left(2\sqrt{2}\right)\\ s/\left(2\sqrt{2}\right) & 4\end{array}\right)\\ =2\hat{I}+\frac{1}{2}\left[4{\hat{\sigma }}_{z}+\frac{s}{\sqrt{2}}{\hat{\sigma }}_{x}\right].$$
(8)

When the lattice is off, this Hamiltonian describes Larmour precession around \({{{{{{\bf{e}}}}}}}_{z}\) with Rabi frequency \(4{E}_{0}/{{\hslash }}\) and when the lattice is on it describes precession about \(4{{{{{{\bf{e}}}}}}}_{z}+\left[s/\sqrt{2}\right]{{{{{{\bf{e}}}}}}}_{x}\) with Rabi frequency \(\sqrt{16+{s}^{2}/2}{E}_{0}/{{\hslash }}\). In the limit \(s\ll 4\sqrt{2}\), the axis of rotation is tipped by \(\theta =4s/\sqrt{2}\), and the Rabi frequency is nearly unchanged from \(4{E}_{0}/{{\hslash }}\). In Supplementary Note 3 Supplementary Fig. 1a plots the top of the Bloch sphere with two example orbits in this limit (dashed lines), both for zero (red) and non-zero s (blue).

The solid curves in Supplementary Fig. 1a show the trajectory for a two pulse sequence that also returns to the origin. In the small s limit, the condition to return to the initial state is \({t}_{{{{{{\rm{d}}}}}}}/{T}_{0}=1/8-{t}_{{{{{{\rm{p}}}}}}}/{T}_{0}\), where td is the delay time between pulses and tp is the pulse duration. Supplementary Fig. 1b plots the probability that the final state returns to k = 0 for a shallow lattice with s = 1 (computed using 7 momentum states). The red line indicates the predicted minimum which is in good agreement with the numerically evaluated optimum configuration.

Supplementary Fig. 1c plots the same quantity, now with s = 10, showing the narrow range of parameters for which our scheme is expected to be successful. For most parameters, the large s simulation is qualitatively different from the small s results, with the exception of very short pulse times and the region following our scheme. In practice we selected \(t_{\rm d} = T_0/10 = 26.5\ \mu{\rm s}\) and \(t_{\rm p} = T_0/32 = 8.2\ \mu{\rm s}\), marked by the red star in Supplementary Fig. 1c.

Conventional parameters

Here we outline the relationships between conventional experimental parameters and the relatively abstract quantities employed in deriving the coupling strength \({g}_{\sigma }\left({{{{{{\bf{k}}}}}}}_{\perp }\right)\) in Eq. (3).

We start with the coherent state amplitude α0 and relate it to the optical intensity

$$\begin{array}{c}I=\frac{1}{2}{\epsilon }_{0}c{\left|E\right|}^{2}={{\hslash }}{\omega }_{{{{{{\rm{ge}}}}}}}c{\left|{\alpha }_{0}\right|}^{2}.\end{array}$$
(9)

In the second statement we inserted the expression

$$\begin{array}{c}{\left|E\right|}^{2}=\frac{2{{\hslash }}{\omega }_{{{{{{\rm{ge}}}}}}}{\left|{\alpha }_{0}\right|}^{2}}{{\epsilon }_{0}}\end{array}$$
(10)

for the magnitude of the electric field. The saturation intensity is a key metric of the light-matter interaction; for arbitrary light polarization

$$\begin{array}{cc}{I}_{{{{{{\rm{s}}}}}}{at}} & = \frac{{\epsilon }_{0}c{\varGamma }^{2}{{{\hslash }}}^{2}}{4{\left|{{{{{{\boldsymbol{\epsilon }}}}}}}_{{\sigma }_{0}}\left({{{{{{\bf{k}}}}}}}_{0}\right)\cdot {{{{{{\bf{d}}}}}}}_{{{{{{\rm{ge}}}}}}}\right|}^{2}}.\end{array}$$
(11)

As detailed in the main text, \({{{{{{\bf{d}}}}}}}_{{{{{{\rm{ge}}}}}}}\) is the dipole matrix element for transitions between the ground and excited state with energy difference \({{\hslash }}{\omega }_{{{{{{\rm{ge}}}}}}}\) and where \({{{{{{\boldsymbol{\epsilon }}}}}}}_{\sigma }\left({{{{{{\bf{k}}}}}}}_{0}\right)\) are the polarization vectors as pairs of orthogonal vectors transverse to \({{{{{{\bf{k}}}}}}}_{0}\). In terms of these parameters the transition linewidth is

$$\begin{array}{cc}\varGamma & =\left(\frac{{\left|{{{{{{\bf{k}}}}}}}_{0}\right|}^{3}}{3\pi {{\hslash }}{\epsilon }_{0}}\right){\left|{{{{{{\bf{d}}}}}}}_{{{{{{\rm{ge}}}}}}}\right|}^{2}.\end{array}$$
(12)

We recall the standard definition for saturation intensity

$$\begin{array}{c}\frac{I}{{I}_{{{{{{\rm{s}}}}}}{at}}}=2{\left|\frac{\varOmega }{\varGamma }\right|}^{2},\end{array}$$
(13)

acquired from a more traditional treatment, where

$$\begin{array}{c}\varOmega =\left|{{{{{{\boldsymbol{\epsilon }}}}}}}_{{\sigma }_{0}}\left({{{{{{\bf{k}}}}}}}_{0}\right)\cdot {{{{{{\bf{d}}}}}}}_{{{{{{\rm{ge}}}}}}}\right|\frac{{E}_{0}}{{{\hslash }}}\end{array}$$
(14)

is the Rabi frequency. We next express Ω in terms of the coupling strength and the optical field amplitude α0 giving

$$\begin{array}{c}\varOmega =2\left|{g}_{{\sigma }_{0}}\left({{{{{{\bf{k}}}}}}}_{0}\right){\alpha }_{0}\right|.\end{array}$$
(15)

These relations allow us to bridge between conventional laboratory parameters and those employed in our model. For example, we combine Eqs. (9) and (11), to obtain

$$\begin{array}{c}\bar{I}=\frac{I}{{I}_{{{{{{\rm{s}}}}}}{at}}}=\frac{8{\left|{\alpha }_{{\sigma }_{0}}{g}_{{\sigma }_{0}}\left({{{{{{\bf{k}}}}}}}_{0}\right)\right|}^{2}}{{\varGamma }^{2}}\end{array}$$
(16)

in agreement with Eqs. (13) and (15).

We now turn to the scattering probability \({P}_{{{{{{\rm{sp}}}}}}}=\varGamma {t}_{{{{{{\rm{m}}}}}}}{P}_{{{{{{\rm{e}}}}}}}\), which contains the excited state probability

$$\begin{array}{cc}{P}_{{{{{{\rm{e}}}}}}} & =\frac{{\left|{\alpha }_{0}{g}_{\sigma }\left({{{{{{\bf{k}}}}}}}_{0}\right)\right|}^{2}}{{\varDelta }^{2}}.\end{array}$$
(17)

This, along with Eq. (16), allows us to rewrite the scattering probability as

$$\begin{array}{c}{P}_{{{{{{\rm{s}}}}}}p}={\left|{\alpha }_{0}{g}_{{\sigma }_{0}}\left({{{{{{\bf{k}}}}}}}_{0}\right)\right|}^{2}\frac{\varGamma {t}_{{{{{{\rm{m}}}}}}}}{{\varDelta }^{2}}=\frac{\varGamma {t}_{{{{{{\rm{m}}}}}}}}{8}\frac{I}{{I}_{{{{{{\rm{sat}}}}}}{}}}\frac{{\varGamma }^{2}}{{\varDelta }^{2}}.\end{array}$$
(18)

This expression is organized into the physically relevant dimensionless quantities \({\bar{t}}_{{{{{{\rm{m}}}}}}}\), \(\bar{I}\) and \(\bar{\delta }\) introduced in the main text. In the main text, we defined the overall measurement strength using these parameters and made the choice to not include the factor of 8 so

$$\begin{array}{c}{g}^{2}=\frac{I}{{I}_{{{{{\rm{sat}}}}}}}\frac{\varGamma {t}_{{{{{{\rm{m}}}}}}}}{{\left(\Delta /\varGamma \right)}^{2}}=8{P}_{{{{{{\rm{sp}}}}}}}.\end{array}$$
(19)

As such, a measurement strength of g2 = 1 signifies a probability of 1/8 for an atom to scatter a single photon at large angle.