Introduction

The spatiotemporal coupling, as an ever-changing optics tool, recently has been well studied to realize kinds of light sources for optical and physical applications1,2,3,4,5,6,7,8,9,10. Two recent representative examples are “flying focus” proposed by Sainte-Marie et al. and Froula et al.11,12 and “ST wave packet” proposed by H.E. Kondakci and A.F. Abouraddy13,14, which are special sets of spatiotemporal structured pulses15 and can propagate at any velocity, i.e., higher or lower than the light speed and forward or backward along the optical axis. The former has already been applied for overcoming dephasing in laser wakefield accelerators16, producing arbitrary velocity ionization waves17, etc. in strong-field optics, and the latter also has great potentials from optical imaging, microscopy, communication to micro-particle manipulation. Apart from wide-range tunable velocities and accelerations18,19,20,21, the ST wave packet has many other features, including diffraction-free22, tunable dispersion23,24, anomalous refraction25, anomalous ST dispersion effect26, veiled Talbot effect27, time diffraction28, etc., which would be certainly as important as “flying focus” in the strong-field optics. However, producing a ST wave packet needs to accurately control its ST spectrum in the Fourier space to introduce a necessary ST correlation that is transverse spatial-frequency dependent quasi-monochromatic spectral-frequency29,30,31, and in this process, a phase spatial light modulator (SLM) or phase plate is required at the Fourier plane of a grating 4-f setup14,32. The low damage threshold of SLM or phase plate determines that the ST wave packet generator cannot operate at a high energy level, and the same problem also occurs with other spatiotemporal optical fields generated by metasurfaces33,34,35. Consequently, an efficient amplifier is required, but which must keep the ST correlation unchanged. Because of a low gain (e.g., ~3 × per 7 mm in a conductive-cooled Yb:YAG36), the high-energy amplification of a population inversion amplifier with an energy-level laser medium requires a long-length propagation and/or a multiple-pass configuration, which consequently is not suitable here. OPA based on the three-wave coupling in a nonlinear crystal can realize a high gain within a thin crystal (e.g., 20 × per 0.5 mm in a 40 fs typeI-BBO OPA37 and 106 × per 15 mm in a 3 ps typeI-BBO OPA38), which might be an ideal amplifier for a ST wave packet. Previously, the phase matching of some localized waves, such as focused wave modes, X-waves, O-waves, etc., in nonlinear crystals has been studied, and the generation/amplification of the above localized waves in the optical parametric process has been investigated39,40,41,42,43. Recently, nonlinear effects of newly reported spatiotemporal pulsed beams with orbital angular momentum, optical vortices, arbitrary vectors, etc. also have been demonstrated44,45,46. All these works show that it is possible to amplify a ST wave packet in OPA.

In this article, we report, under the narrowband approximation, the ST spectrum (angle-dependent phase-matching spectrum) of the type-I collinear OPA has the same analytical expression with that of a ST wave packet, which accordingly is a natural amplifier for a ST wave packet. The amplified signal keeps the ST correlation of the incident ST wave packet, and the simultaneously generated idler also has a high ST correlation which therefore is another ST wave packet, forming a collinear-propagating double ST wave packet. In the non-degenerate OPA, two ST wave packets within the double ST wave packet at short- and long-wavelengths (relative to the degenerate-wavelength) have superluminal and subluminal velocities, respectively; and in the degenerate OPA, it becomes a luminal quasi-monochromatic (the degenerate-wavelength) plane-wave pulse. Our numerical simulation has verified the theoretical prediction and could also be applied in experiments.

Results

ST spectra of ST wave packet and OPA

Figure 1a shows in the Fourier space (momentum space) kx-kz-k that corresponds to the physical space (position space) x-z-t, where x and z are the transverse and longitudinal space axes and t is the time axis, the ST spectrum of a ST wave packet lies in the intersecting curve between the light-cone and a spectral plane parallel to the kx-axis13,14,18,19,20,21,22,23,24,25,26,27,28,29,30,31, and satisfies

$$\cos \varDelta \theta =\frac{{\omega }_{0}+\varOmega\cot \alpha }{{\omega }_{0}+\varOmega }\cdot$$
(1)
Fig. 1: Space-time (ST) spectra of space-time wave packet and optical parametric amplification (OPA).
figure 1

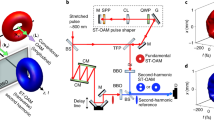
a ST spectrum of a ST wave packet lies in the intersecting curve between the light-cone and a tilted spectral plane parallel to the kx-axis (here two ST wave packets with spectral plane tilt angles α1 > 45° and α2 < 45°). Color of the light-cone schematically illustrates the frequency. b Three-wave coupling in the type-I OPA (here BBO). x-y-z and x’-y’-z’ are lab and crystal coordinates. θp is the pump angle with respect to the z’-axis. p, pump; s, signal; and i, idler. c Phase-matching (momentum conservation) and energy conservation diagrams for collinear OPA, non-collinear OPA, and ST wave packet OPA. Different colors of the arrows schematically illustrate different frequencies. d Phase-matching curves in a 515 nm pumped type-I BBO crystal when the pump angle θp varies from 23.02° to 23.42° every 0.1° (distinguished by colors). Degenerate, nondegenerate, collinear, and non-collinear zones are given. When a signal/idler lies in the solid line and at one side of kx = 0, its idler/signal lies in the dash line and at the other side of kx = 0.

Full size image

ω0 is the vertex frequency defined as the intersecting point between the ST spectrum and the plane kx = 0 at the direction kz > 0, its direction is the propagating direction of the ST wave packet, and its coordinates are (kx, kz, ω/c) = (0, k0, ω0/c). Ω = ω – ω0 is the frequency difference about ω0 of each spectral component, and Δθ is its propagating angle with respect to the direction of ω0 (or the ST wave packet) which is spectral-dependent. α is the tilt angle of the spectral plane with respect to the kz-axis, which determines the velocity of a ST wave packet vg/c = tanα19,29. Figure 1a illustrates a superluminal and a subluminal ST wave packets with α1 > 45° and α2 < 45° at high and low vertex frequencies ω0, respectively.

Figure 1b shows in the type-I (o + o → e) collinear OPA, three waves propagate along the z-axis, and the energy is transferred from the strong pump (e-light) to the amplified signal (o-light) and the generated idler (o-light) in a thin nonlinear crystal (BBO here). We define x-y-z and x’-y’-z’ are the lab and crystal coordinates, respectively; θs, θi, and θp are propagating angles of the signal, idler and pump in the x’-z’ plane of the crystal coordinates x’-y’-z’; and, because the pump always propagates at the z-axis in the lab coordinates x-y-z, Δθs = θs − θp and Δθi = θi − θp are propagating angles of the signal and idler in the lab coordinates x-y-z. The relative rotation angle θp between the x-y-z and x’-y’-z’ coordinates about the y/y’-axis changes the refractive index of the pump (e-light) in the crystal for phase-matching. Traditional collinear and non-collinear phase-matchings (momentum conservation) and energy conservation are illustrated in Fig. 1c. If a ST wave packet can satisfy the amplification condition, Fig. 1c shows the pump spectrum, signal spectral components and idler spectral components should firstly satisfy energy conversion ωs + ωi = ωp and secondly contain a collinear phase-matching ks0 + ki0 = kp for the vertex frequency ω0 of the signal and a series of spatially symmetric non-collinear phase-matchings kscosΔθs + kicosΔθi = kp for other frequencies ω = ω0 + Ω of the signal. And then, the pump beam and the signal and idler ST wave packets approximately form a collinear OPA. Although different spectral components of the signal and the idler have different but spatially symmetric propagating directions, the two propagation-invariant wave packets both propagate at the z-axis. Using a 515 nm pump, phase-matching curves for different pump angles θp from 23.02° to 23.42° every 0.1° are calculated and shown in Fig. 1d. Here, we use solid and dash curves denote the signal and idler, respectively, which are defined relative to each other and are interchangeable. The pump is always along kx = 0, for the collinear phase-matching, both the signal and idler are along kx = 0; and for non-collinear phase-matchings, the signal and idler are at either side of the pump. Comparing the angle-dependent phase-matching spectrum (here also named as ST spectrum) of the signal or idler (see Fig. 1d) with the ST spectrum of a ST wave packet (see Fig. 1a), they have quite similar profiles in the λ-kx (or ω/c-kx) plane, i.e., continuous symmetric conic curves about kx = 0. If two curves overlap with each other, all spectral components including the vertex frequency ω0 and the other frequencies ω = ω0 + Ω of a ST wave packet would be simultaneously amplified by collinear and non-collinear OPAs, respectively, generating an idler that is also a ST wave packet. The amplified signal and the generated idler would have different frequencies for the non-degenerate OPA and the same vertex frequency for the degenerate OPA, respectively.

To verify this judgment, we derived the analytical expression of the angle-dependent phase-matching spectrum (ST spectrum) of the type-I OPA under the narrowband approximation, which satisfies

$$\cos \varDelta {\theta }_{s}\approx \frac{{\omega }_{s0}+{\varOmega }_{s}({\omega }_{s0}{n}_{s}^{2}+\frac{{({\omega }_{p}{n}_{p}-{\omega }_{s0}{n}_{s})}^{2}}{{\omega }_{p}-{\omega }_{s0}})/{\omega }_{p}{n}_{p}{n}_{s}}{{\omega }_{s0}+{\varOmega }_{s}},$$
(2)

where, Δθs is the propagating angle of the frequency ωs = ωs0 + Ωs with respect to the vertex frequency ωs0 within the signal ST wave packet in the x-y-z coordinates, ns and np are angle-independent and angle-dependent refractive indices of the signal vertex frequency ωs0 (o-light) and the pump frequency ωp (e-light), respectively, and a constant ns is used for all frequencies of the signal under the narrowband approximation. By comparing Eq. (2) with (1), the ST spectrum (angle-dependent phase-matching spectrum) of the signal in the type-I OPA has the same expression with that of a ST wave packet, which indicates that a ST wave packet can be amplified by a matched type-I OPA.

Velocities of amplified and generated ST wave packets

From Eqs. (1) and (2), the requirement of amplifying a ST wave packet by a matched OPA is the tilt angle αs of the spectral plane forming the ST wave packet in the Fourier space needs to satisfy

$$\cot {\alpha }_{s}\approx \frac{{\omega }_{s0}{n}_{s}^{2}+\frac{{({\omega }_{p}{n}_{p}-{\omega }_{s0}{n}_{s})}^{2}}{{\omega }_{p}-{\omega }_{s0}}}{{\omega }_{p}{n}_{p}{n}_{s}}.$$
(3)

The refractive indices ns and np in the crystal can be calculated by the Sellmeier equation for ωs0 and ωp, respectively, and the pump angle θp is contained in np. Because three-wave coupling equations show the signal and idler are interchangeable in mathematics [see Eq. (5) in “Methods”], the generated idler is another ST wave packet, whose ST spectrum Δθi(Ωi) and spectral plane tilt angle αi are also respectively described by Eqs. (2) and (3) by simply replacing the subscript s by i. After OPA, a double ST wave packet would appear which contains the amplified signal as well as the generated idler.

When solving the collinear phase-matching [Eq. (5) in “Methods”] in a 515 nm pumped type-I BBO crystal, for every pump angle θp in the phase-matching region, two phase-matched vertex wavelengths λ0 of the signal and idler in a double ST wave packet can be calculated, and by substituting into Eq. (3), their velocities can be obtained (vg/c = tanα). Figure 2 shows the relationship among the pump angle, the vertex wavelength of the signal/idler and the velocity of the ST wave packet, and a signal/idler and its idler/signal lie in red and black curves, respectively. When the pump angle is θp < 23.32° or θp = 23.32°, OPA is nondegenerate or degenerate, respectively, and the double ST wave packet (i.e., signal and idler) has “different wavelengths and velocities” or “same wavelength and velocity”, respectively. In the nondegenerate OPA, the velocities of a double ST wave packet (i.e., signal and idler) are superluminal and subluminal when the vertex wavelengths are shorter and longer than the degenerate-wavelength (1030 nm here), respectively. In this case, the two ST wave packets (i.e., signal and idler) will separate in time during propagation, which can also be separated in spectrum. In the degenerate OPA, the signal and idler have the same vertex wavelength of the degenerate-wavelength (1030 nm here), the same spectral plane tilt angle of 45° in the Fourier space (see Eq. (3)) and accordingly the same velocity of the light speed (as introduced in refs. 19,31), and, in this case, the ST wave packets should become luminal plane-wave pulses. However, Fig. 1d shows because only the vertex wavelength satisfies OPA, other wavelengths cannot be amplified, and the amplified signal and the generated idler would become quasi-monochromatic (the degenerate-wavelength) luminal plane-wave pulses.

Fig. 2: Relationship between vertex wavelength and velocity of space-time (ST) wave packet with pump angle of collinear optical parametric amplification.
figure 2

When the collinear phase-matching is satisfied (515 nm pumped type-I BBO crystal here), each pump angle θp corresponds to two (vertex) wavelengths λ0 (red and black), and the (vertex) wavelength λ0 that is shorter (red) and longer (black) than the degenerate-wavelength (1030 nm here) corresponds to a ST wave packet with a superluminal (red) and a subluminal (black) velocity vg, respectively.

Full size image

Propagation invariance of amplified and generated ST wave packets

In addition to the strict phase-matching (Δk = 0), small phase-mismatchings (Δk → 0) can also support OPAs, and Fig. 3a, b show the gain spectra in a 2 mm thin type-I BBO crystal when the pump wavelength, angle, and intensity are 515 nm, θp = 23°, and 10 GW cm−2, respectively. Although two gain spectra in both short- and long-wave ranges have some ST correlations (see Fig. 3a, b), Fig. 3e, f show the supported pulsed beams have Gaussian ST distributions, which spread out dramatically in space after a 20 mm free propagation (see Fig. 3i, j). Kondakci et al. have defined a parameter of the correlation uncertainty δλ between kx and λ, which is inversely proportional to the propagation-invariant length13. Large correlation uncertainties δλ = 43 and 99 nm at the short- and long-wave gain spectra in Fig. 3a, b destroy high ST correlations, and therefore it is not easy to generate long-distance diffraction-free beams directly in optical parametric generation (OPG), optical parametric oscillation (OPO), etc. However, seeding OPA with a localized wave packet can suppress the optical parametric fluorescence/generation, whose ST correlation is determined by the incident signal instead of OPA, and thereby it may be a good solution. A seed ST wave packet is produced using Eq. (3), whose parameters include a reduced correlation uncertainty δλ = 2 nm, a vertex wavelength λ0 = 855 nm, a spectral bandwidth Δλ = 40 nm, and a spectral plane tilt angle in the Fourier space α = 45.0572°. The ST spectra of the amplified signal and the generated idler are illustrated in Fig. 3c, d, the parameters of the signal almost remain unchanged, and those of the idler include a correlation uncertainty δλ = 4.7 nm, a vertex wavelength λ0 = 1295 nm, a spectral bandwidth Δλ = 105 nm, and a spectral plane tilt angle in the Fourier space α = 44.9111°. The 10 GW cm−2 strong pump enables 400 × small-signal gain for the signal and idler of the same energy level. Figure 3g, h show the pulsed beams supported by the ST spectra of the signal and idler, respectively, and both have a typical distribution of a ST wave packet with a butterfly-like shape and a central peak13,14. Although the “central peaks” are enlarged in space and time (compare Fig. 3g, h and e, f), which almost do not spread out after a 20 mm long-distance free propagation much exceeding the Rayleigh length (see Fig. 3k, l). We can also find some small mis-matchings between the ST spectra of the signal and idler ST wave packets with the strict phase-matching curves (green dash lines in Fig. 3a–d), especially when the wavelengths are far away from the vertex wavelengths, which is because the narrowband approximation for Eq. (2) cannot be strictly satisfied for a broadband pulsed beam. However, the ST spectra of the signal and idler ST wave packets still lie in the gain spectral ranges of OPA [compare Fig. 3c, d and a, b], which therefore doesn’t obviously affect amplification. Figure 4a, b respectively show the ST spectra of the incident and the amplified signal ST wave packets, and the mis-matching reduces the relative intensity at the short-wavelength of the amplified signal (compare parts in the blue rectangles in Fig. 4b with those in Fig. 4a). Figure 4c, d give the local-time integral intensity distributions I(x, z) during a 100 mm long-distance free propagation of the incident and the amplified signal ST wave packets, respectively, and no difference can be observed. In experiments, the perfect phase-matching (amplification condition) can be obtained by reducing both the spectral bandwidth Δλ and the correlation uncertainty δλ of the signal ST wave packet, and in refs. 14,19 which are only Δλ = 0.92 nm & δλ = 30 pm and Δλ = 0.3 nm & δλ = 24 pm, respectively, and much (~50–100 times) smaller than the value Δλ = 40 nm & δλ = 2 nm in this article. Figure 3c also shows when Δλ < 10 nm, the narrowband approximation would work very well.

Fig. 3: Space-time (ST) spectra and supported pulsed beams.
figure 3

In a 515 nm pumped type-I BBO crystal with a pump angle θp = 23°, gain spectra of optical parametric amplification (OPA)/optical parametric generation (OPG)/optical parametric oscillation (OPO) at a short and b long wavelengths for different directions. When seeding a ST wave packet, ST spectra of c amplified signal and d generated idler. Green dash lines in a–d are phase-matching curves. Δθ is the angle in the x–z plane with respect to the pump, uncertainties of ST spectra are around 43, 99, 2, and 4.7 nm in (a–d). Pulsed beams supported by ST spectra in a–d are shown in (e–h), and after 20 mm free propagation those are shown in (i–l). t is the local time, all figures share a normalized color-bar, and profiles and FWHM (full width at half maximum) widths of on-axis pulses and beams are given by curves in (e–l).

Full size image
Fig. 4: Comparison between incident and amplified signal space-time (ST) wave packets.
figure 4

ST spectra of a incident and b amplified signal ST wave packets. Local-time integral intensity distributions during long-distance free propagation I(x, z) of c incident and d amplified signal ST wave packets. All figures share a normalized color-bar, and black curves in c and d are on-axis intensities.

Full size image

Propagation of double ST wave packet

The free propagation of the amplified signal and the generated idler in vacuum are simulated and shown in Fig. 5. OPA happens at the position z = 0, where the signal and idler overlap in space and time. After z = 0, the separation between two ST wave packets increases with propagation due to different velocities of the signal and idler vgs = 1.0020c and vgi = 0.9969c. Figure 5 also shows the propagation-invariant length of the idler is shorter than that of the signal. The first reason is the Rayleigh length for a fixed beam waist w0 decreases with increasing the wavelength (e.g., Gaussian beam ZR = πw02/λ). Here, both central-peak waists of the signal and idler ST wave packets are around w0 = 23.5 μm, however due to a longer wavelength (1295 and 855 nm vertex wavelengths for the idler and signal), the Rayleigh length of the idler ZRi = 1.3 mm is shorter than that of the signal ZRs = 2.0 mm. The second reason is the correlation uncertainty of the idler δλ = 4.7 is larger than that of the signal δλ = 2 and accordingly shortens the propagation-invariant length. Even so, Fig. 5 shows both the propagation-invariant lengths of the signal and idler have far exceeded their Rayleigh lengths of ZRs = 2.0 mm and ZRi = 1.3 mm, respectively.

Fig. 5: Double space-time (ST) wave packet propagation in vacuum.
figure 5

Optical parametric amplification (OPA) is at z = 0, instantaneous ST distributions at z = 0, 10, 20, 30, and 40 mm, containing two ST wave packets of a superluminal signal and a subliminal idler.

Full size image

Discussion

In this article, a general concept of amplifying a ST wave packet in the type-I OPA is studied, and a plane-wave quasi-monochromatic (515 nm) pump pulsed beam without any temporal and spatial phase distortion is considered. However, when the pump pulse has a temporal phase distortion, it will transmit to the amplified signal and the generated idler pulses. In addition, the propagation in the nonlinear crystal can also introduce some temporal dispersions. A current study shows a weak temporal phase distortion cannot affect the propagation invariance of a ST wave packet obviously47. Similarly, when the pump beam has a spatial phase distortion, it will also transmit to the amplified signal and the generated idler beams. Because the beam aperture of a ST wave packet usually is very small (here ~30 μm), the wavefront error of the pump beam within such a narrow size is negligible. Here, the OPA works at a small-signal gain level, and when at a saturation gain level, the amplified signal and the generated idler pulsed beams will contain nonlinear temporal and spatial phase distortions. In general, the amount is very small and therefore does not affect the propagation invariance of the ST wave packet, either. In future, these engineering factors need to be studied in the next-step research for kinds of application. The result in this article is based on the type-I phase-matching, so not only BBO but also other nonlinear crystals, such as LBO, CLBO, KDP, DKDP, YCOD, etc., are applicable. However, the type-II phase-matching, whose angle-dependent phase-matching spectrum is asymmetric about the pump direction, does not fit the result. Moreover, to amplify all components, the pump pulsed beam should be large enough to completely wrap around the incident signal ST wave packet in space-time (e.g., > 600 μm in space and > 500 fs in time in Fig. 3g), and this requirement will reduce the pump-signal conversion efficiency comparing with the traditional OPA, however, which is not a key parameter here.

Conclusions

In summary, we have proposed a principle of amplifying a ST wave packet to high-energy by the type-I collinear OPA, where an idler ST wave packet would be generated simultaneously. Our numerical simulation verified the feasibility of this principle and demonstrated an as yet unreported strong double ST wave packet. In the nondegenerate OPA, two collinear-propagating ST wave packets at short and long wavelengths (compared with the degenerate-wavelength) are superluminal and subluminal, respectively, which accordingly separate in time during propagation. In the degenerate OPA, the double ST wave packet becomes a quasi-monochromatic (the degenerate-wavelength) luminal plane-wave pulse. Amplifying a ST wave packet in energy will introduce this light source to strong-field optics for studying ST-light–matter interactions. Moreover, the simultaneously generated idler can turn a ST wave packet to another wavelength, such as infrared, visible and ultraviolet wavelengths, and switch the velocity between superluminal and subluminal. This discovery will expand the range of application of the ST wave packet and also have some reference values for the nonlinear amplification and conversion of other spatiotemporal structured lights.

Methods

ST spectrum of ST wave packet

In the Fourier space kx-kz-k, the ST spectrum of a ST wave packet is governed by the simultaneous equations of the light-cone and a spectral plane

$${k}_{x}^{2}+{k}_{z}^{2}={k}^{2},$$
(4a)
$$k-{k}_{0}=({k}_{z}-{k}_{0})\tan \alpha ,$$
(4b)

where, k = ω/c (in the vacuum) is the wavenumber, kx = k·sinΔθ and kz = k·cosΔθ are the transverse and longitudinal components, Δθ is the spectral-dependent propagating angle with respect to that of the vertex frequency, and k0 is the vertex wavenumber of the ST spectrum defined as the intersecting point between the ST spectrum and the plane kx = 0 at the direction kz > 0 and has the coordinates (kx, kz, k) = (0, k0, k0). α is the tilt angle of the spectral plane with respect to the kz-axis. By substituting Eq. (4b) into Eq. (4a) and using Ω = ω – ω0, |Δθ| < π/2, |Ω/ω0| < 1 and α ~ π/4, we get the ST spectrum of a ST wave packet that is given by Eq. (1) (see equation derivation in Supplementary Note 1 of Supplementary information).

ST spectrum of type-I OPA

The three-wave coupling among the pump, signal and idler satisfies energy conservation and momentum conservation (phase-matching)

$${\omega }_{s}+{\omega }_{i}={\omega }_{p},$$
(5a)
$${{{{{{\bf{k}}}}}}}_{s}+{{{{{{\bf{k}}}}}}}_{i}={{{{{{\bf{k}}}}}}}_{p},$$
(5b)

where, k is the wavevector in the nonlinear crystal, and the subscript s, i, and p denotes the signal, idler and pump, respectively. The vertex frequency ωs0 of the signal ST wave packet satisfies the collinear phase-matching (Δθs0 = 0), and Eq. (5b) becomes ωs0ns + ωi0ni = ωpnp, where ωi0 is the idler of ωs0, and ns, ni, and np are refractive indices of ωs0, ωi0, and ωp for the type-I phase-matching. By substitution of Eq. (5a), ni is given by

$${{{{{{\rm{n}}}}}}}_{i}=\frac{{\omega }_{p}{n}_{p}-{\omega }_{s0}{n}_{s}}{{\omega }_{p}-{\omega }_{s0}}\cdot$$
(6)

Because the bandwidth of the signal ST wave packet, accordingly that of the generated idler, usually is narrow |Ω/ω0| << 1, we can approximately use constant refractive indices ns and ni for all frequencies of the signal and idler, respectively, which are angle-independent for the type-I phase-matching. Other frequencies ωs = ωs0 + Ωs of the signal ST wave packet satisfy the non-collinear phase-matchings (Δθs ≠ 0), and Eq. (5b) becomes

$${\omega }_{i}^{2}{n}_{i}^{2}={\omega }_{p}^{2}{n}_{p}^{2}+{\omega }_{s}^{2}{n}_{s}^{2}-2{\omega }_{p}{n}_{p}{\omega }_{s}{n}_{s}\,\cos \varDelta {\theta }_{s},$$
(7)

where, Δθs is the non-collinear angle between the signal and pump, which is also the propagating angle of the frequency ωs = ωs0 + Ωs with respect to the vertex frequency ωs0 within the signal ST wave packet in the x-y-z coordinates. By substituting Eqs. (5a) and (6) into Eq. (7), replacing ωs by ωs0 + Ωs, and using the narrowband approximation Ωs2 ≈ 0, we get the angle-dependent phase-matching spectrum (ST spectrum) of the type-I OPA that is given by Eq. (2) (see equation derivation in Supplementary Note 2 of Supplementary information).

Gain spectrum of OPA and amplified intensity

Under the undepleted pump approximation, the gain G of OPA, as well as the output intensities of the signal, Is(L) and idler Ii(L) are given by48

$$G=\left\{\begin{array}{cc}\frac{{\varGamma }^{2}}{{\varGamma }^{2}-{\big(\frac{\varDelta k}{2}\big)}^{2}}{\sinh }^{2}\left[L\sqrt{{\varGamma }^{2}-{\left(\frac{\varDelta k}{2}\right)}^{2}}\right], & {{{{{\rm{for}}}}}}\,{\varGamma }^{2}\ge {\left(\frac{\varDelta k}{2}\right)}^{2}\\ \frac{{\varGamma }^{2}}{{\left(\frac{\varDelta k}{2}\right)}^{2}-{\varGamma }^{2}}{\sin }^{2}\left[L\sqrt{{\left(\frac{\varDelta k}{2}\right)}^{2}-{\varGamma }^{2}}\right], & {{{{{\rm{for}}}}}}\,{\varGamma }^{2} \, < \, {\left(\frac{\varDelta k}{2}\right)}^{2}\end{array} \right.$$
(8a)
$${\varGamma }^{2}=\frac{2{\omega }_{s}{\omega }_{i}{d}_{eff}^{2}{I}_{p}}{{n}_{p}{n}_{s}{n}_{i}{\varepsilon }_{o}{c}^{3}},$$
(8b)
$$\varDelta {{{{{\bf{k}}}}}}={{{{{{\bf{k}}}}}}}_{p}-{{{{{{\bf{k}}}}}}}_{s}-{{{{{{\bf{k}}}}}}}_{i},$$
(8c)
$${I}_{s}(L)={I}_{s}(0)\cdot (1+G),$$
(8d)
$${I}_{i}(L)={I}_{s}(0)\frac{{\omega }_{i}}{{\omega }_{s}}G,$$
(8e)

where, L is the crystal length, deff is the effective nonlinear coefficient, and Ip is the undepleted strong pump intensity.

Propagation of ST wave packet

The angular spectrum method is used to simulate the free propagation of a ST wave packet in vacuum, which from the position z = 0 to the position z is governed by

$$E(x,z,t)=1/2\pi \int E(x,z,\omega )\exp ({{i}}\omega t){{d}}\omega ,$$
(9a)
$$E(x,z,\omega )=1/2\pi \int A({k}_{x},z,\omega )\exp ({{i}}{k}_{x}x){{d}}{k}_{x},$$
(9b)
$$A({k}_{x},z,\omega )=A({k}_{x},z=0,\omega )\exp ({{i}}kz\sqrt{1-{k}_{x}^{2}/{k}^{2}}),$$
(9c)
$$A({k}_{x},z=0,\omega )=\int E(x,z=0,\omega )\exp (-{{i}}{k}_{x}x){{d}}x,$$
(9d)
$$E(x,z=0,\omega )=\int E(x,z=0,t)\exp (-{{i}}\omega t){{d}}t.$$
(9e)

The local-time integral intensity distributions at the position z is given by

$$I(x,z)\propto \int {|E(x,z,t)|}^{2}{{d}}t.$$
(10)