Introduction

At a magic-angle of 1.08∘, theoreticians found moiré flat bands in twisted bilayer graphene (tBLG) with the help of tight-binding models1,2. These nondispersive flat bands are associated with strong correlation due to the Coulomb interaction between the charge carriers3. Numerous studies also suggested the presence of several exotic physical phenomena at the magic-angle condition in tBLG4,5,6. But the significance of the magic angle was fully appreciated when unconventional superconductivity was discovered in tBLG at the same twist angle7. It was later shown that partial filling of the flat bands is responsible for physical phenomena such as striped charge order, pseudogap states, and nematic phase, relating to high-temperature superconductivity in magic-angle tBLG8,9,10. Aside from these rich correlated electron behaviors, magic-angle tBLG also exhibits phononic effects such as the Jahn-Teller effect11 and phonon-driven superconductivity12,13. The central understanding in this field is that interlayer twist angle, which tunes the moiré superlattice formed by regions of commensurability and incommensurability between the lattices, controls the important electronic properties.

At low twist angles, the moiré superlattice relaxes by forming large triangular commensurate AB/BA regions, while the incommensurate AA and SP regions shrink14,15,16. The effect of this in-plane deformation on electronic properties in tBLG has been extensively studied17,18. By contrast, the role of corrugation, or out-of-plane deformation, is unknown despite the fact that previous continuum calculations19 show large out-of-plane deformation. More recently, band flattening and correlated states observed in buckled monolayer graphene20,21 have hinted at the importance of out-of-plane deformation effects on the electronic structure of tBLG.

In this work, we show that large out-of-plane deformation, with displacements of up to several Angstroms, is thermodynamically stable in the low twist angle regime when periods of moiré supercells are sufficiently large. We establish how the detailed nature of the corrugation is connected to partial filling of the flat bands and demonstrate symmetry breaking in the magic-angle tBLG with a simple single particle model. Furthermore, our results explain the experimentally observed vibrational spectra of tBLG as a function of twist angle.

Results and Discussion

Out-of-plane deformation modes in twisted bilayer graphene

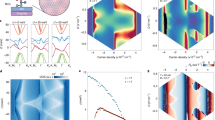
The high corrugation mode in tBLG at 1.08∘ is shown and compared to the conventional corrugation mode in Fig. 1a, based on the results of atomistic calculations described in detail in the "methods" section. Following the predictions of the stability of high corrugation modes at low twist angles19, we refer to the higher corrugation mode as the bending mode (indicated by orange box throughout the manuscript) and the conventional corrugation mode as the breathing mode (indicated by green box throughout the manuscript). The corrugation, or out-of-plane displacement, in the bending mode is an order of magnitude higher than in the breathing mode, as seen in Fig. 1. The largest out-of-plane displacement appears in the AA region of the tBLG. Despite the large corrugation in the bending mode, the variation of interlayer distance in between the tBLG layers remains the same for both breathing and bending mode, as shown in the Supplementary Note 1 and Fig. S1 of the supplementary information. To mimic the tBLG experiments, we incorporate a substrate and take into account the Lennard-Jones interaction between the substrate and the tBLG. The case of the freestanding tBLG structure is also presented in Fig. S2 of the Supplementary information and we explain the effect of the substrate on the corrugation in the Supplementary Note 2.

Fig. 1: Corrugation in magic-angle twisted bilayer graphene (tBLG).
figure 1

a The 3D view (left) of the atomic structure and the profile of the out-of-plane displacement of magic-angle tBLG in the breathing mode (green box) and the bending mode (orange box). A 2D projection of the corrugation of the top layer of the tBLG is also shown by a color plot. The profile of the displacement (right) is obtained by the scan of atomic height along the diagonal of tBLG as shown by the black line in the breathing mode. b Energy density difference between the breathing and bending modes and the total energy per atom of the breathing and bending mode tBLG with reference to the AB bilayer graphene of the same area as a function of twist angle, showing the thermodynamic favorability of the bending mode at low twist angles (θ≤1.61∘). c, d The top view of tBLG in the breathing and the bending modes respectively, showing similar moiré patterns with six-fold symmetry. The region of AA, SP and AB are identified. e Representation of the AA, SP and AB stackings of tBLG.

Full size image

In Fig. 1b, the energetic favorability of the bending mode at low twist angles (θ ≤ 1.61∘) is demonstrated via the energy density difference between the breathing and bending modes, \({{\Delta }}\gamma =\frac{{E}_{Br}-{E}_{Be}}{A}\), where EBr and EBe are the minimized total energies of the tBLG in the breathing and bending modes respectively, and A is the projected area of the tBLG. We also plot the total energy of the tBLG with reference to AB bilayer graphene of the same area as a function of twist angle, which shows a clear transition of stability from breathing to bending mode as twist angle drops below 1.61∘. At 1.6∘ twist angle, the AA regions of the tBLG overlap with each other19, which also points out the transition twist angle between breathing and bending mode. The bending mode also remains as the stable mode at low twist angles if no substrate is present, or if the system has a substrate above and below, as shown in the Supplementary Note 3 and Fig. S3 of the supplementary information. We explain the twist angle dependence of Δγ in terms of dislocation mechanics in the following sections and in the Supplementary Note 4 and Fig. S4–S7 of the supplementary information.

Despite the clear stability of the bending mode, the higher corrugations are not obvious from the top views of tBLG, as shown in Fig. 1c, d. Both breathing and bending modes show moiré patterns with the typical C6 symmetry. Similarly, their differences are not readily apparent from projection-based topology measurement devices such as scanning tunelling microscope (STM). STM measurements combine both electronic and atom position effects. While researchers have attempted to separate their relative contributions by neglecting the electronic effects22, the electronic effects are indeed an important consideration23,24. The quantification of corrugation amplitude is typically done computationally24,25 using density functional theory (DFT) or molecular dynamics (MD) simulations, but these methods are prone to becoming trapped in local minima26,27,28. Although atomic force microscopy (AFM) experiments have been successfully used to quantify corrugation in graphite29,30, the quantification of corrugation in tBLG has not been reported, and the higher corrugation mode – which is thermodynamically more stable in the low twist angle regime – has thus been largely overlooked.

Effect of corrugation on the electronic structure

Our electronic structure calculations show the effect of the bending mode corrugation on the band structure of magic-angle tBLG. In Fig. 2a, the band structure is calculated by a tight binding model31, using atom positions of relaxed configurations obtained from classical potentials. Flat bands form around the Fermi level, as highlighted in the red box. In Fig. 2b, c, we focus on a small energy range around the Fermi level to show the difference between the flat bands of the breathing and the bending modes. We show, for the breathing mode, that each band is either filled or empty, preserving particle-hole symmetry except for the 1.12∘ twist angle case. In tBLG of twist angle 1.12∘, the flat band is the narrowest in the breathing mode, and features partial filling of the states. By contrast, we see the partial filling of the flat bands for bending mode corrugation over a range of twist angles (1.05∘–1.16∘) near the magic angle. This is in agreement with Carr et al.17 who show that the magic angle is not a single value, but rather a range of approximately 0.1∘. So partial filling of the flat bands is a more robust feature in bending mode corrugation occurring not just at a specific twist angle, but over a range of twist angles. This leads to the possibility that bending mode corrugation may play a role in stabilizing superconducting states, given that recent reports suggest that metallic states in twisted bilayer graphene can stabilize the superconductivity32. The flat bandwidth at the high symmetry point Γ is plotted as a function of twist angle in Fig. 2d. Both breathing and bending modes have flat bandwidth of 8 meV at 1.08∘, showing close agreement with the experiments7,33. But the minimum flat bandwidth occurs at 1.12∘ in the breathing mode and at 1.08∘ in the bending mode corrugation. We note that a minimum flat bandwidth can also be found in a flat tBLG structure near the magic angle with no corrugation2,17. Similar features like minimum Fermi velocity and maximum Fermion mass are also apparently dependent on the twist angles of the tBLG instead of the out-of-plane atomic corrugation. However, while these properties suggest the presence of correlated states in magic-angle tBLG, large out-of-plane deformation accompanied by in-plane radial strain show partial filling of the flat bands in the magic-angle regime, hinting at the possibility that superconductivity can be stabilized as a result of the corrugation.

Fig. 2: Band structure and orbital projected density of twisted bilayer graphene (tBLG) near the magic-angle.
figure 2

a Band structure of tBLG at 1.08∘ showing flat bands near the Fermi level in the breathing mode, highlighted inside the red box. b, c Magnified view of the band structure near the Fermi level of tBLG at different twist angles in the breathing mode (green box) and the bending mode (orange box). Each band is denoted by separate colors. d The plot of flat bandwidth at the Γ point as a function of twist angle. This shows a minimum flat bandwidth at twist angle 1.12∘ for breathing mode and at 1.08∘ for bending mode. The shaded region indicates the twist angle regime where flat bands are partially filled for breathing mode (Green) and bending mode (Orange). e, f The orbital projected density near the Fermi level for tBLG of twist angle 1.12∘ in the breathing mode and at 1.08∘ in the bending mode. g Spatial scan of orbital projected density along the vertical direction in the AA region (indicated by red box) showing the spectral weight transfer in the bending mode of the tBLG at 1.08∘.

Full size image

To understand the partially filled flat bands, we also plot the orbital projected density in Fig. 2e,f for tBLG at 1.12∘ in the breathing mode and at 1.08∘ in the bending modes. In the breathing mode, charge density localizes in the AA region of the tBLG. In contrast, the higher corrugation in the bending mode drives a charge redistribution in the AA region, breaking the C6 symmetry. In theory, electron localization, as seen in the breathing mode at 1.12∘, is driven by a smaller atomic corrugation like the breathing mode corrugation34,35. But the localization preserves C6 symmetry and fails to explain essential clues to the superconductivity like spectral weight transfer, striped charge order8, and the presence of nematic phase9,10. In Fig. 2f, the underlying electronic structure reveals a particular breaking of the symmetry by concentrating charge density along a major axis, though the topography shown in Fig. 1d still conforms to a C6 symmetry. Fig. 2f shows a quadrupole geometry in the AA region via the formation of alternating high and low orbital projected density quadrants. This important feature is typically observed in the high-temperature superconductors36,37. To illustrate the broken symmetry, the spatial dependence of the orbital projected density in the AA region is plotted in Fig. 2g. Each line in this figure is a horizontal spatial scan of the AA region, as shown by a red box in Fig. 2f. This spatial scan clearly indicates a charge splitting as the high charge density peaks transfer from left to right along the downward direction. This type of charge transfer can be attributed to spectral weight transfer in the AA region, another phenomenon observed in the unconventional superconductivity of magic-angle tBLG8. Moreover, the center of the AA region (the blue section of the arrow) shows equally distributed peaks, demonstrating a typical feature of pseudogap states in the magic-angle tBLG. This particular broken symmetry and the charge redistribution showing spectral weight transfer can only be observed at the magic-angle regime in presence of the bending mode corrugation (as shown in the Supplementary Note 5 and Fig. S8). Our findings suggest an alternative to the current picture that relies on the simpler breathing mode with a more complex correlated electronic model to explain the broken symmetry10,38,39: we are suggesting a more complex deformation mode, which – even with simpler single particle physics – provides an explanation for the necessary symmetry breaking.

Deformation mechanics in twisted bilayer graphene

To understand the importance of the bending mode of corrugation, we consider the underlying mechanism of this deformation. We show, in Fig. 3a, that the average bond length in the atomistic structure of tBLG varies with twist angle, reaching a maximum at 1.47∘ for the breathing mode and at 1.08∘ for the bending mode. The large deformation in the bending mode, responsible for the reduction in symmetry and charge redistribution, is also responsible for stretching the bonds and for the occurrence of maximum bond length at 1.08∘. We also plotted the experimentally observed micro-Raman ΓG peak as a function of twist angles40, where the full-width half-maximum (FWHM) also occurs at 1.08∘. The micro-Raman G peak relates to the bond stretching between pairs of sp2 atoms41,42. It shows that the bond length and ΓG peak follow the same trend up to 1.47∘. This agreement indicates that the angle dependence of the Raman peak can be explained by the bending mode corrugation. Thus, it provides an indirect support for our suggestion that the large corrugation in bending mode is indeed present in experimental conditions, even though it has not been directly examined until now.

Fig. 3: Stress and energy distribution of magic-angle twisted bilayer graphene (tBLG).
figure 3

a Interatomic bond length and micro-Raman ΓG peak as a function of twist angles. The ΓG peak is shifted to the scale of bond length. The filled markers indicate the twist angles where each mode is stable. The dashed line is a guide for the data of the ΓG peak and bond length for the stable modes. The maximum bond length for the breathing mode occurs at 1.47∘ but shifts to 1.08∘ for the bending mode. Similarly, the full wave half-maximum ΓG peak occurs at 1.08∘. The micro-Raman experimental data are taken from the literature40. b Stress components (σxx and σyy) for top and bottom layer of magic-angle tBLG in the breathing and the bending mode. The bending modes has a reduced symmetry relative to the breathing mode. c Total energy distribution of the magic-angle tBLG to demonstrate the distinctive dislocation behavior between breathing and bending mode. While the SP regions form straight dislocations connecting the AA regions in breathing mode tBLG, the SP regions in bending mode tBLG are kinked, forming wave-like dislocations.

Full size image

In Fig. 3b, the spatial distributions of stress components (σxx and σyy) are shown for the top and bottom layers of magic-angle tBLG in the breathing mode (green) and bending mode (orange). This also reveals a symmetry breaking in the bending mode and demonstrates a tensile stress in the AA region of the tBLG. This causes an in-plane radial expansion of the atoms in the AA region as opposed to pure rotational motion driven by shear stress in the case of the breathing mode. (The in-plane displacements of the atoms in the bending mode have non-zero divergence, as shown in Fig. S4.) Such radial deformation requires high energy for a flat geometry, but requires small energy to relax the structure in the presence of high corrugation. The charge redistribution in tBLG, shown in Fig. 2, can be attributed to this radial deformation in the AA region, which helps to stabilize the symmetry breaking. Numerous studies report on the role of strain in stabilizing symmetry breaking associated with unconventional superconductivity10,39. The connection between bending mode corrugation and in-plane radial strain is further explained in Supplementary Note 6 and illustrated in Fig. S9 and S10. Similarly, higher corrugation in monolayer graphene has been observed in alternating graphene/hexagonal boron nitride heterostructure20,43, where the graphene layer is also strained to obtain a superlattice structure with periodicity. Fig. 3c shows the energy distribution in magic-angle tBLG, which clearly highlights the SP regions, or interlayer dislocations separating regions of AB stacking19,44, and their distinctly different morphologies in the breathing and bending modes. In the bending mode, the SP regions are kinked, in the form of mixed-type (screw+edge) dislocations, while in the breathing mode, the SP regions are straight, in the form of screw-type dislocations.

This specific topology of the dislocation is a key factor in the thermodynamic stability of the bending mode instead of the breathing mode for small twist angles (as shown in fig. 1b). We note that energy difference between the modes can be explained by the 3D dislocation line length and the Moiré wavelength, which have a special relationship in a narrow twist angle range close to the magic-angle. In Fig. S5 of the Supplementary information, we plot a ratio of the two quantities. While this ratio tends to a limit of 1 for very small and large angle limits, it reaches a maximum value at a twist angle 1.47∘, close to the crossover angle that corresponds to the switch between the two deformation modes. The stability between bending and breathing mode is driven by the dislocation mechanics, and a more detailed description of which is found in the Supplementary Note 4.

Conclusions

In magic-angle tBLG, the phase diagram hosts both correlated insulating and superconducting phases, supporting the unconventional nature of superconductivity in the system7,45,46,47. Recent studies, however, illustrate that conventional superconductivity can also appear in magic-angle tBLG, in the absence of correlated insulating phase12,48,49. We report on the critical role of strain in the symmetry breaking associated with unconventional superconductivity in tBLG. We show evidence of the energetically favorable higher corrugation mode, demonstrating pseudogap states and spectral weight transfer by single particle physics. These phenomena are closely connected to similar observations in high-temperature superconductors36,37,50. In a recent study20, highly corrugated monolayer graphene with hexagonal boron nitride (h-BN) as a substrate has also shown the presence of correlated states and broken symmetry. Therefore, large out-of-plane deformation should also be considered in explaining the special properties associated with superconducting states in magic-angle tBLG. The bending mode of corrugation also appears to have an effect equivalent to unscreened electric field induced by the angle disorder51 in magic-angle tBLG as it drives the Fermi level away from charge neutrality. In fact, this type of deformation is a possible way to replace the application of back-gate voltage to tune the generated electric field. Our study suggests that additional work to understand the effect of high corrugation in tBLG is warranted. It may be possible to experimentally address this effect, for example, through application of electric fields, or through the use of substrates to which the tBLG has varying adhesion. This opens the fascinating possibility of controlling superconducting states in magic-angle tBLG, to the extent that we can control the magnitude of corrugation in the tBLG system.

Methods

When two graphene layers rotate relative to one other by a twist angle θ, the system is referred to as twisted bilayer graphene (tBLG). Due to the resulting atomistic incommensurability between layers, a moiré pattern emerges. Our calculations are performed on periodic tBLG in which the two layers form a larger scale commensurate supercell with one other. The commensurate tBLG supercell only occurs at particular twist angles θ34,52. This particular value of θ is an angle in between two lattice vectors d1 = na1 + ma2 and d2 = ma1 + na2, where, n and m are arbitrary integers. As the two vectors d1 and d2 merge after rotation, the lattice vectors of the periodic supercell are \({L}_{1}=m{a}_{1}^{(1)}+n{a}_{2}^{(1)}=n{a}_{1}^{(2)}+m{a}_{2}^{(2)}\) and \({L}_{2}=R(\frac{\pi }{3}){L}_{1}\), where, \(R(\frac{\pi }{3})\) is the two-dimensional rotation matrix of angle π/3. The rotation angle θ, the supercell size Lcell, and the number of atoms N for such a commensurate periodic tBLG can be represented as

$$\cos \theta =\frac{{m}^{2}+4mn+{n}^{2}}{2({m}^{2}+mn+{n}^{2})},$$
(1)
$${L}_{cell}={a}_{0}\sqrt{3({m}^{2}+mn+{n}^{2})},$$
(2)
$$N=8({m}^{2}+mn+{n}^{2}).$$
(3)

Here, a0 is the bond distance in the graphene layers.

We use Large-scale Atomic Molecular Massively Parallel Simulator (LAMMPS)53 to carry out molecular statics calculations to obtain relaxed atomic coordinates. For accurate simulation of interatomic interactions, we use the reactive empirical bond order (REBO) potential54 and the Kolmogorov-Crespi (KC) potential55 for intralayer and interlayer interactions respectively. The REBO potential is known to underestimate the experimental/DFT Young’s modulus and overestimate the experimental/DFT Poisson’s ratio56. However, the binding energy, bending rigidity and bond length obtained with the REBO potential agree well with the experimental and DFT values56. To our understanding, it is difficult to identify a single classical potential, which will perform better in terms of all mechanical properties, although we acknowledge that the development of machine-learned potentials57 clearly shows promise in the classical molecular dynamics simulations field. In the KC potential55,the orientation of the pz orbital is determined by the local environment, where the local normal to an atom is defined by a patch of neighboring atoms. Here, we adopt the parameters of the KC potential from Ouyang et al.58. The atom coordinates are relaxed by minimizing the energy with a conjugate gradient (CG) minimization scheme,59 where the stopping tolerance for energy is 10−11 eV. To obtain the bending mode corrugation in the relaxed structure, a flat tBLG structure is initially perturbed by introducing large bulges in the AA region. Energy minimization of these perturbed structures leads to bending mode corrugation. The magnitude of the bending mode corrugation can be controlled through interactions with a substrate. In this study, we use a Lennard-Jones (LJ) potential to simulate the van der Waals interactions between a substrate and the tBLG.

The atomic coordinates obtained from MD simulations are utilized as an input to the band structure calculation using the tight-binding method. The tight binding Hamiltonian is written as-

$$H=-\mathop{\sum}\limits_{i,j}t({r}_{i}-{r}_{j})\big|{r}_{i}\big\rangle \big\langle {r}_{j}\big|+{{{{{{{\rm{H.c.}}}}}}}},$$
(4)

where, ri are the atomic coordinates obtained from MD simulations and \(|{r}_{i}\rangle\) is the wave function at atomic site i. t(ri − rj) is the hopping integral between atoms i and j, which also accounts for any change in the distance between two atoms due to corrugation. For the hopping integral, we use the formula obtained from Nam et al.31

$$t(d)=-{V}_{pp\pi }(d)\left[1-{\left(\frac{{{{{{{{{\bf{d.e}}}}}}}}}_{z}}{d}\right)}^{2}\right]-{V}_{pp\sigma }(d){\left(\frac{{{{{{{{{\bf{d.e}}}}}}}}}_{z}}{d}\right)}^{2},$$
(5)
$${V}_{pp\pi }(d)={V}_{pp\pi }^{0}\,\exp \left(-\frac{d-{a}_{0}}{{r}_{0}}\right),$$
(6)
$${V}_{pp\sigma }(d)={V}_{pp\sigma }^{0}\,\exp \left(-\frac{d-{d}_{0}}{{r}_{0}}\right).$$
(7)

Here, d = ri − rj is the distance between two atoms, ez is a vector along the normal to the plane of atoms, a0 is the average bond distance, d0 is the average interlayer distance. \({V}_{pp\pi }^{0}\) = −2.7 eV and \({V}_{pp\sigma }^{0}\) = 0.48 eV is the hopping integral between the nearest neighbor atoms within the layers and in between the layers respectively. Tight binding models are sensitive to the choice of hopping terms. Here, we choose the terms from the Nam and Koshino pz tight binding model31, which accurately captures the Fermi velocity reduction when lattice relaxation is accounted for. The same hopping terms used in a different tight binding model35 have led to an accurate magic-angle prediction where flat bands are narrowest. This combination of hopping parameters has been widely used in the literature60,61,62. We also choose a cut-off distance greater than \(\sqrt{3}a\) (a = lattice constant of graphene), where the hopping integral is negligible.