Abstract
Quantum critical fluctuations may prove to play an instrumental role in the formation of unconventional superconductivity. Here, we show that the characteristic scaling of a marginal Fermi liquid is present in inelastic light scattering data of an Fe-based superconductor tuned through a quantum critical point (QCP) by chemical substitution or doping. From the doping dependence of the imaginary time dynamics we are able to distinguish regions dominated by quantum critical behavior from those having classical critical responses. This dichotomy reveals a connection between the marginal Fermi liquid behavior and quantum criticality. In particular, the overlap between regions of high superconducting transition temperatures and quantum critical scaling suggests a contribution from quantum fluctuations to the formation of superconductivity.
Similar content being viewed by others
Introduction
Close to quantum critical points (QCPs) where a second order thermal phase transition is suppressed to absolute zero systems are highly susceptible to small perturbations. The high susceptibility gives rise to various instabilities in materials exhibiting unconventional superconductivity. Although the vanishing temperature at the QCP renders direct experiments impossible, the related critical fluctuations1,2 extend over a wide range of temperatures and manifest themselves under experimentally feasible conditions, yielding direct consequences for the macroscopic properties of materials.
One of the consequences is the deviation from the Landau-Fermi liquid picture observed in many materials such as the cuprates, the Fe-based compounds or the heavy fermion systems3. The linear-in T variation of the resistivity has been considered a landmark experimental manifestation4,5,6,7,8 thereof9, although the interrelation of the resistivity with quantum criticality remains a subject of discussion10. On the other hand, spectroscopic fingerprints strongly indicate a connection between the Ω/T scaling of a marginal Fermi liquid9 and quantum criticality, as observed in a recent study of the optical conductivity11 of the heavy fermion superconductor YbRh2Si212. Theoretical works suggest that quantum fluctuations may have a significant impact in the case for antiferromagnetic13 as well as charge density wave ordering14 and, more specifically, in the enhancement15 or formation16,17 of superconductivity in the iron-based superconductors.
Characteristic for systems with a QCP is the presence of a quantum critical region at temperatures above a crossover temperature T*(x) ~ ∣x − xc∣νz (where ν and z are the correlation length and dynamical critical exponents, respectively, the tuning parameter x, realized in our context by chemical substitution of the metal site, and critical doping xc). Since this broad region of the phase diagram manifests the behavior of the single quantum critical point at x = xc, T = 0, Frerot et al.18 dubbed this region a “magnifying lens” for quantum criticality.
Due to the tunability by doping and the purity of the crystals, we have opted to use as a testbed the compound Ba(Fe1−xCox)2As2, one of the most studied Fe-based superconductors, to investigate this lens. Ba(Fe1−xCox)2As2 exhibits a rich phase diagram19 with overlapping regions of magnetism, nematicity, and superconductivity, and shows a strong enhancement of nematic fluctuations having \({d}_{{x}^{2}-{y}^{2}}\) symmetry (here using the 1-Fe unit cell) close to the nematic transition20,21,22. A plethora of experimental studies20,21,23,24,25,26 indicate the existence of a QCP underneath the superconducting dome in this material, and the Raman response within the superconducting phase bears an imprint of nematic quantum criticality27. Most recently, Worasaran et al.28 provided striking evidence for nematic quantum criticality by observing power-law behavior of the nematic/structural transition temperature as a function of uniaxial strain. However, the influence of the QCP on the high-temperature characteristics, for instance signatures of Ω/T scaling, remain elusive.
In this Article, we provide a comprehensive investigation of the Raman response of Ba(Fe1−xCox)2As2 for doping concentrations on both sides of optimal doping xc ~ 0.061. Specifically, we fill the gap close to xc where Ω/T scaling is expected to be most pronounced and provide a solid experimental basis for an earlier proposal29. We use electronic inelastic light (Raman) scattering which probes fluctuations of various degrees of freedom30,31 and has led to promising results particularly in Fe-based superconductors20,22,32.
Results and discussion
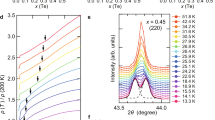
Earlier studies, investigating the low-frequency Raman response of Ba(Fe1−xCox)2As220,22, showed that the contribution of nematic fluctuations presents itself in the B1g (\({d}_{{x}^{2}-{y}^{2}}\)) symmetry of the 1-Fe unit cell whereas the temperature dependence of the A1g response is essentially independent of doping and follows the in-plane resistivity22. This suggests, that the essential critical dynamics of the system is captured by the B1g response. We therefore limit our analysis to the B1g response, with characteristic spectra shown in Fig. 1 for selected Ba(Fe1−xCox)2As2 samples with x < xc, x ~ xc, and x ≫ xc (see Figs. S1 and S2 in Supplementary Note 1 for the complete data set). All spectra have in common that the temperature dependence is limited to low frequencies, while no significant temperature dependence can be detected at higher frequencies.
Depicted is the Raman response function \(R{\chi }_{{{{{{{{\rm{B1g}}}}}}}}}^{^{\prime\prime} }({{\Omega }},T)\) in B1g symmetry (1-Fe unit cell) at selected doping concentrations x and temperatures T where Ω = ωi − ωs stands for the difference of the incident and scattered photon energy ωi and ωs, respectively. Tc refers to the superconducting transition temperature. a For the underdoped compound with x = 0.052, the low-frequency pile-up attributable to classical critical fluctuations exhibits a maximum above the nematic transition and decreases toward Tc. b Close to optimal doping with x = 0.059, the low-frequency response increases monotonically on cooling toward Tc. c For a sample with x ≫ xc, The temperature dependence is weak at all frequencies.
Raman response
The underdoped compound [Fig. 1a] exhibits a nematic transition at approximately Tnem ~ 50 K. Similar to results reported elsewhere for x < xc20,22,32 the strong increase of the spectral weight between 333 and 53 K in the range below 500 cm−1 can be attributed to the presence of (classical) critical fluctuations. The decrease below Tnem, reminiscent of a gap, is characteristic for such transitions in the Fe-based superconductors, and consistent with earlier results22. Closer to optimal doping at x = 0.059 [Fig. 1b] the response increases monotonically upon cooling toward the superconducting transition temperature Tc. Remarkably, the response at this lowest temperature is nearly constant over the entire frequency range. Far away from xc, the temperature dependence is weak even at small energy transfer [Fig. 1c].
Transformation onto the imaginary time axis
To examine the possibility of quantum critical scaling, we have computed \(\beta \tilde{{{\Lambda }}}(\beta /2)\) from each of our measured spectra, with the results shown in Fig. 2. For the underdoped sample [Fig. 2a] the characteristic cusp singularity of the nematic transition is visible29. Notably, a similar increase observed using a sample with x = 0.057 doping in Fig. 2b toward Tc suggests a persisting nematic phase close to the superconducting transition. Yet, from our measurements it cannot be clearly decided whether or not nematicity sets in above Tc. Closer to optimal doping in Fig. 2c, \(\beta \tilde{{{\Lambda }}}(\beta /2)\) develops a broad maximum above Tc, though this cannot be attributed to a nematic phase transition. This maximum occurs roughly at the same temperature as for 5.2% doping and is thus too high in temperature for this doping concentration. Rather, we believe that the increase in the critical fluctuation response starts to freeze out at low temperatures and is then proceedingly compensated by the denominator in Eq. (2). Above xc at x = 0.073 [Fig. 2d], the quantity \(\beta \tilde{{{\Lambda }}}(\beta /2)\) remains constant down to the lowest measured temperature on the order of Tc. Tuning further away from xc [Fig. 2e and f], \(\beta \tilde{{{\Lambda }}}(\beta /2)\) decreases toward low temperatures, where \(\beta \tilde{{{\Lambda }}}(\beta /2)\) is generically required to vanish (see Supplementary Note 2 for a proof of this).
Shown is \(\beta \tilde{{{\Lambda }}}(\beta /2)\), the imaginary time-ordered correlation function \(\tilde{{{\Lambda }}}(\tau )\) derived from the Raman spectra of Ba(Fe1−xCox)2As2 and evaluated at τ = β/2 multiplied by the inverse temperature β = 1/kBT, versus temperature T. The dashed lines correspond to \(\beta \tilde{{{\Lambda }}}(\beta /2,T)={{{{{{{\rm{const}}}}}}}}\), and the blue regions indicate the deviation from this constant behavior, which we use to define the crossover temperatures \({T}_{{{{{{{{\rm{UD}}}}}}}}}^{* }\) and \({T}_{{{{{{{{\rm{OD}}}}}}}}}^{* }\) for x < xc and x > xc, respectively. a At x = 0.052 doping a nematic transition occurs at Tnem ~ 50 K at which \(\beta \tilde{{{\Lambda }}}(\beta /2,T)\) develops a cusp and then decreases toward Tc. b At x = 0.057, \(\beta \tilde{{{\Lambda }}}(\beta /2,T)\) increases toward lower temperatures and develops a maximum above Tc. c Closer to the quantum critical point (QCP) \(\beta \tilde{{{\Lambda }}}(\beta /2,T)\) develops a hump between \({T}_{{{{{{{{\rm{UD}}}}}}}}}^{* }\) and Tc. d On the overdoped side at x = 0.073 the Ω/T scaling persists down to Tc. e Further away, the crossover temperature increases again. f The high crossover temperature at x = 14.6 coincides with a small superconducting transition temperature.
Doping dependence of T*
The dashed horizontal line is a guide to the eye indicating the value of \(\beta \tilde{{{\Lambda }}}\) in the regime of Ω/T scaling. Outside this quantum critical regime, where the response does not scale as Ω/T, the quantity \(\beta \tilde{{{\Lambda }}}(\beta /2)\) from this constant. The shaded regions show the crossover temperatures \({T}_{{{{{{{{\rm{UD}}}}}}}}}^{* }\) and \({T}_{{{{{{{{\rm{OD}}}}}}}}}^{* }\) for x < xc and x > xc, respectively, from Ω/T scaling to regions where other dynamics govern the low-frequency response.
\({T}_{{{{{{{{\rm{UD,OD}}}}}}}}}^{* }(x)\) exhibits a systematic doping dependence, with a global minimum at x = 0.073. To further illustrate this point, \({T}_{{{{{{{{\rm{UD,OD}}}}}}}}}^{* }(x)\) is plotted along with the relevant phase transitions of Ba(Fe1−xCox)2As2 in Fig. 3. The spin-density-wave (SDW) phase is indicated in gray, nematicity in red, and superconductivity in blue. The open red rectangles indicate the crossover temperatures derived from data presented in Lederer et al.29. The dashed lines represent guides to the eye.
The spin-density-wave (SDW) phase is depicted in gray, nematicity in red, and superconductivity (SC) in blue as defined by the superconducting transition temperature Tc. The rectangular and circular data points indicate the crossover temperatures \({T}_{{{{{{{{\rm{UD}}}}}}}}}^{* }\) and \({T}_{{{{{{{{\rm{OD}}}}}}}}}^{* }\) from the region of Ω/T scaling for x < xc and x > xc, respectively. The dashed lines are guides to the eye. Open red squares and circles represent data points from Lederer et al.29. The gray, red, and blue phase separation lines are based on Chu et al.19. The error bars indicate the temperature window of T* depicted in Fig. 2.
Underdoped region
For x < xc Ba(Fe1−xCox)2As2 has an SDW ground state below TSDW, and fluctuations in the temperature range \({T}_{{{{{{{{\rm{SDW}}}}}}}}} \, < \, T \, < \, {T}_{{{{{{{{\rm{UD}}}}}}}}}^{* }\). Above \({T}_{{{{{{{{\rm{UD}}}}}}}}}^{* }\) the Ω/T scaling characteristic for a marginal Fermi liquid is recovered. Moving closer to xc, the magnetic and nematic phases become unstable as signified by the decreasing transition temperatures. In the picture of quantum criticality, this results from a continously increasing superposition of entangled states which manifests itself as a divergence of the coherence length of the quantum fluctuations directly at the QCP. Simultaneously, the region of marginal Fermi liquid behavior with Ω/T scaling begins to persist over wider ranges of temperature with \({T}_{{{{{{{{\rm{UD}}}}}}}}}^{* }\) falling more rapidly after superconductivity sets in.
Overdoped region
On the overdoped side for x > xc, the crossover line re-emerges from the superconducting dome and continues to rise as a function of doping, with a significantly smaller slope than for x < xc. In the absence of a competing magnetic ground state, the quantum fluctuations may support superconductivity over a wider region of doping concentrations.
The endpoints of the dashed lines coincide with the region of optimal doping xc consistent with a scenario in which quantum fluctuations increasingly destroy the long-range order of the ground state for x < xc at temperatures T > 0. Thus, Tc is high where the quantum fluctuations dominate the normal state, and low where “classical” dynamics take over. Therefore the quantum fluctuations appear to have a twofold effect: on the classically ordered side below xc, the competing magnetic ground state is destabilized. On the overdoped side, the quantum fluctuations protect superconductivity at least partially from increasing disorder. This scenario is consistent with quantum criticality being a driving force behind the superconducting state in Ba(Fe1−xCox)2As2.
In the experimental work presented here, we have determined the crossover temperature T* separating the high-temperature quantum critical behavior from the (effectively) classical behavior at low temperatures. To this end, we have introduced a metric to identify the quantum critical regime in terms of the imaginary time response function, \(\tilde{{{\Lambda }}}(\tau )\), which can be inferred directly and unambiguously from experimental inelastic light scattering (Raman) data (see the section “Imaginary time response” in Methods and Lederer et al.29). By focusing on the longest possible imaginary time, τ = β/2 with the inverse temperature β = 1/kBT, we amplify the effect of the singular (power-law) correlations that reflect the critical behavior and maximally avoid contamination by non-universal analytic (short-range in imaginary time) non-critical portions of the imaginary part of the response function χ″. Specifically, if in the critical regime χ″ is a scaling function of Ω/T (i.e., of the marginal Fermi liquid form), this implies that \(\tilde{{{\Lambda }}}(\beta /2)\) is linear in T. In this way, as shown in Fig. 2, we can identify the quantum critical regime for each value of x as the range of (high) T over which \(\tilde{{{\Lambda }}}(\beta /2)\) is T independent, and a crossover scale T*(x) that bounds this regime from below. Applying this analysis to the present work leads to the phase diagram shown in Fig. 3, where for x < xc, the crossover is into a renormalized classical regime in which \(\beta \tilde{{{\Lambda }}}(\beta /2)\) is an increasing function of decreasing T, while for x > xc the crossover is into a quantum disordered regime in which \(\beta \tilde{{{\Lambda }}}(\beta /2)\) is a decreasing function.
Scaling
As a final remark, we wish to comment on the scaling behavior deduced from our data: From equation (S12) in Supplementary Note 2.4, \(\beta \tilde{{{\Lambda }}}(\beta /2)\) should vary as Ty where y = γ/νz. This implies y ~ 0 to be in line with a conventional scaling analysis presented in Supplementary Note 2, and thus one would have to appeal to an extreme value of one or more of these exponents. In this case, the most natural choice would be z = ∞, corresponding to the phenomenology of local quantum criticality33,34 in which only temporal correlations become long ranged at the quantum critical point. Such a scenario is of course exotic. Whether a local quantum critical point that violates scaling is indeed present in Ba(Fe1−xCox)2As2 is beyond the scope of this work and calls for further investigations of quantum criticality in this and related systems.
Conclusions
We tracked the B1g Raman response of Ba(Fe1−xCox)2As2 as a function of doping x. x is tuned from x < xc through a quantum critical point far into the overdoped regime of the phase diagram. From the data, we calculated the temperature dependence of the imaginary time-ordered correlation function \(\tilde{{{\Lambda }}}(\tau )\) at τ = β/2 and extracted crossover temperatures T*(x) above which Ω/T scaling prevails. These temperatures define the boundaries of the quantum critical fan corroborating the existence of a QCP around optimal doping. Thereby we show that the determination of the imaginary time dynamics from spectroscopic data is a straightforward way to reveal the effects of quantum criticality in the normal state of Ba(Fe1−xCox)2As2. The most important distinction is drawn between this analysis and any type of Kramers-Kronig analysis where an upper limit needs to be set. Here, the integral is naturally cut off at kBT by an exponential factor. The analysis is not limited to inelastic light scattering, but can be applied to a wide range of experimental probes as already outlined in Lederer et al.29. We hope that this transformation may enable the comparison of results from different spectroscopic probes directly and on the same footing, allowing a more unified analysis of quantum criticality.
Methods
Raman scattering
We performed inelastic light scattering experiments with the samples (for characterization, see Supplementary Note 3) attached to the cold finger of a 4He flow cryostat. Polarized photons having a wavelength of 577 nm (Coherent GENESIS MX-SLM577-500) hit the sample at an angle of incidence of 68∘. The polarized scattered photons were collected along the surface normal of the sample and focused on the entrance slit of a double monochromator. The photons transmitted at the selected energy were recorded with a CCD detector. The number of photons per second is proportional to the Van-Hove function S(q ≈ 0, Ω) = 1/π[1 + n(Ω, T)]χ″(Ω, T) where n(Ω, T) is the Bose factor and χ″ is the imaginary part of Raman response function which is displayed in Fig. 1. The factor R is the constant of proportionality which absorbs all experimental factors.
Imaginary time response
Following a method proposed in Lederer et al.29, we have used our measurements of the dissipative part of the response function, χ″, to characterize the dynamics of the corresponding imaginary time correlation function \(\tilde{{{\Lambda }}}(\tau )\) using the following exact identity:
with the imaginary time τ ∈ (0, β) and the inverse temperature β = 1/T where kB = 1 along the lines of Lederer et al.29. Since bosonic correlations have period β in imaginary time, the longest time response corresponds to τ ≈ β/2. In the following, it will be convenient to work with the specific quantity
which has the same universal properties as the static susceptibility \({\chi }^{\prime}({{\Omega }}=0,T)\) in the sense that the two quantities have identical scaling with temperature on cooling to both classical and quantum critical points29.
A key property of \(\beta \tilde{{{\Lambda }}}(\beta /2)\) is that it has a power-law dependence on temperature if χ″ obeys Ω/T scaling, and in particular is independent of temperature if χ″(Ω, T) is of marginal Fermi liquid form9, i.e., if it is a function of only Ω/T and not of either variable separately:
One significant virtue of \(\beta \tilde{{{\Lambda }}}(\beta /2)\) in comparison to \(\chi ^{\prime} ({{\Omega }}=0)\) is that it can be unambiguously computed from the measured Raman spectra. Since the measured χ″ (in this and other studies) fails to fall off at high frequency, the Kramers-Kronig integral relating χ″ to \(\chi ^{\prime}\) does not converge, and therefore requires a manual cutoff procedure. By contrast, the denominator in Eq. (2) grows exponentially for frequencies Ω ≫ T, rendering the integral convergent so long as the range of frequencies probed extends to several times the temperature.
Data availability
Data are available from the corresponding authors upon reasonable request.
References
Hertz, J. A. Quantum critical phenomena. Phys. Rev. B 14, 1165–1184 (1976).
Coleman, P. & Schofield, A. J. Quantum criticality. Nature 433, 226–229 (2005).
Fradkin, E., Kivelson, S. A. & Tranquada, J. M. Colloquium: theory of intertwined orders in high temperature superconductors. Rev. Mod. Phys. 87, 457–482 (2015).
Fournier, P. et al. Insulator-metal crossover near optimal doping in Pr2−xCexCuO4: anomalous normal-state low temperature resistivity. Phys. Rev. Lett. 81, 4720–4723 (1998).
Jin, K., Butch, N. P., Kirshenbaum, K., Paglione, J. & Greene, R. L. Link between spin fluctuations and electron pairing in copper oxide superconductors. Nature 476, 73–75 (2011).
Martin, S., Fiory, A. T., Fleming, R. M., Schneemeyer, L. F. & Waszczak, J. V. Normal-state transport properties of Bi2+xSr2-yCuO6+δ crystals. Phys. Rev. B 41, 846–849 (1990).
Cooper, R. A. et al. Anomalous criticality in the electrical resistivity of La2−xSrxCuO4. Science 323, 603–607 (2009).
Licciardello, S. et al. Electrical resistivity across a nematic quantum critical point. Nature 567, 213–217 (2019).
Varma, C. M., Littlewood, P. B., Schmitt-Rink, S., Abrahams, E. & Ruckenstein, A. E. Phenomenology of the normal state of Cu-O high-temperature superconductors. Phys. Rev. Lett. 63, 1996–1999 (1989).
Murthy, C., Pandey, A., Esterlis, I. & Kivelson, S. A. A stability bound on the T-linear resistivity of conventional metals. Preprint at https://arxiv.org/abs/2112.06966 (2021).
Prochaska, L. et al. Singular charge fluctuations at a magnetic quantum critical point. Science 367, 285–288 (2020).
Schuberth, E. et al. Emergence of superconductivity in the canonical heavy-electron metal YbRh2Si2. Science 351, 485–488 (2016).
Scalapino, D. J. A common thread: the pairing interaction for unconventional superconductors. Rev. Mod. Phys. 84, 1383–1417 (2012).
Perali, A., Castellani, C., Di Castro, C. & Grilli, M. d-wave superconductivity near charge instabilities. Phys. Rev. B 54, 16216–16225 (1996).
Lederer, S., Schattner, Y., Berg, E. & Kivelson, S. A. Enhancement of superconductivity near a nematic quantum critical point. Phys. Rev. Lett. 114, 097001 (2015).
Wang, Y., Abanov, A., Altshuler, B. L., Yuzbashyan, E. A. & Chubukov, A. V. Superconductivity near a quantum-critical point: the special role of the first matsubara frequency. Phys. Rev. Lett. 117, 157001 (2016).
Lederer, S., Berg, E. & Kim, E.-A. Tests of nematic-mediated superconductivity applied to Ba1−xSrxNi2As2. Phys. Rev. Res. 2, 023122 (2020).
Frérot, I. & Roscilde, T. Reconstructing the quantum critical fan of strongly correlated systems using quantum correlations. Nat. Commun. 10, 577 (2019).
Chu, J.-H., Analytis, J. G., Kucharczyk, C. & Fisher, I. R. Determination of the phase diagram of the electron-doped superconductor \(\,{{\mbox{Ba}}}\,{({{{\mbox{Fe}}}}_{1-x}{{{\mbox{Co}}}}_{x})}_{2}{{{\mbox{As}}}}_{2}\). Phys. Rev. B 79, 014506 (2009).
Gallais, Y. et al. Observation of incipient charge nematicity in \({{{{{{{{\rm{Ba}}}}}}}}({{{{{{{{\rm{Fe}}}}}}}}}_{1-X}{{{{{{{{\rm{Co}}}}}}}}}_{X})}_{2}{{{{{{{{\rm{As}}}}}}}}}_{2}\). Phys. Rev. Lett. 111, 267001 (2013).
Gallais, Y. & Paul, I. Charge nematicity and electronic Raman scattering in iron-based superconductors. C. R. Phys. 17, 113–139 (2016).
Kretzschmar, F. et al. Critical spin fluctuations and the origin of nematic order in Ba(Fe1−xCox)2As2. Nat. Phys. 12, 560–563 (2016).
Chu, J.-H., Kuo, H.-H., Analytis, J. G. & Fisher, I. R. Divergent nematic susceptibility in an iron arsenide superconductor. Science 337, 710–712 (2012).
Böhmer, A. E. et al. Nematic susceptibility of hole-doped and electron-doped BaFe2As2 iron-based superconductors from shear modulus measurements. Phys. Rev. Lett. 112, 047001 (2014).
Kuo, H.-H., Chu, J.-H., Palmstrom, J. C., Kivelson, S. A. & Fisher, I. R. Ubiquitous signatures of nematic quantum criticality in optimally doped Fe-based superconductors. Science 352, 958–962 (2016).
Palmstrom, J. C. et al. Comparison of temperature and doping dependence of elastoresistivity near a putative nematic quantum critical point. Nat. Commun. 13, 1011 (2022).
Gallais, Y., Paul, I., Chauvière, L. & Schmalian, J. Nematic resonance in the Raman response of iron-based superconductors. Phys. Rev. Lett. 116, 017001 (2016).
Worasaran, T. et al. Nematic quantum criticality in an Fe-based superconductor revealed by strain-tuning. Science 372, 973–977 (2021).
Lederer, S. et al. Measuring the imaginary-time dynamics of quantum materials. Philoso. Mag. 100, 2477–2490 (2020).
Aslamasov, L. & Larkin, A. The influence of fluctuation pairing of electrons on the conductivity of normal metal. Phys. Lett. A 26, 238–239 (1968).
Caprara, S., Di Castro, C., Grilli, M. & Suppa, D. Charge-fluctuation contribution to the Raman response in superconducting cuprates. Phys. Rev. Lett. 95, 117004 (2005).
Thorsmølle, V. K. et al. Critical quadrupole fluctuations and collective modes in iron pnictide superconductors. Phys. Rev. B 93, 054515 (2016).
Si, Q., Rabello, S., Ingersent, K. & Smith, J. L. Locally critical quantum phase transitions in strongly correlated metals. Nature 413, 804–808 (2001).
Varma, C. M. Colloquium: Linear in temperature resistivity and associated mysteries including high temperature superconductivity. Rev. Mod. Phys. 92, 031001 (2020).
Acknowledgements
We thank E. Berg and B. Moritz for fruitful discussions. The work was supported by the Deutsche Forschungsgemeinschaft (DFG, Projekt-IDs 107745057 - TRR 80, HA 2071/8-1 and HA2071/12-1)), the Bavaria-California Technology Center (BaCaTeC, grant no. 21[2016-2]), the Friedrich-Ebert foundation (D.J.) and the Alexander-von-Humboldt foundation (G.H., D.J.). Part of the analysis was performed at the Stanford Institute for Materials and Energy Sciences (SIMES) funded by the U.S. Department of Energy, Office of Basic Energy Sciences, Materials Sciences and Engineering Division (D.J.). J.C.P. was supported by a Gabilan Stanford Graduate Fellowship and a Stanford Lieberman Fellowship. S.L. is supported by the U.S. Department of Energy, Office of Science, National Quantum Information Science Research Centers, Quantum Systems Accelerator (QSA).
Author information
Authors and Affiliations
Contributions
D.J., L.P., G.H., and A.B. contributed approximately equally to the experiments. D.J. and L.P. performed the analysis. J.C.P., M.I., I.R.F., and T.W. prepared and characterized the samples. S.G. performed the SQUID measurements. S.L. worked out the theory. D.J. and R.H. conceived the study and prepared the manuscript with input from all authors, in particular from S.A.K.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks Marco Grilli and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jost, D., Peis, L., He, G. et al. Quantum critical fluctuations in an Fe-based superconductor. Commun Phys 5, 201 (2022). https://doi.org/10.1038/s42005-022-00981-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-022-00981-5
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.