Chiral trabeated metabeam for low-frequency multimode wave mitigation via dual-bandgap mechanism

Abstract

An elastic wave in a physical beam naturally possesses many wave modes, such as flexural, longitudinal, and torsional. Therefore, suppression of all possible vibration modes has been rarely achieved in beam-shaped periodic systems, especially at low frequencies. Here we present a low-frequency complete bandgap mechanism by overlapping the flexural bandgap with the longitudinal-torsional bandgap. To strengthen the general framework, we enforce an extra degree of freedom (rotational and torsional-spring) on the spring-mass system for the flexural and coupled (longitudinal-torsional) modes. The low rotational stiffness provides a low flexural bandgap, whereas the torsional stiffness yields a coupled-mode bandgap. To meet these prerequisites in physical modeling, a chiral trabeated metabeam is conceived, which allows all wave modes to be suppressed by a complete bandgap. Apart from single-mode mitigation, our work provides a route to implementing a low-frequency complete bandgap in a periodic fashion, potentially enabling the use of chirality in elastic structures.

Introduction

Research on metamaterials initiated by Veselago¹ that envisioned negative refractive index has been increasingly applied in diverse fields such as electromagnetics^2,3,4, acoustics^5,6,7 and mechanics^8,9,10 that exploit wave physics. Elastic metamaterials, in particular, can offer remarkable vibration attenuation by exploiting the bandgap property to manipulate elastic wave propagation. The bandgap of elastic metamaterials mainly occurs by decrease in transmission in two ways: the use of Bragg scattering^11,12 causes total reflection, and local resonance^13,14,15 causes massive absorption in the context of the entire metamaterial network, rather than a particular internal constituent.

The notion of elastic metamaterials that exploit local resonance has been thoroughly investigated in the Euler-Bernoulli beam^16,17,18,19, Timoshenko beam²⁰, and beam-shaped periodic structures^21,22 to alleviate flexural waves. The local resonance mechanism intrinsically requires additional local resonators with a linear relation between stiffness and bandgap frequency, and gives rise to a narrow bandgap. Recently, an interesting bandgap mechanism has been reported^23,24,25, in which a newly-considered zero rotational stiffness can shield low-frequency flexural waves in beam-shaped metamaterials. The research employs a quasi-static bandgap by lowering the rotational spring coefficient in the fourth-order dispersion equation that is derived from two-degree-of-freedom (2-DOF) equations of motion that consider shear deformation and rotational bending effects in the continuous Timoshenko beam structure, which accounts for only flexural waves. However, for complete vibration reduction towards a general shielding framework in the same beam-shape structure, longitudinal and torsional waves must be mitigated.

The chiral structure, which arises from the electromagnetic side, is one of the most significant current discussions in elastic or mechanical metamaterials. One proposed 3D chiral mechanical metamaterial²⁶ has the push-to-rotate property that is not allowed in the classical Cauchy continuum mechanics. This chiral metamaterial with push-to-rotate property has an acoustical activity²⁷ that is the mechanical counterpart of optical activity, and further supports the physical understanding of micropolar continuum mechanics²⁸. Accordingly, chiral mechanical metamaterials that can increase push-to-rotate response have been proposed^29,30. A complete bandgap has been observed in alternately arranged chiral mechanical metamaterials^31,32, but the mechanism by which it occurs remains unclear.

Here, we propose a low-frequency complete bandgap mechanism in a beam-shaped structure composed of chiral unit cells. The complete bandgap against all vibration modes is obtained by overlapping two kinds of ‘orthogonal’ bandgaps: a flexural bandgap induced by low rotational stiffness and a longitudinal-torsional bandgap induced by low torsional stiffness. To describe the complete bandgap mechanism, we introduce a generalized spring-mass system and compare it with achiral and chiral trabeated metabeams in the corresponding physical models. The achiral trabeated metabeam achieves a low-frequency flexural bandgap by having low rotational stiffness. Moreover, this achiral model can individually explain the other modes such as longitudinal and torsional modes that are not physically coupled. Here we further assign an additional degree of freedom (i.e., torsional stiffness) to the spring-mass system for the longitudinal-torsional mode. In this case, a low-frequency longitudinal-torsional bandgap is generated by low torsional stiffness. We demonstrate that a chiral trabeated metabeam with low torsional and rotational stiffness can achieve a low-frequency complete bandgap. By calculating dispersion curves and quantifying a measure of chirality in the general spring-mass system, we construct an analytic model that corresponds to a full transition from achiral to chiral trabeated metabeam. The analytically estimated vibration characteristics of the complete bandgap agree well with numerical and experimental results. The findings contribute to our understanding of an elastic analogy of chiral property and lay the groundwork for the complete bandgap mechanism that will be of great help in applying it to vibration devices.

Results and discussion

Dual-bandgap mechanism

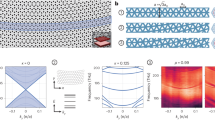
In this section, we seek to explain the dual (flexural and longitudinal-torsional) bandgap mechanism that generates a complete bandgap in the discrete spring-mass system. In general, a conventional beam has four rigid-body fundamental modes: two flexural (Fig. 1a), one longitudinal (Fig. 1b), and one torsional (Fig. 1c). The corresponding acoustic branches (i.e., four rigid vibration modes) in the band structure impede the development of low-frequency bandgaps. Therefore, to obtain a complete bandgap among branches, the mechanism must be clarified.

Fig. 1: Low-frequency flexural and longitudinal-torsional bandgap mechanisms.

Schematic drawings that represent four basic modes of the conventional beam; (a) flexural modes (b) longitudinal mode (c) torsional mode. d–f Spring-mass chain models that represent each wave modes of the beam-shaped structure. g–i Dispersion curves calculated from (d–f), respectively. j Schematic drawing of a longitudinal-torsional coupled mode of the conventional beam. k Two-degree-of-freedom (2-DOF) spring-mass chain model for the longitudinal-torsional coupled mode. l Dispersion curve shows longitudinal-torsional branches that can be tailored by κ and γ supporting the bandgap mechanism. k_x: wave number. a: lattice parameter. M: mass of the unit cell. I_xx: rotational inertia about the x-axis of the unit cell. I_yy: rotational inertia about the y-axis of the unit cell. α: axial stiffness along the z-axis. β: rotational stiffness along the y-axis. κ: axial stiffness along the x-axis. γ: rotational stiffness along the x-axis. u: z-axis displacement. θ: z-axis rotation. v: x-axis displacement. ψ: x-axis rotation. For comparison, M, I_yy, I_xx, a, β, γ are set as 1, and α, κ are set as 10. F-bandgap: flexural bandgap; LT-bandgap: longitudinal-torsional bandgap.

With respect to the flexural modes in the Timoshenko beam that account for shear deformation and rotational bending effects, we consider a 2-DOF spring-mass model with one axial spring for shear deformation u and one rotational spring for rotational bending θ to represent the flexural mode of a beam-shape structure (Fig. 1d). When a beam has four-fold rotational symmetry about the y- and z-axes, a single 2-DOF analytic model can be used to model two flexural modes along the xy-and xz-planes. In this work, we use the xz-plane as a representation.

We develop one-degree-of-freedom (1-DOF) monatomic models for the longitudinal and torsional modes of the beam-shape structure. For longitudinal deformation v, we use one x-axis axial spring with a spring constant κ (Fig. 1e). We also utilize one x-axis rotational spring with a torsion coefficient γ for torsional rotation ψ (Fig. 1f).

The equations of motion in the n^th unit cell of two 1-DOF monatomic models for longitudinal and torsional mode can be written as

$$M\ddot{v}=\kappa \left({v}^{n+1}-{v}^{n}\right)+\kappa \left({v}^{n-1}-{v}^{n}\right),$$

(1)

$${I}_{{xx}}{\ddot{\psi }}^{n}=\gamma \left({\psi }^{n+1}-{\psi }^{n}\right)+\gamma \left({\psi }^{n-1}-{\psi }^{n}\right),$$

(2)

where M is the mass of the unit cell, ${I}_{{xx}}$ is the rotational inertia about the x-axis of the unit cell, v is the x-axis displacement, and ψ is the x-axis rotation movement. Applying the Bloch periodic condition (${u}^{n+1}={u}^{n}{{{{{{\rm{e}}}}}}}^{-{{{{{\rm{i}}}}}}{k}_{x}a}$) and time harmonic displacement ($u={u}_{0}{{{{{{\rm{e}}}}}}}^{{{{{{\rm{i}}}}}}\omega t}$) to the equations of motion yields

$$-M{\omega }^{2}{v}^{n}=2\kappa \left({{{{{\rm{cos }}}}}}\left({k}_{x}a\right)-1\right){v}^{n},$$

(3)

$$-{I}_{{xx}}{\omega }^{2}{\psi }^{n}=2\gamma \left({{{{{\rm{cos }}}}}}\left({k}_{x}a\right)-1\right){\psi }^{n},$$

(4)

where ω is the angular frequency, k_x is the wave number, a is the lattice constant of the unit cell. Equations (3, 4) can be expressed in a matrix form as

$$\left[\begin{array}{cc}M{\omega }^{2}+2\kappa \left({{{{{\rm{cos }}}}}}\left({k}_{x}a\right)-1\right) & 0\\ 0 & I{\omega }^{2}+2\gamma \left({{{{{\rm{cos }}}}}}\left({k}_{x}a\right)-1\right)\end{array}\right]\left[\begin{array}{c}{v}^{n}\\ {\psi }^{n}\end{array}\right]=0.$$

(5)

By solving Det[·] where [·] is the 2 × 2 matrix in Eq. (5), a dispersion relation can be obtained. For simplicity, we determine the parameter set as M = I_xx = a = γ = 1, κ = 10.

The equations of motion in the n^th unit cell of 2-DOF analytic model for flexural mode considering rotational bending effects can be written as²⁵

$$M\ddot{u}= \,\alpha \left({u}^{n+1}-{u}^{n}\right)+\alpha \left({u}^{n-1}-{u}^{n}\right)\\ -\alpha {\zeta }_{{{{{{\rm{f}}}}}}}\left({\theta }^{n+1}+{\theta }^{n}\right)+\alpha {\zeta }_{{{{{{\rm{f}}}}}}}\left({\theta }^{n-1}+{\theta }^{n}\right),$$

(6)

$${I}_{{yy}}{\ddot{\theta }}^{n} = \,\beta \left({\theta }^{n+1}-{\theta }^{n}\right)+\beta \left({\theta }^{n-1}-{\theta }^{n}\right)+\alpha {\zeta }_{{{{{{\rm{f}}}}}}}\left({u}^{n+1}-{u}^{n}\right)\\ -\alpha {\zeta }_{{{{{{\rm{f}}}}}}}\left({u}^{n-1}-{u}^{n}\right)-\alpha {\zeta }_{{{{{{\rm{f}}}}}}}^{2}\left({\theta }^{n+1}+{\theta }^{n}\right)-\alpha {\zeta }_{{{{{{\rm{f}}}}}}}^{2}\left({\theta }^{n-1}+{\theta }^{n}\right),$$

(7)

where I_yy is the rotational inertia about the y-axis of the unit cell, α is the axial stiffness along the z-axis, β is the rotational stiffness along the y-axis. The flexural coupling coefficient (ζ_f = u^*/θ) is a measure of the extent that additional z-axis displacement u^* is induced by the y-axis rotation θ. For example, in the Timoshenko beam, ζ_f = a/2 when deformation is small²⁵.

Similarly as Eqs. (3, 4), dispersion relations of the 2-DOF model for flexural modes can be derived as

$$-M{\omega }^{2}{u}^{n}=2\alpha \left({{{{{\rm{cos }}}}}}\left({k}_{x}a\right)-1\right){u}^{n}+2\alpha {\zeta }_{{{{{{\rm{f}}}}}}}\left({{{{{\rm{i}}}}}}\,{{{{{\rm{sin }}}}}}\left({k}_{x}a\right)\right){\theta }^{n},$$

(8)

$$-{I}_{{yy}}{\omega }^{2}{\theta }^{n}= \,2\alpha {\zeta }_{{{{{{\rm{f}}}}}}}\left(-{{{{{\rm{i}}}}}}\,{{{{{\rm{sin }}}}}}\left({k}_{x}a\right)\right){u}^{n}\\ +2\beta \left({{{{{\rm{cos }}}}}}\left({k}_{x}a\right)-1\right){\theta }^{n}-2\alpha {\zeta }_{{{{{{\rm{f}}}}}}}^{2}\left({{{{{\rm{cos }}}}}}\left({k}_{x}a\right)+1\right){\theta }^{n}.$$

(9)

In a matrix form,

$$ \left[\begin{array}{cc}M{\omega }^{2}+2\alpha \left({{{{{\rm{cos }}}}}}\left({k}_{x}a\right)-1\right) & 2\alpha {\zeta }_{{{{{{\rm{f}}}}}}}\left({{{{{\rm{i}}}}}}\,{{{{{\rm{sin }}}}}}\left({k}_{x}a\right)\right)\\ -2\alpha {\zeta }_{{{{{{\rm{f}}}}}}}\left({{{{{\rm{i}}}}}}\,{{{{{\rm{sin }}}}}}\left({k}_{x}a\right)\right) & {I}_{{yy}}{\omega }^{2}+2\beta \left({{{{{\rm{cos }}}}}}\left({k}_{x}a\right)-1\right)-2\alpha {\zeta }_{{{{{{\rm{f}}}}}}}^{2}\left({{{{{\rm{cos }}}}}}\left({k}_{x}a\right)+1\right)\end{array}\right] \left[\begin{array}{c}{u}^{n}\\ {\theta }^{n}\end{array}\right]=0.$$

(10)

The dispersion curve (Fig. 1g) is calculated using the same fixed parameters (M = I_yy = a = β = 1, α = 10, and ζ_f = 0.5). Contrary to the dispersion curves (Fig. 1h, i) for 1-DOF models, a new optical branch is generated, because an additional degree of freedom is factored into the equation. The broadest and the lowest flexural bandgap can be achieved when α is high and β is low. If ζ_f = 0, the 2-DOF model (Fig. 1d) is decoupled to two separate 1-DOF models (Fig. 1e, f), and the optical branch vanishes. Correspondingly, the bandgap disappears if shear deformation u is not coupled to rotational movement θ.

Here, we deliver a low-frequency longitudinal-torsional bandgap mechanism that extends the flexural bandgap mechanism by evolution of the longitudinal-torsional coupled model (Fig. 1j). If x-axis displacement and x-axis rotation are coupled, the corresponding analytic model (Fig. 1k) can be represented by replacing z-axis axial springs α and y-axis rotational springs β in the flexural mode model (Fig. 1d) with x-axis axial springs κ and x-axis torsional springs γ, respectively. Here, we adopt a longitudinal-torsional coupling coefficient ζ_t.

From the 2-DOF longitudinal-torsional mode-coupled spring-mass model with a coupling coefficient ζ_t, by analogy to the 2-DOF flexural model, the dispersion relations can be written as

$$-M{\omega }^{2}{v}^{n}=2\kappa \left({{{{{\rm{cos }}}}}}\left({k}_{x}a\right)-1\right){v}^{n}+2\kappa {\zeta }_{{{{{{\rm{t}}}}}}}\left({{{{{\rm{i}}}}}}\,{{{{{\rm{sin }}}}}}\left({k}_{x}a\right)\right){\psi }^{n},$$

(11)

$$-{I}_{{xx}}{\omega }^{2}{\psi }^{n}= \,2\kappa {\zeta }_{{{{{{\rm{t}}}}}}}\left(-{{{{{\rm{i}}}}}}\,{{{{{\rm{sin }}}}}}\left({k}_{x}a\right)\right){v}^{n}\\ +2\gamma \left({{{{{\rm{cos }}}}}}\left({k}_{x}a\right)-1\right){\psi }^{n}-2\kappa {\zeta }_{{{{{{\rm{t}}}}}}}^{2}\left({{{{{\rm{cos }}}}}}\left({k}_{x}a\right)+1\right){\psi }^{n},$$

(12)

where ζ_t is a longitudinal-torsional coupling coefficient (v^*/ψ) that quantifies the additional x-axis displacement v^* due to x-axis rotation ψ. In a matrix form,

$$ \left[\begin{array}{cc}M{\omega }^{2}+2\kappa \left({{{{{\rm{cos }}}}}}\left({k}_{x}a\right)-1\right) & 2\kappa {\zeta }_{{{{{{\rm{t}}}}}}}\left({{{{{\rm{i}}}}}}\,{{{{{\rm{sin }}}}}}\left({k}_{x}a\right)\right)\\ -2\kappa {\zeta }_{{{{{{\rm{t}}}}}}}\left({{{{{\rm{i}}}}}}\,{{{{{\rm{sin }}}}}}\left({k}_{x}a\right)\right) & {I}_{{xx}}{\omega }^{2}+2\gamma \left({{{{{\rm{cos }}}}}}\left({k}_{x}a\right)-1\right)-2\kappa {\zeta }_{{{{{{\rm{t}}}}}}}^{2}\left({{{{{\rm{cos }}}}}}\left({k}_{x}a\right)+1\right)\end{array}\right]\left[\begin{array}{c}{v}^{n}\\ {\psi }^{n}\end{array}\right]=0.$$

(13)

Comparisons between Eq. 10 and Eq. 13 made different spring species, so the low-frequency longitudinal-torsional bandgap can be obtained by appropriately adjusting the stiffness of springs, i.e., low γ and high κ (Fig. 1l). In particular, the low γ is directly linked to the low-frequency bandgap. We argue that a monatomic chain effect, i.e., the so-called inertial amplification method^31,33, cannot support the phenomenon. It mainly comes from the dimer chain effect, which is induced by the coupling effect between longitudinal and torsional modes. This complete bandgap mechanism can be applied not only in a single beam-shaped model, but also in a more complicated model with coupled longitudinal and torsional modes. By overlapping two bandgap mechanisms (flexural and longitudinal-torsional modes), we uncover the presence of the complete bandgap, which allows suppression of multiple polarized elastic waves in a beam-shaped 3D periodic model.

Model design

To model the analytic model that has the low-frequency bandgap mechanism, we suggest a toy model called a trabeated metabeam, which is composed of horizontal components (i.e., plates) on vertical components (i.e., columns). Under the four-fold rotational symmetry about the x-axis, we propose achiral and chiral unit cells composed of four columns sandwiched by two plates (Fig. 2a, b). In the achiral case, the columns are parallel to the x-axis. In the chiral case, the columns are tilted to the x-axis, i.e., initially at 90°–Φ_c. Note that the unit cells of the two cases have the same volume because the tilted columns are created using a surface loft between two contact areas that have the same r.

Fig. 2: Visualization of trabeated metabeams.

a The schematic of an achiral and a chiral trabeated metabeams viewed from the xz-plane. b Cubic unit cells of the achiral and chiral trabeated metabeams. a: lattice parameter. b: side length of plate. Φ_A: angle of column (achiral case). Φ_c: angle of column (chiral case). h: thickness of plate. r: radius of contact area between column and plate. d: distance between columns on the plate. c Static simulation showing push-to-rotate property of chiral unit cell. Displacement of the unit cell is normalized.

The achiral trabeated metabeam is constructed by arranging the same achiral unit cells along the x-direction, and the chiral trabeated metabeam is constructed by repeatedly arranging the unit cell and its mirror structure. Therefore, the chiral trabeated metabeam is composed of alternating ‘left-handed’ and ‘right-handed’ chiral unit cells. The push-to-rotate property of the chiral unit cell (Fig. 2c) can couple the longitudinal displacement and torsional rotation of the structure, to yield longitudinal-torsional mode coupling. The achiral trabeated metabeam can only emulate the flexural bandgap mechanism, but the chiral trabeated metabeam can suppress both the flexural and longitudinal-torsional modes by a complete bandgap mechanism.

The unit cells can be described using six parameters (Fig. 2b). Parameter a is the lattice parameter, b is the side length of the square plates and h is their thickness, d is the spacing between the centers of neighboring columns, and r indicates the radius of the contact area between the plate and tilted columns, not the radius of the columns. All columns have the same r and height l. The thick plate (Fig. 2a) has thickness 2 h so the heights l in two trabeated metabeams and the angle Φ_c between tilted columns and plates in chiral trabeated metabeam can be represented as

$$l=a-2h,$$

(14)

$${\phi }_{{{{{{\rm{c}}}}}}}={{{{{\rm{arctan }}}}}}\left(l/d\right).$$

(15)

The angle Φ_A between vertical columns and plates in the achiral trabeated metabeam is 90°. For the analytical and numerical computations, the parameters are set as a = b = 40 mm, h = 6 mm, d = 28 mm, r = 1.5 mm.

Analysis in the previous section confirmed that the low rotational stiffness gives rise to a low-frequency bandgap. Accordingly, we find that both rotational and torsional stiffness are proportional to r⁴. Such a condition can provide an extreme low-frequency complete bandgap at small r. Due to the structural stability, we select r = 1.5 mm, which can be manufactured while keeping the complete low-frequency bandgap.

Analytic spring-mass model for dispersion analysis and dispersion curve calculation

To analyze the dynamic wave properties in the trabeated metabeams, dispersion curves are analytically calculated using the spring-mass model. The achiral trabeated metabeam has three wave modes (flexural, longitudinal, and torsional), whereas the chiral trabeated metabeam has only two modes (flexural and longitudinal-torsional), so we construct separate spring-mass discrete models for the achiral and chiral trabeated metabeams (Fig. 3). We postulate that the plate and columns interact weakly with each other, therefore in the analytic framework, the plate and columns function as a mass and a spring, respectively.

Fig. 3: The analytic model of achiral and chiral trabeated metabeams.

Schematics of trabeated metabeams on the xz-plane and corresponding equivalent analytic spring-mass models. a Flexural mode of the achiral beam. b Longitudinal mode of the achiral beam. c Torsional mode of the achiral beam. d Flexural mode of the chiral beam. e Longitudinal-torsional mode of the chiral beam. a: lattice constant of the achiral and chiral trabeated metabeams do not considering chirality of the unit cell. a_c: lattice constant of the chiral trabeated metabeam considering chirality. M: mass of the unit cell. I_xx: rotational inertia about the x-axis of the unit cell. I_yy: rotational inertia about the y-axis of the unit cell. α: axial stiffness along the z-axis β: rotational stiffness along the y-axis. κ: axial stiffness along the x-axis. γ: rotational stiffness along the x-axis. u: z-axis displacement. θ: z-axis rotation movement. v: x-axis displacement. ψ: x-axis rotation. ψ: x-axis rotation. The subscript A and c denote, respectively, achiral and chiral metabeams.

For the achiral trabeated metabeam (Fig. 3a–c), flexural, longitudinal, and torsional modes are mutually orthogonal, so three spring-mass models are required, one to express each mode. In general, two flexural modes excited by z-axis displacement u_A and y-axis rotation θ_A or y-axis displacement and z-axis rotation each require a 2-DOF mass-spring model. However, the achiral trabeated metabeam has four-fold rotational symmetry about the x-axis, so we can consider only the single 2-DOF flexural model, and obtain degenerate flexural branches. The 1-DOF spring-mass models for longitudinal (Fig. 3b) and torsional (Fig. 3c) modes excited by x-axis displacement v_A and x-axis rotation ψ_A are considered.

However, since the longitudinal and torsional modes of the chiral trabeated metabeam are strongly coupled, the coupled mode should be taken into account. Consequently, two spring-mass models are required, one for the flexural mode and one for the longitudinal-torsional mode. A 2-DOF spring-mass model (Fig. 3d) considers two flexural modes excited by z-axis displacement u_c and y-axis rotation θ_c or y-axis displacement and z-axis rotation. A 2-DOF spring-mass model (Fig. 3e) considers longitudinal-torsional modes excited by x-axis displacement v_c and x-axis rotation ψ_c. To involve the mirror symmetry, the lattice parameter of the chiral trabeated metabeam should be a_c, but the chiral property is not captured in the analytic model with the lattice parameter a (Fig. 3e). Therefore, additional post-processing is required to calculate the appropriate band structure. This stage will be discussed after deriving the dispersion equations of the chiral trabeated metabeam.

Referring to Eqs. 3, 4, 8, and 9, the dispersion relations of the achiral trabeated metabeam can be derived as

$$-M{\omega }^{2}{u}_{{{{{{\rm{A}}}}}}}^{n}=2{\alpha }_{{{{{{\rm{A}}}}}}}\left({{{{{\rm{cos }}}}}}\left({k}_{x}a\right)-1\right){u}_{{{{{{\rm{A}}}}}}}^{n}+2{\alpha }_{{{{{{\rm{A}}}}}}}{\zeta }_{{{{{{\rm{f}}}}}},{{{{{\rm{A}}}}}}}\left({{{{{\rm{i}}}}}}\,{{{{{\rm{sin }}}}}}\left({k}_{x}a\right)\right){\theta }_{{{{{{\rm{A}}}}}}}^{n},$$

(16)

$$-{I}_{{yy}}{\omega }^{2}{\theta }_{{{{{{\rm{A}}}}}}}^{n}= \,2{\alpha }_{{{{{{\rm{A}}}}}}}{\zeta }_{{{{{{\rm{f}}}}}},{{{{{\rm{A}}}}}}}\left(-{{{{{\rm{i}}}}}}\,{{{{{\rm{sin }}}}}}\left({k}_{x}a\right)\right){u}_{{{{{{\rm{A}}}}}}}^{n}\\ +2{\beta }_{{{{{{\rm{A}}}}}}}\left({{{{{\rm{cos }}}}}}\left({k}_{x}a\right)-1\right){\theta }_{{{{{{\rm{A}}}}}}}^{n}-2{\alpha }_{{{{{{\rm{A}}}}}}}{\zeta }_{{{{{{\rm{f}}}}}},{{{{{\rm{A}}}}}}}^{2}\left({{{{{\rm{cos }}}}}}\left({k}_{x}a\right)+1\right){\theta }_{{{{{{\rm{A}}}}}}}^{n},$$

(17)

$$-M{\omega }^{2}{v}_{{{{{{\rm{A}}}}}}}^{n}=2{\kappa }_{{{{{{\rm{A}}}}}}}\left({{{{{\rm{cos }}}}}}\left({k}_{x}a\right)-1\right){v}_{{{{{{\rm{A}}}}}}}^{n},$$

(18)

$$-{I}_{{xx}}{\omega }^{2}{\psi }_{{{{{{\rm{A}}}}}}}^{n}=2{\gamma }_{{{{{{\rm{A}}}}}}}\left({{{{{\rm{cos }}}}}}\left({k}_{x}a\right)-1\right){\psi }_{{{{{{\rm{A}}}}}}}^{n}.$$

(19)

Then referring to Eqs. 8, 9, 11, and 12, the dispersion relations of the chiral trabeated metabeam are written as

$$-M{\omega }^{2}{u}_{{{{{{\rm{c}}}}}}}^{n}=2{\alpha }_{{{{{{\rm{c}}}}}}}\left({{{{{\rm{cos }}}}}}\left({k}_{x}a\right)-1\right){u}_{{{{{{\rm{c}}}}}}}^{n}+2{\alpha }_{{{{{{\rm{c}}}}}}}{\zeta }_{{{{{{\rm{f}}}}}},{{{{{\rm{c}}}}}}}\left({{{{{\rm{i}}}}}}\,{{{{{\rm{sin }}}}}}\left({k}_{x}a\right)\right){\theta }_{{{{{{\rm{c}}}}}}}^{n},$$

(20)

$$-{I}_{{yy}}{\omega }^{2}{\theta }_{{{{{{\rm{c}}}}}}}^{n}= \,2{\alpha }_{{{{{{\rm{c}}}}}}}{\zeta }_{{{{{{\rm{f}}}}}},{{{{{\rm{c}}}}}}}\left(-{{{{{\rm{i}}}}}}\,{{{{{\rm{sin }}}}}}\left({k}_{x}a\right)\right){u}_{{{{{{\rm{c}}}}}}}^{n}\\ +2{\beta }_{{{{{{\rm{c}}}}}}}\left({{{{{\rm{cos }}}}}}\left({k}_{x}a\right)-1\right){\theta }_{{{{{{\rm{c}}}}}}}^{n}-2{\alpha }_{{{{{{\rm{c}}}}}}}{\zeta }_{{{{{{\rm{f}}}}}},{{{{{\rm{c}}}}}}}^{2}\left({{{{{\rm{cos }}}}}}\left({k}_{x}a\right)+1\right){\theta }_{{{{{{\rm{c}}}}}}}^{n},$$

(21)

$$-M{\omega }^{2}{v}_{{{{{{\rm{c}}}}}}}^{n}=2{\kappa }_{{{{{{\rm{c}}}}}}}\left({{{{{\rm{cos }}}}}}\left({k}_{x}a\right)-1\right){v}_{{{{{{\rm{c}}}}}}}^{n}+2{\kappa }_{{{{{{\rm{c}}}}}}}{\zeta }_{{{{{{\rm{t}}}}}},{{{{{\rm{c}}}}}}}\left({{{{{\rm{i}}}}}}\,{{{{{\rm{sin }}}}}}\left({k}_{x}a\right)\right){\psi }_{{{{{{\rm{c}}}}}}}^{n},$$

(22)

$$-{I}_{{xx}}{\omega }^{2}{\psi }_{{{{{{\rm{c}}}}}}}^{n}= \;2{\kappa }_{{{{{{\rm{c}}}}}}}{\zeta }_{{{{{{\rm{t}}}}}},{{{{{\rm{c}}}}}}}\left(-{{{{{\rm{i}}}}}}\,{{{{{\rm{sin }}}}}}\left({k}_{x}a\right)\right){v}_{{{{{{\rm{c}}}}}}}^{n}\\ +2{\gamma }_{{{{{{\rm{c}}}}}}}\left({{{{{\rm{cos }}}}}}\left({k}_{x}a\right)-1\right){\psi }_{{{{{{\rm{c}}}}}}}^{n}-2{\kappa }_{{{{{{\rm{c}}}}}}}{\zeta }_{{{{{{\rm{t}}}}}},{{{{{\rm{c}}}}}}}^{2}\left({{{{{\rm{cos }}}}}}\left({k}_{x}a\right)+1\right){\psi }_{{{{{{\rm{c}}}}}}}^{n},$$

(23)

where ζ_f,A is the achiral flexural coupling coefficient, ζ_f,c is the chiral flexural coupling coefficient, and ζ_t,c is the chiral longitudinal-torsional coupling coefficient. The column is much thinner than the plate, and therefore has less effect on mass and inertia than the plate, so M, I_yy, and I_xx are calculated by neglecting columns. Considering geometric parameters of the unit cell (Fig. 2b), M, I_yy, and I_xx are written as

$$M=2\rho {b}^{2}h,$$

(24)

$${I}_{{yy}}=\frac{1}{12}M\left({b}^{2}+4{h}^{2}\right),$$

(25)

$${I}_{{xx}}=\frac{1}{12}M\left({b}^{2}+{b}^{2}\right).$$

(26)

ζ_f,A, ζ_f,c, and ζ_t,A are unknown coupling coefficients that should be determined. Given geometric conditions (Fig. 4a, b), we can have the achiral flexural coupling coefficient ζ_f,A with ${u}_{{{{{{\rm{A}}}}}}}^{* }$ correlated to ${\theta }_{{{{{{\rm{A}}}}}}}$ as

$${u}_{{{{{{\rm{A}}}}}}}^{* }=\frac{a}{2}{{{{{\rm{sin }}}}}}{\theta }_{{{{{{\rm{A}}}}}}},$$

(27)

where the linear approximation has ${\theta }_{{{{{{\rm{A}}}}}}}\ll 1$. Thus we simply recast Eq. 27 to ζ_f,A as

$${\zeta }_{{{{{{\rm{f}}}}}},{{{{{\rm{A}}}}}}}=\frac{a}{2}.$$

(28)

Fig. 4: Schematic drawing of the geometry for calculating coupling coefficients.

a Achiral and chiral trabeated metabeams with four unit cells, indicating the locations of dashed regions. b 2D view of green dotted region in (a) with rotation ${\theta }_{{{{{{\rm{A}}}}}}}$. c Flexural mode of the achiral trabeated metabeam viewed from xz-plane and xy-plane. d Flexural mode of the chiral trabeated metabeam viewed from xz-plane and xy-plane. e 2D view of blue dash-dotted region in (a) with rotation ${\theta }_{{{{{{\rm{c}}}}}}}$. f 2D view of black solid region in (a) with rotation ψ_c. g 2D view of orange dashed region in (a) with deformation ${v}_{{{{{{\rm{c}}}}}}}^{* }$. a: lattice constant. b: side length of plate. d: distance between columns on the plate. l: height of column.

However, the chiral flexural coupling coefficient ζ_f,c is different from the achiral flexural coupling coefficient ζ_f,A since the flexural ‘twisted’ effect induces additional rotation along the orthogonal direction. It is obvious that the achiral trabeated metabeam has no ‘twisted’ effect (Fig. 4c) unlike the chiral trabeated metabeam (Fig. 4d). For the chiral trabeated metabeam, we measure and find that the ‘twisted’ effect depends on the ratio of l and a, and represent it as a chiral flexural-twist coefficient $\Big(\sqrt{1+{\left(\frac{l}{a}\right)}^{2}}\Big)$. The chiral flexural coupling coefficient ζ_f,c (Fig. 4e) considering the flexural-twist coefficient is therefore determined as

$${\zeta }_{{{{{{\rm{f}}}}}},{{{{{\rm{c}}}}}}}=\frac{a}{2}\sqrt{1+{\left(\frac{l}{a}\right)}^{2}}.$$

(29)

By using the geometry of the chiral trabeated metabeam (Fig. 4f), ${u}_{{{{{{\rm{c}}}}}}}^{* }$ and ${\psi }_{{{{{{\rm{c}}}}}}}$ are related as

$${u}_{{{{{{\rm{c}}}}}}}^{* }=\frac{d}{2}{{{{{\rm{sin }}}}}}{\psi }_{{{{{{\rm{c}}}}}}}.$$

(30)

Considering the geometry of chiral trabeated metabeam (Fig. 4g), ${v}_{{{{{{\rm{c}}}}}}}^{* }$ and ${u}_{{{{{{\rm{c}}}}}}}^{* }$ are expressed as

$$\sqrt{{l}^{2}+{d}^{2}}=\sqrt{{\left(l-{v}_{{{{{{\rm{c}}}}}}}^{* }\right)}^{2}+{\left(d+{u}_{{{{{{\rm{c}}}}}}}^{* }\right)}^{2}}.$$

(31)

Assuming ψ_c $\ll$ 1, then ${{v}_{{{{{{\rm{c}}}}}}}^{* }}^{2}$ and ${{u}_{{{{{{\rm{c}}}}}}}^{* }}^{2}$ become 0. Substituting Eq. (30) into Eq. (31) and solving yields the chiral longitudinal-torsional coupling coefficient ${\zeta }_{{{{{{\rm{f}}}}}},{{{{{\rm{c}}}}}}}$ that represents the relation between ${v}_{{{{{{\rm{c}}}}}}}^{* }$ and ${\psi }_{{{{{{\rm{c}}}}}}}$ as

$${\zeta }_{{{{{{\rm{t}}}}}},{{{{{\rm{c}}}}}}}=\frac{{d}^{2}}{2l}.$$

(32)

The remaining spring coefficients should be determined. These coefficients (${\alpha }_{{{{{{\rm{A}}}}}}}$ = 22.5 kN m⁻¹, ${\beta }_{{{{{{\rm{A}}}}}}}$ = 510 N·m rad⁻¹, ${\kappa }_{{{{{{\rm{A}}}}}}}$ = 2750 kN m⁻¹, ${\gamma }_{{{{{{\rm{A}}}}}}}$ = 9.94 N·m rad⁻¹, ${\alpha }_{{{{{{\rm{c}}}}}}}$ = 356 kN m⁻¹, ${\beta }_{{{{{{\rm{c}}}}}}}$ = 1.19 N·m rad⁻¹, ${\kappa }_{{{{{{\rm{c}}}}}}}$ = 711 kN m⁻¹, and ${\gamma }_{{{{{{\rm{c}}}}}}}$ = 1.90 N·m rad⁻¹) are numerically computed using the COMSOL simulator (see Methods). Because α_c > α_A and β_c < β_A, so the chiral trabeated metabeam should have a lower and broader flexural bandgap than the achiral trabeated metabeam.

Here is a reminder that we should take note of. The chirality should be considered when calculating the dispersion relations, because the proposed analytic model does not adequately include the chirality of the unit cell. Chiral trabeated metabeam is composed of alternating ‘left-handed’ and ‘right-handed’ unit cells, so the lattice parameter becomes a_c (= 2a) when chirality is considered, and a otherwise. We find that the chirality should be considered in the 1st branch of the longitudinal-torsional mode of the chiral trabeated metabeam. Therefore, the 1st branch should be calculated from k_x = 0 to k_x = π/a_c, and two modes are degenerate. However, in the presence of different velocities of two modes, two degenerated modes are lifted in the numerical simulation; these modes will be further discussed in the following section.

Dispersion curves (Fig. 5a, b) are obtained using the analytic spring-mass model (Fig. 3) with band folding mechanism. The achiral trabeated metabeam (Fig. 5a) has a flexural bandgap between 302 Hz and 501 Hz. In contrast, the chiral trabeated metabeam (Fig. 5b) provides lower and broader bandgaps than this in both flexural (182 Hz–1202 Hz) and longitudinal-torsional (91 Hz–1456 Hz) modes. These findings confirm that the proposed chiral trabeated metabeam that has low rotational stiffness can provide vibration shielding for diverse modes.

Fig. 5: Calculated dispersion curves of trabeated metabeams.

a Analytically calculated dispersion curve (band structure) of achiral trabeated metabeam. Orange line with diamond markers: flexural mode; Green line with triangle markers: longitudinal mode. Blue solid line: torsional mode. b Analytically calculated dispersion curve of a chiral model. Orange line with diamond markers: flexural mode. Red solid line: longitudinal-torsional mode. c Numerically calculated dispersion curve of achiral trabeated metabeam. d Numerically calculated dispersion curve of the chiral trabeated metabeam. The schematics below (c, d) show the mode shapes at the colored dot points in the dispersion curve (F1: two degenerate first flexural modes; F2: two degenerate second flexural modes; L1: longitudinal mode; T1: torsional mode; LT1: two degenerate first longitudinal-torsional modes; LT2: second longitudinal-torsional mode; B1: first bending eigenmode of the tilted column; B2: second bending eigenmode of the tilted column). Purple triangles in (d) denote first and second bending eigenfrequencies of the tilted column. Mode shapes of the unit cells of various modes plotted in terms of normalized modal displacements. k_x: wave number. a: lattice constant of the achiral trabeated metabeam. a_c: lattice constant of the chiral trabeated metabeam considering chirality of the unit cell.

Numerical simulation of dispersion curve and mode analysis

To verify the bandgap mechanism in physical models, we conducted a numerical calculation method using finite element method (FEM) based COMSOL Multiphysics (see Methods). Overall, the numerical dispersion curves of the achiral (Fig. 5c) and chiral (Fig. 5d) trabeated metabeams agree well with the corresponding analytical results (Fig. 5a, b). Mode shapes of various vibration modes that can be anticipated by analytic models are presented. While some may argue that a coupling effect exists between the longitudinal-torsional and flexural modes of the chiral trabeated metabeam, the intersection between flexural (F2) and longitudinal (LT2) branches in Fig. 5d provides strong evidence of no coupling effect at least in the low-frequency region. The unexpected flat branches (B1 and B2) not shown in the analytic model are due to the presence of a mass in the physical model that induces bending eigenmodes on the tilted columns that are supposed to function as springs (Fig. 5d). For the sake of comparison, the natural frequencies of columns calculated by using FEM are represented as purple triangles at the center of the first Brillouin zone (k_x = 0). The first and second bending eigenfrequencies of the columns are 1810 Hz and 2540 Hz, respectively.

Lifting of the degeneracy of flexural modes that originates from acoustical activity has been investigated in previous studies^27,28. Such a degeneracy lifting comes from a one-handed chiral unit cell with no mirror symmetry. But we here additionally demonstrate that the degeneracy (Fig. 6a) can be lifted even in longitudinal-torsional modes when mirror symmetry is present (Fig. 6b). As with previous studies^27,28, the splitting between longitudinal-torsional modes is induced by the presence of two decomposed eigenmodes with different phase velocities. We find that when the plate mass of the chiral trabeated metabeam is constant, this splitting can be estimated by measuring the torsion angle of the top surface of the chiral trabeated metabeam when a longitudinal displacement is imposed (see Supplementary Note 1). It indicates that the mode splitting is highly dependent on the geometric characteristics of the chiral trabeated metabeam. Take not that this kind of degeneracy lifting cannot be accomplished with a 2-DOF spring-mass model since the dispersion curve has only two branches (acoustic and optical), demanding the use of a higher degree of freedom model. However, the lifting is negligible because it does not affect the complete bandgap under the given initial geometry parameters (see the Model Design subsection in the Results and Discussion).

Fig. 6: Acoustic branch of longitudinal-torsional modes of the chiral trabeated metabeam.

a Analytical and (b) Numerical dispersion curve of longitudinal-torsional modes of the chiral trabeated metabeam below 0.1 kHz. In (b), A and B show the representative mode shapes in terms of nomalized displacements. The direction of displacement is indicated by black arrows in the mode shapes. a_c: lattice constant of the chiral trabeated metabeam considering chirality of the unit cell.

To confirm that the bandgap mechanism also applies to other geometries, we calculate numerical and analytical dispersion curves for four different geometries (Table 1). In all cases, the results (Fig. 7a–d) show good agreement between the analytical and numerical dispersion curves. The two highest flat modes in numerical dispersion curves indicate the first and second bending eigenmodes of tilted columns. We once again confirm that the degree of the lifting of the degeneracy of longitudinal-torsional modes varies with geometric parameters (Fig. 7(e–h)). Moreover, we conduct numerical simulations of chiral trabeated metabeams with 2 × 2 and 3 × 3 unit cells to verify that the complete bandgap mechanism is applicable to various geometries (see Supplementary Note 2). To achieve broadband wave attenuation, the splitting gap between two modes should be reduced, but it also guarantees an ability to precisely control the gap depending on requirements.

Table 1 Geometric parameters [mm] for four cases.

Fig. 7: Dispersion curves for different geometries.

a–d Dispersion curves of lowest 24 eigenmodes for four cases (Table 1). a Case 1. b Case 2. c Case 3. d Case 4. e–h Zoom of the dispersion curves considering longitudinal-torsional mode below the bandgap. e Case 1. f Case 2. g Case 3. h Case 4. The insets in (e–h) illustrate the models. Black dots denote numerical dispersion curve points (Num.). Orange line indicates flexural mode of the analytical dispersion curves (Ana.) and red line indicates the longitudinal-torsional mode of the analytical dispersion curves. k_x: wave number. a_c: lattice constant of the chiral trabeated metabeam considering chirality of the unit cell.

Transmission simulation and experiment results

To validate the result (Fig. 5), transmission spectra of trabeated metabeams with four unit cells are calculated numerically while keeping the initial geometric parameters (see Methods). Transmission spectra for stacks of four achiral (Fig. 8a–c) and chiral unit cells (Fig. 8d, e) are calculated and compared with the lowest bandgap region calculated from the analytic dispersion curves. Peaks at 1.8 kHz and 2.5 kHz in Fig. 8d, e are generated by the bending eigenmodes on tilted columns that interact weakly with plates. We use four unit cells with lattice parameter a, so four peaks generated by Fabry-Perot resonances appear before the onset frequency of the bandgap (Fig. 8a–d). However, due to the different lattice parameter a_c in the longitudinal-torsional mode of the chiral trabeated metabeam, its transmission exhibits two peaks before the onset frequency of the bandgap (Fig. 8e).

Fig. 8: Numerically calculated tranmission spectra of trabeated metabeams.

Transmission spectrum of (a) flexural wave (b) longitudinal wave (c) torsional wave in four achiral unit cells, and (d) flexural wave (e) longitudinal-torsional wave in four chiral unit cells. Colored region: bandgap region calculated in the analytic model. Yellow dashed region in (e): complete bandgap region.

To verify the simulation result and confirm the difference between the achiral and chiral trabeated metabeams, flexural and longitudinal vibration experiments are conducted (see Methods). Because the transmission peaks in experiments are flattened and lowered under laboratory conditions due to variables such as intrinsic material losses and undesirable experimental noise^17,25,34, we perform the numerical simulation with the assumption that the isotropic loss factor of the photosynthesis resin is 0.05. The experimental findings corroborate the numerical transmission estimates of achiral (Fig. 9a, b) and chiral (Fig. 9c, d) metabeams. The proposed chiral trabeated metabeam suppresses wave propagation for the longitudinal-torsional mode across a wide bandgap (88 Hz–1445 Hz), while the achiral trabeated metabeam maintains a passband. Furthermore, across a wide bandgap, the chiral metabeam robustly prevents flexural mode propagation (151 Hz–1055 Hz). Within the bandgap region, mode shapes manifest stopband behavior, while those beyond the bandgap region represent passband behavior (see Supplementary Note 3). The numerical transmission (Fig. 9) differs from that of Fig. 8 since the boundary conditions and acceleration measurement method have been altered (see Methods). As we use stacks of four unit cells, boundary conditions have an impact on the transmission spectrum. Nevertheless, it has been clearly shown that the chiral metabeam has a low-frequency complete bandgap (151 Hz–1055 Hz), whereas the achiral one only has a flexural bandgap (293 Hz–781 Hz).

Fig. 9: Experimental setups and measurements.

Experimental setup pictures and transmission spectra for (a) flexural mode of the achiral trabeated metabeam, (b) longitudinal mode of the achiral trabeated metabeam, (c) flexural mode of the chiral trabeated metabeam, and (d) longitudinal-torsional mode of the chiral trabeated metabeam. Black line: numerical transmission (Num.) with a material loss factor of zero; Orange line: numerical transmission with the material loss factor of 0.05; Red line: experimental transmission spectrum (Exp.). Scale bars: 4 cm.

Conclusion

In conclusion, we have proposed the low-frequency complete bandgap mechanism in a trabeated metabeam by incorporating two orthogonal bandgaps: flexural and longitudinal-torsional. Periodic mechanical metamaterials can be used to suppress vibrations, and the complete bandgap mechanism in a periodic beam is highly critical due to the presence of various modes such as longitudinal, flexural, and torsional modes. Recently proposed mechanisms to generate low-frequency bandgaps could only explain a single mode protection, especially flexural mode. The low-frequency complete bandgap considering other modes has not been well investigated to date. We analytically clarified the complete bandgap mechanism by establishing two 2-DOF spring-mass systems with coupling coefficients. For physical models, we propose the chiral trabeated metabeam that has both flexural and longitudinal-torsional coupled modes in the low-frequency range, to execute the mechanism. Due to the presence of chirality that cannot be easily examined by the Cauchy continuum, a more-complex mode called ‘longitudinal-torsional coupled mode’ can emerge. The bandgap mechanism is validated using experimental measurements as well as analytical and physical models, and the results are satisfactory. Our proposed design enables the usage of chiral structures with mirror symmetry in vibration insulators for a variety of wave types. Also, using the analytic approach we developed, the bandgap of complicated structures satisfying the complete bandgap mechanism may indeed be readily examined. We hope that this framework can also be utilized to assess the rich physics underpinning it, such as micropolar elasticity and topological edge states.

Methods

Numerical simulations

Numerical simulations are performed using the Solid Mechanics module in COMSOL Multiphysics. In all simulations, we use Young’s modulus E = 3 GPa, Poisson ratio ${v}_{{{{{{\rm{p}}}}}}}$ = 0.4, and density ρ = 1300 kg m⁻³ for metabeams. Geometrical nonlinearities are not considered in this study.

The stiffness coefficients of the unit cells have been calculated using the stationary study. The fixed boundary condition is imposed on the bottom of the unit cell, and a prescribed displacement or rotation condition is applied on the top of the unit cell depending on the axis of stiffness. While other stiffness coefficients do not require postprocessing, β_c must be divided by the square of the chiral flexural-twist coefficient $\left(\sqrt{1+{\left(\frac{l}{a}\right)}^{2}}\right)$, because the chiral flexural ‘twisted’ effect shown in Fig. 4b, c is not considered in the numerical simulation.

The band structures and mode shapes are calculated using Eigenfrequency analysis. In the case of the achiral trabeated metabeam, we impose periodic Bloch boundary conditions on both sides of the designed physical unit cells (Fig. 2b) along the x-axis, and on the remaining boundaries, we impose free boundary conditions. We seek to obtain the reduced wave number k_xπ/a in the first Brillouin zone by solving the ω(k_x) eigenvalue problem. In the case of the chiral trabeated metabeam, periodic Bloch boundary conditions are imposed on both sides of two connected unit cells (one ‘left-handed’ and one ‘right-handed’) along the x-axis, and reduced wave number k_xπ/a_c is obtained by solving the ω(k_x) eigenvalue problem.

For the torsion angle ${\varTheta }_{{{{{{\rm{t}}}}}}}$ calculations, we conduct static simulations. Take note that b and h are fixed to maintain the mass of plates. We enforce a longitudinal displacement (L = l/100) on the top plate and give a fixed boundary condition on the bottom plate. The torsion angle ${\varTheta }_{{{{{{\rm{t}}}}}}}$ is obtained from the central plate.

For the degree of longitudinal-torsional mode splitting s calculations, we calculated numerical dispersion curves with the same process as in Fig. 5. The degree of mode splitting s is estimated by taking the largest difference between two eigenfrequencies of each wavevector $(0\le {k}_{x}\le 2{{{{{\rm{\pi }}}}}}/{a}_{{{{{{\rm{c}}}}}}})$ and dividing it by the eigenfrequency at the edge of the first Brillouin zone (${k}_{x}$ = $2{{{{{\rm{\pi }}}}}}/{a}_{{{{{{\rm{c}}}}}}}$).

The numerical transmission spectra of metabeams (Fig. 8) are calculated using the frequency domain study as a result of steady-state responses due to a sinusoidal load applied to a structure. To excite elastic waves, a harmonic force or moment is applied to the bottom plate along the relevant axis; i.e., a harmonic force along the z-axis to excite flexural waves, a harmonic force along the x-axis to excite longitudinal waves, and a harmonic moment along the z-axis to generate torsional waves. Other boundary conditions are set as stress-free conditions. Transmission can be calculated as

$$T=20\,{{{{{\rm{log }}}}}}({a}_{{{{{{\rm{out}}}}}}}/{a}_{{{{{{\rm{in}}}}}}}),$$

(33)

where a_out and a_in are the average acceleration measured from the top and bottom plate, respectively. In Fig. 8, the Euclidean norm of x-, y-, and z-axis acceleration is used to calculate a_out and a_in. However, when computing the numerical transmission spectra of Fig. 9, boundary conditions that constrain x- and y-axis rotations are imposed to emulate the same conditions with the experimental setup (Fig. 9). In addition, one axis acceleration along the load direction is utilized to determine a_out and a_in. This acceleration is measured from the center of the top surface of the top and bottom plates.

Experimental measurements

The achiral and chiral trabeated metabeam shown in Fig. 9 are fabricated by 3D printing using photocurable epoxy resin (E = 3 GPa, v_p = 0.4, and ρ = 1300 kg m⁻³) with initial geometric parameters (a = b = 40 mm, h = 6 mm, d = 28 mm, r = 1.5 mm).

To enforce a harmonic flexural and longitudinal force to the achiral and chiral trabeated metabeam, an electromagnetic shaker (LDS vibrator V406) is connected to a square aluminum plate that worked as a wave bridge. The excitation signal is a harmonic frequency sweep from 20 to 2500 Hz (chiral) and 20 to 3000 Hz (achiral) in the form of a prescribed acceleration with a constant amplitude, amplified through an amplifier (LDS LPA600) and delivered to the shaker. Input and output accelerations are measured using accelerometers (PCB 356B21) attached to the center of the top side of the top and bottom plates. Take note that for all tests, the x- and y-axis rotations are fixed on the bottom plate. The voltage of the signal over time is captured using an oscilloscope (Keysight DSOX1204A) and transmitted to a computer. Frequency analysis is performed using Fast Fourier Transform (FFT).