Abstract
Exceptional point degeneracies (EPDs) in the resonant spectrum of non-Hermitian systems have been recently employed for sensing due to the sublinear response of the resonance splitting when a perturbant interacts with the sensor. The sublinear response provides high sensitivity to small perturbations and a large dynamic range. However, the resonant-based EPD sensing abides to the resolution limit imposed by the resonant quality factors and by the signal-to-noise ratio reduction due to gain-elements. Moreover, it is susceptible to local mechanical disturbances and imperfections. Here, we propose a passive non-resonant (NR) EPD-sensor that is resilient to losses, local cavity variations, and noise. The NR-EPD describes the coalescence of Bloch eigenmodes associated with the spectrum of transfer matrices of periodic structures. This coalescence enables scattering cross-section cusps with a sublinear response to small detunings away from an NR-EPD. We show that these cusps can be utilized for enhanced noise-resilient sensing.
Similar content being viewed by others
Introduction
Exceptional point degeneracies (EPDs) are spectral singularities corresponding to points in the parameter space of a non-Hermitian operator at which its eigenvalues and the associated eigenvectors coalesce1,2,3. A prominent example includes EPDs in the resonant spectrum of non-Hermitian systems3,4,5,6. In their proximity, a small perturbation \(\varepsilon \ll 1\) leads to a sublinear response (SLR) in the resonant splitting \(\varDelta \omega \propto \root {m} \of {\varepsilon}\gg \varepsilon\) due to a fractional Puiseux expansion of the perturbed frequencies around an \({m}^{{{{{{\rm{th}}}}}}}\) order EPD1,2. Such SLR provides an enhanced sensitivity to small perturbations \(\varepsilon\)7,8,9\(,\) while also offering an additional advantage over other sensing schemes relying on high-Q resonances10: an enhanced dynamic range, which is the ability to measure both small and large perturbation-related detunings. This observation has recently generated a substantial research effort in developing appropriate platforms where resonant EPDs are realized and their SLR is harvested for enhanced sensing application11,12,13,14,15,16,17,18,19.
That said, the implementation of resonant-based EPD sensing has triggered an ongoing debate regarding the resolution limit and the signal-to-noise ratio (SNR) efficiency of such schemes20,21,22. Specifically, the EPD sensing schemes based on purely lossy systems have been hampered by the broadening of the resonance linewidths. The addition of gain-elements can offset the losses, thereby, improving the resolution limit of the EPD sensing, however, they also introduce additional noise which becomes enhanced in the vicinity of the EPD and leads to a degradation of the SNR performance of the sensor. The noise can be intrinsic (e.g., due to amplification) or fundamental (due to the eigenbasis collapse at the EPD) and in some EPD-platforms, might offset the enhanced signal sensitivity, thus leading to an SNR which is not exceptional, but rather conventional19,20,21. Importantly, resonant EPD sensors, alike all resonant-based schemes, are susceptible to local mechanical disturbances (e.g., temperature variations, vibrations, etc.) and cavity imperfections that hamper their sensitivity.
Here, we propose a non-resonant sensing protocol based on EPDs occurring in the spectrum of operators other than the effective Hamiltonian of a resonant system. In our paradigm, the formation of an \({m}^{{{{{{\rm{th}}}}}}}\) order non-resonant EPD (NR-EPD) occurs in the spectrum of transfer matrices of Hermitian periodic structures. Their existence enforces a stationary point in the Bloch dispersion relation \(\omega \left(k\right)\sim {\omega }_{{{{{{\rm{SP}}}}}}}+{(k-{k}_{{{{{{\rm{SP}}}}}}})}^{m},\) where \(m\ge 2\) Bloch modes coalesce and the group velocity \({v}_{{{{{{\rm{g}}}}}}}\equiv \frac{\partial \omega }{\partial k}\sim {(\omega -{\omega }_{{{{{{\rm{SP}}}}}}})}^{\frac{m-1}{m}}\) of a propagating wave inside the structure vanishes23,24,25,26,27,28,29,30,31,32,33,34,35,36. As a result, the differential scattering cross-section \({|{\sigma }_{{{{{{\rm{T}}}}}}}|}^{2}\) of a suitably designed incident wavefront shows a SLR with respect to small global parameter variations \({X}_{{{{{{\rm{SP}}}}}}}\to {X}_{{{{{{\rm{SP}}}}}}}\pm \nu\) occurring in the proximity of the stationary point, i.e.,
where \({W}_{{{{{{\rm{T}}}}}}}\sim {\nu }^{-\alpha }\) is the energy density of the excited (slow) propagating mode. The exponent \(\alpha\) dictates the formation of the cusp in Eq. (1) and its value is controlled by the incident wave via wavefront shaping techniques37,38,39,40. Here, we propose to utilize the sublinear response Eq. (1) of the differential cross-section, near stationary points, as a protocol for hypersensitive sublinear sensing. The special case of \(m=3\) NR-EPDs, known as stationary inflection points (SIPs)23,24,27,28,29,30,31,32,33, monopolizes our attention because of its resilience to common mechanical disturbances, structural imperfections33,41 and losses33,42. Importantly, we show that the proposed SIP-sensing protocol exhibits an enhanced noise-resilient performance, as opposed to existing resonant based-schemes.
Results and discussion
Implementation of SIP platforms
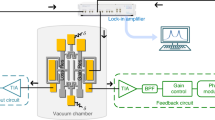
Unlike resonant EPDs, which rely on local perturbations done to the EPD-based platform, the proposed sensing platform (see “Methods”) consists of two distinct units—the probing element and the SIP sensing element (see Fig. 1a). The probing element can be any type of optical or microwave high-Q frequency selective filter (see Fig. 1b, c) whose resonant frequency depends on the applied local perturbation (i.e., acceleration, rotation, particle, etc.). Such arrangement allows to make the probing element extremely compact—thus granting access to measurements on the microscopic scale in a potentially cramped environment, without affecting the measured physics. After being probed, the perturbation is then transduced to the sensing SIP element, which may be placed away from the probe. As a result, the SIP structure can be made sensitive and robust enough without major concern of its size, making such arrangement useful for microscale sensing applications. A proposed experimental implementation of stationary-point-based, on-chip sensors (e.g., accelerometers, gyroscopes, inclinometers), using an optics/microwave framework, is shown in Fig. 1 (see “Methods” for elaboration). Importantly, the proposed platform is scalable and, hence, applicable for various wavelengths ranging from optical to millimeter-wave and radio frequency. The SIP protocol can be utilized in a variety of applications ranging from avionics and temperature variation sensing to bio- and chemical sensing.
a The schematic illustration of the sensing platform. The protocol involves a source which emits a broadband signal to the sensing platform which acts as a high-Q frequency selective filter, with frequency that depends on the applied perturbation. b An optomechanical Fabry–Perot cavity whose one wall is acting as a test-mass. c A whispering-gallery-mode resonator whose resonant frequency is changed due to the Sagnac effect. Different platforms supporting a stationary inflection point (SIP) singularity: d a multilayer structure25,26,32, e a coupled microstrip-waveguide27,28,29,35, where \(H\) indicates an external magnetic field strength, or f a serpentine waveguide36.
Transfer matrices and Bloch dispersion relation
The description of a wave propagating in an \(M\)-channel periodic structure with periodicity \({L}_{0}\) is typically done using the 2M-dimensional unit cell transfer matrix \({{{{{\mathcal{M}}}}}}\left(\omega \right)\,{{\equiv }}\,{{{{{\mathcal{M}}}}}}(z={z}_{0}+{L}_{0},{z}_{0}=0;\omega )\). This non-normal operator connects the wave amplitudes \({{{{{\boldsymbol{\Phi }}}}}}\) of a monochromatic wave at two different spatial positions of the structure at \(z={z}_{0}+{L}_{0}\) and \({z}_{0}\), through the relation
where the real part of the Floquet–Bloch wavenumber \({{{{{\rm{Re}}}}}}(k)\in [-{{\pi }}/{L}_{0},-{{\pi }}/{L}_{0}]\) is defined up to a multiple of \(2{{\pi }}/{L}_{0}\) (first Brillouin zone). At the right-hand-side of Eq. (2) we have imposed the Bloch theorem that requires \({{{{{{\boldsymbol{\Phi }}}}}}}_{k}\left(z={z}_{0}+{L}_{0}\right)={{{{{\rm{e}}}}}}^{{{{{{{{\rm{i}}}}}}}}k{L}_{0}}{{{{{{\boldsymbol{\Phi }}}}}}}_{k}({z}_{0})\), reflecting the periodicity of the underlying structure. Finally, the Bloch dispersion relation \(\omega =\omega (k)\) is evaluated by calculating the \(2M\) eigenvalues \(\lambda \left(\omega \right)\) of the transfer matrix by solving the following secular equation:
where \({\hat{1}}_{2M}\) is a 2M-dimensional identity matrix. When the eigensystem of Eq. (2) has 2\(M\) independent eigensolutions (and under the assumption that the eigensolutions of Eq. (2) can be written in the Bloch form) the transfer matrix \({{{{{\mathcal{M}}}}}}\left(\omega \right)\) is diagonalizable and can be written in the form \({{{{{\mathcal{M}}}}}}\left(\omega \right)={{{{{\mathcal{V}}}}}}\Lambda {{{{{{\mathcal{V}}}}}}}^{-1}\). The nonsingular similarity transformation matrix \({{{{{\mathcal{V}}}}}}\) has columns consisting of the eigenvectors of \({{{{{\mathcal{M}}}}}}\left(z,{z}_{0};\omega \right)\) while \({\Lambda }_{{nm}}={\lambda }_{n}{\delta }_{{nm}}\).
By imposing current conservation, we can show that the transfer matrix \({{{{{\mathcal{M}}}}}}\left(\omega \right)\) satisfies the relation \({{{{{\mathcal{M}}}}}}{\left(\omega \right)}^{{{\dagger}} }\Sigma {{{{{\mathcal{M}}}}}}\left(\omega \right)=\Sigma\) where \(\Sigma ={\Sigma }^{{{\dagger}} }\) is an invertible matrix with \({\Sigma }^{2}=1\), i.e., it belongs to the pseudo-unitary group \(U\left(M,M\right)\). Consequently, \(\left|{{\det }}{{{{{\mathcal{M}}}}}}\left(\omega \right)\right|=1\) while for any frequency \(\omega\) the eigenvalues \({\lambda }_{n}\) satisfy the relations \(\left\{{\lambda }_{n}^{-1}\right\}=\left\{{\lambda }_{n}^{* }\right\}\) corresponding to Bloch wavevectors which are either real (corresponding to propagating waves), or occur in complex conjugate pairs, (corresponding to evanescent modes)23,43. Below, we will refer to the propagating Bloch modes with positive (negative) group velocity \({v}_{{{{{{\rm{g}}}}}}} \, > \, 0\) (\({v}_{{{{{{\rm{g}}}}}}} \, < \,0\)) and to the evanescent Bloch modes with \({{{{{\mathcal{I}}}}}}{{{{{\rm{m}}}}}}\left(k\right) \, > \, 0\) (\({{{{{\mathcal{I}}}}}}{{{{{\rm{m}}}}}}\left(k\right) \, < \,0\)) as forward (backward) waves.
EPDs in the spectrum of transfer matrices and their relation to stationary points in the Bloch dispersion relation
The non-normal nature of the transfer matrix \({{{{{\mathcal{M}}}}}}\) allows for the formation of NR-EPDs in systems with non-trivial topology. Such degenerate points occur in the spectrum of \({{{{{\mathcal{M}}}}}}(X)\) by appropriately tuning one or a few of its parameters \(X\) (e.g., frequency \(\omega ,\) magnetic field, etc.). In this case, a complete basis is formed by augmenting the Bloch eigenvectors with generalized eigenvectors \({{{{{{\boldsymbol{\Phi }}}}}}}_{q}^{{{{{{\rm{r}}}}}}}\). The latter are found by implementing the standard Jordan chain procedure1,2,23,33, defined by the set of vectors that satisfy the recursive equations:
where \(m\) (\(2\le m \, < \,2M\)) is the order of the NR-EPD (NR-EPD\(-m\)), \({{{{{{\boldsymbol{\Phi}}}}}}}_{0}^{{{{{{\rm{r}}}}}}}=0\), \({{{{{{\boldsymbol{\Phi }}}}}}}_{1}^{{{{{{\rm{r}}}}}}}={{{{{{\boldsymbol{\Phi }}}}}}}_{{{{{{\rm{NR}}}}}}-{{{{{\rm{EPD}}}}}}}\) is the regular (Bloch) eigenvector while the remaining \(m-1\) eigenvectors \({{{{{{\boldsymbol{\Phi }}}}}}}_{q \, > \, 1}^{r}\) are the generalized eigenvectors. One can show that the generalized eigenvectors diverge along the propagation direction as \({{{{{{\boldsymbol{\Phi }}}}}}}_{q}\left(z\right)\propto {z}^{q-1}{{{{{\rm{e}}}}}}^{{{{{{{{\rm{i}}}}}}}}{kz}}{{{{{{\boldsymbol{\Phi }}}}}}}_{q}(0).\) At an NR-EPD\(-m\), the transfer matrix \({{{{{\mathcal{M}}}}}}\left({X}_{{{{{{\rm{NR}}}}}}{\mbox{-}}{{{{{\rm{EPD}}}}}}}\right)\) is similar to a Jordan form or a matrix containing Jordan blocks, i.e., \({{{{{\mathcal{M}}}}}}\left({X}_{{{{{{\rm{NR}}}}}}{\mbox{-}}{{{{{\rm{EPD}}}}}}}\right)={{{{{\mathcal{V}}}}}}\Lambda {{{{{{\mathcal{V}}}}}}}^{-1}\), and therefore, it is not diagonalizable1,2,23,33. The similarity transformation matrix \({{{{{\mathcal{V}}}}}}\) has columns consisting of the regular and the generalized eigenvectors. In the case when \({{{{{\mathcal{M}}}}}}\) has only one occurrence of an EPD in its spectrum, the matrix \(\Lambda\) consists of a Jordan block of size \(m\) and a diagonal matrix of size \(2M-m\) with diagonal elements being the eigenvalues \({\lambda }_{n}\) with geometric multiplicity 1. Generally, each Jordan block of size \(m\) will include one propagating Bloch mode with zero group velocity and \(m-1\) generalized eigenvectors with algebraically diverging amplitude with respect to the propagation distance \(z\).
An important feature of an NR-EPD is that any perturbation \({X}_{{{{{{\rm{NR}}}}}}{\mbox{-}}{{{{{\rm{EPD}}}}}}}\to {X}_{{{{{{\rm{NR}}}}}}{\mbox{-}}{{{{{\rm{EPD}}}}}}}+\nu\) that detunes the system away from the degenerate point results in a fractional power series (Puiseux series) of the eigenvalues with respect to the perturbation parameter \(\nu\). In other words, when an NR-EPD\(-m\) transfer matrix \({{{{{\mathcal{M}}}}}}\left({X}_{{{{{{\rm{NR}}}}}}{\mbox{-}}{{{{{\rm{EPD}}}}}}}\right),\) which is similar to a matrix containing at least a Jordan block of size \(m\, \times m\), is perturbed as \({{{{{\mathcal{M}}}}}}\left({X}_{{{{{{\rm{NR}}}}}}{\mbox{-}}{{{{{\rm{EPD}}}}}}}+\nu \right){{{{{\mathcal{\approx }}}}}}{{{{{\mathcal{M}}}}}}\left({X}_{{{{{{\rm{NR}}}}}}{\mbox{-}}{{{{{\rm{EPD}}}}}}}\right)+\nu \cdot \bar{\Delta },\) where \(\bar{\Delta }\) is a constant perturbation matrix, then the degenerate eigenvalues \(\lambda\), will obey the fractional expansion
The perturbed eigenvalue \({\lambda }_{q}\) in Eq. (5) can be also written as \({\lambda }_{q}={{{{{\rm{exp }}}}}}\left[{{{{{\rm{i}}}}}}\left({k}_{{{{{{\rm{NR}}}}}}{\mbox{-}}{{{{{\rm{EPD}}}}}}}+\delta k\right){L}_{0}\right]\approx {\lambda }_{{{{{{\rm{NR}}}}}}{\mbox{-}}{{{{{\rm{EPD}}}}}}}+{\sum }_{n=1}{c}_{n}{\delta k}^{n}\) which allows us to deduce that the perturbed Bloch wavevector (to the first order correction in detuning \(\nu\)) is \(\delta k\sim \root {m} \of{\nu }\). When the associated detuning \(\nu\) from \({X}_{{{{{{\rm{NR}}}}}}{\mbox{-}}{{{{{\rm{EPD}}}}}}}\) is identified with the frequency variation from the NR-EPD frequency \({{\omega }_{{{{{{\rm{NR}}}}}}{\mbox{-}}{{{{{\rm{EPD}}}}}}}=\omega }_{{{{{{\rm{SP}}}}}}}\), we get:
Equation (6) signifies the formation of a stationary point in the Bloch dispersion relation and connects an NR-EPD\(-m\) (and the associated size of the Jordan block) with the order of the stationary point. From Eq. (6) we deduce the presence of a slow-light mode with a vanishing group velocity \({v}_{{{{{{\rm{g}}}}}}}\)
The most familiar example of a stationary point is the regular band-edge (RBE) corresponding to \(m=2\). Higher order stationary points with \(m \, > \, 2\) need to be specifically engineered and are divided into two categories: The stationary points corresponding to even order NR-EPD\(-m^{\prime} s\) that occur at the band-edges, and the odd order NR-EPD\(-m^{\prime} s\) that occur inside the band and form an inflection point in the Bloch dispersion relation. The former are known as degenerate band-edges (DBEs) while the latter as stationary inflection points23,24. As opposed to the RBE, the higher-order stationary points include the presence of degenerate evanescent modes in addition to the propagating modes23,24,31. These evanescent modes contribute significantly in the formation of the cusp anomaly in the differential scattering cross-sections. Their engineered excitation allows us to control the type of divergence that the energy density of the excited (slow) propagating mode \({W}_{{{{{{\rm{T}}}}}}}\) demonstrates, see Eq. (1).
Although these cusp anomalies can occur for both odd and even order-\(m\) NR-EPDs, our focus will be on SIPs. Among all odd \(m\) NR-EPDs, the case of \(m=3\) will be monopolizing our attention. Various reasons led us to this decision: First, an SIP can be engineered in a way that shows a symmetric cusp anomaly with respect to a left/right detuning from the NR-EPD conditions when it is designed to occur in the middle of the band. Second, RBEs and DBEs are often overwhelmed with much more powerful, giant slow wave resonances when the system is turned to a scattering set-up24. Such high-Q resonances destroy the formation of cusps and result in sensing protocols with a small dynamic range10. Third, SIPs are not particularly sensitive to the size and shape of the underlying photonic structure and, when compared to Fabry–Perot or transmission band-edge resonances (where the whole photonic structure acts as a resonator), they are more resilient to absorption and structural imperfections33,41,42. Finally, the SIP of order \(m=3\) has been already implemented experimentally using various photonic platforms (see Fig. 1d–f), for efficient slow-light conversion27,28,29. While in these latter studies, the SIP of order \(m=3\) was promoted due to its high conversion prospects23,24,25,26,27,28,29,30,31,32,33,34,35,36, our sensing scheme takes advantage of the opposite scenario i.e., the possibility of total decoupling between the incident light and the slow mode.
Cusp anomalies in the differential reflectance near a stationary point
Next, we analyze the differential reflectance \(\Delta R(\nu )\) when a control parameter \(X\) (e.g., the frequency \(\omega\) of the incident wavefront) is detuned away from the NR-EPD conditions by \(\nu =X-{X}_{{{{{{\rm{NR}}}}}}{\mbox{-}}{{{{{\rm{EPD}}}}}}}\). For the sake of the argument, we assume only one Jordan block of size \(m\) in the similarity matrix \(\Lambda\). Furthermore, we assume the simplest possible scattering scenario of a lossless semi-infinite SIP structure of order \(m=3\) occupying the positive semi-infinite space \(z\ge 0\). The validity of our conclusions in the case of finite structures (in the presence of losses), has been tested in the next section.
Our presentation below follows closely the study of Figotin and Vitebskiy24. At the interface, the incident \({{{{{{\boldsymbol{\Psi }}}}}}}_{{{{{{\rm{I}}}}}}}\left(\omega ,z\right),\) reflected \({{{{{{\boldsymbol{\Psi }}}}}}}_{{{{{{\rm{R}}}}}}}\left(\omega ,z\right)\) and transmitted \({{{{{{\boldsymbol{\Psi }}}}}}}_{{{{{{\rm{T}}}}}}}\left(\omega ,z\right)\) waves, must satisfy the boundary condition
where the reflection coefficient has been absorbed in \({{{{{{\boldsymbol{\Psi }}}}}}}_{{{{{{\rm{R}}}}}}}\). When the system is detuned away from the NR-EPD (i.e., \(\nu \; \ne \; 0\)), the transmitted wave \({{{{{{\boldsymbol{\Psi }}}}}}}_{{{{{{\rm{T}}}}}}}\left(\omega ,z\right)\) inside the slow-light structure can be decomposed into a superposition of the \(M\) forward Bloch modes \({{{{{{\boldsymbol{\Phi }}}}}}}_{n}^{+}\) (see “Methods”). Specifically,
Furthermore, the energy conservation condition requires that the transmitted and reflected waves satisfy the relation \({S}_{{{{{{\rm{I}}}}}}}+{S}_{{{{{{\rm{R}}}}}}}\left(X\right)={S}_{{{{{{\rm{T}}}}}}}\left(X\right)\), where \({S}_{{{{{{\rm{I}}}}}}}\), \({S}_{{{{{{\rm{T}}}}}}}\left(X\right)\), and \({S}_{{{{{{\rm{R}}}}}}}\left(X\right)\) are the energy fluxes of the incident, transmitted and reflected waves. We further assume that the incident wave is normalized as \({S}_{{{{{{\rm{I}}}}}}}=1\). Since evanescent modes do not contribute to the energy flux, \({S}_{{{{{{\rm{T}}}}}}}\) is
where \({v}_{{{{{{\rm{g}}}}}}}^{(n)}\) indicates the group velocities of the forward propagating Bloch modes inside the structure. In the case that the incident monochromatic wavefront that does not excite any fast-propagating modes inside the medium, Eq. (10) simplifies to \({S}_{{{{{{\rm{T}}}}}}}\propto {W}_{{{{{{\rm{T}}}}}}}{v}_{{{{{{\rm{g}}}}}}}^{{{{{{\rm{slow}}}}}}}\), where \({{W}_{{{{{{\rm{T}}}}}}}\equiv {\left|{{{{{{\boldsymbol{\Phi }}}}}}}_{{{{{{\rm{slow}}}}}}}^{+}\left(z\right)\right|}^{2}\approx \left|{{{{{{\boldsymbol{\Psi }}}}}}}_{{{{{{\rm{T}}}}}}}\left(z\right)\right|}^{2}\) is the energy density carried by the slow mode and \({v}_{{{{{{\rm{g}}}}}}}^{{{{{{\rm{slow}}}}}}}\) is the corresponding group velocity given by Eq. (7). Therefore, the analysis of the exact form of the \({S}_{{{{{{\rm{T}}}}}}}\) singularity collapses to the investigation of the divergence of the energy density \({W}_{{{{{{\rm{T}}}}}}}\sim {\nu }^{-\alpha }\) with respect to the detuning from the NR-EPD.
We first recall that for \(\nu \,\ne\, 0,\) in the specific case of an SIP of order \(m=3\), the excitation \({{{{{{\boldsymbol{\Psi }}}}}}}_{{{{{{\rm{T}}}}}}}\left(z\right)\) can be written as a superposition of a forward slow-propagating Bloch mode \({{{{{{\boldsymbol{\Phi }}}}}}}_{{{{{{\rm{slow}}}}}}}^{+}\left(\omega ,z\right)\) and of a forward evanescent mode \({{{{{{\boldsymbol{\Phi }}}}}}}_{{{{{{\rm{ev}}}}}}}^{+}\left(\omega ,z\right)\) i.e., \({{{{{{\boldsymbol{\Psi }}}}}}}_{{{{{{\rm{T}}}}}}}\left(\omega ,z\right)={{{{{{\boldsymbol{\Phi }}}}}}}_{{{{{{\rm{slow}}}}}}}^{+}\left(\omega ,z\right)+{{{{{{\boldsymbol{\Phi }}}}}}}_{{{{{{\rm{ev}}}}}}}^{+}(\omega ,z)\). Of course, the decaying evanescent contribution to the transmitted wave becomes negligible at a certain distance \({z}_{{{{{{\rm{c}}}}}}}\propto 1/{{{{{\mathcal{I}}}}}}{{{{{\rm{m}}}}}}\left(k\right)\) from the interface and this explains the approximation i.e., \({\left|{{{{{{\boldsymbol{\Phi }}}}}}}_{{{{{{\rm{slow}}}}}}}^{+}\left(z\right)\right|}^{2}\approx {\left|{{{{{{\boldsymbol{\Psi }}}}}}}_{{{{{{\rm{T}}}}}}}\left(z\right)\right|}^{2}\). Nevertheless, the excitation of an evanescent mode is detrimental in the formation of a cusp as it can lead to a finite energy flux \({S}_{{{{{{\rm{T}}}}}}}\propto {\left|{{{{{{\boldsymbol{\Phi }}}}}}}_{{{{{{\rm{slow}}}}}}}^{+}\left(z\right)\right|}^{2}{v}_{{{{{{\rm{g}}}}}}}={{{{{\rm{const}}}}}}.\) under the condition that \({\left|{{{{{{\boldsymbol{\Phi }}}}}}}_{{{{{{\rm{slow}}}}}}}^{+}\left(z\right)\right|}^{2}\sim {\left|{{{{{\rm{\nu }}}}}}\right|}^{-2/3}\). At the same time, we recall that \({\left|{{{{{{\boldsymbol{\Psi }}}}}}}_{{{{{{\rm{T}}}}}}}\left(z\right)\right|}^{2}\approx \left|{{{{{{\boldsymbol{\Phi }}}}}}}_{{{{{{\rm{slow}}}}}}}^{+}\left(z\right)\right|^{2}\) leading to the conclusion that \(\left|{{{\boldsymbol{\Psi}}}}_{{{\mathrm{T}}}}(z)\right|^{2}\sim\left|{{{\mathrm{\nu}}}}\right|^{-2/3}\). Such a field intensity divergence is compatible with the boundary condition Eq. (8) (which dictates that \({{{{{{\boldsymbol{\Psi }}}}}}}_{{{{{{\rm{T}}}}}}}\left(z\right)\) at the boundary \(z=0\) is finite), provided that the incident wave excites both the slow forward propagating and the forward evanescent modes in a way that they are interfering destructively at the interface i.e., \({{{{{{\boldsymbol{\Phi }}}}}}}_{{{{{{\rm{slow}}}}}}}^{+}(z=0)\approx -{{{{{{\boldsymbol{\Phi }}}}}}}_{{{{{{\rm{ev}}}}}}}^{+}\left(z=0\right)\sim {\left|{{{{{\rm{\nu }}}}}}\right|}^{-1/3}.\) The effect of the dramatic amplitude growth of the transmitted wave in the vicinity of an SIP is a feature of the frozen mode regime. Past efforts23,24,25,26,27,28,29,30,31 utilized this generic property of the frozen mode regime for enhancing light–matter interactions. Here, however, our interest lies in the opposite scenario where \({S}_{{{{{{\rm{T}}}}}}}\propto {\left|{{{{{\rm{\nu }}}}}}\right|}^{2/3}\) and, therefore, the transmittance (or the differential reflectance) forms a cusp. From the above discussion, it becomes clear that the formation of the cusp Eq. (1) requires the design of an incident wavefront which does not excite a Bloch evanescent mode. In this case, the differential reflectance in the proximity of an SIP of order \(m=3\) behaves as
where we have assumed that in the lossless scenario at the SIP the reflectance is \(R\left({\omega }_{{{{{{\rm{SP}}}}}}}\right)=1\) (since \({S}_{{{{{{\rm{T}}}}}}}\propto {\left|{{{{{\rm{\nu }}}}}}\right|}^{2/3}\mathop{\to }\limits^{\nu \to 0}0\)), and \(T\left(\omega \right)\equiv {S}_{{{{{{\rm{T}}}}}}}(\omega )/{S}_{{{{{{\rm{I}}}}}}}\) and \(R\left(\omega \right)={S}_{{{{{{\rm{R}}}}}}}(\omega )/{S}_{{{{{{\rm{I}}}}}}}\) are the transmittance and reflectance of the incident wavefront. Equation (11) signifies a sublinear response of the differential reflectance to frequency detuning and can be used as a measurand for enhanced SLR sensing protocols that also demonstrate a large dynamic range. In fact, the above SLR is still applicable for any global parameter variation \(\nu =X-{X}_{{{{{{\rm{NR}}}}}}-{{{{{\rm{EPD}}}}}}}\) which preserves the form Eq. (7) of the slow-light group velocity. Below, we will demonstrate that one such case is associated with variations of the external magnetic field applied to a slow-light structure. Let us finally remark, that a similar argument that led to Eq. (11) for the case of a stationary point of order \(m=3\), can also apply for the stationary point of order \(m=2\) (RBE) leading to a square root cusp i.e., \(\Delta R\left(\nu \right)\sim \sqrt{\nu }.\)
Wave simulations and Coupled Mode Theory (CMT) modeling
We have confirmed our proposed sensing protocol by performing full-wave simulations with a realistic photonic platform that has been experimentally shown to demonstrate an SIP of order \(m=3\) 27,28,29. We consider a semi-infinite periodic system whose unit cell consists of a pair of coupled perfectly conductive microstrip waveguides on a ferrite magnetic substrate (see Fig. 1e and “Methods” for the design details). The unit cell contains one straight waveguide and one meandered waveguide. The waveguides are coupled together in the spatial domain, where they are closely separated from one another. We assumed that there is an applied out-of-plane constant magnetic field \(H\approx 86\) \({{{{{\rm{mT}}}}}}\), resulting in a violation of time-reversal symmetry, necessary for achieving an NR-EPD of order \(m=3\) in the Bloch modes of the \(4 \,\times 4\) transfer matrix \({{{{{\mathcal{M}}}}}}\) which describes the unit cell of the system. Using COMSOL’s finite element method (FEM) solver, we have calculated the S-parameters of the unit cell by probing the system with \(50\Omega\) impedance ports and retrieved the associated transfer matrix \({{{{{\mathcal{M}}}}}}\). This allowed us to calculate the dispersion relation and the Bloch modes, which are required for the analysis of the semi-infinite structure (see “Methods” for details).
In Fig. 2a, we show the calculated dispersion relation which displays an SIP of order \(m=3\) (SIP-3) at the frequency \({f}_{{{{{{\rm{SP}}}}}}}=2.00645\;{{{\mathrm{GHz}}}}\) (see the dashed horizontal line). In the inset of Fig. 2b, we also show the reflectance \(R\) as a function of frequency \(f\). The SIP-3 frequency \({f}_{{{{{{\rm{SP}}}}}}}\), where the reflectance develops a cusp, is shown in the inset by the vertical dotted line. In the main panel of the same figure, we report the differential reflectance \(\Delta R\) as a function of frequency detuning \(\nu\) from the SIP frequency \({f}_{{{{{{\rm{SP}}}}}}}\). The incident wavefront is designed following the criteria specified in the previous section to guarantee the SLR of Eq. (11). The best fit (see black dotted line in Fig. 2b) indicates that the differential reflectance varies with the frequency detuning \(\nu\) as \(\Delta R\sim {\left|\nu \right|}^{0.7}\), which is consistent with the theoretical expectations of Eq. (11). We have also checked the validity of the SLR of \(\Delta R\) with respect to other (global) parameter detunings. In Fig. 2c, we report the response of the differential reflectance \(\Delta R\) with respect to magnetic field variations \(\nu \equiv \Delta H\) from the value of the applied magnetic field strength \({H}_{{{{{{\rm{SP}}}}}}}\) at the SIP. The FEM simulations reveal a scaling \(\Delta R\sim {\left|\Delta H\right|}^{0.66}\) in perfect agreement with Eq. (11).
a The dispersion relation of this platform demonstrates a stationary inflection point frequency fSP which is shown by a dotted black line. b Logarithmic plot of the differential reflectance ΔR (blue dots) as a function of the frequency detuning \(\nu\) from the non-resonant exceptional point degeneracy frequency fSP. The black dashed line indicates the best fitting corresponding to a power law \(\Delta R\propto\left|\nu\right|^{0.7}\). The inset shows the formation of a cusp in the reflectance R spectrum, in the vicinity of fSP (vertical black dashed line). c Logarithmic plot of the differential reflectance ΔR (blue dots) as a function of the magnetic field detuning ΔH from the applied magnetic field strength \({H}_{{{{{{\rm{SP}}}}}}}\) where the order \(m=3\) non-resonant exceptional point degeneracy occurs. The black dashed line is the best fit \(\Delta R\propto\left|\Delta H\right|^{0.66}\).
The scattering properties of the simulated photonic circuit of Fig. 1e in the proximity of the SIP can be analyzed using CMT modeling (see “Methods”). Due to its generality, CMT modeling allows us to extend our conclusions beyond the specific platform of Fig. 1e, to any system that demonstrates stationary points in its Bloch dispersion relation. The geometry of the model is shown in Fig. 3b, while its dispersion relation is reported in the inset of Fig. 3a.
a Logarithmic plot of the differential reflectance \(\Delta R\) (blue line) as a function of the frequency detuning \(\nu\) from the stationary inflection point (SIP) frequency \({\omega }_{{{{{{\rm{SP}}}}}}}\). The black dashed line indicates a variation of the differential reflectance which is \(\Delta R\propto {\left|\nu \right|}^{0.66}\). The inset shows the dispersion relation of the Coupled Mode Theory (CMT) model. The SIP frequency \({\omega }_{{{{{{\rm{SP}}}}}}}\) is indicated by a horizontal dashed line. b Logarithmic plot of the differential reflectance \(\Delta R\) (blue line) as a function of the Peirels’ phase detuning \(\nu =\Delta \phi\) from the critical phase \({\phi }_{{{{{{\rm{SP}}}}}}}\). The black dashed line indicates a variation of the differential reflectance which is \(\Delta R\propto {\left|\nu \right|}^{0.66}\). In the background we show a schematic of the CMT model Eq. (12). c Logarithmic plot of the differential reflectance \(\Delta R\) (color lines) as a function of the frequency detuning \(\nu\) from the SIP frequency \({\omega }_{{{{{{\rm{SP}}}}}}}\) in case of a finite-size system for various number of unit-cells \(L\). The black dashed line indicates a variation of the differential reflectance which is \(\Delta R\propto {\left|\nu \right|}^{0.66}\). In order to optimize the scaling performance, we have used a ramped loss \(\gamma \left(n\right)={\gamma }_{{{\max }}}{\left(\frac{n-1}{L-1}\right)}^{2}\), where \({\gamma }_{{{\max }}}\) is the amount of loss in the last unit cell and \(n\) is the number of the unit cell.
In the main panel of Fig. 3a, we report the differential reflectance \(\Delta R\left(\nu \right)\) versus the detuning \(\nu\) from the SIP frequency. The analysis required the evaluation of the eigenmodes of the transfer matrix of the slow-light structure and the decomposition of the incident wavefront \({{{{{{\boldsymbol{\Psi }}}}}}}_{{{{{{\rm{I}}}}}}}\) in this basis, see Eq. (9). Furthermore, a small imaginary part \(({{{{{\mathcal{I}}}}}}{{{{{\rm{m}}}}}}\left({\varepsilon }_{{{{{\mathrm{0,1}}}}}}\right)\sim {10}^{-5})\) has been introduced (see “Methods”) to simulate natural losses occurring in the structure and to allow us to lift the NR-EPD degeneracy in a controllable manner, in order to implement the decomposition process Eq. (9) numerically.
We have made sure that such a prepared wavefront satisfies the boundary condition Eq. (8) together with the requirements for the appearance of the cusp anomaly in the reflectance, as outlined in the previous section. The data confirms nicely the validity of Eq. (11) for at least three orders of magnitude. The same analysis has been performed using, as a detuning parameter, the variations of the Peirels’ phase from its NR-EPD value \({\phi }_{{{{{{\rm{SP}}}}}}}\) and for fixed incident frequency \(\omega ={\omega }_{{{{{{\rm{SP}}}}}}}.\) These results are also presented in the main panel of Fig. 3b. Furthermore, we have tested that these results are robust for large, but finite, slow-light samples when a small amount of losses are present in the system. These losses are required to suppress Fabry–Perot resonances in the reflectance spectrum which can mask the otherwise robust SLR scaling. Achieving successful scaling in finite samples further indicates the viability of the proposed NR-EPD sensing platform. However, the optimal local loss strength \(\gamma\) with respect to the size of the system \(L\) is expected to be model dependent and determined by the condition that the absorption length \({\xi }_{\gamma }\) in the vicinity of the stationary point is less than the system size. If the loss strength is too high, the impedance mismatch will inevitably deteriorate the desired SLR response. In Fig. 3c, we also show how the finite size of the structure affects the scaling of the differential reflectance \(\Delta R\). From the figure, it is seen that the fractional response is already evident when the number of unit cells is twenty. Larger system sizes result in an increased dynamic range due to reduction of the lower bound of the sublinear scaling.
Noise analysis
While enhanced sensitivity to small perturbations is an important metric, the precision of the measurement is another important characteristic of the efficiency of a sensor. This is defined as the smallest measurable change of the input quantity given by the noise of the sensor output. Noise can stem from a variety of sources, including mechanical vibrations and mesoscopic fluctuations due to environmental thermal fluctuations, signal noise generated by the coupling to the interrogating channels, quantum uncertainty or fundamental detector resolution limits, and it can never be fully eliminated. It is therefore vital to study both—sensitivity and noise—in tandem. Such analysis allows one to estimate how noise in the observable (e.g., \(\Delta R\)) is translated to uncertainty in the measurand (e.g., \(\nu\)), which defines the actual precision of a sensor. The precision of our stationary point sensing protocol due to noise is scrutinized by the computational simplicity that the CMT modeling offers and is reconfirmed by COMSOL simulations for the platform shown in Fig. 1e. Below, we distinguish between two types of noise that might affect the performance of a sensor9: (a) multiplicative noise associated with classical noise sources describing a noisy NR-EPD, and (b) additive noise associated with noisy input channels. For a better assessment of the NR-EPD sensing efficiency we also compare the precision provided by SIP-3 and RBE sensing protocols.
A quantitative description for the precision of the stationary-point-based sensors is provided by analyzing the detuning error \(\sigma (\nu )\) defined as
where \({\sigma }_{\Delta R}\left(\nu \right)\equiv \sqrt{\left\langle \Delta {R}^{2}\left(\nu \right)\right\rangle -{\left\langle \Delta R\left(\nu \right)\right\rangle }^{2}}\) is the standard deviation of \(\Delta R\left(\nu \right)\) due to noise fluctuations and \(\chi \equiv \frac{\partial \left\langle \Delta R\left(\nu \right)\right\rangle }{\partial \nu }\) is the sensitivity of the sensor, where \(\left\langle \cdot \right\rangle\) indicates a noise averaging. The detuning error Eq. (12) provides an estimation of the uncertainty in the evaluation of the detuning \(\nu\) (which is the signature that the perturbing agent leaves when it interacts with the sensing platform) via the output measurement associated with the differential reflectance.
Multiplicative noise
We first analyze the influence of practically inevitable fabrication imperfections or slow fluctuations of the environment associated with, temperature or pressure variations that affect the constituent parameters of the materials, and other types of mesoscopic fluctuations in the system parameters. Such fluctuations are characterized by a very large correlation time implying (quasi-)static disorder and lead to the existence of additional parasitic degrees of freedom of the system44. Therefore, it is instructive to study how these parametric fluctuations are translated to the error in the measured detuning. This situation is modeled by weakly fluctuating frequencies \(\varepsilon_0 +\delta\varepsilon_0\) and \(\varepsilon_1 +\delta\varepsilon_1\) of each resonant mode of the CMT model (see Eq. (22) in “Methods”). For demonstration purposes, we have assumed that both \(\delta\varepsilon_0\) and \(\delta\varepsilon_1\) are independent random variables taken from a uniform distribution \(\left[-W,W\right]\).
We first consider an SIP-3 scenario in a finite-size, disordered system. To mimic the behavior of a semi-infinite structure, we have introduced losses, in such a way that the associated absorption length is smaller than the size of the system (see Methods for details). In Fig. 4a, we report the CMT results for the differential reflectance \(\Delta R\left(\nu \right)\) (gray circles) versus the frequency detuning \(\nu\) from \({\omega }_{{{{{{\rm{SP}}}}}}}\). The ensembled average differential reflectance \(\left\langle {\Delta} R\left(\nu \right)\right\rangle\) is also shown with a blue solid line. We find that the power law scaling \(\left\langle {\Delta} R\left(\nu \right)\right\rangle \sim {\nu }^{\alpha }\) with the best-fitting value of \(\alpha \approx 2/3\) persists for three orders of magnitude in detuning, despite the presence of the disorder. Nevertheless, a smearing of the SIP cusp is unavoidable leading to the formation of a plateau \(\left\langle \Delta R\left(\nu \to 0\right)\right\rangle \sim {W}^{\beta }\) for very small detunings \({\nu }_{{{{{{\rm{c}}}}}}}\sim {W}^{3\beta /2}\) (see inset of Fig. 4a). These detunings define the sensitivity bound of our SIP-sensors as far as the mesoscopic fluctuations are concerned. The numerical analysis gives the best-fit of the exponent, which is \(\beta \approx 2/3\) (see “Methods” for further analysis).
a Logarithmic plot of the differential reflectance ΔR (gray dots) as a function of the detuning \(\nu\) from the frequency ωSP for 104 disorder realizations of the resonant frequencies of the Coupled Mode Theory model. The disorder strength is taken to be \(W = 0.01\). The average value 〈ΔR〉 (blue line) follows the predicted dependence Eq. (11) \(\langle {\Delta} R\rangle\sim\left|\nu\right|^{0.66}\) indicated by the black dashed line. Inset: The sensitivity bound \({\nu }_{{{{{{\rm{c}}}}}}}\) for three different disorder strengths (blue dots). The black dashed line indicates the best fit \({\nu }_{{{{{{\rm{c}}}}}}}\sim W\). b Detuning error \({\sigma }_{\nu }\) as a function of detuning \(\nu\) for three different disorder strengths in case of a regular-band-edge-based sensing scheme (red lines) and of a stationary-inflection-point-based sensing scheme (blue lines). The red highlighted area represents the domain \(\sigma_\nu\; > \;\nu\) where the signal cannot be resolved. The resolution limit for each sensing protocol is defined by the point where the σν line crosses the line \(\sigma_\nu = \,\nu,\) shown by the black dashed line.
Further statistical processing of \(\Delta R\left(\nu \right)\) allows us to evaluate \({\sigma }_{\Delta R}\left(\nu \right)\) and \(\chi\) and from there, via Eq. (12), the detuning error \({\sigma }_{\nu }\). To get a better appreciation of the robustness of the SIP-3 based sensing with respect to disorder, we have also calculated \({\sigma }_{\nu }\) associated with an RBE. The comparison is shown in Fig. 4b for three values of the disorder strength \(W\). In this figure, we have highlighted (red region) the domain where the error in the measured detuning is larger than the detuning itself and, therefore, the precision of the sensor has completely deteriorated. In all cases, \({\sigma }_{\nu }\) is decreasing as we are approaching the corresponding resolution limit (black dashed line). However, for the same disorder strength \(W\), the detuning error of the SIP-3 based sensing is smaller by an order of magnitude than the detuning error of RBE-based sensing protocol indicating its superiority as far as (long-correlation time) multiplicative noise is concerned.
Additive noise
Next, we analyze the effect of noise due to low-frequency thermal fluctuations in the input channels. For this purpose, we have performed Monte-Carlo simulations in a semi-infinite structure associated with the CMT Hamiltonian (see Eq. (22) in “Methods”). From these simulations we have extracted the standard deviation \({\sigma }_{\Delta R}\) of \(\Delta R\left(\nu \right)\) due to the presence of the additive noise and the sensitivity \(\chi\) of the sensor, which allowed us to evaluate the detuning error \({\sigma }_{\nu }\) via Eq. (12).
In Fig. 5a, we report some typical results of the SIP-based sensing scheme, accounting for the influence of input signal noise on the measured differential reflectance \(\Delta R\left(\nu \right)\). The blue solid line indicates the mean value of \(\left\langle \Delta R\left(\nu \right)\right\rangle\) for each specific value of frequency detuning \({{{{{\rm{\nu }}}}}}\). The height of the gray domain surrounding the blue line represents the standard deviation \({\sigma }_{\Delta R}\) of \(\Delta R\left(\nu \right)\) at each value of \({{{{{\rm{\nu }}}}}}\). When comparing the evaluated \({\sigma }_{\Delta R}\) for two distant values of \({{{{{\rm{\nu }}}}}}\) (see black vertical double-sided arrows) it is found that \({\sigma }_{\Delta R}\) does not experience noticeable variations as a function of \({{{{{\rm{\nu }}}}}}\) and remains approximately constant. At the same time, Eq. (12) implies that for \({\sigma }_{\Delta R}\left(\nu \right)\approx {{{{{\rm{const}}}}}}.\), the detuning error will scale inversely proportional to the sensitivity i.e., \({\sigma }_{\nu }\sim {\chi }^{-1}(\nu )\). Therefore, in the limit of small detuning values where the sensitivity is higher, we expect a decreasing detuning error \({\sigma }_{\nu }\). Figure 5b shows the probability density \({{{{{\mathcal{P}}}}}}(\nu )\) of the simulated detuning measurements performed for two distant values of \({{{{{\rm{\nu }}}}}}\) (blue lines). The corresponding values of standard deviation \({\sigma }_{\nu }\) are indicated by double-sided blue arrows. As expected, when the simulated measurements are performed close to the stationary point singularity, the standard deviation \({\sigma }_{\nu }\) decreases, indicating an enhanced precision of the sensor.
a The differential reflectance \(\varDelta R\) as a function of the detuning \(\nu\). Height of the gray domain represents the evaluated standard deviation \({\sigma }_{\varDelta R}\) in the measured differential reflectance for each value \(\nu\) of the frequency detuning. b Probability density of the detuning measurements \({{{{{\mathscr{P}}}}}}(\nu )\) under the influence of input signal noise for two distant values of \(\nu\). The blue double-sided arrows indicate the corresponding standard deviations for the extracted \(\nu\). c Calculated detuning error \({\sigma }_{\nu }\) as a function of the frequency detuning \(\nu\) from the \({\omega }_{{SP}}\) in case of a stationary-inflection-point-based sensor (blue line with circles), in case of a regular-band-edge-based sensor (red line with circles), and in the case of the COMSOL simulated stationary-inflection-point-based sensor shown in Fig. 1e (light-blue line with squares). The dashed blue and light-blue lines indicate a scaling \({\left|\nu \right|}^{1/3}\), while red dashed line indicates a scaling \({\left|\nu \right|}^{1/2}\). The variance of the input signal noise in the Coupled Mode Theory Monte-Carlo simulations is \({\sigma }_{+}^{2}={10}^{-5}\), while for the COMSOL simulations \({\sigma }_{+}^{2}={5\times 10}^{-4}\).
A panorama of \({\sigma }_{\nu }\) versus the detuning \(\nu\), for an SIP-based (blue line) and an RBE-based (red line) sensing protocol is shown in Fig. 5c. In both cases, we have found that \({\sigma }_{\nu }\sim 1/\chi\) (see the blue and red dashed lines corresponding to \({\sigma }_{\nu }{\sim \nu }^{1/3}\) and \({\sigma }_{\nu }\sim {\nu }^{1/2}\), respectively) which is a consequence of the fact that the standard deviation \({\sigma }_{\Delta R}\) remains approximately constant with respect to the detuning from the stationary point frequency \({\omega }_{{{{{{\rm{SP}}}}}}}.\) The smaller detuning error of the RBE sensor compared to the SIP sensor in case of small detuning, does not imply that the RBE sensor is superior to the SIP sensor, since the former is extremely fragile to disorder and losses. In the same subfigure, we report COMSOL results for the case of the coupled microstrip waveguide of Fig. 1e (light blue line). It is instructive to point out that the results of the noise analysis of the Monte-Carlo simulations for the RBE sensing protocol agree with the recent experimental findings of enhanced precision accelerometers operating in the vicinity of a Wigner Cusp Anomaly (WCA)45. The WCAs are square root cusps in the differential scattering cross-section of processes around the frequency threshold of a newly open channel, and they can be seen as a generalization of RBEs.
Conclusions
We have identified a paradigm of enhanced sensing protocols that utilize non-resonant exceptional point degeneracies occurring in the spectrum of transfer matrices of periodic structures. Their presence enforces a stationary point in the Bloch dispersion relation, which leads to a cusp in the reflectance from these structures. We have shown that the reflectance variation with respect to the frequency detuning (or any other global parameter detuning) from the NR-EPD configuration is sublinear and can be used as a measurand for enhanced sensing with a large dynamic range. In this respect, our proposed SLR sensing protocol is complimentary to the resonant-based EPD schemes that detect local perturbations imposed on the system from a perturbing agent. Furthermore, the enhanced sublinear sensitivity is resilient to noise generated by the input channels as opposed to resonant EPDs5,7,8,9,11,12,13,14,15,16,17,18,19,20,21,22 where (fundamental) noise in the proximity of an EPD, due to the resonant eigenbasis collapse, is enhanced and, in some cases (depending on the underlying platform), might offset the enhanced sensitivity19,20,21. Sensors that utilize stationary inflection point NR-EPDs show additional robustness to mesoscopic fluctuations due to environmental temperature variations and fabrication imperfection. Our sensing proposal does not involve active elements, and therefore, it does not suffer from excess noise effects. Although the analysis performed here has been confined to the first two stationary points of order \(m={{{{\mathrm{2,3}}}}}\), it can be extended to higher-order NR-EPDs where one can achieve an even higher sensitivity depending on the number of evanescent modes excited by the incident wavefront. It will be interesting to extend these studies in this direction and analyze the robustness of these schemes to noise.
Methods
Proposed experimental implementation of stationary-point-based avionic sensors
In case of avionic sensing (e.g., acceleration), the probing element can be an optomechanical Fabry-Perot cavity whose one wall is acting as a test-mass (see Fig. 1b). The same concept can be used in microwaves where now the variable cavity consists of an LC circuit with a variable capacitor plate playing the role of the test-mass. When an acceleration is applied, the test-mass is displaced due to the inertia; thus, inducing a variation in the length of the cavity and, consequently, in its resonant frequency. Another possible implementation of the sensing protocol is as a hypersensitive gyroscope. In the optical framework, the probing platform will be a whispering-gallery-mode whose resonant frequency is changed due to the Sagnac effect, which is a shift of the resonant mode frequency by an amount proportional to the angular velocity of the rotating platform (see Fig. 1c). A microwave implementation of the whispering-gallery-mode sensing platform might involve a combination of two microwave accelerometers (see Fig. 1b) which are normal to one another. In both cases (see Fig. 1b, c), the variable resonators act as filtering devices that turn a broadband incident signal into a continuous-wave-like signal with a narrow spectral width around a detuned resonant frequency induced by the motion of the sensing platform. The continuous-wave-signal transmits through the splitter and is reflected by the sensing element which supports an NR-EPD of order \(m=3\) corresponding to a stationary (inflection) point in its Bloch dispersion relation. The reflected signal is measured by a detector and shows a cusp anomaly in the proximity of the stationary point frequency \({f}_{{{{{{\rm{SP}}}}}}}\). The reflectance variations \(\Delta R = \left|R - R_{{{\mathrm{SP}}}} \right|\) with respect to the frequency detuning \(\nu = \left|f - f_{{{\mathrm{SP}}}} \right|\) demonstrate a sublinear response \(\varDelta R\sim {\nu }^{2/3}\) which is used as a measurand for the proposed sensing, see Eq. (1).
Our stationary point sensing scheme utilizes intensity variation measurements (i.e., transmittance/reflectance) near non-resonant EPDs as opposed to resonant shift measurements. The latter might be masked by a linewidth broadening of the resonances that appear in the transmission (or the reflection) spectrum or by the generation of additional noise due to the presence of gain elements. Furthermore, resonant shift sensing requires broadband frequency sweeps, which impose an upper bound on the dynamic range. Such measurements are done in two ways: (i) signal (intensity) measurements, by probing the system at individual frequencies within the scanned domain, (ii) Fourier transform of the temporal signal emitted by the system. In the former case one needs to perform a large number of intensity measurements for each respective frequency, which results either in longer sampling time compared to the direct intensity measurements or worse signal-to-noise ratio. The latter measuring scheme is applicable only to active systems operating at or above the lasing threshold, which, besides adding extra complexity to the platform, also results in the addition of the quantum noise generated by the system.
Decomposition into Bloch modes and wavefront shaping protocol
The analysis of the transport characteristics of a semi-infinite structure is typically based on a scattering matrix approach. The latter can be directly extracted from the analysis of the following three \(2M \times 2M\) transfer matrices: (a) the matrix \({{{{{{\mathcal{M}}}}}}}_{{{{{{\rm{S}}}}}}}\) that determines the wave propagation from a unit cell to a unit cell inside the semi-infinite structure; (b) the transfer matrix \({{{{{{\mathcal{M}}}}}}}_{{{{{{\rm{L}}}}}}}\) that dictates the wave evolution in free space (or the leads), and; (c) the transfer matrix \({{{{{{\mathcal{M}}}}}}}_{{{{{{\rm{I}}}}}}}\) which describes the boundary conditions Eq. (8) that must be satisfied by the field at the interface \(z=0\). The latter can be expressed in a compact form as:
where \(\Psi_j \,(j = 1, 2)\) denote the fields before and after the interface respectively.
While the scattering matrix connects incoming to outgoing waves and, therefore, provides easy access to the transmission/reflection coefficients associated with the scattering process, the transfer matrix formalism allows us to identify the associated Bloch modes of the semi-infinite structure and, via this identification, establish an appropriate basis where the conditions which lead to Eq. (1), for the formation of a cusp in the differential reflectance, can be formulated.
We start with the description of the process that allows us to decompose the fields into the Bloch eigenmodes (see Eq. (9)). First, we diagonalize the transfer matrices \({{{{{{\mathcal{M}}}}}}}_{{{{{{\rm{S}}}}}}}\), \({{{{{{\mathcal{M}}}}}}}_{{{{{{\rm{L}}}}}}}\) in order to extract the Bloch modes and classify them as forward/backward and propagating/evanescent according to their wavenumbers and group velocities as described in the main text. This mode-basis is then arranged as columns of \(2M\times {m}_{j}^{x}\) matrices \({B}_{j}^{x}\), where \({m}_{j}^{x}\) denotes the number of each type \(x\) of the Bloch eigenmodes at a respective frequency. For example, \(x=f\) denotes forward propagating modes, \(x=b\) backward propagating modes, and \(x=e\) evanescent modes which decay away from the interface. Bloch modes that grow away from the interface are excluded from the decomposition based on the physical requirement that the fields must not diverge as \(| z | \rightarrow \infty\). The decomposition proceeds as,
where \({{{{{{\boldsymbol{\alpha }}}}}}}_{j}^{x}\) contain the expansion coefficients in the basis of the Bloch eigenmodes. Inserting Eq. (14) in Eq. (13) leads to the following relation
which, after appropriate re-arrangement, can be written as
Equation (16) relates the incoming propagating and the outgoing propagating and evanescent modes on the right and left sides, respectively.
Next, we want to rewrite the above relation in terms of the incoming \({{{\mathbf{\phi}}}}_+\) (defined in an (\({m}_{1}^{f}+{m}_{2}^{b}\))-dimensional space) and outgoing (propagating and evanescent) modes \({\widetilde{{{{{{\boldsymbol{\phi }}}}}}}}_{-}\) (defined in an \(({m}_{1}^{b}+{m}_{2}^{f}+{m}_{1}^{e}+{m}_{2}^{e})\)-dimensional space). To this end, we first introduce the projection operators \({\varepsilon}_{{{{{\mathrm{1,2}}}}}}^{f}\), \({\varepsilon }_{{{{{\mathrm{1,2}}}}}}^{e},\) and \({\varepsilon }_{{{{{\mathrm{1,2}}}}}}^{b}\) defined as
Substituting in Eq. (16) the expressions for \({{{{{{\boldsymbol{\alpha }}}}}}}_{{{{{\mathrm{1,2}}}}}}^{f,b,e}\) from Eq. (17), we find the relation that connects the incoming with the outgoing (including the evanescent) modes,
Equation (18) defines the non-unitary scattering matrix \(\widetilde{S}\) in terms of the operators \({A}_{+}\), \({\widetilde{A}}_{-}\)
Knowledge of \(\widetilde{S}\) allows us to extract further information about the expansion coefficients \({{{{{{\boldsymbol{\alpha }}}}}}}_{j}^{x}\) and, consequently, identify conditions under which an incident wavefront can (cannot) excite specific Bloch modes inside the semi-infinite stationary point structure.
Let us, for example, analyze the expansion coefficients of a generic incident wavefront that is injected into a semi-infinite structure that supports a stationary point from two single-mode transmission lines. We assume that the wavefront can be written as a linear combination of propagating waves \({{{{{{\boldsymbol{\phi }}}}}}}_{+}^{(n)}={({\delta }_{1,n},{\delta }_{2,n})}^{T}\) (\(n={{{{\mathrm{1,2}}}}}\)) in each of the transmission lines i.e., \({{{{{{\boldsymbol{\phi }}}}}}}_{+}={{{{{{\boldsymbol{\phi }}}}}}}_{+}^{(1)}+\beta {{{{{{\boldsymbol{\phi }}}}}}}_{+}^{(2)}\). The complex amplitude \(\beta\) contains information about the relative magnitudes and phases of the two propagating waves. From superposition principle, we know that the resulting Bloch modal excitation in the semi-infinite structure can be written as a linear combination of the modes that are excited by each individual incident propagating wave \({{{{{{\boldsymbol{\phi }}}}}}}_{+}^{(n)}.\) Since there is only one forward evanescent mode in the SIP structure, the amplitude of the expansion coefficients associated with the evanescent mode \({\alpha }_{2}^{e}(n)\) are evaluated using Eq. (\(18\)). We get
The requirement of zero evanescent mode excitation now translates to the condition \({\alpha }_{2}^{e}(1)+\beta {\alpha }_{2}^{e}(2)=0\) which allows us to extract the wavefront shaping parameter \(\beta\):
The exact value of \(\beta\) might depend on the frequency of the incident wavefront or other parameters \(X\) of the semi-infinite structure. However, our detailed numerical analysis indicated that the extracted value of \(\beta\) at \(X={X}_{{{{{{\rm{SP}}}}}}}\) maintains the sublinear scaling of the differential reflectance.
As a point of caution, Eq. (18) does not assume a flux normalization of the incident wavefront. The latter is crucial when one needs to evaluate transmission coefficients that describe scattering processes between channels that support different group velocities. In our case, we focus on reflectances/transmittances to channels with the same group velocity defined by the dispersion relation of the single mode transmission lines of equal impedance.
Geometry of the unit cell and COMSOL simulations
The full-wave simulations have been performed with a periodic structure which has a unit cell that is shown schematically in Fig. 6. The unit cell consists of a ferrite board (green) with a perfectly conductive grounded bottom surface. The board hosts a pair of perfectly conductive microstrip waveguides indicated with a brown color. The unit cell consists of two spatial domains of length \({l}_{1}=4.318\,{{{\mathrm{mm}}}}\), and \({l}_{2}=5.588\,{{{\mathrm{mm}}}}\), where the two waveguides are separated by distances \(s_1 = 3.5052\,{{{\mathrm{mm}}}}\), and \(s_2 = 0.0889\,{{{\mathrm{mm}}}}\) respectively. Within the first spatial domain, the width of the bent waveguide is \(W_1 = 1.524\,{{{\mathrm{mm}}}}\), while the straight one has a constant width \(W_2 = 0.762\,{{{\mathrm{mm}}}}\) within the whole unit cell. Within the second spatial domain, the width of the bent waveguide is reduced to \(W_3 = 1.016\,{{{\mathrm{mm}}}}\). Finally, the board is made from a magnetic garnet G-810 which has thickness \(T = 1.524\,{{{\mathrm{mm}}}}\). The dielectric permittivity of the board is \(\varepsilon_{{{\mathrm{R}}}} = 14.6\), while the magnetization is \(4\pi M_s = 800 \;{{{\mathrm{G}}}}\).
The platform consists of a board made of a magnetic material (green), which hosts two coupled microstrip waveguides (brown). The vertical purple arrows indicate the applied magnetic field \(H\), Here \(2{l}_{1}\) and \({l}_{2}\) are the lengths of uncoupled and coupled sections of the waveguide, \({W}_{1}\) and \({W}_{3}\) are the widths of the meandered waveguide in the uncoupled and coupled sections, \({W}_{2}\) is the width of the straight waveguide, \(T\) is the thickness of the magnetic substrate, \({s}_{1}\) and \({s}_{2}\) are the separation distances between the waveguides in the uncoupled and coupled sections respectively. Parameter values used in the simulations are provided in the corresponding section of the methods.
Coupled Mode Theory modeling
The lower chain consists of coupled modes with resonant frequencies \({\varepsilon }_{0}\) while the n.n. coupling between them is \({V}_{0}\in {{{{{\mathcal{R}}}}}}\). The upper chain consists of coupled modes with resonant frequencies \({\varepsilon }_{1}=0\) and n.n. coupling between them, which is \({V}_{1}{{{{{\mathcal{\in }}}}}}{{{{{\mathcal{R}}}}}}\). The same n.n. coupling constant describes the coupling between the modes of the first chain with the modes of the second chain. Finally, the diagonal coupling between modes of the first and second chain is \(V_2{{{\mathrm{e}}}}^{i\phi}({V}_{2}\in {{{{{\mathcal{R}}}}}})\). The Peirels’ phase \(\phi\) models a magnetic flux which is responsible for violating the time-reversal symmetry of the system. The effective CMT Hamiltonian of the model has a block-tri-diagonal form,
where the \(2 \times 2\) block matrices have elements, \({H}_{n,n}^{m,{m}^{{\prime} }}={\delta }_{m,2}{\delta }_{m,{m}^{{\prime} }}{\varepsilon }_{0}+{\delta }_{m,{m}^{{\prime} }\pm 1}{V}_{1}\) and \({H}_{n,n+1}^{m,{m}^{{\prime} }}={\delta }_{m,1}{\delta }_{m,{m}^{{\prime} }}{V}_{1}+{\delta }_{m,2}{\delta }_{m,{m}^{{\prime} }}{V}_{0}+{\delta }_{m,1}{\delta }_{m+1,{m}^{{\prime} }}{V}_{2}{e}^{{{{{{\rm{i}}}}}}\phi }\). The corresponding eigenvalue problem can be written in the following form,
where \(\omega\) is the eigenfrequency and \(\langle m\left|{\psi }_{n}\right\rangle\) represents the complex amplitude of the field occupying the site in the \({m}^{{{{{{\rm{th}}}}}}}\) array of the \({n}^{{{{{{\rm{th}}}}}}}\) unit cell. Substituting \(\left|{\psi }_{n}\right\rangle ={{{{{\rm{e}}}}}}^{{{{{{{{\rm{i}}}}}}}}{kn}}\left|A\right\rangle\), where \(k\) is the wavevector and \(\left|A\right\rangle ={\left({A}_{1},{A}_{2}\right)}^{T}\equiv \bar{{{{{{\boldsymbol{A}}}}}}}\), we get
where \(\epsilon_{1} (k)=2V_{1} \cos (k), \epsilon_{2} (k)=\epsilon_{0} + 2V_{0} \cos (K)\) and \(u (k) =V_{1} + V_{2} e^{i(k + \phi)}\). The dispersion relation \(\omega (k)\) is obtained by solving the associated secular equation \({{\det }}\left(\bar{H}\left(k\right)-\omega \left(k\right)\cdot {\hat{1}}_{2}\right)=0\). We get the following two-band dispersion curve
which for an appropriate choice of the model parameters \({\left({\varepsilon }_{0};{V}_{0};{V}_{1};{V}_{2};\phi \right)}_{{{{{{\rm{SP}}}}}}}\approx (4;1;2;3;3.32)\) demonstrates an SIP-3 at \({\omega }_{{{{{{\rm{SP}}}}}}}\approx 6.328\) (\({k}_{{{{{{\rm{SP}}}}}}}\approx -0.507\)), see the inset of Fig. 3a.
The system turns to a scattering setup by coupling each of the left-most resonant modes of the \(n=1\) unit cell of the sample with transmission lines that consist of coupled resonant modes of resonant frequency \({\varepsilon }_{{{{{{\rm{L}}}}}}}=0\) and n.n. coupling \({V}_{{{{{{\rm{L}}}}}}}=-3.5\). Each of the transmission lines supports propagating waves with dispersion relation \(\omega \left(k\right)={\varepsilon }_{{{{{{\rm{L}}}}}}}+2{V}_{{{{{{\rm{L}}}}}}}{{\cos }}(k)\).
Transfer matrix for the CMT model
The calculations reported in Fig. 3 were performed using a CMT formalism where we considered a semi-infinite SIP structure with two single-mode transmission lines attached to each one of the resonant modes of the first unit cell. Our analysis follows closely the steps presented in the second subsection of the “Methods”.
The Bloch modes of the leads have a trivial plane waveform with dispersion relation \(\omega ={\varepsilon }_{{{{{{\rm{L}}}}}}}+2{V}_{{{{{{\rm{L}}}}}}}{{\cos }}\left(k\,a\right)\), where \(a=1\) and \(\left({\varepsilon }_{{{{{{\rm{L}}}}}}},{V}_{{{{{{\rm{L}}}}}}}\right)=\left(0,-3.5\right)\). The Bloch modes of the semi-infinite structure Eq. (23) are extracted from the transfer matrix of the unit cell, which takes the form,
where \({\hat{1}}_{M}\) is the \(M\times M\) identity matrix, \({\hat{0}}_{M}\) is the \(M\times M\) matrix of zeroes, \(|{\Psi }_{n}\rangle ={(|{\psi }_{n+1}\rangle ,{{{{{\rm{|}}}}}}{\psi }_{n}{{\rangle }})}^{T}\), \({\xi }_{1,n}={H}_{n,n+1}^{-1}(\omega {\hat{1}}_{M}-{H}_{n,n})\) and \({\xi }_{2,n}=-{H}_{n,n+1}^{-1}{H}_{n,n+1}^{{{\dagger}} }.\) Finally, the transfer matrix of the interface is given by Eq. (26) by substituting the \(2\times 2\) submatrix \({H}_{n,n+1}^{{{\dagger}} }\) with the hopping matrix \({V}^{{{\dagger}} }\) that connects the transmission lines with the first unit cell and has matrix elements \({\left[V\right]}_{{ij}}={\delta }_{{ij}}{V}_{{{{{{\rm{L}}}}}}}\).
Coalescence parameter of the transfer matrix eigenvectors and EPD
A detailed analysis of the eigenmodes of the transfer matrices associated with the CMT model and of the microstrip waveguide of Figs. 1e and 6 allows us to establish convincing evidence that the SIP occurring in the Bloch dispersion relation is associated with the formation of the EPD in the spectrum of the corresponding transfer matrices.
We start our analysis with the evaluation of the spectrum of the transfer matrix (see Eq. 26) associated with the CMT model. The four eigenvalues of the unit-cell transfer matrix are expressed in terms of the wavevectors \({k}_{q}\) as \({\lambda }_{q}\left(\omega \right)\equiv {e}^{{{{{{\rm{i}}}}}}{k}_{q}{L}_{0}}\) (see Eqs. 2, 3) and can be calculated via direct diagonalization of \({{{{{{\mathcal{M}}}}}}}_{n}\). Two of the four eigenvalues correspond to forward and backward propagating modes and have real \(k\) values (red and green solid lines in Fig. 7a, b respectively). When \(\omega\) is plotted as a function of \(k\), it provides the Bloch dispersion relation of the system \(\omega (k)\), which demonstrates an SIP (see Fig. 7a). The remaining two eigenvalues are associated with one forward and one backward evanescent mode, and they are characterized by a complex \(k\) vector (blue and orange solid lines in Fig. 7a, b respectively). From Fig. 7a, b, we see a third order EPD associated with the coalescence of the slow forward propagating mode (red line) and the forward/backward evanescent modes (blue/orange lines).
Frequency vs a real and b imaginary parts of the wavenumber for each of the four Bloch modes associated with the transfer matrix (see Eq. 26) of the Coupled Mode Theory (CMT) model (see Eq. 22). c Frequency vs coalescence parameter for the CMT model. d–f The same as (a–c), but now for the microstrip waveguide of Fig. 1e. In a, b, d, e, red solid/dotted lines correspond to the slow propagating mode, blue solid/dotted lines correspond to the forward evanescent mode, orange solid/dotted lines correspond to the backward evanescent mode and green solid/dotted lines correspond to the backward fast propagating mode. The black horizontal dashed lined indicates the stationary inflection point frequency.
In Fig. 7c, we further report the eigenvector coalescence parameter defined as46,
where \({{{{{{\boldsymbol{\Phi }}}}}}}_{m}\) refer to the coalescing right eigenvectors of the transfer matrix and \(|\cdot|\) and \(\langle\cdot,\,\cdot\rangle\) indicate the norm and inner product respectively. When \({D}_{{{{{{\rm{H}}}}}}}\to 0\) all vectors involved in the summation are parallel. From the plots, we can immediately recognize the formation of the SIP at frequency \({\omega }_{{{{{{\rm{SP}}}}}}}\) (see horizontal dashed line).
In Fig. 7d–f, we again present the same set of plots, which now are associated with the microstrip system of Fig. 1e. The scattering parameters have been extracted from COMSOL and transformed to the transfer matrix of the unit-cell. A behavior similar to the one found in the CMT model is evident, confirming that the SIP (indicated by a horizontal black dashed line) corresponds to an EPD.
Reflectance in the presence of disorder
The computation of the reflectance in the presence of disorder (see Fig. 4) is performed by considering scattering from a large, but finite, sample. Such a system, in principle is modeled by the temporal CMT equations,
where \(\left|\Psi \right\rangle\) represents the field inside the system and \(|{{{{{{\mathcal{S}}}}}}}^{\pm }\rangle\) represents the time-dependent incoming/outgoing signals to/from the system. \({H}_{{{{{{\rm{eff}}}}}}}\) is the effective Hamiltonian of the system, while \({H}_{0}\) is the Hamiltonian of the isolated system when it is decoupled from the transmission lines. Finally, \(\Delta =\Lambda -\frac{{{{{{\rm{i}}}}}}}{2}D{D}^{{{{{{\rm{T}}}}}}}\) is a diagonal matrix describing the self-energy term associated with the presence of the transmission lines which support plane waves with dispersion characteristics \(\omega ={\varepsilon }_{{{{{{\rm{L}}}}}}}+2{V}_{{{{{{\rm{L}}}}}}}{{\cos}}\,k\). Here, \(\Lambda\) is the purely real normalization matrix accounting for resonant shifts, while the extra loss in the system, due to coupling to the transmission lines, is accounted for by the purely real coupling matrix \(D\). The matrix elements of the self-energy term are \({\left[\Delta \right]}_{{jl}}={V}_{{{{{{\rm{L}}}}}}}{{{{{\rm{e}}}}}}^{{{{{{{{\rm{i}}}}}}}}k}{\delta }_{{jl}}({\delta }_{j1}+{\delta }_{j2}+{\delta }_{j2L-1}+{\delta }_{j2L})\).
The stationary solutions of Eq. (28) admit the following form \(\left|\Psi \right\rangle ={e}^{-{{{{{\rm{i}}}}}}\omega t}\left|\psi \right\rangle\) where we have assumed monochromatic incident waves \(|{{{{{{\mathcal{S}}}}}}}^{\pm }\rangle ={{{{{\rm{e}}}}}}^{-{{{{{\rm{i}}}}}}\omega t}\left|{s}^{\pm }\right\rangle\). Substituting these expressions back in Eq. (28) yields the following equations:
By solving the first equation for \(\left|\psi \right\rangle\) and then applying the result to the second one, we have
where \(S\) is the scattering matrix that describes the scattering process, \(G={\left(\omega {\hat{1}}_{2N}-{H}_{{{{{{\rm{eff}}}}}}}\right)}^{-1}\) is the Green’s function of the system and \({\hat{1}}_{2M}\) is the \(2M\times 2M\) identity matrix.
This formalism allows us to evaluate the reflectance for any incident wavefront. In the case of disordered systems, we have injected an appropriately chosen wavefront that produces the reflectance cusp of Eq. (11) in the corresponding perfect (semi-infinite) case. To mimic the response of the semi-infinite system, a controllable amount of loss is introduced to the model. The amount of loss was chosen in such a way that the corresponding absorption length is smaller than the length of the system. At the same time, we made sure that the loss was gradual along the sample in order to avoid smearing of the cusp due to losses. This scheme allows to prevent reflections from the opposite interface of the finite system and, therefore, leads to the suppression of Fabry–Perot resonances.
In the case of SIP-structures, we distributed the loss following a quadratically-ramped spatial profile, resulting in a loss-growth from \(\gamma =0\) to \(\gamma =1.5\times {10}^{-2}\) over \(L=1000\) unit cells. Our analysis indicated that the RBE is more susceptible to local losses than the SIP. For this reason, in the case of the RBE, we have distributed the quadratically-ramped loss in a way that it increases with a much slower rate over a larger total distance (\(L=5000\) unit cells) from \(\gamma =0\) to \(\gamma =1.5\times {10}^{-3}\).
Phenomenological description of sensitivity bound due to multiplicative noise
The scaling of the sensitivity bound calls for a general argument for its explanation. The following heuristic argument provides some understanding of the power-law for \({\nu }_{{{{{{\rm{c}}}}}}}\sim W\). To this end, we consider a photon propagating inside the semi-infinite structure with velocity \({v}_{{{{{{\rm{g}}}}}}}\). During time \({\tau }_{{{{{{\rm{W}}}}}}},\) related to the Wigner–Smith delay time, the photon will be propagating a distance \({\xi }_{{{\infty }}}={v}_{{{{{{\rm{g}}}}}}}{\tau }_{{{{{{\rm{W}}}}}}}\) inside the structure where \({\xi }_{{{\infty }}}\) is the localization length due to the presence of disorder. On the other hand, the presence of the SIP singularity is resolved in a scattering experiment, whenever the incident wave interacts with the sample for times that are, at least, inversely proportional to the detuning from \({\omega }_{{{{{{\rm{SP}}}}}}}\) i.e., \({\tau }_{{{{{{\rm{W}}}}}}}\sim 1/\nu\). Substituting this estimation, together with the expression Eq. (7) for the group velocity (for \(m=3\)) we get that \({\nu }_{{{{{{\rm{c}}}}}}}\sim {(\frac{1}{{\xi }_{{{\infty }}}})}^{3}\). At the same time, previous scaling analysis for the localization scaling in the proximity of an SIP-3 indicated that \({\xi }_{{{\infty }}}\sim {W}^{-0.4\pm 0.02}\) 41,42 which eventually gives \({\nu }_{{{{{{\rm{c}}}}}}}\sim {W}^{1.2\pm 0.06}\) in reasonable agreement with our numerical findings (see inset of Fig. 4a).
Additive noise analysis
The results presented in Fig. 5 require considering random fluctuations in the incident signal \({{{{{{\bf{s}}}}}}}^{+}\), generated by thermal noise from the transmission lines. The noise at a channel \(n\) has been characterized by the autocorrelation function of its amplitude \({f}_{n}\)
where \({k}_{{{{{{\rm{B}}}}}}}\) is the Boltzmann constant, and \({T}_{n}=T\) is the temperature characterizing the noise fluctuations which in our simulations has been taken to be the same for all channels. The angular frequency bandwidth \(B\) over which the noise is collected by the detector during the data acquisition, along with the continuous-wave signal associated with a carrier frequency, is inversely proportional to the sampling time. In the Monte-Carlo simulations we have accounted for \({10}^{7}\) noise realizations for a specific value of the correlation strength \({\sigma }_{+}^{2}\).
In our CMT (and COMSOL) modeling, this additional noise term \({{{{{\bf{f}}}}}}\) has been accounted for by assuming that the \({i}^{{{{{{\rm{th}}}}}}}\) components \({f}_{i}\) have real and imaginary parts randomly selected from a gaussian distribution with zero mean and variance \({\sigma }_{+}^{2}=\langle {{{{{\rm{Re}}}}}}{({f}_{i})}^{2}\rangle =\langle {{{{{\mathcal{I}}}}}}{{{{{\rm{m}}}}}}{({f}_{i})}^{2}\rangle ={10}^{-5}\) \((5\times {10}^{-4})\). The noisy outgoing field is evaluated using the scattering matrix formalism of the second subsection of the “Methods”,
where the \(S\)-matrix appearing in Eq. (32) is unitary after having projected out the evanescent modes and renormalizing the remaining elements of the non-unitary scattering matrix \(\widetilde{S}\) (see Eq. (18)) with the associated group velocities of the respective modes43. The reflectance is calculated as \(R=\frac{{\left|{{{{{{\bf{s}}}}}}}^{-}\right|}^{2}}{{\left|{{{{{{\bf{s}}}}}}}^{+}\right|}^{2}}\). For better statistical processing, we have simulated the reflected signal over an ensemble of \({10}^{7}\) realizations of the noise. The probability distribution of the extracted detuning \({{{{{\mathcal{P}}}}}}(\nu )\) in Fig. 5b is calculated by mapping the ensemble of differential reflectances to the corresponding detuning values \(\left\{\nu \right\}\), according to the best power-law fit of the mean value \(\langle \Delta R(\nu )\rangle\).
Finally, in the COMSOL simulations, we have acquired a smooth curve for the reflectance data by performing an additional moving averaging window over a length of \(25\) data points. At the same time, the resulting detuning error \({\sigma }_{\nu }\) was averaged over a length of \(10\) data points.
Data availability
The data used to plot the figures are available at Zenodo (https://doi.org/10.5281/zenodo.6626113). All other data are available from the corresponding author upon reasonable request.
Code availability
Most of the code related to the simulations performed in this study, especially pertaining to the CMT model, are available at Zenodo (https://doi.org/10.5281/zenodo.6626113). All other codes are available from the corresponding author upon reasonable request.
References
Kato, T. Perturbation Theory for Linear Operators (Springer, 1995).
Ma, Y. & Edelman, A. Nongeneric eigenvalue perturbations of Jordan blocks. Linear Algebra Appl. 273, 45–63 (1998).
Bender, C. M. Making sense of non-Hermitian Hamiltonians. Rep. Prog. Phys. 70, 947 (2007).
Christodoulides, D. & Yang, J. PT Symmetry and Its Applications (Springer, 2018).
Miri, M.-A. & Alu, A. Exceptional points in optics and photonics. Science 363, 7709 (2019).
El-Ganainy, R. et al. Non-Hermitian physics and PT symmetry. Nat. Phys. 14, 11 (2017).
Wiersig, J. Enhancing the sensitivity of frequency and energy splitting detection by using exceptional points: application to microcavity sensors for single-particle detection. Phys. Rev. Lett. 112, 203901 (2014).
Wiersig, J. Prospects and fundamental limits in exceptional point-based sensing. Nat. Commun. 11, 2454 (2020).
Wiersig, J. Review of exceptional point-based sensors. Phot. Res. 8, 1457 (2020).
Skolianos, G., Aurora, A., Bernier, M. & Digonnet, M. J. Slow-light in Bragg gratings and its applications. J. Phys. D: Appl. Phys. 49, 463001 (2016).
Hodaei, H. et al. Enhanced sensitivity at higher-order EPs. Nature 548, 187 (2017).
Chen, W., Kaya Özdemir, Ş., Zhao, G., Wiersig, J. & Yang, L. Exceptional points enhance sensing in an optical microcavity. Nature 548, 192 (2017).
Dominguez-Rocha, V., Thevamaran, R., Ellis, F. M. & Kottos, T. Environmentally induced exceptional points in elastodynamics. Phys. Rev. Appl. 13, 014060 (2020).
Chen, P.-Y. et al. Generalized parity-time symmetry condition for enhanced sensor telemetry. Nat. Electron. 1, 297 (2018).
Kononchuk, R. & Kottos, T. Orientation-sensed optomechanical accelerometers based on exceptional points. Phys. Rev. Res. 2, 023252 (2020).
Park, J.-H. et al. Symmetry-breaking-induced plasmonic exceptional points and nanoscale sensing. Nat. Phys. 16, 462 (2020).
Xiao, Z., Li, H., Kottos, T. & Alu, A. Enhanced sensing and non-degraded thermal noise performance based on PT-symmetric electronic circuits with a sixth-order exceptional point. Phys., Rev. Lett. 123, 213901 (2019).
Hokmabadi, M., Schumer, A., Christodoulides, D. & Khajavikhan, M. Non-Hermitian ring-laser gyroscopes with enhanced Sagnac sensitivity. Nature 576, 70 (2019).
Lai, Y.-H., Lu, Y.-K., Suh, M.-G. & Vahala, K. K. Enhanced sensitivity operation of an optical gyroscope near an exceptional point. Nature 576, 65 (2019).
Wang, H., Lai, Y.-H., Yan, Z., Suh, M.-G. & Vahala, K. Petermann-factor sensitivity limit near an exceptional point in a Brillouin ring laser gyroscope. Nat. Commun. 11, 1610 (2020).
Langbein, W. No exceptional precision in exceptional-point sensors. Phys. Rev. A 98, 023805 (2018).
Lau, H.-K. & Clerk, A. A. Fundamental limits and non-reciprocal approaches in non-Hermitian quantum sensing. Nat. Commun. 9, 4320 (2018).
Figotin, A. & Vitebskiy, I. Slow light in photonic crystals. Waves Random Complex Media 16, 293 (2006).
Figotin, A. & Vitebskiy, I. Slow wave phenomena in photonic crystals. Laser Photon. Rev. 5, 201 (2011).
Ballato, J., Ballato, A., Figotin, A. & Vitebskiy, I. Frozen light in periodic stacks of anisotropic layers. Phys. Rev. E 71, 036612 (2005).
Figotin, A. & Vitebskiy, I. Frozen light in photonic crystals with degenerate band edge. Phys. Rev. E 74, 066613 (2006).
Stephanson, M. B., Sertel, K. & Volakis, J. L. Frozen modes in coupled microstrip lines printed on ferromagnetic substrates. IEEE Microw. Wirel. Compon. Lett. 18, 305 (2008).
Apaydin, N., Zhang, L., Sertel, K. & Volakis, J. I. Experimental validation of frozen modes guided on printed coupled transmission lines. IEEE Trans. Microw. Theory Tech. 60, 1513 (2012).
Apaydin, N., Sertel, K. & Volakis, J. I. Demonstration of unidirectional printed structures emulating Magnetic Photonic Crystals. IEEE Antennas and Propagation Society Int. Symp. 1 https://doi.org/10.1109/APS.2010.5561940 (IEEE, 2010).
Gutman, N., Hugo Dupree, W., Sun, Y., Sukhorukov, A. A. & Martijn de Sterke, C. Frozen and broadband slow light in coupled periodic nanowire waveguides. Opt. Exp. 20, 3519 (2012).
Gutman, N., Martijn de Sterke, C., Sukhorukov, A. A. & Botten, L. C. Slow and frozen light in optical waveguides with multiple gratings: Degenerate band edges and stationary inflection points. Phys. Rev. A 85, 033804 (2012).
Ramezani, H., Kalish, S., Vitebskiy, I. & Kottos, T. Unidirectional lasing emerging from frozen light in nonreciprocal cavities. Phys. Rev. Lett. 112, 043904 (2014).
Li, H., Vitebskiy, I. & Kottos, T. Frozen mode regime in finite periodic structures. Phys. Rev. B 96, 180301(R) (2017).
Nada, M. Y., Othman, M. A. K. & Capolino, F. Theory of coupled resonator optical waveguides exhibiting high-order exceptional points of degeneracy. Phys. Rev. B 96, 184304 (2017).
Yazdi, F., Mealy, T., Nikzamir, A., Marosi, R. & Capolino, F. Third order modal exceptional degeneracy in waveguides with glide-time symmetry. Phys. Rev. A 105, 052230 (2022).
Parareda, A. H., Vitebskiy, I., Scheuer, J. & Capolino, F. Frozen mode in an asymmetric serpentine optical waveguide. Advanced Photonics Research, Early View, 2100377 https://doi.org/10.1002/adpr.202100377 (2022).
Pichler, K. et al. Random anti-lasing through coherent perfect absorption in a disordered medium. Nature 567, 351 (2019).
Mosk, A. P., Lagendijk, A., Lerosey, G. & Fink, M. Controlling waves in space and time for imaging and focusing in complex media. Nat. Photonics 6, 283 (2012).
Vellekoop, I. M., Lagendijk, A. & Mosk, A. Exploiting disorder for perfect focusing. Nat. Photon. 4, 320 (2010).
Vellekoop, I. M. Feedback-based wavefront shaping. Opt. Exp. 23, 12189 (2015).
Gan, Z. M., Li, H. & Kottos, T. Effects of disorder in frozen-mode light. Opt. Lett. 44, 2891 (2019).
Tuxbury, W., Fernandez-Alcazar, L. J., Vitebskiy, I. & Kottos, T. Scaling Theory of absorption in the frozen mode regime. Opt. Lett. 46, 3053 (2021).
Mello, P. A. & Kumar, N. Quantum Transport in Mesoscopic Systems: Complexity and Statistical Fluctuations (Oxford University Press, 2004).
Mortensen, N. A. et al. Fluctuations and noise-limited sensing near the exceptional point of parity-time-symmetric resonator systems. Optica 5, 1342–1346 (2018).
Kononchuk, R., Feinberg, J., Knee, J. & Kottos, T. Enhanced avionic sensing based on Wigner's cusp anomalies. Sci. Adv. 7, eabg8118 (2021).
Nada, M. Y. & Capolino, F. Frozen mode in three-way periodic microstrip coupled waveguide. IEEE Microw. Wirel. Compon. Lett. 31, 3 (2021).
Acknowledgements
This material is partially based upon work supported by the National Science Foundation under grant no. ECCS 2148318 and is supported in part by funds from OUSD R&E, NIST, and industry partners as specified in the Resilient & Intelligent NextG Systems (RINGS) program. Partial support from Simons Foundation for Collaboration in MPS grant No. 733698 and ONR N00014-19-1-2480 is also acknowledged.
Author information
Authors and Affiliations
Contributions
W.T. performed theoretical calculations. W.T. and R.K. performed COMSOL Multiphysics simulations. T.K. proposed and supervised the project. All authors contributed to the writing of the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks Jan Wiersig and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tuxbury, W., Kononchuk, R. & Kottos, T. Non-resonant exceptional points as enablers of noise-resilient sensors. Commun Phys 5, 210 (2022). https://doi.org/10.1038/s42005-022-00973-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-022-00973-5
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.