Abstract
Collectively coupling molecular ensembles to a cavity has been demonstrated to modify chemical reactions akin to catalysis. Theoretically understanding this experimental finding remains an important challenge. In particular the role of quantum effects in such setups is an open question of fundamental and practical interest. Theoretical descriptions often neglect quantum entanglement between nuclear and electro-photonic degrees of freedom, e.g., by computing Ehrenfest dynamics. Here we discover that disorder can strongly enhance the build-up of this entanglement on short timescales after incoherent photo-excitation. We find that this can have direct consequences for nuclear coordinate dynamics. We analyze this phenomenon in a disordered Holstein-Tavis-Cummings model, a minimal toy model that includes all fundamental degrees of freedom. Using a numerical technique based on matrix product states we simulate the exact quantum dynamics of more than 100 molecules. Our results highlight the importance of beyond Born-Oppenheimer theories in polaritonic chemistry.
Similar content being viewed by others
Introduction
Polaritonic chemistry, or the modification of chemical reactivity using effects of cavity quantum electrodynamics (cavity-QED), is an emerging field of research at the interface of quantum chemistry and physics1,2,3,4,5,6,7,8,9. Experiments have demonstrated that a collective coupling of electronic10,11,12,13,14,15,16,17,18 or vibrational19,20,21,22,23 transitions of large ensembles of molecules to confined non-local electromagnetic fields can provide means to control chemical reactivity. Many experiments have achieved a collective strong coupling regime, where the cavity and the molecules can coherently exchange energy at a rate faster than their decay processes. In such scenarios, the cavity-molecule system has to be considered as one entity with new polaritonic eigenstates, which are collective superpositions of photonic and molecular degrees of freedom. Identifying the underlying mechanisms of collective cavity-modified chemistry remains to be a major challenge. A theoretical understanding of the problem requires to solve complex quantum many-body dynamics in large systems with coupled electronic, photonic, and vibrational degrees of freedom.
Numerically computing the collective time evolution of all degrees of freedom in polaritonic chemistry is an important—yet extremely challenging—task for understanding chemical reaction dynamics, which has been attempted at different levels of approximations. For small systems, the Schrödinger equation can be solved directly24 or using quantum chemistry tools such as multi-configurational time-dependent Hartree-Fock methods25. Density functional theory can be used for ab initio simulations of a few realistic molecules26. For larger systems, stronger approximations are needed. Standard approaches are based on the Born-Oppenheimer approximation. In the Born-Oppenheimer approximation, electro-photonic dynamics are treated as instantaneous compared to nuclear dynamics so that polaritonic (and dark) potential energy surfaces can be computed27. On these adiabatic potential energy surfaces, nuclear dynamics can then be computed. However, this method neglects non-adiabatic couplings between potential energy surfaces and thus fails if the separation between potential energy surfaces becomes small, as is often the case in polaritonic chemistry5,28,29. In order to include the non-adiabatic couplings, two common methods are fewest switches surface hopping30,31,32 or mean-field Ehrenfest dynamics33,34. Ehrenfest dynamics assumes a product state between nuclear and electro-photonic degrees of freedom, completely neglecting any entanglement between them. As a consequence, such entanglement can serve as a measure for the validity of approximations relying on the separability of nuclear and electro-photonic degrees of freedom, and more generally the complexity of the dynamics. Alternatively, vibrationally dressed electronic molecular states have been computed using polaron ansätze35,36,37,38,39. Such approximations allow for the computation of effective transfer rates between these states for very large molecule numbers, but, by construction, they cannot compute the entangled vibrational-electro-photonic dynamics.
The role of quantum effects in molecular dynamics is also a fundamentally interesting research question40,41,42,43. Entanglement is often used to determine the importance of quantum effects by quantifying quantum correlations without classical equivalent44,45,46. In this context, the entanglement between electronic and nuclear degrees of freedom of molecules has been previously studied for single molecules47,48. For cavity-coupled molecules, it is known that a collective cavity-coupling can strongly suppress this entanglement by reducing vibronic couplings, an effect termed “polaron decoupling”35,36. However, this effect neglects local disorder in the electronic level spacings of individual molecules, which is generally present in organic polaritonic setups49,50,51.
Recently, matrix product states (more broadly: tensor networks) have been suggested to numerically tackle dynamics in polaritonic chemistry52 also for larger system sizes. A matrix product state (MPS) can be thought of as a generalization of a product state, which by definition does not include any entanglement, into a larger space with small but finite entanglement. The entanglement of an MPS is limited by a so-called bond dimension, which can be systematically increased until convergence is reached53. Since excessively large entanglement rarely plays an important role in physical dynamics, MPS simulations often become numerically exact. By construction, MPS concepts provide direct access for studying the entanglement dynamics of a system, and they have been used in that context extensively, e.g., for spin-chain or Hubbard-type models in many-body physics45,46.
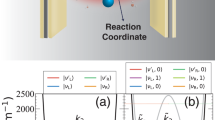
Here, using this numerical approach we study the femtosecond-scale dynamics of more than 100 molecules with electronic transitions collectively strongly coupled to a cavity mode (electronic strong coupling) after an incoherent photo-excitation (see Fig. 1 for a sketch). We analyze a minimal disordered version of the Holstein-Tavis-Cummings (HTC) model35,54,55, which despite its simplicity includes the main ingredients for microscopically understanding modifications of vibrational dynamics in cavity-coupled molecular ensembles, in particular in organic systems. We find that disorder enhances excitation transfer from the initially excited state to a number of molecules selected by a resonance condition (see Fig. 1b, c)56,57,58. This leads to coherent out-of-phase oscillations of the vibrational modes of these molecules. As a consequence, disorder enhances entanglement between vibrations and electronic degrees of freedom several-fold (see the sketch in Fig. 1d). This effect is largest in a regime where disorder is energetically comparable to collective cavity-couplings. Importantly, we find that the disorder-induced focused excitation transfer to a few molecules leads to an enhanced cavity-modified vibrational dynamics on the single-molecule level, compared to a disorder-less scenario where the excitation is diluted among all coupled molecules equally. This effect crucially depends on whether the initial incoherent excitation is absorbed by a single molecule or the cavity, and we analyze both scenarios (see Fig. 1b). We further relate large entanglement to modifications of the shape of the nuclear wave packets, which become broadened and non-Gaussian. In this respect, the vibrational entanglement may have direct consequences for chemical processes.
a We consider toy-model molecules with two harmonic potential energy surfaces (vibrational level spacing ν). Both surfaces are energetically separated by the electronic level spacing ω and displaced by \(\sqrt{2}\lambda\) along the nuclear coordinate x. b An ensemble of molecules is coupled to a cavity with collective strength gc. We analyze dynamics after incoherent photo-excitation of either an individual molecule (red, left) or the cavity (blue, right). An energy level scheme for electro-photonic excitations is sketched. The disorder leads to inhomogeneous broadening by W (left). The coupling of N electronic excitation states (left; gray, red, cyan, orange lines) and a single cavity excitation (right; blue line) lead to new eigenstates (center) that are superpositions with contributions indicated by the different colors. For gc ≫ W, two polariton states at energies ± gc are formed (half gray, half blue), as well as N − 1 dark states (other lines). Due to disorder, the dark states are superpositions of a few energetically resonant electronic excitations. All dark states also acquire a small photon weight (very small blue contribution). After incoherent excitation, energy is transferred through the coupled eigenstates as indicated by straight arrows (transfer probability ξ). For a molecule excitation, energy is predominantly transferred through dark states, for a cavity excitation through polariton states (arrow thickness). c Disorder enhances the transfer away from the initially excited state after molecular (red) or cavity (blue) excitation. The plot shows a time-averaged transfer probability \(\xi =\nu /(2\pi )\int\nolimits_{0}^{2\pi /\nu }dt\,[1-\langle {\hat{O}}^{{{{\dagger}}} }\hat{O}\rangle (t)]\) where \(\hat{O}={\hat{\sigma }}_{1}^{-},\hat{a}\) in a system with 100 molecules. d Excitation transfer leads to a coherent out-of-phase oscillation of different molecules and thus large entanglement entropy, Svib, between electro-photonic (left) and vibrational (right) degrees of freedom.
Results and discussion
Theoretical model
We consider a system of N toy-model molecules coupled to a single-mode optical cavity, i.e., a disordered version of the HTC model35,54,55. Here, each molecule has two electronic energy levels. Different nuclear equilibrium configurations in the ground and excited-state result in two displaced harmonic one-dimensional potential energy surfaces as shown in Fig. 1a. We further include an inhomogeneous broadening, i.e., a disorder of the electronic energy stemming from random energy spacings of the electronic levels59, typically induced by the environment in experiments. The disordered HTC Hamiltonian reads35
The coupling of the cavity is described by the Tavis-Cummings (TC) Hamiltonian, which, in a frame rotating at the cavity frequency ωC, reads (ℏ = 1 throughout this paper)
where \(\hat{a}\) is the destruction operator for a cavity photon, \({\hat{\sigma }}_{n}^{\pm }\) are the raising/lowering operators for the electronic level of the n-th molecule. Δ = ω − ωC is the detuning between the electronic transition frequency at the Condon point ω and ωC, chosen to be Δ = 0 in the remainder of this paper. The coupling strength of a single molecule to the cavity is given by \(g\equiv {g}_{{{{{{{{\rm{c}}}}}}}}}/\sqrt{N}\). In the single-excitation Hilbert space considered here, the TC Hamiltonian has two polariton eigenstates \(\left|\pm \right\rangle ={\hat{a}}^{{{{\dagger}}} }/\sqrt{2}\pm {\sum }_{n}{\hat{\sigma }}_{n}^{+}/\sqrt{2N}{\left|0\right\rangle }_{{{{{{{{\rm{exc+ph}}}}}}}}}\) for the ground state \({\left|0\right\rangle }_{{{{{{{{\rm{exc+ph}}}}}}}}}\) without any excitations, split by the Rabi splitting of 2gc. The other N − 1 eigenstates are degenerate dark states with zero energy.
The nuclear coordinates are described by harmonic potentials
where \({\hat{b}}_{n}\) is the lowering operator of the n-th molecule and ν the molecular oscillation frequency. The eigenstates of \({\hat{H}}_{{{{{{{{\rm{vib}}}}}}}}}\) are Fock states \({\prod }_{n}{({\hat{b}}_{n}^{{{{\dagger}}} })}^{{a}_{n}}\left|{0}_{{{{{{{{\rm{vib}}}}}}}}}\right\rangle\) with an vibrational quanta on the nth molecule and the (undisplaced) total vibrational ground state \(\left|{0}_{{{{{{{{\rm{vib}}}}}}}}}\right\rangle\). We define dimensionless oscillator position and momentum variables as \({\hat{x}}_{n}=({\hat{b}}_{n}+{\hat{b}}_{n}^{{{{\dagger}}} })/\sqrt{2}\) and \({\hat{p}}_{n}=-{{{{{{{\rm{i}}}}}}}}({\hat{b}}_{n}-{\hat{b}}_{n}^{{{{\dagger}}} })/\sqrt{2}\), respectively.
The nuclear coordinate of each molecule is coupled to its electronic state by a Holstein coupling
This corresponds to a shift of the excited state potential energy surface. The dimensionless Huang-Rhys factor λ2 quantifies the minimum of the excited state harmonic potential at position \(\sqrt{2}\lambda\) with energy ω − λ2ν.
Finally, we include disorder by
where ϵn = ωn − ω is the deviation of the electronic transition energy of the n-th molecule from the mean. We take the ϵn as independent, normally distributed random variables with mean 0 and variance W2. Here, we focus on energy disorder in the molecular level spacing, which is a fundamental characteristic of typical organic setups49,50,51. In addition, in real setups typically also the cavity-coupling g is disordered, e.g., due to fluctuations in the molecular orientations and the cavity mode profile. Here, we find that this additional disorder only leads to minor modifications for the entanglement dynamics (see Supplementary Note 1), and we thus do not further consider it in the following.
Dynamics and entanglement
In the following, we analyze the short-time Hamiltonian dynamics on the scale of a single nuclear vibration period, 0 ≤ t ≤ 2π/ν for two different initial states. In one case, a single molecule (n = 1) is excited by the incoherent absorption of a photon, i.e., we consider the initial state \(\left|{\psi }_{0}^{{{{{{{{\rm{m}}}}}}}}}\right\rangle ={\hat{\sigma }}_{1}^{+}{\left|0\right\rangle }_{{{{{{{{\rm{ph}}}}}}}}}{\left|0\right\rangle }_{{{{{{{{\rm{exc}}}}}}}}}{\left|0\right\rangle }_{{{{{{{{\rm{vib}}}}}}}}}\) (Fig. 1b, left). In the other case the photon is incoherently absorbed by the cavity, \(\left|{\psi }_{0}^{{{{{{{{\rm{c}}}}}}}}}\right\rangle ={\hat{a}}^{{{{\dagger}}} }{\left|0\right\rangle }_{{{{{{{{\rm{ph}}}}}}}}}{\left|0\right\rangle }_{{{{{{{{\rm{exc}}}}}}}}}{\left|0\right\rangle }_{{{{{{{{\rm{vib}}}}}}}}}\) (Fig. 1b, right). Here, \({\left|0\right\rangle }_{{{{{{{{\rm{exc,vib,ph}}}}}}}}}\) denote the respective ground states of the bare electronic, vibrational, and photonic Hamiltonian.
In order to analyze entanglement between electro-photonic and nuclear degrees of freedom, we separate the full Hilbert space as \({{{{{{{\mathcal{H}}}}}}}}={{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{ph}}}}}}}}}\otimes {{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{exc}}}}}}}}}\otimes {{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{vib}}}}}}}}}\) into three sub-Hilbert spaces for the cavity photon, electronic excitations, and vibrations, respectively. For a pure state \(\left|\psi \right\rangle\), the entanglement between the two subsystems \({{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{ph}}}}}}}}}\otimes {{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{exc}}}}}}}}}\) and \({{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{vib}}}}}}}}}\) can be quantified by the von Neumann entropy of either subsystem,45,46 e.g.,
where \({\hat{\rho }}_{{{{{{{{\rm{vib}}}}}}}}}\) is the reduced density matrix which can be obtained from the state \(\left|\psi \right\rangle\) by tracing over \({{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{ph}}}}}}}}}\otimes {{{{{{{{\mathcal{H}}}}}}}}}_{{{{{{{{\rm{exc}}}}}}}}}\): \({\hat{\rho }}_{{{{{{{{\rm{vib}}}}}}}}}={{{{{{{{\rm{Tr}}}}}}}}}_{{{{{{{{\rm{ph}}}}}}}}+{{{{{{{\rm{exc}}}}}}}}}(|\psi \rangle \langle \psi |)\). In the case of a product state (or mean-field) assumption, the state of the system would be assumed to factorize throughout the evolution of the system
In this scenario, \({\hat{\rho }}_{{{{{{{{\rm{vib}}}}}}}}}(t)=|{\phi }_{{{{{{{{\rm{vib}}}}}}}}}(t)\rangle \langle {\phi }_{{{{{{{{\rm{vib}}}}}}}}}(t)|\) and Svib(t) = 0 at all times. An entangled state \(|\psi \rangle\) is a linear superposition of many such terms, resulting in Svib > 0. The von Neumann entropy Svib can be readily computed in the MPS framework (see Methods). It is noteworthy that this product state assumption is equivalent to the one made in mean-field Ehrenfest dynamics, where in addition the nuclear motion is treated classically. Since in our case the nuclear wavefunction always stays in a coherent state and thus follows classical equations of motion, our product state results are equivalent to mean-field Ehrenfest results.
Parameter regimes
We choose parameter values that are motivated by a setup with Rhodamine 800, for which strong coupling has been demonstrated60, and which has been previously considered in tensor network studies of strong coupling experiments52. In particular, we set 0.1 ≤ λ ≤ 0.5 and ν = 0.3gc. For an experimentally demonstrated vacuum Rabi splitting of 2gc = 700 meV10, this corresponds to ν = 105 meV and reorganization energies 1 meV ≲ λ2ν ≲ 26 meV, similar to measured values61. Thermal excitation fractions \(\sim \exp (-\nu /{k}_{{{{{{{{\rm{B}}}}}}}}}T)\) are negligible at room temperature (kBT ≈ 26 meV). In particular, in the case of Rhodamine 800 the level spacing is ~2 eV60, for which the Rabi splitting of 700 meV (gc/ω ~ 18%) falls just into a regime beyond the on-set of ultra-strong coupling effects. Note that we still do not include counter-rotating terms in order to derive general results for strong coupling, valid for other molecules with larger level spacings ω or smaller Rabi-splittings gc. Smaller Rabi-splittings will generally lead to an increased ratio of λν/gc and thus additionally induced mixing with vibrational degrees of freedom over the Holstein coupling term \({\hat{H}}_{{{{{{{{\rm{H}}}}}}}}}\).
For our case of λν ≪ ν ≪ gc, the Hamiltonian Eq. (1) can be categorized into strong (W ≪ gc) and weak (W ≫ gc) coupling regimes depending on the relative magnitude of \({\hat{H}}_{{{{{{{{\rm{TC}}}}}}}}}\) and \({\hat{H}}_{{{{{{{{\rm{dis}}}}}}}}}\). The strong coupling regime features polaritonic and dark eigenstates of \({\hat{H}}_{{{{{{{{\rm{TC}}}}}}}}}\) which are mixed perturbatively (Fig. 1b). In perturbation theory, we find that “gray” states \(\left|d\right\rangle\) acquire photo-contributions of \({\sum }_{d}{|\langle d|{1}_{{{{{{{{\rm{ph}}}}}}}}}\rangle |}^{2} \sim {\lambda }^{2}{\nu }^{2}/(2{g}_{{{{{{{{\rm{c}}}}}}}}}^{2})\) and \({\sum }_{d}{|\langle d|{1}_{{{{{{{{\rm{ph}}}}}}}}}\rangle |}^{2}\approx {W}^{2}/{g}_{{{{{{{{\rm{c}}}}}}}}}^{2}\) due to small vibronic coupling and disorder, respectively49,50,58,59 (see Supplementary Notes 2 and 3). In the weak coupling regime, polariton states cease to exist and all eigenstates are structurally similar to the “gray” states in Fig. 1a. We vary 0 ≤ W ≤ 1.5gc analyzing both weak and strong coupling scenarios. The timescale of vibrational evolution t ~ 2π/ν corresponds to tens of femtoseconds, and can be faster than dissipative mechanisms which we do not include explicitly. For quality factors Q ≳ 1000 which have e.g., been achieved for distributed Bragg reflectors, cavity decay is negligible on these timescales62. Similarly, relaxation of molecular excitation into vibrational or electromagnetic reservoirs typically occurs on even slower timescales of picoseconds or nanoseconds, respectively55. In fact, on a microscopic level the coherent dynamics due to disorder and vibronic coupling terms \({\hat{H}}_{{{{{{{{\rm{dis}}}}}}}}}\) and \({\hat{H}}_{{{{{{{{\rm{H}}}}}}}}}\) that we simulate here can be considered as one of the mechanisms responsible for electronic dephasing.
Summary of results
Figure 2 visualizes the main feature of the entanglement and vibrational dynamics after initial molecular (\(\left|{\psi }_{0}^{{{{{{{{\rm{m}}}}}}}}}\right\rangle\), panels a, c, e), and cavity (\(\left|{\psi }_{0}^{{{{{{{{\rm{c}}}}}}}}}\right\rangle\), panels b, d, f) excitation. Strikingly, in both scenarios, we find that increasing the disorder in the range 0 ≤ W ≤ gc leads to a drastically enhanced entanglement entropy build-up, seen in the evolution of the disorder-averaged entropy \(\overline{{S}_{{{{{{{{\rm{vib}}}}}}}}}}\) in Fig. 2a, b. For W = 0, the entanglement entropy remains below values of one, and, in the cavity excitation case only, exhibits oscillatory features which we can attribute to collective Rabi oscillation due to a predominant excitation transfer to the polariton states. For W > gc/2 those features disappear and we observe a strong increase to a maximum value at t ~ 2π/ν and t ~ π/ν in Fig. 2a, b, respectively. This entanglement build-up is matched by modifications of the phase space dynamics (Fig. 2c, d) and the shape of the probability distribution Pi(xi, t) (Fig. 2e, f) of the nuclear coordinate. Below, we will relate all three effects to disorder-enhanced excitation transfer. We will see that neither the entanglement build-up nor the distribution shape changes can be captured by a product state assumption Eq. (7), i.e., they go beyond the mean-field Ehrenfest dynamics.
a, b Time evolution of the disorder-averaged entanglement entropy \(\overline{{S}_{{{{{{{{\rm{vib}}}}}}}}}}\) in the time-range 0 ≤ t ≤ 2π/ν for disorder strengths 0 ≤ W ≤ gc (from light to dark W = 0, gc/4, gc/2, 3gc/4, gc). Stars indicate the final time t = 2π/ν. The left panels (red lines) correspond to the initial molecule excitation state \(\left|{\psi }_{0}^{{{{{{{{\rm{m}}}}}}}}}\right\rangle\), the right panels (blue lines) to the initial cavity excitation \(\left|{\psi }_{0}^{{{{{{{{\rm{c}}}}}}}}}\right\rangle\). c, d Vibrational phase space evolution. Shown are the disorder-averaged expectation values \(\overline{{x}_{i}}\) and \(\overline{{p}_{i}}\) of the oscillator position and momentum operators, \({\hat{x}}_{i}\) and \({\hat{p}}_{i}\), for values of W corresponding to (a). The gray dashed line shows the no-cavity case. In (c) the dynamics of the initially excited molecule is shown, in (d) an additional average overall molecules is taken. e, f Averaged probability distributions of the nuclear coordinate x at time t = 2π/ν (stars in other panels, gray dashed line: no-cavity case). In all panels, we average over 64 disorder realizations, and the error bars represent the error of the mean (not visible when the error is less than the line width). The other parameters are N = 100, ν = 0.3gc, λ = 0.4.
Fig. 2c, d shows the phase space dynamics of the disorder-averaged expectation values \(\overline{{x}_{i}}\) and \(\overline{{p}_{i}}\) of the nuclear coordinate position and momentum operators \({\hat{x}}_{i}\) and \({\hat{p}}_{i}\) on molecule i, respectively. In the molecular excitation case in Fig. 2c, we observe phase space circles for the initially excited molecule (i = 1). In the disorder-less case W = 0, we find an oscillation around the displaced equilibrium position of the excited state oscillator, \(\sqrt{2}\lambda \approx 0.57\). In this case, the evolution is very close to the no-cavity scenario (gray dashed line), for which we obtain a perfect circle around \(\sqrt{2}\lambda\) corresponding to the usual coherent harmonic oscillator evolution.
However, the situation changes drastically for W > 0. Now, the centers of the phase space circles dynamically shift to smaller values of \(\overline{{x}_{1}}\). We note that this behavior can be rationalized without requiring the large entanglement build-up seen in Fig. 2a. Assuming the product state ansatz from Eq. (7), one would expect that the Holstein term \({\hat{H}}_{{{{{{{{\rm{H}}}}}}}}}\) [Eq. (4)] leads to an effective excited state oscillator equilibrium position of \(\sqrt{2}\lambda \langle {\hat{\sigma }}_{1}^{+}{\hat{\sigma }}_{1}^{-}\rangle\) and thus effectively to a time-dependent shift of the minimum depending on \(\langle {\sigma }_{1}^{+}{\hat{\sigma }}_{1}^{-}\rangle (t)\). For W = 0 the initial state \(\left|{\psi }_{0}^{{{{{{{{\rm{m}}}}}}}}}\right\rangle\) is almost a dark eigenstate of \({\hat{H}}_{{{{{{{{\rm{TC}}}}}}}}}\), such that cavity induced excitation transfer is strongly suppressed and the excitation remains on the molecule, \(\langle {\hat{\sigma }}_{1}^{+}{\hat{\sigma }}_{1}^{-}\rangle (t) \sim 1\). In contrast, for finite disorder W > 0, the excitation transfer is significantly enhanced and we perturbatively derive \(1-\langle {\hat{\sigma }}_{1}^{+}{\hat{\sigma }}_{1}^{-}\rangle (t) \sim Wt/N\) for g ≪ W ≪ gc (see Supplementary Note 4). This is in qualitative agreement with recent results predicting that disorder can enhance excitation transfer in models without vibrations56,57,58.
For an initial cavity excitation \(\left|{\psi }_{0}^{{{{{{{{\rm{c}}}}}}}}}\right\rangle\), the phase space evolution traces much smaller circles. As expected, for W = 0 the phase space evolution is approximately centered at \(\overline{{x}_{i}} \sim \sqrt{2}\lambda /(2N)\), and exhibits oscillations at polariton Rabi frequencies. For increasing disorder W → gc, the center of the circle now shifts in the opposite direction compared to Fig. 2c, to roughly twice the value \(\overline{{x}_{i}}\to \sqrt{2}\lambda /N\). This can again be rationalized by looking at the evolution of the expected local molecule excitations \(\langle {\hat{\sigma }}_{i}^{+}{\hat{\sigma }}_{i}^{-}\rangle (t)\). For W = λν = 0, the hybrid nature of the polariton states induces Rabi oscillations between the initial cavity photon state and a collective excitation of all molecules, such that for each molecule the excitation fraction oscillates according to \(\langle {\hat{\sigma }}_{i}^{+}{\hat{\sigma }}_{i}^{-}\rangle (t)={\cos }^{2}({g}_{{{{{{{{\rm{c}}}}}}}}}t)/N\), leading to the observed phase space evolution for W = 0. Finite disorder, however, leads to a photo-contribution of all dark states (perturbatively \(\sim\!\! {W}^{2}/{g}_{{{{{{{{\rm{c}}}}}}}}}^{2}\)). Therefore, excitations are now irreversibly (on our timescale of interest) transferred from the cavity to individual molecules, and one thus expects a disorder-averaged excitation population on each molecule \(\overline{\langle {\hat{\sigma }}_{i}^{+}{\hat{\sigma }}_{i}^{-}\rangle }\to 1/N\) for sufficiently large W. This explains the observed shift. Importantly, the vibrational dynamics only depend on the transfer of excitations from cavity to molecules, independently of whether the molecular excitations are part of polaritons or dark states, such that the relevant timescale for excitation transfer remains 1/gc.
Figure 2e, f shows the probability distribution Pi(xi, t) of the nuclear coordinate at time t = 2π/ν. Without cavity, at this time the distribution is a Gaussian centered at x1 = 0 with variance 1/2, corresponding to a coherent state (gray dashed line). We find that in a cavity and for W = 0, the distribution is extremely close to the no-cavity scenario. For increasing W, however, for the molecular excitation \(\left|{\psi }_{0}^{{{{{{{{\rm{m}}}}}}}}}\right\rangle\), the distribution of the nuclear coordinate of the initially excited molecule P1(x1, t = 2π/ν) clearly shifts to smaller values of x1. In addition, the distribution broadens and acquires an asymmetric shape in Fig. 2e. For an initial cavity excitation \(\left|{\psi }_{0}^{{{{{{{{\rm{c}}}}}}}}}\right\rangle\), we observe that finite W leads to modifications in the tails of the distribution only, i.e., for large values of xi (Fig. 2f). Note that the tail modifications in Fig. 2f seem very small, since a single molecule only receives a ~1/N contribution of the excitation energy (here, N = 100). However, below we see that the cumulative effect on the wavefunction shape can still have important consequences for many molecules.
Excitation transfer dynamics
In Fig. 3, we now exemplify the connection between the time-dependent local molecular excitation and the phase space evolution for an intermediate disorder strength W = gc/2 microscopically. Figure 3a shows the vibrational evolution of each of the 100 molecules for a single disorder realization, after exciting one molecule initially (line with star: excited molecule, other red/cyan/yellow lines: 99 initially unexcited molecules). Strikingly, we observe that the molecules whose dynamics are modified most strongly correspond to the ones with random energy very close to the initially excited one. The reason for this is seen in comparison with Fig. 3b where we plot the excitation numbers of the molecules at t = 2π/ν as a function of their random energy offset ϵi. There we identify the molecules with the strongest phase space modification (cyan square and orange diamond), and the initially excited ones (blue star and vertical line). Crucially, the excitation fraction of these molecules, and thus their phase space dynamics, is much larger than for the disorder-less case with W = 0 (gray lines in Fig. 3a, b, barely visible in a). The same behavior is generally seen also after disorder-averaging (see inset). We attribute a visible asymmetry towards smaller energies in Fig. 3b to additional resonances with states of higher vibrational energies. It is also interesting to point out that in contrast to the initially excited molecule, the phase space variables of the other molecules generally do not complete one revolution until t = 2π/ν (Fig. 3a), and all molecular oscillators evolve out-of-phase.
a Microscopic phase space evolution of 100 molecular oscillators for a single disorder realization with W = gc/2 in the time-range 0 ≤ t ≤ 2π/ν. The black star and line correspond to the initially excited molecule, and the other lines to the 99 initially unexcited ones. The gray line (barely visible around the origin) represents the W = 0 reference. The cyan square and orange diamond are two example molecules with the most strongly modified vibrational dynamics, also identified in (b). b Excitation probability \({\tilde{n}}_{{{{{{{{\rm{ex}}}}}}}}}^{(i)}=\langle {\hat{\sigma }}_{i}^{+}{\hat{\sigma }}_{i}^{-}\rangle (t=2\pi /\nu )\) as a function of the energy offset ϵi of the respective molecule. The inset shows the disorder-averaged excitation probability as a function of the energy difference to the initially excited state for 256 different disorder realizations. The gray horizontal lines are the W = 0 reference. c, d identical plots for a cavity excitation. Parameters: N = 100, ν = 0.3gc, λ = 0.4, disorder drawn from a normal distribution with width W, 256 disorder realizations.
A similar picture presents itself when initially exciting the cavity mode (Fig. 3c, d). The excitation is again primarily transferred from the cavity to several molecules, but now with energies ϵi ~ ± gc close to resonance with the bare polaritons in the strong coupling regime. These molecules acquire much larger excitation fractions than the no disorder reference (gray line in Fig. 3d). As a result, molecular oscillations of molecules with an energy offset ϵn ~ ± gc are most strongly modified, as confirmed in Fig. 3c.
We can deduce the following microscopic picture from our analysis in Fig. 3: While in the W = 0 case the initial excitation is generally diluted throughout the system, disorder W > 0 leads to a strongly enhanced excitation transfer to a few molecules in the energetic vicinity of either the initially excited molecule or the polariton states, depending on the scenario (as sketched in Fig. 1b). In a product state picture, this then modifies the vibrational dynamics of those molecules depending on the amount of local excitation, \(\langle {\hat{\sigma }}_{i}^{+}{\hat{\sigma }}_{i}^{-}\rangle\). However, the product state assumption contradicts the build-up of large vibrational entanglement seen in Fig. 2a, b. Rather, the out-of-phase oscillator dynamics should be considered quantum-mechanically coherent, leading to the large entanglement entropies. In the following, we will study the direct implications of this entanglement.
Nuclear coordinate distribution shapes
We are now interested in the time evolution of the full nuclear coordinate distribution Pn(xn, t) of molecule n and in particular, we will analyze the evolution of its tails in Fig. 4. In a product state ansatz [Eq. (7)], the instantaneous nuclear potential corresponds to a shifted harmonic oscillator. Then, nuclear wave packets of the individual molecules would always stay in a Gaussian shape. Crucially, this is not the case if we allow for finite entanglement. Then, in general, the Holstein coupling \(\propto \sum_n {\hat{x}}_{n}{\hat{\sigma }}_{n}^{+}{\hat{\sigma }}_{n}^{-}\) does not factorize and thus modifies the wave packet shape over time (see e.g., Fig. 2e). To exemplify this, consider a single molecule n with a constant excitation fraction β (without cavity coupling). The time evolution under the Holstein Hamiltonian [Eq. (4)] leads to the following state at time t: \(\left|{\phi }_{\beta }(t)\right\rangle =\sqrt{1-\beta }{\left|0\right\rangle }_{{{{{{{{\rm{exc}}}}}}}}}{\left|0\right\rangle }_{{{{{{{{\rm{vib}}}}}}}}}+\sqrt{\beta }\exp [{{{{{{{\rm{i}}}}}}}}\phi (t)]{\left|1\right\rangle }_{{{{{{{{\rm{exc}}}}}}}}}{\left|x(t)+{{{{{{{\rm{i}}}}}}}}p(t)\right\rangle }_{{{{{{{{\rm{vib}}}}}}}}}\) with the coherent state \({\left|\alpha \right\rangle }_{{{{{{{{\rm{vib}}}}}}}}}=\exp (\alpha {\hat{b}}_{n}^{{{{\dagger}}} }-{\alpha }^{* }{\hat{b}}_{n}){\left|0\right\rangle }_{{{{{{{{\rm{vib}}}}}}}}}\) and the phase ϕ(t) due to the energy difference between states \({\left|0\right\rangle }_{{{{{{{{\rm{exc}}}}}}}}}\) and \({\left|1\right\rangle }_{{{{{{{{\rm{exc}}}}}}}}}\). For β ≠ 0, 1, this is generally an entangled state, and the shape of the nuclear wave packet (after tracing out the spin degree of freedom) is modified from the Gaussian shape, dependent on β.
a, b Time evolution of the cumulative left tail weight ηl (a) and the right tail weight ηr (b) as defined in Eq. (8) for an initial molecule excitation. The dark red solid line is the disorder-averaged exact time evolution for W = gc/2, whereas the red dotted line shows equivalent results computed with a product state approximation [Eq. (7)]. The light red dash-dotted line displays the results for W = 0. The gray dashed line is the no-cavity reference. c, d Results for an initial cavity excitation with analogous line styles. The parameters are N = 100, λ = 0.4, and ν = 0.3gc. Averaged over 256 disorder realizations. The error of the mean is less than the line width.
In order to numerically study the shape of Pn(xn, t) with our exact MPS method, we define its tails by \({x}_{n} \; < \; {x}_{{{{{{{{\rm{thr}}}}}}}}}^{{{{{{{{\rm{l}}}}}}}}}\) and \({x}_{n} \; > \; {x}_{{{{{{{{\rm{thr}}}}}}}}}^{{{{{{{{\rm{r}}}}}}}}}\), respectively. Here we choose a threshold value such that the tails of a ground state molecule include one percent of the weight \({\eta }_{0}=\{1\pm {{{{{{{\rm{erf}}}}}}}}[{x}_{{{{{{{{\rm{thr}}}}}}}}}^{{{{{{{{\rm{l}}}}}}}}/{{{{{{{\rm{r}}}}}}}}}]\}/2=1{0}^{-2}\), which corresponds to \({x}_{{{{{{{{\rm{thr}}}}}}}}}^{{{{{{{{\rm{l}}}}}}}}/{{{{{{{\rm{r}}}}}}}}}\approx \mp 1.6\). We have confirmed that the underlying physics is generally independent of the specific choice of η0 for 0.1 > η0 > 10−4, however, the relative magnitude of the changes generally increases for decreasing η0. We define the time-dependent tail weights:
In a simplified reaction picture, ηl/r(t) may be related to a reaction probability, e.g., for dissociation, if the coordinate x corresponds to the stretching of a critical bond in the system25.
Without cavity, we can analytically solve the dynamics of the tail weights. For an initial single molecular excitation, the (N − 1) ground state molecules exhibit no dynamics, and the excited molecule oscillates between x1 = 0 and \({x}_{1}=2\sqrt{2}\lambda\) according to \({x}_{1}(t)=\sqrt{2}\lambda [1-\cos (\nu t)]\). The tails are then given by \({\eta }^{{{{{{{{\rm{l}}}}}}}}/{{{{{{{\rm{r}}}}}}}}}(t)=(N-1)\times {\eta }_{0}+\{1\pm {{{{{{{\rm{erf}}}}}}}}[{x}_{{{{{{{{\rm{thr}}}}}}}}}^{{{{{{{{\rm{l}}}}}}}}/{{{{{{{\rm{r}}}}}}}}}-{x}_{1}(t)]\}/2\), with \({{{{{{{\rm{erf}}}}}}}}(x)=2\int\nolimits_{0}^{x}dz\exp (-{z}^{2})/\sqrt{\pi }\) the error function. This is shown as gray dashed lines in Fig. 4.
The influence of cavity and disorder on the evolution of ηl/r(t) is shown in Fig. 4 for both an initial molecule excitation (Fig. 4a, b) and the cavity excitation scenario (Fig. 4c, d). We first discuss the disorder-less case W = 0. For the molecule excitation (light dash-dotted lines in Fig. 4a, b), we observe only a minimal modification from the no-cavity case (gray dashed line). In contrast, for an initial cavity excitation (Fig. 4c, d), we find a strong suppression, in particular of the right tail weights due to the cavity. This is a manifestation of the polaron decoupling35.
For W = gc/2, in contrast, we find a distinctively different behavior. Focusing first on the right tail, we observe that disorder on average leads to a reduction of the tail at t ~ π/ν compared to the no-cavity scenario, followed by an increase at later times, seen in Fig. 4b, d. This effect is significantly more pronounced for an initial cavity excitation (Fig. 4d) than for a molecule excitation (Fig. 4b). We attribute the dynamics observed in Fig. 4b, d to the out-of-phase oscillation of the different molecular vibrations (cf. Fig. 3). It implies that nuclear coordinates reach large values of xn at different times and thus reduce the maximum weight of ηr at t ~ π/ν, but lead to a larger tail weight on average at later times. Importantly, we point again out that this out-of-phase oscillation should be considered as a quantum coherent process, i.e., the time-dependent state is a large superposition where the vibrational degrees of freedom enter as linear superposition, as for the single-molecule state \(\left|{\phi }_{\beta }\right\rangle\), but with molecule and time-dependent excitation fractions. The importance of vibrational entanglement for modeling the exact dynamics of the nuclear distribution is strikingly illustrated by the fact that product state simulations in Fig. 4 (dotted lines) fail to describe the correct dynamics.
We note that when we consider a time integration of the right tail weights, \({\eta }_{{{{{{{{\rm{avg}}}}}}}}}^{{{{{{{{\rm{r}}}}}}}}}=\int\nolimits_{0}^{2\pi /\nu }dt\,{\eta }^{{{{{{{{\rm{r}}}}}}}}}(t)\), i.e., the surface under the curves in Fig. 4b, d, we find that for large W, the exact \({\eta }_{{{{{{{{\rm{avg}}}}}}}}}^{{{{{{{{\rm{r}}}}}}}}}\) approximately agrees with the no-cavity scenario. This phenomenon can be rationalized by the fact that, although the excitation is time-dependently distributed over many molecules, in total there still only approximately remains one molecular excitation driving vibrational dynamics. Interestingly, this is not the case when time integrating the left tail weight, \({\eta }_{{{{{{{{\rm{avg}}}}}}}}}^{{{{{{{{\rm{l}}}}}}}}}\). In fact, this integrated weight increases compared to the no-cavity case, which highlights the importance of the broadening and the non-Gaussian shapes of the nuclear distributions.
Parameter scaling
Lastly, we want to systematically investigate the importance of the effects introduced in this paper as a function of disorder strength W, vibronic coupling strength ∝ λ, and molecule number N. In Fig. 5 we focus on the entanglement entropies and the right tail weights at time t = 2π/ν (red: initial molecule excitation, blue: initial cavity excitation). We find that the entanglement entropy Svib and the right tail weight ηr scale extremely similarly with all parameters (comparing a to c and d to f in Fig. 5, respectively). This confirms the close relationship between both quantities. Furthermore, we find that for sufficiently large λ and W, the product state approximation (dotted lines in Fig. 5) breaks down completely and predicts only negligible modifications compared to the exact MPS simulations. This coincides with large values of Svib, and thus underlines the essential role of entanglement between electro-photonic and vibrational degrees of freedom in the dynamics.
a–c show the entanglement entropy Svib, while d–f show the right tail weight ηr [defined in Eq. (8)] as a function of vibronic coupling strength λ (a, d), disorder width W (b, e), and molecule number N (c, f), evaluated at time t = 2π/ν. Red “×” symbols correspond to a molecular excitation, blue “+” symbols correspond to a cavity excitation. The symbols represent individual disorder realizations. The continuous line is a guide to the eye through averages of all 256 disorder realizations. The dotted lines in (b, d, and f) represent the disorder-averaged product state results for reference (the error of the mean is smaller than the line width). η0 = 10−2 is the tail weight in the ground state. We choose the vibrational level spacing ν = 0.3gc, the other parameters are N = 100, λ = 0.4, and W = gc/2 unless specified.
We observe that both Svib and ηr grow with λ (see Fig. 5a, d). As discussed above, both entanglement and modifications to the right tail can be directly attributed to \({\hat{H}}_{{{{{{{{\rm{H}}}}}}}}}\), which scales with λ [Eq. (4)]. For small disorder W < gc/2, i.e., in the strong coupling regime, we find that increasing disorder results in an increase of entanglement entropies and right tail weights (Fig. 5b, e), consistent with disorder-enhanced excitation transfer. Interestingly, Svib and ηr exhibit a peak between the weak and strong coupling limits. It becomes only weakly dependent on W in the weak coupling regime, i.e., for W > gc. This behavior and the clear difference between excitation scenarios exemplify the rich physics in the intermediate coupling regime.
Strikingly, we also observe different scaling behaviors with the molecule number N between both initial states (Fig. 5c, f). For an individually excited molecule, the entanglement and the right tail weight decrease for large N [we subtract the ground state contribution (N − 1)η0 from the tail weight], in line with the analytical estimate for the scaling of excitation transfer between molecules ~Wt/N in the strong coupling regime. In contrast, for an initial cavity-excitation, the entanglement and tail weight remain approximately constant for large N. Here, the excitation transfer from the cavity to molecules occurs on the same timescale as Rabi oscillations, and the total amount of excitation transferred is perturbatively given by \({W}^{2}/{g}_{{{{{{{{\rm{c}}}}}}}}}^{2}\) in the strong coupling regime, and thus to first-order independent of N. This further highlights the important distinction between the two initial states, especially for large molecule numbers.
Conclusions
In summary, we have analyzed the coherent femtosecond dynamics in a disordered HTC model after incoherent photo-excitation. This minimal model features necessary ingredients for analyzing key quantum processes in polaritonic chemistry, including dynamics of electronic, vibrational, and photonic degrees of freedom35. Using a matrix product state approach we have simulated the exact quantum many-body dynamics for realistic parameter regimes for mesoscopic system sizes. We have shown that disorder-enhanced excitation transfer56,57,58, both between the molecules and from the cavity to molecules, leads to coherent out-of-phase oscillations of the individual vibrational modes. Disorder thus strongly enhances the build-up of vibrational entanglement and modifications of the time-dependent nuclear probability distributions, which are not captured in a product state (mean-field Ehrenfest) picture where electronic and nuclear degrees of freedom are treated as separable. We have highlighted that for large molecule numbers, an initial excitation in the cavity leads to much larger modifications than an initial molecular excitation. In general, disorder-enhanced entanglement is a remarkable effect, since typically disorder is known to lead to a suppression of entanglement in various quantum many-body models63.
Our results have direct implications for understanding the role of collective and quantum-mechanical effects in cavity-modified chemistry. While approximations based on wave functions that are separable between the electronic and the vibrational Hilbert space can provide useful insight into disorder-free systems, our work implies that the presence of disorder leads to a breakdown of such approaches. Our work emphasizes that for cavity-modified photo-chemistry with incoherent excitations, it is crucial to distinguish scenarios where the cavity or individual molecules are activated by the photon. The observation of large-scale entanglement entropy build-up on very short femtosecond timescales suggests that quantum effects can play an important role in polaritonic chemistry experiments on timescales faster than the cavity-decay, and thus for experimentally feasible cavities with quality factors of Q ≳ 1000. Our work highlights the general importance of disorder for understanding polaritonic chemistry51,64,65.
In the future, it will be interesting to consider more realistic molecular models, including beyond-harmonic potential energy landscapes with more than one reaction coordinate, and featuring chemical reactions e.g., via electron transfer between multiple electronic levels, or conical intersections of energy surfaces. It will be interesting to extend our analysis to much longer times, when disorder-enhanced transfer becomes even more relevant66. It will be interesting to also investigate the effect of other sources of disorder in more detail, such as random molecular orientations and the cavity mode profile, leading to disordered cavity coupling constants (see Supplementary Note 1). Our numerical approach further allows us to also access regimes with multiple excitations, which will be an interesting regime to explore. Furthermore, our method can also easily include dissipative mechanisms, e.g., using a quantum trajectory approach,67 which has been proposed to lead to further modifications of the involved chemistry32,68,69,70,71, an interesting prospect for future research.
Methods
Matrix product state method
We write the time-dependent quantum state on the full electro-photonic-vibrational Hilbert space in the form
Here, the different indices denote electronic excitation numbers for molecule n, in = 0, 1, the vibrational excitation number on molecule n, \({b}_{n}=0,\ldots ,{n}_{\max }^{{{{{{{{\rm{v}}}}}}}}}\) and the cavity mode occupation number, \(a=0,\ldots ,{n}_{\max }^{{{{{{{{\rm{p}}}}}}}}}\). While in principle \({n}_{\max }^{{{{{{{{\rm{v/p}}}}}}}}}\to \infty\), in practice the vibrational Hilbert space can be truncated at some reasonable occupation number. For this work we found that to capture all relevant physics of the tails of the nuclear coordinate distributions, \({n}_{\max }^{{{{{{{{\rm{v}}}}}}}}}=10\) is sufficient (see Supplementary Figure 2 and Note 5). Due to our choice of the initial state and the conservation of \({\sum }_{n}{\hat{\sigma }}_{n}^{+}{\hat{\sigma }}_{n}^{-}+{\hat{a}}^{{{{\dagger}}} }\hat{a}\), furthermore we can set a photon cutoff at \({n}_{\max }^{{{{{{{{\rm{p}}}}}}}}}=1\) without any approximation. For N = 100 molecules, this implies a full Hilbert space size of 11N2N+1 ≳ 10134, clearly out of reach for any classical computer memory. In order to still make the high-dimensional complex state tensor c amenable for storage in computer memory, we utilize a decomposition into products of smaller tensors, an MPS53. In particular, we utilize an MPS with 2N + 1 tensors:
Here we introduced three-dimensional tensors for the photonic, electronic, and vibrational degrees of freedom, \({{{\Gamma }}}_{a}^{{{{{{{{\rm{[p]}}}}}}}};{\alpha }_{0}{\alpha }_{1}}\), \({{{\Gamma }}}_{{i}_{n}}^{{{{[{{{{\rm{n}}}}_n}]}}};{\alpha }_{m}{\alpha }_{m+1}}\), and \({{{\Gamma }}}_{{b}_{n}}^{{{{[{{{{\rm{v}}}}_n}]}}};{\alpha }_{m}{\alpha }_{m+1}}\), respectively. The tensors are connected by the virtual indices αm with m = 0, …, 2N + 1, and bond dimension χ (except for the edge indices, which are trivially α0 = α2N+1 = 1). The MPS can be brought, and updated, in a canonical form. Then, the virtual indices αm correspond to an orthonormal basis, which is the eigenbasis of the reduced density matrix of the two blocks that the index connects53. This effectively limits the entanglement entropy between the two blocks to \( < {\log }_{2}(\chi )\). For the MPS decomposition to become exact, one would need to choose very large values for \(\chi \sim \exp (N)\). However, limiting χ to computationally treatable magnitudes allows to effectively simulate dynamics on a truncated Hilbert space with restricted entanglement. In our simulations, we verified that all results converge with increasing χ, and therefore that our simulations capture all necessary entanglement and are quasi-exact. In practice, we use χ = 128 for all plots (see Supplementary Figure 3 and Note 5). In our MPS form, tensors can be updated using the time-evolving Block decimation (TEBD) algorithm72. Then, HTC coupling terms can be incorporated with nearest-neighbor gate updates, while cavity-couplings can be incorporated using index-swap gates between the tensors and nearest-neighbor gates. In practice, we choose a second order TEBD decomposition of the Hamiltonian with a time step of gc/100, which we have verified to be sufficiently small for errors due to a finite time step to be negligible (see Supplementary Figure 4 Note 5). In the case of spin-boson dynamics, TEBD in combination with swap gates has been previously shown to exhibit very well-behaved convergence, which is preferable compared to updates that use variational concepts67. Similarly, in order to compute Svib we re-organize all vibrational degrees of freedom into a single block (using swap gates) and compute the entropy over the virtual index into that block. The excitation number conservation can be exploited to enhance the efficiency of tensor contractions and decompositions.
Data availability
The data of this study are available from the corresponding author, J.S., upon reasonable request.
Code availability
The code used for this study is available from the corresponding author, J.S., upon reasonable request.
References
Törmä, P. & Barnes, W. L. Strong coupling between surface plasmon polaritons and emitters: a review. Rep. Prog. Phys. 78, 013901 (2014).
Ebbesen, T. W. Hybrid light–matter states in a molecular and material science perspective. Acc. Chem. Res. 49, 2403–2412 (2016).
Ribeiro, R. F., Martínez-Martínez, L. A., Du, M., Campos-Gonzalez-Angulo, J. & Yuen-Zhou, J. Polariton chemistry: controlling molecular dynamics with optical cavities. Chem. Sci. 9, 6325–6339 (2018).
Flick, J., Rivera, N. & Narang, P. Strong light-matter coupling in quantum chemistry and quantum photonics. Nanophotonics 7, 1479–1501 (2018).
Feist, J., Galego, J. & Garcia-Vidal, F. J. Polaritonic chemistry with organic molecules. ACS Photonics 5, 205–216 (2018).
Hertzog, M., Wang, M., Mony, J. & Börjesson, K. Strong light-matter interactions: a new direction within chemistry. Chem. Soc. Rev. 48, 937–961 (2019).
Herrera, F. & Owrutsky, J. Molecular polaritons for controlling chemistry with quantum optics. J. Chem. Phys. 152, 100902 (2020).
Garcia-Vidal, F. J., Ciuti, C. & Ebbesen, T. W. Manipulating matter by strong coupling to vacuum fields. Science 373, eabd0336 (2021).
Sidler, D., Ruggenthaler, M., Schäfer, C., Ronca, E. & Rubio, A. A perspective on ab initio modeling of polaritonic chemistry: the role of non-equilibrium effects and quantum collectivity. arXiv https://arxiv.org/abs/2108.12244 (2021).
Hutchison, J. A., Schwartz, T., Genet, C., Devaux, E. & Ebbesen, T. W. Modifying chemical landscapes by coupling to vacuum fields. Angew. Chem. Int. Ed. 51, 1592–1596 (2012).
Coles, D. M. et al. Polariton-mediated energy transfer between organic dyes in a strongly coupled optical microcavity. Nat. Mater. 13, 712–719 (2014).
Zhong, X. et al. Non-radiative energy transfer mediated by hybrid light-matter states. Angew. Chem. Int. Ed. 55, 6202–6206 (2016).
Zhong, X. et al. Energy transfer between spatially separated entangled molecules. Angew. Chem. Int. Ed. 56, 9034 (2017).
Munkhbat, B., Wersäll, M., Baranov, D. G., Antosiewicz, T. J. & Shegai, T. Suppression of photo-oxidation of organic chromophores by strong coupling to plasmonic nanoantennas. Sci. Adv. 4, eaas9552 (2018).
Peters, V. N. et al. Effect of strong coupling on photodegradation of the semiconducting polymer P3HT. Optica 6, 318–325 (2019).
Polak, D. et al. Manipulating molecules with strong coupling: harvesting triplet excitons in organic exciton microcavities. Chem. Sci. 11, 343–354 (2020).
Yu, Y., Mallick, S., Wang, M. & Börjesson, K. Barrier-free reverse-intersystem crossing in organic molecules by strong light-matter coupling. Nat. Commun. 12, 1–8 (2021).
Mony, J. et al. Photoisomerization efficiency of a solar thermal fuel in the strong coupling regime. Adv. Funct. Mater. 31, 2010737 (2021).
Thomas, A. et al. Ground-state chemical reactivity under vibrational coupling to the vacuum electromagnetic field. Angew. Chem. Int. Ed. 55, 11462–11466 (2016).
Thomas, A. et al. Tilting a ground-state reactivity landscape by vibrational strong coupling. Science 363, 615–619 (2019).
Vergauwe, R. M. A. et al. Modification of enzyme activity by vibrational strong coupling of water. Angew. Chem. Int. Ed. 58, 15324–15328 (2019).
Lather, J., Bhatt, P., Thomas, A., Ebbesen, T. W. & George, J. Cavity catalysis by cooperative vibrational strong coupling of reactant and solvent molecules. Angew. Chem. Int. Ed. 58, 10635–10638 (2019).
Hirai, K., Hutchison, J. A. & Uji-i, H. Recent progress in vibropolaritonic chemistry. ChemPlusChem 85, 1981–1988 (2020).
Davidsson, E. & Kowalewski, M. Atom assisted photochemistry in optical cavities. J. Phys. Chem. A 124, 4672–4677 (2020).
Vendrell, O. Coherent dynamics in cavity femtochemistry: application of the multi-configuration time-dependent hartree method. Chem. Phys. 509, 55–65 (2018).
Schäfer, C., Ruggenthaler, M., Appel, H. & Rubio, A. Modification of excitation and charge transfer in cavity quantum-electrodynamical chemistry. PNAS 116, 4883–4892 (2019).
Galego, J., Garcia-Vidal, F. J. & Feist, J. Cavity-induced modifications of molecular structure in the strong-coupling regime. Phys. Rev. X 5, 041022 (2015).
Vendrell, O. Collective Jahn-Teller interactions through light-matter coupling in a cavity. Phys. Rev. Lett. 121, 253001 (2018).
Fábri, C., Halász, G. J., Cederbaum, L. S. & Vibók, Á. Born-Oppenheimer approximation in optical cavities: from success to breakdown. Chem. Sci. 12, 1251–1258 (2021).
Fregoni, J., Granucci, G., Coccia, E., Persico, M. & Corni, S. Manipulating azobenzene photoisomerization through strong light-molecule coupling. Nat. Commun. 9, 1–9 (2018).
Luk, H. L., Feist, J., Toppari, J. J. & Groenhof, G. Multiscale molecular dynamics simulations of polaritonic chemistry. J. Chem. Theory Comput. 13, 4324–4335 (2017).
Antoniou, P., Suchanek, F., Varner, J. F. & Foley IV, J. J. Role of cavity losses on nonadiabatic couplings and dynamics in polaritonic chemistry. J. Phys. Chem. Lett. 11, 9063 (2020).
Groenhof, G., Climent, C., Feist, J., Morozov, D. & Toppari, J. J. Tracking polariton relaxation with multiscale molecular dynamics simulations. J. Phys. Chem. Lett. 10, 5476–5483 (2019).
Zhang, Y., Nelson, T. & Tretiak, S. Non-adiabatic molecular dynamics of molecules in the presence of strong light-matter interactions. J. Chem. Phys. 151, 154109 (2019).
Herrera, F. & Spano, F. C. Cavity-controlled chemistry in molecular ensembles. Phys. Rev. Lett. 116, 238301 (2016).
Zeb, M. A., Kirton, P. G. & Keeling, J. Exact states and spectra of vibrationally dressed polaritons. ACS Photonics 5, 249–257 (2018).
Reitz, M., Sommer, C. & Genes, C. Langevin approach to quantum optics with molecules. Phys. Rev. Lett. 122, 203602 (2019).
Martínez-Martínez, L. A., Eizner, E., Kéna-Cohen, S. & Yuen-Zhou, J. Triplet harvesting in the polaritonic regime: a variational polaron approach. J. Chem. Phys. 151, 054106 (2019).
Mauro, L., Caicedo, K., Jonusauskas, G. & Avriller, R. Charge-transfer chemical reactions in nanofluidic Fabry-Pérot cavities. Phys. Rev. B 103, 165412 (2021).
Engel, G. S. et al. Evidence for wavelike energy transfer through quantum coherence in photosynthetic systems. Nature 446, 782–786 (2007).
Mohseni, M., Rebentrost, P., Lloyd, S. & Aspuru-Guzik, A. Environment-assisted quantum walks in photosynthetic energy transfer. J. Chem. Phys. 129, 174106 (2008).
Caruso, F., Chin, A. W., Datta, A., Huelga, S. F. & Plenio, M. B. Highly efficient energy excitation transfer in light-harvesting complexes: The fundamental role of noise-assisted transport. J. Chem. Phys. 131, 105106 (2009).
Collini, E. et al. Coherently wired light-harvesting in photosynthetic marine algae at ambient temperature. Nature 463, 644–647 (2010).
Horodecki, R., Horodecki, P., Horodecki, M. & Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 81, 865 (2009).
Amico, L., Fazio, R., Osterloh, A. & Vedral, V. Entanglement in many-body systems. Rev. Mod. Phys. 80, 517–576 (2008).
Eisert, J., Cramer, M. & Plenio, M. B. Colloquium: area laws for the entanglement entropy. Rev. Mod. Phys. 82, 277–306 (2010).
McKemmish, L. K., McKenzie, R. H., Hush, N. S. & Reimers, J. R. Quantum entanglement between electronic and vibrational degrees of freedom in molecules. J. Chem. Phys. 135, 12B606 (2011).
Vatasescu, M. Measures of electronic-vibrational entanglement and quantum coherence in a molecular system. Phys. Rev. A 92, 042323 (2015).
Agranovich, V., Litinskaia, M. & Lidzey, D. G. Cavity polaritons in microcavities containing disordered organic semiconductors. Phys. Rev. B 67, 085311 (2003).
Michetti, P. & La Rocca, G. C. Exciton-phonon scattering and photoexcitation dynamics in J-aggregate microcavities. Phys. Rev. B 79, 035325 (2009).
Sommer, C., Reitz, M., Mineo, F. & Genes, C. Molecular polaritonics in dense mesoscopic disordered ensembles. Phys. Rev. Res. 3, 033141 (2021).
del Pino, J., Schröder, F. A. Y. N., Chin, A. W., Feist, J. & Garcia-Vidal, F. J. Tensor network simulation of non-markovian dynamics in organic polaritons. Phys. Rev. Lett. 121, 227401 (2018).
Schollwöck, U. The density-matrix renormalization group in the age of matrix product states. Ann. Phys. 326, 96 (2011).
Ćwik, J. A., Reja, S., Littlewood, P. B. & Keeling, J. Polariton condensation with saturable molecules dressed by vibrational modes. EPL 105, 47009 (2014).
Herrera, F. & Spano, F. C. Theory of nanoscale organic cavities: the essential role of vibration-photon dressed states. ACS Photonics 5, 65–79 (2018).
Botzung, T. et al. Dark state semilocalization of quantum emitters in a cavity. Phys. Rev. B 102, 144202 (2020).
Chávez, N. C., Mattiotti, F., Méndez-Bermúdez, J., Borgonovi, F. & Celardo, G. L. Disorder-enhanced and disorder-independent transport with long-range hopping: Application to molecular chains in optical cavities. Phys. Rev. Lett. 126, 153201 (2021).
Dubail, J., Botzung, T., Schachenmayer, J., Pupillo, G. & Hagenmüller, D. Large random arrowhead matrices: multifractality, semilocalization, and protected transport in disordered quantum spins coupled to a cavity. Phys. Rev. A 105, 023714 (2022).
Houdré, R., Stanley, R. P. & Ilegems, M. Vacuum-field Rabi splitting in the presence of inhomogeneous broadening: Resolution of a homogeneous linewidth in an inhomogeneously broadened system. Phys. Rev. A 53, 2711–2715 (1996).
Valmorra, F. et al. Strong coupling between surface plasmon polariton and laser dye rhodamine 800. Appl. Phys. Lett. 99, 051110 (2011).
Christensson, N., Dietzek, B., Yartsev, A. & Pullerits, T. Electronic photon echo spectroscopy and vibrations. Vib. Spectrosc. 53, 2–5 (2010).
Hou, S. et al. Ultralong-Range Energy Transport in a Disordered Organic Semiconductor at Room Temperature Via Coherent Exciton-Polariton Propagation. Adv. Mater. 32, 2002127 (2020).
Abanin, D. A., Altman, E., Bloch, I. & Serbyn, M. Colloquium: Many-body localization, thermalization, and entanglement. Rev. Mod. Phys. 91, 021001 (2019).
Scholes, G. D. Polaritons and excitons: Hamiltonian design for enhanced coherence. Proc. R. Soc. A 476, 20200278 (2020).
Du, M. & Yuen-Zhou, J. Catalysis by Dark States in Vibropolaritonic Chemistry. Phys. Rev. Lett. 128, 096001 (2022).
Botzung, T. Study of strongly correlated one-dimensional systems with long-range interactions. Ph.D. thesis, University of Strasbourg. http://www.theses.fr/2019STRAF062 (2019).
Wall, M. L., Safavi-Naini, A. & Rey, A. M. Simulating generic spin-boson models with matrix product states. Phys. Rev. A 94, 053637 (2016).
Felicetti, S. et al. Photoprotecting Uracil by Coupling with Lossy Nanocavities. J. Phys. Chem. Lett. 11, 8810–8818 (2020).
Wellnitz, D., Pupillo, G. & Schachenmayer, J. A quantum optics approach to photoinduced electron transfer in cavities. J. Chem. Phys. 154, 054104 (2021).
Torres-Sánchez, J. & Feist, J. Molecular photodissociation enabled by ultrafast plasmon decay. J. Chem. Phys. 154, 014303 (2021).
Davidsson, E. & Kowalewski, M. Simulating photodissociation reactions in bad cavities with the Lindblad equation. J. Chem. Phys. 153, 234304 (2020).
Vidal, G. Efficient Simulation of One-Dimensional Quantum Many-Body Systems. Phys. Rev. Lett. 93, 040502 (2004).
Fishman, M., White, S. R. & Stoudenmire, E. M. The ITensor software library for tensor network calculations. arXiv:2007.14822 (2020).
Acknowledgements
We are grateful to Felipe Herrera, Claudiu Genes, David Hagenmüller, Jerôme Dubail and Guido Masella for stimulating discussions. This work was supported by LabEx NIE (“Nanostructures in Interaction with their Environment”) under contract ANR-11-LABX0058 NIE and “ERA-NET QuantERA” - Projet “RouTe” (ANR-18-QUAN-0005-01). This work of the Interdisciplinary Thematic Institute QMat, as part of the ITI 2021-2028 program of the University of Strasbourg, CNRS, and Inserm, was supported by IdEx Unistra (ANR-10-IDEX-0002), SFRI STRAT’US project (ANR-20-SFRI-0012), and EUR QMAT ANR-17-EURE-0024 under the framework of the French Investments for the Future Program. We acknowledge support from ECOS-CONICYT through project nr. C20E01 and the CNRS through the IEA 2020 campaign. G. P. acknowledges support from the Institut Universitaire de France (IUF) and the University of Strasbourg Institute of Advanced Studies (USIAS). Our MPS codes make use of the intelligent tensor library (ITensor)73. Computations were carried out using resources of the High-Performance Computing Center of the University of Strasbourg, funded by Equip@Meso (as part of the Investments for the Future Program) and CPER Alsacalcul/Big Data.
Author information
Authors and Affiliations
Contributions
D.W. and J.S. developed the conceptual approach and performed the simulations. D.W. derived the analytic estimates. J.S. developed the original code. G.P. and J.S. supervised the research. All authors analyzed and discussed the results and wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks Yu Zhang, Joel Yuen-Zhou, and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wellnitz, D., Pupillo, G. & Schachenmayer, J. Disorder enhanced vibrational entanglement and dynamics in polaritonic chemistry. Commun Phys 5, 120 (2022). https://doi.org/10.1038/s42005-022-00892-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-022-00892-5
This article is cited by
-
Cavity-enhanced energy transport in molecular systems
Nature Materials (2024)
-
Thermal disorder prevents the suppression of ultra-fast photochemistry in the strong light-matter coupling regime
Nature Communications (2024)
-
Multi-scale molecular dynamics simulations of enhanced energy transfer in organic molecules under strong coupling
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.