Abstract
The driven quantum asymmetric top is an important paradigm in molecular physics with applications ranging from quantum information to chiral-sensitive spectroscopy. A key prerequisite for these applications is the ability to completely control the rotational dynamics. The inherent degeneracy of quantum rotors poses a challenge for quantum control since selecting a particular rotational state cannot be achieved by spectral selection alone. Here, we prove complete controllability for rotational states of an asymmetric top belonging to degenerate values of the orientational quantum number M. Based on this insight, we construct a pulse sequence that energetically separates population in degenerate M-states. Introducing the concept of enantio-selective controllability, we determine the conditions for complete enantiomer-specific population transfer in chiral molecules and construct pulse sequences for the example of propanediol and carvone molecules for population initially distributed over degenerate M-states. Our work shows how to leverage controllability analysis for the solution of practical quantum control problems.
Similar content being viewed by others
Introduction
Molecular chirality—the fact that a chiral molecule cannot be superimposed with its mirror image by rotations and translations—is as ubiquitous as it is intriguing. The left-handed and right-handed versions of a chiral molecule share almost all of their physical properties. Yet, the chemical and biological behavior of the two enantiomers typically differs dramatically. Detection of chirality and the ability to separate enantiomers, therefore, play a central role across the natural sciences. To this end, chiroptical spectroscopy, the interrogation of chiral molecules with electromagnetic radiation1, has been a method of choice since the very discovery of molecular chirality. For the detection of enantiomeric excess, for example, several new techniques have recently been brought forward, including resonant phase-sensitive microwave three-wave mixing2,3,4,5 and ultrafast spectroscopies based on photoelectron circular dichroism6,7,8 or high-harmonic generation9,10. They share, as a common feature, a sufficiently high sensitivity allowing for application in gas phase samples of randomly oriented molecules.
Among these techniques, resonant phase-sensitive microwave three-wave mixing2,3,4,5 holds the promise of separating enantiomers in a racemic mixture with electromagnetic fields alone. A precursor—enantiomer-selective population excitation transfering right-handed molecules to a different energy level than left-handed ones—has already been demonstrated experimentally11,12,13, albeit with efficiencies of at most a few percent. If the efficiency of the population transfer can be brought close to 100%, an enantiopure sample can be distilled out of the racemate by e.g., ionizing all molecules in one of the two levels. Such an ability to completely separate enantiomers in energy would benefit e.g., high-resolution searches of parity violation11,14,15. In experiments to date11,12,13, the efficiency of the enantiomer-selective population transfer has been limited by two factors. One is the temperature of the sample or, more precisely, thermal population in the excited states targeted by the three-wave mixing. A solution to this problem consists in addressing levels which are sufficiently highly excited such that their thermal population vanishes16,17. The second limitation is due to degeneracies within the rotational spectrum. Chiral molecules are typically asymmetric top rotors. Denoting the rotational quantum number by J, every energy level of a rigid asymmetric top consists of 2J + 1 states with a different orientational quantum number M. Theoretical descriptions of resonant three-wave mixing have most often ignored the presence of degenerate energy levels2,17,18,19,20,21,22,23. However, transfer efficiencies are then predicted correctly only for cycles which start from the non-degenerate rotational ground state (J = 0)16,24,25. Otherwise, cyclic excitation involves a number of coupled, partially incomplete three-level systems, limiting the efficiency of enantiomer-selective population transfer24, even in the absence of thermal population in the excited states.
The orientational degeneracy of rotational states in asymmetric top molecules is an obstacle also in applications beyond resonant microwave three-wave mixing, for example, in laser cooling26,27 and quantum computing28. More generally, driven or “kicked” top rotors are an important paradigm of quantum control with a long-standing history in quantum chaos29 and molecular alignment30. The ability to control a quantum system such as a driven rotor can be tackled by controllability analysis. It refers to the question of whether a control target can be reached, given the interaction of the system with external fields31. Degeneracies may pose a problem because state-selectivity cannot simply be reached by spectral selection32. For molecular rotations, the simplest example of degeneracy is that of a linear rotor. The degeneracy is due to isotropy of space which can be broken by using controls with more than one polarization direction. This was first proven for finite-dimensional subspaces of the linear rotor spectrum33,34. Development of a rigorous theory to decouple a finite-dimensional subspace from the rest of an infinite-dimensional spectrum two decades later35,36,37 has allowed to extend the controllability proof for the linear rotor to unitary evolutions38, a prerequisite for e.g., using molecular rotations in quantum computing28,39. In contrast to linear rotors, symmetric top molecules are not controllable40,41 since no mechanism exists to break the additional symmetry with respect to the molecule-fixed axis. In asymmetric top molecules, this symmetry is absent, as in the case of a linear rotor. However, the asymmetric top energy level structure is much more complex than that of the linear rotor, involving additional transitions between states with ΔJ = 0, depending on the orientational quantum number M. Controllability of the asymmetric top is thus a nontrivial problem. It has recently been proven for the complete infinite-dimensional spectrum42. This does not, however, imply that a particular subsystem addressed in an experiment is controllable as well. For example, it does not guarantee the three rotational levels involved in microwave three-wave mixing are controllable. For practical purposes, it is, therefore, necessary to prove controllability of rotational subsystems. Addressing rotational subsystems instead of the complete spectrum also allows for identifying the number of different control fields that is required to control the subsystem.
Here, we show how to completely control the rotational dynamics in asymmetric top molecules, with electric fields chosen such as to break the orientational degeneracy, which we will refer to as orientation-selective control. To this end, we first prove controllability for asymmetric tops in finite-dimensional subspaces for arbitrary initial states (within these subspaces), building on recent advances in the controllability of quantum rotors38,40,41,43,44. We then consider the simultaneous controllability of left-handed and right-handed asymmetric top molecules interacting with the same electric fields and prove enantiomer-sensitive controllability within any rotational subspace corresponding to three rotational energies with quantum numbers J and J + 1. Based on this mathematical insight, we solve two control problems. As a first example, we consider population that initially is incoherently distributed over degenerate rotational states and derive pulse sequences that energetically separate them. This can be used as a precursor for distilling a specific orientation. We then combine control over degenerate rotational states with cyclic population transfer to achieve complete control over enantiomer-selective excitation in degenerate rotational levels. The solution consists in amending the three-wave mixing pulse sequence to consist of at least five different combinations of the three polarization directions and three frequencies. The corresponding modified cycles are closed for all levels in the degenerate manifold, avoiding population loss; and they can be synchronized for complete population transfer, accounting for the M-dependent Rabi frequencies. By identifying the required light-matter couplings and deriving practical pulse sequences, we solve the problem of orientational degeneracy in resonant microwave three-wave mixing.
Model
Chiral molecules as asymmetric top rotors
We consider the interaction of chiral molecules with electromagnetic radiation, described by the Hamiltonian
where the subscript (±) denotes the two enantiomers. The molecular Hamiltonian \({\hat{H}}_{0}\) is the same for both enantiomers, except for a very small, parity-violating energy shift which we neglect here. In contrast, the interaction of the molecule with external electric fields, \({\hat{H}}_{{{{{{{{\rm{int}}}}}}}}}^{(\pm )}\) differs since at least one of the Cartesian projections of the molecule’s electric dipole moment onto the molecular frame changes sign when changing enantiomers3,22,45. It is this sign change that is at the core of phase-sensitive resonant microwave mixing2,22. Exploiting the sign change in cyclic population transfer, enantiomer-selective excitation is achieved by creating destructive interference for molecules of one handedness and constructive interference for the other handedness19.
The dynamics of each enantiomer, induced by the electromagnetic field, are obtained by solving the time-dependent Schrödinger equation,
Since we consider rotational dynamics of molecules in the electronic and vibrational ground state, there are no dissipative mechanisms relevant to the timescale of the dynamics. Expectation values for a racemic mixture are obtained via the density operator \(\hat{\rho (t)}=\frac{1}{2}{\sum }_{\pm }|{\psi }^{(\pm )}(t)\rangle \langle {\psi }^{(\pm )}(t)|\).
We assume the molecules to be sufficiently rigid to model them as asymmetric tops. The molecular Hamiltonian \({\hat{H}}_{0}\) then becomes46
where \({\hat{J}}_{a}\), \({\hat{J}}_{b}\), and \({\hat{J}}_{c}\) are the angular momentum operators with respect to the principal molecular axes, and A > B > C are the rotational constants. We adopt the standard approach46 of expressing the asymmetric top eigenstates as superpositions of symmetric top eigenstates \(\left|J,K,M\right\rangle\),
with prolate symmetric top eigenenergies
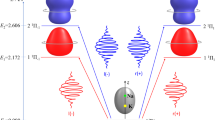
where J denotes the rotational quantum number, J = 0, 1, 2, …, and M and K are the projection quantum numbers, M = − J, − J + 1, …, J and K = − J, − J + 1, …, J, which describe the orientation with respect to a space-fixed and a molecule-fixed axis. Note that in Eq. (4), states with different K but the same J and M are mixed. For each J, the coefficients \({c}_{K}^{J}\) and the asymmetric top eigenenergies EJ,τ are obtained by diagonalizing the corresponding (2J + 1)-dimensional matrix. The index τ = − J, − J + 1, …, J counts the asymmetric top states corresponding to a given J, starting with the one with lowest energy. Note that in rotational spectroscopy, the asymmetric top states are often denoted by \(\left|J,| {K}_{a}| ,| {K}_{c}| ,M\right\rangle\), where Ka and Kc are the projection quantum numbers of the corresponding prolate and oblate symmetric top, respectively. For our purpose, it is more convenient to use the notation \(\left|J,\tau ,M\right\rangle\). For a given J, the asymmetric top states with the lowest energy can thus be denoted either by \(\left|J,0,J,M\right\rangle\) or, in our notation, by \(\left|J,-J,M\right\rangle\), the ones with the largest energy by \(\left|J,J,0,M\right\rangle\) or \(\left|J,J,M\right\rangle\), and the states in between can be matched accordingly. The spectrum of a near-prolate asymmetric top is sketched in Fig. 1a.
a Energies eigenvalues are sketched up to E2,2 and labeled by the quantum numbers J, τ. The degenerate eigenstates in each level are labeled by the orientational quantum number M. By choosing a set of microwave fields resonant to particular transitions, only selected rotational levels are addressed. This is highlighted for the frequencies ω1 = (E2,−1 − E1,−1)/ℏ, ω2 = (E2,0 − E2,−1)/ℏ, and ω3 = (E2,0 − E1,−1)/ℏ in example (i), and ω1 = (E1,0 − E0,0)/ℏ, ω2 = (E1,1 − E1,0)/ℏ, and \({\omega }_{3}=({E}_{1,1}-{E}_{0,0})\left.\right)/\hslash\) in example (ii). b (i) and (ii) The subsystems of the asymmetric top resulting from resonant microwave driving with set of frequencies depicted in a (i) and a (ii), respectively, with the colored lines indicating transitions induced by x−, y−, and z− polarized fields with frequencies ω1 (orange), ω2 (pink), and ω3 (turquoise). Here, μa, μb, and μc are the Cartesian components of the dipole moment responsible for the transition indicated by the vertical bars. The small numbers indicate the states of the subsystems.
In the electric dipole approximation, the interaction of an asymmetric top with f electric fields linearly polarized along one of the laboratory frame directions can be written as
We denote the electric fields by Ei(t) = eiEifi(t) with polarization vector ei (equal to either ex, ey, or ez) and maximal amplitude Ei. The time-dependence of the field is denoted by \({f}_{i}(t)={{{{{{{{\mathcal{E}}}}}}}}}_{i}(t)\cos ({\omega }_{i}t+{\varphi }_{i})\). Here, \({{{{{{{{\mathcal{E}}}}}}}}}_{i}(t)\) is the dimensionless envelope and ωi and φi are frequency and phase of the field, and we assume spatially uniform electric fields. In Eq. (6), the dipole moments, given in the laboratory-fixed frame with \({\hat{\mu }}_{i}^{(\pm )}\) equal to \({\hat{\mu }}_{x}^{(\pm )}\), \({\hat{\mu }}_{y}^{(\pm )}\), or \({\hat{\mu }}_{z}^{(\pm )}\), are connected to the dipole moments \({\mu }_{\sigma }^{(\pm )}=({\mu }_{a}^{(\pm )},{\mu }_{b}^{(\pm )},{\mu }_{c}^{(\pm )})\) in the molecule-fixed frame by a rotation16,47,
where \({D}_{MK}^{J}\) denote the elements of the Wigner D-matrix. Note that each element of the Wigner D-matrix represents an operator due to its dependence on the Euler angles. For chiral molecules with C1-symmetry, all three components \({\mu }_{\sigma }^{(\pm )}\) are non-zero. Moreover, \(| {\mu }_{\sigma }^{(+)}| =| {\mu }_{\sigma }^{(-)}|\) and
i.e., the two enantiomers differ in the sign of one of the Cartesian components of the dipole moment22. Equation (8) is the basis of enantiomer-specific three-wave mixing2.
In the asymmetric top eigenbasis (4), the interaction Hamiltonian contains matrix elements of the form
with
The Wigner 3j-symbols in Eq. (10) determine the selection rules, namely \(J^{\prime\prime} -J^{\prime} =0,\pm 1\) and \(K^{\prime\prime} =K^{\prime} +K\) as well as \(M^{\prime\prime} =M^{\prime} +M\) where the value of M is determined by the electric field polarization in Eq. (6). Since the quantization axis of the rotor is chosen to be parallel to the space fixed z-axis, M = 0 for z-polarized fields. The interaction with linearly polarized fields with polarization axis along the space fixed x- or y-axis allows transitions with both, M = 1 and M = − 1. The transition matrix elements for x- and y-polarized fields only differ by their relative phases. Note that the transition matrix element (10) is equal to zero if \(J^{\prime} =J^{\prime\prime}\) and \(M=M^{\prime} =M^{\prime\prime}\), i.e., transitions with ΔM = 0 are forbidden for \(J^{\prime} =J^{\prime\prime}\).
Control problem
Our goal is to transfer population which is initially distributed over a degenerate manifold into quantum states which are energetically separated. Such a transfer can serve as precursor for distilling population out of an incoherent mixture.
For a racemic mixture of chiral molecules, the two enantiomers initially occupy the same rotational states since they possess the same rotational spectrum. The initial state is thus described by the density matrix
At non-zero temperatures, the state of each enantiomer is given by a thermal ensemble,
where \({p}_{{J}_{0},{\tau }_{0}}\) is the Boltzmann weight of the rotational level denoted by J0 and τ0 and the incoherent sum over the degenerate M0-states accounts for the isotropic angular distribution of molecules in the gas phase.
We seek to achieve the population transfer with narrow-bandwidth pulses such that only resonant transitions (with \({E}_{J^{\prime\prime} ,\tau ^{\prime\prime} }-{E}_{J^{\prime} ,\tau ^{\prime} }=\hslash {\omega }_{i}\), where \(J^{\prime\prime} =J^{\prime}\) or \(J^{\prime\prime} =J^{\prime} \pm 1\)) need to be considered. In broadband microwave three-wave mixing experiments this assumption is justified if the differences between transition frequencies are larger than ~50−150 MHz, depending on experimental conditions for example the intensity of the microwave fields. This condition has been met in microwave three-wave mixing experiments to date2,4,5,11,12,13 where the triple of rotational levels was chosen such that non-resonant couplings are indeed negligible. The assumption of resonant transitions reduces the number of non-zero matrix elements in the interaction Hamiltonian to those with the appropriate combination of frequency ωi and electric field polarization ei. Moreover, for f combinations of polarization and frequency, we obtain f linearly independent interaction matrices \({{{{{{{{\bf{H}}}}}}}}}_{i}^{(\pm )}\), expressing the interaction Hamiltonian (6) on the basis of the asymmetric top states. Since a given set of microwave fields addresses only a finite number of rotational levels, we can describe the dynamics in a comparatively small rotational subsystem. Figure 1b shows two examples of such subsystems that are relevant for microwave three-wave mixing in chiral molecules: Fields with frequencies ω1 = (E2,−1 − E1,−1)/ℏ, ω2 = (E2,0 − E2,−1)/ℏ, and ω3 = (E2,0 − E1,−1)/ℏ couple the states with rotational energies E1,−1, E2,−1, and E2,0, cf. Fig. 1b (i), while in Fig. 1b (ii) the states with E0,0, E1,0, and E1,1 are addressed.
At zero temperature, when \({\rho }^{(\pm )}=\left|0,0,0\right\rangle \left\langle 0,0,0\right|\), excitation with three microwave pulses with x-, y-, and z-polarization and frequencies ω1, ω2, and ω3, as shown in Fig. 1b (ii), is predicted to lead to 100% enantiomer-selective excitation16,24. However, in the microwave three-wave experiments performed so far, rotational states with J = 1 and J = 2 were addressed, as shown in Fig. 1b(i), or with J = 2 and J = 34,11,12 where all levels with given J0, τ0 are (2J0 + 1)-fold degenerate. This degeneracy results in incomplete enantio-selective population transfer in state-of-the-art three-wave mixing2,4,5,11,12, even if temperature effects are not considered. Below we will show that complete enantiomer-selective excitation into energetically separated quantum states can be achieved in a racemic mixture, cf. Eq. (11), despite the M-degeneracy of the rotational states when using the rotational levels EJ,τ, \({E}_{J+1,{\tau }^{\prime}}\), and \({E}_{J+1,{\tau }^{^{\prime\prime} }}\). In passing, we furthermore show that population distributed over degenerate levels in Eq. (12) can also be energetically separated.
Theoretical framework for controllability analysis
Given the model of a quantum system and its interaction with external fields, controllability analysis consists in addressing the question of whether a control target can or cannot be reached. This is in contrast to control synthesis which devises the shapes of external fields that drive the system to the target in the best possible way48. Controllability is thus a prerequisite for control synthesis.
Controllability may refer to a single quantum system or an ensemble of quantum systems that shall be controlled simultaneously with only a few control fields48. Here, we adapt the notion of simultaneous controllability to the specific task of enantiomer-selective population transfer. We first recall the basic mathematical concepts for controllability analysis before defining enantio-selective controllability.
Lie rank condition and spectral gap excitation
A quantum system is said to be controllable if we can steer it, in a finite time that may depend on the target, from any initial state to any final state by suitably choosing possibly time-dependent external fields. Here, state refers to either a wave function, a density matrix, or a set of orthogonal Hilbert space vectors. In the latter case, controllability implies that arbitrary unitary evolution operators can be realized. If one is able to prove evolution operator-controllability (also called controllability on the group), this entails density matrix-controllability, i.e., an arbitrary initial density matrix can be transformed into any unitarily equivalent density matrix. That is, any incoherent initial state can be steered to any final state with the same purity31. Note that, if a system is density matrix-controllable, it is also wavefunction-controllable31. However, wavefunction-controllability does not imply density matrix-controllability. In the subsection “Controllability of asymmetric quantum rotors" below, we will prove evolution operator-controllability, i.e., the strongest of the three properties.
We consider a finite dimensional system, described by the Hamiltonian
where H0 is the Hamiltonian of the system and Hi are the interaction Hamiltonians connected with the control fields fi(t). A necessary and sufficient condition for the system to be evolution operator-controllable is requiring the Lie algebra of its Hamiltonian to be of full rank31,
where N denotes the Hilbert space dimension and Lie {iH0, …, iHf} the maximal real vector space of matrices consisting of the matrices iH0, …, iHf and all of their nested commutators (Lie brackets). We consider here, without loss of generality, traceless Hamiltonians. Otherwise, the dimension in Eq. (13) should be N2 for a system to be controllable. A quantum system is not completely controllable if the field-free system possesses a symmetry which is not broken by the control fields. The existence of a symmetry operator, i.e., an operator that commutes with the total Hamiltonian, is equivalent to the existence of a conserved quantity. As a result, the Hamiltonian can be written in block-diagonal form, without transition matrix elements connecting the blocks such that the system can be controlled only within the symmetry-enforced subsystems.
When accounting only for resonant transitions, the Lie rank condition (13) can be checked efficiently on the reduced Hamiltonians38. More precisely, one considers only frequencies ω ∈ Σ, where Σ = {∣λi − λj∣, i, j = 1, …, N} denotes the set of energy level spacings, and matrices Hω,a defined by
where \(|{\psi }_{1}\rangle ,\ldots ,|{\psi }_{N}\rangle\) and λ1, …, λN are the eigenstates and eigenvalues of \({\hat{H}}_{0}\). Then, if one can find frequencies {ω1, …, ωk} ⊂ Σ such that
the system is evolution operator-controllable38. Equations (13) and (15) are equivalent necessary and sufficient conditions for evolution operator controllability35,38. Equation (15) implies that the Lie algebra generated by H0 and the various \({{{{{{{{\bf{H}}}}}}}}}_{{\omega }_{i},a}\) is all of \({\mathfrak{s}}{\mathfrak{u}}(N)\), i.e., the Lie algebra of traceless N × N skew-Hermitian matrices.
The conditions for controllability, Eqs. (13) and (15), hold for a finite-dimensional system whereas the spectrum of a quantum rotor is, in principle, infinite-dimensional. The remedy consists in introducing the notion of approximate controllability. Two steps are required to extend a proof of controllability from a finite-dimensional system to one of approximate controllability of an infinite-dimensional system. First, for a finite-dimensional subsystem of a system with an infinite number of energy levels, Eq. (15) can be used to check approximate controllability. As an additional condition, all frequencies ω ∈ Σ connecting states within the subsystem that are required for controllability should be off-resonant with all frequencies connecting states inside the subsystem with states outside of it. (The presence of the same transition frequency for two states that are both outside the subspace does not pose any problem to the approximation.) If such a condition fails to hold, the finite-dimensional subsystems may all be controllable, even if the infinite-dimensional system is not approximately controllable49. Approximate controllability then means that each target of the subsystem can be reached by the infinite-dimensional system with arbitrary precision. This is based on the fact that, if a frequency ω ∈ Σ is resonant with a finite number of energy level spacings only, the operators Hω,a do not address transitions in the total rotational state space, but only within a finite-dimensional part of it. Second, treating the truncation of an infinite-dimensional Hilbert space by a finite-dimensional subspace as a Galerkin approximation allows for quantifying the error due to the truncation, making the proof rigorous36. To this end, one introduces the set of energy level spacings Σn = {∣λi − λj∣, i, j = 1, …, n}, and defines the n-th approximation of H0 as the truncation of (the infinite-dimensional) H0 such that all Σn with n = 1, 2, … are contained in the truncated Hamiltonian. The set of energy level spacings that connect the finite-dimensional subspace with its (infinite-dimensional) complement are \({\hat{{{\Sigma }}}}_{n}=\{| {\lambda }_{i}-{\lambda }_{j}| ,\ i=1,\ldots ,n,\ j=n+1,n+2,\ldots\}\). Moreover, one defines \({{{\Xi }}}_{n}=\{\omega \in {{{\Sigma }}}_{n}| \omega \, \ne\, 0,\ \omega \,\notin\, {\hat{{{\Sigma }}}}_{n}\}\) as the set which contains those frequencies in Σn that do not connect the finite-dimensional and infinite-dimensional subspaces. Then if, for any n0, one can find an n > n0 such that
the system is approximately controllable, i.e., it is possible to steer any initial state arbitrarily close to any desired final state38. Equation (16), called Lie–Galerkin condition, is a sufficient condition for approximate controllability of infinite-dimensional systems. Moreover, if the Lie–Galerkin condition holds, the finite-dimensional projections are exactly controllable, that is, one can find a time T such that the finite-dimensional projections of the infinite-dimensional propagator are exactly the finite-dimensional projections of the target propagator44.
Enantio-selective controllability
For a rigid asymmetric top, we can apply the controllability analysis according to Eq. (15) by identifying the matrices \({{{{{{{{\bf{H}}}}}}}}}_{{\omega }_{i},a}\) with the f linearly independent interaction matrices \({{{{{{{{\bf{H}}}}}}}}}_{i}^{(\pm )}\). If such a molecule, evolving according to Eq. (2), is controllable, one can—at least in principle—find electric fields which steer a given initial state, \(|{\psi }^{(+)}(t=0)\rangle\) or ρ(+)(0), to a desired target state, \(|{\psi }_{{{{{{{{\rm{target}}}}}}}}}^{(+)}\rangle\) or \({\rho }_{{{{{{{{\rm{target}}}}}}}}}^{(+)}\) (with same purity). However, controllability of Eq. (2) does not imply that one can, with the same set of control fields, steer \(|{\psi }^{(+)}(0)\rangle\) to \(|{\psi }_{{{{{{{{\rm{final}}}}}}}}}^{(+)}\rangle\) and \(|{\psi }^{(-)}(0)\rangle\) to \(|{\psi }_{{{{{{{{\rm{final}}}}}}}}}^{(-)}\rangle\) simultaneously. To capture such a control target, we introduce the concept of enantio-selective controllability. It corresponds to the problem of simultaneously controlling two evolutions, i.e., the evolution of the two enantiomers, governed by the same molecular Hamiltonian \({\hat{H}}_{0}\) and controlled with the same fields Ei(t).
We call an asymmetric top enantio-selective controllable if both enantiomers are simultaneously controllable with the same set of external fields. To analyze enantio-selective controllability, we construct a composite system, defined on a Hilbert space which is the tensor sum \({{{{{{{\mathcal{H}}}}}}}}\oplus {{{{{{{\mathcal{H}}}}}}}}\) of the (identical) rotational state spaces of the two enantiomers. The corresponding Hamiltonian is block-diagonal,
with H0 and \({{{{{{{{\bf{H}}}}}}}}}_{{{{{{{{\rm{int}}}}}}}}}^{(\pm )}(t)\) being the matrix representations of \({\hat{H}}_{0}\) and \({\hat{H}}_{{{{{{{{\rm{int}}}}}}}}}^{(\pm )}\) in the asymmetric top eigenbasis, Eq. (4). The block-diagonal structure of the Hamiltonian in Eq. (17) is a result of parity conservation in a rigid rotor, i.e. within the rigid rotor approximation enantiomers cannot be converted into each other. A system described by a block-diagonal matrix with two blocks of the size N × N is controllable if its Lie algebra has the dimension 2(N2 − 1). In other words, due to the block structure of Eq. (17), the system is enantio-selective controllable if its Lie algebra is \({\mathfrak{s}}{\mathfrak{u}}(N)\oplus {\mathfrak{s}}{\mathfrak{u}}(N)\). This corresponds to the sufficient condition for simultaneous controllability50,51. The Lie rank condition for enantio-selective controllability is equivalent to generating (by taking enough commutators) any operator of the form A ⊕ 0 and 0 ⊕ B for all \( A,B\in {\mathfrak{s}}{\mathfrak{u}}(N)\). This provides a physical intuition for the enantio-selective controllability condition since A ⊕ 0 changes the state of the first enantiomer while leaving the state of the second enantiomer unchanged (and vice versa for 0 ⊕ B), and having any operator of this form implies the ability to carry out any evolution for the single enantiomers.
Controllability of asymmetric quantum rotors
In this section, we use the concepts for controllability analysis to analyze controllability and enantio-selective controllability of rigid asymmetric top rotors. Generally, controllability of quantum rotors is difficult to prove due to the presence of the M- (and for symmetric tops K-) degeneracies. Controllability of molecular rotation has first been investigated for the linear rotor, and the combination of three orthogonal polarization directions was identified to yield controllability33. A complete rigorous proof has been made possible by the Lie-Galerkin approximation38. The extension from a linear to a symmetric top is non-trivial due to the additional presence of two-fold K-degeneracies, and controllability can only be shown for accidentally symmetric top molecules whereas generic symmetric tops are uncontrollable40,41. While the K-degeneracies of the symmetric top are lifted for the asymmetric top, suggesting better prospects for controllability, the presence of transitions with ΔJ = 0 is an important difference compared to the linear rotor. It is thus not possible to simply transfer the intuition of three orthogonal polarization directions from the linear to the asymmetric top.
In addition to controllability of a single asymmetric top, we are interested here in the enantio-selective controllability. The fact that enantio-selective excitation can be obtained by three control fields with orthogonal polarization directions11,12,22 is a good starting point but does not automatically imply enantio-selective controllability. This is most easily seen by an example: Consider a three-wave mixing process that starts in the manifold of states with J0 = 1, τ0 = −1. Applying the control scheme used in experiment12, the cycles with M0 = ±1 are not closed, leading to population loss. Enantio-selective controllability, on the other hand, would guarantee complete enantiomer-selective population transfer.
Below we will prove controllability and enantio-selective controllability for asymmetric top rotors in finite-dimensional subspaces, as encountered in resonant microwave three-wave mixing, cf. Fig. 1b (i) and (ii). For the complete infinite-dimensional spectrum of an asymmetric top, only approximate controllability can be proven42, whereas accidentally symmetric tops are provably not enantio-selective controllable since their K-degeneracy prevents the simultaneous controllability of the two enantiomers. Our analysis goes beyond a purely mathematical exercise by providing practical information on (enantio-selective) controllability, in terms of the number and properties of the fields required for controllability. We proceed by first introducing generalized Pauli matrices as a useful tool to carry out the calculations. We then apply them to the enantio-selective controllability of specific rotational subsystems.
Generalized Pauli matrices
To analyze controllability of an asymmetric top molecule, described by the truncated H0 and interacting with a set of f electromagnetic fields via the interaction Hamiltonians \({{{{{{{\rm{i}}}}}}}}{{{{{{{{\bf{H}}}}}}}}}_{{\omega }_{i},a}\), we need to construct the corresponding Lie algebra and verify Eq. (15). To this end, it is useful to express \({{{{{{{\rm{i}}}}}}}}{{{{{{{{\bf{H}}}}}}}}}_{{\omega }_{i},a}\) as linear combinations of the generalized Paul matrices40,
where ej,k is the matrix whose entries are all zero except for the entry in row j and column k which is equal to one. Since the operators (18) (with j, k = 1, …, n) span the Lie algebra \({\mathfrak{s}}{\mathfrak{u}}(n)\), we need to show that repeatedly taking commutators between \({{{{{{{\rm{i}}}}}}}}{{{{{{{{\bf{H}}}}}}}}}_{{\omega }_{i},a}\) and iH0 yields elements of the Lie algebra which are proportional to each of the operators Gj,k, Fj,k, and Dj,k alone. For these computations, we will exploit the following properties of the generalized Paul matrices: Their commutator relations read
and
Operators which couple disjunct pairs of states commute,
with T, U ∈ {G, F, D}. Finally, the commutators with the rotational Hamiltonian are given by
where ΔEk,j is the energy level spacing between states j and k.
Complete controllability and enantio-selective controllability of rotational subsystems of the type \({E}_{J,\tau }/{E}_{J+1,\tau ^{\prime} }/{E}_{J+1,\tau ^{\prime\prime} }\)
We consider the rotational subsystem made up of all states with energies EJ,τ, \({E}_{J+1,\tau ^{\prime} }\), and EJ+1,τ″, cf. Fig. 1b (i) and (ii) for two examples with J = 0, respectively J = 1. In order to determine controllability and enantio-selective controllability, we diagonalize \({\hat{H}}_{0}\) for this subsystem and compute the Lie algebra generated by a set of control fields. The proof involves two steps. First, we prove evolution-operator controllability for the rotational subsystem with EJ,τ, \({E}_{J+1,\tau ^{\prime} }\), and EJ+1,τ″ of a single enantiomer. This result by itself is already quite significant. It implies that each level, including the degenerate ones, can be addressed separately with electric fields alone, and it is not necessary to lift the degeneracy, for example with a magnetic field. To carry out this part of the proof, we need to consider at least four control fields with linear polarization directions pi and frequencies \({\omega }_{1}=({E}_{J+1,{\tau }^{\prime}}-{E}_{J,\tau })/\hslash\) and \({\omega }_{2}=({E}_{J+1,{\tau }^{^{\prime\prime} }}-{E}_{J+1,{\tau }^{\prime}})/\hslash\), cf. Fig. 1b (i) and (ii) for examples with J = 0 and J = 1, chosen such as to induce transitions via the dipole moments μb and μa, respectively. The corresponding interaction Hamiltonians \({{{{{{{{\bf{H}}}}}}}}}_{{\omega }_{1},{p}_{1}}\), \({{{{{{{{\bf{H}}}}}}}}}_{{\omega }_{1},{p}_{2}}\), \({{{{{{{{\bf{H}}}}}}}}}_{{\omega }_{2},{p}_{3}}\), and \({{{{{{{{\bf{H}}}}}}}}}_{{\omega }_{2},{p}_{4}}\) are expressed in terms of the generalized Pauli matrices (18). We analyze the resulting Lie algebra by repeatedly taking commutators. Since the dimension of the subsystems is lJ = (2J + 1) + 2(2J + 3), the Lie algebra has to contain \({\mathfrak{s}}{\mathfrak{u}}({l}_{J})\) for the subsystem to be controllable. In a second step, we prove enantio-selective controllability by adding a control field with frequency \({\omega }_{3}={\omega }_{1}+{\omega }_{2}=({E}_{J+1,{\tau }^{^{\prime\prime} }}-{E}_{J,\tau })/\hslash\) and interaction Hamiltonian \({{{{{{{{\bf{H}}}}}}}}}_{{\omega }_{3},{p}_{5}}\). As indicated in Fig. 1b (i) and (ii) for examples with J = 0 and J = 1, such a field couples rotational states via the dipole moment μc. The corresponding Lie algebra has to contain \({\mathfrak{s}}{\mathfrak{u}}({l}_{J})\oplus {\mathfrak{s}}{\mathfrak{u}}({l}_{J})\) for the subsystem to be enantio-selective controllable. In the following, we work out the proof for the simplest example, with J = 0, cf. Fig. 1b (ii), which illustrates the relevant steps. Representing the asymmetric top Hamiltonian on a graph and constructing the Lie algebra inductively52 allows us to generalize the proof to arbitrary J. We find that independent of the choice of J, four (five) different fields are necessary and sufficient to prove evolution-operator (enantio-selective) controllability.
We start by writing the rotational Hamiltonian in the asymmetric top eigenbasis,
and consider a set of four interaction operators,
with polarization directions p1 = x, p2 = z, p3 = y, and p4 = z which is one specific choice but not necessarily the only one possible. We have to show that
since the Hilbert space \({{{{{{{{\mathcal{H}}}}}}}}}^{(\pm )}\) coincides with \({{\mathbb{C}}}^{7}\). Using Eqs. (6), (7), and (9), we can write the interaction operators as linear combinations of the generalized Pauli matrices,
Since the coefficients \({c}_{K}^{J}(\tau)\) in Eq. (9) do not depend on M, the summation over these coefficients only results in a common prefactor, which is not relevant for the proof of controllability. For simplicity of notation, we denote the interaction Hamiltonians without these prefactors (see also ref. 52). The matrix elements are labeled according to Fig. 1b (ii). For example, \({{{{{{{\rm{i}}}}}}}}{{{{{{{{\bf{H}}}}}}}}}_{{\omega}_{1},x}={\mu }_{b}{E}_{{\omega}_{1},x}({{{{{{{{\bf{G}}}}}}}}}_{1,4}-{{{{{{{{\bf{G}}}}}}}}}_{1,2})\) means that the field with x-polarization and frequency ω1 couples the state \(\left|0,0,0\right\rangle\) (labeled 1) to the states \(\left|1,0,1\right\rangle\) and \(\left|1,0,-1\right\rangle\) (labeled 4 and 2). With the commutator relations (19), we find
and
Taking the sum and the difference, we obtain
In this way, we generate operators that separately address the transitions 1 ↔ 5 and 1 ↔ 7, i.e., that act separately on two degenerate M-states. Moreover, we find
So far, we have obtained all elements Gj,k with j = 1. Applying Eq. (19a) to these elements, we get all remaining elements Gj,k, j, k ∈ {1, …, 7}, and using Eqs. (19d) and (19b), we obtain all elements Fj,k and Dj,k, j, k ∈ {1, …, 7}. Since the elements Gj,k, Fj,k, Dj,k span \({\mathfrak{s}}{\mathfrak{u}}(7)\), we have proven that the Lie algebra contains \({\mathfrak{s}}{\mathfrak{u}}(7)\). The subsystem is thus controllable with the set of control fields \({{{{{{{{\mathcal{X}}}}}}}}}_{1}\). In the same way, it can also be shown that the system is not controllable if any of the four fields contained in \({{{{{{{{\mathcal{X}}}}}}}}}_{1}\) is left out. When generalizing this proof to a system consisting of three rotational levels EJ,τ, \({E}_{J+1,\tau ^{\prime} }\), EJ+1,τ″ with arbitrary J, the Hilbert space dimension becomes 6J + 7. Thus, we need to show that
with the set of interaction operators defined in Eq. (20) but replacing ω2 by ω3, in order to address all degenerate rotational states. Making use of an inductive argument, we construct the operator basis of the Lie algebra52, analogously to the argument provided above for J = 0. This allows us to conclude that any rotational subsystem \({E}_{J,\tau }/{E}_{J+1,\tau ^{\prime} }/{E}_{J+1,\tau ^{\prime\prime} }\) is controllable with four control fields.
In the second step, we extend the proof to the composite system of both enantiomers, showing enantio-selective controllability. Without loss of generality, we assume that the dipole moments of the two enantiomers are \(({\mu }_{a}^{(+)},{\mu }_{b}^{(+)},{\mu }_{c}^{(+)})=({\mu }_{a},{\mu }_{b},{\mu }_{c})\) and \(({\mu }_{a}^{(-)},{\mu }_{b}^{(-)},{\mu }_{c}^{(-)})=({\mu }_{a},{\mu }_{b},-{\mu }_{c})\). For the interaction Hamiltonians, it follows that \({{{{{{{{\bf{H}}}}}}}}}_{{\omega }_{1},{p}_{i}}^{(+)}={{{{{{{{\bf{H}}}}}}}}}_{{\omega }_{1},{p}_{i}}^{(-)}\) and \({{{{{{{{\bf{H}}}}}}}}}_{{\omega }_{2},{p}_{i}}^{(+)}={{{{{{{{\bf{H}}}}}}}}}_{{\omega }_{2},{p}_{i}}^{(-)}\) since, according to Eq. (22), these matrices are proportional to μa and μb. Thus the four fields contained in \({{{{{{{{\mathcal{X}}}}}}}}}_{1}\) applied to the composite system result in
as matrices acting on the vector space \({{{{{{{{\mathcal{H}}}}}}}}}^{(+)}\oplus {{{{{{{{\mathcal{H}}}}}}}}}^{(-)}={{\mathbb{C}}}^{7}\oplus {{\mathbb{C}}}^{7}\). For the Lie algebra to contain \({\mathfrak{s}}{\mathfrak{u}}(7)\oplus {\mathfrak{s}}{\mathfrak{u}}(7)\), an additional control field with frequency ω3 is required which leads to the interaction operator
with \({{{{{{{\rm{i}}}}}}}}{{{{{{{{\bf{H}}}}}}}}}_{{\omega }_{3},x}={\mu }_{c}{E}_{{\omega }_{3},x}({F}_{1,5}-{F}_{1,7})\) and the minus sign in the lower block occuring because of \({\mu }_{c}^{(+)}=-{\mu }_{c}^{(-)}\). To prove that the system is enantio-selective controllable with the set of five control fields generating the interaction operators
we need to show that
since
To do so, we consider the matrix
which is an element of the Lie algebra generated from the four fields contained in \({{{{{{{{\mathcal{X}}}}}}}}}_{1}\), see Eq. (23). Moreover,
with
We see that V and \({{{{{{{\bf{J}}}}}}}}({{{{{{{\rm{i}}}}}}}}{{{{{{{{\bf{H}}}}}}}}}_{{\omega }_{3},x}^{{{{{{{{\rm{chiral}}}}}}}}})\) differ by the sign of the matrix elements belonging to the second enantiomer. Taking the sum and difference of the two matrices, we obtain
and
which are two operators belonging to the Lie algebras acting only on the first and the second enantiomer, respectively. Furthermore,
and finally the sum
which is a basis element for the Lie algebra acting on the first enantiomer only. Replacing \({{{{{{{\bf{J}}}}}}}}({{{{{{{\rm{i}}}}}}}}{{{{{{{{\bf{H}}}}}}}}}_{{\omega }_{3},x}^{{{{{{{{\rm{chiral}}}}}}}}})+{{{{{{{\bf{V}}}}}}}}\) with \({{{{{{{\bf{J}}}}}}}}({{{{{{{\rm{i}}}}}}}}{{{{{{{{\bf{H}}}}}}}}}_{{\omega }_{3},x}^{{{{{{{{\rm{chiral}}}}}}}}})-{{{{{{{\bf{V}}}}}}}}\) in (30) and (31), we obtain a matrix proportional to \(\left(\begin{array}{ll}0&0\\ 0&{{{{{{{{\bf{G}}}}}}}}}_{1,5}\end{array}\right),\) which is a basis element for the Lie algebra acting on the second enantiomer only. To complete the proof, it suffices to compute commutators between these elements and the elements of Eq. (27), e.g.,
and
for all k = 1, …, 7. Since from the elements G1,k we obtain all Gj,k, Fj,k, and Dj,k using the relations (19a), (19c), and (19d), the Lie algebra generated by the five fields contained in \({{{{{{{\mathcal{X}}}}}}}}\) contains \({\mathfrak{s}}{\mathfrak{u}}(7)\oplus {\mathfrak{s}}{\mathfrak{u}}(7)\) which proves enantio-selective controllability. A generalization to rotational subsystems \({E}_{J,\tau }/{E}_{J+1,\tau ^{\prime} }/{E}_{J+1,\tau ^{\prime\prime} }\) with arbitrary J is given in Supplementary Notes I.
Summarizing, we have demonstrated for the subsystem comprising all rotational states with energies EJ,τ, \({E}_{J+1,\tau ^{\prime} }\), EJ+1,τ″ that a single enantiomer is controllable with four fields with frequencies \({\omega }_{1}=({E}_{J+1,{\tau }^{\prime}}-{E}_{J,\tau })/\hslash\) and \({\omega }_{2}=({E}_{J+1,{\tau }^{^{\prime\prime} }}-{E}_{J+1,{\tau }^{\prime}})/\hslash\), while for enantio-selective control five fields with frequencies ω1, ω2, and \({\omega }_{3}={\omega }_{1}+{\omega }_{2}=({E}_{J+1,{\tau }^{^{\prime\prime} }}-{E}_{J,\tau })/\hslash\) are necessary and sufficient. Here, we chose the polarizations to be p1 = x, p2 = z, p3 = y, p4 = z, and p5 = x. Other choices of the polarization directions also result in controllability and enantio-selective controllability as long as the pairs p1, p2, and p3, p4 are not the same and all three polarization directions x, y, z are present. In the section “Application: Derivation of practical pulse sequences for carvone molecules", we show how to exploit these minimal sets of fields for the example of the propanediol molecule.
Controllability and enantio-selective excitation
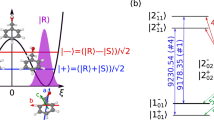
Evolution-operator enantio-selective controllability as shown in the previous subsection is a sufficient, but not a necessary condition for realizing complete separation of two enantiomers in a racemic mixture. In the following, we construct an example where complete separation of the enantiomers can be achieved within a subset of states. The idea is sketched in Fig. 2 for an example with J = 1, cf. Fig. 1b(i), and relies on the assumption that only the states with the lowest energy are populated initially. For the example of Fig. 2,
where \(\left|J=1,\tau =-1,M\right\rangle\) are asymmetric top eigenstates. Then enantio-selective excitation of the initial state (32) can be obtained by considering only the set of reachable states, i.e., the set of rotational states to which population can be transferred by the control fields. These are the states labeled by 1–3, 6–8, and 10–12 in Fig. 2. The complete rotational subsystem shown in Fig. 2 is obviously not controllable by the indicated choice of fields, since two of the rotational states are not addressed at all.
The subsystem consists of the states \(\left|J=1,\tau =-1,M\right\rangle\), \(\left|J=2,\tau =-1,M\right\rangle\) and \(\left|J=2,\tau =0,M\right\rangle\), where J, τ, and M are the quantum numbers of the asymmetric top. The orange, (pink, and turquoise) lines indicate the transitions which are induced by fields with polarization σ+ (σ−, z) and frequencies ω1 (ω2, ω3), respectively. The transition in transparent magenta is not part of any of the three-wave mixing cycles. The small numbers indicate the states of the subsystem.
In order to construct three-wave mixing cycles as those shown in Fig. 2, we need to employ circular polarization directions, σ± = x ± iy. Assuming that the polarization directions of the fields with frequencies \({\omega }_{1}=({E}_{J+1,{\tau }^{\prime}}-{E}_{J,\tau })/\hslash\) and \({\omega }_{2}=({E}_{J+1,{\tau }^{^{\prime\prime} }}-{E}_{J+1,{\tau }^{\prime}})/\hslash\) are σ+ and σ−, the resulting (anti-Hermitian) interaction Hamiltonians are
and
with
The set of interaction operators then becomes
where again ω3 = (EJ+1,τ″ − EJ,τ)/ℏ. It can be thought of as derived from the following interaction Hamiltonians with linear polarization directions,
which are not sufficient for controllability since (p1 = x, p2 = y) = (p3 = x, p4 = y).
In the example of Fig. 2, the set of reachable states is divided into three isolated subsystems, each consisting of three states. As a whole, the subsystem consisting of these nine states is not controllable either. However, a sufficient condition for complete enantio-selective excitation of population in the lowest level is that the three isolated subsystems are simultaneously enantio-selective controllable. This requires the Lie algebra to contain
since each of the three-level systems is controllable if its Lie algebra contains \({\mathfrak{s}}{\mathfrak{u}}(3)\) and enantio-selective controllable if its Lie algebra contains \({\mathfrak{s}}{\mathfrak{u}}(3)\oplus {\mathfrak{s}}{\mathfrak{u}}(3)\).
In order to determine the Lie algebra for a single enantiomer, we first consider the interaction Hamiltonians
and show that, together with iH0, they generate \({\mathfrak{s}}{\mathfrak{u}}(3)\oplus {\mathfrak{s}}{\mathfrak{u}}(3)\oplus {\mathfrak{s}}{\mathfrak{u}}(3)\). Using Eq. (19d), we find
with \({{{{{{{\bf{J}}}}}}}}({{{{{{{\rm{i}}}}}}}}{{{{{{{{\bf{H}}}}}}}}}_{{\omega }_{1},{\sigma }_{+}})\) defined in Eq. (33). Moreover, abbreviating commutators as \({{{{{{{{\rm{ad}}}}}}}}}_{A}^{n+1}B=[A,{{{{{{{{\rm{ad}}}}}}}}}_{A}^{n}B]\) with \({{{{{{{{\rm{ad}}}}}}}}}_{A}^{0}B=B\), we note that
with s = 0, 1, 2, … Thus,
with
The matrix V is invertible since the entries \(1,\sqrt{3},\sqrt{6}\) are all different which implies that \({{{{{{{{\bf{G}}}}}}}}}_{1,6},{{{{{{{{\bf{G}}}}}}}}}_{2,7},{{{{{{{{\bf{G}}}}}}}}}_{3,8}\in {{{{{{{\rm{Lie}}}}}}}}\{{{{{{{{\rm{i}}}}}}}}{{{{{{{{\bf{H}}}}}}}}}_{0},{{{{{{{\rm{i}}}}}}}}{{{{{{{{\bf{H}}}}}}}}}_{{\omega }_{1},{\sigma }_{+}}\}.\) From the commutation rules of the generalized Pauli matrices (19), it follows that also
We then calculate the commutators
and, using again the commutation relations of the generalized Pauli matrices and the rotational Hamiltonian, we find
Since
we have proven that the three isolated three-level systems are simultaneously controllable with the interaction operators \({{{{{{{\rm{i}}}}}}}}{{{{{{{{\bf{H}}}}}}}}}_{{\omega }_{1},{\sigma }_{+}}\) and \({{{{{{{\rm{i}}}}}}}}{{{{{{{{\bf{H}}}}}}}}}_{{\omega }_{2},{\sigma }_{-}}\).
To obtain enantio-selective control of each of these three cycles, we consider the interaction with the third field, namely
or, for the composite system consisting of the two enantiomers,
The interaction operators
for (ωi, a) = (ω1, σ+) and (ω2, σ−) together with \({{{{{{{\rm{i}}}}}}}}{{{{{{{{\bf{H}}}}}}}}}_{0}^{{{{{{{{\rm{chiral}}}}}}}}}\) create, among others, the operators G1,6 ⊕ G1,6 and G1,10 ⊕ G1,10. We compute the double bracket
and taking the sum and difference with G1,10 ⊕ G1,10, the operators G1,10 ⊕ 0 and 0 ⊕ G1,10 are generated. In the same manner, all operators
can be generated. Since the operators Xi,j span the Lie algebra \({\mathfrak{s}}{\mathfrak{u}}(3)\oplus {\mathfrak{s}}{\mathfrak{u}}(3)\oplus {\mathfrak{s}}{\mathfrak{u}}(3)\), the operators (38) span \({\mathfrak{s}}{\mathfrak{u}}(3)\oplus {\mathfrak{s}}{\mathfrak{u}}(3)\oplus {\mathfrak{s}}{\mathfrak{u}}(3)\oplus {\mathfrak{s}}{\mathfrak{u}}(3)\oplus {\mathfrak{s}}{\mathfrak{u}}(3)\oplus {\mathfrak{s}}{\mathfrak{u}}(3)\), and thus the three three-level systems are simultaneously enantio-selective controllable.
As a result, for the initial state (32), complete enantio-selective excitation can be obtained by two circularly polarized and one linearly polarized fields. This result can be generalized to any \({E}_{J,\tau }/{E}_{J+1,\tau ^{\prime} }/{E}_{J+1,\tau ^{\prime\prime} }\) subsystem, where the three fields create 2J + 1 “parallel” three-level cycles, and the interaction Hamiltonian (35) is a linear combination of 2J + 1 generalized Pauli matrices with different prefactors. The matrix V, generalizing Eq. (37), has 2J + 1 different entries in the first row and is invertible52. Simultaneous controllability of 2J + 1 three-level cycles using two circularly polarized fields and the corresponding enantio-selective controllability with an additional linearly polarized field can thus be proven for any J. As we shall see for the example of carvone in the following section, those isolated three-level systems are particularly suited for enantio-selective excitation in real molecules.
Application: derivation of practical pulse sequences for propanediol and carvone molecules
We now show how to use the controllability results of the previous section to derive actual pulse sequences in order to control the rotational dynamics in propanediol and carvone molecules. In all examples presented below, the control target is to energetically separate an initially incoherent mixture of degenerate rotational states, as encountered in gas phase experiments with randomly oriented molecules. We simulate the rotational dynamics for the R- and S-enantiomers of propanediol and carvone. Details of the numerical calculations are provided in Supplementary Notes 2. The molecular parameters for propanediol and carvone are listed in Table 1. Table 1 also shows the frequencies of the microwave fields interacting with the molecules. At these frequencies, spatial inhomogenities do not noticeably influence the microwave three-wave mixing experiments (this is expected to become relevant only at frequencies above ~15 GHz, depending on the experimental conditions), which justifies our assumption of spatially uniform fields.
Our choice of example is motivated by experiments demonstrating for carvone an enantiomeric enrichment of 6% with enantiomer-selective population transfer12. Enantiomeric enrichment is mainly limited by the thermal population of rotational levels. This can be overcome by depleting the population in the excited rotational levels53 or by addressing excited rotational levels in a vibrationally excited state with effectively zero thermal population16,17. The latter requires a combination of microwave and infrared pulses, and the three-wave mixing can well be achieved within the coherence time of the excited vibrational state16. A second limiting factor is a degeneracy with respect to the orientational quantum number M, which is relevant whenever the initial state is chosen with J > 0. This is the problem we address here. The control strategies presented below are applicable to both purely microwave three-wave mixing11,12 as well as three-wave mixing combining microwave and infrared excitation16,17. In other words, our pulse sequences will induce the maximal degree of orientational, respectively enantiomer-selectivity, that is compatible with the purity of the initial ensemble, and temperature can simply be factored in.
We present two different strategies to energetically separate population initially distributed over M-degenerate states. First, we exploit evolution operator-controllability of the complete rotational subsystem, in particular the insight into which fields are required, for orientational, respectively enantiomer-specific, state transfer. Second, we use the simultaneous controllability of “parallel” three-level cycles for enantiomer-specific state transfer. The working principle of both strategies is to combine enantio-selectivity (due to the sign difference in one of the dipole moments) with an energetic separation of population residing initially in degenerate states. We first demonstrate controllability of a single enantiomer by showing that initially degenerate rotational states can be separated in energy. Note that in this case, the rotational dynamics of the two enantiomers is identical. We then demonstrate enantio-selective controllability, where we show that we can energetically separate the two enantiomers.
In the subsections “Orientation-selective excitation exploiting complete controllability” and “Enantiomer-selective control exploiting complete controllability”, the pulses drive transitions within the E0,0/E1,0/E1,1 rotational submanifold, cf. Fig. 3. Even in this comparatively small manifold, the pulse sequence for enantiomer-selective population transfer consists of 12 pulses sampled from five different fields, i.e., five different combinations of polarization directions and frequencies. In order to obtain a simpler sequence, we forego full evolution operator-controllability in subsection “Complete enantiomer-selective population transfer using synchronized three-wave mixing” and use a sequence of three pulses which partitions the rotational submanifold into isolated subsystems and drives simultaneously several three-wave mixing cycles. For this strategy to succeed, the initial rotational submanifold needs to have the smallest degeneracy factor gJ = 2J + 1. We, therefore, consider transitions within the E1,−1, E2,−1, E2,0 rotational submanifold.
Choice of four, respectively five, microwave fields, which are sufficient to ensure evolution operator-controllability (a) and enantio-selective evolution operator-controllability (b) in the rotational subsystem consisting of the asymmetric top states \(\left|J=0,\tau =0,M=0\right\rangle\), \(\left|J=1,\tau =0,M\right\rangle\). and \(\left|J=1,\tau =1,M\right\rangle\), with quantum numbers J, τ, and M. The orange and pink lines in a indicate the four fields which yield complete controllability of this subsystem for a single enantiomer. The polarization of the fields is denoted by x, y, and z, and μa, μb, and μc are the Cartesian components of the dipole moment responsible for the transitions indicated by the vertical bars. The additional field which is required for enantio-selective control is indicated in b by turquoise lines. The frequencies ω1, ω2, and ω3 of propanediol are given in Table 1.
Orientation-selective excitation exploiting complete controllability
The simplest rotational subsystem that allows for enantiomer-selective population transfer using three-wave mixing spectroscopy consists of the rotational states \(\left|J,\tau ,M\right\rangle =\left|0,0,0\right\rangle\), \(\left|1,0,M\right\rangle\), and \(\left|1,1,M\right\rangle\) with M = − 1, 0, 1, and rotational energies EJ,τ = E00, E10, and E11, cf. Fig. 3. Note that, from here on, all states we refer to are asymmetric (and not symmetric) top eigenstates. A single enantiomer is completely controllable with four (microwave) fields, for example two fields with frequency ω1 = (E10 − E00)/ℏ and x-, respectively z-polarization and two fields with frequency ω2 = (E11 − E10)/ℏ and y-, respectively z-polarization. The transitions induced by these fields are indicated by orange and pink lines in Fig. 3a; they form closed loops connecting the four states \(\left|0,0,0\right\rangle\), \(\left|1,0,\pm \!1\right\rangle\), \(\left|1,1,\pm \!1\right\rangle\), and \(\left|1,0,0\right\rangle\). Complete controllability implies that population in any initial state within the rotational manifold can be driven into any other initial state within that manifold. This means in particular that population in degenerate states, for example \(\left|1,0,\pm \!1\right\rangle\), can be driven into states with different energy. Such an energetic separation can serve as precursor for complete enantio-selective excitation, as we show below. It also has further applications and could, for example, be used towards purifying an incoherent ensemble with electric fields only or distilling a specific molecular orientation.
We, therefore, consider the following control problem for a single enantiomer: Given that the initial state is an incoherent ensemble of the two degenerate \(\left|1,0,M\right\rangle\) states,
find a pulse sequence that drives the population with M = + 1 into a final state with different rotational energy than the M = − 1 component. As an example, we have chosen \(\left|0,0,0\right\rangle\) and \(1/\sqrt{2}(\left|1,1,-1\right\rangle +\left|1,1,1\right\rangle )\) as target states. The initial and desired final states are sketched as gray dots in the bottom panels of Fig. 4, the upper panel of which shows the pulse sequence that drives the corresponding rotational dynamics. In detail, starting from the initial states \(\left|1,0,-1\right\rangle\) (see Fig. 4a and b) and \(\left|1,0,1\right\rangle\) (see Fig. 4c and d), the state \(\left|1,0,0\right\rangle\) (purple line in the middle panel) can be reached by two different excitation pathways: via the states \(\left|1,1,\pm \!1\right\rangle\) and via \(\left|0,0,0\right\rangle\). The 1st, 2nd, and 4th pulse transfer 50% of the population to state \(\left|1,0,0\right\rangle\) via the first pathway, while pulses 1 and 3 transfer the other half of the initial population along the second pathway. Interference between the two pathways in \(\left|1,0,0\right\rangle\) is constructive for the initial state \(\left|1,0,-1\right\rangle\) and destructive for the initial state \(\left|1,0,1\right\rangle\) (see purple lines in the middle panel of Figs. 4a, c near t = 350 t0). Therefore, the initial state \(\left|1,0,-1\right\rangle\) is transferred to \(\left|1,0,0\right\rangle\) while the initial state \(\left|1,0,1\right\rangle\) is transferred to \(1/\sqrt{2}(\left|1,1,-1\right\rangle +\left|1,1,1\right\rangle )\) at the end of pulse 4. Finally, the 5th pulse transfers the population from \(\left|1,0,0\right\rangle\) to the desired final state \(\left|0,0,0\right\rangle\) in Fig. 4a while not affecting the population in \(\left|1,1,\pm \!1\right\rangle\), cf. Fig. 4c. The two initially degenerate states thus become energetically separated using four fields, with two different frequencies and two polarization components.
a and b These depict the population dynamics for the initial state \(\left|J=1,\tau =0,M=-1\right\rangle\) and c and d display the dynamics for the initial state \(\left|J=1,\tau =0,M=1\right\rangle\), where J, τ, and M are the quantum numbers of the asymmetric top. a and c show the population in the rotational levels J, τ = 1, 1, J, τ = 1, 0 and J, τ = 0, 0. The population dynamics of the degenerate states are depicted by green (M = −1), purple (M = 0), and orange (M = 1) lines. The envelope of the pulses is indicated by the orange (frequency ω = ω1) and pink (ω = ω2) shapes, and x, y, and z denote the polarization of the corresponding fields. Time is given in units of t0 = ℏ/B. The initial (t = 0) and final (t = T) states are sketched in b and d. The gray dots indicate the initially populated states \(\left|J=1,\tau =0,M=-1\right\rangle\) (b) and \(\left|J=1,\tau =0,M=1\right\rangle\) (d), as well as the states populated at t = T, \(\left|J=0,\tau =0,M=0\right\rangle\) (b) and \(\left|J=1,\tau =1,M=\pm \!1\right\rangle\) (d). The vertical bars show the frequencies ω1 and ω2.
Enantiomer-selective control exploiting complete controllability
For enantiomer-selective control, an additional field with frequency ω3 = ω1 + ω2 is required to allow for three-wave mixing. In our example, we choose x-polarization for ω3 such that we have three mutually orthogonal fields with \({{{{{{{{\bf{H}}}}}}}}}_{{\omega }_{1},z}\) (central orange line in Fig. 3b), \({{{{{{{{\bf{H}}}}}}}}}_{{\omega }_{2},y}\) (pink lines), and \({{{{{{{{\bf{H}}}}}}}}}_{{\omega }_{3},x}\) (turquoise lines). If the initial state is the ground rotational state, three-wave mixing results in complete separation of the enantiomers into energetically separated levels16. This requires, however, preparation of the molecules close to zero temperature. For typical experimental conditions, the initial state has to be chosen with J > 011,12 and thus contains degenerate rotational states. Then, three fields are not sufficient to obtain complete enantio-selectivity. Therefore, we consider the initial ensemble (11) with
The initial states \(\left|1,0,-1\right\rangle\) and \(\left|1,0,1\right\rangle\) are depicted in Fig. 5 c and f with the gray circles indicating that both enantiomers occupy the same states. The control aim is to drive the two enantiomers into rotational states with different energies, cf. the red and blue shades in Fig. 5c, f.
a–c They depict the population dynamics for the initial states \(\left|J=1,\tau =0,M=-1\right\rangle\) and d–f, display the dynamics for the initial state \(\left|J=1,\tau =0,M=1\right\rangle\), where J, τ, and M are the quantum numbers of the asymmetric top. a and d These show the population in the rotational levels J, τ = 1, 1, J, τ = 1, 0 and J, τ = 0, 0, averaged over the degenerate M-states for a pulse sequence with five different fields which ensure complete enantiomer-selective control. For comparison, b and e display the incomplete enantiomer-selective state transfer in standard three-wave mixing cycles. The two enantiomers are denoted by solid blue and dashed red lines. The pulse envelopes are indicated by orange (ω = ω1), pink (ω = ω2), and turquoise (ω = ω3) shapes. The height of these shapes indicates the maximal electric field strength (in arbitrary units) and the polarization is denoted by x, y, and z. Time is given in units of t0 = ℏ/B, where B is a rotational constant. The details of the pulse shapes are given in Supplementary Information 2. c and f illustrate the initial (t = 0) and final (t = T) populations. The gray circles mark the states which are initially populated by both enantiomers. The blue (red) shapes indicate which states are finally populated by enantiomer 1 (enantiomer 2). The vertical bars show the frequencies ω1 (orange), ω2 (pink), and ω3 (turquoise).
The combination of fields \({{{{{{{{\bf{H}}}}}}}}}_{{\omega }_{1},z}\), \({{{{{{{{\bf{H}}}}}}}}}_{{\omega }_{2},y}\), and \({{{{{{{{\bf{H}}}}}}}}}_{{\omega }_{3},x}\), indicated in Fig. 3b, which works if the initial state is \(\left|0,0,0\right\rangle\), obviously fails for Eq. (11) since it does not create three-wave mixing cycles for the \(\left|1,0,M\right\rangle\) states. This can be remedied by choosing instead a sequence containing the fields \({{{{{{{{\bf{H}}}}}}}}}_{{\omega }_{1},x}\), \({{{{{{{{\bf{H}}}}}}}}}_{{\omega }_{2},z}\), and \({{{{{{{{\bf{H}}}}}}}}}_{{\omega }_{3},y}\). However, due to insufficient controllability with three fields in the presence of M-degeneracy, the population transfer is only partially enantiomer-selective, cf. the corresponding rotational dynamics in Fig. 5b, e, where the solid blue and dashed red lines present the two enantiomers. For complete enantio-selective excitation, all five fields depicted in Fig. 3b are required, as illustrated by Fig. 5a, d.
The pulse sequence, which leads to complete separation of the enantiomers into energetically separated levels, consists of 12 pulses: The first four pulses are the same as the pulse sequence shown in Fig. 4. Transferring the initial states \(\left|1,0,-1\right\rangle\) and \(\left|1,0,1\right\rangle\) into \(\left|1,0,0\right\rangle\), respectively \(1/\sqrt{2}(\left|1,1,-1\right\rangle +\left|1,1,1\right\rangle )\), they lead to an energetic separation of the two initially degenerate M states, but are not yet enantiomer-selective. Two more pulse sequences realize enantiomer-selective three-wave mixing cycles for the two initial states separately. First, enantiomer-selective transfer for the initial state \(\left|1,0,-1\right\rangle\) is obtained by three-wave mixing with the fields \({{{{{{{{\bf{H}}}}}}}}}_{{\omega }_{1},z}\), \({{{{{{{{\bf{H}}}}}}}}}_{{\omega }_{3},x}\), and \({{{{{{{{\bf{H}}}}}}}}}_{{\omega }_{2},y}\) (pulses 5, 6, and 7). Analogously, pulses 9, 10, and 11 form a three-wave mixing cycle for the initial state \(\left|1,0,1\right\rangle\). After pulse 11 the enantiomers of both initial states are separated in energy. The two cycles for the different M-states are synchronized by applying pulse 12 (at the same time as pulse 11), such that all population of one enantiomer is collected in the highest rotational state (blue lines) while all population of the other enantiomer is excited to the intermediate level (dashed red lines). Figure 5a, d thus confirms complete enantio-selective state transfer in a racemic mixture of initially degenerate M-states for a set of microwave fields for which enantio-selective controllability is predicted.
The analysis of enantio-selective controllability yields the minimal number of different fields, which are required for enantiomer-selective population transfer, but does not make any predictions about the temporal shape of the fields. In particular, it does not predict the number of individual pulses. The control sequence shown in Fig. 5a, d contains 12 individual pulses applied either sequentially or overlapping. Here, complete enantio-selectivity is obtained by constructing an individual three-wave mixing cycle for every initial state. This implies that population initially in the degenerate M-states first has to be separated in energy so that they can be addressed individually. If the degeneracies become larger (for higher J), the pulse sequences become more complicated, because more degenerate states have to be separated in energy and three-wave mixing cycles for each of these states have to be constructed. Such pulse sequences may experimentally not be feasible or at least technically very challenging to implement. This is true in particular for rotational subsystems with higher rotational quantum numbers as in earlier microwave three-wave mixing experiments 12, where cycles with J = 1/2/2 or J = 2/3/3 have been addressed because of their better frequency match and higher Boltzmann factors. For these cases, circularly polarized fields resulting in simpler pulse sequences may be better suited. This will be discussed next.
Complete enantiomer-selective population transfer using synchronized three-wave mixing
Another route to enantiomer-selective state transfer is provided by partitioning the relevant rotational manifold into subsystems that form individual three-wave mixing cycles and uncontrollable “satellites” Provided that the initial state contains population only within the various three-level cycles, the lack of complete controllability does not preclude enantiomer-selective population transfer. In other words, one needs to consider manifolds \(\left|J,\tau ,M\right\rangle\), \(\left|J+1,\tau ^{\prime} ,M\right\rangle\), \(\left|J+1,\tau ^{\prime\prime} ,M\right\rangle\) and choose the transitions realizing the three-wave mixing such that the initial state resides in the manifold with lower J. An advantage of this approach is that three different fields, if properly chosen, are sufficient.
As an experimentally relevant example, we consider the rotational subsystem made up of \(\left|1,-1,M\right\rangle\), \(\left|2,-1,M\right\rangle\), and \(\left|2,0,M\right\rangle\) and construct a pulse sequence that achieves complete enantiomer-selective population transfer despite M-degeneracy. We assume that, initially, only the lowest rotational levels, those with J = 1, are populated. This initial condition can be realized if all or at least the two excited rotational states are in a higher vibrational state such that the thermal population of the higher rotational levels is negligible16. The racemic mixture is then described by Eq. (11) with
Applying a standard three-wave mixing pulse sequence with linearly polarized fields with orthogonal polarization directions results at most in about 80% enantio-selectivity (data not shown). In contrast, circularly polarized fields allow for a complete separation of the enantiomers. This can be seen in Fig. 6.
a, b, and c Depict the rotational dynamics for the initial states J, τ = 1, − 1 with M = − 1, M = 0, and M = 1, respectively, where J, τ, and M are the asymmetric top quantum numbers, showing the population in the levels J, τ = 2, 0, J, τ = 2, − 1 and J, τ = 1, − 1. The two enantiomers are denoted by solid blue and dashed red lines. The envelope of the pulses is indicated by the orange (ω = ω1), pink (ω = ω2), and turquoise (ω = ω3) shapes. The height of these shapes indicates the maximal electric field strength (in arbitrary units) and the polarization is denoted by σ+, σ− and z. Time is given in units of t0 = ℏ/B, where B is a rotational constant. The initial (t = 0) and final (t = T) states are sketched in d, e, and f. The gray circles indicate which states are initially populated by both enantiomers, the blue (red) circles show which states are finally populated by enantiomer 1 (enantiomer 2). The transitions induced by the three fields are indicated by the orange, pink, and turquoise lines with the transition affecting the respective initial state highlighted. The frequencies ω1, ω2, and ω3 for carvone are listed in Table 1.
The three subsystems, which are isolated by applying left- and right-circularly polarized light are indicated in the bottom panels of Fig. 6: The field with σ+-polarization (orange line) induces transitions between \(\left|1,-1,M\right\rangle\) and \(\left|2,-1,M\,+\,1\right\rangle\), while the σ−-polarized field (pink line) drives transitions between \(\left|2,-1,M\right\rangle\) and \(\left|2,0,M\,-1\right\rangle\), and the linearly z-polarized field (turquoise line) closes the cycles. For all the initially populated, degenerate M-states, the population is thus trapped into a three-level subsystem and cannot spread over the whole manifold, as it would happen when using three linearly polarized fields with orthogonal polarization directions.
The corresponding rotational dynamics is depicted in Fig. 6a–c. The pulse sequence that leads to complete enantio-selective excitation is essentially a three-wave mixing cycle: The first pulse creates a 50/50 coherence between the ground and first excited rotational level of each three-level system. The second pulse transfers the population from the intermediate state to the highest state and the third, z-polarized pulse induces the enantiomer-specific interference between the ground state and highest excited state. There is, however, an important difference to the standard three-wave mixing cycles used so far—the pulses are chosen such that they synchronize the three subsystems, allowing to reach a 50/50 coherence between the ground and first excited state for each of the subsystems. As can be seen in Fig. 6, the Rabi frequencies of each subsystem are different, due to the different Clebsch-Gordon coefficients, respectively the different elements of the Wigner D-matrix, in Eq. (9). A 50/50 coherence for all three subsystems occurs after three Rabi oscillations for the subsystem depicted in a, five oscillations for b, and seven oscillations forc. The synchronized three-level cycles then lead to complete separation of the enantiomers into energetically separated levels, by applying a sequence of only three pulses, cf. Fig. 6. When choosing the pulse amplitude and duration, it is important to realize that the subsystems undergo either all an even or all an odd number of Rabi oscillations, so that they accumulate the same phase. Otherwise, the interference effects induced by the third pulse will cancel each other.
In the present example, synchronized three-wave mixing with circularly polarized pulses improves the enantio-selectivity from 80% for standard three-wave mixing with linearly polarized pulses to almost 100%, assuming no thermal population in the two upper levels. Without this assumption, synchronized three-wave mixing enhances the 6% enrichment to ~8% for conditions as reported in12. It is a small but clearly measurable enhancement, which corresponds to the maximal enrichment that any unitary evolution can achieve for the given thermal occupation. Independent of temperature, for subsystems with higher J and thus larger degeneracy, enantiomeric enrichment with the standard three-wave mixing decreases24 and the improvement due to our scheme becomes even more significant. Indeed, our excitation scheme can be easily extended to rotational manifolds with larger J, since the manifolds can always be broken up into isolated subsystems where three pulses are sufficient to energetically separate the enantiomers. The number of pulses is thus independent of the number of degenerate states in the initial ensemble. The pulse duration of the first pulse may have to be longer (or its amplitude larger), since, for larger J, this pulse needs to synchronize Rabi oscillations of more three-level cycles. However, this does not pose a fundamental difficulty. In more detail, the main difference when comparing to existing microwave three-wave-mixing experiments12 is the use of circular instead of linearly polarized pulses. Moreover, due to the synchronization of the Rabi-cycles, the first pulse in our excitation scheme is, for the same field intensity, about 14 times longer than an average π/2-pulse in standard microwave three-wave mixing, and the complete cycle is approximately two times longer than the cycles applied in previous experiments. Since the pulse durations are determined by the respective Rabi-frequencies, one can alternatively increase the field strength of the pulses by a factor of two to obtain the same duration as in the previous microwave three-wave mixing experiments. Synchronized three-wave mixing cycles driven with two circularly polarized and one linearly polarized field, when combined with a strategy to eliminate thermal population in the two excited levels16,17, will thus enable complete enantiomer-selective population transfer in three-wave mixing experiments.
General design principles
Figures 4, 5, and 6 show three pulse sequences achieving M-sensitive, respectively enantiomer-selective, population transfer. Each of these sequences represents only one among many possible solutions to the respective control problem. One could, for example, replace our combination of π- and π/2-pulses by a sequence inducing adiabatic passage19,20,21 or by one derived from shortcuts to adiabaticity23. When adapting a given pulse sequence designed to start from the non-degenerate J = 0-level to addressing a degenerate one (J > 0), the following design principles will ensure selectivity despite M-degeneracy.
First, one needs to select the appropriate combination of frequencies and polarizations, i.e., four different fields including all three linear polarization directions and two resonant frequencies for evolution operator-controllability in a EJ,τ/EJ+1,τ/EJ+1,τ manifold; five different fields including all three linear polarization directions and three resonant frequencies for enantio-selective evolution operator-controllability in a EJ,τ/EJ+1,τ/EJ+1,τ manifold; and three different fields with three resonant frequencies, two with opposite circular polarization directions and one linearly polarized one, for enantio-selective control in “parallel” three-level cycles. The specific choice of the fields determines the states that will be addressed.
The pulse sequence then needs to be chosen such that it creates closed cycles for population transfer and constructive, respectively destructive, interference. The case most similar to three-wave mixing starting from J = 0 is enantiomer-selective population transfer in “parallel” three-level cycles, where the replacement of linear by circular polarization for two of the fields breaks the symmetry between transitions with M ↔ M + 1 and those with M ↔ M − 1. All that is required in addition is synchronization of the cycles due to the M-dependent transition matrix elements. The interference for enantio-selectivity is achieved as before16,19,20,22. In case of rotational state transfer with M-selectivity, Fig. 4, four states (in three levels) are involved since four fields are required for evolution-operator controllability. The sequence is chosen such that it creates constructive and destructive interference for states with opposite M. In order to generalize our example in Fig. 4, with initial population in the states M = ±1, to higher degeneracies, one would need to combine ± M-selectivity with synchronization, to account for the ∣M∣-dependent transition matrix elements. Finally, pulse sequences, based on evolution-operator controllability, driving enantiomer-selective population transfer in a mixture of degenerate rotational states concatenate M-selective four-state cycles with enantio-discriminating three-level cycles, as in Fig. 5.
Conclusions
We have used Lie-algebraic techniques of controllability analysis to determine the number and type (in terms of frequency and polarization direction) of electric fields that allow to completely control the rotational dynamics of an asymmetric top molecule, despite the degeneracy with respect to the orientational quantum number M. Specifically, four different combinations of frequency and polarization direction are required for the rotational subsystem made up of the levels with energy EJ,τ, \({E}_{J+1,{\tau }^{\prime}}\), and \({E}_{J+1,{\tau }^{^{\prime\prime} }}\). This result implies that it is not necessary to lift the degeneracy, e.g., with a magnetic field, in order to selectively address each rotational level. Rather, selectivity can be achieved by exploiting differences of the electric dipole transition matrix elements, similarly to the case of linear rotors33,38. To the best of our knowledge, this insight has not yet been appreciated by the wider atomic and molecular physics community.
To demonstrate how this type of controllability can be utilized, we have constructed a pulse sequence that energetically separates population incoherently distributed over degenerate levels, as a precursor for distilling a specific molecular orientation. The insight gained from the rather abstract mathematical analysis of controllability can thus directly be used to extract practical information for a subset of rotational states that are addressed in a particular experiment. Exploiting complete controllability of rotational states despite the M-degeneracy may also be helpful for laser cooling of asymmetric molecules26,27 or their use in robust qubit encodings28.
We have then introduced the concept of enantiomer-selective controllability, in order to analyze simultaneous controllability of the two enantiomers of a chiral molecule, driven by the same set of external fields. This analysis was motivated by microwave three-wave mixing spectroscopy aiming to energetically separate enantiomers in a racemic mixture, with current protocols suffering from population loss due to partially incomplete three-level cycles11,12,13. We have proven that complete enantio-selective controllability can be achieved with five different, suitably chosen combinations of frequency and polarization direction. This result implies the existence of microwave three-wave mixing protocols that allow for complete enantiomer-selective population transfer despite the M-degeneracy. It is relevant also for all other enantiomer-specific processes, which rely on rotational dynamics, such as the non-resonant excitation of rotational wave packets by interaction with induced dipole moments54,55,56,57.
For the example of microwave three-wave mixing, knowledge of the necessary light-matter couplings has allowed us to design a pulse sequence, which drives enantiomer-specific population transfer. Our numerical simulations of the rotational dynamics for the examples of propanediol and carvone confirm nearly 100% enantio-selectivity, provided the two upper rotational levels do not contain any thermal population16,25. The sequence consists of 12 pulses, sampled from five fields driving the same type of transitions as those used in the earlier microwave experiments11,12,13. Admittedly, the pulse sequence is rather complicated, even for the smallest rotational subsystem. Therefore, we have identified, based on the controllability analysis of subsets of states, an alternative control strategy that relies on isolating “parallel” three-level cycles for each degenerate state in a single manifold. We have shown that simultaneous control of the “parallel” cycles yields complete enantio-selective excitation with a much simpler protocol containing only three fields, chosen to synchronize the population transfer in all of the cycles. The corresponding pulse sequence requires one left-circularly, one right-circularly, and one linearly polarized field and is within the capabilities of current microwave technology. Our proposal eliminates an important obstacle toward complete enantiomer-selective state transfer in three-wave mixing experiments11,12. The control strategies derived here are general, i.e., they can be applied to all molecules which are amenable to chiral-sensitive techniques in the gas phase. This implies, in terms of the size of the molecules, an upper limit toward biochemically relevant molecules, due to difficulties of preparing samples of very large molecules in the gas phase. Our results are thus most relevant to the wider atomic and molecular physics community, where the interest in small polyatomic molecules has seen a recent surge, due to prospective applications in fundamental physics15,26, quantum information science28, or optical enantiomer-selective control9,10,54,55,56,57, in addition to microwave three-wave mixing2,4,5,11,12,13.
More broadly, our work testifies to the value of mathematical controllability analysis in general and the Lie–Galerkin approximation in particular for topical problems in quantum control. The same techniques can in principle also be applied to many-body dynamics or open quantum systems, where the spectral gap condition required to invoke the Lie–Galerkin approximation will translate into a timescale separation argument. It will be interesting to see in these cases how far controllability despite degeneracy can be pushed. While in our example of asymmetric quantum rotors, the key to controllability despite degeneracy is found in the 3D nature of the light-matter coupling, it is presently an open question which mechanisms could be leveraged for the control of many-body dynamics or open quantum systems.
Data availability
All data generated or analyzed during this study are included in this published article (and its supplementary information files).
Code availability
The code used for solving the time-dependent Schrödinger equation is available from the corresponding author upon reasonable request.
References
Berova, N., Polavarapu, P. L., Nakanishi, K. & Woody, R. W. (eds.) Comprehensive Chiroptical Spectroscopy: Instrumentation, Methodologies, and Theoretical Simulations (John Wiley & Sons, New York, 2012).
Patterson, D., Schnell, M. & Doyle, J. M. Enantiomer-specific detection of chiral molecules via microwave spectroscopy. Nature 497, 475–477 (2013).
Grabow, J.-U. Fourier transform microwave spectroscopy: handedness caught by rotational coherence. Angew. Chem. Int. Ed. 52, 11698–11700 (2013).
Shubert, V. A., Schmitz, D., Patterson, D., Doyle, J. M. & Schnell, M. Identifying enantiomers in mixtures of chiral molecules with broadband microwave spectroscopy. Angew. Chem. Int. Ed. 53, 1152–1155 (2014).
Lobsiger, S., Pérez, C., Evangelisti, L., Lehmann, K. K. & Pate, B. H. Molecular structure and chiral detection by Fourier transform microwave spectroscopy. J. Phys. Chem. Lett. 6, 196–200 (2015).
Fanood, M. M. R., Ram, N. B., Lehmann, C. S., Powis, I. & Janssen, M. H. M. Enantiomer-specific analysis of multi-component mixtures by correlated electron imaging-ion mass spectrometry. Nature Commun. 6, 7511 (2015).
Kastner, A. et al. Enantiomeric excess sensitivity to below one percent by using femtosecond photoelectron circular dichroism. ChemPhysChem 17, 1119–1122 (2016).
Comby, A. et al. Real-time determination of enantiomeric and isomeric content using photoelectron elliptical dichroism. Nature Commun. 8, 5212 (2018).
Baykusheva, D. & Wörner, H. J. Chiral discrimination through bielliptical high-harmonic spectroscopy. Phys. Rev. X 8, 031060 (2018).
Neufeld, O. et al. Ultrasensitive chiral spectroscopy by dynamical symmetry breaking in high harmonic generation. Phys. Rev. X 9, 031002 (2019).
Eibenberger, S., Doyle, J. & Patterson, D. Enantiomer-specific state transfer of chiral molecules. Phys. Rev. Lett. 118, 123002 (2017).
Pérez, C. et al. Coherent enantiomer-selective population enrichment using tailored microwave fields. Angew. Chem. Int. Ed. 56, 12512–12517 (2017).
Pérez, C., Steber, A. L., Krin, A. & Schnell, M. State-specific enrichment of chiral conformers with microwave spectroscopy. J. Phys. Chem. Lett. 9, 4539–4543 (2018).
Quack, M., Stohner, J. & Willeke, M. High-resolution spectroscopic studies and theory of parity violation in chiral molecules. Annu. Rev. Phys. Chem. 59, 741–769 (2008).
Hutzler, N. R. Polyatomic molecules as quantum sensors for fundamental physics. Quantum Sci. Technol. 5, 044011 (2020).
Leibscher, M., Giesen, T. F. & Koch, C. P. Principles of enantio-selective excitation in three-wave mixing spectroscopy of chiral molecules. J. Chem. Phys. 151, 014302 (2019).
Zhang, Q., Chen, Y.-Y., Ye, C. & Li, Y. Evading thermal population influence on enantiomeric-specific state transfer based on a cyclic three-level system via ro-vibrational transitions. J. Phys. B: At., Mol. Opt. Phys. 53, 235103 (2020).
Shapiro, M., Frishman, E. & Brumer, P. Coherently controlled asymmetric synthesis with achiral light. Phys. Rev. Lett. 84, 1669–1672 (2000).
Král, P. & Shapiro, M. Cyclic population transfer in quantum systems with broken symmetry. Phys. Rev. Lett. 87, 183002 (2001).
Li, Y., Bruder, C. & Sun, C. P. Generalized Stern-Gerlach effect for chiral molecules. Phys. Rev. Lett. 99, 130403 (2007).
Li, X. & Shapiro, M. Spatial separation of enantiomers by coherent optical means. J. Chem. Phys. 132, 041101 (2010).
Hirota, E. Triple resonance for a three-level system of a chiral molecule. Proc. Jpn. Acad., Ser. B 88, 120–128 (2012).
Vitanov, N. V. & Drewsen, M. Highly efficient detection and separation of chiral molecules through shortcuts to adiabaticity. Phys. Rev. Lett. 122, 173202 (2019).
Lehmann, K. K. Influence of spatial degeneracy on rotational spectroscopy: three-wave mixing and enantiomeric state separation of chiral molecules. J. Chem. Phys. 149, 094201 (2018).
Ye, C., Liu, B., Chen, Y.-Y. & Li, Y. Enantio-conversion of chiral mixtures via optical pumping. Phys. Rev. A 103, 022830 (2021).
Augenbraun, B. L., Doyle, J. M., Zelevinsky, T. & Kozyryev, I. Molecular asymmetry and optical cycling: laser cooling asymmetric top molecules. Phys. Rev. X 10, 031022 (2020).
Dickerson, C. E. et al. Franck-Condon tuning of optical cycling centers by organic functionalization. Phys. Rev. Lett. 126, 123002 (2021).
Albert, V. V., Covey, J. P. & Preskill, J. Robust encoding of a qubit in a molecule. Phys. Rev. X 10, 031050 (2020).
Haake, F., Gnutzmann, S. & Kuś, M. Quantum Signatures of Chaos (Springer, 2018).
Stapelfeldt, H. & Seideman, T. Colloquium: aligning molecules with strong laser pulses. Rev. Mod. Phys. 75, 543–557 (2003).
D’Alessandro, D. Quantum Control and Dynamics (Chapman and Hall (CRC), 2008).
Brumer, P. & Shapiro, M. Principles and Applications of the Quantum Control of Molecular Processes (Wiley Interscience, 2003).
Judson, R., Lehmann, K., Rabitz, H. & Warren, W. Optimal design of external fields for controlling molecular motion: application to rotation. J. Mol. Struct. 223, 425–456 (1990).
Turinici, G. & Rabitz, H. Multi-polarization quantum control of rotational motion through dipole coupling. J. Phys. A 43, 105303 (2010).
Chambrion, T. Periodic excitations of bilinear quantum systems. Autom. J. IFAC 48, 2040–2046 (2012).
Chambrion, T., Mason, P., Sigalotti, M. & Boscain, U. Controllability of the discrete-spectrum Schrödinger equation driven by an external field. Ann. Inst. H. Poincaré Anal. Non Linéaire 26, 329–349 (2009).
Boussaїd, N., Caponigro, M. & Chambrion, T. Weakly coupled systems in quantum control. IEEE Trans. Automat. Control 58, 2205–2216 (2013).
Boscain, U., Caponigro, M. & Sigalotti, M. Multi-input Schrödinger equation: controllability, tracking, and application to the quantum angular momentum. J. Differ. Equ. 256, 3524–3551 (2014).
DeMille, D. Quantum computation with trapped polar molecules. Phys. Rev. Lett. 88, 067901 (2002).
Boscain, U., Pozzoli, E. & Sigalotti, M. Classical and quantum controllability of a rotating symmetric molecule. SIAM J. Control Optim. 59, 156–184 (2021).
Boscain, U., Sigalotti, M. & Pozzoli, E. Reachable sets for a 3D accidentally symmetric molecule. IFAC-PapersOnLine 53, 1943–1948 (2020). 21st IFAC World Congress.
Pozzoli, E. Classical and Quantum Controllability of a Rotating Asymmetric Molecule. Appl Math Optim 85, 8 https://doi.org/10.1007/s00245-022-09821-y (2021).
Boscain, U., Caponigro, M., Chambrion, T. & Sigalotti, M. A weak spectral condition for the controllability of the bilinear Schrödinger equation with application to the control of a rotating planar molecule. Comm. Math. Phys. 311, 423–455 (2012).
Caponigro, M. & Sigalotti, M. Exact controllability in projections of the bilinear Schrödinger equation. SIAM J. Control Optim. 56, 2901–2920 (2018).
Ordonez, A. F. & Smirnova, O. Generalized perspective on chiral measurements without magnetic interactions. Phys. Rev. A 98, 063428 (2018).
Koch, C. P., Lemeshko, M. & Sugny, D. Quantum control of molecular rotation. Rev. Mod. Phys. 91, 035005 (2019).
Zare, R. N. Angular Momentum (Wiley, 1988).
Glaser, S. J. et al. Training Schrödinger’s cat: quantum optimal control. Strategic report on current status, visions and goals for research in Europe. Eur. Phys. J. D 69, 279 (2015).
Mirrahimi, M. & Rouchon, P. Controllability of quantum harmonic oscillators. IEEE Trans. Automat. Control 49, 745–747 (2004).
Dirr, G. Ensemble controllability of bilinear systems. Oberwolfach Rep. 9, 674–676 (2012).
Belhadj, M., Salomon, J. & Turinici, G. Ensemble controllability and discrimination of perturbed bilinear control systems on connected, simple, compact Lie groups. Eur. J. Control 22, 23–29 (2015).
Pozzoli, E., Leibscher, M., Sigalotti, M., Boscain, U. & Koch, C. P. Lie algebra for rotational subsystems of a driven asymmetric top. J. Phys. A: Math. Theor. In press https://doi.org/10.1088/1751-8121/ac631 (2022).
Lee, J. et al. Quantitative Study of Enantiomer-Specific State Transfer Phys. Rev. Lett. 128, 173001 (2022).
Yachmenev, A. & Yurchenko, S. N. Detecting chirality in molecules by linearly polarized laser fields. Phys. Rev. Lett. 117, 033001 (2016).
Tutunnikov, I., Gershnabel, E., Gold, S. & Averbukh, I. S. Selective orientation of chiral molecules by laser fields with twisted polarization. J. Phys. Chem. Lett. 9, 1105–1111 (2018).
Milner, A. A. et al. Controlled enantioselective orientation of chiral molecules with an optical centrifuge. Phys. Rev. Lett. 122, 223201 (2019).
Tutunnikov, I. et al. Observation of persistent orientation of chiral molecules by a laser field with twisted polarization. Phys. Rev. A 101, 021403 (2020).
Moreno, J. R. A., Huet, T. R. & González, J. J. L. Conformational relaxation of S-(+)-carvone and R-(+)-limonene studied by microwave Fourier transform spectroscopy and quantum chemical calculations. Struct. Chem. 24, 1163–1170 (2013).
Acknowledgements
We would like to thank Sandra Eibenberger and Valery Milner for helpful discussions, and we gratefully acknowledge financial support from the Deutsche Forschungsgemeinschaft through CRC 1319 ELCH and from the European Union’s Horizon 2020 research and innovation program under the Marie Sklodowska-Curie grant agreement Nr. 765267 (QuSCo). M.S. and U.B. also thank the ANR projects SRGI ANR-15-CE40-0018 and Quaco ANR-17-CE40-0007-01.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
The work reported here was conceived by M.L., E.P., and C.P.K. and supervised by M.S., U.B., and C.P.K. The controllability analysis has been carried out by E.P., the pulse sequences were designed by M.L. who also carried out all numerical calculations. Experimental realization of the excitation schemes has been discussed between M.L., C.P.K., C.P., and M.Sch. C.P. and M.Sch have also provided experimental data on microwave 3WM. All authors contributed to the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks Emil Zak and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Leibscher, M., Pozzoli, E., Pérez, C. et al. Full quantum control of enantiomer-selective state transfer in chiral molecules despite degeneracy. Commun Phys 5, 110 (2022). https://doi.org/10.1038/s42005-022-00883-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-022-00883-6
This article is cited by
-
Inducing transient enantiomeric excess in a molecular quantum racemic mixture with microwave fields
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.