Micro-object pose estimation with sim-to-real transfer learning using small dataset

Abstract

Three-dimensional (3D) pose estimation of micro/nano-objects is essential for the implementation of automatic manipulation in micro/nano-robotic systems. However, out-of-plane pose estimation of a micro/nano-object is challenging, since the images are typically obtained in 2D using a scanning electron microscope (SEM) or an optical microscope (OM). Traditional deep learning based methods require the collection of a large amount of labeled data for model training to estimate the 3D pose of an object from a monocular image. Here we present a sim-to-real learning-to-match approach for 3D pose estimation of micro/nano-objects. Instead of collecting large training datasets, simulated data is generated to enlarge the limited experimental data obtained in practice, while the domain gap between the generated and experimental data is minimized via image translation based on a generative adversarial network (GAN) model. A learning-to-match approach is used to map the generated data and the experimental data to a low-dimensional space with the same data distribution for different pose labels, which ensures effective feature embedding. Combining the labeled data obtained from experiments and simulations, a new training dataset is constructed for robust pose estimation. The proposed method is validated with images from both SEM and OM, facilitating the development of closed-loop control of micro/nano-objects with complex shapes in micro/nano-robotic systems.

Introduction

Scanning electron microscopy (SEM), which enables high-resolution imaging of micro/nano-scale objects, is a common tool for micro/nano-robotics development¹. For example, previous work has demonstrated the use of SEM for assembling^2,3,4, handling and characterizing nanomaterials^5,6,7,8, nanowires, carbon nanotubes, and other nanoscale objects^9,10. In addition, optical microscope (OM) has been widely integrated with micro-robotic systems. For example, optical micro-manipulation systems integrated with OM have been developed for cell manipulation or other biomedical applications¹¹. Therefore, accurate perception of micro/nano-objects has been shown to be essential for closed-loop micro/nano-manipulation and visual servoing, as laboratory-based experiments are often conducted under microscopic observations.

Thus far, most of the micro/nano-scale operations are conducted by an operator using a manual joystick, keyboard¹² or a haptic device^13,14. To develop a semi- or fully automatic micro/nano-manipulation platform, three-dimensional (3D) pose estimation of the micro/nano-objects is needed, which relies on the microscopic imaging as feedback^15,16. Previous research has utilized the microscope camera view to estimate the position of micro/nano-objects in 2D with applications in nano-manipulation systems integrated with SEM^17,18, optical tweezers¹⁹ integrated with OM, magnetic microscopic system²⁰, and atomic force microscopy²¹. However, accurate 3D pose estimation for individual and group-wise robot manipulation has not been fully explored, due to the challenges of 3D pose estimation using monocular microscopic images. Therefore, real-time reliable visual pose estimation of end-effectors and target objects for high-speed micro/nanomanipulation will be the main focus of this paper.

Hitherto, template matching methods have been widely used for the pose estimation of micro/nano-objects. However, the accuracy can be limited as it’s difficult to obtain labeled templates for all possible 3D poses. An alternative method is to use simulated images as templates. However, the inaccuracy of micro-fabrication and the characteristics of different image modalities may cause varying appearances of the microrobots in the images obtained from different domains, which is known as the domain gap. The inherent domain gap between the simulated data and the experimental data may induce errors in matching the templates with the real object poses. Feature-based methods, which rely on triangulation with stereo camera views are currently not applicable to microscopic images due to the nature of how the images are acquired. To this end, it is necessary to investigate other new methods for accurate micro/nano-object pose estimation.

Pose estimation for micro/nano-scale systems, such as experimental setups inside SEM, has been investigated based on a geometrical solution²². Model-based tracking of magnetic intraocular micro/nanorobots has also been proposed²³. However, the work mentioned above cannot be used for optical micro/nanorobots due to the transparency of the materials used and the variance of blurriness. Compared to traditional approaches, machine learning based methods can provide more generic solutions for micro/nano-object pose estimation supporting different experimental setups^24,25,26. Recent advances in machine learning have offered new opportunities for performing data classification, identification of molecular characteristics²⁷, consequences prediction and optimal design of materials or nano-devices in nanoscience^{28,29,30,31,32}. Recent studies have shown promising results in carrying out accurate predictions even with limited data. Therefore, we aim to investigate machine learning based techniques to assist the perception of micro/nanoscale objects in 3D.

In recent years, artificial neural networks have been investigated for pose estimation of objects at the macroscale level, such as PoseCNN³³, SSD-6D³⁴, BB8³⁵, and other methods constructed via deep convolutional neural networks³⁶. At the microscale, a CNN-based method for estimating the 3D pose and depth of optically transparent microrobots has been developed¹⁹. This method relies on a large volume of labeled data of each microrobot with different poses for training, which is expensive due to the high cost of micro/nano-fabrication and difficulty in accurately controlling the pose of the microrobots. To this end, pose estimation of micro/nano-object using a relatively small dataset should be explored to lower the development cost and enable the research in autonomic microrobotic control.

Few-shot learning represents a type of machine learning where the training dataset contains limited labeled data for different classes, contrary to the conventional deep learning which employs a large volume of data for model training³⁷. To enable few-shot learning for micro/nano-object pose estimation, labeled data generated in simulation can be used to assist the model training when the experimental data is limited³⁸. However, for many tasks, artificial neural network models trained on simulated data do not work well with real experimental data. To bridge the gap between simulated and real data, domain adaptation has been investigated³⁹. These include using abstract representations, training invariant feature extractors⁴⁰, learning the mapping between feature spaces⁴¹, and image-to-image translation^42,43. However, some of the aforementioned methods have inherent limitations. For example, abstract representations may not be effective when the image data obtained from different domains have large differences, training invariant feature extractors requires a large dataset, while image-to-image translation may induce artefacts in the images.

To address the limitations mentioned above, a sim-to-real learning-to-match approach is proposed in this paper, which is developed based on the combination of image-to-image translation and training invariant feature extractors. The work presented here is developed based on the few-shot learning concepts, circumventing the need of collecting a large amount of data for model training like most of the existing work⁴⁴. Comparisons are made between the traditional template matching approach and the proposed method for pose estimation of micro/nanorobot based on the image data obtained from various types of image modalities, including SEM and OM images.

Results

The workflow of the proposed method for micro/nano-object pose estimation is illustrated as follows.

• (1) Step 1: to reduce the domain gap between the simulated data and the experiment data, a Generative Adversarial Network (GAN) model is developed to learn a mapping from the simulated data to the experimental data, which can translate the labeled images obtained from the source domain (simulation) to the target domain (experiment).

• (2) Step 2: to further reduce the discrepancy between the generated data and the experimental data, a feature embedding model is developed for domain adaptation, which minimizes the differences between the images of the micro/nano-objects with the same pose.

• (3) Step 3: the embedded domain-invariant features are used to train a multi-layer perception (MLP) model for pose estimation.

• (4) Step 4: at test, the pose of the micro/nano-object is predicted online by combining the feature embedding model and the MLP model.

Dataset construction

We assume that the image data obtained from simulation is denoted as S, while the images of the micro/nano-objects collected via experiments are denoted as M. Let ${{{{{{{{\mathcal{D}}}}}}}}}_{{{{{{{{\mathcal{T}}}}}}}}}^{s}={\{({x}_{i}^{s},{y}_{i}^{s})\}}_{i}^{{N}_{1}}$ denotes a large training dataset made of pairs of simulated data (${{{{{{{{\mathcal{D}}}}}}}}}_{{{{{{{{\mathcal{T}}}}}}}}}^{s} \sim {{{{{{{\boldsymbol{S}}}}}}}}$), where N₁ denotes the number of samples in the simulation domain, ${x}_{i}^{s}$ denotes the image of a micro/nano-object generated from the simulator and ${y}_{i}^{s}$ denotes the corresponding pose value of image ${x}_{i}^{s}$. Let ${{{{{{{{\mathcal{D}}}}}}}}}_{{{{{{{{\mathcal{T}}}}}}}}}^{m}={\{({x}_{i}^{m},{y}_{i}^{m})\}}_{i}^{{N}_{2}}$ denote a small training dataset made of pairs of data obtained in physical experiments (${{{{{{{{\mathcal{D}}}}}}}}}_{{{{{{{{\mathcal{T}}}}}}}}}^{m} \sim {{{{{{{\boldsymbol{M}}}}}}}}$), where N₂ represents the number of samples in the experimental data domain, ${x}_{i}^{m}$ is the image of a micro/nano-object captured during the physical experiments, ${y}_{i}^{m}$ is the corresponding pose value for image ${x}_{i}^{m}$.

To reduce the domain gap between ${{{{{{{{\mathcal{D}}}}}}}}}_{{{{{{{{\mathcal{T}}}}}}}}}^{s}$ and ${{{{{{{{\mathcal{D}}}}}}}}}_{{{{{{{{\mathcal{T}}}}}}}}}^{m}$, a GAN-based technique is applied for image-to-image translation, which transfers the simulated data to the experimental data domain. This leads to a new dataset ${{{{{{{{\mathcal{D}}}}}}}}}_{{{{{{{{\mathcal{T}}}}}}}}}^{m^{\prime} }={\{({x}_{i}^{m^{\prime} },{y}_{i}^{m^{\prime} })\}}_{i}^{{N}_{1}}$ (${{{{{{{{\mathcal{D}}}}}}}}}_{{{{{{{{\mathcal{T}}}}}}}}}^{m^{\prime} } \sim {{{{{{{{\boldsymbol{M}}}}}}}}}^{\prime}$), where ${{{{{{{{\boldsymbol{M}}}}}}}}}^{\prime}$ denotes the generated data domain. After the sim-to-real transfer, we assume that the features obtained from M and ${{{{{{{\boldsymbol{M}}}}}}}}^{\prime}$ are of similar distributions. The discrepancy between M and ${{{{{{{\boldsymbol{M}}}}}}}}^{\prime}$ can be further minimized by training a feature embedding model.

Let θ and γ denote the out-of-plane rotation angle along the X and Y axis respectively. The predictions of angle θ for two microrobots (microrobot A and microrobot B) are used as examples to verify the proposed method in detail. In this case, label ${y}_{i}^{* }(* =s,m)$ is equal to θ in both datasets (${{{{{{{{\mathcal{D}}}}}}}}}_{{{{{{{{\mathcal{T}}}}}}}}}^{s}$ and ${{{{{{{{\mathcal{D}}}}}}}}}_{{{{{{{{\mathcal{T}}}}}}}}}^{m}$). For a more general situation, ${y}_{i}^{* }(* =s,m)$ is a vector constructed by θ and γ, where ${{{{{{{\bf{{y}}}}}}}_{i}^{* }}}=[\theta ,\gamma ](* =s,m)$. An example about how to estimate the two out-of-plan angles θ and γ simultaneously is introduced in Supplementary Note 5 with experimental verification, while the results are shown in Supplementary Fig. 6.

The definitions of the coordinate and the out-of-plane rotation angle of microrobot A and microrobot B are illustrated in Fig. 1a, b. All the microrobots used for experiments were fabricated using the Two-Photon Polymerization, while the SEM samples were coated with gold using a metal sputtering deposition system (HEX, Korvus Technology) (see Methods section).

Fig. 1: Overview of the microrobots used for experimental validation.

a The definition of the coordinate system and the out-of-plane pose of microrobot A. b The definition of the coordinate system and the out-of-plane pose of microrobot B. c Different poses of the microrobot B obtained from the simulator, and the images obtained from Scanning Electron Microscopy (SEM) and Optical Microscope (OM). d Images obtained from the simulator, the SEM and the OM of microrobot A with the same pose (θ = 0°). e Images obtained from the simulator, the SEM and the OM of microrobot B with the same pose (θ = 0°).

For data collection, an SEM (Tescan, Czech) and an OM (Zeiss, UK) were employed to obtain the images of the microrobots with various poses as experimental data (see Methods section). Figure 1c takes microrobot B as an example and demonstrates the images of microrobot B with different out-of-plane poses obtained from the simulator, the SEM and the OT respectively. For the images of the microrobot with the same pose, the domain gaps are significant. Figure 1d, e shows the examples of images obtained from the simulator, the SEM and the OM of microrobot A and microrobot B with the same pose (θ = 0° is used as an example). For the OM data, the images of the microrobot with the same pose look significantly different, since the images obtained at different depth levels compared to the focal plane of the OM have different levels of blurriness.

For each image collected, it has a corresponding label of θ, which represents the out-of-plane rotation angle along X axis, as shown in Fig. 1a, b. The minimal displacement between the rotation of the microrobots along the X axis is k degree during the experimental data collection process. Let min(θ) and max(θ) represent the minimal and maximum out-of-plane rotation along X axis respectively, min(θ) = 0° and max(θ) = 90° are used in this paper. Suppose that I represents the number of microrobots required to be fabricated for the data collection, it can be computed based on the following equation:

$$I=[max(\theta )-min(\theta )]/k+1$$

(1)

For a microrobot printed at a specific pose, K images are collected. N represents the total number of images used to construct the small dataset of the experimental data (${{{{{{{{\mathcal{D}}}}}}}}}_{{{{{{{{\mathcal{T}}}}}}}}}^{m}$). Therefore, we have N = I × K number of images collected in total. The smaller the value of k is, the more precise the pose estimation can be, the more image data we can obtain to construct ${{{{{{{{\mathcal{D}}}}}}}}}_{{{{{{{{\mathcal{T}}}}}}}}}^{m}$ for model training.

Sim-to-real transfer via GAN

A GAN model can be used for domain adaptation, enabling the sim-to-real transfer⁴⁵. When learning a GAN model, a generator G and a discriminator D are trained in an adversarial manner. In the context of domain adaptation for visual inputs, the generator G takes images from the source domain, and tries to generate output images matching those from the target domain. In the meantime, a discriminator D is trained to distinguish the generated target images and the real experimental images.

Pixel level image translation based on a Pix2Pix model has been developed for image translation⁴⁶. However, paired image data is required, which cannot be applied to sim-to-real transfer since the data from different domains are difficult to pair. CycleGAN⁴⁷, DiscoGan⁴⁸ and DualGan⁴⁹ introduce a cycle-consistent loss to enforce an inverse mapping from the target domain to the source domain in an unsupervised manner, which ensures the translated images can be easily translated back to the original image domain. In this paper, we implement the CycleGAN for image translation, which aims at reducing the domain gap between the simulated data and the experimental data for micro/nano-object pose estimation.

The target of sim-to-real transfer is to learn a mapping function G(.): S → M, which is known as a generator. Let ${{{{{{{{\boldsymbol{M}}}}}}}}}^{\prime}$ denote the generated images obtained via CycleGAN via ${{{{{{{{\boldsymbol{M}}}}}}}}}^{\prime}={{{{{{{\boldsymbol{G}}}}}}}}({{{{{{{\boldsymbol{S}}}}}}}})$. We assume that ${{{{{{{{\boldsymbol{M}}}}}}}}}^{\prime}$ has reduced domain gap from M. A domain discriminator D_M is used to classify whether a data point is drawn from M or ${{{{{{{{\boldsymbol{M}}}}}}}}}^{\prime}$, which is optimized according to an adversarial loss. Suppose that ${{{{{{{{\boldsymbol{G}}}}}}}}}^{\prime}(.):{{{{{{{\boldsymbol{M}}}}}}}}\to {{{{{{{\boldsymbol{S}}}}}}}}$ is an inverse generator, D_S is a domain discriminator for classifying whether a data point is drawn from S or ${{{{{{{{\boldsymbol{S}}}}}}}}}^{\prime}$.

An overview of the CycleGAN for image data translation between simulated data and experimental data of the microrobots is shown in Fig. 2, where ${x}_{i}^{m^{\prime} }={{{{{{{\boldsymbol{G}}}}}}}}({x}_{i}^{s})$, ${x}_{i}^{s^{\prime} }={{{{{{{{\boldsymbol{G}}}}}}}}}^{\prime}({x}_{i}^{m})$. To make the generated images indistinguishable from the original images, an adversarial loss is adopted, through which the samples from different domains are not distinguishable after the model training.

Fig. 2: Image data translation between simulated data and experimental data of microrobots and the illustration of the CycleGAN approach.

An image ${x}_{i}^{s}$ obtained from source domain S (simulation domain) is translated to ${x}_{i}^{m^{\prime} }$ in the target domain ${{{{{{{{\boldsymbol{M}}}}}}}}}^{\prime}$, while an image ${x}_{i}^{m}$ obtained from the target domain M (experiment domain) can be translated back to ${x}_{i}^{s^{\prime} }$ in the source domain ${{{{{{{{\boldsymbol{S}}}}}}}}}^{\prime}$. Microrobot A is used for the demonstration of the sim-to-real transfer approach based on CycleGAN. G(. ) is a generator; ${{{{{{{{\boldsymbol{G}}}}}}}}}^{\prime}(.)$ is an inverse generator; ${{{{{{{{\mathcal{L}}}}}}}}}_{\,{{{{\mathrm{cyc}}}}}}^{1}$ and ${{{{{{{{\mathcal{L}}}}}}}}}_{\,{{{{\mathrm{cyc}}}}}\,}^{2}$ represent the cycle consistency loss (see Eq. (7)); D_S and D_M are domain discriminators.

In this unpaired image-to-image translation setting, the inverse generator ${{{{{{{{\boldsymbol{G}}}}}}}}}^{\prime}(.)$ is used to map the observations in the target domain back to the source domain (${{{{{{{\boldsymbol{S}}}}}}}}\approx {{{{{{{{\boldsymbol{S}}}}}}}}}^{\prime}={{{{{{{{\boldsymbol{G}}}}}}}}}^{\prime}({{{{{{{\boldsymbol{G}}}}}}}}({{{{{{{\boldsymbol{S}}}}}}}}))$). A cycle consistency loss ${{{{{{{{\mathcal{L}}}}}}}}}_{{{{{\mathrm{cyc}}}}}}({{{{{{{\boldsymbol{G}}}}}}}},{{{{{{{{\boldsymbol{G}}}}}}}}}^{\prime})$ is defined, which is the sum of ${{{{{{{{\mathcal{L}}}}}}}}}_{\,{{{{\mathrm{cyc}}}}}\,}^{1}$ and ${{{{{{{{\mathcal{L}}}}}}}}}_{\,{{{{\mathrm{cyc}}}}}\,}^{2}$, as indicated in Fig. 2. The cycle consistency loss is used to ensure that the generated images can preserve the content of its original images to some extent. The optimization is formulated as a min-max problem:

$${{{{{{{{\boldsymbol{G}}}}}}}}}^{* },{{{{{{{{\boldsymbol{G}}}}}}}}}^{^{\prime} * }=\arg \mathop{\min }\limits_{{{{{{{{\boldsymbol{G}}}}}}}},{{{{{{{{\boldsymbol{G}}}}}}}}}^{\prime}}\mathop{\max }\limits_{{{{{{{{{\boldsymbol{D}}}}}}}}}_{{{{{{{{\boldsymbol{S}}}}}}}}},{{{{{{{{\boldsymbol{D}}}}}}}}}_{{{{{{{{\boldsymbol{T}}}}}}}}}}{{{{{{{\mathcal{L}}}}}}}}\left({{{{{{{\boldsymbol{G}}}}}}}},{{{{{{{{\boldsymbol{G}}}}}}}}}^{\prime},{{{{{{{{\boldsymbol{D}}}}}}}}}_{{{{{{{{\boldsymbol{S}}}}}}}}},{{{{{{{{\boldsymbol{D}}}}}}}}}_{{{{{{{{\boldsymbol{T}}}}}}}}}\right)$$

(2)

The details of the constructions of loss functions are presented in Methods section. The trained generator G(.) is then applied to translate the labeled simulated images to the generated experimental data, with the pose label simply passed on after translation. After sim-to-real transfer, the learning-to-match approach is employed to capture the domain-invariant features with effective embedding, and ensure precise pose estimation by utilizing a large amount of generated data and the limited labeled experimental data. The learning-to-match approach further reduces the gap between the generated data and the experimental data, which is detailed as follows.

As shown in Supplementary Fig. 5, some checkboard patterns can be observed in the generated image, which is the fundamental issue of GAN-based approaches. With the learn-to-match approach described in the next section, the patterns in the background will not influence the pose estimation results. Since the feature embedding model can learn to map images of the microrobots with the same pose to the same location, regardless of the patterns in the background.

Model construction and training

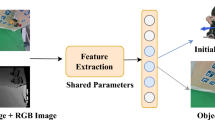
An overview of the learning-to-match approach is demonstrated in Fig. 3. Examples of the generated data obtained via sim-to-real transfer based on CycleGAN and the corresponding experimental data with the same pose for microrobot A is shown in Fig. 3a. Figure 3b illustrates the concept of the learning-to-match approach and the overall structure of the pose estimation model. The motivation of the proposed method is to save the computation time by enabling the model to be adapted to new experimental setups quickly. A feature embedding model is trained to project images with different angles to different locations and map images with the same pose angle to the same location in 1D space. Therefore, given a new dataset, the raw image can be compressed while the useful information of the original image is encoded in the 20-dimensional vector. To enable the precise pose estimation using the new dataset obtained in new environments, we only need to retrain the MLP using the compact features obtained via the feature embedding model for the calibration purpose. In this way, the efficiency of domain adaptation of the proposed method can be ensured.

Fig. 3: Overview of the learning-to-match model.

a Examples of the generated data obtained via sim-to-real transfer based on CycleGAN and the corresponding experimental data with the same pose. An example of the sampling of an anchor frame with θ = 45°, a positive frame with θ = 45° and a negative frame with ${\theta }^{\prime}=1{5}^{\circ }$. b Concept illustration of the learning-to-match approach and overall structure of the pose estimation model. G(.) represents the generator; F(.) is the feature embedding model; f(.) is the multi-layer perception (MLP) network.

Let ${{{{{{{{\mathcal{D}}}}}}}}}_{{{{{{{{\mathcal{T}}}}}}}}}^{m^{\prime} }$ denote the dataset constructed by the images from domain $M^{\prime}$. We combine the generated images obtained via GAN (domain transferred simulated data) ${{{{{{{{\mathcal{D}}}}}}}}}_{{{{{{{{\mathcal{T}}}}}}}}}^{m^{\prime} }$ and the real experimental data ${{{{{{{{\mathcal{D}}}}}}}}}_{{{{{{{{\mathcal{T}}}}}}}}}^{m}$ as ${{{{{{{{\mathcal{D}}}}}}}}}_{{{{{{{{\mathcal{T}}}}}}}}}$. Therefore, ${{{{{{{{\mathcal{D}}}}}}}}}_{{{{{{{{\mathcal{T}}}}}}}}}={\{({x}_{i},{y}_{i})\}}_{i}^{{N}_{1}+{N}_{2}}$ consists of images from two domains, i.e. the domain transferred simulated data and the real experimental data with labels. In ${{{{{{{{\mathcal{D}}}}}}}}}_{{{{{{{{\mathcal{T}}}}}}}}}$, we define anchor image data as X^a. Suppose that the pose label of X^a is θ, we select two images (X^p and Xⁿ) randomly among the remaining images in ${{{{{{{{\mathcal{D}}}}}}}}}_{{{{{{{{\mathcal{T}}}}}}}}}$, where the pose label of X^p is θ and the pose label of Xⁿ is ${\theta }^{\prime}$ (${\theta }^{\prime}\ne \theta$). The target is to train an embedding model F(.) to represent high-dimensional data X^*(* = a, p, n) effectively, where the embedded feature vector is generated by x^* = F(X^*)(* = a, p, n).

The aim is to minimize the distance of embedded features between the anchor image and the positive image of the same pose ${D}_{A}={\left\Vert F\left({X}_{i}^{a}\right)-F\left({X}_{i}^{p}\right)\right\Vert }_{2}^{2}$, while at the meantime maximize the distance of features between the anchor image and the negative sample ${D}_{B}={\left\Vert F\left({X}_{i}^{a}\right)-F\left({X}_{i}^{n}\right)\right\Vert }_{2}^{2}$. Thus, we aim to learn a feature embedding model F(. ) such that

$$\begin{array}{l}\phi\ < \ {L}_{embed}={\left\Vert F\left({X}_{i}^{a}\right)-F\left({X}_{i}^{n}\right)\right\Vert }_{2}^{2}-{\left\Vert F\left({X}_{i}^{a}\right)-F\left({X}_{i}^{p}\right)\right\Vert }_{2}^{2}\\ \forall \left(F\left({X}_{i}^{a}\right),F\left({X}_{i}^{p}\right),F\left({X}_{i}^{n}\right)\right)\in {{{{{{{{\mathcal{D}}}}}}}}}_{T}\end{array}$$

(3)

where ϕ is a margin range. This can be formulated as a triplet loss for model training. Suppose that we sample J frames of X^a and J frames of X^p from ${{{{{{{{\mathcal{D}}}}}}}}}_{{{{{{{{\mathcal{T}}}}}}}}}$ with pose label θ as anchor frames, J frames of Xⁿ from ${{{{{{{{\mathcal{D}}}}}}}}}_{{{{{{{{\mathcal{T}}}}}}}}}$ with pose label ${\theta }^{\prime}({\theta }^{\prime}\ne \theta )$ as negative frames.

The embedding function F(.) provides a compact and domain-invariant representation of the microrobot images. This effective feature embedding model can map the images of microrobots with the same pose but from different domains to the same cluster, while the distance between the centers of different clusters is increased, resulting in different clusters are used to represent microrobots with different poses. Subsequently, the embedded feature vector can be fed into the MLP network for pose estimation.

Figure 3b demonstrates the concept of the learning-to-match approach and the overall structure of the pose estimation model. The details of the architecture of the feature embedding model are depicted in Fig. 4a, which includes four convolutional layers and two fully connected layers. The input of the model is the preprocessed image, while the output is an embedded feature vector with the size 1 × 20.

Fig. 4: Neural network architecture for the implementation of learning-to-match approach.

a The feature embedding model. b A multi-layer perception (MLP) model for pose estimation.

After training of F(.), the image data x_i (i = 1, 2, ... ,N) in ${{{{{{{{\mathcal{D}}}}}}}}}_{{{{{{{{\mathcal{T}}}}}}}}}$ is translated to ${x}_{i}^{\prime}$(i = 1, 2, ... ,N), which forms a new compact dataset ${{{{{{{{\mathcal{D}}}}}}}}}_{{{{{{{{\mathcal{T}}}}}}}}}^{\prime}$ for model training of pose estimation. The details of the architecture of the MLP neural network model for pose estimation are depicted in Fig. 4b. ${{{{{{{{\mathcal{D}}}}}}}}}_{{{{{{{{\mathcal{T}}}}}}}}}^{\prime}$ is fed to the MLP neural network model for pose estimation, which is constructed by three fully connected layers, with 128, 64 and 32 neurons respectively. Each fully connected layer is followed by a ‘ReLU’ activation function before connecting to the next layer. The final fully connected layer is followed by a ‘ReLU’ activation function and a dropout function to avoid over-fitting, while ‘SoftMax’ activation is used to map the feature vector to the target pose value. This MLP model is therefore used for pose value classification. In fact, the MLP model can be easily formulated as a regression model. The main difference comes from the activation function. The ‘SoftMax’ activation can be changed to a ‘linear’ activation function if pose value regression is needed. Overview of the MLP neural network model for pose estimation based on regression mode is shown in Supplementary Fig. 2.

Results and analysis

Results for SEM images

For the experimental evaluation, five images are collected for a specific pose of a microrobot (K = 5) while k is set as 10° (k = 10). According to Eq. (1), 10 different classes of microrobots with different pose values are included in the training dataset (I = 10), while 50 frames of a microrobot were collected in total to form the small dataset in the domain M (N = 50). Examples for sim-to-real transfer based on SEM data can be found in Supplementary Fig. 5.

The training and validation loss of embedding model using SEM data for microrobot A and B in both cases are shown in Fig. 5a, b. For microrobot A and B, the training loss is reduced from the original value of 0.20 and converged to 0.03. As for the validation, the loss value is reduced from 0.20 and converged to 0.01 and 0.02 for microrobot A and B respectively.

Fig. 5: Model training and results for the evaluation of the proposed method using scanning electron microscope (SEM) data.

a, b The training and validation loss for learning-to-match model of microrobot A and microrobot B respectively. c, d Clustering results based on t-distributed stochastic neighbor embedding (t-SNE) for microrobot A and microrobot B respectively after feature extraction. Different colors represent different clusters with different pose values. The qualitative results indicate that the feature embedding model is desired to separate the features of microrobots with different poses to different clusters. e, f Comparisons between ground truth data and predicted results of pose values for microrobot A, microrobot B respectively.

We qualitatively evaluate the learned embedding features using t-distributed stochastic neighbor embedding (t-SNE) representations^50,51. The embedded feature vector has a size of 1 × 20, while t-SNE can be used to represent the data points in 2D space through non-linear dimensionality reduction in an unsupervised learning manner. The t-SNE based clustering results for the extracted features of microrobots with different pose values are visualized in Fig. 5c, d. It can be seen that the microrobots with different poses can be separated into different clusters with a clear boundary. The visualization of the comparisons between ground truth data and predicted results of SEM images for microrobot A and microrobot B are shown in Fig. 5e, f. During the test, three groups of tests are conducted by randomly selecting 50 images to calculate the average error of pose estimation. The mean errors and standard deviation for the quantitative evaluation of microrobot pose estimation based on the proposed method and the traditional template matching method are shown in Table 1.

Table 1 Mean errors for pose estimation of microrobots using scanning electron microscopy (SEM) data.

The results indicate that the average pose estimation errors for microrobot A and B are 3.31° and 3.23° respectively when using the proposed method. As for the template matching approach, the average pose estimation errors are higher compared to the ones obtained via our proposed method (5.13° vs. 3.23° for microrobot A; 6.43° vs. 3.50° for microrobot B).

Moreover, the computation time for pose estimation of the microrobots based on the proposed method and the template matching method is 0.002 and 0.028 seconds respectively. The computation time of template matching is much longer compared to the proposed method, which limits its online applications with real-time computation requirements. Therefore, the proposed sim-to-real learning-to-match approach can yield higher accuracy and require less computation time, which is essential for online pose estimation of micro/nano-objects.

Results for OM images

For the data collected via the OM, we define two cases for experimental validation, which depend on how we organize the training dataset and the testing dataset.

• Case A: for the training dataset, k is set to 10° and K is 5. According to Eq. (1), 10 different classes of microrobots with different pose values are included in the training dataset, while 50 microscopic images of a microrobot were collected in total. For the testing dataset, k is set as 5°, K is set as 8. According to Eq. (1), 19 different classes of microrobots with different pose values are included in the testing dataset. Different from data included in the training dataset, another 152 OM images of a microrobot were collected, which includes new values of pose that have not been included in the training dataset. In this case, microrobots with pose values of θ = 0°, 10°, ⋯  , 80°, 90° are used for model training. During the testing phase, the pre-trained model can be used for microrobot pose estimation with labels of θ = 5°,15°, ⋯  , 75°, 85°, the data of which are not included in the model training process.

• Case B: for both training and testing dataset, k is set to 5°, K is set as 8. According to Eq. (1), 19 different classes of microrobots with different pose values are included in the testing dataset. In all, 152 microscopic images of a microrobot were collected in total. After constructing the dataset with data augmentation, 80% of the data was used to construct the training dataset while the remaining 20% was used to construct the testing dataset.

For experiments in both cases, the images of a microrobot have either different values of pose or depth levels, which means that the training and testing data have significant differences. For Case A, the number of classes used for training and testing is different. The model is trained by using the data obtained from 10 different classes of pose values, while tested by using the data obtained from 19 different classes of pose values. This demonstrates the advantages of the proposed method. During the model training process, we do not need to collect data with all the labels that we need to predict during the testing phase. The training process is target at finding a reasonable feature embedding method to map the data to a feature vector that contains useful information for few-shot adaptation using the MLP model for pose prediction. During the model training, the generated data contains pose values of θ = 0°, 5°, 10°, 15°, ⋯  , 75°, 80°, 85°, 90°, while the real data (experimental data) of microrobots contains pose values of θ = 0°, 10°, ⋯  , 80°, 90°. During the testing phase, when given new experimental data of microrobot with new pose values of θ = 5°,15°, ⋯  , 75°, 85° that have not been demonstrated during the model training process, the embedding model can map this new data to the generated data with the same pose labels. Following that, the extracted feature vectors can lead to high accuracy of pose prediction, even though the data with new labels have not been demonstrated during the model training process.

As for Case B, the number of classes used for training and testing is the same. Experiments of Case A are designed to demonstrate the data-efficiency of the proposed method, which indicates that we do not need to collect the images of every specific pose of the microrobots to construct the training dataset, while the proposed method can still be effective for pose estimation when unseen pose values present in the testing dataset.

The training and validation loss of embedding model training using OM data for microrobot A and B in both cases are shown in Supplementary Fig. 1. For microrobot A and B in Case A, the training loss is reduced from the original value of 0.12 to 0.02. As for the validation, the loss value is reduced from 0.08 and converged to 0.01. This means that the embedding model is effective to capture similar features from both the experimental data and the generated data, and can discover the differences between microrobots with different pose values across both domains. The same conclusions can be drawn for the model training in Case B using the dataset of microrobot A and B.

The clustering results based on t-SNE dimension reduction is shown in Fig. 6a, which indicates that the feature embedding model can map the microrobots with the same pose to the same cluster, while the distance between different centers of the clusters is evident. This means that the feature embedding model is desired to separate the features of microrobots with different poses to different clusters.

Fig. 6: Model training and results for the evaluation of the proposed method using optical microscope (OM) data.

a The clustering results based on t-distributed stochastic neighbor embedding (t-SNE) dimension reduction for OM data. Different colors represent different clusters with different pose values. Comparison between ground truth data and predicted results of pose values for OM images using the testing dataset for b microrobot A in Case A, c microrobot B in Case A, d microrobot A in Case B, e microrobot B in Case B.

Validation is conducted using the testing dataset for comparisons between the ground truth data and predicted results for robot out-of-plane pose estimation, where 100 data points are shown in Fig. 6b–e. It can be seen that in both cases, the predicted pose values are almost similar to the ground-truth values. The quantitative evaluation results are shown in Table 2, where the average errors of pose estimation for microrobots using the OM images are calculated. Template matching based on normalized correlation matching approach is used as the baseline for comparative study⁵². S→M represents using the simulation data as the templates for pose estimation of the experimental data, while M→M represents using the experimental data as the templates.

Table 2 Results for pose estimation of microrobots using optical microscope (OM) data.

The results indicate the applicability of the proposed method for pose estimation of microrobots under OM, since the pose estimation error is within 10°, which cannot be differentiated by the operators’ eyes. In Case B, the average pose estimation error for microrobot A and microrobot B is 1.48° and 1.29° respectively. The pose estimation errors in Case A are higher than that in Case B, since there are some unseen pose values in Case A and the data for training is less than that in Case B.

Due to the domain gap between the simulation data and the experimental data, it does not make sense to use the images obtained from simulation as templates and apply them to experimental data for template matching. The pose estimation accuracy is high when using templates from the experimental data. For microrobot A and microrobot B, the average errors of pose estimation using labeled simulation data as templates are 32.39° and 30.17° respectively, while the average errors can be reduced to 6.03° and 13.81° respectively when using labeled experimental data as templates. However, it is difficult to collect all the image data with different poses and depth levels during experiments for template matching, which can be known as one of the limitations of using this approach for the pose estimation of micro/nanorobots.

Discussion

Few-shot learning represents a type of machine learning where the training dataset contains limited labeled data for different classes, contrary to the conventional deep learning which employs a large volume of data for model training. The problem addressed in this paper is related to supervised domain adaptation for few-shot learning, where only very few target labeled data are available for model training. However, the model trained on one robot cannot be applied to another microrobot directly with different or more complex shapes without retraining. For a new robot, we need several labeled image data for calibration. With our proposed method based on few-shot learning concept, we eliminate the need of collecting a large amount of data for supervised learning.

Transfer learning method can be used as an extension of the proposed method. That is to say, the model obtained for angle prediction of microrobot A can be fine-tuned and applied to angle prediction of microrobot B, which saves time for model re-training. The accuracy for angle prediction can reach similar performance, while the computation time can be reduced. To further enhance the generalizability of the proposed method, meta learning approach can be investigated. Meta learning, such as model agnostic meta learning⁵³, can be used to enable the proposed method to be adapted to the pose estimation for multiple microrobots with ease.

The quality of SEM images may get affected by the electrical charging of the samples or other environmental factors. The issues of image drift may cause inaccuracy of the pose estimation results without in situ calibration. Therefore, the robustness of the proposed methods can be further enhanced by automatic artefact removal methods. Real-time monitoring of micro/nano-robots with precise tracking and pose estimation for closed-loop control can be investigated, which is the first step towards the construction of intelligent and versatile SEM-based or OM-based micro/nano-robotic platforms for nanoscience or biomedical applications.

To summarize, we have proposed a sim-to-real learning-to-match model in this article, which enables micro/nano-object pose estimation based on limited labeled experimental data, while simulated data is used to enlarge the dataset for training. The domain gap between the simulated data and the experimental data is reduced via CycleGAN, which implements sim-to-real transfer to translate the simulated data to the experimental data with corresponding labels to form a new enlarged dataset. To further minimize the domain gap, a learning-to-match approach is developed to train a feature embedding model to map the generated data and the experimental data to the same low-dimensional space. Combining the experimental data and the generated data, the new dataset is compressed via the feature embedding model, and is employed to train a simple MLP model for micro/nano-object pose estimation. In addition, we conduct a series of ablation studies (see Supplementary Notes 1–4). The results of which are detailed in Supplementary Tables 1–4.

Two microrobots with different shapes were fabricated and used for experimental validation. Both the SEM and OM images were collected for model training. Comparisons are made between the template matching approach and the proposed approach. Results indicated that few-shot learning can be implemented for the pose estimation of microrobots using the proposed method. The pose estimation error for SEM images is smaller than 4°, which is considerably better than those using the template matching approach. The pose estimation error for OM images is within a reasonable range (<6°).

For an SEM-integrated micro/nanomanipulation system, the operator normally relies on the monocular view for the perception of the target micro/nano-objects for operation. To observe the samples from different views, the stage that is used to hold the specimen (micro/nano-objects) is required to be tilted. However, the adjustment of the tilting angle is not intuitive, and cannot be applied for real-time operation. Therefore, with the pose estimation method for micro/nano-object or robotic end-effectors, we can provide a 3D virtual views generation interface for SEM-integrated micro/nanomanipulation, through which we can observe the target object with desired customized viewing angle. The details for this application is illustrated in Supplementary Note 6 as an example, where the results are shown in Supplementary Fig. 7.

This proposed method allows pose estimation of micro/nano-objects using a single image obtained from SEM or OM as the visual feedback. This work is applicable to transmission electron microscopy (TEM) based systems or other imaging systems. Moreover, it can be extended to many applications which may involve micro/nano-robotic systems, and benefit other research fields.

Methods

Microrobot fabrication

The microrobots used for experimental verification were fabricated using the Two-Photon Polymerization⁵⁴. Photoresist (Nanoscribe, IP-L 780) was used as the material for printing the microrobots via the micro 3D printing system (Nanoscribe GmbH, Germany). The details of the printing process can be found in our previous work¹¹.

Data collection

For the data collection of the microrobots with different poses via SEM, 12.0 kx magnification was used, while the high voltage (HV) was set to be 5.0 kV and working distance (WD) was set to be ~13.7 mm.

Image preprocessing

Image preprocessing with data augmentation is necessary before model training to reduce the noises in the data. Given the images collected during experiments, a bounding box is manually placed to identify the initial position of the microrobot of interest. Gaussian filter is applied to remove the noises from the images.

Subsequently, a binary segmentation of the microrobot is generated by thresholding intensity. The threshold is manually tuned to segment the main body of the microrobot. Illustration of the threshold tuning process is shown in Supplementary Fig. 3. The original threshold of intensity is set to be 210, and is gradually decreased until the segmented main body of the microrobot has a clear boundary. For example, 120 is used as the threshold for microrobot B during image preprocessing.

Subsequently, the 2D position of the centroid [x_c, y_c] of the segmented microrobot can be computed from the center of mass of this binary image. Each image is cropped to have the dimension of 256 × 256 pixels, the central point of which is coincided with [x_c, y_c]. To this end, we can crop the image with the microrobot located in the central area of the image. To reduce the computation time, the cropped image is resized to 100 × 100 pixels. Illustration of the image preprocessing is shown in Supplementary Fig. 4, where microrobot B is used as an example.

Data augmentation is performed to enlarge the dataset via horizontal flipping, translation with a range of 20 pixels. For both the training and testing data, pre-processing of the image is conducted. Pixel intensities are rescaled to the range of [−0.5, 0.5] as follows.

$$p({x}^{\prime},{y}^{\prime})=p(x,y)/255-0.5$$

(4)

Loss functions definitions

Suppose that n is the total number of samples used for calculating the loss function, the adversarial loss on the observation samples in domain M can be calculated as follows:

$${{{{{{{{\mathcal{L}}}}}}}}}_{{{{{{{{\rm{adv}}}}}}}}}\left({{{{{{{\boldsymbol{G}}}}}}}},{{{{{{{{\boldsymbol{D}}}}}}}}}_{{{{{{{{\boldsymbol{M}}}}}}}}},{{{{{{{\boldsymbol{S}}}}}}}},{{{{{{{\boldsymbol{M}}}}}}}}\right)=\frac{1}{n}\mathop{\sum }\limits_{i=1}^{n}{\left({{{{{{{{\boldsymbol{D}}}}}}}}}_{{{{{{{{\boldsymbol{M}}}}}}}}}\left({x}_{i}^{m}\right)-1\right)}^{2}+\frac{1}{n}\mathop{\sum }\limits_{i=1}^{n}{\left({{{{{{{{\boldsymbol{D}}}}}}}}}_{{{{{{{{\boldsymbol{M}}}}}}}}}\left({{{{{{{\boldsymbol{G}}}}}}}}\left({x}_{i}^{s}\right)\right)\right)}^{2}$$

(5)

Similarly, the adversarial loss on the observation samples in domain S can be calculated as follows:

$${{{{{{{{\mathcal{L}}}}}}}}}_{{{{{{{{\rm{adv}}}}}}}}}\left({{{{{{{{\boldsymbol{G}}}}}}}}}^{\prime},{{{{{{{{\boldsymbol{D}}}}}}}}}_{{{{{{{{\boldsymbol{S}}}}}}}}},{{{{{{{\boldsymbol{M}}}}}}}},{{{{{{{\boldsymbol{S}}}}}}}}\right)=\frac{1}{n}\mathop{\sum }\limits_{i=1}^{n}{\left({{{{{{{{\boldsymbol{D}}}}}}}}}_{{{{{{{{\boldsymbol{S}}}}}}}}}\left({{{{{{{{\boldsymbol{G}}}}}}}}}^{\prime}\left({x}_{i}^{m}\right)\right)\right)}^{2}+\frac{1}{n}\mathop{\sum }\limits_{i=1}^{n}{\left({{{{{{{{\boldsymbol{D}}}}}}}}}_{{{{{{{{\boldsymbol{S}}}}}}}}}\left({x}_{i}^{s}\right)-1\right)}^{2}$$

(6)

The cycle consistency loss can be calculated as follows.

$${{{{{{{{\mathcal{L}}}}}}}}}_{{{{{\mathrm{cyc}}}}}}({{{{{{{\boldsymbol{G}}}}}}}},{{{{{{{{\boldsymbol{G}}}}}}}}}^{\prime})=\; {{{{{{{{\mathcal{L}}}}}}}}}_{\,{{{{\mathrm{cyc}}}}}\,}^{1}+{{{{{{{{\mathcal{L}}}}}}}}}_{\,{{{{\mathrm{cyc}}}}}\,}^{2}=\frac{1}{n}\mathop{\sum }\limits_{i=1}^{n}\left[\parallel {{{{{{{{\boldsymbol{G}}}}}}}}}^{\prime}({{{{{{{\boldsymbol{G}}}}}}}}({x}_{i}^{s}))-{x}_{i}^{s}{\parallel }_{1}\right]\\ +\frac{1}{n}\mathop{\sum }\limits_{i=1}^{n}\left[\parallel {{{{{{{\boldsymbol{G}}}}}}}}({{{{{{{{\boldsymbol{G}}}}}}}}}^{\prime}({x}_{i}^{m}))-{x}_{i}^{m}{\parallel }_{1}\right]$$

(7)

where ∣∣.∣∣ represents the L1 norm (Manhattan norm). The overall loss is computed by adding the adversarial loss of G and ${{{{{{{{\boldsymbol{G}}}}}}}}}^{\prime}$ as well as the cycle consistency loss, which is defined as follows:

$${{{{{{{\mathcal{L}}}}}}}}\left({{{{{{{\boldsymbol{G}}}}}}}},{{{{{{{{\boldsymbol{G}}}}}}}}}^{\prime},{{{{{{{{\boldsymbol{D}}}}}}}}}_{{{{{{{{\boldsymbol{S}}}}}}}}},{{{{{{{{\boldsymbol{D}}}}}}}}}_{{{{{{{{\boldsymbol{M}}}}}}}}}\right)={{{{{{{{\mathcal{L}}}}}}}}}_{{{{{{{{\rm{adv}}}}}}}}}\left({{{{{{{\boldsymbol{G}}}}}}}},{{{{{{{{\boldsymbol{D}}}}}}}}}_{{{{{{{{\boldsymbol{M}}}}}}}}},{{{{{{{\boldsymbol{S}}}}}}}},{{{{{{{\boldsymbol{M}}}}}}}}\right)+{{{{{{{{\mathcal{L}}}}}}}}}_{{{{{{{{\rm{adv}}}}}}}}}\left({{{{{{{{\boldsymbol{G}}}}}}}}}^{\prime},{{{{{{{{\boldsymbol{D}}}}}}}}}_{{{{{{{{\boldsymbol{S}}}}}}}}},{{{{{{{\boldsymbol{M}}}}}}}},{{{{{{{\boldsymbol{S}}}}}}}}\right)+\lambda {{{{{{{{\mathcal{L}}}}}}}}}_{{{{{{{{\rm{cyc}}}}}}}}}({{{{{{{\boldsymbol{G}}}}}}}},{{{{{{{{\boldsymbol{G}}}}}}}}}^{\prime})$$

(8)

where λ is a parameter for controlling the relative importance between the adversarial loss and the cycle consistency loss.

The loss function ${\mathbb{L}}$ for training F(.) is listed as follows.

$${\mathbb{L}}=\mathop{\sum }\limits_{j}^{J}max({\Vert F({X}_{j}^{a})-F({X}_{j}^{p})\Vert }_{2}^{2}-{\Vert F({X}_{j}^{a})-F({X}_{j}^{n})\Vert }_{2}^{2}+\phi ,0)$$

(9)

Model training

The model was implemented in Python based on Keras⁵⁵, and was trained on a PC with an Intel Core i5-8300H CPU (2.30 GHz), a GeForce GTX 1050 GPU (NVidia Corporation) and 8 GB of RAM.

The model was trained for 200 epochs with a learning rate of 0.0001 based on the Adam optimizer, while the batch size was set to be 80. The loss function was constructed by mean-square-error (MSE) for feature embedding model training.