Introduction

Magnetoelasticity, which is the coupling of spin and strain, is a universal phenomenon in magnetic materials and enables active control of the spin states by modifying the material dimensions1. Thus far, it has been investigated that the spin dynamics after ultrafast spin angular momentum transfer by photo-excitation2,3,4,5,6,7 is governed by time-dependent effective fields with origins such as magnetocrystalline8, dipole, Zeeman9, exchange10,11,12, terahertz13,14, magnetoelasticity15,16, and spin current17,18,19. These have been described mainly by electron and spin degrees of freedoms, while the lattice degree of freedom was highlighted only recently20.

The increase in lattice temperature by photo-excitation generates two types of strain, which are the propagating strain ηp(z, t) with a few-ps temporal width and the quasi-static strain (QSS: ηqss(t)) at a penetration length scale with a heat dissipation time. In the recent decade, the interaction of spins with ηp has attracted considerable research attention from diverse points of view15,16,21,22,23. On the other hand, QSS has not been a major focus despite its comparable amplitude to that of ηp. As principal reasons, the QSS and thermal dependence of materials are inextricable, particularly in photo-induced experiments. Moreover, the QSS is difficult to quantify only with a differential reflectivity that is typical measurement data in a pump–probe experiment. Therefore, great care must be taken in determining ηqss(t). In general, the three temperatures model is used to extract the time-dependent temperature information of the sub-systems by fitting with the experimental curves of spin and reflectivity dynamics. These temperature profiles can account for the only temperature contribution to the reflectivity, not the strain contribution. This might deliver improper messages and hinder unveiling the new physics of ultrafast dynamics. The earlier work describes the contributions of the QSS and thermal effects to the spin dynamics of a galfenol film depending on the external magnetic field strength24. In addition, for an integrated understanding, the experimental quantification of the QSS and its competition with the thermal effect by various experimental conditions remain to be proven. As the QSS and the thermal effects have different contributions to dynamics (the former changes the plasmonic25 or electronic bands26 and the latter changes the electron populations), systematic and comprehensive measurement approaches to separate the two effects are required for the complete analysis of the fundamental mechanism of the ultrafast photo-induced spin dynamics.

Using ultrafast Sagnac interferometry (USI) and a magneto-optical Kerr effect (MOKE) instrument, we demonstrate in this work that the QSS in ferromagnetic films governs the ultrafast spin dynamics from the first ps to the ns timescale. In particular, USI is used to prove the existence of QSS by measuring the lattice expansion dynamics directly. Here, three important sets of evidence that could not be explained by the thermal effect are as follows: (i) the increase in spin precession frequency with the pump intensity, (ii) π-phase inversion of the precession, and (iii) the pronounced background distinguished from incoherent phonons and magnons. The model calculation of the Landau–Lifshitz–Gilbert (LLG) equation incorporating the time-dependent QSS strongly supports that all features mentioned are elucidated by one concept of QSS. The scenario is consolidated with full consistency using other ferromagnets (Co, Ni, and NixFe1-x) to adjust the competition between strain and thermal effects.

Results

Experimental configurations of MOKE and USI measurements

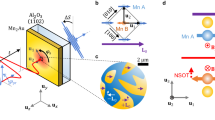
The measurement geometries are shown in Fig. 1a. The bilayer structure of Al2O3(5 nm)/Co(25 nm)/Al2O3(substrate) and the trilayer structure of Co(200 nm)/Al2O3(15 nm)/Co(25 nm)/Al2O3(substrate) were prepared by magnetron sputtering (nm in thickness are omitted hereafter). The Al2O3(5) layer in the bilayer structure was deposited to prevent oxidation. In the trilayer structure, the Al2O3(15) was used both to suppress the possible propagation of thermal magnons from the top Co layer and to match acoustic impedance with Co. The acoustic impedance Z is given by a product of mass density χ and sound velocity υ. The acoustic reflection coefficient rac = (ZCo − ZAl2O3)/(ZCo + ZAl2O3) between Co and Al2O3 with χCo = 8.9 × 103 kg m−3, υCo ~ 5.8 km s−1 27 and χAl2O3 = 3.98 × 103 kg m−3, υAl2O3 ~ 11.2 km s−1 28 is ~0.07 showing the good impedance matching.

Fig. 1: Measurement geometry and ultrafast Sagnac interferometric data.
figure 1

a Simple images of the pump–probe magneto-optical Kerr effect (MOKE) and ultrafast Sagnac interferometry (USI) measurements. For MOKE, the front-pump and front-probe for the bilayer (a-I), the front-pump and back-probe schemes for the trilayer (a-II) were used. The back-pump and front-probe for the bilayer (a-III) were used for the Sagnac measurements. b Dynamic strain pulse profiles η(z, t) calculated for the top Co layer in the trilayer structure at t = 7 (blue curve) and 20 ps (green curve): the propagating bipolar pulse ηp(z) and the quasi-static strain ηqss(z). c Sagnac interferometric curves for Co bilayer: ρ = ΔR/2 R (c-I: ρ—relative change in reflectance induced by the pump pulse and ΔR—differential reflectivity) and the lattice displacement u(0, t) (c-II: experimental data (blue circles) and reproduced one by calculation (yellow line)). d ηqss(t) profile extracted from the reproduced data u(0, t).

Full size image

For MOKE measurements, we used Ti:sapphire regenerative amplified laser pulses with a repetition rate of 10 kHz, a temporal width of 40 fs, and a center wavelength of 800 nm (The details of the MOKE setup are given in Methods). The frequency-doubled pump pulses (λpu = 400 nm) excite the front sides of samples and probe pulses (λpr = 800 nm) measure the differential Kerr rotation Δθ(t) and reflectivity ΔR(t) either of the front side for the bilayer or the back side for the trilayer, as shown in Fig. 1a-I, a-II, respectively. The strain pulse generated in the Co(200) surface in the trilayer propagates and triggers the spin precession in Co(25) layer through magnetoelastic coupling. For USI measurement, the front pump-front probe geometry we first tried partially degrades the quality of probe polarization. Therefore, in the current experiment, we make the pump pulses excite the back side of Co, and the probe pulses measure the front side (Fig. 1a-III). In Fig. 1b, we present the simulated strain profiles η(z, t) at t = 7 (blue) and 20 ps (green) for the top Co layer in the trilayer structure for a better understanding of the time evolution of ηp(z) propagating into the film depth and ηqss(z) biding at a penetration length scale. For simplicity, we used ηqss(t) = η(0, t) hereafter.

The main purpose of USI29 is to measure unambiguously the lattice displacement dynamics u(z = 0, t) and extract \({{\eta }_{{{{{{\rm{qss}}}}}}}(t)=\partial u(z,t)/\partial z|}_{{{{{{\rm{z}}}}}}=0}\) in the end. The USI was built with a Ti:sapphire oscillator system operating at a repetition rate of 80 MHz, a temporal width of 40 fs, and a center wavelength of 800 nm. To avoid possible heat accumulation by a prepulse, the repetition rate is lowered down to 1 MHz by an electro-optic modulator (see “Methods” and Supplementary Note 1 for more details of the USI instrument). We confirmed that all data measured here have no heat accumulation from a prepulse by assuring zero background offset. Although ΔR(t) resulted from a change in a complex refractive index \(\tilde{n}\) is linked to η(z, t) through the relation \(\varDelta \tilde{n}=(\partial \tilde{n}/\partial T)\varDelta T+(\partial \tilde{n}/\partial \eta )\varDelta \eta\), it is relatively difficult to extract η(z, t) directly because of an unknown piezo-optic property (\(\partial \tilde{n}/\partial \eta\)) of materials except for Ni, Cr, and Au at specified wavelengths30,31. Instead, as a circumvention, ηqss(t) was obtained without introducing unknown coefficients by solving the one-dimensional wave equation incorporating the lattice temperature profile used as a driving source (see the strain calculation and parameter values in “Methods” for more details). The lattice temperature profile was calculated using a three temperatures model with proper parameter values of a bulk Co. In addition, the pump intensity calibration between the two different instruments (MOKE and USI) was performed by matching their signal levels of ΔR(t)/R. Figure 1c shows the real part of the Sagnac signal ρ = ΔR/2 R (Fig. 1c-I) and the converted lattice displacement u(0, t) = λprδϕ/4π (Fig. 1c-II) from the imaginary part (δϕ) of δr/r ~ ρ + iδϕ for the bilayer structure (blue circles for the measurement and the yellow line for the reproduction from the calculation). Here, r is defined as the complex amplitude-reflection coefficient of the sample, ρ the relative change in reflectance, and δϕ the phase change induced by the pump pulse. In principle, ηqss(t) can be obtained from the relation \(\eta (z,\,t)=\partial u(z,t)/\partial z\). However, as u(0, t) measured from USI is only one particular case of u(z, t), it is not possible to directly obtain \({{\eta }_{{{{{{\rm{qss}}}}}}}(t)=\partial u(z,t)/\partial z|}_{z=0}\). To bypass this problem, we first obtain a trial solution u(z, t) by calculating the wave equation combined with the three temperature models (see “Methods”). Then, by iteratively adjusting the pump intensity parameter and unknown heat coupling coefficients gij, we find the final solution u(z, t) that best matches u(0, t) to the experimental curve measured by USI. Now that u(z, t) is known based on the measurement quantity, ηqss(t) can be reproduced as shown in Fig. 1d. The positive value of ηqss stands for a tensile strain resulted from the lattice expansion by a sign convention.

In contrast to the reproduced yellow curve in Fig. 1c-II, the experimental data u(0, t) shows a sharp positive peak at the first ps, indicating lattice contraction into the film direction. This may be explained by several possible candidates, such as the electronic stress by photo-excitation32 and the magnetic stress driven by ultrafast demagnetization in FePt nanogranular structures33,34,35. However, the continuous film case in ref. 35 showed that the compressive strain was not produced due to the in-plane constraints upon the lattice expansion. This is a different result from our experimental data u(0, t) shown in Fig. 1c-II. However, identifying the origin is beyond the current scope of this paper, and the lattice contraction has not been considered in the reproduction process.

Variation of spin precession frequency as a function of pump intensity

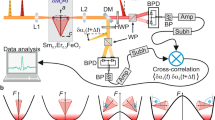
The solid circles in Fig. 2a show Δθ(t) of the Co bilayer under the magnetic field Hext = 0.4 T and φ = 60° (φ: the magnetic field angle from out-of-plane direction) with various pump intensities Ip. The experimental curves for other field angles (φ = 15, 30, and 45°) are presented in Supplementary Note 2. The precession frequency f was obtained by fitting the experimental curves with the following damped sinusoidal function:

$$\varDelta \theta (t)=A\exp \left(-\frac{t}{{\tau }_{1}}\right)\sin (2\pi ft+{\delta }_{0})+B\exp \left(-\frac{t}{{\tau }_{2}}\right)+C$$
(1)

where τ1 is the spin relaxation time, τ2 the decay time of the background signal, δ0 the initial phase of the precession, A and B the amplitudes of the first two terms on the right-hand side, and C defined as the background offset. The solid line in Fig. 2a denotes the fit curve for the highest Ip. Figure 2b shows that the change in the precession frequency (Δf/fm = (f − fm)/fm) increases with Ip for all magnetic field angles (φ = 15°: black, 30°: red, 45°: green, 60°: blue circles. The error bars are marked on the data points). Here, fm is defined as the precession frequency for the minimum Ip and corresponds to 13.8, 20.0, 24.4, and 27.6 GHz for the respective angles of φ (15, 30, 45, and 60°). This frequency variation observed for the polycrystalline Co film has an opposite trend to what would be expected from the conventional magnetic energy terms such as the magneto-crystalline, dipolar, and Zeeman energy. The magnitude of the effective magnetic field Heff(t) in such case would decrease with the increasing temperature of the sub-systems or the increasing Ip.

Fig. 2: Spin precession as a function of the pump intensity of the Co bilayer.
figure 2

a Differential magneto-optical Kerr rotations Δθ(t) of the Co(25) bilayer as a function of pump intensity Ip under the magnetic field Hext = 0.4 T and φ = 60° (φ: the magnetic field angle from out-of-plane direction). b Summary of the frequency change of the spin precession Δf/fm for the bilayer as a function of Ip and φ (15°: black, 30°: red, 45°: green, 60°: blue circles). Here fm is defined as the precession frequency for the minimum Ip. The pink circles present Δf/fm obtained from the Co(25) in the trilayer. All data points are presented with error bars obtained from the least-square fit. c Model calculation results of Δf/fm based on the Landau-Lifshitz-Gilbert (LLG) equation for the presence (solid lines) and absence (dashed lines) of ηqss, respectively. d Δθ(t) induced by ηp for the trilayer under Hext = 0.4 T and φ = 60°.

Full size image

In order to figure out the effect of ηqss(t) on the precession frequency f, we solved the following LLG equation.

$$\frac{d{{{{{\bf{M}}}}}}}{dt}=-{\gamma}_{{{\rm{s}}}}{\mu }_{0}({{{{{\bf{M}}}}}}\times {{{{{{\bf{H}}}}_{{{\bf{eff}}}}}}})+\frac{{\alpha}_{{{\rm{d}}}}}{{M}_{{{{{{\rm{s}}}}}}}}\left({{{{{\bf{M}}}}}}\times \frac{d{{{{{\bf{M}}}}}}}{dt}\right)$$
(2)

where Ms is the saturation magnetization, Heff the effective magnetic field vector defined as \({{{{{{\bf{H}}}}_{{{\bf{eff}}}}}}}=-\partial {F}_{{{\rm{tot}}}}/{\mu }_{0}\partial {{{{{\bf{M}}}}}}\), γs = 1.63 × 1011 rad s−1 T−1 the gyromagnetic ratio36, and the phenomenological damping constant αd = 0.015 is assumed. The total magnetic free energy (Ftot) consists of the magnetocrystalline, dipole, Zeeman, and the magnetoelastic energy terms as follows:

$${F}_{{{{{{\rm{tot}}}}}}}= \, {K}_{{{{{{\rm{u}}}}}}}(M){\sin }^{2}\vartheta +\frac{1}{2}{\mu }_{0}\mathop{\sum} \limits_{i}{N}_{i}{M}_{i}^{2}(t)-{\mu }_{0}\mathop{\sum}\limits _{i}{M}_{i}(t){H}_{{{{{{\rm{ext}}}}}},i}\\ -\frac{3}{2}{\lambda }_{{{\rm{s}}}}{\sigma }_{{{\rm{s}}}}{\cos }^{2}\vartheta$$
(3)

For the polycrystalline Co film, we used following parameter values: uniaxial magnetic anisotropy coefficient Ku ~ 0, the magnetostriction value λs = −62 μ37 the mechanical stress σs = 3(1 + ν)(1 − ν)−1Bηqss(t), Poisson’s ratio ν = 0.31, the bulk modulus B = 190 GPa27, and the demagnetizing factor Nx = Ny = 0, Nz = 1. \(\vartheta\) is defined as the angle between the magnetization M and σs (out-of-plane) direction. From the time-dependent profiles of Ku(t), M(t), ηqss(t), and ϑ(t) calculated after solving both the three temperatures model and the wave equation based on the measurement curve u(t), the magnetization dynamics \(d{{{{{\bf{M}}}}}}/dt\) is obtained (see “Methods” for calculation details about the three temperatures model and the wave equation).

After calculating the spin precession and extracting f from \(d{{{{{\bf{M}}}}}}/dt\), the simulation results are summarized in Fig. 2c. The values of Δf/fm considering ηqss(t) (solid lines, on the left axis) are in good agreement with experimental data of Fig. 2b, showing an increase in Δf/fm up to 2% for a wide range of φ. In contrast, for the absence of ηqss(t), Δf/fm decreased by 1.6% (dashed lines, on the right axis), as expected with conventional energy terms. We also checked the case when the spin precession was involved in neither thermal nor QSS effects. This requirement was met by the back-side measurement of the trilayer structure. The strain pulse ηp(z, t) generated from the Co top layer propagates to the Co underlayer without carrying the thermal energy and contributes only to triggering spin precession through magnetoelastic coupling. From Δθ(t) with a function of Ip under φ = 60° in Fig. 2d (the fit curve with Eq. (1) for the highest Ip is denoted by the solid line), Δf/fm did not show a noticeable change within the experimental uncertainty (see the pink curve in Fig. 2b). Here Ip = 2.6 mJ cm−2 corresponds to ~70% of the burning threshold for the Co top layer.

Ferromagnetic resonance frequency dependence on T, φ, and η qss

To obtain the comprehensive picture of the QSS effect on f over a wide range of temperature T and field angle φ, the ferromagnetic resonance frequency fr was calculated using the classical Kittel equation with the magnetic free energy F, as used in the dynamics case.

$${f}_{{{{{{\rm{r}}}}}}}={\gamma }_{{{{{{\rm{s}}}}}}}\frac{{({F}_{\varsigma \varsigma }{F}_{\xi \xi }-{F}_{\varsigma \xi }^{2})}^{1/2}}{2\pi M(T)\sin \,{\varsigma }_{{{{{{\rm{eq}}}}}}}},$$
(4)

where \({F}_{{{{pq}}}}={\partial }^{2}F/\partial p\partial q\). The symbols \(\varsigma\) and ξ denote the polar and azimuthal angles in a spherical coordinate system, respectively. \({\varsigma }_{{{{{{\rm{eq}}}}}}}\) is defined as the equilibrium angle of magnetization, and ξ = π/2 is set due to the azimuthal symmetry of the sample. As the classical Kittel equation generally treats the static regime, the QSS is assumed to be a constant supposing no thermal relaxation after a thermal equilibrium among the sub-systems. Hence, the QSS can be handled simply with thermal strain ηth(T) = βΔT (thermal expansion coefficient of Co27: β = 13.7 μ). Figure 3a, b present the contour map of fr with the control parameters of T (x-axis) and φ (y-axis) under Hext = 0.4 T for the absence and presence of ηth(T), respectively. Figure 3a shows that fr decreases monotonically with increasing T at a fixed value of φ (along the yellow line). In contrast, Fig. 3b indicates that fr increases gently with T up to ~800 K (blue box region). This is because ηth(T) increases almost linearly with T, unlike the barely altered M(T) owing to its high Curie temperature Tc. Hence, the effect of magnetoelasticity plays a dominant role over those of the conventional magnetic energy terms. At a higher T (orange box region), the rapid drop of M(T) reduces the effective field strength, leading to the inflection point of fr around 800 K.

Fig. 3: Ferromagnetic resonance frequency with the control parameters T, φ, and ηqss.
figure 3

Contour maps of a ferromagnetic resonance frequency fr calculated using the classical Kittel equation as a function of temperature T and magnetic field angle φ under Hext = 0.4 T, for the absence (a for Co) and presence (b for Co and c for Ni) of ηqss, respectively. The fr decreases monotonically with increasing T for case a, but increases moderately showing the inflection point around 800 K for case b, implying competition between the thermal and strain effects. The shaded boxes in b stand for the domains where fr increases (blue) and starts to slow down (red) as T increases. d Selected curves of Δf/fm at φ = 25, 45, and 60° from c. e Δθ(t)/θ of Ni(270)/SiO2 under Hext = 0.4 T and φ = 25° as a function of Ip. Unlike the Co bilayer, the sign of Δf/fm changes, as shown in the inset, confirming the competition between the thermal and the quasi-static strain (QSS) effects. All data points in the inset are presented with error bars obtained from the least-square fit.

Full size image

This is not a special case only for Co but can be generalized to a broad class of magnetoelastic materials. We can expect that for low Tc materials, a faster decrease of M(T) shows up at a lower T or Ip, where the QSS effect on fr is comparatively weaker. The Ni can be a good tester to examine the competition of the thermal and strain effects. The Ni has low values of Tc = 630 K and M = 525 emu cm−3 which are the key parameters for enhancing the thermal effect, but similar λs, β, and B values to Co which are related to the strain effect. Figure 3c shows the contour map of fr including the QSS effect for Ni, and Fig. 3d presents Δf/fm for φ = 25, 45, and 60° selected from the contour map. In contrast to the Co case, fr decreases first at a low T, meaning that the thermal effect is dominant, and is switched to the increase with increasing T. To prove those results experimentally, Δθ(t) of Ni(270)/SiO2 at φ = 25° and Ip ≤ 2.2 mJ cm−2 was measured and plotted in Fig. 3e. As presented in the inset, after fitting the data with Eq. (1) (denoted as the solid line for the highest Ip), Δf/fm becomes first negative and then positive as Ip increases (the error bars are marked on the data points). These curves reproduce the calculation (Fig. 3d) in excellent agreement supporting our analysis on thermal and QSS effects.

Governing role of QSS on ultrafast spin dynamics

We address that the QSS has a decisive role in determining the initial status of spin dynamics judged by further features that have been underrated. The first point is the phase of the spin precession. Figure 4a presents the calculated curves of ΔMz(t)/Mz for the absence (red) and presence (blue curve) of ηqss(z, t) under Hext = 0.54 T and φ = 60°. Here the spin precessions in Co and Ni (Figs. 2a and 3e) correspond to the blue curve, leading to a π-phase inversion compared to conventional free energy analysis.

Fig. 4: Quasi-static strain (QSS) effect governing spin dynamics.
figure 4

a Calculated curves of spin dynamics based on the Landau–Lifshitz–Gilbert (LLG) equation for the absence (red) and presence (blue curve) of ηqss under Hext = 0.54 T and φ = 60°. The π-phase inversion is clearly observed around 20 ps. The yellow dashed curve marks the monotonic-decaying background originated by a coherent rotation of Heff(t) to the in-plane direction. Inset: schematic diagram describing the rotation direction of Heff(t) depending on either QSS (blue) or thermal effect (red). b Experimental verification of the π-phase inversion of the spin precession for materials with negligible magnetoelastic energy (Ni0.36Fe0.64 (red): the thermal expansion coefficient β ~ 0, Ni0.8Fe0.2 (blue circles): the magnetostriction value λs ~ 0).

Full size image

The pictorial description of the inset explains the π-phase difference concisely. According to conventional energy analysis, the sudden decrease in M(t) after photo-excitation results in a rotation of Heff(t) (yellow solid arrow) to the out-of-plane direction (H′eff(t)—red dashed arrow) due mainly to the decrease in dipolar energy (for polycrystalline or isotropic materials) and starts precessing around the new axis H′eff(t). This aspect takes place when the thermal effect dominates the QSS effect for such conditions of λsηqss ≥ 0 (λs ≥ 0, β ≥ 0 or λs ≤ 0, β ≤ 0) and even λsηqss ≤ 0 (λs ≤ 0, β ≥ 0) provided the magnitude of λs is small. On the other hand, for λsηqss ≪ 0, the QSS effect prevails over the thermal effect and drives the rotation of Heff(t) towards the in-plane direction (H″eff(t)—blue dashed arrow). Then, the spins start the precession around the H″eff(t) axis. This orientation is determined at the initial stage of the precession, immediately after demagnetization. NixFe1-x(180)/Al2O3 films were tested experimentally to verify this scenario, as plotted in Fig. 4b. As the alloys of x ~ 0.36 and 0.8 have negligible β and λs values, respectively, it is expected that they have low magnetoelastic energy (∝ λsβΔT). These cases rotate Heff(t) towards H′eff(t), inducing negative values of signals at the first half period (20–30 ps) as the conventional analysis does, as shown with the red graph in Fig. 4a.

The second feature is the pronounced decaying background (yellow dashed line in Fig. 4a). This in general has been considered as incoherent thermal phonons and magnons with nonzero wavenumbers38, which have the heat dissipation timescale. Rather, our analysis suggests that this needs to be interpreted as the contribution of coherent rotation of Heff(t) because of the QSS effect. This was clearly verified from the fact that Co and Ni with high magnetoelastic energy have much larger decaying offsets than those of NiFe alloys. These all features mentioned above, including the frequency increase in the spin precession, are reproduced through the model calculation incorporating only one concept of the QSS effect with the full consistency with the experimental data.

Discussion

By decoupling the thermal and the QSS effects using USI and the MOKE, we proved that the QSS has a governing role over the thermal effect on the overall behavior of ultrafast spin dynamics over a wide range of time scales. The ultrafast photo-excitation can strengthen the effective magnetic field due to the QSS effect. This leads to a higher frequency of spin precession and accounts for the π-phase inversion determined from the initial stage of the precession. Besides, the long-lived offset with the relaxation timescale of the QSS was interpreted as extra gain induced by the contribution of a coherent rotation of Heff(t). This study shows that the QSS is involved universally in a wide family of magnetoelastic materials and should be treated fundamentally.

The strain of 0.1–1% generated by photo-excitation is high enough to induce the modification of the electronic band structure26 even at ultrafast time scales39. Therefore, it can be predicted that the QSS modifies the dielectric tensors bringing about features such as derivative-like changes in differential magneto-optics. And this will lead to inequivalence between its real and imaginary parts of magneto-optic signal, and involuntary extra gains in differential reflectivity as well even after thermal equilibrium timescale. To date, considerable effort has been made to identify genuine magnetism and the origin of demagnetization3,20,40,41,42,43,44,45,46. Our demonstration that the QSS governs the spin dynamics provides an interpretation of ultrafast magneto-optics and therefore helps to better understand the physical mechanisms behind ultrafast phenomena by considering both strain and thermal effects.

Methods

Time-resolved pump–probe MOKE

We used Ti:sapphire regenerative amplified laser pulses with a repetition rate of 10 kHz, a temporal width of 40 fs, and a center wavelength of 800 nm. The pump pulses are frequency-doubled with a beta Barium Borate crystal and have a temporal width of 60 fs at a sample position. The pump and probe pulses were focused on the sample with diameter sizes of 150 and 30 μm, respectively, and their intensity ratio was set to ~1000:1. The reflected probe pulses from the samples were split into orthogonal polarizations using a Wollaston prism and analyzed into the differential Kerr rotation Δθ(t) and differential reflectivity ΔR(t). An external magnetic field of Hext = 0.4 T was applied with various angles φ from the normal to the sample plane.

Ultrafast Sagnac interferometer

An ultrafast Sagnac interferometer based on a Ti:sapphire oscillator system issued with a center wavelength of 800 nm and a temporal width of 40 fs was employed to obtain a quantitative profile of the time-resolved lattice thermal expansion after the pump excitation. After passing through an electro-optic modulator operating at 1 MHz, the dispersed pulse was compressed to 45 fs by pairs of negative-chirped mirrors. The pump pulses were frequency-doubled by a 500-μm-thick BiB3O6 crystal with a conversion efficiency of 25% and had a temporal width of 65 fs at a sample position. The probe and pump pulses were focused on the front and back sides of the samples in normal incidence. The numerical apertures of the objective lenses used in each beam line were 0.55 and 0.4, respectively. The temporal delay between p-pol. (arrives at a negative delay) and s-pol. probes (arrives at a positive delay) at the sample position were fixed to ~1 ns and the s-pol. probes measure the pump-induced optical responses (ρ and δϕ) (Supplementary Note 1 for more details of the setup schematics and characteristics).

Strain calculation and parameter values

To obtain η(z, t), it is necessary to solve the three temperatures model and one-dimensional wave equation in the Co(25)/Al2O3 structure. The three temperatures model (Eq. (5)) is described as follows:

$${C}_{i}({T}_{i})\frac{\partial {T}_{i}}{\partial t}={\delta }_{i{{{{{\rm{e}}}}}}}\left[\frac{\partial }{\partial z}\left(\kappa \frac{\partial {T}_{i}}{\partial z}\right)+P(z,t)\right]-{g}_{ij}\varDelta {T}_{ij}$$
(5)

where i, j = e, l, s stand for electrons, lattice, and spins, respectively. The Ci and κ are the heat capacity per unit volume of bath i and the thermal conductivity. The gij is the coupling coefficient between two baths i and j, and P(z, t) the laser source term. The ΔTij is defined as Ti − Tj, the temperature difference between two baths i and j. Using boundary conditions—continuities of both the heat transfer at air/Co \(({0={\kappa }_{{{{{{\rm{Co}}}}}}}\frac{\partial {T}_{{{{{{\rm{e}}}}}}}}{\partial z}|}_{{{{{{\rm{z}}}}}}=0,{{{{{\rm{Co}}}}}}})\), Co/Al2O3 \(({{\kappa }_{{{{{{\rm{Co}}}}}}}\frac{\partial {T}_{{{{{{\rm{e}}}}}}}}{\partial z}|}_{{{{{{\rm{z}}}}}}={{{{{\rm{d}}}}}},{{{{{\rm{Co}}}}}}}={{\kappa }_{{{{{{\rm{Al2O3}}}}}}}\frac{\partial {T}_{{{{{{\rm{l}}}}}}}}{\partial z}|}_{{{{{{\rm{z}}}}}}={{{{{\rm{d}}}}}},{{{{{\rm{Al2O3}}}}}}})\) and the temperatures at Co/Al2O3 \(({{T}_{{{{{{\rm{e}}}}}}}(z,t)|}_{{{{{{\rm{z}}}}}}={{{{{\rm{d}}}}}},{{{{{\rm{Co}}}}}}}={{T}_{{{{{{\rm{Al2O3}}}}}}}(z,t)|}_{{{{{{\rm{z}}}}}}={{{{{\rm{d}}}}}},{{{{{\rm{Al2O3}}}}}}})\)—temperature profiles of the three baths were obtained (d is a film thickness). Here, since there is an arbitrariness for the selection of pump intensity and unknown value of Cs, we carefully chose the value by matching with the experimental data of both u(z = 0, t) of the Sagnac measurement and the demagnetization ΔθL(t)/θL (longitudinal Kerr geometry) under Hext = 0.5 T and φ = 90°. That is, Tl(z, t) obtained from three temperature models calculation (Eq. (5)) is linked to u(z, t) through the one-dimensional wave equation (Eq. (6)) as follows:

$$\frac{{\partial }^{2}u(z,t)}{\partial {t}^{2}}={\upsilon }^{2}\frac{{\partial }^{2}u(z,t)}{\partial {z}^{2}}-\frac{3\beta B}{\rho }\frac{\partial {T}_{{{{{{\rm{l}}}}}}}}{\partial z}$$
(6)

where ρ is the mass density, υ the sound velocity, β the linear thermal expansion coefficient, and B the bulk modulus. Using boundary conditions, continuities of both the stress at air/Co \((3\frac{1-\nu }{1+\nu }B\frac{\partial u}{\partial z}=3\beta B\varDelta {T}_{{{{{{\rm{l}}}}}}})\), Co/Al2O3 \((3\frac{1-\nu }{1+\nu }B\frac{\partial u}{\partial z}-3\beta B\varDelta {T}_{{{{{{\rm{l}}}}}}}=3\frac{1-{\nu }_{{{{{{\rm{Al2O3}}}}}}}}{1+{\nu }_{{{{{{\rm{Al2O3}}}}}}}}{B}_{{{{{{\rm{Al2O3}}}}}}}\frac{\partial u}{\partial z})\), and the displacements at Co/Al2O3 \(({u(z,t)|}_{{{{{{\rm{z}}}}}}={{{{{\rm{d}}}}}},{{{{{\rm{Co}}}}}}}={u(z,t)|}_{{{{{{\rm{z}}}}}}={{{{{\rm{d}}}}}},{{{{{\rm{Al2O3}}}}}}})\) − u(z, t) were solved. Then, \({{\eta }_{{{{{{\rm{qss}}}}}}}(t)=\partial u(z,t)/\partial z|}_{{{{{{\rm{z}}}}}}=0}\) was determined by matching u(0, t) with the Sagnac measurement curve, as shown in Fig. 1c. The parameter values used in the simulation are as follows: Ce = 6.6 × 102 Te, Cl = 3.5 × 106 47, Cs = −WmdM2/dTs J m−3 K−1 48 where a molecular field prefactor Wm was assumed to be 4.5 × 108 for Co, and Cl = 3.1 × 106 for Al2O349. κCo = 6447, κAl2O3 = 20 W m−1 K−1 50 at 500 K, B = 190 GPa, ν = 0.31 for Co27. For dynamic heat coupling coefficients between two sub-systems, we used the following values: gel = 1.3 × 1018, gls = 5.0 × 1017, and ges = 3.5 × 1017 W m−3 K−1 to match with the ΔθL(t)/θL and u(0, t) curves qualitatively. For the Curie–Weiss curve, M(T) = Ms(1 − 1.058(T/Tc)α)ζ was extracted by fitting the data in ref. 51, here Ms = 1360 emu cm−3, Tc = 1380 K, α = 3.15, and ζ = 0.50.