All-optical quasi-monoenergetic GeV positron bunch generation by twisted laser fields

Abstract

Generation of energetic electron-positron pairs using multi-petawatt (PW) lasers has recently attracted increasing interest. However, some previous laser-driven positron beams have severe limitations in terms of energy spread, beam duration, density, and collimation. Here we propose a scheme for the generation of dense ultra-short quasi-monoenergetic positron bunches by colliding a twisted laser pulse with a Gaussian laser pulse. In this scheme, abundant γ-photons are first generated via nonlinear Compton scattering and positrons are subsequently generated during the head-on collision of γ-photons with the Gaussian laser pulse. Due to the unique structure of the twisted laser pulse, the positrons are confined by the radial electric fields and experience phase-locked-acceleration by the longitudinal electric field. Three-dimensional simulations demonstrate the generation of dense sub-femtosecond quasi-monoenergetic GeV positron bunches with tens of picocoulomb (pC) charge and extremely high brilliance above 10¹⁴ s⁻¹ mm⁻² mrad⁻² eV⁻¹, making them promising for applications in laboratory physics and high energy physics.

Introduction

Ever since the positron was discovered in 1930s by Anderson¹, extensive theoretical modeling, numerical simulations and experiments have been carried out to investigate the generation and application of positrons in various fields^2,3, such as material science, particle physics, medical treatments as well as laboratory astrophysics. Spontaneous pair production by a single laser beam in vacuum was predicted by Schwinger⁴ when the electric field reaches E_S ≈ 1.32 × 10¹⁸ V m⁻¹. This corresponds to a laser intensity of 10²⁹ W cm⁻², which is far beyond the current laser technology capability. Although it has been proved theoretically that the threshold could be lowered down to 10²⁶ W cm⁻² by colliding laser beams⁵, the intensity is still at least three orders of magnitude larger than the achievable magnitude in the current laboratories. Several other approaches with seeded particles have been also proposed and extensively investigated in the past decades. For example, the trident process^6,7 relies on the energetic (hot) electrons direct interaction with the Coulomb field of the nuclei, while the Bethe–Heitler (BH) process^{8,9,10,11,12,13,14,15} refers to the positron generation by the interaction of bremsstrahlung γ-photons with heavy nucleus. In case of two γ-photons collision, the Breit-Wheeler (BW) process¹⁶ dominates the electron-positron pair production, by which pure light can be transformed into matter. Although the linear BW process has weak probability, researchers have managed to observe this process on the Relativistic Heavy Ion Collider (RHIC)¹⁷. Different from the pure linear BW process, a significant number of pairs can be generated via the nonlinear BW process, where the energetic γ-photon beams propagate through an electromagnetic field, e.g., a laser pulse. This makes it possible to generate copious positrons in a configuration of laser-laser or laser-electron collisions. The famous SLAC-E144 experiment performed twenty years ago is a typical example^18,19 of the latter choice, where a 46.6 GeV electron beam first created high-energy γ-photons and then underwent multiple collisions with the laser pulses from a Nd:glass laser at 527 nm wavelength. Finally, a signal of 106 ± 14 positrons with a broad energy spectrum in the range of 5–20 GeV was detected. However, such positron beams are not suitable for practical applications due to the trivial positron number produced.

With the advent of multi-petawatt (PW) lasers, significant efforts have been recently dedicated to obtaining high-energy-density electron-positron pairs by use of extremely intense laser-plasma interactions in various configurations^{20,21,22,23,24,25,26,27,28,29,30,31,32,33,34}, such as thin foil target^20,21,22, laser-electron collision in gas plasma²⁷, cone target filled with near critical density (NCD) plasma²⁹ and plasma channel³⁴, some of which have the potential to be prolific positron yield factories and may be tested on the upcoming multi-PW laser systems. Although dramatic progress has been made on the generation of copious numbers or high-energy-density positrons^{35,36,37,38,39,40,41,42,43,44}, there are some other restrictions on the practical usage of positrons generated from BH or BW processes, such as the separation of positrons from the plasma background and the preservation of the positron beam quality. Besides, the control of energy spread and duration of the generated positron beam driven by lasers is still extremely challenging and remains to be solved, which is essential for further applications in particle physics, e.g., as positron injection source in electron-positron collider and defect probing in materials. To the best of our knowledge, the methods to achieve dense short monoenergetic positron beams by use of multi-PW lasers in an all-optical way are yet to be explored.

In order to achieve both high yields of positrons and follow-up manipulation on the positron beam properties, here we propose an all-optical scheme for the generation of dense ultra-short quasi-monoenergetic positron bunches by use of a twisted laser pulse. At the first stage of the scheme, a relativistic Laguerre–Gaussian (LG) laser pulse is focused onto a cylindrical NCD plasma with a parabolic transverse density gradient, which can accelerate electrons directly from the background plasma to form sub-femtosecond electron bunches with energy up to several GeV. Then these energetic electrons quiver strongly in the LG laser fields and collide head-on with a high-intensity scattering Gaussian laser field in the second stage, emitting abundant γ-photons via the nonlinear Compton scattering (NCS) process. At the final stage, the multi-photon BW process is triggered and copious numbers of positrons are generated. Due to the unique structure of LG laser fields, these positrons are compressed by the radial electric field and suffer phase-locked-acceleration (PLA) by the longitudinal electric field. As a result, dense sub-femtosecond quasi-monoenergetic GeV positron bunches are generated, which can be further accelerated in vacuum.

Results

Motivation of the scheme

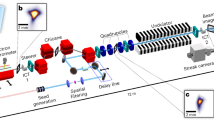
Generally, it is difficult to couple the generation, injection, and acceleration of high-energy-density positrons in an all-optical setup. In past decades, thin foils have been extensively employed for dense positron generation^20,21,22. However, once the ultra-intense laser pulse propagates through the foil plasma, its profile will be modified significantly, making it very difficult to control the positron beam quality without additional laser and beam facilities. Another issue is the fast dispersion of positrons by the drive pulse, whose ponderomotive force pushes the particles off the laser axis. Although ideally suited for electron acceleration, laser wakefields in plasma are not adequate for positron acceleration since positrons are easily expelled away from the bubble in the transverse direction⁴⁵. Therefore, several methods have been proposed to mitigate this problem on positron wakefield acceleration from simulations^46,47 and experiments⁴⁸, but they generally require the pre-injection of monoenergetic positron beams, and these positrons are generally produced via the BH process. It has been shown that appropriate time and spatial waveform of laser fields could potentially manipulate the properties of charged particles. Vortex light⁴⁹ is one of the examples, which has been widely used in quantum information⁵⁰, communication⁵¹, micromanipulation⁵², etc. The LG laser is a typical vortex light characterized by a hollow intensity distribution with a spiral equiphase surface and carrying orbital-angular-momentum (OAM). It has been proved that the LG laser pulse could be used to drive particle acceleration with high OAM^53,54,55, generate γ-ray vortex^56,57 as well as harmonics vortex⁵⁸. In our scheme, we propose a configuration composed of a relativistic circularly polarized LG laser pulse with an intensity of order of 10²² W cm⁻² and parabolic NCD plasma channel. This laser pulse has been shown to be achievable by a normal Gaussian pulse incident on optical devices like spiral phase plate^59,60, by Raman amplification in plasma⁶¹, or by plasma holograms⁶². With the help of a cone structure⁶³, the intensity of LG laser can even be increased to beyond 10²² W cm⁻². Unlike solid targets, the drive laser can keep its profile almost intact in the NCD plasma, which plays a key role in the manipulation of positron bunches. Figure 1 schematically illustrates the three stages of our scheme, which has been simulated by full three-dimensional (3D) particle-in-cell (PIC) simulations (see Methods). It is shown that dense ultra-short quasi-monoenergetic GeV positron bunches can be generated by 10 PW-scale lasers, which may open up potential applications in particle physics.

Fig. 1: Schematic diagram of quasi-monoenergetic positron bunches generation by twisted lasers in near critical density (NCD) plasma.

The scheme is divided into three stages: (I) The Laguerre–Gaussian (LG) drive laser is incident onto the NCD plasma from the left-side, accelerating electrons from the background plasma to form sub-femtosecond electron bunches at multi-GeV energy. (II) Copious γ-photons are generated via the nonlinear Compton Scattering (NCS) process when the electron bunches collide head-on with a time-delayed scattering laser pulse traveling inside the NCD plasma. (III) Prolific electron-positron pairs are generated via the multi-photon Breit-Wheeler (BW) process, which are further compressed transversely, and accelerated longitudinally via the phase-lock-acceleration (PLA), resulting in the generation of sub-femtosecond quasi-monoenergetic positron bunches. The bunches can be accelerated further and sustain their properties for tens of laser cycles when propagating in vacuum.

Dense electron bunches formation

When the LG laser propagates into the NCD plasma, it picks up electrons from the background via the radial electric field, forming a dense electron bunch train as shown in Fig. 2a. This can be attributed to the special structure of the LG laser electric fields. Here, the laser radial electric field can be written as^54,64 $E_r = E_y \cdot \cos \alpha + E_z \cdot \sin \alpha = \frac{{E_0f^2r}}{{\sigma _0\left( {f^2 + x^2} \right)}}{{{{{{{\mathrm{e}}}}}}}}^{ - \left( {\frac{r}{\sigma }} \right)^2}G\left( \phi \right)$, where E₀ is the peak value of the laser electric field, α is the direction angle of electric field in the y−z plane, σ₀ is the focal spot radius, σ is the spot radius related to x coordinates, G(ϕ) is the temporal shape of the laser which is Gaussian in our simulations, $f = \frac{{\pi \sigma }}{\lambda }$ is the Rayleigh length and λ is the wavelength of the laser. The phase factor $\phi = \omega _0t - k_0\left( {x + \frac{{r^2}}{{2r_l}}} \right) - 2arctan\left( {\frac{x}{f}} \right)$, ω₀ is the angular frequency, $r = \sqrt {y^2 + z^2}$, $k_0 = 2\pi /\lambda$ is the wave number and $r_l = x + \frac{{f^2}}{x}$ is the radius of curvature of the wavefront. When $\phi = \pi /2 + 2n\pi\,\left( {n = 0,1,2 \cdots } \right)$, E_r points outward and has the maximum value that pushes the electrons towards the laser axis; when $\phi = 3\pi /2 + 2n\pi$, E_r points inward and has the maximum value that drives electrons off the laser axis. This results in the formation of an electron bunch train with a sub-femtosecond scale duration and 7.8 nC charge per bunch (see Supplementary Note 1).

Fig. 2: Formation and acceleration of GeV electron bunches.

Dense sub-femtosecond electron bunches are formed with a high cutoff energy (~2 GeV), large energy density (~10⁵ MeV·n_c) and sub-femtosecond full width at half maximum (FWHM) duration (~825 as). a Energy density distribution of electrons at t = 45T₀. Here the on-axis electron density distribution is illuminated in the x−z plane. b Evolution of the electron energy spectrum. c Electron angle-energy distribution right before the laser-electron collision (t = 50T₀).

On the other hand, the longitudinal electric field of the LG laser can be written as⁵⁵

$$E_x = \frac{{\sqrt {2e} E_0\sigma _0}}{{k_0\sigma ^2}}{{{{{{{\mathrm{e}}}}}}}}^{ - \left( {\frac{r}{\sigma }} \right)^2}G(t)\left[ {2\left( {\frac{{r^2}}{{\sigma ^2}} - 1} \right)cos\phi - \frac{{k_0r^2}}{{r_l}}sin\phi } \right],$$

(1)

where e ≈ 2.718 is the Euler number. It is shown that E_x reaches the maximum $E_{x,max} = - 2\frac{{\sqrt {2e} E_0\sigma _0}}{{k_0\sigma ^2}}cos\psi$ on the laser axis (r = 0). Thus, the strong longitudinal electric field can accelerate the electrons near the axis most efficiently. This also decreases the dephasing rate⁶⁵ $R = \gamma _e - p_x/m_ec$, leading to a much longer distance of acceleration, where γ_e is the relativistic factor of electron, p_x and m_e represent the longitudinal momentum and rest mass of electrons, respectively. The laser radiation pressure also plays an important role in the electron bunch acceleration, which can be written as $F_{rad} = P \cdot \frac{{dS}}{{n_edV}} = \frac{1}{{cn_el}}\sqrt {\frac{{\varepsilon _0}}{{\mu _0}}} \cdot \frac{{2eE_0^2r^2\sigma _0^2}}{{\sigma ^4}}{{{{{{{\mathrm{e}}}}}}}}^{ - 2\left( {\frac{r}{\sigma }} \right)^2}.$ Obviously, the force depends on the electron density and position. It reaches the maximum at $r = \sigma /\sqrt 2$, and is one order of magnitude larger than $q_eE_{x,max}$ when $n_e = 10n_c$. Here, $n_c = m_e\omega _0/4\pi q_e^2 \approx 1.1 \times 10^{21}cm^{ - 3}$ is the critical density at the laser wavelength of 1 μm, where q_e is the charge of an electron. This interprets the fact that the off-axis electrons with lower density are able to be accelerated to much higher energy than the electrons on the laser axis. Figure 2b presents the evolution of electron energy spectrum. It shows that these electrons have a cutoff energy of more than 2 GeV at t = 50T₀ and reach a peak energy density of 10⁵ MeV·n_c. Afterwards, the cutoff energy decrease, which is due to the γ-photon emission via the subsequent NCS process at the stage II. The different acceleration mechanisms for the electrons around the axis and off-axis lead to the double-peak structure in the angle-energy distribution of electrons as indicated in Fig. 2c.

Energetic γ-photon emission

The high-energy electrons quiver quickly in the LG laser field so that a large quantity of photons could be emitted in the quantum radiation dominated regime. At this stage, the intensity of photon emission process can be characterized by the quantum invariant $\chi _e = \left( {\frac{{\gamma _e}}{{E_s}}} \right)\scriptstyle\sqrt {( {\overrightarrow \beta \times c\overrightarrow B + \overrightarrow E })^2 - ( {\vec \beta \cdot \vec E} )^2}$, where $\overrightarrow \beta = \overrightarrow v _e/c$ is the normalized electron velocity, $\gamma _e = 1/\sqrt {1 - \beta ^2}$, and c is the speed of light in vacuum. Figure 3a illustrates the distribution of χ_e along the x axis in the collision zone at t = 50T₀. It is shown that χ_e is between 0.1 and 0.6, exciting the emission of sufficient γ-ray photons when the energetic electron bunches head-on collide with the scattering laser. Due to the short bunch structure, these photons have a similar distribution to the electrons with a peak density of 300n_c. Figure 3b presents the photon energy spectrum evolution, which shows a cutoff energy of photons as high as 1 GeV before the collision and 1.5 GeV after the collision. The significant increase of photon energy and number are mainly attributed to the NCS process during the collision. By integrating the energy spectrum, we also see that the radiation power from the quivering electrons in the LG laser field is about 0.27 PW, while the peak radiation power via the NCS process is increased up to 6 PW, an order of magnitude higher than in the former process. Meanwhile, these photons also show a double-peak structure in the angle-energy space as indicated in Fig. 3b. Different from the electron bunches above, the high-energy photons are mainly resided within a smaller divergence angle about 15°. Although the off-axis electrons have larger velocity and energy, the incident scattering laser is Gaussian and has the maximum value on the axis, leading to much larger χ_e around the laser axis. Thus, the higher energy photons resulting from the NCS process are generated by the electron bunches near the axis instead of the off-axis electrons. This results in the smaller divergence angle and higher photon energy as indicated in Fig. 3b. This small divergence angle leads to the high peak-brightness of the photon bunch of $8.04 \times 10^{25}photons\,s^{ - 1}mm^{ - 2}mrad^{ - 2}\left( {0.1\% bandwidth} \right)^{ - 1}$ with the photon energy centered at 13.13 MeV and the bunch size of 1 μm (see Supplementary Note 2 and 3), the value is comparable to the average-brightness of X-ray free-electron lasers. By use of stronger lasers, one may achieve brighter γ-photon beams (from MeV to GeV) with much higher peak-brightness approaching EuXFEL⁶⁶ centered at 25 keV.

Fig. 3: Generation of γ-photons.

a Distribution of quantum invariant χ_e in the collision area at t = 50T₀. b Angular distribution of γ-photons at t = 55T₀. The inset shows the evolution of photon energy spectrum.

Positron bunches generation

The generated γ-photons continue propagating forward and collide with the counter-propagating Gaussian laser field coming from the right side at around t = 55T₀, hence initiating the multi-photon BW process. At this stage, the quantum invariant determining the electron-positron pair emissivity is $\chi _\gamma = \hbar \omega _0\left| {\vec E_ \bot + \vec k \times c\vec B} \right|/\left( {2m_ec^2E_S} \right)$, where $\vec E_ \bot$ is the electric field perpendicular to the velocity of γ-photons, and $\vec k = \frac{{2\pi \vec v}}{{\lambda _{ph}c}}$ is the wave vector of the emitted photon. Here, λ_ph is the wavelength of the photon and $\vec v$ is the speed vector of the photon. Figure 4a presents the 2D distribution of χ_γ in the x−y plane of the collision zone. The result shows that χ_γ reaches 0.6, implying the generation of copious electron-positron pairs. Moreover, χ_γ is much larger near the laser axis due to higher energy of γ-photons and stronger transverse field of Gaussian laser fields there, leading to the creation of copious electron-positron pairs around the laser axis. Figure 4b demonstrates that most positrons are distributed within a small range in the transverse direction, which shows a similar distribution to the transverse laser electric field.

Fig. 4: Quasi-monoenergetic positron bunch generation.

a Distribution of quantum invariant χ_γ in the collision zone at t = 50T₀. b Distribution of positrons and their relative position to the E_y field at t = 50T₀. c Density distribution of positron bunches at t = 78T₀. d The corresponding energy spectrum of each positron bunch as marked in (c).

Figure 4c presents the density distribution of positrons at t = 78T₀. One can see that the positrons are characterized by a train of position bunches each with a duration of about 680 as and a peak density of 8n_c (see Supplementary Note 3). The energy spectrum of each positron bunch is presented in Fig. 4d. It is apparent that the positron bunches are quasi-monoenergetic and the cutoff energy of the first bunch is as high as 1 GeV with total charge of about 55 pC. At t = 78T₀, the absolute FWHM energy spread of the second positron bunch is δE ≈ 60 MeV with the center energy of E ≈ 530 MeV. Thus, the minimum relative energy spread is δE/E ≈ 11.3% (see Supplementary Note 4), which is much less than those obtained in the previous work via the BH process^14,15. To the best of our knowledge, it is the first time to report such dense quasi-monoenergetic positron bunch generation via the multi-photon BW process. Compared with the BH case¹⁴ at a similar laser intensity, the positron number density is about five orders of magnitude higher. Furthermore, the skin depth of the pair plasma $l_s \approx 2.24\,\mu m$ is smaller than the transverse plasma size of 2.51 μm, inducing weak collective effects of plasmas and making the hot dense pair plasma potential candidate as a test bed for pair plasma physics as well as nonlinear QED physics^2,29.

Acceleration and propagation of positron beams

As the positron bunches co-propagate along with the LG laser pulse, they experience compression and acceleration in the transverse and longitudinal direction, respectively (see Supplementary Note 5). In the transverse direction, the positron bunches are well confined by the negative radial electric field E_r, forming collimated energetic positron bunches. For a more intuitive description, we show the 2D distribution of transverse electric and magnetic field force $\vec F_ \bot = \vec E_ \bot q_e + q_e\left( {\vec v \times \vec B} \right)_ \bot$ experienced by positrons in the y−z plane at t = 65T₀ in Fig. 5a. It is interesting to see that the positrons within the red dashed circle ($r = \sigma /\sqrt 2$) are well confined with a very small transverse velocity, while the positrons outside of the circle are scattered off the laser axis by the laser field. This phenomenon can be attributed to the transverse ponderomotive force of the LG laser pulse:

$$F_{tr} = \left[ {2\left( {\frac{r}{\sigma }} \right)^2 - 1} \right]\frac{{F_0f^2}}{{k_0\sigma _0\left( {f^2 + x^2} \right)}}{{{{{{{\mathrm{e}}}}}}}}^{ - \left( {\frac{r}{\sigma }} \right)^2},$$

(2)

where $F_0 = \sqrt {2{{{{{{{\mathrm{e}}}}}}}}} q_eE_0$. It is shown that, when $r\, > \,\sigma /\sqrt 2$, the transverse ponderomotive force F_tr > 0, so that the positrons beyond the circle are pushed outward. On the contrary, as $r \, < \, \sigma /\sqrt 2$, F_tr > 0, positrons are confined within a small range. These are in good agreement with our simulation results as shown in Fig. 4b. Thus, the transverse compression of positrons can be achieved by the special field distribution of LG laser without applying extra magnetic fields as in previous researches¹⁵. It is in sharp contrast to the case of using normal Gaussian drive laser, where the generated positrons are dispersed quickly in space and there are no obvious positron bunches formed (see Supplementary Note 6). Due to the limited transverse motion, the positrons are well directed with a small divergence angle of 12°, as presented in Fig. 5b. Additionally, the geometric emittance of the positron bunches ${\it{\epsilon }}_s = \scriptstyle\sqrt { < s^2 > < \theta _s^2 > - < s\theta _s > ^2}$ in y and z direction is ${\it{\epsilon }}_y = 0.036\,mm \cdot mrad$ and ${\it{\epsilon }}_z = 0.034\,mm \cdot mrad$, respectively, which are two orders of magnitude smaller than that recently acquired in experiments⁶⁷. Here, s represents the direction in space (x, y, z), <s> is the average particle position in the s direction, and $< \theta _s >$ is the average angle between the particle momentum p and the s axis. Correspondingly, the peak beam brilliance is $B_{e^ + } = \frac{{N_{e^ + }/\tau _{e^ + }}}{{{\it{\epsilon }}_y{\it{\epsilon }}_zE_{e^ + }}} = 1.03 \times 10^{14}$ $s^{ - 1}\,mm^{ - 2}\,mrad^{ - 2}eV^{ - 1}$ with the source size of 1 μm, ten million times brighter than the reactor-based positron source NEPOMUC⁶⁸, where $N_{e^ + }$, $\tau _{e^ + }$, $E_{e^ + }$ are the total number, duration, and energy of a positron bunch, respectively.

Fig. 5: Phase space distribution of positrons.

a Transverse electric and magnetic field force experienced by typical positrons located at x = 68 μm in the y−z plane at t = 65T₀. The red dashed circle with $r = \sigma /\sqrt 2$ indicates the location of the positron bunch. b Angle-energy distribution of positrons. The inset shows the magnitude of the longitudinal electric force E_xq and the ponderomotive force F_x versus r. c Positron distribution in x − p_x phase space at t = 70T₀. Here, the green shadow indicates the location of positrons phase-locked and accelerated (E_x > 0, E_r < 0). d Evolution of the first positron bunch in x − px phase space.

In contrast with electrons, the positrons are accelerated dominantly by the positive longitudinal electric field E_x. Here, the positron dephasing rate can be rewritten as $R = 1 - \frac{{q_e}}{{m_ec}}{\int} {E_xdt^\prime }$. In our case, E_x > 0, the positrons are rapidly accelerated to near the speed of light accompanying with a much longer acceleration length due to the decreasing R, so that they are swiftly phase-locked and accelerated in the NCD plasma. Since the positrons are well confined within a small zone near the laser axis, the positron acceleration is thus dominated by the longitudinal electric field. However, the off-axis positrons are also accelerated by the laser ponderomotive force $F_x = - \partial V_{pond}/\partial x \approx \frac{{2\lambda ^2x}}{{\pi ^2\sigma ^2\sigma _0^2}}\left( {1 - \frac{{r^2}}{{\sigma ^2}}} \right)\frac{{\sqrt {2e} E_0q_er\sigma _0}}{{k_0\sigma ^2}}{{{{{{{\mathrm{e}}}}}}}}^{ - \left( {\frac{r}{\sigma }} \right)^2}$, which is positive inside the laser spot (r < σ) except on the laser axis (F_x = 0). Here F_x is of the same order of magnitude as the longitudinal electric field force q_eE_x. On the one hand, F_x equals zero on the laser axis and increases gradually along the radial direction; on the other hand, the decreased longitudinal electric field force q_eE_x along with the radial direction compensate the increased F_x force, as seen in Fig. 5b, so that the positrons in each bunch can be accelerated as a whole. The unified positron acceleration results in eventually the generation of quasi-monoenergetic positron bunches as shown in Fig. 4d.

Figure 5c presents the x−p_x phase space distribution of positrons at t = 70T₀, which indicates a clear sub-femtosecond bunch structure as observed in Fig. 4c. It is shown that the phase-locked positron bunches are well confined by the negative radial electric field E_r. Especially, the E_x field shows an approximately linear roll-off for a large number of positrons, which plays a crucial role for the positron micro-bunching. Similar to the proton acceleration in the phase-stable-acceleration (PSA) regime^69,70,71, the phased-locked tail positrons experience larger longitudinal electric field forces and can catch up with the positrons in the front, leading to the micro-bunching of positrons. In order to illustrate this, we present the evolution of micro-bunching process of positrons in the x−p_x space, as shown in Fig. 5d. It shows that the positron bunch is discrete in the x−p_x phase space and is characterized by a typical micro-bunching structure, leading to the generation of quasi-monoenergetic positron bunches.

Moreover, the positron bunches can be accelerated further and sustain their structure for a few tens of laser periods after they propagate into vacuum at t = 88T₀, as shown in the inset of Fig. 5d. For example, the first positron bunch can be accelerated from 1.2 GeV to 3.8 GeV and maintain its structure after traveling for 40 laser cycles in vacuum (see Supplementary Note 7). Although these bunches show somewhat spatial diffusion in the transverse direction, their energy spread and duration are well maintained. It is interesting to note that the protons from the NCD plasma dephase quickly due to their low energy and large mass, compared with the positrons. Thus, the positron bunches can be well separated from the NCD plasma background, facilitating the further manipulation for potential applications. Figure 6 presents a possible experimental setup. Based on some previous researches^54,55, a left-handed circularly polarized LG pulse is chosen as the drive laser to generate short particle bunches. Since the generated electron and positrons are highly-collimated and confined near the laser axis, they may be separated from the laser pulses and γ-ray beams by using magnets, e.g., dipole, quadrupole, and sextupole magnets. However, electron-positron separation with dense beams is still challenging nowadays and should be considered carefully in future experiments. In particular, by use of few-cycle laser pulses, isolated ultra-short electron and X/γ-photon bunches can be generated^72,73, so that a single positron bunch also can be expected via the BW process.

Fig. 6: Proposal of an experiment set-up to acquire high-quality positron beams.

The LG laser pulse can be obtained by irradiating a phase plate with a usual Gaussian laser pulse (see Methods), for example, a 16/32 stair phase plate with the stair-height of tens nanometers employed in previous experiments⁶⁰ can be used here. Then, the LG laser pulse interacts with the nanotube foam target and collide with the scattering laser, generating abundant γ-ray and electron-positron pairs. Finally, the collimated electron and positron beams can be separated from the laser pulses and γ-ray beams by use of magnetic fields.

Discussion

In order to demonstrate the robustness of the scheme, we perform additional simulations to investigate the laser energy and angular momentum conversion efficiency into γ-photons and positrons. Firstly, we vary the drive laser intensity from a_d = 180 to 265 while keeping a_s = 150. Since the on-axis electrons are accelerated mainly by the longitudinal electric field E_x, the energy of electrons depends on a_d and the acceleration length. As mentioned before, with such strong drive laser intensity (a_d ≧ 180), electrons could be accelerated to near the speed of light within one laser cycle and are phase-locked in the acceleration phase, so that the acceleration length approximates the same. Thus, the energy conversion efficiency from the lasers to electrons scales as $\varepsilon _e = E_e/E_{laser} \propto a_d/\left( {a_d^2 + a_s^2} \right) \sim a_d^{ - 1}$. In the near QED regime, the radiation power of energetic electrons can be estimated by $P_\gamma \approx \frac{2}{3}N_eq_eE_sc\alpha _f\overline {\chi _e^2g\left( {\chi _e} \right)}$, where N_e is the electron number, α_f is the fine structure constant, $\chi _e \propto \gamma _e\left| {E_ \bot } \right| \sim \left( {a_d^2 + a_s^2} \right)a_d \sim a_d^3$, $\overline {\chi _e^2g\left( {\chi _e} \right)}$ is the average radiation power factor, and $g\left( {\chi _e} \right) \approx \left( {1 + 12\chi _e + 31\chi _e^2 + 3.7\chi _e^3} \right)^{ - 4/9}$ is the quantum weaken factor. The energy of emitted γ-photons is estimated as $E_\gamma \propto E_e\overline {\chi _e^2g\left( {\chi _e} \right)}$, thus we can get the simple approximation of the laser energy conversion efficiency to the γ-photons as $\varepsilon _\gamma = E_\gamma /E_{laser} \sim a_d^{1/3}$, in accordance with the simulation results in Fig. 7a. The approximate form of the function determining the rate of electron-positron pair production is²⁸ $T_ \pm ( {\chi _\gamma } ) \approx 0.16\frac{{K_{1/3}^2\left[ {2/( {3\chi _\gamma } )} \right]}}{{\chi _\gamma }}$, where K is the modified Bessel function of the second kind. When χ_γ < 8, $T_ \pm ( {\chi _\gamma } ) \propto {{{{{{{\mathrm{exp}}}}}}}}\left[ { - 2/( {3\chi _\gamma } )} \right]$, and $\chi _\gamma \propto \gamma _e^2\left| {E_ \bot } \right|^2 \sim a_d^6$. Since the positron acceleration is dominated by the laser longitudinal electric field, the laser energy conversion efficiency to the positrons is thus $\varepsilon _{e^ + } \propto \varepsilon _\gamma T_ \pm ( {\chi _\gamma } )a_d \sim a_d^{4/3}{{{{{{{\mathrm{exp}}}}}}}}\left[ { - 2/\left( {3a_d^6} \right)} \right]$, agreeing well with the simulation results shown in Fig. 7a. Especially, when we decrease a_d, e.g., to a_d = 180, the generated positron bunches are still quasi-monoenergetic. The laser pulse with this intensity will be soon attainable on several laser facilities⁷⁴ e.g., ELI-NP, SULF and CoReLS.

Fig. 7: Laser energy conversion efficiency to electrons, γ-photons and positrons.

Energy conversion efficiency (a) with different a_d and a fixed a_s; (b) with different a_s and a fixed a_d.

Secondly, we keep a_d = 265, but vary a_s from a_s = 100 to a_s = 200. The energy conversion efficiency from the laser pulses to the electrons and positrons shows a similar scaling except for photons, as shown in Fig. 7b. Different from the charged particles, the laser energy conversion efficiency to the γ-photons keeps almost unchanged with the increase of a_s. Here, the radiated γ-photons originate from two parts, the quivering electrons in the drive laser field and the NCS process. Although the NCS process depends on the intensity of both laser pulses, the first part of γ-photons is determined only by the drive laser, resulting in different scaling of energy conversion efficiency with a_d and a_s. Our simulations show that the final laser energy conversion efficiency to photons grows at the same rate as the total laser energy.

It is interesting to see that the OAM of LG laser pulse is also transferred to electrons and positrons efficiently. Here, the angular momentum of laser field is $L_{laser} = \left| {\vec r \times \left( {\vec E \times \vec B} \right)} \right|$, while the angular momentum of particles can be calculated by $L_{part} = \left| {\vec r_{part} \times \vec p_{part}} \right|$, where $\vec r_{part}$ and $\vec p_{part}$ are the transverse position and the momentum of particles, respectively. In the case of a_d = 265 and a_s = 150, the OAM conversion efficiency from laser pulses to positrons can reach 2% which is an order of magnitude higher than previous study³⁰. When we increase the scattering laser intensity, the laser angular momentum conversion efficiency to the positrons is also increased efficiently (see Supplementary Note 8). Here, the angular momentum provides the GeV positron bunches an extra degree of freedom so that they may have many potential applications in high energy physics, such as discovering new particles, solving the underlying physics in the collision of e⁻e⁺ and investigating fundamental QED processes. Meanwhile, the attosecond-scale positron bunches are not only separated in space, but also in energy, enabling ultra-short time resolution in detecting and accurate injection into accelerators.

In conclusion, we propose an all-optical scheme for the generation, acceleration, and compression of positrons to form dense GeV sub-femtosecond positron bunches with 10 PW-scale lasers. In this scheme, high-energy incoherent γ-photons are efficiently generated via the NCS process. Once the γ-photons collide head-on with the scattering laser pulse, abundant positrons are generated via the multi-photon BW process. Owing to the PLA, sub-femtosecond quasi-monoenergetic positron bunches are produced. The high-quality positron bunches are sustainable for tens of laser periods when propagating into vacuum along with the drive laser. Besides the short-time duration and narrow energy bandwidth, OAM is also transferred efficiently from the LG laser pulse to the γ-photons and positrons with the efficiency of about 30 and 2%, respectively. In the near future, several laser facilities^75,76 under construction will be capable of delivering ultra-high intensity laser pulses of 10²²−10²⁴ W cm⁻² with the peak power at 10 PW and above, which is high enough to test our scheme. The bright quasi-monoenergetic sub-femtosecond positron bunches with tunable energy and OAM may find wide applications in science and engineering, such as ultra-fast dynamics, laboratory astrophysics and particle collision experiments.

Methods

Numerical modeling

3D PIC simulations are carried out using the open-source PIC code EPOCH, with both QED and collective plasma effects included^21,28. In the simulations, a left-handed circularly polarized LG laser pulse and a linearly polarized Gaussian laser pulse are incident from the left and right boundaries of the simulation box with a time delay of 23T₀. Except for the parameter scanning, the main results of this manuscript are based on the following laser parameters. The drive laser has an intensity of a_d = 265, focal spot radius of r₀ = 3λ₀, pulse duration ofτ_L = 12T₀ (with Gaussian profile), laser period of T₀ = 3.3 fs, and laser wavelength of λ₀ = 1 μm. As for the scattering laser, a_s = 150, r₀ = 5λ₀, and τ_L = 10T₀. While the parameter scanning results in Discussion are acquired with all other parameters unchanged except the laser intensities (details are given in the previous section). From the parameter scanning results, the minimum laser intensity required for quasi-monoenergetic positron bunch generation in our scheme is as low as a₀ = 150 for both drive and scattering lasers. Thus, the corresponding laser power is only 8 PW, smaller than that in several available laser facilities^74,77, like SULF and ELI-NP. For the sake of maintaining positron bunch quality, the laser fluctuations need to be less than half of the laser spot radius. The simulation box is x × y × z = 80λ₀ × 9λ₀ × 9λ₀, sampled by cells of 1000 × 225 × 225 with 16 macro-particles per cell. A cylindrical NCD plasma (r = 9λ₀) with parabolic density distribution is applied to focus the incident laser and enhance the laser absorption. The plasma exists from 2λ₀ to 78λ₀ with the transverse distribution defined by n₀ = (1 + 0.11r²)n_c. The intensity of both lasers is tunable in the simulations and the NCD plasma can be manufactured by focusing the laser pulses on gas jets⁷⁸ or foams⁷⁹. The electron dynamics and photon emission have been verified by the Virtual Laser Plasma Lab (VLPL) code⁸⁰.

Intense twisted laser pulse generation

It has been already proved that intense twisted laser pulse can be generated through irradiating a spiral-shaped phase plate (light fan) by an intense Gaussian laser pulse⁵⁹. Recently, femtosecond twisted laser pulse with an intensity of 6.3 × 10¹⁹ W cm⁻² has been successfully generated in experiments where a 32-stair plate with the step-height of 17.5 nm was used⁶⁰. Here, we investigate numerically the generation of such an ultra-intense twisted laser pulse via the light fan by using the 3D-PIC code EPOCH, as shown in Fig. 8a. The parameters of incoming Gaussian laser (LG₀₀) are: a₀ = 265, r₀ = 3λ₀, τ_L = 12T₀ (with Gaussian profile), and λ₀ = 1 μm. The phase plate is a plastic foil with eight stairs whose height is Δ = λ₀/16 = 62.5 nm to produce a total phase shift of λ₀/2, and the minimum thickness of the foil is 2 μm. After the Gaussian pulse is completely reflected by the phase plate, an ultra-intense twisted LG₀₁ pulse with a₀ ≈ 200 is acquired, as indicated in Fig. 8b, c. In theory, the laser mode of the reflected pulse can be expanded by a series of LG modes and the expansion coefficients can be defined as^81,82:

$${{{{{\mathrm{a}}}}}}_{{{{{\mathrm{st}}}}}} = \left\langle{{{{{\mathrm{LG}}}}}}_{{{{{\mathrm{st}}}}}}\left|{{{{{\mathrm{exp}}}}}}\left(- {{{{{\mathrm{i}}}}}}\Delta\upphi\right)\right|{{{{{\mathrm{LG}}}}}}_{00}\right\rangle \\ = {\int\!\!\!\!\int}{\rm rdrd}\upphi\left(\frac{{\rm C}_{{\rm st}}}{{\upsigma}_{{\rm st}}}\right)\exp \left(\frac{{\rm ik}_{0}{\rm r}^{2}}{2{\rm R}_{{\rm st}}} - \frac{{\rm r}^{2}}{{\upsigma}_{{{{{{\mathrm{st}}}}}}}^{2}}\right) \times {{{{{\mathrm{exp}}}}}}\left[{{{{{\mathrm{i}}}}}}\left({{{{{\mathrm{s}}}}}} - {{{{{\mathrm{t}}}}}} \right)\upphi\right](-1)^{{{{{{\mathrm{min}}}}}}({{{{{\mathrm{s}}}}}},{{{{{\mathrm{t}}}}}})}\left(\frac{{\rm r}\sqrt{2}}{{\upsigma}_{{{{{{\mathrm{st}}}}}}}}\right)^{|{{{{{\mathrm{s}}}}}}-{{{{{\mathrm{t}}}}}}|}\\ \times {{{{{\mathrm{L}}}}}}_{\min({{{{{\mathrm{s}}}}}},{{{{{\mathrm{t}}}}}})}^{|{{{{{\mathrm{s}}}}}}-{{{{{\mathrm{t}}}}}}|}\left( \frac{{{{{{\mathrm{r}}}}}}^{2}}{{\upsigma}_{{{{{\mathrm{st}}}}}}^{2}}\right){{{{{\mathrm{exp}}}}}}\left(-{{{{{\mathrm{i}}}}}}\Delta\upphi\right)\left(\frac{{{{{{\mathrm{C}}}}}}_{00}}{{\upsigma}_{0}}\right){{{{{\mathrm{exp}}}}}}\left(- \frac{{{{{{\mathrm{ik}}}}}}_{0}{{{{{\mathrm{r}}}}}}^{2}}{2{{{{{\mathrm{R}}}}}}_{{{{{\mathrm{st}}}}}}} - \frac{{{{{{\mathrm{r}}}}}}^{2}}{{\upsigma} _{{{{{\mathrm{st}}}}}}^{2}}\right)$$

(3)

Here,${\Delta}\phi = \mathop {\sum}\nolimits_{n = 0}^7 {H\left( {\phi - \pi /4n} \right)} H\left( {\pi /4n + \pi /4 - \phi } \right)2\pi /8n$, C_st is a normalization constant, R_st = (f² + x²)/x and H(x) is the Heaviside function. Thus, the reflected pulse is composed of several laser modes and the percentage of each mode is given by $I_{st} = \left| {a_{st}} \right|^2$. Because of Δϕ ≈ ϕ in our simulations, the laser modes with the azimuthal mode index l = s − t = 1 contribute the most in the ϕ integral. In our case, the resulting I₁₀ = 78.5% means that the LG₀₁ mode dominates the reflected pulse, which agrees well with the PIC simulation results as shown in Fig. 8b, c.

Fig. 8: Schematic diagram of generating ultra-intense LG₀₁ laser pulses.

a A circularly polarized Gaussian laser pulse is incident onto the phase plate, and a LG₀₁ model dominated reflected pulse can be obtained. b Transverse electric field E_y at (b) x = 9.44λ₀ and (c) x = 9.95λ₀.