On the dual effect of obstacles in preventing silo clogging in 2D

Abstract

Placing an obstacle in front of a bottleneck has been proposed as a sound alternative to improve the flow of discrete materials in a wide variety of scenarios. Nevertheless, the physical reasons behind this behavior are not fully understood and the suitability of this practice has been recently challenged for pedestrian evacuations. In this work, we experimentally demonstrate that for the case of inert grains discharging from a silo, an obstacle above the exit leads to a reduction of clog formation via two different mechanisms: i) an alteration of the kinematic properties in the outlet proximities that prevents the stabilization of arches; and ii) an introduction of a clear anisotropy in the contact fabric tensor that becomes relevant when working at a quasi-static regime. Then, both mechanisms are encompassed using a single formulation that could be inspiring for other, more complex, systems.

Introduction

The placement of obstacles has been suggested as a smart strategy to prevent clog formation when a discrete system flows through a constriction. This, a priori counter-intuitive behavior, was originally proposed to improve pedestrian evacuation from a room with a small exit¹. After this work, the increment of the flow rate by suitably placing an obstacle in front of the gate has been taken as a hallmark of pedestrian dynamics and, accordingly, it has been reproduced by most of the recently proposed models^{2,3,4,5,6,7,8}. Nevertheless, a robust experimental demonstration of the obstacle effectiveness in pedestrian dynamics is still lacking given that the existing results are contradictory^{9,10,11,12,13,14,15,16}. Paradoxically, this experimental evidence exists for other systems as (i) the passage of animals such as sheep^17,18 or mice¹⁹ through narrow doors, and (ii) the discharge of granular matter from a silo^20,21,22,23.

It is precisely the granular scenario the one that allows a better and more detailed analysis of the system behavior^24,25,26,27; first because of the simpler interaction rules among inert grains, and second because it allows the performance of as many experimental repetitions as desired. In this way, it has been found that placed at the optimal distance from the orifice, a circular obstacle reduces the clogging probability more than one hundred times without affecting the flow rate^20,21. When the obstacle position is raised above the optimal location, the effect progressively reduces, whereas if it is placed too close to the outlet, clogging increases abruptly as arches start to form between the obstacle and the silo bottom instead of above the orifice²⁰.

Furthermore, experiments of grains discharging from a silo have revealed that the key aspect behind clogging reduction is the creation of an empty region just below the obstacle²². Thus, when a group of particles coincides above the orifice and form an arch, its stabilization becomes very difficult in comparison with the case without obstacle (where the beads above the arch restrict the motion of the particles conforming it²⁰). An indirect quantification of this behavior consisted in computing the ratio of particles moving upwards in the outlet region with respect to the total, a measure that revealed a net correlation to clogging reduction: the higher the ratio of upwards displacements, the lower the probability of clogging. In addition, Endo et al.²² reported an associated effect of the obstacle on clogging reduction consisting in increasing the granular temperature of the sample in the horizontal direction.

The existing explanations that justify the effect of an obstacle on clogging are related to the system dynamics. Therefore, it could be expected that if the motion of the grain is minimized, the obstacle impact will become barely important. In this work, we demonstrate that this is not the case by implementing a granular extraction mechanism consisting of a belt placed below the orifice that permits discharging the silo quasistatically²⁸ (see “Methods” section). Indeed, we discover that in quasi-static discharges, the presence of the obstacle introduces a clear anisotropy in the contact fabric tensor that justifies the reduction of clogging probability.

Results and discussion

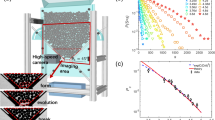
The main objective of this work is to investigate how the presence of the obstacle above the exit of a silo affects the emergence of clogging when the kinematic effects are progressively reduced (up to the quasi-static limit). For this purpose, we performed experiments in a two-dimensional silo with an obstacle above the orifice and a conveyor belt below the silo, as shown in Fig. 1a. An automated measurement protocol, visually explained in Supplementary Movie 1, enables the computation of the clogging probability p_c from the avalanches distribution in each experimental configuration. Additional kinematic information is extracted from video recordings (see “Methods” section), a single frame of which is shown as an example in Fig. 1b.

Fig. 1: Outline of the experimental setup.

a Photograph of the bottom part of the silo where the obstacle, the orifice, and the conveyor belt can be distinguished. b Frame taken from a film recorded with the high-speed camera where the orifice size is defined. The blue box is the region located at the outlet where the velocity of particles is averaged to compute v. The red box is the representative area above the orifice and below the obstacle where the magnitudes are averaged to obtain v_x, v_z, and the solid fraction ϕ. The coordinate system (where for convenience, positive values are considered in the downwards direction) is also shown in this figure. c Experimental data of the mean velocity of the particles when exiting the silo v, versus the belt velocity v_b, in the silo with the obstacle, for the two orifice sizes indicated in the legend. Uncertainties are smaller than the point size as the velocities come from averages over a large amount of data.

Although changes in kinematics are achieved by means of tuning the velocity of the extracting belt (v_b), the parameter that we will use here to characterize the system dynamics is v, the mean particle velocity at the very outlet (more specifically, in the blue box displayed in Fig. 1b). This strategy was proved to be useful in previous works²⁸ permitting a successful encompassing of the results obtained for different gaps between the belt and the silo bottom (the other parameter that affects the particle velocities apart from the belt velocity²⁹). Indeed, in agreement with the findings reported in these works for standard silos, when the obstacle is placed above the orifice we find a non-linear relationship between the mean particle velocity at the outlet and the belt velocity (Fig. 1c). Note that grains moving downwards have positive velocities, as depicted in Fig. 1b. For low v_b the dependence is rather linear because the belt is mainly controlling the extraction dynamics; but then, as v_b increases, the orifice starts to screen the grains passage and their velocity saturates in what it was called the “free discharge regime” because of its similarity with a scenario in which the discharge is just driven by gravity (without belt). As expected, the saturation value is lower for the smaller outlet size (D) as in a freely discharged silo the velocities of the grains at the outlet scale with D^1/230.

Clogging

Once we know the mean velocity of the particles when crossing the exit for each experimental condition, we compute the corresponding clogging probability p_c. This quantity, which accounts for the probability that a particle clogs the system when it is exiting the silo, can be easily calculated from the exponential distribution of avalanche sizes (measured as the number of particles, s, flowing out of the silo before an arch produces a clog)^25,26,27,28 (see “Methods” section). Clearly, Fig. 2a reveals a decreasing trend of p_c with v, a result that qualitatively resembles the one obtained without obstacle²⁸. Indeed, for the two outlet sizes investigated, the curves can be successfully fitted with the expression proposed in that work:

$${p}_{{{{{{\mathrm{c}}}}}}}={(a+bv)}^{-{(D/{d}_{{{{{{\mathrm{p}}}}}}})}^{2}}$$

(1)

in which, d_p is the particle diameter, v the velocity of the grains, and b and a are two fitting parameters that account, respectively, for the effect of the system dynamics and geometrical properties of arches.

Fig. 2: Clogging probabilities in different scenarios.

a Probability of clogging as a function of the mean velocity of particles v at the outlet, for the orifice sizes shown in the two legends. Empty symbols correspond to the experiments performed in this work, while solid symbols are the experimental data already reported in Gella et al.²⁸ for the silo without obstacle. The solid lines are representations of Eq. (1) with a = 1.33 and b = 0.0128 scm⁻¹, the parameters found in Gella et al.²⁸ for a silo without obstacle. Dotted lines correspond to the same expression with a = 1.406 and b = 0.0153 scm⁻¹, the parameters corresponding for the obstacle position implemented in this work. b Probability of clogging as a function of the aspect ratio D/d_p in the quasi-static regime. Purple diamonds correspond to the experimental data of this work, while green triangles are the experimental data already reported in Gella et al.²⁸ for the quasi-static regime. Dashed lines are representations of Eq. (1) with the same values of a introduced above for the obstacle and no-obstacle cases. Note that the value of b in Eq. (1) is irrelevant in the quasi-static regime as v → 0. In all cases, the uncertainties associated to the clogging probabilities are smaller than the point size.

Figure 2a evidences a systematic deviation between the data obtained with and without obstacle: the obstacle reduces the clogging probability to <50% of the reference value without obstacle for all velocities, including the limit scenario of a quasi-static discharge (i.e., v → 0). This reflects on the different fitting parameters obtained when the obstacle is present (a = 1.406 ± 0.004 and b = 0.0153 ± 0.0004 scm⁻¹) than when it is not (a = 1.33 and b = 0.0128 scm⁻¹)²⁸. Both, the geometrical and dynamics parameters vary when placing the obstacle, suggesting a dual role of it in what concerns clogging prevention. Indeed, although the explanations given in the literature about the obstacle role were related to an alteration of the system dynamic properties near the orifice, it is rather clear that, at the quasi-static limit, there is a net difference among the two pairs of curves shown in Fig. 2a.

Aiming to confirm this feature and to evaluate its generality when the outlet size is varied, we implemented a series of experiments at the quasi-static limit (Fig. 2b), using the smallest value of v_b available (v_b = 0.1 cm s⁻¹). Univocally, the presence of the obstacle leads to a reduction of the clogging probability even when the particle dynamics is expected to play a negligible role. Consistently, the results obtained can be nicely fitted with Eq. (1) using v = 0 and then, a single fitting parameter a = 1.406. Of course, the value of a is the same as the one obtained when fitting the p_c vs v curves for the scenario with obstacle in Fig. 2a.

From these results, we can infer that the obstacle should have a dual effect on the system properties: on one side, it may affect the geometrical arrangements occurring in the quasi-static regime, but on the other, it should also lead to an alteration of the system dynamics. Therefore, in order to confirm this idea, we proceed to analyze the effect of the obstacle in several kinematic and static (geometrical) magnitudes that may be related to the development of clogging.

Dynamics

In this section, we explore the behavior of various quantities related to the system dynamics in the region between the obstacle and the orifice; i.e., the position at which clogging arches develop. In particular, we have chosen a 1.2 × 1.2 cm² region just above the orifice as depicted in Fig. 1b. The reason for this choice is to cover the largest region possible but keeping apart from the orifice borders and the obstacle, where a particle may get eventually stacked and distort the statistics. Undoubtedly, the region election determines the obtained values as both the orifice and the obstacle induce strong gradients in their vicinities. Nevertheless, we have observed similar qualitative results provided that the analyzed area is centered with the outlet and covers its proximities. We start displaying in Fig. 3a, b the distributions of particles velocities, both in the horizontal direction (v_x) and in the vertical one (v_z). Clearly, the distributions of v_x are slightly wider for the scenario with the obstacle than without it, a result that can be understood if we think that the obstacle forces the particles to detour around it, hence increasing the horizontal component of the velocity and reducing the vertical one. This can be effectively corroborated by looking at the distributions of vertical velocities, which is evidence that the obstacle leads to a small reduction of large positive velocities (recall that downwards velocities have positive values). This feature is accompanied by a widening of the distribution tails towards negative values. Indeed, for the cases without obstacles, all these tails seem to fall relatively on top of each other, whereas when the obstacle is placed, they seem to broaden as the extraction rate augments. From this, we can conclude that the presence of the obstacle favors the upwards motion of the particles above the orifice. This feature, which was already related to an arch destabilization process in a freely discharged silo²⁸, seems to be more important as the extraction rate and grains velocities increase.

Fig. 3: Dynamic features of the system.

Experimental probability density functions (pdf) of (a) horizontal and (b) vertical velocity components measured in the region indicated with a red box in Fig. 1b for an orifice size of D = 1.53 cm and the belt velocities indicated in the legend. Dashed lines account for the experiments with the obstacle while solid ones make reference to the experiments without it. In c and d the averages of these distributions (using the absolute value in the case of v_x) are reported as a function of v, the particles velocities when crossing the outlet. e Proportion of upwards displacements (computed as the number of negative velocities ${V}_{Z}^{-}$ divided by the total number of velocities ${V}_{Z}^{T}$ analyzed in the red box of Fig. 1b) versus the particles velocities when crossing the outlet. f Two-dimensional solid fraction in the area signaled with a red box in Fig. 1b as a function of the particles velocities when crossing the outlet. The dashed line shows ${\phi }_{{{{{{\mathrm{CP}}}}}}}=\pi \sqrt{3}/6$, the maximum value available for ϕ in this system which corresponds to the close packing of circles in 2D. The uncertainties of the mean quantities are smaller than the points size since they come from averaging a large amount of data.

Then, in order to confirm this instance and better characterize the effect of the obstacle in the particle dynamics when the velocity of the grains crossing the exit v is varied, 〈∣v_x∣〉 and 〈v_z〉 are represented as a function of v (Fig. 3c, d). The detouring of particles around the obstacle explained above is confirmed as 〈∣v_x∣〉 augments and 〈v_z〉 reduces in the obstacle presence. This feature becomes more important when v increases as the difference among the obstacle and no-obstacle curves is enhanced. Complementarily, the upwards motion of the grains in the outlet vicinity is characterized by computing the number of upwards displacements ${V}_{Z}^{-}$ with respect to the total number of displacements detected ${V}_{Z}^{T}$ in the analyzed region; or, in other words $\int\nolimits_{-\infty }^{0}pdf({v}_{z})d{v}_{z}/\int\nolimits_{-\infty }^{\infty }pdf({v}_{z})d{v}_{z}$. The dependence of this proportion is represented as a function of the grains exit velocity in Fig. 3e revealing an interesting behavior. In absence of the obstacle, the proportion of upwards displacements for high exit velocities is negligible but, when reducing v, this augments considerably up to almost 15% for the lowest value of v. The same curve shape is observed for the scenario with the obstacle, but in this case all data are shifted upwards; i.e., the obstacle favors upwards displacements when v is high. In addition, when v is reduced the growth of ${V}_{Z}^{-}/{V}_{Z}^{T}$ is less pronounced for the scenario with the obstacle, hence provoking that both curves approach each other when v → 0. From this, we can interpret that the effect of the obstacle in the kinematic properties of the system above the orifice is minimized when reducing the velocity with which the particles are extracted from the silo. If this is the case, the reason for which the obstacle considerably reduces the clogging probability in the quasi-static limit as observed in Fig. 2, remains undisclosed.

A first indicator that would justify a possible origin of the clogging reduction in the quasi-static limit comes from the analysis of the two-dimensional solid fraction ϕ in the region comprised between the exit and the obstacle. Indeed, as shown in Fig. 3f, the obstacle presence induces the formation of an empty gap below it, reducing the solid fraction by about 0.1 units. This effect seems to be rather independent of the extraction velocity, hence persisting in the quasi-static limit. Therefore, lower packing fractions would correspond to reduced probabilities of particles touching each other above the outlet, and then to a smaller probability of getting arches formed^31,32. Alternatively, lower packing fractions can be also assumed to give rise to smaller pressures at the region of arch development, hence preventing their stabilization. Indeed, although increasing the pressure may trigger the destabilization of arches developed in systems composed of deformable particles^33,34, the same action has been proved to increase the robustness of arches formed by hard grains submitted to an external vibration¹⁷.

Statics

From the findings reported above, a better characterization of the quasi-static regime seems necessary. Therefore, in this section, we will spatially analyze the particle-particle contacts in the outlet region for the obstacle and no-obstacle scenarios. To this end, we have evaluated the whole registered region for several static configurations. As the flow is intrinsically intermittent³⁵, in order to avoid sampling repeatedly identical arrangements, we have decided to explore the system every time the flow is temporarily arrested (without a clogging arch formed) after a rearrangement. In Fig. 4a we show the temporal evolution of the kinetic energy E_k in the system, defined as the sum of the kinetic energy of all beads in the visual field of the camera in each frame. The specific moments we have considered for the analysis are indicated with circles; as illustrated, one configuration is evaluated every time that the grains rearrange and stop again.

Fig. 4: Static features of the system.

a Example of the temporal evolution of the kinetic energy of the grains in the whole recorded region (above the orifice) for the quasi-static regime. Red circles indicate the moments at which the fabric tensor is analyzed. b–e Maps of the horizontal f_xx and vertical f_zz components of the fabric tensor averaged over around 40 different configurations. The results correspond to a silo with an orifice size of D = 1.53cm without obstacle (top row panels) and with it (bottom row panels). f, g Corresponding maps of the rescaled difference between the horizontal and vertical components of the contact fabric tensor (f_xx − f_zz)/(f_xx + f_zz).

To assess the network orientation of contacts we computed the second-order contact fabric tensor, a magnitude able to characterize statistically the microstructure of a granular assembly. This tensor can measure the degree of anisotropy in the directions of the contacts between the grains composing the sample and is defined for each particle i as ${f}_{\alpha \beta }^{i}=\frac{1}{{N}_{{{{{{\mathrm{c}}}}}}}}\mathop{\sum}\nolimits_{{{{{{\mathrm{c}}}}}}}{n}_{\alpha }^{{{{{{\mathrm{c}}}}}}}{n}_{\beta }^{{{{{{\mathrm{c}}}}}}}$. Here, N_c is the number of contacts of that particle, while $\overrightarrow{{n}^{{{{{{\mathrm{c}}}}}}}}$ is the normalized branch vector that links the center of the particle i with the ones of its contacting particles. From these data, we built continuous fields of this quantity (see “Methods” section) which result to be strongly dependent on the obstacle presence. The maps of the horizontal component of the fabric tensor (f_xx) reveal a notable increase of f_xx in the region below the obstacle (Fig. 4c), a behavior that is clearly coupled with a reduction in the values of the vertical component f_zz (Fig. 4e). Then, the roughly similar values of f_xx and f_zz developed above the orifice for the no-obstacle scenario (that correspond to isotropic arrangements), become unbalanced due to the presence of the obstacle. This suggests that the obstacle introduces a marked anisotropic distribution of contacts, a behavior that is better reflected by the rescaled difference between the horizontal and vertical components of the contact fabric tensor ((f_xx − f_zz)/(f_xx + f_zz)). Effectively, the values obtained above the outlet are close to zero in the no-obstacle configuration (Fig. 4f), whereas patently take positive values due to the obstacle weight screening (Fig. 4g). From this result, one could argue that the obstacle prevents the development of vertical contacts in the arch formation region, while it favors the horizontal ones. Assuming that this behavior holds for the orientation of the forces, it follows that a typical arch (semicircular in average) would be squeezed in the horizontal direction and, quite possibly, destabilized.

Conclusions

In summary, in this work, we have experimentally demonstrated that placing an obstacle above a silo exit prevents clog formation via two different mechanisms that become more or less prevalent depending on the granular extraction rate. In quasi-static discharges, the obstacle induces an alteration of the contact fabric tensor below it (above the orifice): contacts in the horizontal direction become more abundant than in the vertical one. If we consider that isotropically charged arches are more stable than those charged mostly from the sides, it follows that the clogging probability gets reduced in the presence of the obstacle. For high extraction rates (or free discharges), the mechanism behind clog reduction relates to the empty gap formed below the obstacle and the augmentation of horizontal velocities in this region. The combination of these two features renders difficult the complete stabilization of particles coinciding above the orifice to form a clogging arch. Typically, grains undergo horizontal collisions that, given the lack of confinement in the vertical direction, lead to upwards ejections that impede clog formation.

All this complex behavior can be encompassed with a single equation (proposed before for the silo without obstacle) that describes the clogging probability as a function of particles velocities and the outlet size, using only two fitting parameters. As these two parameters (one related to the particles dynamics and the other with the quasi-static condition) are different for the obstacle and no-obstacle case, we speculate a dependence of them on the obstacle properties and position that should be studied elsewhere.

Finally, let us point out that the findings discovered in this work may help to shed light on the sometimes contradictory role that an obstacle has in other systems such as pedestrians, animals or active matter in general. Importantly, from a physical point of view, the analogy with a freely discharged silo does not seem the best choice for these systems, which are characterized by having a limit velocity instead of moving under a constant acceleration field; hence resembling the case of a silo discharged with a conveyor belt more than the freely discharged one. Having said that, it is essential to address the important differences existing among our ideal hard spherical particles and the constituents of most of these other real systems. In particular, the effect of using particles of complex shapes^23,36 and their deformability^33,34 (which may lead to different global responses to pressure) should be investigated in the near future.

Methods

Experimental setup

The system is a two-dimensional silo built by sandwiching two parallel glass sheets of 70 cm wide and 160 cm high. Between them, two 0.4 cm thick aluminum gauges supplemented by thin cardboards play the role of lateral sides. Then, only a single layer of granular material, monodisperse spheres of AISI 420 stainless steel (diameter d_p = 0.4000 ± 0.0002 cm, density ρ_M = 7.75 g cm⁻³), fits in between the panes. The silo bottom consists of two wedge-shaped stainless steel pieces whose separation defines the outlet size D through which the grains flow out. The conveyor belt is placed below the orifice, with a separation of 0.67 ± 0.03cm between their upper protrusions and the lowest part of the steel pieces of the silo bottom. This device can operate in a range of belt velocities between 0.1 and 16 cm s⁻¹. In some runs, a circular obstacle (4 cm diameter) made of methacrylate has been glued at a vertical distance of 1.56 ± 0.03 cm from its lowest edge to the orifice center. In the x direction, the obstacle has been centered with the orifice. Additionally, a hopper situated at the top permits the manual filling of the silo.

Clogging probability

The probability that a bead clogs the system when it is crossing the orifice, p_c, is computed from the distribution of avalanche sizes s, defined as the amount of material discharged between two clogging events. In particular, the values of p_c correspond to the negative slopes of the survival functions (ccdf) of s in semi-logarithmic scale, taking into account that ${{{{{{\mathrm{ln}}}}}}}\,[{{{{{{{\rm{ccdf}}}}}}}}(s)]\simeq -s{p}_{{{{{{\mathrm{c}}}}}}}$ (see PhD thesis of D. Gella³⁷ for a detailed explanation). To obtain these distributions, in each experimental configuration, an automated measurement protocol synchronizes several devices which have been incorporated into the system: a balance with a bucket on it placed at the end of the belt, a web camera, and a vibration system to break the clogging arches. Once the silo is manually filled, the protocol is launched. Its steps are summarized in Supplementary Movie 1 and detailed hereafter. First, the balance is tared and the conveyor belt starts running at the desired velocity, discharging the granular material. During this time, the web camera is continuously evaluating the sum of pixels in a region located just below the area in which arches form. Then, if a clogging event occurs, there will be no beads in that area and the pixels will be mostly white, leading the sum above a predetermined threshold. If this situation carries on for 4 s, the arch is considered stabilized. When this occurs, the belt pours all the grains discharged from the silo into the bucket and stops. Then, the avalanche size is registered by the balance, the shaker vibrates to break the arch, and the conveyor belt resumes its motion. This process is repeated until having around 1000 avalanches per experimental configuration. In all cases, the survival function of the avalanche sizes is computed and the corresponding value of p_c is extracted from a linear fitting of the natural logarithm of these distributions. This is shown in Fig. 5, where the experimental survival functions for D = 1.53 cm and several values of v_b are represented together with their corresponding fits in the semi-logarithmic scale. The goodness of the fits together with a large amount of points (around 1000) lead to uncertainties associated to p_c which are smaller than the size of the points in Fig. 2. Finally, the quasi-static regime has been achieved by using the smallest value of v_b available (v_b = 0.1 cm s⁻¹) in the conveyor belt. The results derived from this method are analogous to the ones obtained by evaluating p_c as a function of v and then fitting them to Eq. (1) for each orifice size²⁸.

Fig. 5: Avalanche sizes distributions.

Experimental survival functions of the avalanche sizes for D = 1.53 and the values of v_b indicated in the legend. Note the semi-logarithmic scale. The solid lines are the linear fits in the semi-logaithmic scale used to compute the clogging probabilities p_c.

Kinematic and geometrical magnitudes

Using a Photron ®FASTCAM-1024PCI high-speed camera, we recorded several films of the motion of the grain at the area surrounding the orifice and the obstacle (Fig. 1b). High-contrasting images are achieved thanks to a LED panel at the rear which provides backlighting illumination. For each experimental configuration, three videos have been recorded with a frame rate of 500 fps and a duration of around 7 s. A homemade image processing software has been developed to detect the bead centers with subpixel resolution and track their trajectories. To ensure good accuracy in the detection of the centers position, the spatial resolution of the frames has been chosen in such a way that each particle diameter covers around 40 pixels (i.e., around 10 pix per mm). From their centers and radii, the particles are reconstructed in each frame, allowing the computation of the two-dimensional solid fraction as the proportion of space occupied inside a characteristic area. Furthermore, the particle velocities are calculated as the ratio between their displacements and the time between two frames (1/500 s). The individual velocity data is averaged over a characteristic area (Fig. 1a) depending on the situation to express the information required in each case. As the amount of data used in this process is very large (from around 7000 in the worst case to around 100,000 in the best one), the uncertainties associated to these averaged quantities are really minor (about the point size in the figures). Finally, the contact fabric tensor has been computed from the branch vectors between contacting particles, defined as the ones whose centers are separated less than 1.05d_p. Then, a coarse-grained method inspired in the work of Gorldhirsch³⁸ has been used to build macroscopic continuous fields. Given the contact fabric tensor data linked to each position and time, ${f}_{\alpha \beta }^{i}(t)$, the mean field has been computed as ${f}_{\alpha \beta }(\overrightarrow{r},t)=\frac{{\sum }_{i}{f}_{\alpha \beta }^{i}(t){{\Theta }}(\overrightarrow{r}-{\overrightarrow{r}}_{i}(t))}{{{\Theta }}(\overrightarrow{r}-{\overrightarrow{r}}_{i}(t))}$. In this expression, ${{\Theta }}(\overrightarrow{r}-{\overrightarrow{r}}_{i}(t))$ is the coarse-graining function, a 2D Gaussian function, ${{\Theta }}(\overrightarrow{r}-{\overrightarrow{r}}_{i}(t))=\frac{1}{2\pi {w}^{2}}\exp (-| \overrightarrow{r}-{\overrightarrow{r}}_{i}| /2{w}^{2})$ with w = d_p/2. For computational reasons, this function has been cut off for distances larger than 3w from each particle center. Finally, f_xx and f_yy have been averaged over all frames considered to obtain the amounts represented in the article, ${f}_{xx}(\overrightarrow{r})=\langle {f}_{xx}(\overrightarrow{r},t)\rangle$ and ${f}_{yy}(\overrightarrow{r})=\langle {f}_{xx}(\overrightarrow{r},t)\rangle$.