Scale invariance of cell size fluctuations in starving bacteria

Abstract

In stable environments, cell size fluctuations are thought to be governed by simple physical principles, as suggested by recent findings of scaling properties. Here, by developing a microfluidic device and using E. coli, we investigate the response of cell size fluctuations against starvation. By abruptly switching to non-nutritious medium, we find that the cell size distribution changes but satisfies scale invariance: the rescaled distribution is kept unchanged and determined by the growth condition before starvation. These findings are underpinned by a model based on cell growth and cell cycle. Further, we numerically determine the range of validity of the scale invariance over various characteristic times of the starvation process, and find the violation of the scale invariance for slow starvation. Our results, combined with theoretical arguments, suggest the relevance of the multifork replication, which helps retaining information of cell cycle states and may thus result in the scale invariance.

Introduction

Recent studies on microbes in the steady growth phase suggested that the cellular body size fluctuations may be governed by simple physical principles. For instance, Giometto et al.¹ proposed that size fluctuations of various eukaryotic cells are governed by a common distribution function if the cell sizes of a given species are normalized by their mean value (see also ref. ²). In other words, the distribution of cell volumes v, p(v), can be described as follows:

$$p(v)={v}^{-1}F(v/V),$$

(1)

with a function F( ⋅ ) and V = 〈v〉 being the mean cell volume. This property of distribution is often called scale invariance. Interestingly, this finding can account for power laws of community size distributions, i.e., the size distribution of all individuals regardless of species, which were observed in various natural ecosystems^3,4. Scale invariance akin to Eq. (1) was also found for bacteria^5,6 for each cell age, and the function F( ⋅ ) was shown to be robust against changes in growth conditions, such as the temperature.

Those results, as well as theoretical models proposed in this context^1,7,8, have been obtained under steady environments, for which our understanding of single-cell growth statistics has also been significantly deepened recently^9,10,11. By contrast, it is unclear whether such a simple concept as scale invariance is valid under time-dependent conditions, where different regulations of cell cycle kinetics may come into play in response to environmental variations. In particular, when bacterial cells enter the stationary phase from the exponential growth phase, they undergo reductive division, during which both the typical cell size and the amount of DNA per cell decrease^12,13,14,15. Although this behavior itself is commonly observed in batch cultivation, little is known about single-cell statistical properties during the transient. The bacterial reductive division is therefore an important stepping stone for studying cell size statistics under time-dependent environments and understanding the robustness of the scale invariance against environmental changes.

To investigate size distributions of large bacterial populations under time-dependent growth conditions, we should care about experimental methods. A microfluidic device called the mother machine¹⁶ consists of many small separate chambers of cells supplied with medium and thus allows for tracking of bacteria trapped therein. Although this type of device has also been used for time-dependent problems as well^{17,18,19,20,21}, for our purpose involving size fluctuations of a large population of cells, it is not obvious if they are equivalent to those of a collection of many independent small populations. More precisely, since the size of a cell depends strongly on its age, it is reasonable to use large enough chambers so that the chamber size may not affect the age distribution. This led us to develop another system that can deal with large enough populations in each chamber and uniformly control non-steady environments without delicate optimization.

In this study, we develop a microfluidic device, which we name the “extensive microperfusion system” (EMPS). This device can culture cells uniformly by supplying fresh medium through a porous membrane, similarly to previously reported systems^22,23,24, but here we realize wide quasi-two-dimensional traps of dense bacteria in such a system. We confirm that bacteria can freely swim and grow inside and evaluate the uniformity and the switching efficiency of the culture condition. Then we use this system for quantitative observations of bacterial reductive division processes, triggered by abrupt switching to non-nutritious medium. We observe Escherichia coli cells and find that the distribution of cell volumes, collected irrespective of cell ages, maintain the scale invariance as in Eq. (1) at each time, with the mean cell size that gradually decreases. On the other hand, the rescaled distribution function F is found to depend on the growth condition before starvation, slightly but significantly. To obtain theoretical insights on these experimental findings, we devise a cell cycle model describing reductive division processes, by extending the Cooper–Helmstetter (CH) model and its variants^25,26,27 for steady growth environments. We numerically find that this model indeed shows the scale invariance under starvation conditions, confirming the robustness of this property. We also provide theoretical descriptions on the time evolution of the cell size distribution and propose a condition for the scale invariance. Finally, we numerically show the range of validity of the scale invariance over various characteristic times of the starvation process, revealing that the number of multifork replications may be important for the scale invariance.

Results

Development of the EMPS

To achieve uniformly controlled environments with dense bacterial suspensions, we adopt a perfusion system, which supplies fresh medium through a porous membrane attached over the observation area. Among several existing devices of this kind^22,23,24, here we choose the one developed in ref. ²² as a prototype. In this device, bacteria are confined in microwells made on a coverslip, covered by a cellulose porous membrane attached to the coverslip via biotin–streptavidin bonding. Note that cellulose cannot be metabolized by E. coli strains common for laboratory use²⁸, which we confirmed explicitly with MG1655 (Supplementary Fig. 1g). The pore size of the membrane is chosen so that it can confine bacteria and also that it can exchange nutrients and waste substances across the membrane. To continuously perfuse the system with fresh medium, a polydimethylsiloxane (PDMS) pad with a bubble trap is attached above the membrane by a two-sided frame seal (Fig. 1a and Supplementary Fig. 1a). This set-up can maintain a spatially homogeneous environment for cell populations in each microwell, in particular if the microwells are sufficiently shallow so that all cells remain near the membrane. However, because the soft cellulose membrane may droop and adhere to the bottom for wide and shallow microwells, the horizontal size of such quasi-two-dimensional microwells has been limited up to a few tens of micrometers, preventing from characterization of the instantaneous cell size distribution.

Fig. 1: Sketch of the extensive microperfusion system (EMPS).

a Entire view of the device. Microwells are created on a glass coverslip. We attach a polydimethylsiloxane (PDMS) pad on the coverslip with a square frame seal to fill the system with liquid medium. b Cross-sectional view inside the PDMS pad. A polyethylene terephthalate (PET)–cellulose bilayer porous membrane is attached via the biotin–streptavidin bonding. Note that there are two outlets as in (a).

By the EMPS, we overcome this problem and realize quasi-two-dimensional wells sufficiently large for statistical characterization of cell populations. This is made possible by introducing a bilayer membrane, where the cellulose membrane is sustained by a polyethylene terephthalate (PET) porous membrane via biotin–streptavidin bonding (Fig. 1b, Supplementary Fig. 1b, and “Methods”). Because the PET membrane is more rigid than the cellulose membrane, we can realize extended area without bending of the membrane.

Here we conducted several experiments to evaluate how well the experimental condition inside the EMPS can be controlled (see also Supplementary Note 2). We first examined the flatness of the observation area using motile bacteria. If a cellulose membrane alone is used, it is bent and adheres to the bottom of the well (Supplementary Fig. 1c, d and Supplementary Movie 1). However, if it is replaced by our PET–cellulose bilayer membrane, it keeps flat enough so that bacteria can freely swim in the shallow well (Supplementary Fig. 1e, f and Supplementary Movie 2). We also show that, using non-motile bacteria, growth rate of the bacteria is spatially uniform (Supplementary Fig. 2 and Supplementary Movies 3 and 4). The doubling time of the cell population was 59 ± 10 min, which is comparable to that in the previous system without the PET membrane^22,29,30. Furthermore, similarly to other microfluidic devices, we can also switch the culture condition by changing the medium to supply. We evaluate how efficiently the medium in the well is exchanged, by using fluorescent dye and non-motile bacteria. We found that the medium exchange was almost completed within 5 min (Supplementary Fig. 3), much shorter than the length of the bacterial cell cycle. On the other hand, since medium exchange in EMPS relies on diffusion of molecules through the membrane, other devices that can replace medium more directly, such as mother machines in which medium is poured to a main channel connected to observed growth channels^{17,18,19,20,21}, may be advantageous in this respect. Since this difference may affect, e.g., the amount of molecules that can remain on the surface of the observation area, cellular states may also change differently after an environmental switch. In this respect, advantages of EMPS in environmental changes may be in the fact that (i) we can control the environment without hydrodynamic perturbations and, simultaneously, (ii) we can observe cells in large space under a uniform and time-dependent environment without mechanical trapping. The absence of hydrodynamic perturbations can be seen from Brownian motion of non-motile cells in Supplementary Movies 5 and 6, which is hardly affected by relatively strong medium flow above the membrane used to switch the medium. Therefore, EMPS is indeed able to change the growth condition for cells in large space uniformly, without noticeable fluid flow perturbations, which is a unique strength of our device.

Characterization of bacterial reductive division by EMPS

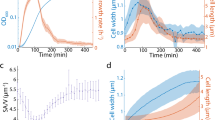
Now we observe the reductive division of E. coli MG1655 in the EMPS, triggering starvation by switching from nutritious medium to non-nutritious buffer. In the beginning, a few cells are trapped in a quasi-two-dimensional well (diameter 55 μm and depth 0.8 μm) and grown in nutritious medium, until a microcolony composed of approximately 100 cells appear. We then quickly switch the medium to a non-nutritious buffer, which is continuously supplied until the end of the observation (see “Methods” for more details). By doing so, we not only trigger cell starvation but also intend to remove various substances secreted by cells, such as autoinducers for quorum sensing and waste products, to reduce their effects on cell growth^31,32,33,34. Note that 5 min required to exchange the medium in the trap is sufficiently shorter than the typical length of the cell cycle of E. coli, which is several tens of minutes. This implies that starvation is triggered abruptly for cells. Throughout this experiment, the well is entirely recorded by phase contrast microscopy. We then measure the length and the width of all cells in the well, to obtain the volume v of each cell by assuming the spherocylindrical shape, at different times before and after the medium switch. Here we mainly show the results for the case where the medium is switched from Luria-Bertani (LB) broth to phosphate-buffered saline (PBS) (denoted by LB → PBS) in Fig. 2, while the results for M9 medium with glucose (Glc) and 12 amino acids (a.a.) → PBS, M9 medium with glucose (Glc) → PBS, M9 medium with glycerol (Glyc) → PBS, and M9 medium with glucose (Glc) → M9 medium with α-methyl-d-glucoside (αMG), a glucose analog that cannot be metabolized³⁵, are also presented in Supplementary Fig. 4. We observe that, after switching to the non-nutritious buffer, the growth of the total volume decelerates, and the mean cell volume rapidly decays because of excessive cell divisions (Supplementary Movies 7–11, Fig. 2a, b, and Supplementary Fig. 4), until cells eventually stop growing and dividing. Note that, unlike other cases (Supplementary Fig. 4), cell growth did not stop completely in the case of LB → PBS, but we consider that this will not affect our analysis because the ultimately remaining growth rate $\sim 1{0}^{-4}\ {\min }^{-1}$ (Supplementary Fig. 9a) was sufficiently low compared to the time scale of the volume reduction $\sim 1{0}^{2}\ \min$ (Fig. 2c) and all other time scales relevant in this study. Concerning the volume reduction, it is mostly due to the decrease of the cell length, while we notice that the mean cell width may also change slightly (Supplementary Fig. 5). We consider that this is not due to osmotic shock³⁶, because then the cell width would increase when the osmotic pressure is decreased, which is contradictory to our observation for LB → PBS (Supplementary Table 1 and Supplementary Fig. 5). Such a change in cell widths was also reported for a transition between two different growth conditions³⁷. In any case, Fig. 2d shows how the distribution of the cell volumes v, p(v, t), changes over time; as the mean volume decreases, the histograms shift leftward and become sharper. However, when we take the ratio v/V(t), with V(t) = 〈v〉 being the mean cell volume at each time t, and plot vp(v, t) instead, we find that all those histograms overlap onto a single curve (Fig. 2e). In other words, we find that the time-dependent cell size distribution during the reductive division maintains the following scale-invariant form all the time:

$$p(v,t)={v}^{-1}F(v/V(t)).$$

(2)

This is analogous to Eq. (1) previously reported for the steady growth condition, but here importantly the mean volume V(t) changes over time significantly (Fig. 2c). The scale invariance also holds for the length distribution (Supplementary Fig. 6); this is expected because the length changes are dominant in the studied volume changes.

Fig. 2: Results from the observations of reductive division.

a Snapshots taken during the reductive division process of E. coli MG1655 in the EMPS. The medium is switched from LB broth to phosphate-buffered saline (PBS) at t = 0. See also Supplementary Movie 7. b, c Experimental data (blue symbols) for the total cell volume V_tot(t) (b), the growth rate λ(t) (b inset, see also Supplementary Fig. 9a showing the same data in logarithmic scale), the mean cell volume V(t) (c), and the number of the cells n(t) (c inset) in the case of LB → PBS, compared with the simulation results (red curves). The error bars indicate segmentation uncertainty in the image analysis (see “Methods”). t = 0 is the time at which PBS enters the device (black dashed line). The data were collected from 15 wells recorded in a single experiment. d Time evolution of the cell size distributions during starvation in the case of LB → PBS at $t=0,5,30,60,90,120,180,240,300,360,420,480\ \min$ from right to left. The sample size is n(t) for each distribution (see (c) inset). e Rescaling of the data in (d). The overlapped curves indicate the function F(v/V(t)) in Eq. (2). The dashed line represents the fitted log-normal distribution (σ = 0.34(2)). f The coefficient of variation (CV) and the skewness (Sk) (Eq. (3)) against V(t) = 〈v〉. The error bars were estimated by the bootstrap method with 1000 realizations.

To further test the scale invariance of the distribution, we evaluate the coefficient of variation (CV) and the skewness (Sk) defined by

$${{{{{{{\rm{CV}}}}}}}}\equiv \frac{\sqrt{\langle \delta {v}^{2}\rangle }}{\langle v\rangle },\quad {{{{{{{\rm{Sk}}}}}}}}\equiv \frac{\langle \delta {v}^{3}\rangle }{{\langle \delta {v}^{2}\rangle }^{3/2}},$$

(3)

with δv ≡ v − 〈v〉. Both quantities measure the shape of the distribution function of v/V(t) and are not affected by variation of V(t). The results in Fig. 2f indeed confirm that both CV and Sk remain essentially constant, so that the function F( ⋅ ) remains unchanged and the scale invariance holds during the reductive division. Remarkably, we reach the same conclusion for all combinations of the growth and starving conditions that we test, as shown in Fig. 3a–c and Supplementary Fig. 7 (see Fig. 2f and Supplementary Fig. 4 for the results of CV and Sk). Our results therefore indicate that the scale invariance as in Eq. (2), which has been observed for steady conditions^1,2, also holds in non-steady reductive division processes of E. coli rather robustly.

Fig. 3: Rescaled cell size distributions.

a The results for M9(glucose (Glc) + amino acids (a.a.)) → PBS. The dashed line represents the fitted log-normal distribution (σ = 0.31(2)). The data were taken from 17 wells recorded in a single experiment. The sample size ranges from n(0) = 685 to n(180) = 1260 (see Supplementary Fig. 4). (Inset) Time evolution of the non-rescaled cell size distributions at $t=0,10,20,30,40,50,60,90,120,180\ \min$. b The results for M9(glucose (Glc)) → PBS. The dashed line represents the fitted log-normal distribution (σ = 0.29(2)). The data were taken from 26 wells recorded in a single experiment. The sample size ranges from n(0) = 836 to n(200) = 2160 (see Supplementary Fig. 4). (Inset) Time evolution of the non-rescaled cell size distributions at $t=0,10,20,30,40,50,60,80,100,150,200\ \min$. c Experimental results of F(v/V(t)) = vp(v, t) for the three cases studied in this work. The raw data obtained at different times are shown by thin lines with relatively light colors, and the time-averaged data are shown by the bold lines. The time-averaged distributions (bold lines) are found to be slightly but significantly different among the three cases. The difference can also be seen in the instantaneous distributions (thin lines; see the inset for enlargement near the peak). d Fitting of the experimentally obtained F(x) (solid lines; time-averaged data in (c) are shown) to the log-normal distribution (yellow dotted line). Also shown is the fitting result by Giometto et al.¹ for unicellular eukaryotes (green dotted line). σ is the standard deviation parameter of the log-normal distribution (see text).

In addition to the robustness of the scaling relation (2), the functional form of the scale-invariant distribution, i.e., that of F(x), is of interest. We detect weak dependence of F(x) on the choice of the medium in the growth phase (Fig. 3c). More specifically, we find the trend that the fluctuations of the rescaled cell volumes are larger for richer growth conditions (Supplementary Fig. 7h, i), consistently with a past observation in ref. ³⁸. The lower the nutrient level of the growth medium is, the sharper the function F(x) becomes, and therefore, the smaller the variance is. We have also confirmed that the variation in F(x) among different sets of media is more significant than that among biological replicates (Supplementary Fig. 7h, i). This is somewhat unexpected in view of the past studies reporting the robustness of cell size fluctuations against varying temperatures and other environmental factors^1,5,7.

Moreover, we find that our observations for E. coli are significantly different from those for unicellular eukaryotes reported by Giometto et al.¹ (Fig. 3d). More precisely, they showed that the rescaled cell size distribution for unicellular eukaryotes is well fitted by the log-normal distribution, $\propto (1/x)\exp (-{({{{{{{\mathrm{log}}}}}}}\,x-m)}^{2}/2{\sigma }^{2})$ with m = − σ²/2 (due to the normalization 〈x〉 = 1) and obtained σ = 0.471(3). We find that our data for E. coli can also be fitted by the log-normal distribution (Figs. 2e and 3a, b, d and Supplementary Fig. 7), but here the value of σ, evaluated by the standard deviation of ${{{{{{\mathrm{log}}}}}}}\,x$, is found to be around σ = 0.3 (σ = 0.34(2) for LB → PBS, σ = 0.30(2) for M9(Glc+a.a.) → PBS, and σ = 0.29(2) for M9(Glc) → PBS), much lower than σ = 0.471(3) for the unicellular eukaryotes. In the literature, a previous study on Bacillus subtilis³⁹ reported values of σ from 0.24 to 0.26, which are comparable to our results for E. coli. Compared to this substantial difference between bacteria and unicellular eukaryotes, the dependence on the environmental factors seems to be much weaker (Fig. 3d).

Modeling the reductive division process

To obtain theoretical insights on the experimentally observed scale invariance of the cell size distributions, we construct a simple cell cycle model for the bacterial reductive division. For the steady growth conditions, a large number of studies on E. coli have been carried out to clarify what aspect of cells triggers the division event^9,10. Significant advances have been made recently to provide molecular-level understanding^{9,27,37,40,41,42,43,44}. Here we extend such a model to describe the starvation process.

One of the most established models in this context is the CH model^25,45, which consists of cellular volume growth and multifork DNA replication. The multifork replication is the phenomenon that a cell replicates its DNA not only for its daughters but also for its granddaughters, before the birth of the daughter cells (Fig. 4a, b)—a phenomenon well known for fast growing bacteria such as E. coli and B. subtilis^25,45. In the CH model, completion of the DNA replication triggers the cell division, and this gives a homeostatic balance between the DNA amount and the cell volume. An unknown factor of the CH model is how DNA replication is initiated, and a few studies attempted to fill this gap to complement the CH model^27,40. Ho and Amir²⁷ assumed that replication is initiated when a critical amount of “initiators” accumulate at the origin of replication. In the presence of a constant concentration of autorepressors, expressed together with the initiators, this assumption means that the cellular volume increases by a fixed amount between two initiation events, regardless of the absolute volume at the initiation. This “adder” principle between initiations is now supported by several observations^42,43,44. By the initiation considered above, the cell starts the C period of the bacterial cell cycle, which is followed by the D period, and eventually the cell divides^25,45. While Ho and Amir assumed that a constant time is needed to complete the C+D period ("timer” principle)²⁷, further experimental investigations by Witz et al. clarified that the model assuming the adder principle for the C+D period captured single-cell behavior better²⁶. Clarifying the mechanism of cell division control is currently a target of intensive studies and different models have also been proposed^42,43,44. In the present work, we choose to extend Witz et al.’s model²⁶ to cope with the switch to the non-nutritious condition and measure the cell size fluctuations during the reductive division process. We also checked that our main conclusions do not change if we use instead Ho and Amir’s model²⁷ as the starting point.

Fig. 4: Model of reductive division and simulation results.

a, b Single (a) and multifork (b, where #ori = 4) intracellular cycle processes. See Eq. (4) for the criterion that triggers the initiation. Progress of each cycle is represented by a coordinate ${X}_{i}^{{{{{{{{\rm{CD}}}}}}}}}(t)$, which increases at speed μ_i(t) and ends at ${X}_{i}^{{{{{{{{\rm{CD}}}}}}}}}(t)={X}_{i}^{{{{{{{{\rm{CD,th}}}}}}}}}$ by triggering cell division. c Illustration of cell cycles in this model. Each colored arrow represents a single intracellular cycle process. d Overlapping of the rescaled cell size distributions during starvation in the model for LB → PBS. The dashed line represents the fitted log-normal distribution (σ = 0.25(2)). (Inset) The non-rescaled cell size distributions at $t=0,5,30,60,90,120,180,240,300,360,420,480\ \min$ from right to left. e Numerically measured division rate, B(v, t), in the model for LB → PBS. See Supplementary Note 4.B for the measurement method. (Inset) Test of the condition of Eq. (9). Here B_t(0)/B_t(t) is evaluated by B_t(0)/B_t(t) = ∫B(xV(0), 0)dx/∫B(xV(t), t)dx, with x running in the range 0 ≤ x ≤ 1.8. Overlapping of the data demonstrates that Eq. (9) indeed holds in our model.

The model consists of two processes that proceed simultaneously, namely, the volume growth and the intracellular cycle. The volume of each cell (indexed by i), v_i(t), grows as $\frac{{{{{{{{\rm{d}}}}}}}}{v}_{i}}{{{{{{{{\rm{d}}}}}}}}t}=\lambda (t){v}_{i}(t)$, with a time-dependent growth rate λ(t). Following Witz et al.’s model²⁷, we assume that the volume growth is coupled to the intracellular cycle as follows. To begin with the simplest case, suppose that a newborn cell i has a single origin of replication in its chromosome and that the replication starts at some point in time (Fig. 4a, red star). By this initiation of replication, the cell starts to have two origins of replication. Then, the next initiation is triggered when the cell volume v_i(t) increases by a fixed amount δ_i,1 per origin, i.e., when v_i(t) increases by δ_i,1 × 2, since the last initiation (Fig. 4a, blue stars). Note that this criterion does not change whether a cell divides or not before the initiation; if a cell divides and produces daughter cells i₁ and i₂, the initiation in the daughter cells occurs when ${v}_{{i}_{1}}(t)+{v}_{{i}_{2}}(t)-{v}_{i}({t}_{{{{{{{{\rm{init}}}}}}}}})={\delta }_{i,1}\times 2$, where t_init is the time at which the last initiation occurred. Similarly, if multifork replication takes place in a single cell (i.e., #ori = 2^j with j ≥ 2), the threshold for the added volume is given by δ_i,j × #ori (see Fig. 4b for an example with #ori = 4). The criterion therefore reads:

$$\left(\mathop{\sum}\limits_{{i}^{\prime}\in \,{{\mbox{offspring of}}}\,i}{v}_{{i}^{\prime}}(t)\right)-{v}_{i}({t}_{{{{{{{{\rm{init}}}}}}}}})={\delta }_{i,j}\times \#{{{{{{{\rm{ori}}}}}}}}.$$

(4)

Following the experimental results by Si et al.⁴¹, we assume that δ_i,j does not depend on environmental conditions. On the other hand, to take into account stochastic nature of division events, we generate δ_i,j randomly from the Gaussian distribution with mean 〈δ_i,j〉 = δ_mean and standard deviation Std[δ_i,j] = δ_std.

After an initiation, the cell undergoes the C+D period and finally divides. Here, for the sake of simplicity, the progression of the C and D period is collectively expressed by a coordinate ${X}_{i}^{{{{{{{{\rm{CD}}}}}}}}}(t)$, which starts form zero and increases at time-dependent speed μ_i(t), $\frac{{{{{{{{\rm{d}}}}}}}}{X}_{i}^{{{{{{{{\rm{CD}}}}}}}}}}{{{{{{{{\rm{d}}}}}}}}t}={\mu }_{i}(t)$. When ${X}_{i}^{{{{{{{{\rm{CD}}}}}}}}}(t)$ reaches a threshold ${X}_{i}^{{{{{{{{\rm{CD,th}}}}}}}}}$, the cell divides (Fig. 4b), leaving two daughter cells of volumes ${v}_{{i}_{1}}(t)={x}^{{{{{{{{\rm{sep}}}}}}}}}{v}_{i}(t)$ and ${v}_{{i}_{2}}(t)=(1-{x}^{{{{{{{{\rm{sep}}}}}}}}}){v}_{i}(t)$. Here x^sep is randomly drawn from the Gaussian distribution with mean 0.5 and standard deviation 0.0325, the latter value being deduced from experimental observations (see “Methods” and Supplementary Fig. 8). To deal with the multifork replication, the index i of ${X}_{i}^{{{{{{{{\rm{CD}}}}}}}}}(t)$ denotes the cell to divide by the considered cell cycle progression. Therefore, if #ori = 2 when the initiation is triggered, a pair of cell cycles for the future daughter cells, represented by ${X}_{{i}_{1}}^{{{{{{{{\rm{CD}}}}}}}}}(t)$ and ${X}_{{i}_{2}}^{{{{{{{{\rm{CD}}}}}}}}}(t)$, start and run simultaneously (Fig. 4c). Similarly to δ_i,j, we also assume that ${X}_{i}^{{{{{{{{\rm{CD,th}}}}}}}}}$ is a Gaussian random variable, with $\langle {X}_{i}^{{{{{{{{\rm{CD,th}}}}}}}}}\rangle =1$ and ${{{{{{\mathrm{Std}}}}}}}\,[{X}_{i}^{{{{{{{{\rm{CD,th}}}}}}}}}]={X}_{{{{{{{{\rm{std}}}}}}}}}^{{{{{{{{\rm{CD,th}}}}}}}}}$.

Now we are left to determine the two time-dependent rates, λ(t) and μ_i(t). Here we consider the situation where growth medium is switched to non-nutritious buffer at t = 0; therefore, t denotes time passed since the switch to the non-nutritious condition. First, we set the volume growth rate λ(t) on the basis of the Monod equation⁴⁶, assuming that substrates in each cell are simply diluted by volume growth and consumed at a constant rate, without uptake because of the non-nutritious condition considered here. As a result, we obtain

$$\lambda (t)={\lambda }_{0}\frac{1-A}{{e}^{ct}-A},$$

(5)

with constant parameters A and c and the growth rate λ₀( = λ(0)) in the exponential growth phase (see Supplementary Note 3.A for details).

For the cycle progression speed μ_i(t), we propose a functional form that conforms with the type of the principle assumed in the original model for the C+D period in steady conditions, i.e., the adder principle for Witz et al.’s model and the timer principle for Ho and Amir’s model. We first note that the C+D period mainly consists of DNA replication, followed by its segregation and the septum formation⁴⁵. Most parts of those processes involve biochemical reactions of substrates, such as deoxynucleotide triphosphates for the DNA synthesis. Here we can consider different molecular mechanisms for the cycle progression, depending on the type of the principle to adopt. For the case of the adder principle (à la Witz et al.), we can assume that division occurs when a given amount of relevant molecules, such as DNA, is produced. We assume that such relevant molecules are synthesized from substrates through enzyme catalyses, according to the Michaelis–Menten equation. Considering dilution due to the volume growth too, we obtain μ_i(t) ∝ [S_C+D]v_i(t)/(K + [S_C+D]), with [S_C+D] being the concentration of the corresponding substrates and K an adjustable parameter (see Supplementary Note 3 for details). For simplicity, here we assume that [S_C+D] is common to all cells. Note that, since [S_C+D] is constant in steady conditions, μ_i(t) ∝ v_i and this results in the adder principle as considered in Witz et al.’s model. For the starvation process, we consider that [S_C+D] decreases by dilution due to volume growth, degradation, and consumption. Those are assumed to be independent of #ori, based on the experimental results that the duration of the C+D period is independent of #ori in steady environments⁴¹. From those considerations, we finally obtain the following equation for the cycle progression speed:

$${\mu }_{i}(t)=\frac{{\mu }_{0}}{{v}_{0}}\frac{k+1}{k\exp (t/\tau )+1}{v}_{i}(t),$$

(6)

with parameters k and τ, the mean cycle progression speed μ₀, and the mean cell size v₀ in the exponential phase (see Supplementary Note 3.A). In the case of the timer principle for the C+D period in steady environments (à la Ho and Amir), we consider instead that assembly processes of molecules such as deoxynucleotide triphosphates control the cycle progression speed. As a result, we obtain a formula of μ_i(t) without v_i dependence (see Supplementary Note 3). In the following, however, we mostly present results from the model à la Witz et al. unless otherwise stipulated, while we checked that the main conclusions did not change if the model à la Ho and Amir was used instead.

The parameter values are determined from the experimentally measured total cell volume and the cell number, which our simulations turn out to reproduce very well (Fig. 2b, c and Supplementary Fig. 4a, b), with the aid of relations reported by Wallden et al.⁴⁰ for some of the parameters (see Table 1 for the parameter values used in the simulations and “Methods” for the estimation method). With the parameters fixed thereby, we measure the cell size fluctuations at different times and find the scale invariance similar to that revealed experimentally (Fig. 4d and Supplementary Fig. 9b, e). The constancy of CV and Sk is also confirmed (Supplementary Fig. 9c, f). Interestingly, the scale invariance emerges despite the existence of characteristic scales in the model definition, such as the typical volume added between initiations, δ_mean. To check the robustness of those results, we also extended Ho and Amir’s model along the same line (see Supplementary Note 3.B for details) and confirmed the scale invariance of similar quality (Supplementary Fig. 9g, h). These findings suggest the existence of a statistical principle underlying the scale invariance, which is not influenced by details of the model.

Table 1 Parameters used for the simulations.

Theoretical conditions for the scale invariance

To seek for a possible mechanism leading to the scale invariance, here we describe, theoretically, the time dependence of the cell size distribution in a time-dependent process. Suppose N(v, t)dv is the number of the cells whose volume is larger than v and smaller than v + dv. If we assume, for simplicity, that a cell of volume v can divide to two cells of volume v/2, at probability B(v, t), we obtain the following time evolution equation:

$$\frac{\partial N(v,t)}{\partial t}= \, -\frac{\partial }{\partial v}[\lambda (t)vN(v,t)]\\ \, - B(v,t)N(v,t)+4B(2v,t)N(2v,t).$$

(7)

Note that this equation has been studied by numerous past studies for understanding stable distributions in steady conditions^{1,47,48,49,50,51,52}, but here we explicitly include the time dependence of the division rate, B(v, t), for describing the transient dynamics. To clarify a condition for this equation to have a scale-invariant solution, here we assume the scale-invariant form, Eq. (2), where p(v, t) = N(v, t)/n(t) and n(t) is the total number of the cells, and obtain the following self-consistent equation (see Supplementary Note 4.A for derivation):

$$F(x)=-x\frac{\partial F(x)}{\partial x}-\frac{B(v,t)}{\bar{B}(t)}F(x)+2\frac{B(2v,t)}{\bar{B}(t)}F(2x).$$

(8)

Here x = v/V(t) and $\bar{B}(t)=\int dvB(v,t)p(v,t)$. For the scale invariance, Eq. (8) should hold at any time t. This is fulfilled if B(v, t) can be expressed in the following form (see Supplementary Note 4.A):

$$B(v,t)={B}_{v}(v/V(t)){B}_{t}(t).$$

(9)

This is a sufficient condition for the cell size distribution to maintain the scale-invariant form, Eq. (2), during the reductive division. Note that ref. ⁶ proposed a similar scale-invariant form of the division rate for the steady environment. It is also important to remark that, as opposed to Eq. (7), Eq. (8) does not include the growth rate λ(t) explicitly. The scale-invariant distribution F(x) is therefore completely characterized by the division rate B(v, t) in this framework.

To test whether the condition of Eq. (9) is satisfied in our model, we measure the division rate B(v, t) in our simulations (Fig. 4e). The data overlap if B(v, t)B_t(0)/B_t(t) is plotted against v/V(t), demonstrating that Eq. (9) indeed holds here. On the other hand, our theory does not seem to account for the functional form F(x) of the scale-invariant distribution; the right hand side of Eq. (8) differs significantly from the left hand side, if the numerically obtained B(v, t) is used together with the function F(x) from the simulations or the experiments (Supplementary Fig. 10). The disagreement did not improve by taking into account the effect of septum fluctuations (see Supplementary Note 4.C). The lack of quantitative precision is probably not surprising given the simplicity of the theoretical description, which incorporates all effects of intracellular cycles into the simple division rate function B(v, t). The virtue of this theory is that it clarifies that the intracellular cycle seems to have important relevance in the scale invariance and the functional form of the cell size distribution. The significant difference in F(x) identified between bacteria and unicellular eukaryotes (Fig. 3d) may be originated from the different replication mechanisms that the two taxonomic domains adopt.

Violation of the scale invariance

Here we investigate the robustness of the scale invariance during the reductive division. In particular, we aim to clarify whether it breaks down for other starvation conditions, and if so, what the condition is for the scale invariance to hold. As shown in Fig. 3c and Supplementary Fig. 7, the form of F(x) obtained by our experiments depends on the growth environment before starvation. This suggests that F(x) may change if one switches between two growth media in a quasistatic manner, i.e., the scale invariance may break down in this case. Motivated by this hypothesis, we numerically investigate whether there is a lower bound on the relaxation speed of the cellular state, below which the scale invariance breaks down. For simplicity, we consider that the environment starts to change at t = 0, and the volume growth rate λ(t) and the cycle progression speed μ_i(t) decrease as follows:

$$\lambda (t)={\lambda }_{0}\exp (-t/{\tau }_{\lambda }),$$

(10)

$${\mu }_{i}(t)=\frac{{\mu }_{0}}{{v}_{0}}\exp (-t/{\tau }_{\mu }){v}_{i}(t).$$

(11)

We regard τ_λ, τ_μ, and λ₀ as free parameters, while the parameters μ₀ and v₀ were set as follows (see also Supplementary Note 3.C.2 for details). For μ₀, we determined it from λ₀ using empirical relation reported by Wallden et al.⁴⁰ for steady environments. For v₀, we set its value self-consistently, so that the mean cell volume 〈v_i〉 obtained numerically in the exponential phase with μ_i = (μ₀/v₀)v_i falls within 1% error from the given value of v₀. The number of cells is set to be approximately 50,000 at t = 0 and kept constant afterward during the starvation process, by eliminating one of the daughter cells produced by division (see “Methods” for details).

First we evaluate the mean cell volume 〈v〉 and the coefficient of variation, ${{{{{{{\rm{CV}}}}}}}}=\sqrt{\langle \delta {v}^{2}\rangle }/\langle v\rangle$, in the exponential growth phase under steady conditions, by varying the growth rate λ₀ from 0.01 to $0.03\ {\min }^{-1}$. As shown by the black squares in Fig. 5a, b, lower growth rates (smaller mean volumes) lead to lower CVs. This is consistent with our experimental results (Fig. 3c and Supplementary Fig. 7). We then investigate how the mean volume 〈v〉 and CV change during the starvation process, starting at t = 0 from the growth phase with ${\lambda }_{0}=0.03\ {\min }^{-1}$ (Fig. 5a, the top right black square). As expected, our data showed that the mean cell volume decreases if τ_μ > τ_λ and increases otherwise; therefore, in the following, we deal with the case of τ_μ > τ_λ, which corresponds to the reductive division. The color curves in Fig. 5 show trajectories in the 〈v〉–CV space during the starvation process, each curve corresponding to a different τ_μ( > τ_λ) with τ_λ fixed at ${\tau }_{\lambda }=40\ \min$. Remarkably, these trajectories overlap to a single curve with an extended plateau region, which indicates that CV is kept constant, i.e., the scale invariance. Each curve stops in the middle of the master curve, the location of the endpoint (at t → ∞, shown by the open circles) being determined by τ_μ. Importantly, for small τ_μ, the trajectories stop in the plateau region, so that the scale invariance holds during the entire process. By contrast, for large τ_μ, the trajectories go over the plateau and CV decreases abruptly; in other words, the scale invariance breaks down. Next, Fig. 5b shows the master curves for different τ_λ, each constructed by using the trajectories for all τ_μ greater than τ_λ. We find that the smaller τ_λ is, the more extended the plateau region is. Finally, we show the phase diagram for various combinations of τ_μ and τ_λ in Fig. 5c. This clearly shows a region in which the scale invariance is maintained during the entire starvation process, bordered by a transition line over which the scale invariance breaks down. Note that the scale-invariant region becomes narrower for larger τ_λ and τ_μ and seem to disappear eventually; this is consistent with our expectation described at the beginning, that the scale invariance does not hold for quasistatic changes. All those results were also confirmed when the extension of Ho and Amir’s model was used instead (Supplementary Fig. 11; see Supplementary Note 2.B for the model definition).

Fig. 5: Numerical results on the range of validity of the scale invariance.

The initial growth rate is fixed at $\lambda (0)={\lambda }_{0}=0.03\ {\min }^{-1}$ unless otherwise stipulated. a Trajectories in the 〈v〉–CV space for different τ_μ (from 50 to $150\ \min$), with ${\tau }_{\lambda }=40\ \min$ fixed. The endpoint of each trajectory is indicated by a colored open circle. The black squares represent the states in steady growth conditions with the growth rate λ₀ ranging from 0.01 to $0.03\ {\min }^{-1}$. The dashed plateau indicates the initial CV at ${\lambda }_{0}=0.03\ {\min }^{-1}$. b The master curves of the 〈v〉-CV trajectories for different τ_λ. Those are obtained by taking the average of the CV values at each 〈v〉 over different τ_μ(>τ_λ). τ_λ ranges from 10 to $90\ \min$. c Phase diagram. ×: the scale invariance breaks down. Blue ○: the scale invariance holds. Green △: near the boundary. Black dots: the scale invariance holds but the mean volume increases. d Pseudocolor plot of ρ for different τ_λ and τ_μ. See the main text for the definition of ρ. The black region indicates ρ = 0. The white line represents the transition line obtained from c. The boundaries (△) are not included in the region where the scale invariance breaks down.

To understand what triggers the violation of the scale invariance, we focus on the state of the multifork replications, since our theory suggested the importance of the division rate, which is controlled by the state of the cell cycle. As illustrated in Fig. 4c, the first few divisions after the onset of starvation are tied to the initiation that occurred in the exponential growth phase. We may expect that these division events retaining “memories” from the growth phase are less affected by the starvation and therefore may not violate the scale invariance. Based on this expectation, we investigate the state of the cell cycle as follows. First, we observe that the change in the number of origins of replication (#ori) during the growth phase is rather stable, doubling (by initiation) and decreasing (by division) between #ori = 2^j−1 and 2^j with a fixed j for the majority of cells (j = 3 in the case of Fig. 4c; note that j − 1 and j correspond to the numbers of parallel arrows therein). This number is maintained for a while in the starvation process, but eventually it may decrease, because a cell may divide without initiating a new replication during the life. We therefore measure the fraction of such cells, ρ. To be precise, with J being j of each cell in the growth phase, ρ is the fraction of cells such that the C+D period with j < J is initiated during the lifetime, and that this C+D period ends and triggers a cell division afterward, before the cell cycle progression completely stops (note that, since μ_i(t) → 0, not all cell cycles complete). It is measured at the final time point of the simulations (specifically $t=600\ \min$) and shown in Fig. 5d for ${\lambda }_{0}=0.03\ {\min }^{-1}$. Intuitively, ρ corresponds to the fraction of cells that lost memories from the growth phase. Here we find ρ = 0 indeed in most part of the scale-invariant region, while ρ > 0 when the scale invariance breaks down. We therefore consider that the state of the multifork replications may be a key factor that determines whether the scale invariance holds or not during the reductive division. Note that, for gradual environmental changes, actual cells are known to emit signals such as ppGpp^53,54 that control growth and cycle progression, which are not taken into account in our model. Investigating the effect of such signals in this problem is an interesting problem left for future studies.

Discussion

In this work, we developed a membrane-based microfluidic device that we named the extensive microperfusion system (EMPS). Advantages of this device are that we can realize a uniformly controlled environment for wide-area observations of microbes and can switch it without hydrodynamic perturbations. Those advantages may be useful for applications in a wide range of problems with dense cellular populations, including living active matter systems^55,56 and biofilm growth^57,58,59. In this work, we focused on statistical characterizations of single-cell morphology during the reductive division of E. coli. Thanks to the EMPS, we recorded the time-dependent distribution of cell size fluctuations and revealed that the rescaled distribution is scale invariant and robust against the abrupt environmental change, despite the decrease of the mean cell size (e.g., Fig. 2). We confirmed the robustness of the result against different combinations of the growth and non-nutritious media, while we also found that the shape of the rescaled distribution does depend on the choice of the growth medium before the switch (Fig. 3). Moreover, those findings were successfully reproduced by simulations of a model based on the CH model^26,27, which we propose as an extension for dealing with time-dependent environments (Fig. 4). We further inspected theoretical mechanism behind this scale invariance and found the significance of the division rate function B(v, t). We obtained a sufficient condition for the scale invariance, Eq. (9), which was indeed confirmed in our numerical data. Finally, we numerically clarified the range of validity of the scale invariance during the reductive division, showing that the state of the multifork replications may play a crucial role (Fig. 5).

Notably, our experiments (on the growth condition dependence) and simulations suggest that the scale invariance breaks down for slow starvation. Further investigations of cell size fluctuations in such cases, both experimentally and theoretically, will be an important step toward clarifying what determines the critical time scale of environmental changes for the violation of the scale invariance. Elucidating the (τ_λ, τ_μ) phase diagram is particularly important, because it may serve as a further test of the two cell cycle models used here, which predicted significantly different diagrams (Fig. 5c and Supplementary Fig. 11b). It is a challenge experimentally, but may also be possible with EMPS, by combining a technique to control the progression speed of the C+D period, such as the one developed in ref. ⁴¹.

It is also worth noting that the cell size distribution we measured is that of the entire population, which is given by p(v) = ∫p(v∣a)p_age(a)da with the size distribution p(v∣a) of cells at a given age a and the age distribution p_age(a) of the population. Since those distributions have also been studied in the past for steady conditions (e.g., refs. ^5,6 for p(v∣a), ref. ³⁰ for p_age(a)), it is an important future work to understand how these distributions change under time-dependent conditions and how they contribute to the scale invariance. It is also important to understand the dependence on the population size, which will be a crucial point to consider an analogous experiment in the mother machine.

In the context of possible follow-up experiments using the mother machine, another aspect that deserves attention is the way nutrients are delivered to cells and removed. As we have mentioned, EMPS relies on diffusion of molecules and is therefore prone to have a slight amount of residual nutrients in the observation area. While this may better correspond to natural conditions, in which the surrounding medium is not necessarily replaced by a strong flow as in the mother machine^{17,18,19,20,21}, we cannot exclude the possibility that the slightly remaining nutrients might affect the cellular state after starvation in EMPS. Therefore, it would be interesting to investigate whether the scale invariance, which our study has shown to be robust in various starvation conditions in EMPS and in models, can also be verified in the mother machine.

After all, our results backed by the cell cycle model suggest that mechanism of intracellular replication processes may have direct impact on the scale-invariant distribution, which may account for the significant difference we identified between bacteria and eukaryotes (Fig. 3d). Since the number of species studied in each taxonomic domain is rather limited (E. coli (this work) and B. subtilis³⁹ for bacteria, 13 protist species for eukaryotes¹), it is of crucial importance to test the distribution trend further in each taxonomic domain and to clarify how and to what extent the cell size distribution is determined by the intracellular replication dynamics. The influence of cell-to-cell interactions, e.g., quorum sensing^32,33, may also exist. Theoretical approaches, such as models considering the cellular age⁶⁰, knowledge from the universal protein number fluctuations^61,62,63, and renormalization group approaches for living cell tissues⁶⁴, may also be useful. We hope that our understanding of the population-level response against nutrient starvation will be further refined by future experimental and theoretical investigations.

Methods

Strains and culture media

We used wild-type E. coli strains (MG1655 and RP437) and a mutant strain (W3110 ΔfliC Δflu ΔfimA) in this study. Culture media and buffer are listed in Supplementary Table 1. The osmotic pressure of each medium was measured by the freezing-point depression method by the OSMOMAT 030 (Genotec, Berlin, Germany). Details on the strains and culture conditions in each experiment are provided below (see also Supplementary Note 1).

Fabrication of the EMPS

The EMPS consists of a microfabricated glass coverslip, a bilayer porous membrane, and a PDMS pad. The microfabricated coverslip and the PDMS pad were prepared according to refs. ^22,30. We fabricated the bilayer porous membrane by combining a streptavidin-decorated cellulose membrane and a biotin-decorated PET membrane. The streptavidin decoration of the cellulose membrane (Spectra/Por 7, Repligen, Waltham, MA, molecular weight cut-off 25,000) was realized by the method described in refs. ^22,30. The PET membrane (Transwell 3450, Corning, Corning, NY, nominal pore size 0.4 μm) was decorated with biotin as follows. We soaked a PET membrane in 1 wt% solution of 3-(2-aminoethyl aminopropyl) trimethoxysilane (Shinetsu Kagaku Kogyo, Tokyo, Japan) for 45 min, dried it at 125 °C for 25 min and washed it by ultrasonic cleaning in Milli-Q water for 5 min. This preprocessed PET membrane was stored in a desiccator at room temperature, until it was used to assemble the EMPS.

The EMPS was assembled as follows. The preprocessed PET membrane was cut into 5 mm × 5 mm squares, soaked in the biotin solution for 4 h, and dried on filter paper. The biotin-decorated PET membrane was attached with a streptavidin-decorated cellulose membrane, cut to the size of the PET membrane, by sandwiching them between agar pads (M9 medium with 2wt% agarose). In the meantime, a 1 μl droplet of bacterial suspension was inoculated on a biotin-decorated coverslip (see also details below). We then took the bilayer membrane from the agar pad, air-dried for tens of seconds, and carefully put on the coverslip on top of the bacterial suspension. The bilayer membrane was then attached to the coverslip via streptavidin–biotin binding as shown in Supplementary Fig. 1b. We then air-dried the membrane for a minute and attached a PDMS pad on the coverslip by a double-sided tape.

Observation of the bacterial reductive division

We used a wild-type strain MG1655. Before the time-lapse observation, we inoculated the strain from a glycerol stock into 2 ml growth medium in a test tube. The same medium as for the main observation was used (LB broth, M9(Glc+a.a.) or M9(Glc)). After shaking it overnight at 37 °C, we transferred 20 μl of the incubated suspension to 2 ml fresh medium and cultured it until the optical density (OD) at 600 nm wavelength reached 0.1–0.5. The bacterial suspension was finally diluted to OD = 0.05 before it was inoculated on the coverslip.

For this experiment, we used a substrate with wells of 55 μm diameter and 0.8 μm depth. The well diameter was chosen so that all cells in the well can be recorded. The device was placed on the microscope stage, in the incubation box maintained at 37 °C. The microscope we used was Leica DMi8, equipped with a ×100 (N.A. 1.30) oil immersion objective and operated by Leica LasX. To fill the device with growth medium, we injected fresh medium stored at 37 °C from the inlet (Supplementary Fig. 1), at the rate of 60 ml h⁻¹ for $5\ \min$ by a syringe pump (NE-1000, New Era Pump Systems).

In the beginning of the observation, growth medium was constantly supplied at the rate of 2 ml h⁻¹ (flow speed approximately 0.2 mm s⁻¹ above the membrane). When a microcolony composed of approximately 100 cells appeared, we quickly switched the medium to a non-nutritious buffer (PBS or M9 medium with αMG, see Supplementary Table 1) stored at 37 °C, by exchanging the syringe. The flow rate was set to be 60 ml h⁻¹ for the first 5 min, then returned to 2 ml h⁻¹. Throughout the experiment, the device and the media were always in the microscope incubation box, maintained at 37 °C. Cells were observed by phase contrast microscopy and recorded at the time interval of $5\ \min$. The data for obtaining each distribution are taken from several wells (stated in the figure captions) in a single experiment.

The cell volumes were evaluated as follows. We determined the major axis and the minor axis of each cell, manually, by using a painting software. By measuring the axis lengths, we obtained the set of the length L_i and the width w_i for all cells (indexed by i). We estimated the uncertainty in manual segmentation at ±0.15 μm. However, the measurement of the individual cell widths is less accurate than that of the lengths, essentially because the width depends on the choice of the section of the cell. To estimate the cell volume, therefore, we neglected the fluctuation of the width among the cells as follows. We measured the width w_i at the center of each cell and took the ensemble average 〈w_i〉. Together with the cell length L_i, we obtained the volume of this cell, v_i, by ${v}_{i}=\frac{4\pi }{3}{\left(\frac{\langle {w}_{i}\rangle }{2}\right)}^{3}+\pi {\left(\frac{\langle {w}_{i}\rangle }{2}\right)}^{2}({L}_{i}-\langle {w}_{i}\rangle )$. Note that the scale invariance holds for the length distribution as well (Supplementary Fig. 6), which suggests that neglecting the width fluctuation does not affect the main finding of the paper.

Finally, let us note that there may be some technical limitation specific to the combination of the LB medium and the EMPS. When we used LB medium in the growth phase, the bacteria continued growing, albeit very slowly, even long time after the medium was switched to PBS (see Supplementary Movie 7), while they stopped growing completely in all cases where we used chemically defined medium before the switch (Supplementary Fig. 4 and Supplementary Movies 8–11). This may be because some nutrient molecules specific to LB might remain on the well surface or inside the membrane. However, since we are focusing on the earlier stage of the starvation process, in which the typical cell sizes change most significantly, we believe that this remaining slow growth in the case LB → PBS does not affect our main results. More quantitatively, from Supplementary Fig. 9a, we can evaluate the rate of this remaining cell growth observed in the case LB → PBS to be nearly $1{0}^{-4}\ {\min }^{-1}$ or eventually even less. Because the corresponding time scale $\gtrsim 1{0}^{4}\ \min$ is much longer than the time scales relevant to the scale invariance we found, which are around $100\ \min$, there is a clear scale separation, from which we can expect that the remaining slow cell growth will not affect our main finding. We also noticed relatively poor reproducibility of experiments using LB medium (Supplementary Fig. 7), which may be attributed to its chemical undefinedness⁶⁵, since the experiments using defined media recorded good reproducibility (see the same figure).

Simulation

The parameters used in the simulations were evaluated as follows. First, from the observations of the exponential growth phase, we determined the growth rate λ₀ and the mean cell size v₀ directly. This allowed us to set the cycle progression speed μ₀ too, by using the relation ${\mu }_{0}^{-1}\simeq (1.3{\lambda }_{0}^{-0.84}+42)$ proposed by Wallden et al.⁴⁰ (the values of λ₀ and μ₀ in the unit of ${\min }^{-1}$ are used here). Concerning the volume threshold for initiating the replication, we found such a value of δ_mean (or ${v}_{{{{{{{{\rm{mean}}}}}}}}}^{{{{{{{{\rm{th}}}}}}}}}$) that reproduced the experimentally observed mean cell volume in the growth phase. The standard deviation δ_std (or ${v}_{{{{{{{{\rm{std}}}}}}}}}^{{{{{{{{\rm{th}}}}}}}}}$) was set to be 10% of the mean δ_mean (${v}_{{{{{{{{\rm{mean}}}}}}}}}^{{{{{{{{\rm{th}}}}}}}}}$), based on the relation on the initiation volume found by Wallden et al.⁴⁰. They also measured the fluctuations of the time length of the C+D period; this led us to estimate ${X}_{{{{{{{{\rm{std}}}}}}}}}^{{{{{{{{\rm{CD,th}}}}}}}}}$ at 5% of 〈X^CD,th〉, i.e., ${X}_{{{{{{{{\rm{std}}}}}}}}}^{{{{{{{{\rm{CD,th}}}}}}}}}=0.05$. On the septum positions, we measured their fluctuations and found little difference in ${x}_{{{{{{{{\rm{std}}}}}}}}}^{{{{{{{{\rm{sep}}}}}}}}}$ among the different growth conditions we used and also in the non-nutritious case (Supplementary Fig. 8). We therefore used a single value ${x}_{{{{{{{{\rm{std}}}}}}}}}^{{{{{{{{\rm{sep}}}}}}}}}=0.0325$ for all simulations. Note that, without this stochastic asymmetric division, the cell size distribution exhibited periodic oscillations, presumably because cellular states between siblings were strongly correlated then.

In the following, we describe how the remaining parameters were evaluated and how the simulations were carried out for each set of the simulations presented in this work.

Methods for the results that reproduced the experimental observations

We evaluated the time-dependent rates λ(t) and μ_i(t) as follows. The growth rate λ(t) can be determined independently of the cell divisions, because the total volume V_tot(t) = ∑_iv_i(t) grows as ${V}_{{{{{{{{\rm{tot}}}}}}}}}(t)={V}_{{{{{{{{\rm{tot}}}}}}}}}(0)\exp (\int\nolimits_{0}^{t}\lambda (t){{{{{\rm{d}}}}}}t)$. With λ(t) given by Eq. (5), we compared V_tot(t) with experimental data and determined the values of A and c (Fig. 3c). Finally, only k and τ in Eq. (6) remained as free parameters. We tuned them so that the mean cell volume V(t) and the number of the cells n(t) observed in the simulations reproduced those from the experiments (Fig. 3d). The parameter values determined thereby are summarized in Table 1 for the simulations for LB → PBS and M9(Glc+a.a.) → PBS.

We started the simulations from 10 cells with volumes in the range of 0.07–1.13 μm³, randomly generated from the uniform distribution. The cells grew in the exponential phase (with the constant growth rate λ₀ and the cycle progression speed μ_i = (μ₀/v₀)v_i) until the number of cells reached 100,000. We then randomly picked up 10 cells from this “precultured” sample and grew them until the number of cells exceeded 500. Those cells were kept growing for 1,000 min to sufficiently mix cell cycle progressions in the population. During this process, we kept the number of cells constant, by eliminating one of the daughter cells after each division. We then used them as the initial population of each simulation. To precisely compare the number of cells in simulations with the experimentally obtained population ${n}_{\exp }(t)$ (Fig. 2c and Supplementary Fig. 4b), the numerically obtained population ${n}_{{{{{{{{\rm{sim}}}}}}}}}(t)$ is rescaled by multiplying ${n}_{\exp }(0)/{n}_{{{{{{{{\rm{sim}}}}}}}}}(0)$.

Methods for the results on violation of the scale invariance

The functional forms of λ(t) and μ_i(t) were given by Eqs. (10) and (11), with variable parameters τ_λ and τ_μ. For μ₀, we determined it from λ₀ using the empirical relation reported by Wallden et al.⁴⁰. For v₀, we set its value self-consistently, so that the mean cell volume 〈v_i(0)〉 obtained numerically in the exponential phase with μ_i = (μ₀/v₀)v_i falls within 1% error from the given value of v₀. As a result, we obtained v₀ = 1.9, 2.5, 3.2, 4.0, 5.0 μm³ for $\lambda =0.01,0.015,0.02,0.025,0.03\ {\min }^{-1}$, respectively. These values satisfy the growth law, i.e., the mean cell size increases exponentially with the growth rate⁵². The other parameters were fixed at δ_mean = 0.25 μm³, δ_std = 0.025 μm³, ${X}_{{{{{{{{\rm{std}}}}}}}}}^{{{{{{{{\rm{CD,th}}}}}}}}}=0.05$, and ${x}_{{{{{{{{\rm{std}}}}}}}}}^{{{{{{{{\rm{sep}}}}}}}}}=0.0325$. We started the simulations from 50 cells with volumes in the range of 0.07–1.13 μm³, randomly generated from the uniform distribution. The cells grew in the exponential phase until the number of cells reached 500,000. We then randomly picked up 50 cells and grew them until the number of cells exceeded 50,000. Those cells were kept growing for 1,000 min to sufficiently mix cell cycle progressions in the population, with the number of cells kept constant by eliminating one of the daughter cells produced by division. Using them as the initial population (at t = 0), we started the simulations for t ≥ 0, with the number of cells still kept constant by the same method. Strictly, this situation with a constant number of cells is different from the experimental setting, but we confirmed that this change did not influence the validity of the scale invariance and had only a minor effect on the value of CV, at least for the situation shown in Fig. 4c. Therefore, for the results on the violation of the scale invariance (Fig. 5), we carried out simulations with a constant number of cells as described above, to reduce the computation time.

Reporting summary

Further information on research design is available in the Nature Research Reporting Summary linked to this article.