Abstract
Two-dimensional (2D) surface of the topological materials is an attractive channel for the electrical conduction reflecting the linearly-dispersive electronic bands. Thickness-dependent sheet conductance measurement is a reliable method to evaluate the 2D and three-dimensional (3D) electrical conducting channel separately but has rarely been applied for Weyl semimetals. By applying this method to thin films of a Weyl semimetal Co3Sn2S2, here we show that the 2D conducting channel clearly emerges under the ferromagnetic phase, indicating a formation of the Fermi arcs projected from Weyl nodes. Comparison between 3D conductivity and 2D conductance provides the effective thickness of the surface conducting region being estimated to be approximately 20 nm, which would reflect the Weyl feature of electronic bands of the Co3Sn2S2. The emergent surface conduction will provide a pathway to activate quantum and spintronic transport features stemming from a Weyl node in thin-film-based devices.
Similar content being viewed by others
Introduction
The surface of the films forms interface with substrate or capping layer, which usually plays an active role for the electrical conduction in addition to the bulk region. Various origins for the interface conduction in trivial semiconductors have been explored as charge discontinuity at oxide interface1, charge transfer2, dipoles effect3, and electric polarization effect4,5. The effective thickness of the two-dimensional (2D) conducting channel is basically dominated by charge accumulation based on Poisson equation. Besides these interface effects, the emergent topological materials hold intrinsic surface conducting channels that are a Dirac surface state in three-dimensional (3D) topological insulator (TI)6 and Fermi arc in Dirac and Weyl semimetals7,8. The surface conduction in the topological materials exhibits the intriguing features of linearly-dispersive electronic bands such as spin-momentum locking9,10, quantum anomalous Hall effect11,12, and magnetoresistance oscillation at the Weyl orbits13,14. As another important feature, the surface states of TIs suddenly disappear by hybridization between two surfaces of top and bottom in ultrathin films. While the dominant factor of the penetration function along thickness direction has been experimentally15,16 and theoretically17 investigated, the critical thickness for 3D-TIs is about 5 nm for Bi2Se3 (ref. 15) and 2 nm for Bi2Te3 (ref. 16). However, surface conduction in Weyl semimetal (WSM) has been rarely explored in thin films. Recently, a Co-kagome magnet of Co3Sn2S2, crystal structure of which is shown in Fig. 1a, has been extensively investigated as a Dirac semimetal (DSM) at paramagnetic phase and a WSM at ferromagnetic phase18,19,20,21,22,23. Among proposed Weyl semimetals, Co3Sn2S2 is an ideal material for the electrical detection of surface conduction because (i) the Weyl points are very close to the Fermi level18, (ii) the linearly-dispersive bands dominantly contribute to density-of-states at the Fermi level18, (iii) the Curie temperature (TC) of ~180 K is relatively high as a kagome-lattice ferromagnet with electrical conduction. Large anomalous Hall conductivity has been focused with perpendicular magnetic anisotropy owing to large contribution of Berry curvature in the Weyl nodes18. By tilting the symmetric line of the two Weyl nodes from z-axis, surface Fermi arc has been observed by spectroscopies21,22,23. The contribution of the projected Weyl nodes would be detected in electrical conduction for ultrathin films with suppressed bulk conduction though it has not been apparently obtained in bulk Co3Sn2S2.
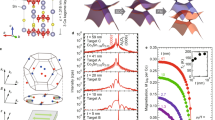
a Crystal structure of Co3Sn2S2. b Concept of electrical conduction of Co3Sn2S2 thin films in the bulk Gbulk and at the surface Gsurf. Below Curie temperature, perpendicular magnetization M (green arrows) induces anomalous Hall effect (AHE). c Cross-section of thin films with thickness t-dependent \(G_{{\mathrm{bulk}}}^{2{\mathrm{D}}}\) and t-independent \(G_{{\mathrm{surf}}}^{2{\mathrm{D}}}\). Sheet conductance in the bulk \(G_{{\mathrm{bulk}}}^{2{\mathrm{D}}}\) is evaluated by three-dimensional conductivity of bulk Co3Sn2S2 \(\sigma _{{\mathrm{bulk}}}^{3{\mathrm{D}}}\) × t.
The electrical conduction in thin films at zero magnetic field is generally expected to follow the Ohm’s law based on the 3D uniform conductivity σxx (Ω−1cm−1) in whole region of the film; \(G = \frac{I}{V} = \sigma _{xx}\frac{{tW}}{L}\), where G is the conductance of the sample, I current, V applied voltage, W width, L length, and t thickness of the channel. The sheet conductance is experimentally calculated by \(G_{\mathrm{s}} = \frac{{IL}}{{VW}} = t\sigma _{xx}\). When the surface or interface contributes to the electrical conduction in the films, the sheet conductance of the film \(G_{{\mathrm{total}}}^{2{\mathrm{D}}}\) sums up the t-dependent conductance in bulk region Gbulk = \(t\sigma _{{\mathrm{bulk}}}^{3{\mathrm{D}}}\) and the t-independent 2D surface conductance \(G_{{\mathrm{surf}}}^{2{\mathrm{D}}}\), \(G_{{\mathrm{total}}}^{2{\mathrm{D}}} = t\sigma _{{\mathrm{bulk}}}^{3{\mathrm{D}}} + G_{{\mathrm{surf}}}^{2{\mathrm{D}}}\) as shown in Fig. 1b, c, where \(\sigma _{{\mathrm{bulk}}}^{3{\mathrm{D}}}\) is the 3D conductivity of the bulk region. Experimentally, t dependence of the 2D sheet conductance \(G_{{\mathrm{total}}}^{2{\mathrm{D}}}\) can separately elucidate the conducting channel at 3D bulk and 2D surface when these contributions are comparable in thin films. However, it is often difficult to achieve the electrical conduction in the ultrathin layers because the island-like grains initially disconnect each other. This is so-called a dead layer at the interface, which is usually evaluated by the t-dependent conductance measurement. To accurately evaluate the bulk conductivity \(\sigma _{{\mathrm{bulk}}}^{3{\mathrm{D}}}\) of the thin films, therefore, the t-dependent measurement is reliable with elimination of the additional conduction at the surface and/or with accurate thickness contributing conduction except for a dead layer. In this study, we applied this analysis to the Co3Sn2S2 thin films to elucidate the dimensionality of the conducting channels at bulk and surface separately. The films holding WSM phase are intensively discussed in thickness 23–61 nm. The metallic conduction of the films at the WSM phase strongly relates to the superior surface conduction.
Results
Temperature dependence of electrical resistivity
Temperature dependent resistivity ρxx of two Co3Sn2S2 films with thicknesses of 41 and 40 nm is shown in Fig. 2a with a reference ρxx of bulk crystal18. The two films are typical examples for 12 films with various thicknesses t (23–61 nm), prepared by radio-frequency sputtering (Methods section)24,25. Atomic force microscopy observation detected comparable surface roughness values on SiOx cap layers of the two films (Supplementary Fig. 1). All three traces in Fig. 2a clearly present a kink ~180 K coming from the ferromagnetic transition, corresponding to a phase transition from DSM at T > TC to WSM at T < TC. This feature is in fact detected in magnetization and anomalous Hall conductivity24,25. Since metallic conduction is more pronounced in the WSM phase, here we define the residual resistivity ratio (RRR = ρxx (T = 300 K)/ρxx (T = 2 K)) to characterize the metallicity of the films. This RRR is a good measure to classify the films into two groups while the structural qualities of these films are comparable in the inspection by x-ray diffraction25. In Fig. 2b, the RRR for all the films measured in this study is summarized with the bulk value18 to classify the films into Groups A (blue) and B (red), in which the border for classification is RRR ∼ 4. Typical ρxx values for the film #1 of Group A and the film #2 of Group B with comparable t ∼ 40 nm represent large and small RRR in Fig. 2a, respectively. In comparison with the reference ρxx of bulk crystal with large RRR ∼ 8.5, ρxx of #1 at low temperature is comparable to that of the bulk but the ρxx of both the films at high temperature is largely different.
a T dependence of resistivity ρxx for a reference of bulk (black curve from Liu et al.18), film #1 (blue curve; t = 41 nm) from Group A, and film #2 (red curve; t = 40 nm) from Group B. b Residual resistivity ratio RRR for the films as a function of thickness, which guided to categorize the films to Group A and B by the criteria at roughly RRR = 4. The bulk value of RRR = 8.5 (Liu et al.18) is included for comparison. c, d To detect the t-independent conductance, sheet conductance \(G_{{\mathrm{total}}}^{2{\mathrm{D}}}\) for various thickness films at T = 300 K and 2 K are plotted, respectively. The slope corresponds to three-dimensional conductivity \(\sigma _{{\mathrm{bulk}}}^{3{\mathrm{D}}}\). The detection of intercept in d indicates the emergence of t-independent two-dimensional surface conductance \(G_{{\mathrm{surf}}}^{2{\mathrm{D}}}\). The experimental data in a and d are replotted from Ikeda et al.25.
Detection of 2D surface conductance in WSM phase
Thickness t dependence of sheet conductance (Gs = 1/Rs, where Rs is sheet resistance) at T = 300 K and 2 K is plotted as a function of t in Fig. 2c, d, respectively. In DSM phase at 300 K, the sheet conductance linearly depends on t. In addition, the intercept of the fitting line is close to the origin, holding a dead layer thickness of roughly 1 nm. This linear trend and the small intercept, as well as the negligibly small strain as revealed by transmission electron microscopy analysis (Supplementary Fig. 2), support the validity of this t-dependent analysis based on the uniform crystalline quality of the films. The slope in this plot corresponds to the conductivity of the bulk \(\sigma _{{\mathrm{bulk}}}^{3{\mathrm{D}}}\) as a usually discussed fundamental physical parameter. In contrast, the intercept of the fitting line at T = 2 K in Fig. 2d apparently reveals the emergence of t-independent 2D conducting channel at extrapolated t = 0 nm, corresponding to the 2D surface conductance \(G_{{\mathrm{surf}}}^{2{\mathrm{D}}}\). This dramatic variation of the intercept in the fitting line from 300 K to 2 K (also see Supplementary Fig. 3) strongly indicates the unique surface transport of the Fermi arc states, relating on the spontaneous symmetry breaking and Fermi energy. The Fermi energy in the non-magnetic phase is far from the Dirac point26, being the maximum density of state that relates on the Stoner criterion for the ferromagnetism in Co3Sn2S2. By contrast, the Fermi energy becomes rather close to the Weyl nodes below TC (refs. 18,26), which is the origin for the distinct appearance of the surface state in only WSM phase.
Evaluation of 2D and 3D conducting channel separately
At the various temperatures, t-dependent analysis was carried out to elucidate the \(\sigma _{{\mathrm{bulk}}}^{3{\mathrm{D}}}\) and \(G_{{\mathrm{surf}}}^{2{\mathrm{D}}}\). In addition, the total conductivity \(\sigma _{xx}\) of the films is calculated by conventional scheme \(\sigma _{xx} = {\textstyle{{\rho _{xx}} \over {\left( {\rho _{xx}^2 + \rho _{yx}^2} \right)}}}\), where ρxx is resistivity and ρyx Hall resistivity for estimation under the assumption of uniform conduction in whole region. Figure 3a, b shows the σxx (black line) for the films #1 and #2 and the analyzed \(\sigma _{{\mathrm{bulk}}}^{3{\mathrm{D}}}\) (red circles) as discussed in Fig. 2c, d for the Group A and B, respectively. Above TC ∼ 180 K, the analyzed \(\sigma _{{\mathrm{bulk}}}^{3{\mathrm{D}}}\) matches well with the σxx, meaning that the analysis is valid for estimation of bulk conductivity for DSM phase. In WSM phase below TC, the \(\sigma _{{\mathrm{bulk}}}^{3{\mathrm{D}}}\) (red closed circles) gradually increases with decreasing temperature, implying the suppression of spin disorder scattering and/or magnon-phonon scattering19,27,28,29 as like half-metallic ferromagnetic materials. Moreover, the σxx for #1 (black line) represents superior metallic behavior at low temperature, the value of which is much higher than the \(\sigma _{{\mathrm{bulk}}}^{3{\mathrm{D}}}\). This deviation indicates the contribution of additional conducting channel to that of the t-dependent bulk, which is the t-independent surface conduction (blue region). By contrast, in Fig. 3b, the σxx for #2 (black line) is comparable to the \(\sigma _{{\mathrm{bulk}}}^{3{\mathrm{D}}}\) (red open circles) for Group B. Considering the comparable \(\sigma _{{\mathrm{bulk}}}^{3{\mathrm{D}}}\) for Group A and B, the superior metallic conduction of σxx for #1 is mainly driven by the surface conduction.
a, b The \(\sigma _{{\mathrm{bulk}}}^{3{\mathrm{D}}}\) is estimated by the slope in t-dependent sheet conductance for Group A and B as shown in Fig. 2c, d. Temperature dependence of the analyzed \(\sigma _{{\mathrm{bulk}}}^{3{\mathrm{D}}}\) is plotted with the obtained conductance data for the representative film #1 in A and #2 in B (black line). The deviation between the black line and \(\sigma _{{\mathrm{bulk}}}^{3{\mathrm{D}}}\) corresponds to the contribution of electrical conduction at the surface \(\sigma _{{\mathrm{surf}}}^{3{\mathrm{D}}}\). The error bars represent the standard deviations of the calculated \(\sigma _{{\mathrm{bulk}}}^{3{\mathrm{D}}}\).
Effective thickness of 2D surface conducting channel
The analyzed \(G_{{\mathrm{surf}}}^{2{\mathrm{D}}}\) for Group A and B is plotted as a function of temperature in Fig. 4a. The \(G_{{\mathrm{surf}}}^{2{\mathrm{D}}}\) increases with decreasing temperature in WSM phase for both Groups. The steep increase of \(G_{{\mathrm{surf}}}^{2{\mathrm{D}}}\) for Group A induces the large σxx of the films in Group A. Judging from the consistent trend between the σxx shown in Fig. 3 and the \(G_{{\mathrm{surf}}}^{2{\mathrm{D}}}\) in Fig. 4a, the difference between the observed σxx (black line) and the analyzed \(\sigma _{{\mathrm{bulk}}}^{3{\mathrm{D}}}\) (red circles) in Fig. 3; \(\sigma _{xx} - \sigma _{{\mathrm{bulk}}}^{3{\mathrm{D}}} = \sigma _{{\mathrm{surf}}}^{3{\mathrm{D}}}\), corresponds to the contribution of 2D \(G_{{\mathrm{surf}}}^{2{\mathrm{D}}}\). Considering the units of \(\sigma _{{\mathrm{surf}}}^{3{\mathrm{D}}}\) and \(G_{{\mathrm{surf}}}^{2{\mathrm{D}}}\), we estimate the effective thickness of the surface conduction \(t_{{\mathrm{surf}}}^{{\mathrm{eff}}}\) by a following equation \(\sigma _{{\mathrm{surf}}}^{3{\mathrm{D}}} \times t_{{\mathrm{surf}}}^{{\mathrm{eff}}} \times 2 = G_{{\mathrm{surf}}}^{2{\mathrm{D}}}\) where the factor of 2 corresponds to two surfaces of the films. Although the error bar is large in Fig. 4b, the t-independent 2D conduction region is estimated to be roughly 20 nm constant against t-variation. This value is rather thicker than that of 3D-TI for example 5 nm of Bi2Se3 (ref. 15). The distribution of surface Fermi arc along z-direction may be related to the broadness of the projection of Weyl nodes with narrow gap17. Based on empirical facts that weakening of spin–orbit coupling tends to increase the critical thickness in 3D-TIs such as Bi2Se3 and Bi2Te3 (refs. 15,16,17), the weaker spin–orbit coupling of Co3Sn2S2 composed of lighter elements may induce the weak confinement of surface state, resulting in the large effective thickness. While we here assume uniform \(G_{{\mathrm{surf}}}^{2{\mathrm{D}}}\) to estimate the averaged effective thickness, the penetration function of the surface conduction region should be more carefully considered to be rapid decay along z-direction as like 3D-TIs17,30. It will be important to clarify the correspondence between the estimated \(t_{{\mathrm{surf}}}^{{\mathrm{eff}}}\) and the real-space distribution of the surface states. While the values of \(\sigma _{{\mathrm{bulk}}}^{3{\mathrm{D}}}\) and \(G_{{\mathrm{surf}}}^{2{\mathrm{D}}}\) are influenced by the defects in bulk and surface region, the \(t_{{\mathrm{surf}}}^{{\mathrm{eff}}}\) is likely valid owing to the independent analysis for the estimation of bulk and surface contribution. In this study, apparent detection of the t-independent conductance reveals the possibility of surface Fermi arc conduction in the Co3Sn2S2 thin films.
a Temperature dependence of the surface conduction \(G_{{\mathrm{surf}}}^{2{\mathrm{D}}}\) by the analysis as shown in Fig. 2d for the data of Group A (blue) and B (red). b Under the assumption of uniform electrical conduction at the surface region, the effective thickness of surface conduction \(t_{{\mathrm{surf}}}^{{\mathrm{eff}}}\) is calculated by \(t_{{\mathrm{surf}}}^{{\mathrm{eff}}} = \frac{{G_{{\mathrm{surf}}}^{2{\mathrm{D}}}}}{{2\sigma _{{\mathrm{surf}}}^{3{\mathrm{D}}}}}\) at T = 2 K. The error bars represent the standard deviations of the calculated \(G_{{\mathrm{surf}}}^{2{\mathrm{D}}}\) and \(t_{{\mathrm{surf}}}^{{\mathrm{eff}}}\) in a and b, respectively.
Discussion
Here we discuss the origin for the appearance of t-independent surface conduction in the films. The robust t-independent current path is experimentally detected by the analysis of sheet conductance of the films. The thickness of the films is thick enough to form uniform crystalline structure and to hold a feature of WSM with large anomalous Hall conductivity25. The top and bottom surfaces of the films form the interface with a capping layer of SiOx and Al2O3 substrate, respectively. Such interface between oxide insulator and sulfide metal is likely to be basically inactive for the electrical conduction. Other extrinsic defect formation contributing to the metallic electrical conduction can be excluded. As intrinsic origins, the surface projected Fermi arc is possibly located at the inert interface. Moreover, the appearance of surface conduction below TC should be noticeable to the Weyl nodes stemming from WSM phase. However, the origin for different values of RRR in two groups is not obvious from the structural quality. In fact, the analyzed value of \(\sigma _{{\mathrm{bulk}}}^{3{\mathrm{D}}}\) for both group is comparable. The resultant \(G_{{\mathrm{surf}}}^{2{\mathrm{D}}}\) originating from clear classification of Group A and B in Fig. 2d is mainly related to the difference of RRR. As shown in Fig. 2b, most of the films in Group A are roughly thicker than those in Group B, implying that 40 nm ∼2 × \(t_{{\mathrm{surf}}}^{{\mathrm{eff}}}\) looks criteria for the large surface conduction. The surface conduction in the WSMs may be weakened by hybridization each other. Single crystalline bulk also presents large RRR (Liu et al.18), even though the electrical conduction is dominated by the Gbulk due to thick limit. To be consistent with the bulk results, the detected surface conduction is likely to shed light on the thin films with less contribution of bulk conduction. In addition, the surface termination might be a plausible origin for holding different Fermi surface contributing to the electrical conduction7,21,22,31, although determination of the surface termination of Co3Sn2S2 thin film is difficult in the present sample structure. The superior metallic surface conduction in Group A may link to the rich surface Fermi arc by sulfur termination. On the sulfur terminated surface, the sulfur vacancies detected by tunneling spectroscopy might influence the 2D surface conduction via a local modification of the electronic states22,32. By contrast, the less surface conduction in Group B may be terminated by Sn. The further studies on specific interface formation need to clarify the termination and contribution to the charge distribution.
Conclusions
Systematic thickness dependence of conductance reveals the emergence of t-independent 2D conducting channel in the Co3Sn2S2 films under Weyl semimetal phase. Based on the analysis for two group films, superior metallic conduction at surface dominates the large RRR of the films. Origin for the appearance of 2D metallic conducting channel is likely the surface Fermi arc projected from Weyl nodes. Broad penetration of the 2D surface state comes from material specific parameters of Weyl semimetal Co3Sn2S2 such as strength of spin–orbit coupling and gap size at Weyl point. The interface formation with the Co3Sn2S2 will provide an attractive arena for quantum transport and spintronic phenomena based on the intriguing 2D metallic surface state.
Methods
Film preparation
Co3Sn2S2 thin films were prepared by radio-frequency sputtering. The growth procedure is following and detail information can be found in previous studies24,25. Firstly, a Co3Sn2S2 film was deposited on Al2O3 (0001) substrate at 400 °C. Then, a SiOx capping layer was deposited on the Co3Sn2S2 film. The film was annealed at 800 °C in vacuum for 1 h. The crystal structures and composition were characterized by x-ray diffraction and energy-dispersive x-ray spectroscopy. The t (23–61 nm) was controlled by the deposition duration, which was confirmed by the Laue fringe in x-ray diffraction patterns.
Electrical transport measurement
Electrical measurements were carried out in physical property measurement system (PPMS, Quantum Design)25. The films were scratched to make Hall-bar shape with indium contact electrodes. In the previous studies, the large anomalous Hall conductivity was observed in all films, indicating that the WSM phase is materialized.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Ohtomo, A. & Hwang, H. Y. A high-mobility electron gas at the LaAlO3/SrTiO3 heterointerface. Nature 427, 423–426 (2004).
Chen, W., Chen, S., Qi, D. C., D., Gao, X. Y. & Wee, A. T. S. Surface transfer p-type doping of epitaxial graphene. J. Am. Chem. Soc. 129, 10418–10422 (2007).
Chua, L.-L. et al. General observation of n-type field-effect behaviour in organic semiconductors. Nature 434, 194–199 (2005).
Olsson, L. Ö. et al. Charge accumulation at InAs surfaces. Phys. Rev. Lett. 76, 3626–3629 (1996).
Ambacher, O. et al. Two dimensional electron gases induced by spontaneous and piezoelectric polarization in undoped and doped AlGaN/GaN heterostructures. J. Appl. Phys. 87, 334–344 (2000).
Hasan, M. Z. & Kane, C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Yan, B. & Felser, C. Topological materials: Weyl semimetals. Annu. Rev. Condens. Matter Phys. 8, 337–354 (2017).
Armitage, N. P., Mele, E. J. & Vishwanath, A. Weyl and Dirac semimetals in three-dimensional solids. Rev. Mod. Phys. 90, 015001 (2018).
Mellnik, A. R. et al. Spin-transfer torque generated by a topological insulator. Nature 511, 449–451 (2014).
Soumyanarayanan, A., Reyren, N., Fert, A. & Panagopoulos, C. Emergent phenomena induced by spin-orbit coupling at surfaces and interfaces. Nature 539, 509–517 (2016).
Chang, C.-Z. et al. Experimental observation of the quantum anomalous Hall effect in a magnetic topological insulator. Science 340, 167–170 (2013).
Tokura, Y., Yasuda, K. & Tsukazaki, A. Magnetic topological insulators. Nat. Rev. Phys. 1, 126–143 (2019).
Potter, A. C., Kimchi, I. & Vishwanath, A. Quantum oscillations from surface Fermi arcs in Weyl and Dirac semimetals. Nat. Commun. 5, 5161 (2014).
Moll, P. J. W. et al. Transport evidence for Fermi-arc-mediated chirality transfer in the Dirac semimetal Cd3As2. Nature 535, 266–270 (2016).
Zhang, Y. et al. Crossover of the three-dimensional topological insulator Bi2Se3 to the two-dimensional limit. Nat. Phys. 6, 584–588 (2010).
Li, Y.-Y. et al. Intrinsic topological insulator Bi2Te3 thin films on Si and their thickness limit. Adv. Mater. 22, 4002–4007 (2010).
Zhang, W., Yu, R., Zhang, H.-J., Dai, X. & Fang, Z. First-principles studies of the three-dimensional strong topological insulators Bi2Te3, Bi2Se3 and Sb2Te3. New J. Phys. 12, 065013 (2010).
Liu, E. et al. Giant anomalous Hall effect in a ferromagnetic kagome-lattice semimetal. Nat. Phys. 14, 1125–1131 (2018).
Wang, Q. et al. Large intrinsic anomalous Hall effect in half-metallic ferromagnet Co3Sn2S2 with magnetic Weyl fermions. Nat. Commun. 9, 3681 (2018).
Li, G. et al. Surface states in bulk single crystal of topological semimetal Co3Sn2S2 toward water oxidation. Sci. Adv. 5, eaaw9867 (2019).
Jiao, L. et al. Signatures for half-metallicity and nontrivial surface states in the kagome lattice Weyl semimetal Co3Sn2S2. Phys. Rev. B. 99, 245158 (2019).
Morali, N. et al. Fermi-arc diversity on surface terminations of the magnetic Weyl semimetal Co3Sn2S2. Science 365, 1286–1291 (2019).
Liu, D. F. et al. Magnetic Weyl semimetal phase in a Kagomé crystal. Science 365, 1282–1285 (2019).
Fujiwara, K. et al. Ferromagnetic Co3Sn2S2 thin films fabricated by co-sputtering. Jpn. J. Appl. Phys. 58, 050912 (2019).
Ikeda, J. et al. Critical thickness for the emergence of Weyl features in Co3Sn2S2 thin films. Commun. Mater. 2, 18 (2021).
Ozawa, A. & Nomura, K. Two-orbital effective model for magnetic Weyl semimetal in Kagome-lattice shandite. J. Phys. Soc. Jpn 88, 123703 (2019).
Goodings, D. A. Electrical resistivity of ferromagnetic metals at low temperatures. Phys. Rev. 132, 542–558 (1963).
Furukawa, N. Unconventional one-magnon scattering resistivity in half-metals. J. Phys. Soc. Jpn. 69, 1954–1957 (2000).
Bombor, D. et al. Half-metallic ferromagnetism in the Heusler compound Co2FeSi. Phys. Rev. Lett. 110, 066601 (2013).
Muechler, L. et al. Emerging chiral edge states from the confinement of a magnetic Weyl semimetal in Co3Sn2S2. Phys. Rev. B. 101, 115106 (2020).
Xu, Q. et al. Topological surface Fermi arcs in the magnetic Weyl semimetal Co3Sn2S2. Phys. Rev. B. 97, 235416 (2018).
Xing, Y. et al. Localized spin-orbit polaron in magnetic Weyl semimetal Co3Sn2S2. Nat. Commun. 11, 5613 (2020).
Acknowledgements
The authors are grateful to S. Ito and M. Nagasako for the transmission electron microscopy analysis and K. Kobayashi, Y. Yanagi, M.-T. Suzuki, and Y. Motome for fruitful discussions. This work was performed under the Inter-University Cooperative Research Program of the Institute for Materials Research, Tohoku University (Proposal No. 19G0410). This work was supported by JSPS KAKENHI (Grant No. 20H01830) and JST CREST (JPMJCR18T2).
Author information
Authors and Affiliations
Contributions
J.I. and K.F. grew the films and measured the electrical transport properties. J.S. performed the magnetoresistance measurements. K.F. performed the magnetization measurements under the support by J.S., T.S., and K.T.; J.I. and K.F. analyzed the measured data. K.N. contributed to theoretical interpretations of the experimental results. J.I., K.F., and A.T. wrote the manuscript with input from other authors. All authors discussed the results. A.T. supervised the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Communications Physics thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ikeda, J., Fujiwara, K., Shiogai, J. et al. Two-dimensionality of metallic surface conduction in Co3Sn2S2 thin films. Commun Phys 4, 117 (2021). https://doi.org/10.1038/s42005-021-00627-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-021-00627-y
This article is cited by
-
Magnetic, transport and topological properties of Co-based shandite thin films
Communications Physics (2024)
-
Non-volatile chirality switching by all-optical magnetization reversal in ferromagnetic Weyl semimetal Co3Sn2S2
Communications Physics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.