Introduction

Moiré is a kind of geometrical interference that appears when two nearly identical lattices are aligned with a small angle mismatch (Fig. 1a). The discovery of moiré in a stack of h-BN and graphene1,2 has led to numerous studies associated with superstructures of graphene formed by incommensurate substrates3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18. The moiré structure virtually gives graphene another periodic structure, and therefore, these systems can be regarded as superlattices19,20. The conventional understanding of superlattices is that an energy gap forms at the boundary of the Brillouin zone of the superlattice. However, recent findings in monolayer graphene have shown that Dirac cones are formed by locally closing the energy gap, and this results in additional peaks in the carrier density dependence of resistance3,4,5,6,7,11. Further studies have indicated that the secondary Dirac cones are formed at the K or K’ point of the superlattice Brillouin zone21,22,23,24. The moiré potential forms a band gap of about 20 meV at the secondary Dirac cone in the hole branch8,13. In addition, the superlattice potential forms a band gap of about ∼35 meV at the primary Dirac cone in the case of perfect alignment, which appears at the charge neutrality point4,5,6,7,8,13,25,26. These band-gap values are highly dependent on the alignment angle and sample structure4,13.

Fig. 1: Sample characterization.
figure 1

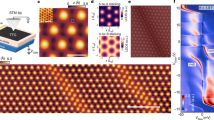
a Schematic drawing of moiré structure formed by stacking two honeycomb lattice sheets. The arrows indicate the periodic structure. b Low energy dispersion relation of AB-stacked tetralayer graphene in the absence a perpendicular electric flux density, calculated for Slonczewski-Weiss-McClure (SWMcC) parameters of graphite. \(k_0 = \frac{{2\gamma _1}}{{\surd 3\gamma _0a}}\) (a is the lattice constant of graphene). c Low energy dispersion of AB-stacked tetralayer graphene in the presence a perpendicular electric flux density. FLB stands for the nearly flat part in the band. Be (Bh) is an electron-like (hole-like) heavy mass bilayer-like band; be (bh) is an electron-like (hole-like) light mass bilayer-like band. d Optical micrograph of a sample. Hall bar equipped with top and bottom gate electrodes. The bar is 10 μm long. e Bottom gate voltage (Vb) dependence of resistivity (ρ) measured for zero top gate voltage (Vt = 0 V). \(T = 4.2\,{\mathrm{K}}\,{\mathrm{and}}\,B = 0\,{\mathrm{T}}.\) The peak for charge neutrality (\(V_{\mathrm{b}} \approx 0\)V) and satellite peaks (\(V_{\mathrm{b}} \approx 40\,{\mathrm{and}}\, - 45\)V) are discernible.

Full size image

Although there have been a number of studies on moiré superlattices of h-BN/single layer graphene heterostructures, there have only few studies on moiré superlattices of graphene with multiple layers. As far as the authors know, bilayer graphene has been studied in terms of Hofstadter butterfly’s diagram in the energy spectrum obtained in a magnetic field10,24,27. The superlattice potential due to the moiré would primarily influence the surface layer of graphene in contact with it. Therefore, it is not clear how the electronic band structure is modified by the moiré potential in graphene with multiple layers. Moreover, trigonal warping of the band structure becomes increasingly dominant as the number of layers increases28,29. This effect would be important in forming an energy gap due to the moiré structure, and it would also be important in reconstructing the Fermi surface. In this work, we studied the electronic band structure of a moiré superlattice of AB-stacked tetralayer graphene, as an example of multilayer graphene, by conducting low-temperature transport experiments. We found features intrinsic to the moiré superlattice of multilayer graphene.

The band structure of AB-stacked tetralayer graphene consists of two bilayer-like bands (light and heavy mass) as shown in Fig. 1b. A simplified band model indicates that the tetralayer graphene should have a semi-metallic band in which there is an overlap of the electron and hole bands near E = 0; however, mixing between the heavy and light-mass bilayer-like bands creates local energy gaps, and thus, the band overlap of the conduction and valence bands is expected to be considerably smaller than predicted by the simplified band model30,31,32,33. The band overlap vanishes by applying a perpendicular electric field; an energy gap opens at the bottoms of the bilayer-like bands31,32 as in the case of bilayer graphene34,35,36,37,38,39,40,41,42 (Fig. 1c). The bottoms of the heavy-mass and light-mass bilayer-like bands become nearly flat31,32,33. However, trigonal warping locally closes the energy gap, resulting in mini-Dirac cones at the bottom of the heavy-mass bilayer-like band. These characteristic structures in the dispersion relation were revealed by studying the intrinsic resistance peaks that as a function of carrier density and perpendicular electric flux density31,32,43,44.

Results and discussion

Experimental results

Figure 1d shows an optical micrograph of an AB-stacked tetralayer graphene sample that consisted of encapsulated graphene with a top and a bottom gate electrode. The graphene sample is encapsulated with two h-BN flakes with different crystallographic orientations. Relative angle of crystal axis between graphene and bottom h-BN flake was set to be approximately parallel (actually 0.35 degrees) which forms moiré superlattice. On the other hand, the angle between top h-BN and graphene was about 16 degrees and the moiré structure due to top h-BN is negligible. The low-temperature electrical mobility of this device was above 4 × 104 cm2V−1s−1. As shown in Fig. 1e, peaks which arise from moiré superlattice appear in the plot of resistivity (ρ) against bottom gate voltage (Vb). In addition to the clear main peak at Vb ≈ 0 V, a couple of side peaks are discernible at Vb ≈ 40 and −45 V, which are reminiscent of superlattice peaks due to the secondary Dirac points in a moiré superlattice formed with h-BN and monolayer (or bilayer) graphene.

The resistivity traces (ρ vs Vb) showed significant variation with top gate voltage (Fig. 2a), and detailed measurements of the resistivity map revealed a fine structure of resistivity peaks (Fig. 2b). The straight ridge from the top left to bottom right of Fig. 2b is the condition of charge neutrality, which is given by ntot = 0, where ntot is the carrier density induced by the top and bottom gate voltage,

$$n_{{\mathrm{tot}}} = (C_{\mathrm{t}}V_{\mathrm{t}} + C_{\mathrm{b}}V_{\mathrm{b}})/e.$$
(1)

Here, Ct and Cb are the specific capacitances for the top and bottom gate electrodes. The perpendicular electric flux density (D⊥), which is roughly proportional to the strength of the perpendicular electric field, can be calculated as

$$D_ \bot = (C_{\mathrm{t}}V_{\mathrm{t}} - C_{\mathrm{b}}V_{\mathrm{b}})/2.$$
(2)
Fig. 2: Resistance peaks due to moiré superlattice.
figure 2

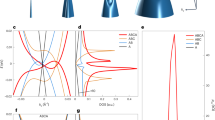
a Vb-dependence of ρ for different Vt. (T = 4.2 K). b Map of ρ plotted as a function of Vb and Vt (T = 4.2 K). c Map of ρ plotted as a function of carrier density (ntot) and perpendicular electric flux density (\(D_ \bot\)). Some of the salient ridges are labeled as A+, A−, B+, B−, C+, C−, bb+, bb-, and MDP. \(T = 4.2\) K and \(B = 0\) T. d Map of longitudinal resistivity \(\rho _{xx}(B)\) vs. \(n_{{\mathrm{tot}}}\). \(T = 4.2\) K. Perpendicular electric flux density (\(D_ \bot\)) was kept at zero by tuning Vb and Vt. The arrow indicates Landau levels that are reminiscent of those of the secondary Dirac cone in the moiré superlattice of the h-BN/ single layer graphene heterostructures. e Map of ρ numerically calculated by using the effective mass approximation with the SWMcC parameters of graphite. The effective moiré potential derived by Moon and Koshino24 was used with a mismatch angle of 0.35°. The amplitude of the moiré potential was scaled with a factor of 0.5. Labels correspond to those in panel c. Ridges BB+ and BB−, which are not clearly visible in c, arose from the bottom of the heavy-mass bilayer-like band.

Full size image

Figure 2c is a replot of the map. One can see ridges of resistivity (bb+, bb−, MDP) that were recently found in AB-stacked tetralayer graphene31,32,33,43,44. Ridges bb+ and bb- reflect the bottoms of the light-mass bilayer-like bands, whose dispersions are nearly flat in a perpendicular electric field. MDP is due to mini-Dirac cones. However, the other ridges (A+, B+, C+, etc.) are absent from pristine AB-stacked tetralayer graphene.

The peaks in the trace of the gate voltage dependence of resistivity are reminiscent of superlattice peaks in the moiré superlattice of h-BN/monolayer graphene: one can calculate the period of the moiré potential3,4,5,6,7 from the size of the superlattice Brillouin zone, which can be estimated from the carrier density of the resistivity peak due to the superlattice (nFBZ)3,4,5,6,7. The mismatch angle ϕ can be estimated as3,4,5,6,7,

$$n_{FBZ} = \frac{8}{{\sqrt 3 \lambda ^2}}$$
(3)

where

$$\lambda = \frac{{\left( {1 + \delta } \right)a}}{{\sqrt {2\left( {1 + \delta } \right)\left( {1 - {\mathrm{cos}}\phi } \right) + \delta ^2} }}.$$
(4)

Here, λ is the wave length (or lattice constant) of the moiré potential, δ is the difference between the lattice constants of h-BN and graphene, and a is the lattice constant of graphene3. Because the tetralayer graphene has two low energy bands, nFBZ cannot generally be determined from carrier density of the superlattice in the trace of gate voltage vs. resistivity. However one can roughly estimate λ if one ignore contribution of the smaller Fermi surface. In our case, the lower limit of λ was about 12.4 nm using \(|n_{\mathrm{tot}}|\) of A+ (A−) ridge at \(|D_ \bot | = 0\). Corresponding mismatch angle was estimated to be \(\phi \approx 0.52^ \circ\). On the other hand the upper limit is the perfect aligned case which is about 14 nm, so that λ of our tetralayer graphene moire superlattice lies between them. The estimated values are close to the experiment in monolayer graphene3,7,9,10.

The Landau levels were also influenced by the moiré structure. Figure 2d shows a map of longitudinal resistivity (ρxx), which was measured as a function of ntot and magnetic field (B) for \(D_ \bot = 0\,{\mathrm{cm}}^{ - 2}{\mathrm{As}}\). Each streak indicated by bright and dark lines is a Landau level and the energy gap between them. The Landau level structure between \(n_{{\mathrm{tot}}} = - 2 \times 10^{12}\,{\mathrm{and}}\,2 \times 10^{12}\) cm−2 are specific to pristine AB-stacked tetralayer graphene31,32,33,45 which ensured that our sample was AB-stacked tetralayer. In addition, at \(n_{{\mathrm{tot}}} \sim 3.5 \times 10^{12}\,{\mathrm{cm}}^{ - 2}\), one can see a Landau fan reminiscent of that for the secondary Dirac cones in the case of moiré superlattice in bilayer graphene. Around this carrier density, ridge A+ appears (Fig. 2c).

Numerical simulation

Although Ridges A+(A−), B+(B−), and C+(C−) would be the satellite peaks similar to those in the moiré superlattice for mono- and bilayer graphene, they showed unusual response to the perpendicular electric field: the ridges exhibited significant variation with respect to \(|D_ \bot |\). Such behavior was not observed in the case of bilayer graphene (see Supplementary Note). To study the origin, we compared the results of the experiment with a theoretical calculation. Figure 2e shows a map of resistivity that was numerically calculated from the dispersion relations by using Boltzmann transport theory with the constant relaxation time approximation (see Supplementary Method). The band structure calculation took account of an effective moiré potential based on the h-BN-graphene hopping model presented by Moon and Koshino24. The amplitude of the effective potential and mismatch angle of the crystal axes between h-BN and graphene were adjusted so that the calculation reproduced the experimental results (see Supplementary Discussion). The experimental map was approximately reproduced for θ = 0.35°. The period of the moiré potential was 13.0 nm (about 53 times the lattice constant of graphene). This value is slightly different from the rough estimation (λ = 12.4 nm, θ = 0.52°) The calculation approximately reproduced the experimental map of resistivity, which indicates that the moiré potential significantly influenced the band structure of the multilayer graphene even though the potential is present at the first layer of graphene contacting h-BN. The ridges bb+ and bb− are intrinsic to AB-stacked tetralayer graphene31,32,43,44. By studying the relation between the shape of the Fermi surface (the energy contour of the dispersion relation) and carrier density, it was found that the other ridges appeared when an energy gap associated with the superlattice potential opened. These resistivity peaks (ridges) are due to formation of an energy gap associated with overlapping of the Fermi surfaces which are translated by reciprocal vectors in the extended zone scheme, as shown in Fig. 3a–c. These show the numerically calculated Fermi surface(s) for different energies in the case of \(\left| {D_ \bot } \right| = 3.2 \times 10^{12}\,{\mathrm{cm}}^{ - 2}{\mathrm{As}}\). Reciprocal vectors of the moiré potential is shown in Fig. 3d. The Fermi surface of AB-stacked tetralayer graphene consists of trigonally warped circles. It changes its topology by opening an energy gap when the Fermi surfaces are overlapped in the superlattice potential as shown schematically in Fig. 3e–g. Opening an energy gap reduces the electronic states available for electrical conduction, and thereby reduces conductivity. Ridge A+ (A−) are for overlapping of the Be (Bh) band. (Be (Bh) is an electron-like (hole-like) heavy mass bilayer-like band; be (bh) is an electron-like (hole-like) light mass bilayer-like band.) Ridges B+ (B−) and C+ (C−) are for overlapping of Be (Bh) and be (bh), which occur at different carrier densities (energies) because of the trigonally warped Fermi surface (Fig. 3b–c, f, g). For higher carrier densities, overlapping be (bh) with itself would possibly occur and it should result in a corresponding resistance ridge.

Fig. 3: Topological transition of Fermi surface.
figure 3

Energy contours of the numerically calculated dispersion relation for a E = 0.0386 eV \((n_{{\mathrm{tot}}} = 2.08 \times 10^{12}\,{\mathrm{cm}}^{ - 2})\), b E = 0.0684 eV \((n_{{\mathrm{tot}}} = 4.32\, \times 10^{12}\,{\mathrm{cm}}^{ - 2})\) and c E = 0.0894 eV \((n_{{\mathrm{tot}}} = 5.95\, \times 10^{12}\,{\mathrm{cm}}^{ - 2})\). For all the cases, \(\left| {D_ \bot } \right| = 3.2 \times 10^{ - 7}\,{\mathrm{cm}}^{ - 2}{\mathrm{As}}\). Hexagon XYXYXY is the first Brillouin zone of the superlattice potential. For a weak potential, the energy gap does not open on the Brillouin zone boundary. d G1-G6 are reciprocal vectors of the superlattice. Panels e–g are schematic illustrations for a–c, respectively. The energy gap opens at the point where the Fermi surfaces in a different Brillouin zone are overlapped (shown by circles). This results in a topological transition of the Fermi surface. Panel e shows the case of overlapping of Be with itself. Panels f and g show different cases of overlapping of be and Be. Panels h–j show schematic illustration of dispersion relations for different \(|D_ \bot |\) in the extended zone scheme. Energy gaps open at the points of band crossings where Fermi surfaces separated by a reciprocal vector are overlapped (shown by the open circles). This results in resistivity peaks when the chemical potential is swept. At the chemical potential where A+ appears (dashed line), there are two electron bands for \(D_ \bot = 0\) (panel h). With increasing \(|D_ \bot |\), the difference in energy between the bottoms of Be and be increases. Accordingly, the carrier density decreases, as shown by the size of the Fermi surface of be (FSbe) in Panel i. The Fermi surface of be disappears at the critical\(|D_ \bot |\) (panel j).

Full size image

Figure 3h–j show simplified band diagrams in the extended zone scheme to explain the opening of the energy gap; FBZ is the first Brillouin zone, and identical band diagrams are translated by reciprocal vectors. Small energy gaps open when bands cross each other, and this results in resistance ridges A+, B+, C+, etc.; for example, ridge A+ occurs when band Be crosses itself in the neighboring zone; ridge B+ occurs when be crosses Be, etc. Because the band structure is trigonally warped28,29, the energy gaps associated with the overlapping generally occur at wave numbers other than on the Brillouin zone boundary, as can be seen in the figure.

The complicated dependence of the peaks (ridges) on ntot and \(D_ \bot\) is due to the multiband property relevant to the variation of dispersion relations through the perpendicular electric field. The energy gaps among be, Be, Bh and bh widen with increasing \(|D_ \bot |\), as shown in Fig. 3h–j. Accordingly a chemical potential in the vicinity of the energy gap for peak A+ (A−) (the dashed line), generally varies by \(|D_ \bot\)|. However, the shape of the fermi surfaces of Be (Bh) does not vary largely at that energy, so that carrier density in Be (Bh) band (for the energy) is approximately unchanged by \(|D_ \bot\)|. On the other hand, the difference in energy between the bottom of be and the bottom of Be increases with increasing \(|D_ \bot\)|, and Ridge A+ (A−) bends to smaller |ntot| with increasing \(|D_ \bot\)| because the number of carriers in be decreases (Fig. 3h, i). Above the critical \(|D_ \bot\)|, the energy of the bottom of be (bh) becomes larger than the chemical potential (dashed line), and only the Fermi surface of Be (Bh) is present (Fig. 3j). This transition can be seen in the map (Fig. 2c, e) as crossings of ridge A+ (A−) and bb+ (bb−) at \(\left| {n_{{\mathrm{tot}}}} \right| \sim 2.3 \times 10^{12}{\mathrm{cm}}^{ - 2}\)and \(\left| {D_ \bot } \right| \sim 3.5 \times 10^{ - 7}\,{\mathrm{cm}}^{ - 2}{\mathrm{As}}\). The electron-hole asymmetry in the map can be similarly explained by considering the electron-hole asymmetry in the dispersion relation. The Fermi surface areas of the light-mass bilayer-like band and the heavy-mass one have different ratios in electron and hole regimes because of this asymmetry.

As shown above, the resistance peaks (ridges) due to the moiré superlattice can be explained by energy gaps opening. It is commonly accepted that energy gaps form on the Brillouin zone boundary of the superlattice. Indeed, the energy gap is expected to open at the Brillouin zone boundary in moiré superlattice for monolayer graphene which is approximately isotropic. However, it can open inside the Brillouin zone in an anisotropic electron system (Fermi surface) as in the case of AB-stacked graphene with multiple layers. Textbooks on solid-state physics tell us that, in the presence of a periodic potential, an energy gap opens via interference of wave functions \(\phi \left( {\mathbf{k}} \right)\) and \(\phi ({\mathbf{k}} \pm {\mathbf{G}})\), where k is a wave vector and G is one of the reciprocal vectors. If the original band structure satisfies \(E\left( {\mathbf{k}} \right) = E\left( {{\mathbf{k}} \pm {\mathbf{G}}} \right)\), an energy gap should open on a boundary of the Brillouin zone. On the other hand, if the original band is anisotropic, as in the case of AB-stacked multilayer graphene, the condition, \(E({\mathbf{k}}) = E({\mathbf{k}} \pm {\mathbf{G}})\), can be satisfied and an energy gap should form even though k is not on the boundary of but rather inside the Brillouin zone, as can be seen in Fig. 3a. Similar phenomena arising from anisotropy have recently been discussed in photonic crystals46 and phonic crystals47,48,49; Bragg reflection occurs inside the Brillouin zone in anisotropic media, rather than on the boundary. In addition, an energy gap opens when the Fermi surfaces of different bands are overlapped. The wave functions in band 1, \(\phi _1({\mathbf{k}}_1)\), and in band 2, \(\phi _2({\mathbf{k}}_2)\), which are orthogonal to each other in the absence of moiré potential, anti-cross when \(E({\mathbf{k}}_1) = E({\mathbf{k}}_2 \pm {\mathbf{G}})\) is satisfied. This can be seen in Fig. 3b, c. Energy gaps open and the Fermi surfaces change their topology when be and Be are overlapped.

Effective moiré potential

The detailed structure of the numerically calculated dispersion relation is highly dependent on the models of the effective moiré potential and its amplitude. However, the essential feature of the Fermi surface topology is unchanged by the choice of model. We calculated the dispersion relations and resistivity maps for h-BN-graphene hopping models22,23,24,50, the 2D charge modulation model51, and the potential modulation model3,22,50 (see Supplementary Discussion). The h-BN-graphene hopping models approximately reproduce the experimental resistivity map if the potential amplitude is less than about half of those given in the theoretical works22,23,24,50. Using any of these models, the resistivity map was approximately reproduced for a sufficiently small potential amplitude, which indicates that the topological transitions of the Fermi surface due to overlapping occur regardless of the model used.

Trigonal warping

If the resistivity peaks (ridges) originate from overlapping of the Fermi surface, the resistivity maps should show a significant dependence of the trigonal warping because the overlapping is significantly influenced by the shape of the Fermi surface. Figure 4a–c shows the maps calculated for different values of γ3 of the SWMcC parameters, which tunes the trigonal warping; γ3 = 0 eV is for circular Fermi surfaces; γ3 = 0.3 eV approximates the experiment. Overlapping of Be and be (Bh and bh) can occur at different points, and thereby, at different energies (or carrier densities) in the trigonally warped case as illustrated in Fig. 3f–h. This results in separate ridges B+ (B−) and C+ (C−) (γ3 = 0.3 eV; Fig. 4c). With decreasing γ3, ridges B+ and C+ (B− and C−) merge into a single ridge (γ3 = 0 eV; Fig. 4a). In this case, the energy gap should open on the boundary of the superlattice Brillouin zone.

Fig. 4: Effect of trigonal warping on superlattice peaks.
figure 4

Numerically calculated maps of ρ for a \(\gamma _3\) = 0 eV, b \(\gamma _3\) = 0.1 eV, and c \(\gamma _3\) = 0.3 eV. Panel d shows the experimental results. Some of the characteristic ridges are labeled. With decreasing  trigonal warping, ridges B+ (B−) and C+ (C−) merge into a single ridge BC+ (BC−). This indicates that the superlattice peaks are strongly dependent of the shape (or symmetry) of the Fermi surface.

Full size image

Conclusions

The moiré superlattice of a h-BN/AB-stacked tetralayer graphene heterostructures were studied by conducting low-temperature transport measurements. It was found that the carrier density dependence of the resistivity showed superlattice peaks reminiscent of those in the monolayer case. The electronic band structure was strongly influenced by the moiré potential which would act only the outermost layer of graphene that contacts h-BN. A multiband property was observed in the significant dependence of the superlattice peaks on the perpendicular electric field. These peaks were significantly influenced by the trigonal warping of the band structure. The peaks occurred when the Fermi surfaces translated through a reciprocal vector are overlapped, which resulted in the energy gap opening and a topological transition of the Fermi surface. The energy gap opens inside the superlattice Brillouin zone rather than on its boundary. These are aspects of the moiré superlattice of the h-BN/graphene heterostructures and two-dimensional superlattices with anisotropic band structures.

Methods

The sample was h-BN-encapsulated AB-stacked tetralayer graphene formed on Si substrate covered with SiO2. The h-BN and graphene flakes were prepared by mechanical cleaving using adhesive tape. The stack was formed using dry transfer process with polypropylene carbonate (PPC) film52. The sample was equipped with top and bottom gate electrodes. The top one was made of a few-layer graphene and the bottom one was the Si substrate which was heavily doped and remained conducting down to liquid helium temperatures. The sample was patterned into a Hall bar via reactive ion etching using a mixture of low-pressure CF4 and O2 gas. The electric contacts to the graphene were formed by using the edge-contact-technique52. The number of graphene layers was roughly determined by making optical contrast measurements53,54,55. Then, the number of layers and stacking were verified via a Landau fan diagram, which is a map of resistivity measured as a function of carrier density and magnetic field. The structure of the Landau levels characterizes the electronic band structures of graphene. It is different for different numbers of layers and stackings, and accordingly, the fan diagrams exhibit specific patterns. By comparing the diagram with those in the past studies45, the present sample was identified to be AB-stacked tetralayer graphene.

Resistivity measurements were performed by using standard lock-in technique. Magnetic fields were applied by using superconducting solenoid.