Abstract
Single crystals of URu2Si2 show below 17.5 K a transition into an ordered state with a significantly reduced entropy. The low temperature phase is called the hidden order (HO) state, because its microscopic origin is still unknown—there are no charge, structural or magnetic transitions associated to HO. Here we report a one-dimensional (1D) charge modulation within the HO state of URu2Si2. We perform detailed Scanning Tunneling Microscopy (STM) experiments with high resolution on many atomically flat surfaces of URu2Si2 obtained by fracturing single crystals at cryogenic temperatures and find a 1D charge density wave with a large wavevector. We show that the 1D modulation is connected to the dynamical magnetic excitations of the HO through a moiré construction and appears as a consequence of excitations quenched through the interaction between the travelling fracture front and the dynamic modes of the crystal. The combination of fracture dynamics and the dynamics of the solid provides a method to create ground states and shows that charge interactions are among the most relevant features competing with HO in URu2Si2.
Similar content being viewed by others
Introduction
The HO state of URu2Si2 puzzles experimentalists and theoreticians alike since its discovery more than three decades ago1,2,3. It consists of a phase transition below THO = 17.5 K in which there is a large entropy change4. However, neutron scattering experiments do not show any sign of static magnetic nor structural order5. Instead, there are dynamical modes of Ising-like magnetic excitations with a strong fluctuating magnetic moment, μ ≈ 1 − 2μB, located at q0 = (0, 0, 1) and q1 = (0.6, 0, 0)5,6,7. These modes are quenched into an antiferromagnetic order above 5 kbar with the q0 wavevector3,5,8 and with the q1 wavevector at high magnetic fields8,9,10. The magnetic field also modifies the Fermi surface, producing nesting at q111. In addition, several measurements indicate that at zero field the bandstructure has a hotspot for scattering at q1, so that there is a strong interaction between electronic degrees of freedom and the dynamical modes9,11,12,13.
Here we use Scanning Tunneling Microscopy (STM) to study high quality single crystals of URu2Si2. Contrasting previous STM work14,15, we find a 1D charge modulation in the HO state. We characterize the modulation, which consists of a long wavelength pattern and find that it can be explained by a moiré combination between the crystal lattice and a charge modulation at q1. Moiré patterns can lead to fundamentally new electronic behavior when formed between two atomic lattices slightly shifted with respect to each other16,17,18,19,20,21,22. A solid is, however, not just characterized by the atomic lattice, but also by dynamical charge or magnetic excitations that do not need to be commensurate to the lattice. These excitations can be quenched giving rise to static charge, magnetic, or orbital order. Our experiment suggests that a moiré can be generated between quenched dynamic modes and the atomic lattice, through the interaction with a transient phenomenon as a fracture. Furthermore, we show that the symmetry breaking field of the 1D modulation is related to the path followed by the fracture front during cryogenic cleaving of the sample.
Results and discussion
Atomic size patterns obtained with STM and 1D charge modulation in URu2Si2
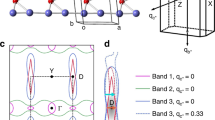
Figure 1a shows the crystal structure of URu2Si2. In Fig. 1b we show atomically resolved images of the U square atomic lattice, with the in-plane lattice parameter a = 420 pm, similar as in previous work14,15,23. We focus here on features obtained from the STM topography on samples fractured, as schematically shown in Fig. 1c at liquid Helium temperatures. Spectroscopic features are mentioned in the Supplementary Information (Supplementary Note 1) and coincide with previous work. We also discuss the atomic termination in the Supplementary Information (Supplementary Note 2), which mostly consists of the square U atomic lattice.
a URu2Si2 tetragonal crystalline structure (a = 420 pm and c = 960 pm), with U atoms in green, Ru atoms in blue and Si atoms in grey. b Atomic resolution STM image showing the square U surface. The white line provides the path for the scan shown in the inset. The bias voltage is of 5.5 mV and the current is held constant at 3 nA. White arrows show the in-plane crystalline directions and the color scale the height difference, following the color bar on the upper left (from zero, black to 40 pm, green). White scale bar is 1.3 nm long. c Schematic behavior of the fracture process. At low temperatures (below 4.2 K), the sample (gray rectangular bar) is broken by bringing it close to a blade (shown in yellow). During breaking, the fracture front travels through the sample following the violet arrow and an instanteanous pressure front travels (pressure shown by the color scale from blue (0 Gpa) to red (8 GPa)). d Schematic picture of the in-plane Fermi surface of pristine URu2Si2. Red and blue lines represent the two main bands crossing the Fermi level in the paramagnetic state above the hidden order state critical temperature THO = 17.5 K and in the plane of the tetragonal Brillouin zone. Thick violet arrow represents the travel direction of the fracture front. The interaction with electronic modes (thin violet arrows) leaves a permanent trace, which consists of a moiré whose wavenumber qM is determined by half the reciprocal unit cell a* and the vector q1.
Let us review briefly a few aspects of the bandstructure of URu2Si2. A part relevant to the HO are an electron and a hole band, schematically represented as cuts through the Fermi surface in the plane of the tetragonal Brillouin zone (blue and red lines in Fig. 1d). These three-dimensional bands suffer nesting along the c-axis below THO. As a consequence, the bands split into a set of eight pockets leaving out the areas highlighted in yellow in Fig. 1d9,11,12,24. There is a tendency to form in-plane four-fold periodic structures along q1 = (0.6, 0, 0), as shown by magnetic field induced nesting at this wavevector11. The sample breaks along the plane of the tetragonal crystal structure, leaving the U-atom surface Fig. 1b exposed. Locally, during fracture, a high pressure front builds up at the wedge (bottom panels of Fig. 1c). The fracture direction (violet arrow in Fig. 1c, d) defines a symmetry breaking field which allows for 1D interactions between hotspots remaining in bandstructure of the HO state close to q1. We observe that this interaction results in an electronic modulation at q1 which is observed as a moiré pattern between the reciprocal lattice constant a* and q1 (Fig. 1d), with a wavevector \({{\bf{q}}}_{M}=| \frac{1}{2}{a}^{* }-{{\bf{q}}}_{1}|\).
In fields of view that are sufficiently large and free of steps we observe a certain pattern, which repeats on the image and is 1D (Fig. 2a, b). The pattern corresponds to height changes which vary from place to place and are very small, of at most 2 pm, i.e., less than 1% of the c-axis unit cell size. The period and the direction of the 1D pattern can be determined from the Fourier transforms of the topographic images. The Bragg peaks associated to the 1D modulation (Fig. 2c, d) repeat at integer multiples of qM. We determine qM from the reciprocal space distance between consecutive peaks and obtain that qM = 0.17 nm−1 (Fig. 2c, d). This corresponds to a modulation of period dM = 1/qM ≈ 6 nm (dM ≈ 14a). The 1D modulation is nearly parallel to an in-plane crystalline direction. We observed the modulation in many fields of view on five different samples, each one cleaved at low temperatures (more details in the Supplementary Information, Note 3), up to magnetic fields of 4 T (parallel to the c-axis) and temperatures several K above liquid helium. At higher temperatures and above THO we were unable to detect it because the amplitude of the modulation is too small to detect in presence of temperature induced drift in the STM. As discussed in the Supplementary Information (Supplementary Note 4) in detail, the observed features are associated to fracturing the sample at low temperatures and appear in subsequent steps whose height difference is half the c-axis unit cell lattice constant (Supplementary Note 5).
a, b Atomic resolution Scanning Tunneling Microscopy (STM) images in two different fields of view. Notice that these show the behavior over many atomic lattice constants. We mark the 1D modulation of wavelength dM by dashed lines and the arrow. The current is constant at 0.05 nA and the bias voltage is of 4 mV in left panel and 5 nA and 5 mV in the right panel. The colored bars provide the vertical scale, with 20 pm from black to green in left panel and 37 pm in right panel. Horizontal scale bars are 5 nm long. c, d Fourier transform of the images in a and b, respectively. We observe the usual atomic Bragg peaks due to the square surface atomic lattice and also multiple peaks at reciprocal space distances qM. We mark with white circles the Bragg peaks of the atomic lattice and the wavevector of the modulation qM. Horizontal scale bars are 1.2 nm−1 long. The Fourier amplitude is given by the vertical bars, with 0.12 pm in left panel and 0.16 pm in right panel, from black to green. Insets show profiles of the Fourier amplitude along the white lines in the Fourier transform. White dots are points of the image and the dashed line is a guide to the eye. Similar dM are obtained in 24 different fields of view acquired in 5 different samples. We show further details of the modulation in the Supplementary Notes 1, 2, 5, 6, and 8 and Supplementary Figs. 1, 3, 6, 9, 10, and 12.
A modulation observed in STM topographic images superimposed to the atomic lattice can often be related to charge order. The Fermi surface has mainly a four-fold symmetry and there are no features in the Fermi surface, which could lead to a charge density wave along one axis12,25. Features of the Fermi surface are instead four-fold, showing nesting at q0 along the c-axis. Nesting occurs in-plane at q1 too at sufficiently high magnetic fields11. At the level of the local atomic size density of states measured by in-plane topographic imaging with STM, we might be sensitive to effects related to the mode at q1, which is clearly an in-plane hotspot in the Fermi surface (Fig. 1d). As we show in the following, qM is related to q1 through a moiré pattern and the direction of qM is determined by the direction of the propagation of the crack front during fracture.
Origin of the long wavelength pattern observed in the STM images
First, let us establish the relation between q1 and qM, knowing that q1 ≫ qM. The superposition of 1D modulations with similar periodicities λ1 and λ2 (λ1 ≈ λ2) leads to an additional modulation, the moiré pattern, at a scale which is far above λ1 and λ2 and is given by \({d}_{M}=\frac{{\lambda }_{1}\cdot {\lambda }_{2}}{| {\lambda }_{1}-{\lambda }_{2}| }\)26,27. If λ2 = a and λ1 ≈ na with n an integer (and of course λ1 ≠ na), the moiré adopts a “fractional” form and \({d}_{M}=\frac{{\lambda }_{1}\cdot a}{| {\lambda }_{1}/n-a| }\) (more details in Supplementary Note 6). The moiré is then composed of n cosine functions of wavelength dM phase-shifted to each other by 2π/n. In STM images made at constant tunneling current, we measure the variations in the local density of states (LDOS) integrated between the Fermi level and the bias voltage as a function of the position. The LDOS can be understood as a combination of localized orbitals and itinerant electrons mostly from the topmost layer (here U as shown in the Supplementary Information, Note 2), with some influence from layers below28,29. Let us consider a periodic modulation with wavevector close to q1 (for instance at ≈ (0.5700)). The LDOS is determined by the LDOS from the U atoms and an additional periodic modulation at q1. The atomic lattice and the modulation at q1 combine into the moiré pattern observed in our images. As λ1 ≈ 2λ2, with λ1 the modulation at q1, λ1 = 1/q1, and λ2 = a, the resulting moiré pattern consists of two inverted cosines, each one with a periodicity \({d}_{M}=\frac{{\lambda }_{1}\cdot a}{| {\lambda }_{1}/2-a| }\) and shifted by π (see also Supplementary Information, Note 6 and Supplementary Fig. 10). Thus, the features observed at dM are a consequence of a moiré combination between modulations at q1 and at the atomic lattice constant.
Second, to understand the symmetry breaking, let us discuss the origin of the modulation. The modulation is not present in any of the STM images shown in previous work14,15, although their resolution was of the same order as ours. In those experiments samples were plate-like, whereas we use a small bar shaped sample and break it perpendicular to its long axis at very low temperatures (below liquid helium). Breaking a long, hard single crystal produces brittle fracture. It is a fast procedure by which the bonds are broken first on one side of the sample and then a crack front travels through the sample in a short amount of time (see Fig. 1c and Supplementary Information, Note 4 and Supplementary Fig. 8). The propagation of the crack front during cleavage leaves permanent modifications of the surface30. These modifications can be due to acoustic waves that are emitted when a crack front crosses defects during the cleaving process or due to other forms of local interaction of the crack front and the crystalline lattice and have been extensively studied in materiales such as Si, sapphire or tungsten30,31,32,33. From a careful optical and electron microscopy analysis of surfaces of URu2Si2 broken at room temperatures and at low temperatures (see Supplementary Information, Note 4) we obtain that samples cleaved at low temperatures have a set of linear features created during crack and oriented close to a crystalline axis. These features define a fixed direction which is close to one of the main in-plane crystalline axis and produce the 1D symmetry breaking field. We note that we observe the modulation in five samples cut differently, in spite that each one has slightly different shape, different crack initiation points, and different internal structure of defects.
Our scans show the Bragg peaks due to the moiré pattern just at the center of the Fourier transform. To understand this observation, let us describe a modulation through a vector \({\boldsymbol{D}}({\boldsymbol{r}})={\boldsymbol{A}}\cos ({\boldsymbol{q}}{\boldsymbol{r}}+\phi )\), with A the vector of the absolute value of the modulation, q the wavevector of the modulation and ϕ a phase shift34. As we show in the Supplementary Information (Supplementary Note 7) the corresponding Fourier transform shows satellite peaks around lattice Bragg peaks when the displacement vector is in-plane along A = (A0, 0, 0) or A = (0, A0, 0). If the displacement is out-of-plane, A = (0, 0, A0), the image shows satellite peaks around the center of the Fourier transform. The latter is always observed in our images. Thus, we are mostly observing an amplitude modulation of the charge (out-of-plane), without in-plane atomic displacements.
Induced strain and the 1D charge modulation
We have calculated the strain field in several images, following refs. 35,36. We show in Fig. 3a a STM image where we can observe the 1D modulation, also in its Fourier transform, Fig. 3b. The strain field of this image is essentially a random featureless map. Thus, there is no 1D strain that follows the modulation. We see that we observe atomic size defects in Fig. 3a. Measuring the height differences around these defects and comparing with images obtained elsewhere on the sample (see Supplementary Fig. 4), we obtain that these defects are mostly Si atoms on top of the U surface. Around these defects, we observe a modification of the in-plane strain, consisting of four-fold contraction and elongation of the in-plane lattice (Fig. 3c). In some fields of view (see Fig. 3d and its Fourier transform Fig. 3e) we observe a slight modification of the strain pattern around defects. The observed in-plane strain at defects has a slight tendency to show an elongated shape (Fig. 3f). We generally observe such a tendency when the c-axis amplitude of the modulation is large, as in Fig. 3d. The observed compression and extension in the strain map M(r) occurs preferentially along an axis that is parallel to the 1D modulation. This shows that, although the modulation itself does not have an accompanying strain field, there is an interaction between the 1D modulation and the strain field produced by individual defects. It is useful to remind that Nuclear Magnetic Resonance (NMR) measurements highlight the relevance of charge disturbances and in particular show a two-fold lineshape on Si associated to defects37,38,39. Our results suggest that Si defects are influenced by charge disturbances such as the 1D charge modulation.
In a we show a topographic image (tunneling current of 0.2 nA and bias voltage of 9 mV). The corresponding Fourier transform is shown in b. In c we show the in-plane strain map of the orange square shown in a. In d we show the topography of another field of view (tunneling current of 0.5 nA and bias voltage of 4 mV), in e its Fourier transform and in f the strain on the area marked with an orange square shown in d. Black scale bars in a, d are 5 nm long. White scale bars in b and e are 3 nm−1 long. The color scale of the topographic images is shown on the bottom left of a and d and goes from 0 pm (black) to 20 pm (green). The color scale of the strain is shown on the bottom right of c and f, and ranges ±5% of the in-plane lattice constant a.
Finally, let us note that we observe defects in the 1D pattern in some fields of view. As we show in the Supplementary Note 8, the stripes associated to the modulation are sometimes displaced at certain locations.
Interaction between the 1D charge modulation and dynamic modes of the HO state
We should note that crack front velocity is of order of sound velocity (see Supplementary Information, Note 4, and refs. 30,31,32,33). Thus, we can link together the external action (crack front), atomic displacement modes (phonons) and the electronic susceptibility of URu2Si2 (fluctuations at q1). The phonon dispersion in URu2Si2 shows no strong features connected to the HO transition40. However, there is an anomalous phonon mode broadening, which suggests strong anharmonicity and coupling to magnetic excitations40,41,42. The dispersion relation of the q1 modes provides a velocity \(v=\frac{d\epsilon }{dk}\approx 1{0}^{4}\frac{m}{s}\)40. Most remarkably, crack front velocity, sound velocity and the velocity of the magnetic q1 modes are all of the order of tens of km/s.
The time required for each of these three modes to cross a single unit cell is in the femtosecond regime. Interestingly the quasiparticle lifetime at q1 is observed to increase significantly in the HO phase43, suggesting that ultrafast dynamics might be strongly sensitive to cryogenic cleaving of URu2Si2 and that this could unveil further insight into the interaction between the modes of the HO phase and the lattice.
The energy-dependent density of states, discussed in detail in the Supplementary Information, Note 1, and in refs. 14,15,23 shows features indicating strong hybridization between bands, according to the modifications in the bandstructure that lead to the Fermi surface schematically depicted in Fig. 1d. Interestingly, it has been suggested that there is a wave inside the HO phase that is due to the hybridization of light and heavy electron bands and that such a hybridization wave can create a charge modulation at q1, which would be, however, very weak44,45,46. It has been also proposed that the density of states might show a nematic component at the hybridization gap, not at the Fermi level47. Clearly, there is no symmetry breaking modulation in refs. 14,15,23, although in our case there is a modulation that leads to the observed one-dimensional moiré pattern. As we discuss above, fracture at low temperatures is a differentiating ingredient of our experiments. This suggests that there is a wave pattern, be it a tiny hybridization wave or fluctuating magnetic modes, in the HO phase which is enhanced or stabilized by cryogenic fracture into a visible charge pattern at q1. How this 1D modulation influences macroscopic experiments is not easy to establish without a careful analysis of the morphology of samples, which could point out defects or features associated to strain or fracture. New experiments on probes particularly sensitive to the density of states at the Fermi level, such as the thermopower11, could provide further insight in the light of our results.
Notice that moiré patterns arise on surfaces or few layer systems because of displacements or rotations of atomic lattices16,17,18,19,20,21,22. Rotations among atomic layers provide a control parameter, the relative angle between layers, to modify the moiré17. In our case, moiré modulations can arise with any characteristic vector from the electronic bandstructure. That is, with wavevectors located inside the Brillouin zone and lying close to an integer fraction of the unit cell lattice. To modify the moiré, we need to modify the bandstructure, with the usual control parameters as doping, stress or magnetic field. For very large values of n in \({d}_{M}=\frac{{\lambda }_{1}\cdot a}{| {\lambda }_{1}/n-a| }\), the moiré pattern might rapidly acquire a very long wavelength, which should make it quite difficult to distinguish from a large defect or distortion. However, for small n (and with a sufficient difference between λ1 and na), the moiré combinations proposed here could lead to a variety of new modulated phenomena.
Conclusion
In summary, we observe that the high susceptibility of URu2Si2 at q1 results in a quenched charge modulation when there is a sufficiently strong interaction with a cracking process. We are not just condensing a magnetic or orbital excitation into a charge modulation at q1 through fracture. The moiré between the atomic lattice and the q1 modulation leads to a real pattern observed in STM, which breaks the in-plane C4 symmetry. Of course such a pattern is not a property of the HO found in pristine URu2Si2. But it is related to HO through one of the wavevectors that lead to the moiré. Our observation supports the claim that in the HO phase electric interactions might play a key role, as proposed by NMR experiments39 and more recent experiments in the related compound UPt2Si248, and suggest that controlled fracture can be used as a means to study ground state excitations.
Methods
We use a STM setup described in refs. 49,50 that features a movable sample holder which we use to cleave in situ the sample and change in situ the scanning window49. The single crystals of URu2Si2 have been grown as described in previous work51,52. We first screened crystals for high quality, from different growths. Systematic studies on different crystals show than the HO phase itself is quite robust on sample purity. We then cut crystals into needles of about 0.5 × 0.5 × 2 mm. We inserted each needle into a hole made on a gold substrate and glued them with silver epoxy. The needles were positioned into the sample holder in such a way that they hit a sharp ceramic blade when pulling on the sample holder. Slightly below 4.2 K we pulled on the holder through a manual mechanism located at room temperature and connected to the holder with a piano cord. We felt resistance when the sample touched the blade. We continued pulling until we heard a characteristic “crack”. At this point, the sample was broken. The noise created during crack, which we heard outside the dilution refrigerator, evidences generation of sound waves during fracture. This was made with the tip far from the sample. We then approached the tip to the sample, scanned and obtained the results discussed here. We provide results of five succesful cleaves, obtaining each time atomically flat surfaces in cryogenic vacuum. In each crystal, we were able to study several tens of scanning windows, each limited by the scanning range of our piezotube (2 × 2 μm)49. We present almost exclusively topographic STM images made at 150 mK and with the STM on constant current mode held by a feedback loop, with a setpoint of a fraction of nA and at a bias voltage of order of 10 mV.
Data availability
All data in this publication and in its supplementary information are available upon reasonable request at the corresponding authors.
References
Flouquet, J. On the heavy fermion road. Prog. Low Temp. Phys. 15, 139 (2005).
Mydosh, J. A. & Oppeneer, P. M. Colloquium : Hidden order, superconductivity, and magnetism: the unsolved case of URu2Si2. Rev. Mod. Phys. 83, 1301 (2011).
Mydosh, J. A., Oppeneer, P. M. & Riseborough, P. S. Hidden order and beyond: an experimental–theoretical overview of the multifaceted behavior of URu2Si2. J. Phys. Condens. Matter 32, 143002 (2020).
Wang, L. et al. Electronic nematicity in URu2 Si2 revisited. Phys. Rev. Lett. 124, 257601 (2020).
Bourdarot, F., Raymond, S. & Regnault, L.-P. Neutron scattering studies on URu2Si2. Philos. Mag. 94, 3702–3722 (2014).
Broholm, C. et al. Magnetic excitations and ordering in the heavy-electron superconductor URu2Si2. Phys. Rev. Lett. 58, 1467 (1987).
Broholm, C. et al. Magnetic excitations in the heavy-fermion superconductor URu2Si2. Phys. Rev. B 43, 12809 (1991).
Villaume, A. et al. Signature of hidden order in heavy fermion superconductor URu2Si2 : resonance at the wave vector q0 = (1, 0, 0). Phys. Rev. B 78, 012504 (2008).
Wiebe, C. R. et al. Gapped itinerant spin excitations account for missing entropy in the hidden-order state of URu2Si2. Nat. Phys. 3, 96 (2007).
Knafo, W. et al. Field-induced spin-density wave beyond hidden order in URu2Si2. Nat. Commun. 7, 13075 (2016).
Pourret, A. et al. Fermi surface reconstruction inside the hidden order phase of URu2Si2 probed by thermoelectric measurements. J. Phys. Soc. Japan 82, 034706 (2013).
Elgazzar, S., Rusz, J., Amft, M., Oppeneer, P. M. & Mydosh, J. A. Hidden order in URu2Si2 originates from Fermi surface gapping induced by dynamic symmetry breaking. Nat. Mater. 8, 337 (2009).
Morr, D. K. Theory of scanning tunneling spectroscopy: from Kondo impurities to heavy fermion materials. Rep. Prog. Phys. 80, 014502 (2016).
Aynajian, P. et al. Visualizing the formation of the Kondo lattice and the hidden order in URu2Si2. Proc. Natl Acad. Sci. USA 107, 10383 (2010).
Schmidt, A. R. et al. Imaging the Fano lattice to hidden order transition in URu2Si2. Nature 465, 570 (2010).
Bistritzer, R. & MacDonald, A. H. Moiré bands in twisted double-layer graphene. Proc. Natl Acad. Sci. USA 108, 12233 (2011).
Cao, Y. et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 556, 80 (2018).
Xie, Y. et al. Spectroscopic signatures of many-body correlations in magic-angle twisted bilayer graphene. Nature 572, 101 (2019).
Choi, Y. et al. Electronic correlations in twisted bilayer graphene near the magic angle. Nat. Phys. 15, 1174 (2019).
Jiang, Y. et al. Charge order and broken rotational symmetry in magic-angle twisted bilayer graphene. Nature 573, 91 (2019).
Lu, X. et al. Superconductors, orbital magnets and correlated states in magic-angle bilayer graphene. Nature 574, 653 (2019).
Peng, L. et al. Unusual electronic states and superconducting proximity effect of Bi films modulated by a NbSe2 substrate. ACS Nano 13, 1885 (2019).
Zhang, W. et al. ARPES/STM study of the surface terminations and 5f -electron character in URu2Si2. Phys. Rev. B 98, 115121 (2018).
Santander-Syro, A. F. et al. Fermi-surface instability at the hidden-order transition of URu2Si2. Nat. Phys. 5, 637 (2009).
Bourdarot, F. et al. Precise study of the resonance at q0=(1,0,0) in URu2Si2. J. Phys. Soc. Japan 79, 064719 (2010).
Zhou, S. et al. Fourier-based analysis of moiré fringe patterns of superposed gratings in alignment of nanolithography. Opt. Express 16, 7869 (2008).
Oster, G. & Nishijima, Y. Moirépatterns. Sci. Am. 208, 54 (1963).
Tersoff, J. & Hamann, D. R. Theory and application for the scanning tunneling microscope. Phys. Rev. Lett. 50, 1998 (1983).
Tersoff, J. & Hamann, D. R. Theory of the scanning tunneling microscope. Phys. Rev. B 31, 805 (1985).
Deegan, R. D. et al. Wavy and rough cracks in silicon. Phys. Rev. E 67, 066209 (2003).
Sherman, D. & Be’ery, I. From crack deflection to lattice vibrations-macro to atomistic examination of dynamic cleavage fracture. J. Mech. Phys. Solids 52, 1743 (2004).
Kermode, J. R. et al. Macroscopic scattering of cracks initiated at single impurity atoms. Nat. Commun. 4, 2441 (2013).
Zhao, L., Bardel, D., Maynadier, A. & Nelias, D. Velocity correlated crack front and surface marks in single crystalline silicon. Nat. Commun. 9, 1298 (2018).
El Baggari, I. et al. Nature and evolution of incommensurate charge order in manganites visualized with cryogenic scanning transmission electron microscopy. Proc. Natl Acad. Sci. USA 115, 1445 (2018).
Lawler, M. J. et al. Intra-unit-cell electronic nematicity of the high-Tc copper-oxide pseudogap states. Nature 466, 347 (2010).
Zeljkovic, I. et al. Strain engineering Dirac surface states in heteroepitaxial topological crystalline insulator thin films. Nat. Nanotechnol. 10, 849 (2015).
Kambe, S. et al. NMR study of in-plane twofold ordering in URu2Si2. Phys. Rev. Lett. 110, 246406 (2013).
Kambe, S., Tokunaga, Y., Sakai, H. & Walstedt, R. E. Distributed twofold ordering in URu2Si2. Phys. Rev. B 91, 035111 (2015).
Kambe, S. et al. Odd-parity electronic multipolar ordering in URu2Si2 : conclusions from Si and Ru nmr measurements. Phys. Rev. B 97, 235142 (2018).
Buhot, J. et al. Lattice dynamics of the heavy-fermion compound uru2si2. Phys. Rev. B 91, 035129 (2015).
Butch, N. P. et al. Symmetry and correlations underlying hidden order in URu2Si2. Phys. Rev. B 91, 035128 (2015).
Gardner, D. R. et al. Inelastic x-ray scattering measurements of phonon dynamics in URu2Si2. Phys. Rev. B 93, 075123 (2016).
Dakovski, G. L. et al. Anomalous femtosecond quasiparticle dynamics of hidden order state in URu2Si2. Phys. Rev. B 84, 161103 (2011).
Dubi, Y. & Balatsky, A. V. Hybridization wave as the “hidden order” in URu2Si2. Phys. Rev. Lett. 106, 086401 (2011).
Hu, D., Dong, J.-J. & Yang, Y.-f Hybridization fluctuations in the half-filled periodic Anderson model. Phys. Rev. B 100, 195133 (2019).
Su, J.-J., Dubi, Y., Wölfle, P. & Balatsky, A. V. A charge density wave in the hidden order state of URu2Si2. J. Phys. Condens. Matter 23, 094214 (2011).
Chandra, P., Coleman, P. & Flint, R. Hastatic order in URu2Si2 : hybridization with a twist. Phys. Rev. B 91, 205103 (2015).
Lee, J. et al. Charge density wave with anomalous temperature dependence in UPt2Si2. Phys. Rev. B 102, 041112 (2020).
Suderow, H., Guillamon, I. & Vieira, S. Compact very low temperature scanning tunneling microscope with mechanically driven horizontal linear positioning stage. Rev. Sci. Instrum. https://doi.org/10.1063/1.3567008 (2011).
Galvis, J. A. et al. Three axis vector magnet set-up for cryogenic scanning probe microscopy. Rev. Sci. Instrum. 86, 013706 (2015).
Matsuda, T. D. et al. Details of sample dependence and transport properties of URu2Si2. J. Phys. Soc. Japan 80, 114710 (2011).
Aoki, D. et al. Field re-entrant hidden-order phase under pressure in URu2Si2. J. Phys. Condens. Matter 22, 164205 (2010).
Acknowledgements
We acknowledge discussions with F. Guinea, A. Levy Yeyati, and with S. Vieira and support by the Spanish MINECO (FIS2014-54498-R, MDM-2014-0377), by the Comunidad de Madrid through program NANOMAGCOST-CM (Grant No. S2018/NMT-4321) and by Cost Action CA16218 (Nanocohybri). I.G. acknowledges support by the European Research Council PNICTEYES grant agreement 679080. We also acknowledge the support of Departamento Administrativo de Ciencia, Tecnología e Innovación, COLCIENCIAS (Colombia) Convocatoria 784 - 2017 and the Cluster de investigación en ciencias y tecnologías convergentes de la Universidad Central (Colombia). J.A.G. acknowledges support from MinCiencias, Colombia (Grant No. 122585271058). We also acknowledge SEGAINVEX at UAM.
Author information
Authors and Affiliations
Contributions
E.H. and I.G. spotted the 1D modulation and worked through its characterization. The experiment was proposed by D.A. and J.F. and designed by E.H., I.G. and H.S. V.B. searched for possible combinations of modulations, identified the moiré and calculated the strain, with the supervision of H.S., E.H. and I.G. W.J.H. and J.A.G. provided support to the interpretation and in analyzing fracture, together with E.H. and with input from H.S. J.C. made the corresponding simulations. D.A. prepared and characterized samples. The paper was written by E.H., V.B., I.G., J.F. and H.S. with contributions from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Herrera, E., Barrena, V., Guillamón, I. et al. 1D charge density wave in the hidden order state of URu2Si2. Commun Phys 4, 98 (2021). https://doi.org/10.1038/s42005-021-00598-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-021-00598-0
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.