Abstract
Non-line-of-sight (NLOS) imaging is attractive for its potential applications in autonomous vehicles, robotic vision, and biomedical imaging. NLOS imaging can be realized through reconstruction or recognition. Recognition is preferred in some practical scenarios because it can classify hidden objects directly and quickly. Current NLOS recognition is mostly realized by exploiting active laser illumination. However, passive NLOS recognition, which is essential for its simplified hardware system and good stealthiness, has not been explored. Here, we use a passive imaging setting that consists of a standard digital camera and an occluder to achieve a NLOS recognition system by deep learning. The proposed passive NLOS recognition system demonstrates high accuracy with the datasets of handwritten digits, hand gestures, human postures, and fashion products (81.58 % to 98.26%) using less than 1 second per image in a dark room. Beyond, good performance can be maintained under more complex lighting conditions and practical tests. Moreover, we conversely conduct white-box attacks on the NLOS recognition algorithm to study its security. An attack success rate of approximately 36% is achieved at a relatively low cost, which demonstrates that the existing passive NLOS recognition remains somewhat vulnerable to small perturbations.
Similar content being viewed by others
Introduction
Non-line-of-sight (NLOS) imaging is a technique of detecting the hidden objects behind obstacles or around corners by exploiting the scattered light, which has attracted intensive interest for its fundamental importance in several application fields, such as autonomous vehicles, robotic vision, and biomedical imaging. NLOS imaging can be realized through reconstruction or recognition, depending on the application scenarios. NLOS reconstruction aims to make a visual representation of the hidden objects, while NLOS recognition just focuses on classifying the hidden objects.
The vast majority of NLOS imaging is based on an active detection strategy, like light detection and ranging (LIDAR)1,2,3,4,5,6,7,8,9, correlation-based imaging10,11,12,13, and holographic approaches14,15. The LIDAR technique allows for 3D scene reconstruction using a streak camera or single-photon avalanche photodiode detector and short-pulsed laser1,2,3,4,5,6,7,8,9. However, it faces severe practical limitations, including high costs, low photon efficiency, and typically long acquisition time3,4,5,6,7. The correlation-based and holographic NLOS imaging can also realize robust shape recovery with less expensive hardware, yet the former one is limited for sparse hidden objects with a small field of view10,11,12,13, and the latter one faces severe difficulties in recording holograms in practical scenarios14,15. NLOS recognition can provide labels for the hidden objects directly. Active NLOS recognition using the LIDAR technique realizes 76.6% accuracy on human pose estimation behind scattering media16. And that using optical coherence achieves 90% accuracy on the modified National Institute of Standards and Technology (MNIST) dataset of handwritten digits and 78.18% accuracy on human body posture dataset around corners17.
Unlike the active techniques, passive NLOS imaging utilizes weak scattered light or thermal radiation from the hidden objects without the need for a probing laser. Passive NLOS imaging is essential in some practical scenarios due to its simplified hardware system and good stealthiness. However, passive NLOS imaging is challenging and has limited programmable control. Different methods have been proposed to address this problem, including using a partial occluder18,19,20,21, thermal information22,23, or polarization cues24 in a NLOS system designed for imaging around corners, and using aperture masks25 or deep neural networks26,27 in an NLOS system for imaging through scattering media. The existing passive imaging is all realized through reconstruction. For example, the occluder-based passive NLOS reconstruction recovers 2D scenes by solving an inverse problem20,21, whereas the existing methods either demand prior information of the setting20 or yield low-quality recovery due to the partial knowledge of the occluder21. Moreover, they require a few minutes to process the occluder’s estimation and tens of seconds more for reconstruction, which is unrealistic for real-time NLOS applications. Deep neural networks have been used for passive NLOS reconstruction through scattering media to improve recovery quality26,27. However, the reconstruction quality is worse when the handwritten digit is illuminated by ultra-weak laser light on the same side27, which is the particular situation of passive NLOS imaging that the useful signal is extremely weak. It is hard to identify the hidden objects when the recovery quality is poor, whereas NLOS recognition can avoid this problem and meanwhile accelerate the imaging process. To our knowledge, passive NLOS recognition has not been explored thus far.
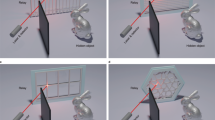
In this study, we perform passive NLOS recognition around corners using a pin-speck experimental setup, which consists of a standard digital camera and an occluder (Fig. 1). The rays of light from the monitor scene that go towards the secondary surface are partially blocked by the occluder, producing a penumbra. The camera captures the penumbra on the secondary surface, which contains category information and can be labeled by an elaborately trained convolutional neural network (CNN) model. The proposed NLOS recognition system is demonstrated with high and robust performance under increasingly complex scenes. For uncalibrated setups placed in a dark room, the recognition accuracy exceeds 97% on the well-known MNIST dataset of handwritten digits28 with less than 1 s per image. The proposed NLOS recognition system is also generalized on more sophisticated datasets of hand gestures29,30, human postures31, and fashion-MNIST32. The recognition accuracy varies from 81.58% to 93.95%, higher than the active NLOS recognition results of human postures16,17. When a homogeneous ambient light is added to the setup, the recognition accuracy still maintains above 94% on the MNIST handwritten digit dataset. When varying ambient light is added to the setup by using 0–3 plates to cast shadows on the secondary surface, the recognition accuracy remains above 88.28% on the MNIST handwritten digit dataset. The system also reveals good generalizability with an accuracy above 60% when different number of people walk around the system and cast shadows on the secondary surface.
The origin of the x-axis is placed at the lower-right corner of the monitor. The origin of the y- and z-axes is placed at the intersection of the optical table and secondary surface. The position parameters of the screen, occluder, and camera are calibrated using coordinates relative to the origin (0, 0, 0). The black dashed and red solid arrows denote the light path and data flow, respectively.
On the flip side, we further consider the security threats of NLOS recognition. Here we mainly concern about the fragility arising from the NLOS recognition algorithm based on CNNs. CNNs are vulnerable to attacks in line-of-sight (LOS) image classification33,34,35,36, which limits their use in this domain. Whether are CNNs fragile in NLOS recognition? There is no consensus in the literature regarding this topic. Therefore, we conduct attacks on the NLOS-recognition process in this study using a white-box decoupled direction and norm (DDN) attack method37. Results show that an attack success rate of approximately 36% can be achieved with a relatively low cost even using uncalibrated settings, indicating that NLOS recognition is somewhat vulnerable to perturbations. Although beyond the scope of this paper, NLOS recognition’s robustness to active adversaries38,39 should be investigated in the future.
Results
Passive NLOS recognition
NLOS recognition is beyond human capacities and thereby relies on computational methods. CNNs40,41 are particularly appealing for NLOS-recognition applications due to their ability to seize invariants, reduce the dimensionality of high-dimensional noisy data, and classify objects. We construct a CNN model for NLOS recognition using a similar experimental setup to that proposed by Saunders et al.20, which consists of a standard digital camera, a liquid-crystal display monitor, and an occluder as shown in Fig. 1. Two deep CNN models, SimpleNet17 and ResNet1842, are used as classifiers. Further details about the two CNN models can be found in the “Methods” section and Supplementary Note 1. We evaluate the proposed NLOS recognition system under increasingly complex scenes: (1) dark room; (2) homogeneous ambient light; (3) varying ambient lighting conditions; and (4) practical test.
Dark room
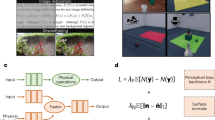
First, we fix the parameter settings of the hardware system (Supplementary Table 3), which is referred to as a fixed setup. The occluder is rectangular with a width of 7.5 cm and a height of 7.7 cm. The support stand is 0.7 cm wide and 23.1 cm high. The center of the occluder is located at (0.3980, 0.5000, 0.2695) m relative to the origin, as indicated in Fig. 1. The monitor screen is 37.75 cm in width and 30.20 cm in height. The lower-right corner of the screen has coordinates of (0.0185, 1.0000, 0.0940) m. The center of the camera is fixed at a position of (0.5835, 1.0400, 0.2800) m with a FOV size of 47 cm. To evaluate the proposed NLOS recognition system in a dark room, we train the CNN with data acquired both from simulations and camera measurements on the MNIST dataset28 of handwritten digits, which contains ten categories and includes 60,000 training images and 10,000 test images. Simulated images are synthesized with the traditional forward transport model, in which the original images of the MNIST dataset are pre-multiplied by the light transport matrix A, which was computed using prior information of the setting (see details in Supplementary Notes 2.1). Several examples of simulated images are shown in Fig. 2. As shown in Table 1, regardless of using SimpleNet or ResNet18, the recognition accuracy of the model trained with the simulated images is comparable to that of the model trained with the original images, both exceeding 99% and confirming that the light transport matrix A preserves category information perfectly. Compared to the simulation results, the recognition accuracy of the model trained on the measured images is marginally lower but remains above 98% using both SimpleNet and ResNet18, as shown in Table 1. These results demonstrate that the noise contained in the NLOS imaging system from system modeling errors, background noise, etc. is tolerable. Therefore, the proposed method of directly identifying a hidden object based on measured images is feasible.
To benchmark the proposed method, we also perform image reconstruction using the spatial differencing reconstruction method (see details in Supplementary Notes 2.2 and 2.3). As shown in Fig. 2, the quality of the restored handwritten-digit images is significantly deteriorated compared to the original images, which will inevitably increase the subsequent misclassification rate by humans or computers. For example, it is difficult for humans to classify the reconstruction results of digits 2, 4, 5, 8, and 9 (Fig. 2). We observe that the recognition following image reconstruction has worse performance that the accuracy decreases from 99% with the original dataset to approximately 94%, which is even lower than the accuracy of the NLOS recognition model (~98%). This observation is reasonable because the data processing in image reconstruction will lose the information. To improve recognition accuracy, it would take considerable effort and time to optimize the algorithm to increase the reconstruction quality. Even when using the traditional forward transport model, an additional 2 min is required to reconstruct an image, while only 0.87 s is required with the proposed CNN-trained NLOS recognition model.
We also use the proposed passive NLOS recognition method on more sophisticated datasets that contain hand gestures29,30, human postures31, and fashion-MNIST32 (see Supplementary Note 3.1). Examples of original, simulated, and measured images for four sophisticated datasets are shown in Supplementary Fig. 6. The recognition process of each image is completed in less than 1 s, and the recognition accuracy varies from 81.58% to 93.95%, as shown in Supplementary Table 5. Therefore, the proposed NLOS-recognition system also achieves good performance on more sophisticated objects hidden around the corner.
Considering the application of the proposed method in a real situation, it is impossible to obtain all NLOS data in a fixed setup because real setups will vary. To train a CNN model that is invariant to parameter settings, we collect data with changes in the occluder shapes and the positions of the monitor, occluder, and camera within given ranges. This case is referred to as the mixed setup. The shape of the occluder is changed from a rectangle into a triangle, a circle, and even the shape of a cup. The parameter setting ranges for the mixed setup are shown in Supplementary Table 3. This model achieves recognition accuracies of 97.16% and 98.26% with SimpleNet and ResNet18, respectively, within the trained range.
In addition, we performed a simulation to study the effect of camera sensor noise on the NLOS recognition accuracy. A 96% recognition accuracy can be achieved as long as the signal-to-noise ratio of the image captured by the camera sensor is greater than 20 dB, as shown in Supplementary Note 3.2.
Homogeneous ambient light
Additionally, to verify the robustness of NLOS recognition models to ambient light, we added an incandescent lamp with adjustable light intensity in the experimental setting. As shown in Table 2, the recognition accuracy of the NLOS recognition model (SimpleNet or ResNet18) decreases as the light intensity increases. However, the recognition accuracy can still reach more than 94%, even in the presence of intense ambient light as high as 4.2 Lux, while the signal of interest is only 0.3 Lux. Therefore, NLOS recognition models are robust to homogeneous ambient light within a specific intensity range.
Varying ambient lighting conditions
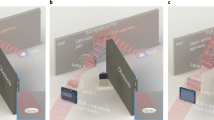
Because there is no way to control ambient lighting in practice, we also study the robustness of the trained NLOS recognition model in varying ambient lighting conditions. Specifically, we study the effect of people walking nearby and casting shadows on the secondary wall. A house-shaped occluder-based NLOS system was placed in an exhibition hall with an intense ambient light of 610 Lux (Supplementary Fig. 8). Ambient light remains as high as 120 Lux measured in front of the camera lens after an L-shaped translucent acrylic plate was placed around the system (Fig. 3a). The NLOS recognition accuracy is 84.73% in this situation when recognizing digits shown on the monitor. Different numbers of opaque plates of approximately 1.70 m height are used to cast shadows on the secondary surface to simulate people in the vicinity of the proposed system (Fig. 3a–d). As shown in Table 3, the recognition accuracy of the CNN model trained in the experimental setting without plates (referred to as ResNet18-0) drops from 84.73% to 71.84–77.58% when 1–3 plates are placed around the proposed system. We also test ResNet18-0 when a person walks around the system. The recognition capability is affected with an accuracy of around 70%, which is comparable to the simulation results and indicates that the passive NLOS recognition model trained under one fixed lighting condition is not robust to varying ambient lighting.
To improve the robustness of the recognition model, we retrain the network with the data collected under a mixed lighting condition with 0, 1, 2, and 3 plates in the setting (referred to as ResNet18-M). As shown in the left panel of Table 3, the recognition accuracy under different ambient lighting conditions was markedly improved by 1–15% using ResNet18-M. To improve the generalizability of the NLOS recognition model, we add Gaussian noise, random horizontal flip, and random rotation to the measured images for data augmentation. Comparing the left and right panels of Table 3, it is shown that the recognition accuracy of ResNet18-M with data augmentation improves by approximately 2%, higher than 88.28%.
Practical test
To demonstrate the effectiveness of ResNet18-M with data augmentation under real varying ambient lighting due to movements of nearby objects, practical tests are implemented on the house-shaped passive NLOS recognition system in an exhibition hall (Supplementary Fig. 9). We write a script to automatically display the 10,000 test images of the MNIST dataset on the monitor screen and calculate the accuracy when different numbers of people walk around the system with casual poses and gestures. The recognition accuracy of ResNet18-M with data augmentation remains above 60% with three rounds of the practical test, indicating good generalizability.
NLOS attack
The security of CNNs is an active topic within deep learning communities. Attacks33,34,35,36 can manipulate CNNs using generated adversarial examples (AEs) to misclassify data, in which AEs are essentially indistinguishable from legitimate ones by adding small perturbation. In this study, we use an existing white-box attack method called DDN37 to generate AEs, in which the cost is evaluated by the L2 norm of perturbations (see details in “Methods”). The lower the L2 noise of attacks, the more fragile the recognition system. The attacks performed in this study are all untargeted (i.e., the perturbations to a digit force the CNN to classify the digit as another unspecific output).
An example is shown in Supplementary Fig. 10a to demonstrate the process of a LOS attack. Learnable perturbations are added to the original image to produce an AE, which is indistinguishable from the original image by human beings but is misclassified by CNNs as another digit with high confidence. Supplementary Figure 10b shows several AEs generated for the SimpleNet and ResNet18 models trained on the MNIST handwritten digit dataset. We achieve a 97.7% success attack rate with L2 of 0.5779 for SimpleNet. The cost is expensive, as digits 2 and 4 have been severely distorted to mislead SimpleNet. Conversely, a 100% success attack rate is achieved for ResNet18 with a much smaller L2 of 0.0999. The distortion is too small to be perceived by humans. ResNet18 has deeper layers and stronger recognition capability than SimpleNet, yet it is much easier to be attacked by the DDN method. Many studies have demonstrated that CNNs are vulnerable to active attacks in LOS classification33,34,35,36; however, attacks on a NLOS-recognition CNN model have not been investigated.
Two different attack strategies are designed to perform attacks on NLOS classifiers (Fig. 4). One strategy is called attack on the monitor screen, where digits with designed small image perturbations are shown on the monitor. The AEs (i.e., digits with image perturbations) on the monitor are clear to a LOS viewer, yet cause distorted information on the secondary surface and then mislead the NLOS recognition system. The other strategy is called attack on the secondary surface, where small wall perturbations are added onto the penumbra of the digits on the secondary surface either by an additional light projection, wallpaper, or wall painting. The generated AEs on the secondary surface, which are indistinguishable from the original penumbra of the digits, can be directly captured by the camera and cause misclassification of the NLOS recognition system.
Attack strategy #1 attack on the monitor screen: image perturbations are added on the original image to create an adversarial example, which is displayed on the monitor screen to cause misclassification; Attack strategy #2 attack on the secondary surface: wall perturbations are added on the secondary surface to change the measured image and cause misclassification.
To produce NLOS AEs used in real-world attacks, we first perform simulations of attacks on the NLOS classifiers. In the scenario of attacks on the secondary surface, we use the same process as the LOS attacks to generate AEs to misdirect the NLOS classifiers based on the assumption that the captured penumbra of the digits on the secondary surface is the measured image (Supplementary Fig. 11). In the scenario of attacks on the monitor screen, we generate AEs shown on the monitor to disturb the NLOS classifiers by introducing the forward transport model to approximate the relationship between the image on the monitor and the captured penumbra on the secondary surface (Supplementary Fig. 12).
Supplementary Figure 13 shows simulated AEs on the monitor screen and secondary surface. To achieve a 100% attack success rate for SimpleNet, the L2 norm of the distortion on the secondary surface is 0.0241/0.0221 against the fixed/mixed NLOS classifier, which is much below the L2 value of 0.5779 in the LOS attack (Table 4). This result likely occurs because the measured images on the secondary surface are just high-frequency shadows that lose large amounts of information compared to the original images. The L2 norm of the distortion on the monitor screen is 0.2249/0.2225 intending to totally disable the fixed/mixed NLOS classifier, which is larger than the corresponding L2 value of attacks on the secondary surface. This result likely occurs because more information is contained on the monitor screen than on the secondary surface; thus, the attack cost is increased considerably. The NLOS attack cost of the mixed setup is near that of the fixed setup in simulation, and the attack scenarios for ResNet18 are similar to those for SimpleNet, as shown in Table 4. Overall, the image or wall perturbations to achieve a 100% attack success in NLOS recognition are small based on the simulation results, indicating the moderate fragility of the NLOS recognition system.
In order to test the effectiveness of the AEs generated by the simulation method in reality, a natural idea is that we display the simulated AEs (i.e., digits with image perturbations) on the monitor screen and later capture the corresponding distorted penumbra on the secondary surface. Then we feed the measured image into NLOS classifiers to test whether it can cheat the NLOS recognition model. This process is called a real-world attack. If the measured image is misclassified, this attack is called a successful attack. Otherwise, it is called a failed attack. Unfortunately, the attack does not work both in the fixed and mixed NLOS setups if we directly display previously simulated AEs on the monitor. The large discrepancy in the success rates of the real world and simulated attacks can be attributed to the perturbations using the DDN37 method with 100 iterations being much lower than the noise in the system.
To overcome this problem, we increase the perturbations of AEs. Besides, we find that the estimation of background noise (item b in Supplementary Eq. (2) is important in a real-world attack (see details in Supplementary Note 4.3). Therefore, AEs on the monitor for a real-world attack are generated after considering item b in the forward model and using an increased L2 norm. Figure 5 shows AEs on the monitor screen for real-world attacks in the fixed/mixed setup. When the L2 norm of the perturbations is approximately 0.60 for SimpleNet, the increased success rates against the fixed and mixed setup classifiers are 49.31% and 36.23%, respectively. The attack success rate in the mixed setup is much lower than that in the fixed setup, which demonstrates that the mixed setup classifier is more robust than the fixed setup classifier by considering the variability of parameters. These situations also apply to the attack on ResNet18, as shown in Table 4. In summary, the experimental results demonstrate that the high-precision classifiers trained in the fixed/mixed NLOS setup can be attacked in real-world scenarios. Therefore, the CNN model based on NLOS data is susceptible to AEs.
Discussion
Thus far, we have shown that the proposed NLOS recognition system is accurate, efficient, and practical but somewhat fragile to elaborately crafted perturbations. Our passive NLOS recognition system has demonstrated the robustness to part of the parameters of the NLOS hardware system, including occluder shape, positions of the screen, occluder, and camera, and lighting conditions. Recent work in passive NLOS reconstruction also shows that the hidden scenes can be recovered using an unknown occluder21, revealing robustness to the occluder shape. The occluder information is estimated by exploiting motions in the scene. However, the occluder estimation takes more time and the reconstruction quality deteriorates due to lack of full knowledge about the occluder shape. We note that our method is only designed for a white secondary surface of uniform albedo, while the real secondary surface may have varying albedo such as checkered tiles and wallpaper of different patterns. A recent passive NLOS work by Seidel et al.43 provides a possible path to solve this task that they recover 1D projection of the hidden scene behind a wall with real floors of varying albedo patterns by exploiting priors on the floor albedo and hidden scene from a single photograph.
We perform attacks on the NLOS CNN recognition algorithm in this study, which represent an initial but essential step to developing a robust NLOS CNN recognition system. The robustness of the proposed CNN recognition system could be improved further by applying defenses to mitigate the effects of AEs. Although such defense strategies38,39 are out of the scope of this study, they can be briefly summarized into two categories: (1) enhance the learning model via methods like adversarial training44 and defense distillation45 and (2) detect adversarial samples via methods like principal component analysis46 and feature squeezing47. White-box attacks36 are used to generate AEs using prior knowledge of the target network. In practice, we may have no access to the underlying training policy. Therefore, gray- or black-box attacks33 should be investigated in future work. Additionally, a targeted attack should also be investigated to produce labels specified in advance.
Attacks on the secondary surface would be easier than attacks on the monitor screen based on the lower L2 norms of the simulated attacks. However, it is challenging to perform these types of attacks because the perturbation on the secondary surface changes with the images shown on the monitor screen. To address this problem, a universal perturbation with L2 equal to 0.4545 is learned, as shown in Fig. 6a, which could deceive the ResNet18 recognition model and is invariant to the original images on the monitor. As shown in Fig. 6b, the difference between AEs and the original measured images of penumbra is imperceptible by humans, which is the main difference between the attack strategy on the secondary surface in this work and the robustness issues caused by using different patterns on the secondary surface43. The universal perturbation severely distorts the measured images, and the attack success rate of this method can reach 89.67% in the simulation. The AEs in this study can also be used for defenses to improve the robustness of the proposed NLOS recognition system.
Thus, we demonstrate a passive NLOS recognition technique that is invariant to changes in calibration parameters. The setup is simple and inexpensive with a standard digital camera and an occluder. We performed experiments to verify its feasibility, and results show that passive NLOS recognition can achieve high accuracy of between 81.58% and 98.26% in a dark room with different datasets that contain images of handwritten digits, hand gestures, human postures, and fashion-MNIST with processing time less than 1 s per image. Moreover, high recognition accuracy can be maintained under more complex lighting conditions. On the other side, white-box attacks are conducted on the NLOS recognition model. Although the positions of the experimental setup vary, an attack success rate of approximately 36% can be achieved with a relatively low cost. Therefore, existing NLOS-recognition methods remain somewhat vulnerable to well-designed perturbations. The robustness of the proposed recognition model will be improved further by applying defense methods in the future.
Methods
Hardware configuration
Our capture system includes an HP LCD monitor model P19A, which has a 5:4 aspect ratio and 1280 × 1024 resolution; a FLIR Grasshopper3 camera with a resolution of 2048 × 2048 using a Tamron M118FM16 lens with a 16 mm focal length and f/1.4 aperture; a black occlude; and a white foam board that is visibility diffuse. There is no LOS from the monitor screen to the camera.
Data acquisition from the camera
A Python script was used to control data acquisition and the exposure time was 0.7 s per snapshot. Each snapshot is an 8-bit raw image with 2048 × 2048 pixels in a Bayer filter RGBG pattern storage format. To obtain a three-channel GRB mode image, the two green channels are averaged, and then the images in each channel are sampled using 16 × 16 blocks. Finally, a color image with 128 × 128 pixels is obtained, which is used to train the deep learning model or is fed into the CNN model to identify its category.
Deep neural networks for passive NLOS recognition
SimpleNet
Inspired by the deep network model built by Lei et al.17, we cherry-pick a convolutional network, as shown in Supplementary Fig. 1. Its overall structure is represented in Supplementary Table 1. Dropout was added to the top two fully connected layers to prevent overfitting. The number of fully connected layers of the last layer of the model is set to 10, which represents the number of categories in the MNIST dataset. The input sizes of the original image, simulated image, and measured image are 32 × 40, 128 × 128, and 128 × 128, respectively. For the simple MNIST dataset, we used an SGD optimizer48 with a momentum of 0.9 and an initial learning rate of 0.01. With a batch size of 64, 20 epochs were trained on the training set. Furthermore, every five training iterations, the learning rate is multiplied by 0.9.
ResNet18
ResNet’s unique residual structure makes it one of the most significant architectures in the field of computer vision. This unique residual structure is used to mitigate the performance degradation problem caused by the increased depth of the neural network. This study modifies and fine-tunes the ResNet18 model published on the PyTorch official website42, as shown in Supplementary Fig. 2. Its overall structure is represented in Supplementary Table 2. Because the image in the experimental datasets is grayscale, its input channel is modified to 1 and the output number of neurons in the last layer of the fully connected layer is adjusted to the number of categories in the experimental datasets. The training strategy of this network is consistent with that of SimpleNet on the MNIST dataset. For the sophisticated datasets, we modify the number of training epochs to 60. For the training strategy, we use a weight decay of 0.0001. In the 20th and 50th epochs, the learning rate is multiplied by 0.1 and the other parameters of the network remain unchanged. Additionally, we use data augmentation, such as Gaussian noise, random horizontal flip, and random rotation to avoid overfitting.
DDN for NLOS attack
DDN37 is an existing white-box attack method that is designed to generate AEs with a low perturbation norm in a few iterations for a given input image. The objective of the non-targeted attack is to minimize the likelihood of correct classification with a given maximum norm of the disturbance constraint. This problem can be described as
where \({\it{y}}_{{\mathrm{true}}}\) denotes the ground-truth label corresponding to the sample \({\mathbf{x}}\); \({\mathbf{x}} + {\mathbf{\updelta }}\) represents the AEs; \(P\left( {y|{\mathbf{x}},\theta } \right)\) is the probability that sample \({\mathbf{x}}\) is predicted to be \({\it{y}}\) when the model parameter \(\theta\) is known; \({\it{\upvarepsilon }}\) and \(M\) represent the maximum norm of the disturbance and the maximum value of each pixel, respectively; and \({\it{n}}\) represents the size of the image \({\mathbf{x}}\).
DDN using the projected gradient descent method49 to refine the perturbation iteratively for a given input image works by calculating the cumulative gradient direction based on the misclassification loss function, and updates the perturbation by multiplying an adaptive step size by a unit vector of the computed gradient:
where \({\mathrm{clip}}_{\left( {0,1} \right)}\) limits the adversarial perturbation to [0,1]. For the kth iteration, when given the perturbation step \({\it{\upalpha }}\), the current gradient direction \({\mathbf{g}}\) of the input image is calculated by the loss function \({\it{L}}\), \({\mathbf{g}} = {\it{\upalpha }}\frac{{\nabla _{{\tilde{\mathbf{x}}}_{k - 1}}L({\tilde{\mathbf{x}}}_{k - 1},y,\theta )}}{{\left\| {\nabla _{{\tilde{\mathbf{x}}}_{k - 1}}L({\tilde{\mathbf{x}}}_{k - 1},y,\theta )} \right\|_2}}\), which are aggregated to the current cumulative gradient direction \({\mathbf{\updelta }} _{k - 1}\) to obtain the next cumulative gradient direction \({\mathbf{\updelta }}_k\), \({\mathbf{\updelta }}_k = {\mathbf{\updelta }}_{k - 1} + {\mathbf{g}}\). \({\it{\upvarepsilon }}_k\) is the step size corresponding to the \({\mathbf{\updelta }}_k\). For a given adaptive factor \({\it{\upgamma }}\), if the current \({\tilde{\mathbf{x}}}_{k - 1}\) sample is adversarial, the step size \({\it{\upvarepsilon }}_k\) will be decreased to minimize the perturbation norm, \({\it{\upvarepsilon }}_k{\mathrm{ = }}\left( {{\mathrm{1}} - \gamma } \right){\it{\upvarepsilon }}_{k - 1}\); otherwise, the step size \({\it{\upvarepsilon }}_k\) will be increased, \({\it{\upvarepsilon}}_k = \left( {{{1}} + \gamma } \right){\it{\upvarepsilon}}_{k - 1}\). This method is suitable for targeted and non-targeted attacks in white-box scenarios and achieves the best overall performance in terms of attack success rate, low disturbance, and convergence speed.
Because the dimensions of the original image and the measured image are different, this study employs the relative L2 norm rather than the L2 norm to measure the distance between the AE and the given input image to be perturbed. The specific formula is
where \({\mathbf{x}}\) and \({\tilde{\mathbf{x}}}\) represent the given input image to be perturbed and the AE, respectively. The size of the L2 value measures the robustness of the model against attacks: the smaller the value is, the lower the cost of the attack model. The parameter settings against LOS and NLOS attacks are summarized in Supplementary Table 6.
The authors affirm that informed consent for publication of the images in Supplementary Fig. 9 was obtained from the identifiable individuals.
Data availability
The datasets generated during and/or analyzed during the current study are available at https://pan.baidu.com/s/1YwSxNWl1zu1ZtGZytfHRhQ with the password of “iy7d”.
Code availability
The codes generated during and/or analyzed during the current study are available on https://github.com/zyaqin/Passive-None-Line-of-Sight-Recognition.
References
Velten, A. et al. Recovering three-dimensional shape around a corner using ultrafast time-of-flight imaging. Nat. Commun. 3, 745 (2012).
Pawlikowska, A. M., Halimi, A., Lamb, R. A. & Buller, G. S. Single-photon three-dimensional imaging at up to 10 kilometers range. Opt. Express 25, 11919–11931 (2017).
O’Toole, M., Lindell, D. B. & Wetzstein, G. Confocal non-line-of-sight imaging based on the light-cone transform. Nature 555, 338–341 (2018).
Lindell, D. B., Wetzstein, G. & O’Toole, M. Wave-based non-line-of-sight imaging using fast f-k migration. ACM Trans. Graph. 38, 116 (2019).
Liu, X. et al. Non-line-of-sight imaging using phasor-field virtual waveoptics. Nature 572, 620–623 (2019).
Liu, X., Bauer, S. & Velten, A. Phasor field diffraction based reconstruction for fast non-line-of-sight imaging systems. Nat. Commun. 11, 1645 (2020).
Rapp, J. et al. Seeing around corners with edge-resolved transient imaging. Nat. Commun. 11, 5929 (2020).
Chopite, J. G., Hullin, M. B., Wand, M. & Iseringhausen, J. Deep non-line-of-sight reconstruction. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), (eds Eric, M. M. M.) 960–969 (Institute of Electrical and Electronics Engineers (IEEE), 2020).
Isogawa, M., Yuan, Y., Toole, M. O. & Kitani, K. Optical non-line-of-sight physics-based 3D human pose estimation. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), (eds Eric, M. M. M.) 7011–7020 (Institute of Electrical and Electronics Engineers (IEEE), 2020).
Gupta, M., Nayar, S. K., Hullin, M. B. & Martin, J. Phasor imaging: a generalization of correlation-based time-of-flight imaging. ACM Trans. Graph. 34, 156 (2015).
Kadambi, A. et al. Coded time of flight cameras: sparse deconvolution to address multipath interference and recover time profiles. ACM Trans. Graph. 32, 167 (2013).
Heide, F., Xiao, L., Heidrich, W. & Hullin, M. B. Diffuse mirrors: 3D reconstruction from diffuse indirect illumination using inexpensive time-of-flight sensors. In IEEE Conference on Computer Vision and Pattern Recognition, (eds Eric, M. S. F.) 3222–3229 (Institute of Electrical and Electronics Engineers (IEEE), 2014).
Metzler, C. A. et al. Deep-inverse correlography: towards real-time high-resolution non-line-of-sight imaging. Optica 7, 63–71 (2020).
Singh, A. K., Naik, D. N., Pedrini, G., Takeda, M. & Osten, W. Looking through a diffuser and around an opaque surface: a holographic approach. Opt. Express 22, 7694–7701 (2014).
Willomitzer, F., Li, F., Balaji, M. M., Rangarajan, P. & Cossairt, O. High resolution non-line-of-sight imaging with superheterodyne remote digital holography. In Imaging and Applied Optics 2019 (COSI, IS, MATH, pcAOP), CM2A.2 (Optical Society of America, 2019).
Satat, G., Tancik, M., Gupta, O., Heshmat, B. & Raskar, R. Object classification through scattering media with deep learning on time resolved measurement. Opt. Express 25, 17466–17479 (2017).
Lei, X. et al. Direct object recognition without line-of-sight using optical coherence. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), (eds William, B. M. R. A. & Eric, M.) 11729–11738 (Institute of Electrical and Electronics Engineers (IEEE), 2019).
Torralba, A. & Freeman, W. T. Accidental pinhole and pinspeck cameras: revealing the scene outside the picture. In IEEE Conference on Computer Vision and Pattern Recognition, (ed. Mortensen, E.) 374–381 (Institute of Electrical and Electronics Engineers (IEEE), 2012).
Bouman, K. L. et al. Turning corners into cameras: principles and methods. In IEEE International Conference on Computer Vision (ICCV), (ed. Mortensen, E.) 2289–2297 (Institute of Electrical and Electronics Engineers (IEEE), 2017).
Saunders, C., Murraybruce, J. & Goyal, V. K. Computational periscopy with an ordinary digital camera. Nature 565, 472–475 (2019).
Yedidia, A. B., Baradad, M., Thrampoulidis, C., Freeman, W. T. & Wornell, G. W. Using unknown occluders to recover hidden scenes. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), (eds William, B. M. R. A. & Eric, M.) 12231–12239 (Institute of Electrical and Electronics Engineers (IEEE), 2019).
Kaga, M. et al. Thermal non-line-of-sight imaging from specular and diffuse reflections. IPSJ Trans. Comput. Vis. Appl 11, 8 (2019).
Maeda, T., Wang, Y., Raskar, R. & Kadambi, A. Thermal non-line-of-sight imaging. In IEEE International Conference on Computational Photography (ICCP), (ed. Lalonde, J.-F.) 1–11 (Institute of Electrical and Electronics Engineers (IEEE), 2019).
Tanaka, K., Mukaigawa, Y. & Kadambi, A. Enhancing passive non-line-of-sight imaging using polarization cues. Preprint at https://arxiv.org/abs/1911.12906 (2019).
Boger-Lombard, J. & Katz, O. Passive optical time-of-flight for non line-of-sight localization. Nat. Commun. 10, 3343 (2019).
Sun, Y., Shi, J., Sun, L., Fan, J. & Zeng, G. Image reconstruction through dynamic scattering media based on deep learning. Opt. Express 27, 16032–16046 (2019).
Sun, L., Shi, J., Wu, X., Sun, Y. & Zeng, G. Photon-limited imaging through scattering medium based on deep learning. Opt. Express 27, 33120–33134 (2019).
LeCun, Y., Cortes, C. & Burges, C. J. THE MNIST DATABASE of handwritten digits. http://yann.lecun.com/exdb/mnist/ (2013).
Aistudio. Hand Gesture Recognition Dataset. https://aistudio.baidu.com/aistudio/datasetdetail/51629 (2020).
Kaggle. Sign Language MNIST: Drop-In Replacement for MNIST for Hand Gesture Recognition Tasks. https://www.kaggle.com/datamunge/sign-language-mnist (2017).
Kumar, A. & Raj, E. D. Silhouettes for Human Posture Recognition. IEEE Dataport, https://doi.org/10.21227/9c9b-3j44 (2020).
Xiao, H., Rasul, K. & Vollgraf, R. J. A. Fashion-MNIST: a novel image dataset for benchmarking machine learning algorithms. Preprint at https://arxiv.org/abs/1708.07747 (2017).
Wiyatno, R. R., Xu, A., Dia, O. & Berker, A. D. Adversarial examples in modern machine learning: a review. Preprint at https://arxiv.org/abs/1911.05268 (2019).
Carlini, N. & Wagner, D. Towards evaluating the robustness of neural networks. In IEEE Symposium on Security and Privacy (SP), (ed. Ciocarlie, G.) 39–57 (Institute of Electrical and Electronics Engineers (IEEE), 2017).
Moosavi-Dezfooli, S.-M., Fawzi, A. & Frossard, P. Deepfool: a simple and accurate method to fool deep neural networks. In IEEE Conference on Computer Vision and Pattern Recognition, (ed. Russakovsky, O.) 2574–2582 (Institute of Electrical and Electronics Engineers (IEEE), 2016).
Szegedy, C. et al. Intriguing properties of neural networks. Preprint at https://arxiv.org/abs/1312.6199 (2014).
Rony, J. et al. Decoupling direction and norm for efficient gradient-based L2 adversarial attacks and defenses. In IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), (ed. Brendel, W.) 4322–4330 (Institute of Electrical and Electronics Engineers (IEEE), 2019).
Meng, D. & Chen, H. MagNet: A two-pronged defense against adversarial examples. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, (eds G.P. Yvo Desmedt, Daniel Xiapu Luo, Barbara Carminati) 135–147 (Association for Computing Machinery, 2017).
Papernot, N. et al. The Limitations of deep learning in adversarial settings. In IEEE European Symposium on Security and Privacy (EuroS&P), (ed. Stock, B.) 372–387 (Institute of Electrical and Electronics Engineers (IEEE), 2016).
Krizhevsky, A., Sutskever, I. & Hinton, G. ImageNet classification with deep convolutional neural networks. In Proceedings of the 25th International Conference on Neural Information Processing Systems, (eds Yvo, G. P., Desmedt, Luo, D. X. & Carminati, B.) 1097–1105 (Association for Computing Machinery, 2012).
LeCun, Y. et al. Backpropagation applied to handwritten zip code recognition. Neural Comput 1, 541–551 (1989).
GitHub. Inc. vision/torchvision/models at master pytorch/vision GitHub.: p. https://github.com/pytorch/vision/tree/master/torchvision/models.
Seidel, S. W. et al. Corner occluder computational periscopy: estimating a hidden scene from a single photograph. In IEEE International Conference on Computational Photography (ICCP), (ed. Lalonde, J.-F.) 1–9 (Institute of Electrical and Electronics Engineers (IEEE), 2019).
Madry, A., Makelov, A., Schmidt, L., Tsipras, D. & Vladu, A. Towards deep learning models resistant to adversarial attacks. Preprint at https://arxiv.org/abs/1706.06083arXiv Mach. Learn. (2018).
Papernot, N., McDaniel, P., Wu, X., Jha, S. & Swami, A. Distillation as a defense to adversarial perturbations against deep neural networks. In IEEE Symposium on Security and Privacy (SP), (ed. Sonalker, A.) 582–597 (Institute of Electrical and Electronics Engineers (IEEE), 2016).
Hendrycks, D. & Gimpel, K. Early methods for detecting adversarial images. Preprint at https://arxiv.org/abs/1608.00530 (2016).
Xu, W., Evans, D. & Qi, Y. Feature squeezing: detecting adversarial examples in deep neural networks. In Network and Distributed Systems Security Symposium (NDSS), 18–21 (Internet Society, 2018).
Kingma, D. P. & Ba, J. Adam: a method for stochastic optimization. Preprint at https://arxiv.org/abs/1412.6980 (2015).
Figueiredo, M. A. T., Nowak, R. & Wright, S. J. Gradient projection for sparse reconstruction: application to compressed sensing and other inverse problems. IEEE J. Sel. Top. Signal Process. 1, 586–597 (2007).
Acknowledgements
This work was supported by the Beijing Nova Program of Science and Technology under Grant Z191100001119129 and the National Natural Science Foundation of China under Grant 61702520.
Author information
Authors and Affiliations
Contributions
L. Xiao and X.X. conceived the idea of this study and supervised the study. Y. Wang and Z.C. designed and performed the experiments. M.H. and Y. Zhang conceived the algorithm, performed the calculations, and analyzed the data. Y. Jia and Y. Weng contributed to the data acquisition script. Y. Wang, M.H., and Y. Zhang wrote the manuscript. All authors discussed the results and contributed to the final version of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wang, Y., Zhang, Y., Huang, M. et al. Accurate but fragile passive non-line-of-sight recognition. Commun Phys 4, 88 (2021). https://doi.org/10.1038/s42005-021-00588-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-021-00588-2
This article is cited by
-
Research Advances on Non-Line-of-Sight Imaging Technology
Journal of Shanghai Jiaotong University (Science) (2024)
-
Attention-based network for passive non-light-of-sight reconstruction in complex scenes
The Visual Computer (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.